Computers, Materials & Continua DOI:10.32604/cmc.2021.019092
Article

An Efficient Hybrid PAPR Reduction for 5G NOMA-FBMC Waveforms

Arun Kumar1,*, Sivabalan Ambigapathy2, Mehedi Masud3, Emad Sami Jaha4, Sumit Chakravarty5 and Kanchan Sengar1

1Department of Electronics and Communication Engineering, JECRC University, Jaipur, 303905, India
2Center for System Design, Chennai Institute of Technology, India
3Department of Computer Science, College of Computers and Information Technology, Taif University, Taif, 21944, Saudi Arabia
4Department of Computer Science, Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah, Saudi Arabia
5Department of Electrical and Computer Engineering, Kennesaw State University, GA, USA
*Corresponding Author: Arun Kumar. Email: arun.kumar1986@live.com
Received: 01 April 2021; Accepted: 02 May 2021

Abstract: The article introduces Non-Orthogonal Multiple Access (NOMA) and Filter Bank Multicarrier (FBMC), known as hybrid waveform (NOMA-FBMC), as two of the most deserving contenders for fifth-generation (5G) network. High spectrum access and clampdown of spectrum outflow are unique characteristics of hybrid NOMA-FBMC. We compare the spectral efficiency of Orthogonal Frequency Division Multiplexing (OFDM), FBMC, NOMA, and NOMA-FBMC. It is seen that the hybrid waveform outperforms the existing waveforms. Peak to Average Power Ratio (PAPR) is regarded as a significant issue in multicarrier waveforms. The combination of Selective Mapping-Partial Transmit Sequence (SLM-PTS) is an effective way to minimize large peak power inclination. The SLM, PTS, and SLM-PTS procedures are applied to the NOMA-FBMC waveform. This hybrid structure is applied to the existing waveforms. Further, the correlated factors like Bit Error Rate (BER) and Computational Overhead (CO) are studied and computed for these waveforms. The outcome of the work reveals that the NOMA-FBMC waveform coupled with the SLM-PTS algorithm offers superior performance as compared to the prevailing systems.

Keywords: 5G; NOMA-FBMC; SLM-PTS; PAPR; BER; OFDM

1  Introduction

Due to the increased requirement of cellular capacity, there is an urgency to design an advanced radio network. It is anticipated that the cellular capacity will increase by 30%, which cannot be supported by the current fourth-generation (4G) cellular network. Additionally, technologies such as the Internet of Things (IoT), Device to Device communications (D2D), and smart health care require high spectral efficiency. To fulfill these requirements, the advanced waveform implementation plays a key role in the standardization of the fifth-generation (5G) {network}. Presently, 4G is based on Orthogonal Frequency Division Multiplexing (OFDM). OFDM is implemented by splitting a single carrier into several orthogonal sub-carriers. The key parameters in the structure of OFDM consist of Inverse Fast Fourier Transform (IFFT), Fast Fourier Transform (FFT), and Cyclic Prefix (CP). The purpose of IFFT is to generate a composite signal, FFT is used to detect the desired signal, and CP is utilized to mitigate Inter-Symbol Interference (ISI). Though OFDM is utilized in several applications [1], it is not recommended as a suitable candidate for the 5G network. OFDM consists of several drawbacks. The use of CP result in loss of spectrum [2], and filtering in OFDM is not suitable for cognitive applications. Frequency characteristics of OFDM are poor, not suitable to support huge data traffic, and its performance degrades for Digital Subscribers Line (DSL) applications. Hence, the regularization of the 5G network requires an efficient waveform scheme. Filter Bank Multicarrier (FBMC) and Non-Orthogonal Multiple Access (NOMA) is the most popular advanced waveform for the 5G radio network. In FBMC, a poly-phase filter is used at the transceiver of the framework. A PHYDYAS filter is applied to the sub-carriers’ group, which mitigates the effect of ISI between the sub-carriers. Further, the spectral performance of FBMC is better than the OFDM structure. However, it is observed that the performance of FBMC degrades with Multiple Inputs and Multiple Outputs (MIMO) or Cognitive Network Systems (CNS). Additionally, the requirement of a multi-tap detection system for each sub-carrier is seen severe disadvantage of the FBMC waveform [3]. On the other hand, NOMA is hugely popular and even regarded as the top waveform contender for the 5G network. It efficiently utilizes the spectrum and allows multiple subscribers to access the resources in both the time and frequency domain. The subscribers are multiplexed in either time or code domain, resulting in enhanced throughput of the framework. It also supports a large number of subscribers as compared to OFDM or FBMC [4]. It is observed that NOMA significantly supports weak users, which results in a better probability of outage than FBMC or OFDM. The integration of NOMA and massive MIMO also enables user overload more effectively than FBMC system. NOMA provides excellent service even if subscribers’ number exceeds the number of users allocated per base station [5]. The NOMA structures comprise of the components: IFFT, Successive Interference Cancellation (SIC), FFT, and Super Coding (SC). IFFT is used to generate the sub-carriers, SC allows the users to simultaneously access the spectrum resources, and SIC helps in the detection of the signal. The ability to serve a massive number of devices, provide high spectral access, enable low propagation delay, or low probability of outage are the novelties of the NOMA structure. Hence, it is more appropriate as a 5G candidate, than the FBMC or OFDM. In the projected framework, a cluster of filters is applied to a group of sub-carriers, and thereby allowing them to maintain signal separation, enabling system compatibility with cognitive radio, overcoming frequency and temporal domain error etc. The NOMA-FBMC is considered an important contender for 5G radio due to its several advantages: large device connectivity, efficient utilization of spectrum, high data speed, better connectivity, high capacity, and amenability to the use of advanced techniques [6]. Peak to Average Power Ratio (PAPR) is a common problem in multicarrier schemes such as OFDM, FBMC, and NOMA. PAPR is the ratio of the power of transmitted symbols to the symbol's average power. PAPR is seen as an important concern in the rollout of the 5G radio network. PAPR degrades the power amplifier's gain and reduces the Signal-to-Noise Ratio (SNR) [7]. Though PAPR cannot be eliminated, it can be reduced by using PAPR minimization algorithms. PAPR algorithms are grouped into: a. signaling methods [8], b. distortion minimization [9] and c. scrambling methods [10]. Several PAPR conventional reduction algorithms can be utilized in OFDM and can efficiently reduce the amplitude power [11]. The conventional PAPR algorithms cannot apply to the advanced waveforms due to their different structural arrangement as {compared} to the OFDM. The recent studies reveal that the conventional algorithms perform poorly when applied to the FBMC structure [12]. In this work, advanced PTS-SLM hybrid algorithms are applied to the OFDM, FBMC, NOMA and, NOMA-FBMC structures. The conventional PTS and SLM lower down the multicarrier waveforms peak power but increase the framework's computational complexity's [13]. The proposed PTS-SLM efficiently minimizes the PAPR and the complexity of the waveforms. Various reduction algorithms are studied and an advanced Discrete-SLM-Circulation Transformation algorithm is introduced to decrease the peak power of advanced waveforms. It is seen that the proposed algorithm enhances the throughput of the structure, although the complexity and BER of the systems are significantly increased. The PAPR analysis on SC-OFDM is estimated and analyzed for different PAPR minimization algorithms. It is found that the peak power and the complexity are significantly decreased in the projected structure in comparison to the traditional methods [14]. OFDM is widely used in many applications, but it is not suitable for the 5G network. The gain of the power amplifier is adversely affected by the high peak power. A technique like Tone reservation (TR) is an efficient method to minimize the PAPR, and increases the hardware overhead. The combination of TR and Fast Iterative Shrinkage Threshold Algorithm (FISTA) is designed to improve the PAPR performance of OFDM [15]. In [16], the OFDM symbols’ amplitude is analyzed and estimated in the time domain. The large amplitude OFDM symbols are reduced by multiplying with the scaling elements. The proposed algorithm minimizes the peak power from 13 to 7 dB. Hence, the efficiency of 53% is achieved. In [17], the combination of PTS-PSO was introduced to enhance the efficiency of PA in the OFDM structure. The simulation outcomes reveal a remarkable improvement in the throughput of the system. The peak power reduction based on PTS and Genetic Algorithm (GA) is implemented for the OFDM framework [18]. The experimental outcomes reveal that the projected algorithm significantly lowers the PAPR while sustaining a moderate arithmetical overhead. The key contributions of the proposed work are as follows:

a.   A significant reduction in PAPR is obtained by introducing a PTS-SLM algorithm. Further, the optimal PAPR is obtained by experimenting with different sub-blocks and phase elements.

b.   Proposed a hybrid PAPR reduction applied to the combination of NOMA and FBMC. The performance of the Hybrid waveform is better than the OFDM, FBMC, or NOMA.

c.   The proposed PTS-SLM considerably reduces the complexity overhead of the structure.

2  System Model

2.1 PAPR in Multicarrier System

The structure of the multicarrier system is given in Fig. 1.

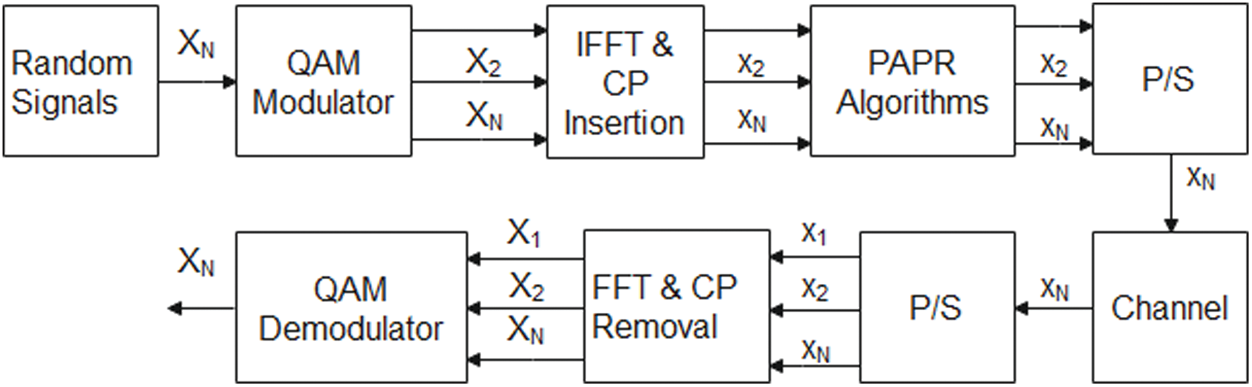
Figure 1: OFDM

Let us consider an N-sub-carrier to modulate the OFDM symbols:

X=[X0,X1,…,XN−1]T(1)

An IFFT is applied on Eq. (1) to generate a time-domain OFDM symbols (L), given as:

x(n)=1N∑L=0N−1⁡XLej6.28LKN(2)

where n=0,1,…,KN−1 and K is the overlapping factor. The PAPR of the OFDM symbols in the transmitter is given as:

PAPR=Maximum|x(n)|2Average|x(n)|2(3)

To estimate the peak power of the OFDM symbols in dB is given as:

PAPRdB=10log10Maximum|x(n)|2Average|x(n)|2(4)

To analyze the efficiency of peak power of OFDM system, it is important to estimate the complementary cumulative distribution function (CCDF), given as:

F(y)=1−exp(−x)(5)

The average value of the OFDM symbol (Average|y(n)|2) is one.

The PAPR for different threshold value is given as:

(PAPR<x)=f(x)2=(1−expx)L(6)

(PAPR>x)=f(x)2=1−(PAPR≤x)=1−(1−expx)L(7)

2.2 PAPR in NOMA-FBMC

The schematic of the projected waveform is given in Fig. 2.

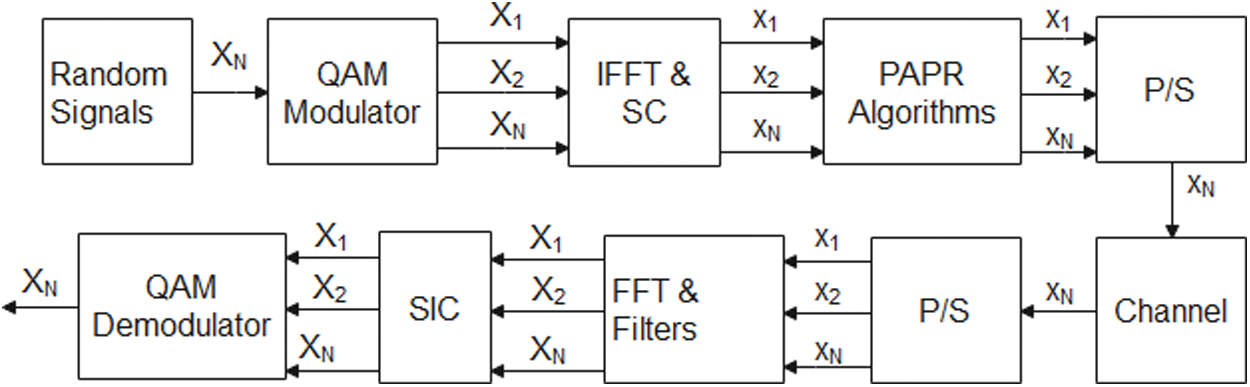
Figure 2: NOMA-FBMC

The NOMA symbols are expressed as:

Y=[Y0,Y1,…,YN−1]T(8)

The modulated NOMA symbols form-subcarriers (S) are given by:

ym,j[m]=1S∑k=0S−1⁡Yiexp⁡(i6.28nkS),0≤n≤S−1(9)

A cluster of filters is applied to the ym,j[m], given by:

ymj,k=ym,j[m]∗Fc(10)

where Fc is the group of filters. The filtered symbols are added to reconstruct the NOMA-FBMC symbols represented as:

yj=∑k=0M−1⁡yˇmJ,K(11)

yj denotes the NOMA-FBMC symbols multiplexed in the power domain. Let P be the total power allocated to the NOMA subs-carriers, given as:

y=∑j=1L⁡Pj∗yj(12)

The PAPR of the NOMA-FBMC is expressed as:

PAPR=Maximum|yj(n)|2Average|yj(n)|2(13)

The CCDF of the NOMA-FBMC is given by:

Prob(PAPR>PAPRo)=1−(1−exp(−yj(n))S(14)

2.3 Selective Mapping (SLM)

The conventional arrangement of SLM is given in Fig. 3. It is one of the most adopted PAPR approaches due to its numerous benefits.

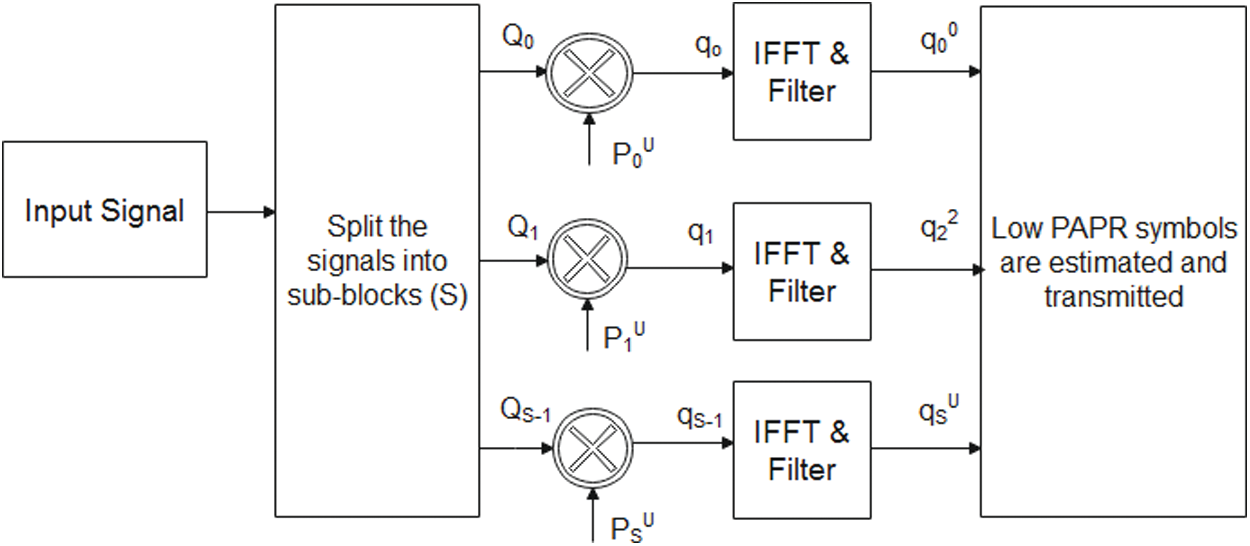
Figure 3: SLM

The symbols are segregated into the cluster of blocks, which can be represented as:

Qs=[Qs,0Qs,1,…,Qs,N−1]T(15)

The clusters of phase sequence u are given as:

U=[p0u,p1u,…,pS,N−1u]T(16)

The symbols (Qn) are multiplied with the clusters of phase sequence U:

qsu=Qs∗U(17)

Applying IFFT to the Eq. (17)

qsu(n)=1N∑n=0N−1⁡qsuexpi6.28nSKN(18)

The symbols (qsu(n)) with low amplitudes are estimated and transmitted to the receiver.

2.4 PTS (Partial Transmission Sequence)

The structure of PTS is given in Fig. 4.

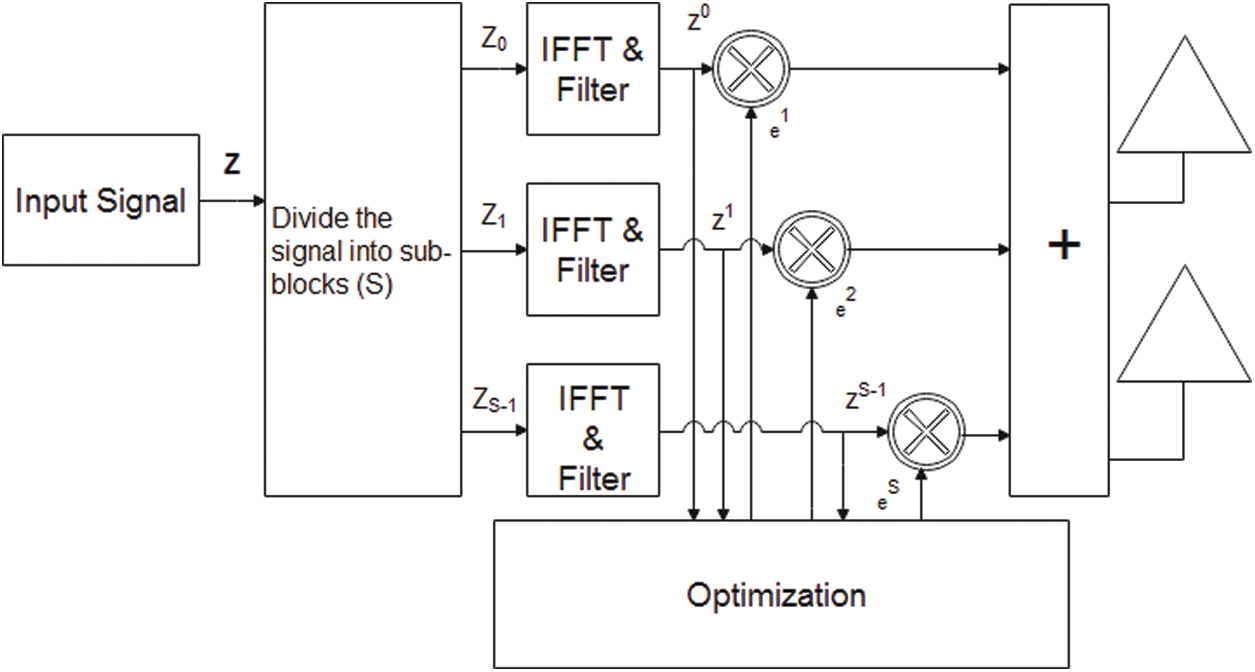
Figure 4: PTS

The PTS method reduces the PAPR by splitting the multicarrier signals (Z) into the number of sub-blocks (S).

Z=∑sS⁡Zs(19)

The signals (Zs) are weighted by constant phase elements (es) to lower down the peak power. The phase element vector is express as:

e=e1+e2,…,es(20)

where e is written as:

e=es=exp⁡(i2πS/P)(21)

P is the acceptable phase elements limited to {±1}, {±1,±i}:

An IFFT is applied to the sub-blocks to estimate the large peak values of the signals, expressed as:

z=es{∑sS⁡IFFT(Zs)}=∑sS⁡eszs(22)

The minimal PAPR is obtained by finding the best phase elements given as:

{e1+e2,…,es}=minmum1≤p≤P⁡|∑sS⁡eszs|(23)

2.5 Proposed SLM-PTS

The structural arrangement of SLM-PTS is given in Fig. 5. SLM's spectral and PAPR performance is superior to the PTS, but SLM results in high computational overhead as equated to the PTS. The primary concern is to lower the value of peak power while reducing the framework's complexity. Hence, we proposed to integrate PTS-SLM for advanced waveforms.

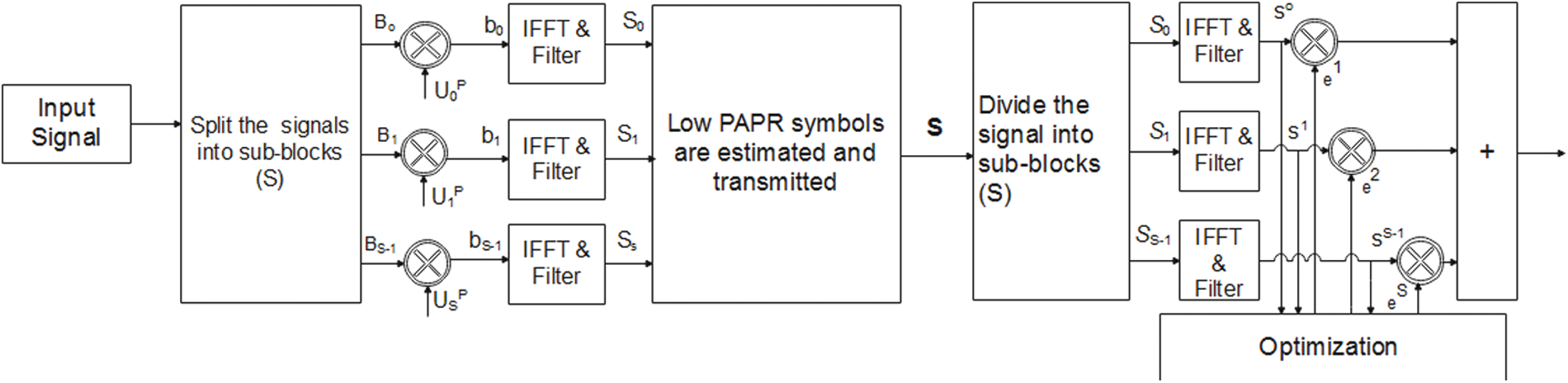
Figure 5: Proposed SLM-PTS

Let us consider multicarrier signals separated into several sub-blocks (S) is given by:

Bs=[Bs,0Bs,1,…,Bs,N−1]T(24)

The phase sequence ∅p is given as:

∅p=[u0∅p,u1∅p,…,uN−1∅p]T(25)

The symbols (BS) and phase elements (∅p) are multiplied given as:

bpsU=∅p∗BS(26)

Applying IFFT to the Eq. (26)

S(n)=1N∑n=0N−1⁡bpsUexpi6.28nSKN(27)

The low amplitudes of SLM symbols (S (n)) are selected and transmitted to the PTS system. The PTS method reduces the complexity by splitting SLM symbols into the number of sub-blocks given as:

sˇ=∑sS⁡Sˇs(28)

The signals (Sˇs) are weighted by constant phase elements (es) to lower down the peak power. The phase element vector is express as:

e=e1+e2,…,es(29)

where e is written as:

e=es=exp⁡(i2πS/P)(30)

An IFFT is applied to the sub-blocks to estimate the large peak values of the signals, expressed as:

sˇ=es{∑sS⁡IFFT(Sˇs)}=∑sS⁡essˇs(31)

The minimum PAPR is expressed as:

{e1+e2,…,es}=minmum 1≤p≤P⁡maximumn=0,1,…,N−1⁡|∑sS⁡essˇs|(32)

3  Results

The projected method is implemented and studied by using MATLAB v2014 on a Core i7 system. The BER, PAPR, and spectral accessing performance have been explored for the OFDM, FBMC, NOMA, and NOMA-FBMC centered PTS, SLM, and SLM-PTS algorithms. Tab. 1 shows the simulation constraints of the projected work.

Complexity is one of the major apprehensions in PAPR procedures. The complexity of the different waveforms can be obtained as [19]:

Complexity=PS−1N−1(33)

We consider arithmetic operational as the intricacy of this work. The addition (Add) and multiplication (Mul) of PTS [20], SLM [21], and proposed SLM-PTS are given below:

PTSAdd=S(2Nlog2N)(34)

PTSMul=S(N2log22N)(35)

SLMAdd=S(Nlog2N2)(36)

SLMMul=S(N2Slog2S+N)(37)

SLM−PTSAdd=PS−1N(S−1)(38)

SLM−PTSMul=PS−1N(S+1)(39)

Fig. 6 indicated the spectral and Out of Band Emission (OOBE) comparison of OFDM, FBMC, NOMA, and NOMA-FBMC. It is seen that the OOBE of the SLM-PTS is −115 dB as compared with the NOMA (−87 dB), FBMC (−80 dB), and OFDM (−55 dB). It is noted that the spectral leakage of NOMA-FBMC is very low. Hence, it is concluded that the projected hybrid waveform is superior to the standard or advanced waveforms.

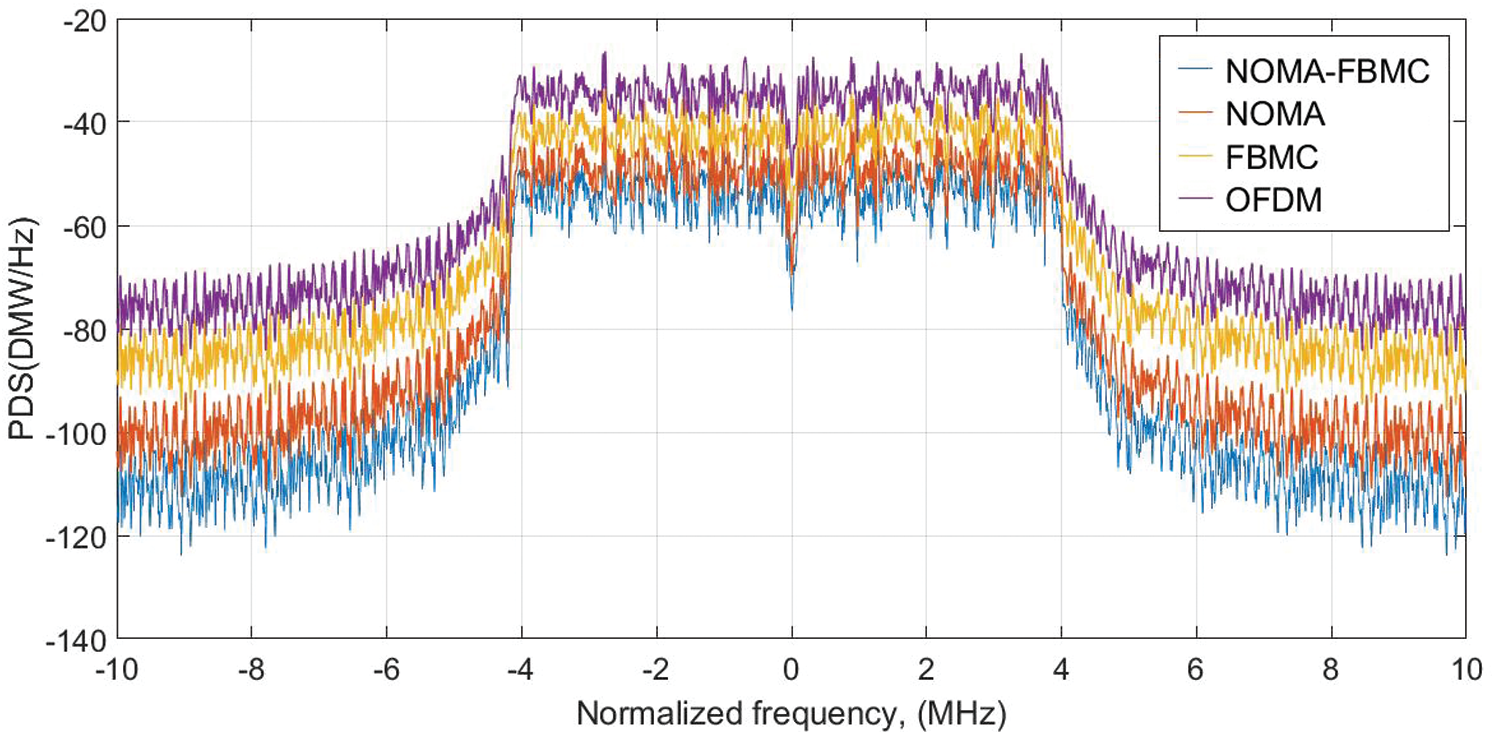
Figure 6: Spectrum leakage performance

The BER estimation of the OFDM structure for the PAPR minimization method is given in Fig. 7. The projected SLM-PTS obtained a BER of 10−3 at SNR of 7.2 dB in comparison to the SLM (7.2 dB) and PTS (8.4 dB), respectively. It is seen that the SLP-PTS enhanced the throughput of the OFDM by 24% as compared with the SLM (18%) and PTS (12%). It is concluded that SLM-PTS is a novel PAPR algorithm and can be applied to the conventional waveforms scheme.

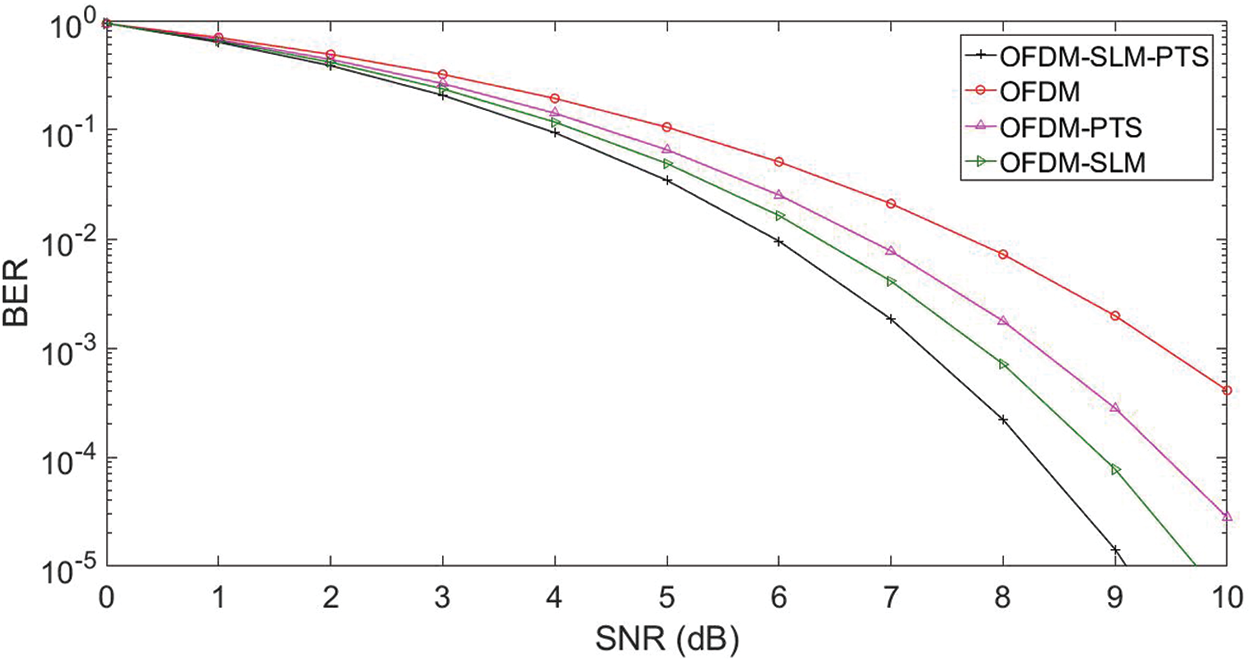
Figure 7: BER OFDM

In Fig. 8 we evaluate the CCDF of OFDM structure for PAPR algorithms. The original signal's peak power without applying the reduction algorithm is 9.6 dB at the CCDF of 10−3. It is seen that the SLM and PTS enlarge the peak of the OFDM signals, hence increases the PAPR to 7 and 6.6 dB. However, the projected SLM-PTS scales down the peak of the symbols, consequently reducing the PAPR to 6.6 dB. It is observed that the SLM-PTS obtained a gain of 0.4 and 1.1 dB as compared to the SLM and PTS.

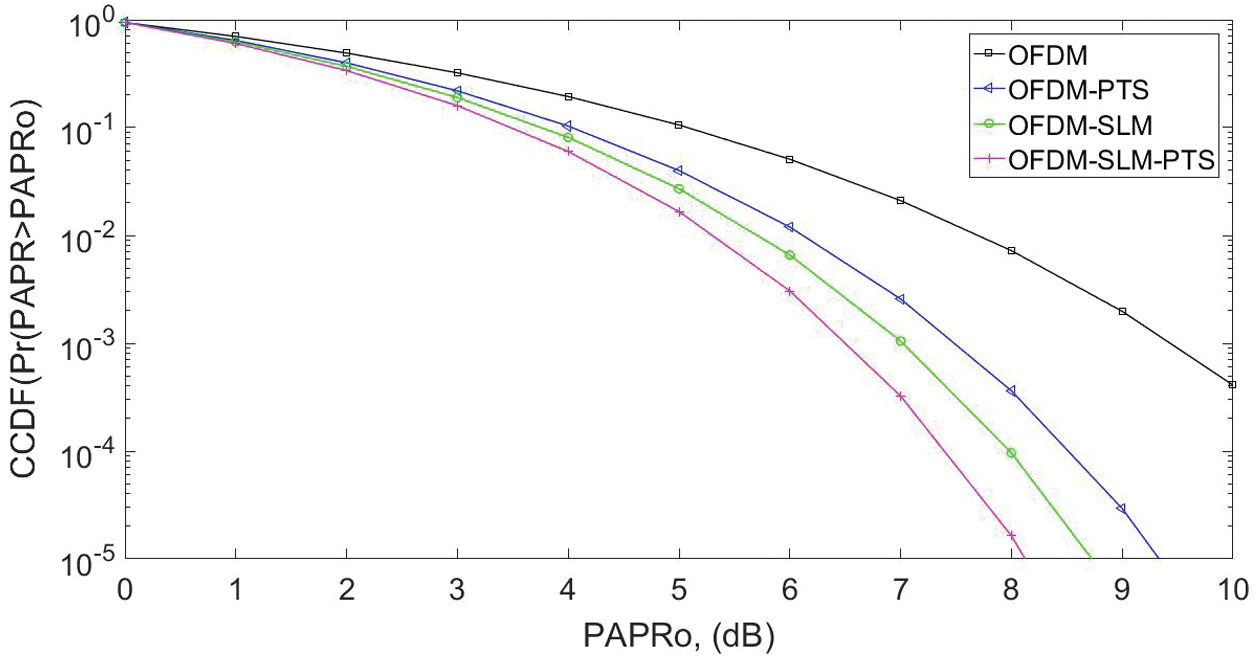
Figure 8: OFDM PAPR

The analysis of BER curves of FBMC arrangement for different PAPR algorithms is given in Fig. 9. The SLM-PTS, SLM, and PTS achieved an efficiency of 38%, 30%, and 25%, respectively. Hence, it is concluded that projected SLM-PTS performance is better when applied to the FBMC structure than the OFDM.

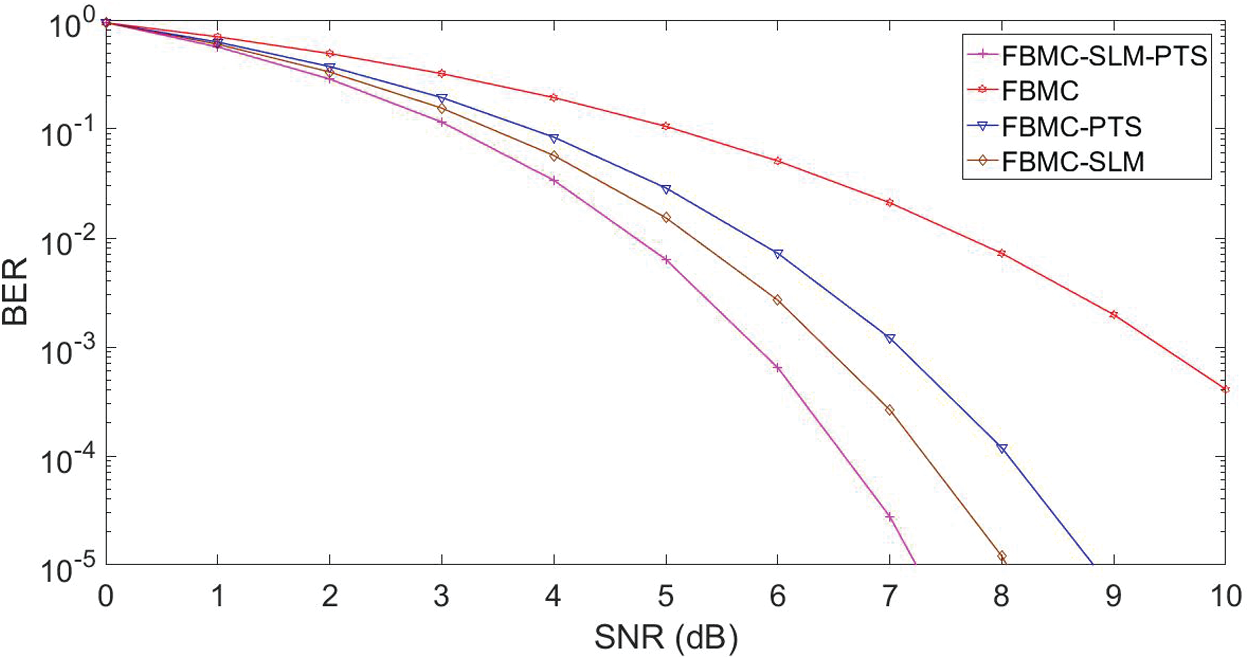
Figure 9: FBMC BER

The CCDF of the FBMC structure is given in Fig. 10. It is noted that the SLM-PTS, SLM, and PTS decrease the peak power to 5.4, 6.2, and 6.8 dB, respectively, at the CCDF of 10−3. Hence, it is concluded that the SLM-PTS clipped the OFDM signal's peak at the desired level, thus enhancing the structure's PAPR performance.

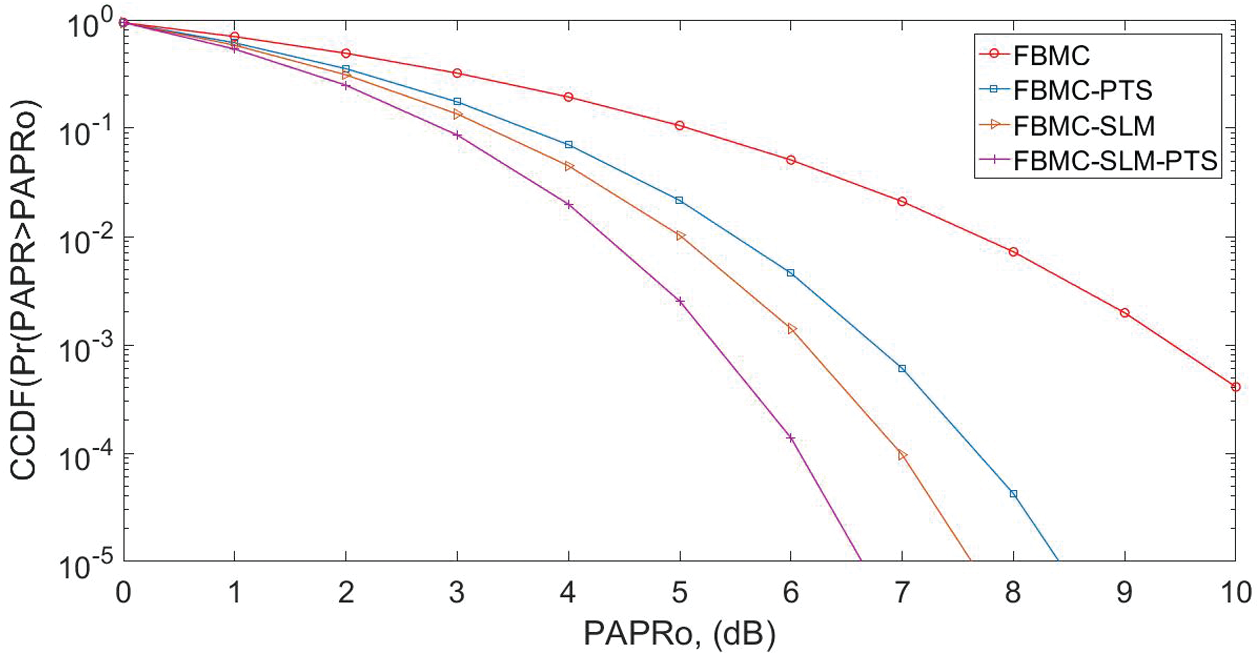
Figure 10: FBMC PAPR

The BER estimation of the NOMA waveform structure is given in Fig. 11. It is seen that the efficiency of BER performance is greatly improved at the lower SNRs prerequisite. The SLM-PTS, SLM, and PTS enhanced the efficiency of the framework by 43%, 37%, and 28%, respectively. Hence it is concluded, the overall throughput of the NOMA arrangement is greatly enhanced as compared to the OFDM and FBMC structure.

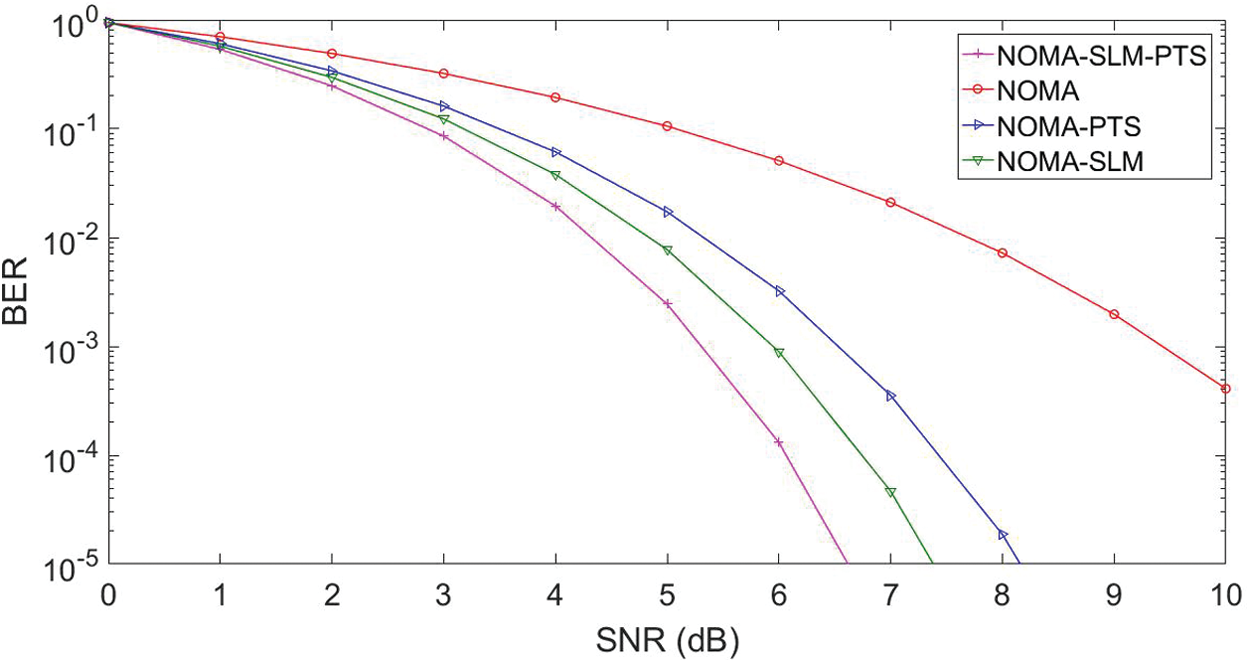
Figure 11: NOMA BER

The CCDF estimation of the NOMA structure is given in Fig. 12. The NOMA signal's peak power is 9.6 dB at the CCDF of 10−3, without applying the PAPR algorithms. The peak power is minimized to 4.6 dB for SLM-PTS, 5.2 dB for SLM, and 6 dB for PTS. Hence, it is concluded that the PAPR performance of the NOMA is superior to the FBMC and OFDM structure.

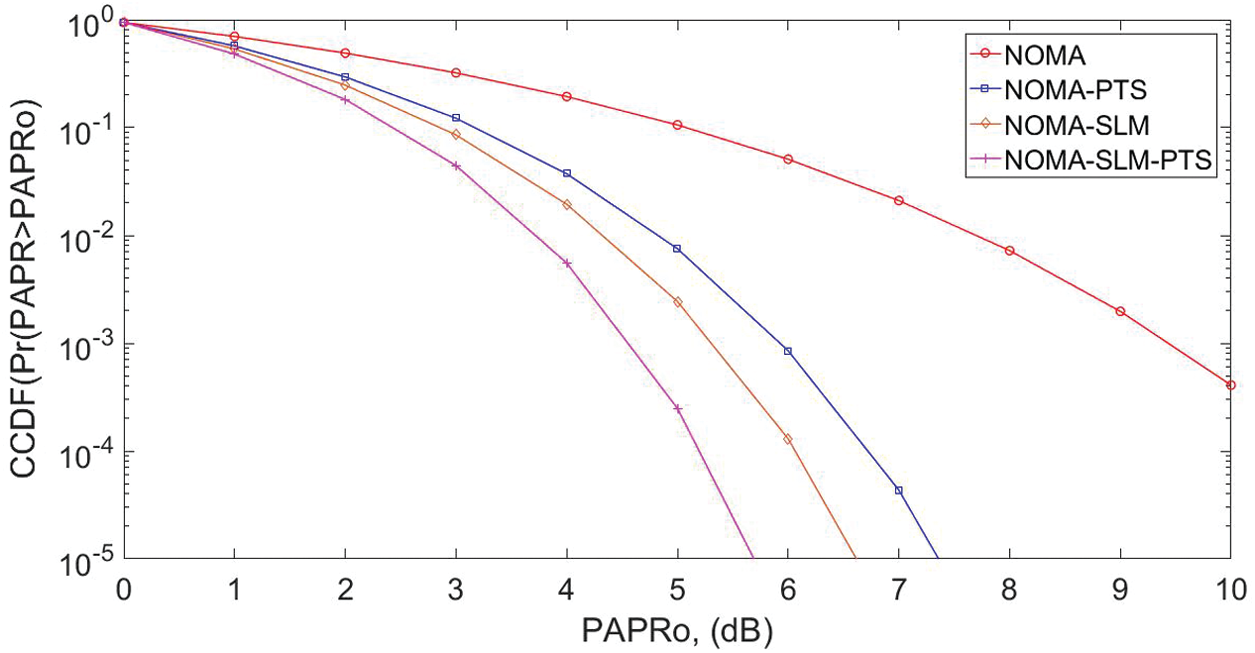
Figure 12: NOMA PAPR

The BER analysis of the Hybrid waveform for different PAPR minimization schemes is given in Fig. 13. The BER of 10−3 is obtained at the SNR of 9.6 dB, 4.4, 5.3, and 6 dB for NOMA-FBMC, SLM-PTS, SLM, and PTS respectively. It is seen that the SNR requirement is drastically reduced for the hybrid waveform scheme. Further, the projected SLM-PTS obtained an efficiency of 54%, due to which it becomes a more desired candidate for 5G radio.

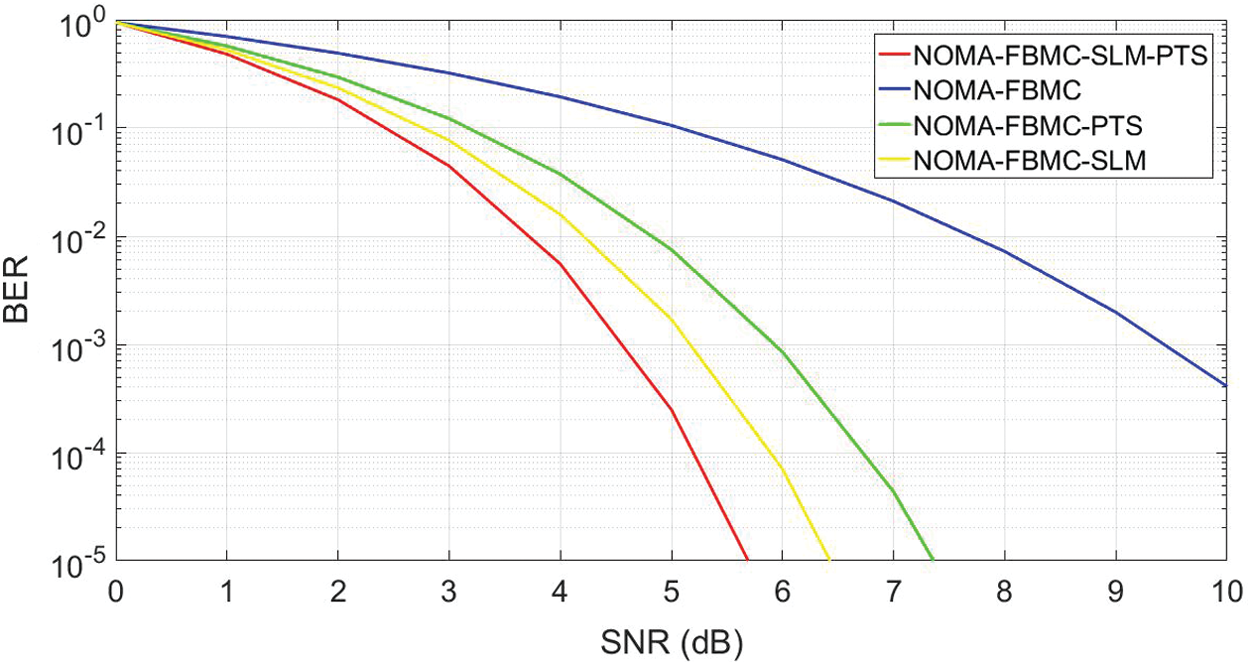
Figure 13: NOMA-FBMC BER

To estimate the effect of PAPR algorithms, the CCDF analysis of NOMA-FBMC is given in Fig. 14. The CCDF of NOMA-FBMC at 10−3 for SLM-PTS, SLM, and PTS is 3, 4.2, and 5.4 dB, respectively, in comparison to the original signal (9.6 dB). Hence, it is noted that the PAPR performance of the projected algorithm is highly optimized in hybrid-scheme.

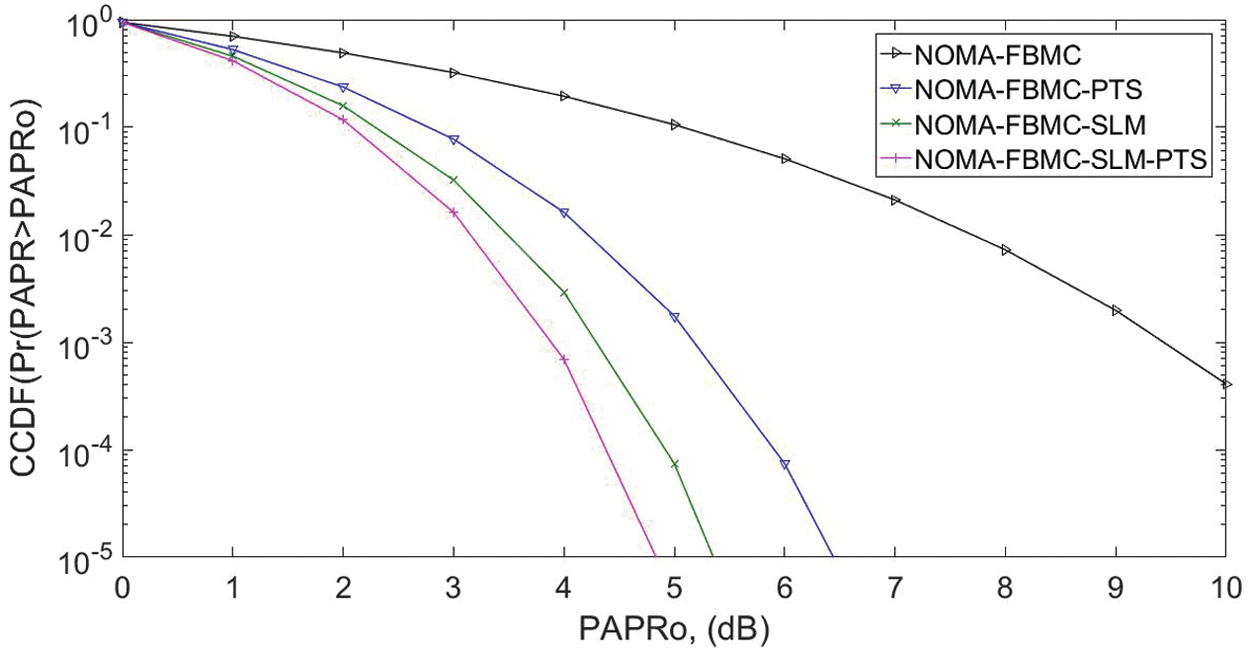
Figure 14: NOMA-FBMC PAPR

4  Conclusion

The BER, PAPR, and spectral performance of the conventional, advanced, and projected hybrid-waveforms are analyzed. The projected SLM-PTS, SLM, and PTS algorithms are applied to the radio waveforms, and simulation results are rigorously investigated. In the first part of the work, we examined and compared the radio waveforms’ spectral performance. However, from the existing literature, it is revealed that the currently used waveforms like OFDM may not serve the key requirements of the 5G radio. Hence, we designed a hybrid NOMA-FBMC waveform to mitigate the drawbacks of current waveforms. It is noted that the spectrum leakage and utilization capability of NOMA-FBMC are better than the existing radio waveforms. In the second part of the work, we mitigate the PAPR effect of multicarrier waveforms. SLM and PTS lower down the PAPR, but the computational overhead is large. Hence, a hybrid SLM-PTS algorithm is suggested to enhance the PAPR and BER performance while sustaining the framework's complexity overhead. The outcome of the work reveals that the projected SLM-PTS surpasses the performance of standard PAPR algorithms.

Acknowledgement: The authors would like to thank for the support from Taif University Researchers Supporting Project Number (TURSP-2020/10), Taif University, Taif, Saudi Arabia and the Centre of Artificial Intelligence, Chennai Institute of Technology, INDIA, vide funding number CIT/CAI/2021/RP-002.

Funding Statement: Taif University Researchers Supporting Project Number (TURSP-2020/10).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

Reference

 1.  R. Saxena and H. Joshi, “OFDM and its major concerns: A study with way out,” IETE Journal of Education, vol. 54, no. 1, pp. 26–49, 2013. [Google Scholar]

 2.  L. Uryvskyiand and S. Osypchuk, “OFDM signal energy characteristics research in channel with permanent parameters,” Telecommunication Sciences, vol. 4, no. 2, pp. 22–27, 2013. [Google Scholar]

 3.  A. Kumar, “A novel hybrid PAPR reduction technique for NOMA and FBMC system and its impact in power amplifiers,” IETE Journal of Research, 2019. https://doi.org/10.1080/03772063.2019.1682692. [Google Scholar]

 4.  R. W. Bauml, R. F. Fischer and J. B. Huber, “Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping,” Electronics Letter, vol. 32, no. 22, pp. 2056–2057, 1996. [Google Scholar]

 5.  V. K. Trivedi, K. Ramadan, P. Kumar, M. I. Dessouky and F. E. Samie, “Enhanced OFDM-NOMA for next-generation wireless communication: A study of PAPR reduction and sensitivity to CFO and estimation errors,” AEU–International Journal of Electronics and Communication, vol. 102, pp. 9–24, 2019. [Google Scholar]

 6.  A. Kumar and M. Gupta, “A comprehensive study of PAPR reduction techniques: Design of DSLM-CT joint reduction technique for advanced waveform,” Soft Computing, vol. 24, pp. 11893–11907, 2020. [Google Scholar]

 7.  A. Kumar, “PAPR reduction of FBMC using hybrid and k-hybrid techniques,” Radio Electronics and Communications System, vol. 62, pp. 501–509, 2019. [Google Scholar]

 8.  A. Kumar and M. Gupta, “A review on activities of fifth-generation mobile communication system,” Alexandria Engineering Journal, vol. 57, no. 2, pp. 1125–1135, 2018. [Google Scholar]

 9.  F. H. Raab, P. Asbeck, S. Cripps, P. B. Kenington, Z. B. Popovic et al., “Power amplifier and transmitters for RF and microwave,” IEEE Transactions Microwave Theory and Techniques, vol. 50, no. 3, pp. 814–826, 2002. [Google Scholar]

10. M. Laabidi and R. Bouallegue, “Three implementations of the tone reservation PAPR reduction scheme for the FBMC/OQAM system,” IET Communication, vol. 13, no. 7, pp. 918–925, 2019. [Google Scholar]

11. J. Moon, Y. Nam and J. Kim, “PAPR reduction in the FBMC-OQAM system via segment-based optimization,” IEEE Access, vol. 6, pp. 4994–5002, 2018. [Google Scholar]

12. L. Dai, B. Wang, Y. Yuan, S. Han, I. C. Lin et al., “Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends,” IEEE Communication Magazine, vol. 53, no. 9, pp. 74–81, 2015. [Google Scholar]

13. A. Jayalath, C. Tellambura and H. Wu, “Reduced complexity PTS and new phase sequences for SLM to reduce PAP of an OFDM signal,” in IEEE VTC, 2000 IEEE 51st Vehicular Technology Conf. Proc. (Cat. No. 00CH37026Tokyo, Japan, pp. 1914–1917, 2000. [Google Scholar]

14. S. Rajasekaran, M. Vameghestahbanati, M. Farsi, H. Yanikomeroglu and H. Saeedi, “Resource allocation-based PAPR analysis in uplink SCMA-OFDM systems,” IEEE Access, vol. 7, pp. 162803–162817, 2019. [Google Scholar]

15. T. Zhang, Y. Zou, J. Sun and S. Qiao, “Improved companding transform for PAPR reduction in ACO-OFDM-based VLC systems,” IEEE Communications Letters, vol. 22, no. 6, pp. 1180–1183, 2018. [Google Scholar]

16. A. M. Rateb and M. Labana, “An optimal low complexity PAPR reduction technique for next generation OFDM systems,” IEEE Access, vol. 7, pp. 16406–16420, 2019. [Google Scholar]

17. M. H. Aghdama and A. A. Sharifib, “PAPR reduction in OFDM systems: An efficient PTS approach based on particle swarm optimization,” ICT Express, vol. 5, pp. 178–181, 2019. [Google Scholar]

18. J. K. Lain, S. Y. Wu and P. H. Yang, “PAPR reduction of OFDM signals using PTS: A real-valued genetic approach,” Eurasip Journal on Wireless Communications and Networking, vol. 126, 2011. https://doi.org/10.1186/1687-1499-2011-126. [Google Scholar]

19. F. Sandoval, G. Poitau and F. Gagnon, “Hybrid peak-to-average power ratio reduction techniques: Review and performance comparison,” IEEE Access, vol. 5, pp. 27145–27161, 2017. [Google Scholar]

20. S. G. Kang, J. G. Kim and E. K. Joo, “A novel sub block partition scheme for partial transmit sequence OFDM,” IEEE Transaction Broadcasting, vol. 45, no. 3, pp. 333–338, 1999. [Google Scholar]

21. Z. T. Ibraheem, M. M. Rahman, S. N. Yaakob, M. S. Razali, R. A. Kadhim et al., “Performance of PTS techniques with varied partition size in PAPR reduction of OFDM system,” in Proc. IEEE Int. Conf. Computer, Communications, and ControlTechnology, (I4CTLangkawi, Malaysia, pp. 21–25, 2014. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.