Computers, Materials & Continua DOI:10.32604/cmc.2021.018939
Article

Augmented Node Placement Model in t-WSN Through Multiobjective Approach

Kalaipriyan Thirugnansambandam1, Debnath Bhattacharyya2, Jaroslav Frnda3, Dinesh Kumar Anguraj2 and Jan Nedoma4,*

1School of Computer Science and Engineering, VIT University, Chennai Campus, Tamilnadu, India
2Department of Computer Science and Engineering, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, India
3Department of Quantitative Methods and Economic Informatics, Faculty of Operation and Economics of Transport and Communications, University of Zilina, 010 26 Zilina, Slovakia
4Department of Telecommunications, Faculty of Electrical Engineering and Computer Science, VSB-Technical University of Ostrava, 708 33 Ostrava-Poruba, Czech Republic
*Corresponding Author: Jan Nedoma. Email: jan.nedoma@vsb.cz
Received: 27 March 2021; Accepted: 28 April 2021

Abstract: In Wireless Sensor Network (WSN), coverage and connectivity are the vital challenges in the target-based region. The linear objective is to find the positions to cover the complete target nodes and connectivity between each sensor for data forwarding towards the base station given a grid with target points and a potential sensor placement position. In this paper, a multiobjective problem on target-based WSN (t-WSN) is derived, which minimizes the number of deployed nodes, and maximizes the cost of coverage and sensing range. An Evolutionary-based Non-Dominated Sorting Genetic Algorithm-II (NSGA-II) is incorporated to tackle this multiobjective problem efficiently. Multiobjective problems are intended to solve different objectives of a problem simultaneously. Bio-inspired algorithms address the NP-hard problem most effectively in recent years. In NSGA-II, the Non-Dominated sorting preserves the better solution in different objectives simultaneously using dominance relation. In the diversity maintenance phase, density estimation and crowd comparison are the two components that balance the exploration and exploitation phase of the algorithm. Performance of NSGA-II on this multiobjective problem is evaluated in terms of performance indicators Overall Non-dominated Vector Generation (ONGV) and Spacing (SP). The simulation results show the proposed method performs outperforms the existing algorithms in different aspects of the model.

Keywords: Focused wireless sensor network; m–coverage k-connectivity problem; non-dominated sorting; NSGA-II

1  Introduction

Wireless Sensor Networks (WSN) is one among the predominant domain where ‘n’ number of problems grasps the researchers for achieving reliability, accuracy, the efficiency of the network. This contribution exponentially increased when the applications of WSN are expanded in the environments such as health care, disaster tracking system, military-based applications, etc. In recent years a significant number of optimization problems are solved using nature inspired algorithms [1]. IoT based Pay-AsYou-Go Smart Parking System is proposed which uses the unused garbage spaces [2]. Another recent model, which uses digital contact tracing to handle the epidemic situations like Covid-19 using IoT [3]. In WSN, the sensor nodes are used to sense the data surrounds it and report it to the base station either using a single hop or multi-hop communication process. Sensor node deployment is of two different types, namely ad-hoc and pre-determined manner [4]. The ad-hoc type deployment plays a significant role in regions like a deep forest, aquatic nature, etc. Usage of ad-hoc in such regions requires many sensor nodes for effective coverage of the respective region and proper connectivity between deployed sensor nodes. Manual deployment (pre-determined) of sensor nodes is easy to access and requires fewer sensors. However, coverage and connectivity issues are common in both types since the node’s transmission range is less than its restricted power source. The use of wireless connection gets disrupted due to bad weather, etc. Thus, covering targets and maintaining connectivity between sensors that enhance the network lifetime has been considered one of the significant aspects of WSN.

This paper addresses k-coverage m-connected augmented node deployment model in WSN as a multiobjective problem where Non-dominated sorting Genetic Algorithm-II is used to optimize it. The problem is described in this section. Given k target regions and P available positions for node deployment, the objective is to cover k targets using m sensor nodes where m⊆P. As it is given in Fig. 1, Let T={λ1,λ2,…,λ10} be the available target regions to be sensed using S={s1,s2,…,sm} deployed nodes. As per Fig. 1 number of sensor nodes in S is six out of 10 available positions of P. Target λ2 is covered by a Deployed sensor s1 since the target is within the sensing range of the deployed sensor s2 which is deployed in the available position p2 and the deployed node can transfer the data to a base station through the available positions p3 and p4. By allocating the sensor nodes concerning its coverage and connectivity range, the minimum objective number of deployed nodes to cover all targets are efficiently achieved. This problem is considered an NP-complete problem [5]. Achieving optimization in this problem is highly preferable since exact methods take more high time complexity when compared to the optimization approach.

2  Related Work

In the past few decades, research contributions on optimizing WSN problems using heuristic and metaheuristics are higher than earlier research exposure [5–9]. In this literature, coverage and connectivity related algorithms are described with their predominant features.

A detailed Survey has been recorded on different methods for effective node placement in WSN by [10]. In [5] a contradictory set of objectives are taken for effective node placement in WSN, namely energy cost, sensible area, and network reliability. The flaws in their approach are the inadequate coverage of complete targets in the given region. The use of meta-heuristics failed to achieve this particular issue which made the algorithm an ineffective one. A new approach for solving the WSN issue is dividing a region into a disjoint sub-region and imposed active and passive mode of operations in it by [11]. The proposed methodology of Cardie was later redefined in [5] to enhance the lifetime of the network by imposing redundant nodes. Irrespective of coverage and connectivity, this approach achieves better results along with improved disjoint sets.

Figure 1: Two-covered one-connected network

Research on the optimization of resource allocation algorithm in WSN is discussed by [12]. The lifetime of network and connectivity are the objectives considered in this paper, which takes the sensor positions and transmission power level as their attributes to solve the problem. MOEA/D is used to solve the given problem to achieve the objectives with fewer deployed sensor nodes. Coverage was not handled in this paper. Author Harizan et al. [13] proposed an NSGA-II with modified dominance has been proposed for the scheduling problem. The multiple parameters as coverage, connectivity and residual energy of the sensor nodes are considered. A probabilistic sensing model (PSM) and harmony search algorithm (HSA) approach are used in the same type of problem in WSN to achieve the balance between the network coverage performance and the network cost [14].

In 2012, a multi coverage based WSN problem is handled in [15], three different coverage, namely simple coverage, k and Q coverage. For the optimization process, an exhaustive cover set defining process is used in this approach. For the inclusion of connectivity in the proposed algorithm, an M-connected approach is included for optimization. The algorithm’s time complexity is higher since the algorithm flow included each node one by one and check for all possible combinations in the set for adaptive placement of nodes.

A simulation-based approach for effective node placement is proposed by [16], where several available positions to place the sensor nodes are given. Without colliding the connectivity between sensor nodes, the nodes should be placed with the minimal number–-another approach based on GA proposed in [17] as relay sensor node placement algorithm. This paper’s defined objective is to efficiently place the nodes in the given positions, thus minimizing the number of sensors without colliding its connectivity between relay nodes. Using GA, another approach for attacking coverage problem in WSN is proposed to enhance its lifetime. In this approach, sensing targets are not used for simulation. Only the sensors nodes are placed to cover the simulation region without any targets in it. In our proposed method, this problem is addressed. Another GA based approach for addressing the same issue as our proposed method has been made in [4]. However, this method reproduces offspring so that it becomes invalid, and a solution repair process is needed here. In our proposed algorithm, a multiobjective optimization algorithm NSGA-II is used to address this issue and Pareto set solutions.

3  Multiobjective Optimization

This section comprises the prescribed definition of the multiobjective optimization problem [18] and Pareto dominance operators, which helps to understand the proposed work better.

Given a problem with solution set P=[C1,C2,…,Cn] with n individuals where each individual Ci=[Gi,1,Gi,2,…,Gi,j,…,Gi,m] with m decision variables intents to find a vector Ci*→=[Gi,1*,Gi,2*,…,Gi,m*] which satisfies p equality constraints ui(C→)=0,i=1,2,…,p, q inequality constraints vi(C→)=0,i=1,2,…,q and finds a minimized vector function f(C→)=[f1(C→),f2(C→),…,fk(C→)] where k is the number of objectives.

From the solution space given in this definition P=[C1,C2,…,Cn], an individual C1=[G1,1,G1,2,…,G1,m] is said to dominate C2=[G2,1,G2,2,…,G2,m] iff fi(C1→)≤fi(C2→)∀iϵk and fi(C1→)<fi(C2→)∃iϵk and this can be represented as C1→≺C2→. Two individuals said to be non-dominated to each other if neither C1→≺C2→ nor C2→≺C1→ and this can be represented as C1→≼C2→.

Fig. 2 shows an example for dominated and non-dominated solutions. Let us consider a multiobjective problem that consists of two objectives f1() and f2(). Three individuals C1→,C2→andC3→ are plotted in Fig. 1 based on their objective values. From the given definition, we can claim that individual C1→ dominates individual C2→ and C3→ and this can be represented as C1→≺{C2→,C3→}. And individual C2→ and C3→ are non-dominated to each other since it satisfies the given definition of the non-dominated solution set and this can be represented as C2→≼C3→.

Figure 2: Dominance relation

4  Problem Formulation

In this section the the formulation of t-WSN problem is defined with an example along with the objectives.

4.1 Network Model

Let us assume that the simulation region for target-based WSN is of the two-dimensional region. Our model positions the positions to deploy the sensor nodes randomly based on the available targets. The target points and sensor nodes are static for some available positions. In our proposed model, the available position to sense targets are given with a different range, as shown in Tab. 1. Similarly, communication between nodes are given as coverage range which is listed in same Tab. 1.

4.2 Problem Definition

Let us define the notations that are used to create the system model.

1. Set of Target points T={λ1,λ2,…,λk}

2. Set of available positions of sensor nodes to cover targets P={ρ1,ρ2,…,ρh}

3. Set of deployed sensor nodes in available positions S={s1,s2,…,sm|d≤m}

4. ℝcomm represents sensor node communication range.

5. ℝsen represents sensor node sensing range.

6. d(λi,sj) represents the distance between the target point λi to Deployed Sensor sj

7. Cov(λi) denotes the sensor nodes that cover the target points λi. This can be represented as:

Cov(λi)={sj⊆S∣d(λi,sj)≤ℝsen}(1)

8. Tcov(si) denotes the target points that are covered by si. This can be represented as:

Cov(si)={λj⊆T∣d(λj,si)≤ℝsen}(2)

9. Comm(si) denotes the sensor nodes that are covered by sj. This can be represented as:

Comm(si)={sj⊆S∣d(sj,si)≤ℝcomm}(3)

Boolean representation is used to define whether the target i is covered by node j. Points 7–9 is represented as follows:

aij={1iftargetλicoveredusingnodesj0elsebij={1ifsiisconnectedtosj0elsecij={1ifρhisselectedtobinS0else(4)

with inequality constraints ∑i=1Maij≥k and ∑i=1Maij≥m where k represents the target and m represents sensor nodes.

4.3 Objectives

There are three objectives of coverage, and connected problem are considered in this paper. The objectives are defined as follows:

1. Minimize the number of Deployed Nodes: The first objective is defined to minimize the number of deployed sensor nodes from the available positions h. It can be formulated as

Minimize|S||P|(5)

2. Maximize the cost of coverage: It can be represented as:

Maximize1T×k∑i=1TCostCov(λi)(6)

where CostCov={kif|Cov(λi)|≥kk-|Cov(λi)|else and k∈T and Cov(λi)⊆S

3. Maximize the cost of connection: Mathematical representation can be stated as:

Maximize1S×m∑i=1SCostComm(sj)(7)

where CostCov={mif|Comm(si)|≥mm-|Comm(si)|else and m∈S and Cov(λi)⊆T.

5  Non-Dominated Sorting Genetic Algorithm II on Coverage-Connected Problem

This section holds a four-folded algorithm for optimizing coverage-connected problem using NSGA II [19]. In this section, a discussion on the Non-dominated sorting method followed by preservation of diversity will be explained in the second fold, and reproduction operators are discussed. In the final fold, a complete algorithm for solving the coverage-connected problem using NSGA-II is described. NSGA-II is chosen to solve m −connected k −coverge problem over other multiobjective optimization techniques due to its following advantages.The advantages are listed as follows: Non-Dominated sorting techniques are utilized to enhance the solution search towards pareto-optimal solutions. The use of crowding distance improvises the diversity of search. The usage of Elitist technique preserves the optimal solution in every iteration [20].

5.1 Non-Dominated Sorting and Density Estimation

Non-dominated sorting is the process of sorting the individuals based on its domination set. It is a rank-based selection method to accentuate the Pareto front individuals to improve the algorithm’s search capability. A detailed description of Non-Dominated sorting is given in Algorithm 1. This algorithm is considered as a function to be called by NSGA-II in Algorithm 3.

5.2 Preserving Diversity

A multiobjective evolutionary algorithm is supposed to hold two properties such as:

•   Convergence towards Pareto front individuals.

•   A diversified search should be done during the run.

In NSGA-II, two methods are used to handle this diversity preservation: density estimation and crowded comparison operator. This method eliminates the process of user-dependent feature.

Density estimation denotes the dense population around an individual i∈Υi. It is represented as Υi(dk) for individual i. When m is represented as objectives, then fm(i) represents the fitness of individual i with respective to objective m then fmmax represents the maximum value of objective function m from the entire population t and fmmin represents the minimum value. Algorithm 2 represents the crowding distance function.

5.3 Crowd Comparison (≺n )

For selecting an individual, the crowding comparison operator can be used in the crowded population. Crowd comparison operator is used when both the individual obtains the same rank in non-dominated sorting. Each individual C∈P consists of attributes, namely 1. Non-dominated Ranking (Crank) and crowd distance (Cd). C1≺nC2 if it falls in two conditions which are:

Crank1<Crank2 (8)

Crank1=Crank2 and Cd1>Cd2 (9)

when an individual fall into these two conditions, then the individual with a lower rank will be selected.

5.4 Process of NSGA-II on m-Connected k-Coverage

The individuals are represented as chromosomes, and a complete solution set can be represented as population P. Boolean representation is used to represent each individual C. For Reproduction (Offspring), simulated binary crossover and 2-point mutation are used for effective diversification. After initializing the population, the offspring is done with the parent population. Children are produced and appended along with their parents. The detailed flow of NSGA-II is given in Algorithm 3.

6  Experimental Results & Discussion

The experimental setup for evaluating the proposed algorithm’s performance on the k-coverage m-connected problem, NSGA-II, is implemented on the problem using MATLAB version 8.4 in the system configured with Intel Core i7 processor, 3.4 GHz processor speed, and 4 GB RAM. The designed testbed for this paper’s described problem, two different grid-based scenarios are generated, namely WSN1 with a 300-m × 300-m grid and WSN2 with a 500-m × 500-m grid. The base station for WSN1 and WSN2 were set in the position coordinates of (300, 150) and (500, 250), respectively. The available positions for sensor nodes and targets are randomly placed in the grid. The parameters are given in Tab. 1.

6.1 Performance Metrics

Performance measures using for evaluating the proposed algorithm are F-value, Computation time in seconds. F-value: F-value is the ratio between the number of available positions to the number of deployed sensors in it (a higher value is better). It can be formulated as:

F-Value=#AvailablePositions#DeployedSensors(10)

Computational Time: Computational time is defined as the algorithm’s time to perform its entire run. In this simulation, the computational time is given in seconds.

The simulation results are tabulated in Tab. 2.

Figure 3: Simulation setup of WSN1 (300 × 300)

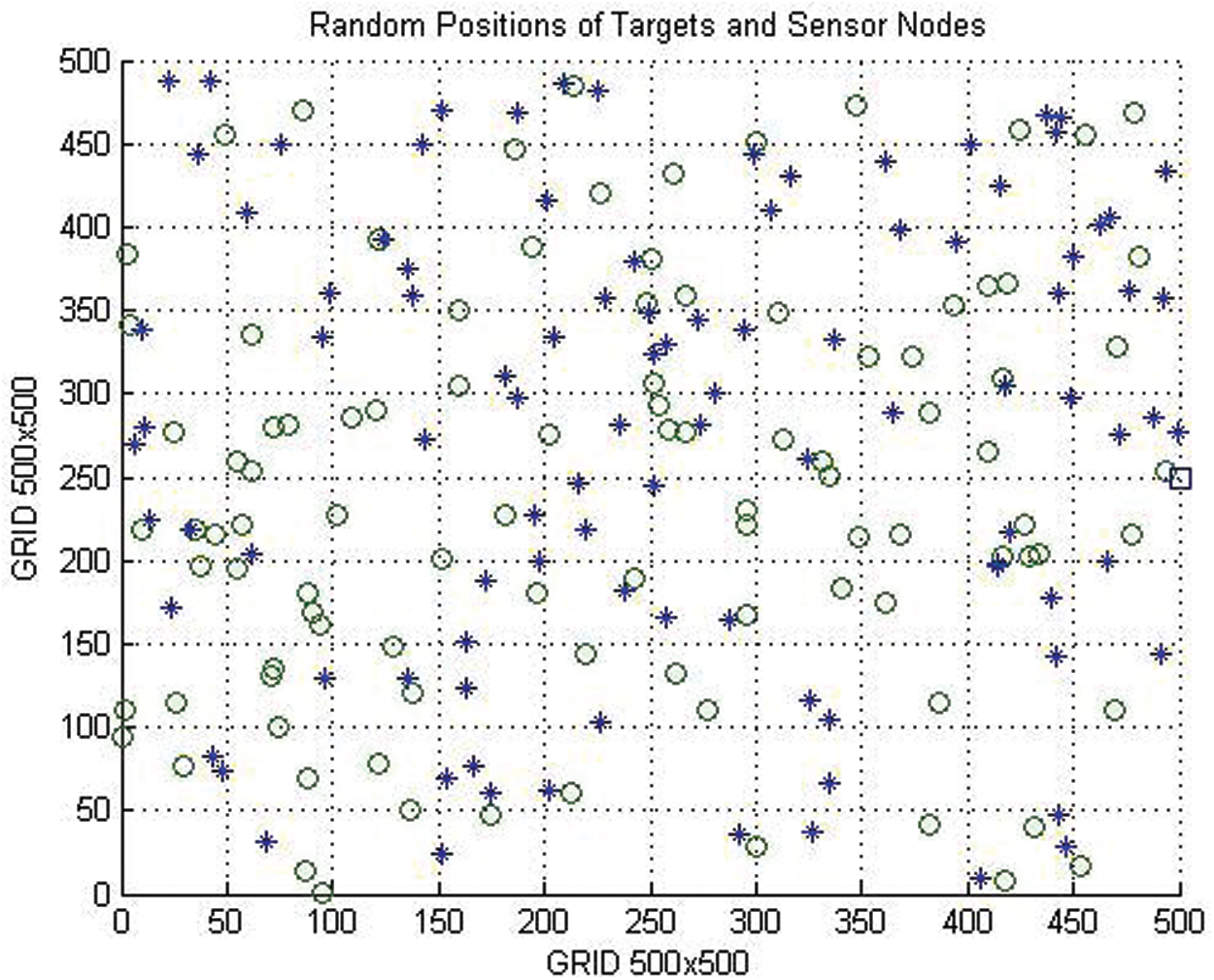
Figure 4: Simulation setup of WSN2 (500 × 500)

6.2 Performance Measures Using Multiobjective Performance Indicators

Figs. 3 and 4 are showing the performance of the proposed algorithm in terms of multiobjective solutions, two effective unary indicators are evaluated with Pareto front solutions, namely Overall non-dominated vector generation (ONGV) and Spacing (SP). To evaluate the performance of the proposed algorithm in terms of multiobjective solutions, two effective unary indicators are evaluated with Pareto front solutions, namely Overall non-dominated vector generation (ONGV) [21] and Spacing (SP) [22]. ONGC and SP are formulated as follows:

ONGV=|γ|c (11)

SP=1|γ|c-1∑j=1|γ|c(d¯-dj)2 (12)

|γ|c denotes the number of individuals in the Pareto front and dj=mink(∑lm∥fmj-fmk∥)∀j,k∈|γ|c for each objective f() with m objectives and d¯ is denoted as the mean of dj. In terms of ONGV higher, the values depict the algorithm’s efficiency in finding Pareto front solutions. SP value depicts a complete solution set efficiency, and when the value is near 0, it obtains a higher performance impact. For evaluating other algorithms in terms of multiobjective performance indicators, their final iteration solutions are considered. The performance measures are shown in Tab. 3.

6.3 Result Analysis

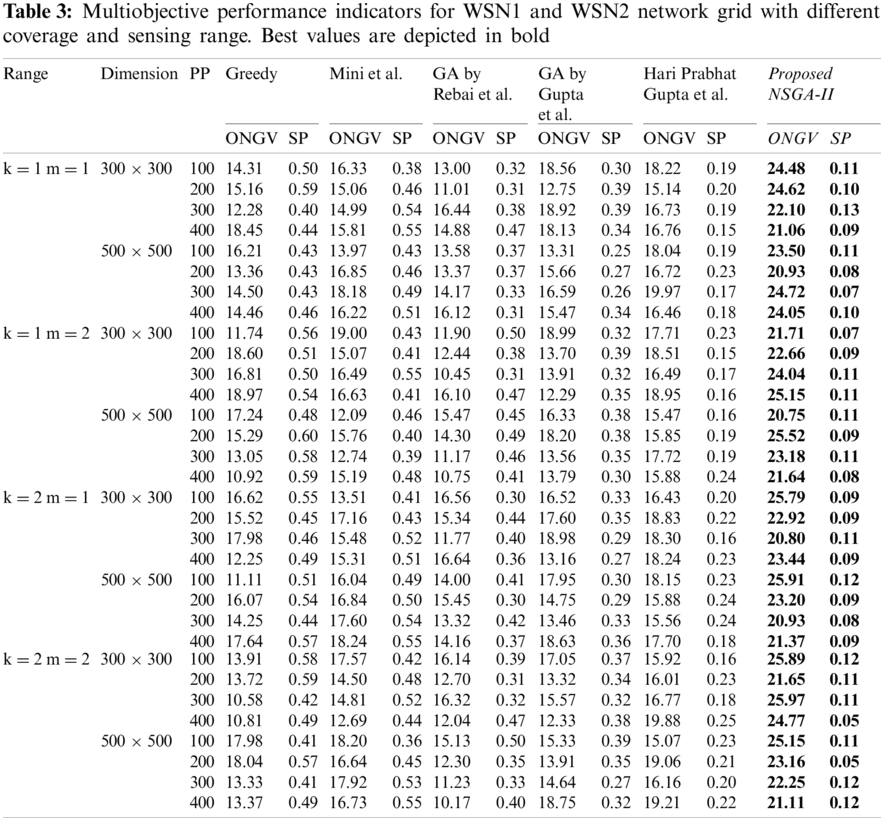
For comparison purpose, we simulated other existing algorithms, namely heuristic-based method Greedy Method and GA based method [15–17,23] and GA in [1]. Tabs. 2 and 3 comprises the results in terms of efficiency and Pareto front individuals, respectively. From Tab. 2, the results of the proposed algorithm show significant performance in terms of F-value on coverage and connection range (k, m) values (1, 1) and (2, 2). Tab. 3 holds the ONGV and SP metric results, which are performance indicators for evaluating the multiobjective problem. Figs. 5 and 6 shows the performance comparison of deployed sensor nodes for all algorithm with different coverage and connectivity range and the performance comparison of WSN1 and WSN2. From the given results, it is justified that the proposed algorithm’s performance outperforms with appropriate performance measures.

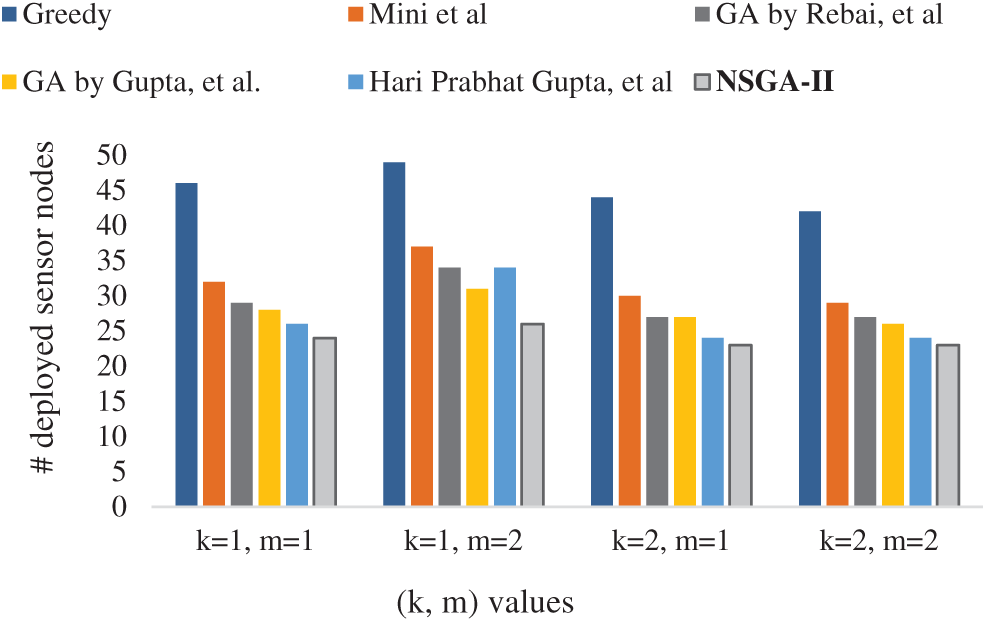
Figure 5: Comparison of # deployed nodes w.r.t coverage and connectivity range for WSN1

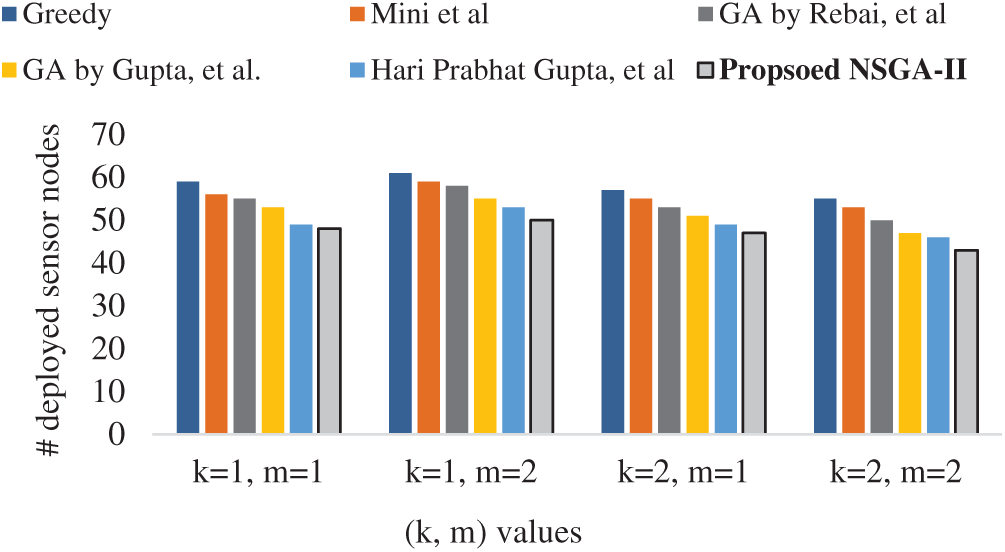
Figure 6: Comparison of # deployed nodes w.r.t coverage and connectivity range for WSN2

7  Conclusion

In this paper, the NSGA-II optimization algorithm is used to handle the multiobjective coverage connectivity problem in WSN. The described objectives were efficiently handled using NSGA-II to obtain a high number of Pareto front set solutions. The proposed NSGA-II on coverage connectivity was tested with different grid size, communication and sensing range. In terms of F-Value, the proposed method performance with superior values for most of the simulations. Also, in terms of computational time, the proposed algorithm outperforms when compared with the existing algorithms. For justifying the proposed algorithm, five existing techniques were simulated with the same grid, and the values were tabulated in terms of F-Value and Computational time. For comparing the results in terms of multiobjective performance indicators, the final iteration individuals are taken to count with respect to its Euclidian distance.

The future directions of the proposed model can be enhanced by solving more number of objectives. On the other hand, improvising heterogeneous algorithms for solving m-connected k-coverge problem is also an another scope of the research.

Funding Statement: This research has been funded with the support of the project SP2021/45, assigned to VSB-Technical University of Ostrava, the Ministry of Education, Youth and Sports in the Czech Republic.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S.-C. Chu, Z.-G. Du and J.-S. Pan, “Discrete fish migration optimization for traveling salesman problem,” Data Science and Pattern Recognition, vol. 4, no. 2, pp. 1–18, 2020. [Google Scholar]

 2.  A. Sant, L. Garg, P. Xuereb and C. Chakraborty, “A novel green IoT-based pay-as-you-go smart parking system,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3523–3544, 2021. [Google Scholar]

 3.  L. Garg, E. Chukwu, N. Nasser, C. Chakraborty and G. Garg, “Anonymity preserving IoT-based COVID-19 and other infectious disease contact tracing model,” IEEE Access, vol. 8, pp. 159402–159414, 2020. [Google Scholar]

 4.  M. Rebai, M. Le berre, H. Snoussi, F. Hnaien and L. Khoukhi, “Sensor deployment optimization methods to achieve both coverage and connectivity in wireless sensor networks,” Computers & Operations Research, vol. 59, no. 3, pp. 11–21, 2015. [Google Scholar]

 5.  L. Liu, B. Hu and L. Li, “Energy conservation algorithms for maintaining coverage and connectivity in wireless sensor networks,” IET Communications, vol. 4, no. 7, pp. 786, 2010. [Google Scholar]

 6.  K. D. Kandris, A. Alexandridis, T. Dagiuklas, E. Panaousis and D. D. Vergados, “Multiobjective optimization algorithms for wireless sensor networks,” Wireless Communications and Mobile Computing, vol. 2020, no. 3, pp. 1–5, 2020. [Google Scholar]

 7.  P. Kuila and P. K. Jana, “A novel differential evolution based clustering algorithm for wireless sensor networks,” Applied Soft Computing, vol. 25, no. 4, pp. 414–425, 2014. [Google Scholar]

 8.  P. Kuila and P. K. Jana, “Energy efficient clustering and routing algorithms for wireless sensor networks: particle swarm optimization approach,” Engineering Applications of Artificial Intelligence, vol. 33, pp. 127–140, 2014. [Google Scholar]

 9.  M. A. Jamshed, M. Ur-Rehman, J. Frnda, A. A. Althuwayb, A. Nauman et al., “Dual band and dual diversity four-element MIMO dipole for 5G handsets,” Sensors, vol. 21, no. 3, pp. 767, 2021. [Google Scholar]

10. M. Younis and K. Akkaya, “Strategies and techniques for node placement in wireless sensor networks: A survey,” Ad Hoc Networks, vol. 6, no. 4, pp. 621–655, 2008. [Google Scholar]

11. D.-R. Chen, L.-C. Chen, M.-Y. Chen and M.-Y. Hsu, “A coverage-aware and energy-efficient protocol for the distributed wireless sensor networks,” Computer Communications, vol. 137, no. 2, pp. 15–31, 2019. [Google Scholar]

12. X. Hao, N. Yao, L. Wang and J. Wang, “Joint resource allocation algorithm based on multi-objective optimization for wireless sensor networks,” Applied Soft Computing, vol. 94, no. 10, pp. 106470, 2020. [Google Scholar]

13. S. Harizan and P. Kuila, “A novel NSGA-II for coverage and connectivity aware sensor node scheduling in industrial wireless sensor networks,” Digital Signal Processing, vol. 105, pp. 102753, 2020. [Google Scholar]

14. B. Al-Fuhaidi, A. M. Mohsen, A. Ghazi and W. M. Yousef, “An efficient deployment model for maximizing coverage of heterogeneous wireless sensor network based on harmony search algorithm,” Journal of Sensors, vol. 2020, no. 6, pp. 1–18, 2020. [Google Scholar]

15. S. Mini, S. K. Udgata and S. L. Sabat, “M-connected coverage problem in wireless sensor networks,” ISRN Sensor Networks, vol. 2012, pp. 1–9, 2012. [Google Scholar]

16. S. Misra, N. E. Majd and H. Huang, “Constrained relay node placement in energy harvesting wireless sensor networks,” in IEEE Eighth Int. Conf. on Mobile Ad-Hoc and Sensor Systems, Valencia, Spain, pp. 25–34, 2011. [Google Scholar]

17. S. K. Gupta, P. Kuila and P. K. Jana, “Genetic algorithm approach for k-coverage and m-connected node placement in target based wireless sensor networks,” Computers & Electrical Engineering, vol. 56, no. 12, pp. 544–556, 2016. [Google Scholar]

18. C. C. Coello, G. B. Lamont and D. A. van Veldhuizen, Evolutionary Algorithms for Solving Multi-Objective Problems. Berlin, Germany: Springer, 2007. [Online]. Available: https://www.springer.com/gp/book/9780387332543. [Google Scholar]

19. K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. [Google Scholar]

20. G. Subashini and M. C. Bhuvaneswari, “Comparison of multi-objective evolutionary approaches for task scheduling in distributed computing systems,” Sadhana, vol. 37, no. 6, pp. 675–694, 2012. [Google Scholar]

21. B. Barán, Bio-Inspired Computation in Telecommunications, 1st ed., Amsterdam, Netherlands: Elsievier, 2015. [Online]. Available at: https://www.elsevier.com/books/bio-inspired-computation-intelecommunications/yang/978-0-12-801538-4. [Google Scholar]

22. K. Zheng, R.-J. Yang, H. Xu and J. Hu, “A new distribution metric for comparing pareto optimal solutions,” Structural and Multidisciplinary Optimization, vol. 55, no. 1, pp. 53–62, 2016. [Google Scholar]

23. H. P. Gupta, P. K. Tyagi and M. P. Singh, “Regular node deployment for k-coverage in m-connected wireless networks,” IEEE Sensors Journal, vol. 15, no. 12, pp. 7126–7134, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.