DOI:10.32604/cmc.2021.018761

| Computers, Materials & Continua DOI:10.32604/cmc.2021.018761 |  |
| Article |
Optimization of the Active Composition of the Wind Farm Using Genetic Algorithms
1Department of Artificial Intelligence, Lviv Polytechnic National University, Lviv, 79013, Ukraine
2Department of Automared Systems Control, Lviv Polytechnic National University, Lviv, 79013, Ukraine
3Faculty of Management, Comenius University, Bratislava, 81499, Slovakia
*Corresponding Author: Nataliya Shakhovska. Email: nataliya.b.shakhovska@lpnu.ua
Received: 19 March 2021; Accepted: 20 April 2021
Abstract: The article presents the results of research on the possibilities of using genetic algorithms for solving the multicriteria optimization problem of determining the active components of a wind farm. Optimization is carried out on two parameters: efficiency factor of wind farm use (integrated parameter calculated on the basis of 6 parameters of each of the wind farm), average power deviation level (average difference between the load power and energy generation capabilities of the active wind farm). That was done an analysis of publications on the use of genetic algorithms to solve multicriteria optimization problems. Computer simulations were performed, which allowed us to analyze the obtained statistical data and determine the main optimization indicators. That was carried out a comparative analysis of the obtained results with other methods, such as the dynamic programming method; the dynamic programming method with the general increase of the set loading; the modified dynamic programming method, neural networks. It is established that the average power deviation for the genetic algorithm and for the modified dynamic programming method is located at the same level, 33.7 and 28.8 kW, respectively. The average value of the efficiency coefficient of wind turbine used for the genetic algorithm is 2.4% less than for the modified dynamic programming method. However, the time of finding the solution by the genetic algorithm is 3.6 times less than for the modified dynamic programming method. The obtained results provide an opportunity to implement an effective decision support system in energy flow management.
Keywords: Wind farm; genetic algorithm; active composition of the wind farm; optimization
Wind energy has several features that significantly distinguish it from traditional energy. First of all, we are talking about the instability of energy generation. In the conditions of fast change of energy potential of wind or direction, the important task is the maintenance of the set level of power of a generation of the electric power. One way to solve this problem is to use decision support systems (DSS), which would continuously monitor changes in environmental parameters and provide recommendations to the operator in real-time. This requires that the system monitor the efficiency of each wind turbine and find such sets of wind farms (hereinafter active composition), the use of which would best meet the needs of consumers for possible instantaneous power and other technical parameters for each wind turbine.
Therefore, the development of methods and tools that would allow to quickly justify the active composition of wind farms, and analysis of the advantages and disadvantages of using the developed methods for specific conditions, is an actual scientific task. Not only can the results be used in the design of DSS, but also to improve the management of existing wind turbines.
The main purpose of this research is to determine the possibility and feasibility of using genetic algorithms (GA) to solve the problem of finding the active components of a wind farm. The task of determining the active composition of wind farms is a multi-criteria optimization problem, the essence of which is to find such a set of wind turbines to maximize the average efficiency of plants included in the set and minimize the difference between load capacity and energy generation capacity. Determine the optimal parameters for GA, such as population size, crossing operator, mutation operator, and others.
Investigating the advantages and disadvantages of GA compared to other methods, such as the method of dynamic programming, the dynamic programming method with a reasonable increase in the specified load, the modified dynamic programming method, neural networks.
The main contribution consists of the following:
• new genetic algorithm to solve the problem of finding the active components of a wind farm; multi-point and uniform crossover showed a slightly better result than single-point crossover;
• average indication of the difference between the load to be provided and the capacity of the active component of the wind farm for genetic algorithm is 15% higher than for modified dynamic programming method,
• the average power deviation for the genetic algorithm and for the modified dynamic programming method is located at the same level, 33.7 and 28.8 kW, respectively.
This paper consists of several sections. In the Literature review section, the methods of wind farm optimization are given. In the Methods and means section, new genetic algorithm to solve the problem of finding the active components of a wind farm is proposed. The next section presents result of calculation and data interpretation. The last section concludes this paper containing the probable decision of appraisal technique.
There are several approaches to formalizing the task of determining the active composition of wind farms. One of the simplest is to formalize this task as a Knapsack task [1]. Then, in order to find the active composition of wind farms, it is necessary to find such a set of wind turbines so that the total wind power of the set was less than or equal to the power to be generated and the sum of wind efficiency coefficients of the set was maximum. That is:
where, n—sequence number of wind turbines, dn—a binary value that shows the included n-th wind turbine in the set (dn = 1), or not (dn = 0), wn—power of n-th wind turbine, W—power to be generated. The objective function has the form:
where, cn—efficiency coefficient of the n-th wind turbine. The efficiency coefficient of the wind turbine is an integral value calculated on the basis of technical parameters of the wind turbine, such as indicators of technical condition, number of on/offs, amount of energy produced, number of hours worked, etc. An additive function is used to determine the efficiency coefficient of the wind turbine:
where, aj—he weighting factor of the j-th parameter, Kj—normalized value of the j-th parameter. Since the described parameters have different dimensions, each of them is normalized so that the value was within [0; 1]. Methods of normalization are described in more detail in the research [2]. Determination of weights is done by forming a matrix of pairwise comparisons by experts and finding the vector of weights using Saati method [3].
This method of formalizing the task of determining the active composition of wind farms is described in the works [4,5].
One of the ways to somewhat eliminate the first drawback is the dynamic programming method with a reasonable increase in the required power (DP+) [5]. The idea of the method is to statistically determine the average difference between the power to be generated and the power of the active component of the wind farm, and to increase the required power by this value in advance. The method has a number of disadvantages. First of all, it is difficult to determine analytically by what amount it is necessary to increase the power. The magnitude of the power increase depends on many factors, such as required power, instantaneous wind turbine power, the number and type of wind turbine that are part of the wind farm, and others. Some of these parameters are not static and can change over time, which significantly reduces the accuracy of the method.
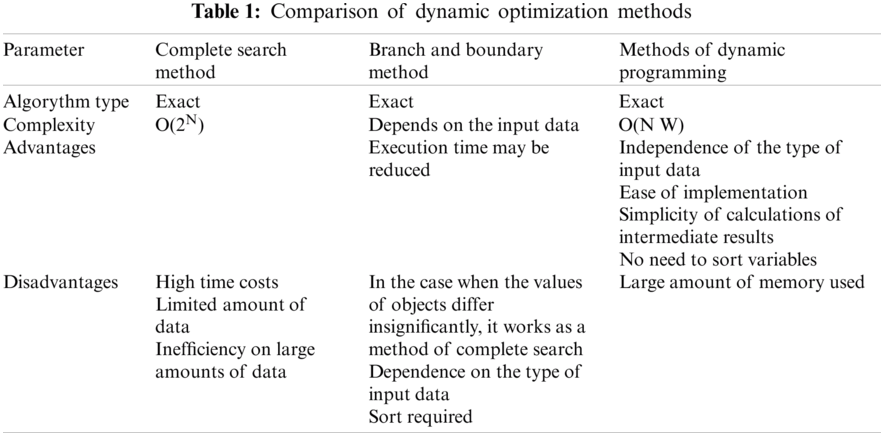
In the works [6–9] the use of methods is investigated: Gaussian-based wake model, the method of complete search, the branches and bound method, the dynamic programming method to solve the problem. It is established that among the studied methods, the use of the method of complete search, the branches and bound method is almost impossible in practice, due to the high computational complexity of these methods. Thus, the computational complexity of the method of complete search is O(2n), and the complexity of the branches and bound method is not more than O(2n), the complexity of the dynamic programming method is O(N · W), where N—number of wind turbines, W—required power. The speed of solving the problem by different methods is given in Fig. 1. The speed of solving the problem by the dynamic programming method for 35 wind turbines does not exceed 0.6 s.
However, the formalization of the task of determining the active composition of the wind farm, as a classic task of packing a backpack, has a number of limitations. According to expression (1) the total capacity of the active component of the wind farm should be less than or equal to the capacity to be generated, which makes it difficult to meet the needs of consumers in all cases. Also, due to the specifics of the target function, the most priority for inclusion in the active composition are wind turbines for which the ratio between efficiency and power is maximum. Which leads to more intensive use of wind turbines of lower capacity (if there are any).

Figure 1: The relationship between the speed of solving problems and the number of wind turbines
The use of a modified dynamic programming method (MDP) [10] eliminates both shortcomings. The main idea of the method is to change the constraints and the objective function so as to minimize deviations and maximize the efficiency of the wind farm, and use dynamic programming method to find the active composition of the wind farm. The objective function is:
where, bn—a binary value that shows the included n-th wind turbine in the set (bn = 1) or not (bn = 0), pn—power of the n-th wind turbine, kn—efficiency coefficient of the n-th wind turbine, P—power to be generated, ∆P—the difference between the load to be provided and the capacity of the active composition of the wind farm,
The analysis of researches of methods of dynamic optimization (Tab. 1) has shown expediency of use of a method of dynamic programming. It provides the best performance with large amounts of data.
Not only the methods described above can be used to solve the problem of finding the active composition of wind farms, but also artificial neural networks (ANNs). Research on this topic was conducted in [11]. ANNs have shown extremely high performance, which allows the use of ANNs in the cases where speed is the determining factor. The speed of solving the problem for ANN is 85 higher than for MDP. However, ANNs are significantly inferior inaccuracy. Thus, the average indication of the difference between the power to be generated and the power of the active component of the wind farm for MDP is 30 times less than for ANN [12].
To solve the problems of combinatorial optimization, this class includes the problem of determining the active composition of wind turbines, you can use genetic algorithms. Research on this topic was conducted in [13–15]. Research have shown that classical GAs are an effective method for solving combinatorial problems (salesman’s problems and others). However, the use of GA is complicated by the fact that there is no analytical way to determine the optimal configuration of GA (selection method, crossing operator, mutation operator, population size, number, etc.). The parameters can vary greatly depending on the characteristics of the task [16]. GA consists of three main elements: the method of selection, the crossing operator, the mutation operator.
The method of selection is a method that selects chromosomes to the next generation. There is an extremely large number of different selection methods, among all the variety can be distinguished, such as:
• Boltzmann selector–using this method, the probability of chromosome selection (P(x)) is determined as [17]:
where, N—the total number of chromosomes, b—the parameter responsible for the intensity of selection, F(x)—the fitness function. Positive values of b increase the probability of selecting a chromosome with high fitness. Negative values of b increase the probability of selecting a chromosome with low fitness. If b is zero, the probability of choosing all phenotypes is the same.
• Linear rank selector–using this selector, the chromosomes are sorted by fitness. Rating N is assigned to the best and rating 1 to the worst. The probability of selection of chromosome i is linearly assigned to individuals according to their rank [18]:
where,
• Exponential rank selector—in contrast to the linear rank selector, the probability of chromosome selection is determined by an exponential function:
where, c—selection factor. A small value of c increases the probability of selecting the best phenotypes. If c is set to zero, the probability of choosing the best phenotype is equal to one. The probability of selection of all other phenotypes is zero.
• Monte-Carlo selector—this selector chooses chromosomes from the population at random. The selector can be used to measure the efficiency of other selectors.
• Roulette wheel selector—the probability of choosing a chromosome, this selector, is directly proportional to the value of the fitness function, that is:
• Stochastic universal selector—this selector minimizes random oscillations because only one random number is used, unlike the K numbers in the roulette wheel. Imagine a roulette on which K points are placed, so that they divide the roulette at the level of the part. In this case, only one point needs to be found (wheel offset relative to the starting point), and the others will be determined automatically [19].
• Tournament selector—the selector selects the s chromosome in the tournament. A chromosome will only win a tournament if its fitness exceeds that of other participants (s - 1). The worst chromosome never survives, and the best chromosome wins in all the tournaments in which it participates. The selection pressure can be changed by changing the size of the tournament.
• Truncation selector—using this selector, the chromosomes are sorted by fitness. The chromosomes at the end of the list are cut off. The percentage of chromosomes that need to be cut off is set by a special parameter.
The crossing operator is an operator that allows you to create two completely new chromosomes (offspring) by combining the genes of a pair of parents. In classical GA, the crossing operator plays an extremely important role, in contrast to the mutation used only occasionally. Among the most common methods of crossing are such methods as:
• Single point crossover—a point inside a chromosome (breakpoint) is randomly determined, at which both chromosomes divide into two parts and exchange them.
• Multi-point crossover—unlike single-point crossover, multi-point crossover allows you to specify the number of breakpoints. If specify one point of intersection, then the multi-point crossover method behaves like a single point crossover.
• Uniform crossover—this crossing operator replaces individual genes between two chromosomes, rather than whole ranges, as in single- and multi-point crossing.
• Partially matched crossover (PMC)—ensures that all genes occur exactly once on each chromosome. No gene will be duplicated by this crossbreeding method. This feature can be useful for solving problems for which the value of the fitness function depends on the ordering of genes in the chromosome (salesman's task and others) [20].
The mutation operator is another method of gene recombination. Unlike crossbreeding, a mutation does not combine existing chromosomes, but randomly alters one or more genes. Even if crossbreeding plays a much larger role in finding the chromosome with the highest value of the fitness function, the mutation can play an important role in providing the diversity required for crossbreeding. Among the mutation operator can be distinguished such as [21]:
• Uniform mutator—the simplest mutator, which according to the law of uniform distribution determines the new value of the gene.
• Swap mutator—a feature of this mutation operator is that it changes the order of genes in the chromosome, not the meaning of the genes themselves. Like PMC, this mutation operator can also be used to solve problems for which the value of the fitness function depends on the ordering of genes in the chromosome.
Papers [22–24] describe modifications of GA, particularly elephant algorithm.
So, the aim of this research is to determine the possibility and feasibility of using genetic algorithms (GA) to solve the problem of finding the active components of a wind farm
To substantiate the configuration of the GA, which would better solve the problem of finding the active composition of the wind farm, 500 experiments were performed for different combinations of the above methods of selection, crossing operators and with different parameters (hereinafter the combination). The chromosome consists of N genes, where N is the total number of wind turbines. Each gene can take two values 1 or 0, which respectively indicates the included wind turbine in the active composition of the wind farm or not. Expression (6) is used as a function of fitness. The size of the population is 100 chromosomes, and the number of generations is limited to 50. These parameters are determined experimentally, so that none of the combination could not find the optimal solution, which allowed to evaluate the effectiveness of the combination.
Efficiency evaluation (Kcom) of the combination of the selection method and the crossing operator is performed on the average value of the fitness function for the chromosome with the highest value of this function in the last generation. That is:
where, M–number of experiments,
where, fHop—the normalized value of the fitness function, f—not the normalized value of the fitness function, fmin—the smallest value of the fitness function among the combinations, fmax—the greatest value of the fitness function among the combinations. The combination of single-point crossover and Monte-Carlo selector showed the worst result among the studied combinations. The value of the fitness function for this combination is 0.8055. The best result was shown by the combination of Uniform crossover and Linear rank selector with the value of the fitness function 0.8613 (Tab. 2).
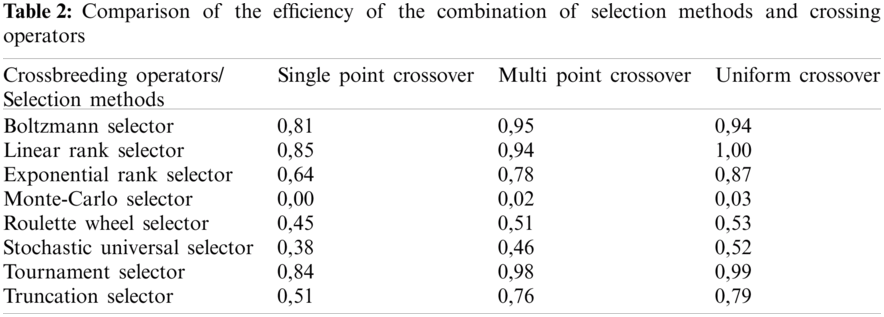
Combinations with PMC are not listed in the Tab. 2, because during the experiments it was found that the peculiarities of the PMC lead to significant time delays for the conditions described above. Time delays make it almost impossible to use this operator in practice and solve the problem of finding the active composition of wind farms.
Analyzing the results, we can say that multi-point and uniform crossover showed a slightly better result than single-point crossover. However, the difference between multi-point, uniform crossover, and single-point crossover is insignificant. The method of selection showed a much greater influence on the value of the fitness function. Thus, the fitness functions during the using linear rank and tournament selector are 6.9% higher than when using the Monte–Carlo selector. Further research was performed for a combination of the linear rank selector with a selection factor

Figure 2: Dependence between the best value of the fitness function in the generation and the number of generations
In the second stage, to improve the obtained results, additional experiments were performed with the mutation operators described above. The experiments were performed under identical conditions. In the Tab. 3 presents data on how the use of the mutation operator allows increasing the value of the fitness function compared to the values obtained without the use of the mutation operator.

Based on the obtained values, it cannot be stated unequivocally that the use of the mutation operator improves or degrades efficiency of solving the problem of finding the active composition of wind farms. Because the obtained results are on the verge of statistical error.
In the third stage, to investigate the advantages and disadvantages of using sound configurations of GA compared to the described methods of solving the problem, 500 experiments were also performed for each of the known methods of finding the active composition of wind farms under identical conditions. GA is stopped if the result has not been improved during the last 50. And, the size of the GA population has been increased to 600 chromosomes. Experimentally, it was found that at a constant value of time, this population size allows achieving a higher value of the fitness function. In Fig. 3 is presented the relationship between population size and the value of the fitness function.
In Fig. 4 is shown the relationship between the best value of the fitness function in a generation and the number of generations for a combination of 1 and 2 for one of the experiments.

Figure 3: Dependence between population size and the value of the fitness function

Figure 4: The relationship between the best value of the fitness function in the generation and the number of generations
For results comparison the recurrent neural network (RNN) with one hidden layer and 3 last layers responsible for discretization is used. The topology of RNN is given in Fig. 5. Training process consists of 10,000 epochs, the role of the teacher was performed by modification of dynamic programming. Input_1 is array of wind turbine capacities, input_2 is array of wind turbine efficiency coefficients, input_3 shows how much energy needs to be generated.

Figure 5: The topology of RNN
Statistical analysis of the results obtained by different methods is given in the Tab. 4.
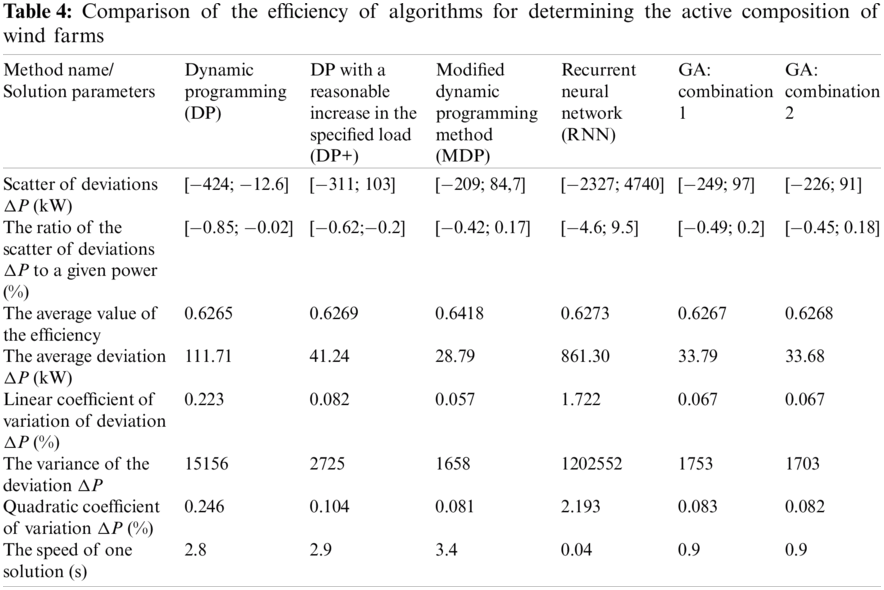
MDP showed the best results of all analised methods. The average value of the efficiency coefficient for MPD is 2.3%–2.4% higher than in other studied methods. The average power deviation for MDP is 15% less than for GA, which is situated in the second place based on this parameter. However, in terms of speed, MDP is inferior to 3 and 85 times GA and RNM, respectively. GA showed a pretty good result. It is worse only than MDP in the average power deviation and worse only than RNN in speed. In turn, DP and DP+ showed not the best results for all parameters. Thus, the average power deviation for DP is 3.9–2.7 times greater than for other methods, except for RNN. RNN showed extremely high speed, but the lowest accuracy, among all the studied methods. Thus, the speed for RNN is 85 times higher than for MDP, and the average power deviation is 30 times higher.
Analyzing the results of the first stage of this research, we can say that among the studied combinations of the selection method and the crossing operator, the best results were shown by two combinations:
• the linear rank selector with a selection factor
• tournament selector with a tournament size of 3–5 and a uniform crossover with identical parameters (hereinafter combination 2).
The values of the fitness function for combinations 1 and 2 are almost at the same level, 0.86139 and 0.86107, respectively. Experiments with mutation operators showed that the values of the fitness function for combination of 1 and 2 of the studied mutation operators and without is within the statistical error.
Comparing the results of the application of GA and other methods, we can conclude that the use of GA to solve the problem of finding the optimal composition of wind farms. GA showed a slightly larger average power deviation than MDP. That is the average indication of the difference between the load to be provided and the capacity of the active component of the wind farm for GA is 15% higher than for MDP. Other parameters are almost on par with MDP. One of the features of GA is the relatively high speed of problem-solving, which is 3.6 times higher than for MDP, but 22 times lower than for RNN. Sufficiently high accuracy and high speed make GA a reasonable alternative to MDP in the case when the speed of doing is an important indicator (in extreme conditions, with significant amounts of wind turbines).
The obtained results can be used in the design and implementation of effective decision support systems for energy flow management in integrated power supply systems in the presence of wind farms.
Acknowledgement: The research was supported by Ministry of Education and Science of Ukraine and National Research Foundation of Ukraine.
Funding Statement: This research was funded by National Research Foundation of Ukraine, Grant Number 2020.01/0025.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. Quan and H. M. Kim, “A tight upper bound for quadratic knapsack problems in grid-based wind farm layout optimization,” Engineering Optimization, vol. 50, no. 3, pp. 367–381, 2018. [Google Scholar]
2. Y. Wu and K. He, “Group normalization,” in 15th European Conf. on Computer Vision, Munich, Germany, pp. 3–19, 2018. [Google Scholar]
3. S. Saati, A. Hatami-Marbini, P. J. Agrell and M. Tavana, “A common set of weight approach using an ideal decision making unit in data envelopment analysis,” Journal of Industrial and Management Optimization, vol. 8, no. 3, pp. 623–637, 2012. [Google Scholar]
4. M. Khanali, S. Ahmadzadegan, M. Omid, F. K. Nasab and K. W. Chau, “Optimizing layout of wind farm turbines using genetic algorithms in Tehran province,” Iran International Journal of Energy and Environmental Engineering, vol. 9, no. 4, pp. 399–411, 2018. [Google Scholar]
5. K. Yang, G. Kwak, K. Cho and J. Huh, “Wind farm layout optimization for wake effect uniformity,” Energy, vol. 183, pp. 983–995, 2019. [Google Scholar]
6. L. Parada, C. Herrera, P. Flores and V. Parada, “Wind farm layout optimization using a Gaussian-based wake model,” Renewable Energy, vol. 107, no. 1, pp. 531–541, 2017. [Google Scholar]
7. S. Jadhav, “Optimal power flow in wind farm microgrid using dynamic programming,” in 2018 Int. Conf. on Emerging Trends and Innovations in Engineering and Technological Research, Ernakulam, India, pp. 357–361, 2018. [Google Scholar]
8. J. Feng and W. Z. Shen, “Optimization of wind farm layout: A refinement method by random search,” in Int. Conf. on Aerodynamics of Offshore Wind Energy Systems and Wakes, Lygnby, Denmark, pp. 624–633, 2013. [Google Scholar]
9. M. Fischetti and D. Pisinger, “Mathematical optimization and algorithms for offshore wind farm design: An overview,” Business & Information Systems Engineering, vol. 61, no. 4, pp. 469–485, 2019. [Google Scholar]
10. Y. Tang, H. Hev and W. J. Liu, “Power system stability control for a wind farm based on adaptive dynamic programming,” IEEE Transactions on Smart Grid, vol. 6, no. 1, pp. 166–177, 2014. [Google Scholar]
11. J. Park and J. Park, “Physics-induced graph neural network: An application to wind-farm power estimation,” Energy, vol. 187, no. 9, pp. 115883, 2019. [Google Scholar]
12. L. Ekonomou, S. Lazarou, G. Chatzarakis and V. Vita, “Estimation of wind turbines optimal number and produced power in a wind farm using an artificial neural network model,” Simulation Modelling Practice and Theory, vol. 21, no. 1, pp. 21–25, 2012. [Google Scholar]
13. J. Edward and A. Ferris, “Genetic algorithms for combinatorial optimization: The assemble line balancing problem INFORMS,” Journal on Computing, vol. 6, no. 2, pp. 161–173, 1994. [Google Scholar]
14. P. Zhang, “Combinatorial optimization problem solution based on improved genetic algorithm,” in AIP Conf. Proc., Chongqing City, China, vol. 1864, pp. 20206, 2017. [Google Scholar]
15. M. Li, S. Fan and An Luo, “A Partheno-genetic algorithm for combinatorial optimization,” in Int. Conf. on Neural Information, Berlin, Heidelberg, Springer, pp. 224–229, 2004. [Google Scholar]
16. R. S. Luciano, T. Ricardo and V. Marley, “Quantum-inspired genetic algorithms applied to ordering combinatorial optimization problems,” in IEEE World Congress on Computational Intelligence, Brisbane, Australia, pp. 10–15, 2012. [Google Scholar]
17. L. Chang-Yong, “Entropy-Boltzmann selection in the genetic algorithms,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 33, no. 1, pp. 138–149, 2003. [Google Scholar]
18. T. Blickle and L. Thiele, “A Comparison of selection schemes used in evolutionary algorithms,” Evolutionary Computation, vol. 4, no. 4, pp. 361–394, 1996. [Google Scholar]
19. T. Pencheva, K. Atanassov and A. Shannon, “Modelling of a stochastic universal sampling selection operator in genetic algorithms using generalized nets,” in Tenth Int. Workshop on Generalized Nets, Sofia, Bulgaria, pp. 1–7, 2009. [Google Scholar]
20. S. Massinanke and C. Z. Zhang, “Application of genetic algorithm on travelling salesman person,” Advanced Materials Research, vol. 1048, pp. 526–530, 2014. [Google Scholar]
21. D. Goldber, Genetic Algorithms in Search, Optimization, and Machine Learning. vol. 102. Boston, USA: Addison-Wesley Publishing Company, pp. 414–420, 1989. [Google Scholar]
22. A. Wagan and M. Shaikh, “A new hybrid metaheuristic algorithm for wind farm micrositing,” Mehran University Research Journal of Engineering and Technology, vol. 36, no. 3, pp. 635–648, 2017. [Google Scholar]
23. H. Hakli, “BinEHO: A new binary variant based on elephant herding optimization algorithm,” Neural Computing and Applications, vol. 32, no. 22, pp. 16971–16991, 2020. [Google Scholar]
24. T. Nguyen, A. Truong and T. Phung, “A novel method based on adaptive cuckoo search for optimal network reconfiguration and distributed generation allocation in distribution network,” International Journal of Electrical Power & Energy Systems, vol. 78, no. 1, pp. 801–815, 2016. [Google Scholar]
25. L. Bauer and S. Matysik, “Enercon E-53-800,00 kW-wind turbine,” 2020. [Online]. Available: https://en.wind-turbine-models.com/turbines/530-enercon-e-53. [Google Scholar]
26. L. Bauer and S. Matysik, “Enercon E-44-900,00 kW-Wind turbine,” 2020. [Online]. Available: https://en.wind-turbine-models.com/turbines/531-enercon-e-44. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |