Computers, Materials & Continua DOI:10.32604/cmc.2021.018159
Article

Monarch Butterfly Optimization for Reliable Scheduling in Cloud

B. Gomathi1, S. T. Suganthi2,*, Karthikeyan Krishnasamy3 and J. Bhuvana4

1Department of Information Technology, Hindusthan College of Engineering and Technology, Coimbatore, 641032, India
2Department of Computer Networking, Lebanese French University, Erbil, 44001, Iraq
3Department of Information Technology, Coimbatore Institute of Technology, Coimbatore, 641014, India
4Department of MCA, School of Computer Science and IT, Jain (Deemed to be) University, Bangalore, 560069, India
*Corresponding Author: S. T. Suganthi. Email: suganthi@lfu.edu.krd
Received: 27 February 2021; Accepted: 03 May 2021

Abstract: Enterprises have extensively taken on cloud computing environment since it provides on-demand virtualized cloud application resources. The scheduling of the cloud tasks is a well-recognized NP-hard problem. The Task scheduling problem is convoluted while convincing different objectives, which are dispute in nature. In this paper, Multi-Objective Improved Monarch Butterfly Optimization (MOIMBO) algorithm is applied to solve multi-objective task scheduling problems in the cloud in preparation for Pareto optimal solutions. Three different dispute objectives, such as makespan, reliability, and resource utilization, are deliberated for task scheduling problems.The Epsilon-fuzzy dominance sort method is utilized in the multi-objective domain to elect the foremost solutions from the Pareto optimal solution set. MOIMBO, together with the Self Adaptive and Greedy Strategies, have been incorporated to enrich the performance of the proposed algorithm. The capability and effectiveness of the proposed algorithm are measured with NSGA-II and MOPSO algorithms. The simulation results prompt that the proposed MOIMBO algorithm extensively diminishes the makespan, maximize the reliability, and guarantees the appropriate resource utilization when associating it with identified existing algorithms.

Keywords: Improved monarch butterfly optimization; cloud computing; makespan; reliability; fuzzy dominance; task scheduling

1  Introduction

Cloud Environment is an internet-based service that provides virtual resources to users based on their demand [1]. An efficient task scheduling technique must utilize an upgraded resource utilization in the cloud data center to dispatch the application tasks to cost-effective virtual resources,. The simultaneous provision of heterogeneous resources to the cloud data center causes a task scheduling problem and makes it an NP-hard problem. Many heuristics algorithms in past research have proposed to resolve this problem to improve the service quality in the cloud environment. Improved Genetic Algorithm [2] is a suggested algorithm for task scheduling in the cloud environment and it is considered to reduce the makespan and upgrade the resource utilization. Priority-based self-adaptive learning Particle Swarm Optimization(PSO) [3] is adopted to schedule the tasks in a cloud environment. This process is done by elastically choosing velocity updating techniques, guaranteeing the QoS at the user level and enhancing the trustworthiness and economic benefit of the cloud provider. To provide an uninterrupted cloud service, cloud data centers host hundreds of thousands of commodity servers. There is a probability of hardware failure that will affect the enactment of the cloud environment. Nowadays, hardware failure needs to be focused on when processing takes place in the cloud data center. In preparation for sinking the impact of cloud system failures, an Optimal MOIMBO task scheduling algorithm is used to put forward the back-and-forth approach to exploit the reliability and reduce the makespan.

Based on previous works [4], the classical optimization methods has been utilized to pool multi-objectives into a particular objective which produced only one solution at a time. The classical method has proved to be successful when run several times, which takes more significant execution time leading to optimal solutions during each execution. To overcome these problems, the Epsilon-fuzzy dominance-based Multi-Objective Improved Monarch Butterfly Optimization (MOIMBO) algorithm is recommended to resolve the multiple objectives task scheduling problem in the cloud environment. The suggested algorithm is utilized to consider different contradictory objectives like makespan, reliability, and consumption of cloud resources and provide faster convergence towards the Pareto front in a short duration while preserving reasonable diversity solutions to produce better efficiency. The Cloudsim toolkit simulates the task scheduling problem in the data center and castoff to compare the prominence connection with the proposed approach along with the well-known task scheduling algorithms like NSGA-II [5], MOPSO [6] in the cloud environment.

The following details are given in the rest of the paper. Section 2 contains the related work of the task scheduling problem. The problem formulation is specified in Section 3. The following section presents a multi-objective optimization approach. Section 5 gives the information about the Epsilon-fuzzy dominance-based Multi-Objective Improved Monarch Butterfly Optimization algorithm. Section 6 mentioned the usage of the simulation environment and the performance evaluation of the proposed approach. Finally, the last section contributes to the conclusion.

2  Related Work

Nowadays, researchers are focused on generating robust schedules to handle multi-objective under-task scheduling problems. When task scheduling problems are solved, scheduling criteria such as makespan, reliability, execution cost, etc., are considered. Authors in [7] put forward to design reliability-based scheduling architecture using reliability ware scheduling algorithm. Dependency between precedence constrained tasks was designed using a directed acyclic graph and duplicated to achieve high quality of reliability on a heterogeneous distributed system. However, scheduling length is not considered. Reference [8] handled precedence constrained tasks in a heterogeneous computing system while considered reliability and energy constraint simultaneously. That algorithm is comprised of three phases such as building a topological order among application tasks, picking out energy-efficient frequency to complete each task, and mapping tasks with a suitable processor to maximize system reliability with minimum energy consumption. Reference [9] anticipated a fault tolerance flexible scheduling technique in the data center. The backup model was utilized for fault tolerance purposes and an adaptable resource allocation technique to improve the resource application. However, the fault tolerance mechanism fails to take scheduling length into account.

In [10], the author proposed different scaling techniques to enhance the reliability of heterogeneous distributed embedded systems along with energy and response time criteria in the Automatic Cyber-Physical Systems. Simultaneously, the pessimistic energy pre-allocation method was used to decrease the reply time of function during energy constraint time. A Failure-aware VM consolidation mechanism [11] was proposed for VM considering failure and physical machines’ hazard rates. It helped to avoid more failures and recreation of VMs by allocating VMs on reliable physical machines, thus improving energy efficiency. The failure prediction technique helped to trigger the fault tolerance mechanism with less computation time. However, it failed to consider the presence of correlation failures.

In [12], they were presented to solve reliability redundancy allocation. This multi-objective algorithm was aimed to maximize system reliability while minimizing the system cost simultaneously. The Continuous-time Markov Chain Model has been applied to compute the precise value of reliability in a standby system. Refrence [13] presented fault-tolerant scheduling algorithms that also considered energy efficiency for real-time applications in a 5G cloud-based network. The proactive strategy was adopted to upturn the processing capability. The Rearrange technique improved Resource usage. While reducing energy consumption, the primary backup model was used to handle fault tolerance in the cloud environment. Reference [14] proposed optimal communication path search algorithm and reliability-driven lookahead scheduling maximizes performance and reliability by considering communication and processor failure in heterogeneous distributed systems. Iterative duplication strategy utilized for reliability improvement.

The non-DVFS and DVFS [15] methods have been proposed to improve reliability and energy efficiency under embedded systems with heterogeneous nature. When assigning tasks for execution, tasks’ reliability goal determined choosing a processor with opted energy efficiency. Here, the applications’ reliability goal was transformed into each task later assigned to the processor that gratifies energy efficiency and reliability [16]. put forward a reliability-conscious resource allocation technique in fog based cloud environment. Fog integrated resource allocation mechanism mapped industry applications with VMs by considering replication of VM and reliability threshold. To generate an optimal solution, an exhaustive search algorithm was proposed for the VM placement problem.

In literature, there are references of numerous reliable scheduling algorithms that improve the reliability, it may produce high scheduling length, and many practical scheduling algorithms that minimize makespan and may also minimize the reliability. It can be concluded that the scheduling algorithm must give importance to both the makespan and the reliability of the system to diminish the execution time at the charge of high reliability. Simultaneously, the above aforementioned multi-objective algorithms were utilized to generate the Pareto optimal solutions in the multiple objectives problem; Solutions in the Pareto set were considered equal and unable to measure how another solution dominates one solution. Hence, the proposed Epsilon-fuzzy dominance-based Improved Monarch Butterfly Optimization is utilized to estimate the comparative fitness of non-dominated individuals in the Pareto optimal set. This method helps to minimize both makespan and failure probability system as well as to provide the better and quicker convergence than other algorithms like NSGA-II and MOPSO especially when the number of objectives is more significant.

3  Problem Formulation

To confirm the parallel and distributed cloud environment, the dynamic batching mode is chosen. The required tasks are collected in a set that is analyzed for mapping instead of mapping tasks into resources as they arrive. According to the collected information, such as the actual status of resources and task details, a more reasonable scheduling strategy can be designed in the cloud environment. In this paper, a Multi-objective Improved MBO scheduling algorithm using an epsilon-fuzzy mechanism is suggested to discover the optimal schedule by minimizing the finishing time of allocated tasks, maximizing system reliability will stabilize the load all over the resources.

To formulate a multi-objective task scheduling problem, the set of n mutually independent tasks are represented as Ti, where i ={0, 1…,n −1} and set of m heterogeneous resources are represented as Rj, where j ={0, 1,…,m −1}. Suppose the execution time Pi, j for task j on resource i is known. Furthermore, tasks are considered non-preemptive. The task scheduling helps assign tasks to resources for their execution. In task scheduling, the following constraints assure that processing resources can execute only one task at a time (constraint 2). An individual task is assigned to accurately processing one resource at a time (condition 1). The permutation matrix entry Xi, j (as shown in Tab. 1) is defined as,

Xi,j={1,if  task  j  is  assigned  to  resource  i0,otherwise}(1)

∑i=1mXi,j=1,     1≤j≤n(2)

Let nj be the number of tasks assigned for resource Rj such that∑j∈{1..m}nj=n The completion time of the assigned tasks on resource Rj is,

Cj=∑i∈{1…nj}Pi,j*Xi,j(3)

The makespan [17] of the task schedule is the last task’s finishing point in the schedule.

Minimize MS=max1≤j≤mCj(4)

Hardware failure cannot be ignored when processing occurs in the cloud environment where large quantity of resources are interconnected. The reliability of the schedule depends on the success of the execution of the schedule on the resources. The resources are assumed to be fail-silent [18]. There is an assumption that failure only affect the current tasks running on the failure resource, but not the following tasks. Consider that failures are independent events. The failure model follows Poisson’s law where the failure rate of resource Ri is represented by constant parameters λi. The probability that all the tasks are completed on resource Ri is expressed by exponential law as follows,

  psucci=e-λiCi(5)

Assume that the failures are independent, so the reliability of assigned tasks on the set of resources can be defined as,

Maximize  Rs=e-λi  ∑iCi(6)

The failure probability of schedule is defined as

  Minimize  Fp=λi  ∑iCi(7)

Reducing the failure probability of schedule is equivalent to maximizing the reliability of schedule in the cloud environment. Hence, the MOIMBO task scheduling algorithm is used to minimize the makespan and failure probability of the schedule to maximize the reliability of the whole schedule. Due to the heterogeneous nature of resources in the cloud, processing capability varies from resource to resource. When allocating processing resources to task set, most of the tasks are assigned for the better processing capability resources which will get more workload than other idle resources. A third objective, such as Load Balancing Index (β), is also considered in our problem to balance the load across different processing resources. β is computed to gauge the deviations of load on processing resources as follows [19].

β=∑i=1mLi-L̄m(8)

where Li is the load of the resource, i and L is the average load of all resources. The lesser β shows the enhanced load balance in the cloud environment. To augment task scheduling performance in the cloud, the load will be balanced across resources and maximize their utilization and reliability while minimizing makespan in the cloud environment.

4  Method to Handle Multiple Objectives Optimization Problem

The concurrent optimization of different objectives in the optimization problem is called a multi-objective optimization problem (MOP) [20,21]. The multi-objective optimization problem is well-defined as follows:

MinimizeS(x)=(S1(x),S2(x),…,ST(x))(9)

Let T be the number of objectives in the problem, Si(x) is the ith objective function, and X is the solution. Many traditional methods like the weighted method, distance method, and min-max formulation method are available to optimize multiple objectives. However, these methods combine multiple objectives into a single objective that may provide the single incorrect solution and need prior information about the optimum before optimization. In this situation, the rank-based non-dominance sorting algorithm was used to generate a Pareto dominance solution for multi-objective optimization.

Let us take the Pareto dominance relation, which shows that a minor reduction in few objectives is typically allowed if an outstanding upgrading in other objectives is capable of being attained. Let us take two solution vectors x1 and x2, then x1 is defined as dominate x2 (also written as x1≺x2) if and only if the below two constraints carry:

A solution is called a Non-dominated or Pareto-optimal solution if there is no feasible solution that improves one objective without reducing another objective. The collection of Pareto-optimal solutions is called the Pareto set, and the boundary of mapping the Pareto solutions in solution space is called Pareto-Front. Since all the non-dominated solutions in the Pareto set must be considered as an equal rank-based method is not able to measure how one solution extends to dominate another solution. It is provided by the new dominance relation called the Fuzzy dominance [22] method. Let us assume to reduce T quantity of objectives functions Si(x), i = 1…, T in the multi-objective optimization problem. The solution set is represented as Ψ⊂Rn, where n is the dimensionality.

4.1 Solution and its Fuzzy Dominance

Solution u∈Ψ is defined as fuzzy dominate solution v∈Ψ iff ∀i∈{1, 2,…, T}, u≻iS v holds. This association can be designated as u≻Sv. The degree of fuzzy dominance can be represented by entreating the concept of fuzzy intersection and expending t-norm and is calculated as

μdom (u≻Sv)=∩i=1Tμidom(u≻iSv)(10)

In the prior fuzzy dominance work [22], the membership functions μdom(.), which were utilized to assess the fuzzy dominance, were said to be zero for negative arguments. Hence, if Si(u)¿Si(v), the degree of fuzzy dominance u≻iSv was zero mandatorily. Hence, non-dominated solutions shall not be allotted zero values mandatorily with the help of ε. The membership functions utilized are trapezoidal, yielding non-zero values at whatever time their arguments are equivalent to threshold ε. Mathematically, the membership function μidom(u≻iSv  ) is said to be:

μidom(ΔSi)={0,ΔSi≤-εΔSiΔi,ε-<ΔSi<Δi-ε1ΔSi≥Δi-ε}(11)

where Si=Si(v)-Si(u) If many solutions have a similar ε-fuzzy dominance value, at that time, the diversity fitness function, which is equivalent to the perimeter of the most significant M dimensional hypercube in the objective space, can be used. The value of perimeter I (y) for any solution y is given by:

I(y)=∑i=1T(Si(x)-Si(z))/(max(Si)-min(Si))  (12)

where x and z are the next to the solutions to y while merging the population in rising order giving to the ith objective, Si. Boundary solutions are assigned ∞ values when relating multiple solutions with the same ε -fuzzy dominance values, the priority is specified to solutions with more significant I(y).

4.2 Fuzzy Dominance in a Population

Given a population of solutions P⊂Ψ, a solution v∈P is said to be fuzzy dominated in P if it is fuzzy dominated by any other solution u∈P. In this case, the degree of fuzzy dominance can be computed by performing a union operation over every possible μdom (u≻Sv), carried out using t-co norms as,

μdom(P≻Sv=)=∪u∈Pμdom(u≻Sv)(13)

Similarly, an individual solution is allocated a particular measure to represent the quantity it takes over the others in a population. Improved solutions within the set are allocated lower fuzzy dominance values. The global best solution can be selected by this sorting method after the completion of each iteration.

5  Multi-Objective IMBO Algorithm

Monarch Butterfly Optimization (MBO) suggested by [23] to influence the behavior of Monarch Butterflies. Since MBO requires fewer computational parameters and more appropriate for parallel processing, researchers attempt to extend the MBO to resolve multi-objective optimization problems and showed that the MBO algorithm’s performance is competitive to other swarm intelligence algorithms. The proposed Multi-Objective Improved Monarch Butterfly Optimization (MOIMBO) algorithm is utilized to resolve the multi-objective task scheduling problem in the data center. The main features of the proposed MOIMBO are as follows: (a) Improved MBO is proposed to solve task scheduling problem in the cloud (b) To balance exploitation and exploration ability, a self-adaptive technique is applied by changing the population sizes dynamically, this gives on to magnify the exploitation outcome of the MBO algorithm (c) Greedy strategy is applied to allow new butterfly individuals with better fitness value into the next generation. It guides to revamp the proposed algorithm’s convergence speed (d) Non-dominated solutions are maintained with the Pareto archive set’s help. The proposed Multi-Objective Improved Monarch Butterfly Optimization (MOIMBO) algorithm is described in the upcoming section.

5.1 Monarch Butterfly Optimization (MBO)

Monarch Butterfly Optimization (MBO) is a swarm-based intelligent optimization method that mimics monarch butterflies’ relocation activities based on seasonal conditions in nature. However, the entire swarms of butterflies are partitioned into swarm_1 and swarm_2, respectively. The butterfly migration operator as well as adjusting operator are the critical processes used in the search process.

5.1.1 Butterfly Migration Operator (BMO)

BMO creates information exchange between individuals of swarm_1 and swarm_2. Suppose the number of individuals staying in swarm_1 and swarm_2 is called Nsa and Nsb, calculated as ceil(r*Ns) and (Ns-Nsa). Whereas r and Ns represent the ratio of individuals in swarm_1 and whole individuals in both swarms. The variable v is calculated for the migration operator as follows:

v=rand*mp(14)

Let rand is the random value produced using the Uniform distribution function, and mp is the migration period. However, if v≤r, then the novel place of the nth individual is modified by utilizing the migration operator in the following way:

Pn,k(t+1)=Pv1,k(t)(15)

Pn,k(t+1) represents the kth element of Pm that denotes the nth butterfly position in Iteration t+1. Similarly, Pv1,k(t), is the kth element of Pv1 for current iteration t. Besides, v1 is an individual in swarm_1 that is selected randomly. When v ¿ r, then the kth element of a new position for nth butterfly is computed by using,

Pn,k(t+1)=Pv2,k(t)(16)

where Pv2,k(t) is the kth portion of Pv2 for current iteration t. Besides, v2 is an individual in swarm_2 that is selected randomly.

5.1.2 Self-Adaptive Strategy

In the basic MBO algorithm, the number of individuals in swarm_1 and swarm_2 are fixed during the whole optimization process to expand basic MBO; self-adaptive strategy [24] is used to resolve the high dimensional optimization problem. The following dynamic technique is used to update variable by using the self-adaptive strategy as shown below:

r=c + dt(17)

Let t is the present iteration, c and d are constants which are generated by using,

c=rmintm-rmaxtm-1(18)

d=rmax-rmintm-1(19)

Here, tm is the maximum iteration. In the same way, rmin and rmax are the minimum and maximum bound values of variable r. The value of  rmin and rmax lies in the range [0, 1]. Using Eq. (17), the value of r is updated in a linear fashion from rmin and rmax.

5.1.3 Greedy Strategy

Every afresh produced butterflies are allowed as fresh butterflies for upcoming iteration in the basic MBO algorithm. If the recently produced butterflies give the worst performance, it leads to reduce convergence speed. By using a Greedy strategy [24], new butterflies with superior fitness value can enter into the upcoming iteration. The new individual will be decided by using the below greedy strategy in minimal problem,

Pi,new(t+1)={Pit+1,f(Pit+1)<f(Pit)Pit,else}(20)

where  f(Pit+1) and f(Pit)are the fitness value of individuals Pit+1 and Pit respectively. Pi,new(t+1) is the new individual that will be moved to the next iteration.

5.1.4 Butterfly Adjustment Operator (BAO)

Furthermore, the location of butterflies can also be modified by using the below Butterfly Adjustment Operator. Like BMO, when arbitrarily created variable rand ≤ r, then the location of mth butterfly can be modified as follows:

Pm,k(t+1)=Pbest,k(t)(21)

where, Pm,k(t+1) represents the position of a kth element of mth individual at iteration t+1. Moreover,  Pbest,    k(t) indicates the position of the kth component of best individual among swarm_1 and swarm_2 in current iteration t. In contrast, if rand is greater than r, then the position can be modified for mth individual as follows:

Pm,k(t+1)=Pv3,k(t)(22)

whereas Pv3 represents the position of a kth element of v3 individual, this is randomly chosen from swarm_2. With this condition, individual adjustment rate α is compared with the rand variable. If rand¿α, then the below equation is used to alter the position of mth individual as follows:

Pm,k(t+1)=Pm,k(t+1)+β*(dpk- 0.5)(23)

Here, β is the weighting factor given at current iteration t as follows:

β=swmax/t2(24)

where swmax is the highest step walk done by an individual in one step, and dpk is the step walk of mth individual that can be computed by using Levy fight

dp=Levy(Pmt)(25)

According to Eq. (24), the high value of β makes lengthy step length that causes enhancement in the proposed algorithm’s exploration ability. In contrast, the small value of β reduces step size to expand the proposed algorithm’s exploitation capability.

Hence, an Improved MBO algorithm with Self-Adaptive and Greedy techniques are suggested to resolve the scheduling problem in the data center. The Self-Adaptive technique is utilized to enhance the searching ability to prevent sticking to the local optimum. A greedy technique is proposed to magnify the convergence speed of the MOIMBO algorithm.

5.2 Multi-Objective Improved Monarch Butterfly Optimization (MOIMBO) Algorithm for Task Scheduling

To resolve the task scheduling problem in the data center, the Basic MBO algorithm is modified as Improved Monarch Butterfly Optimization incorporates Pareto dominance relation to resolve the problems with multiple objectives as shown below.

Initialize number of tasks as n, number of VMs as m, iteration counter as c, and maximum iteration as CG

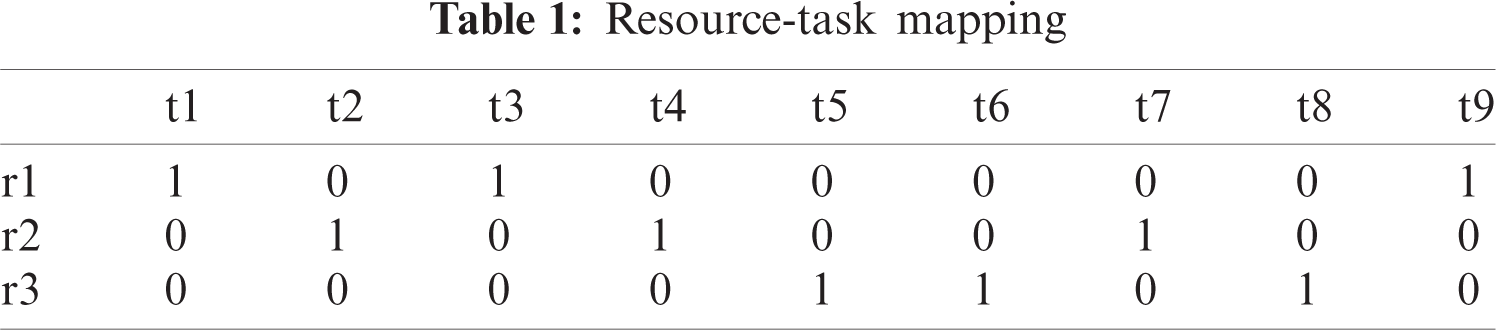
Set the two swarm sizes as Nsa and Nsb. Each individual in both the swarms are initialized randomly, as shown in Tab. 1

Assess the individuals against fitness function. Order the individuals in the whole swarm derived from the ef-dominance method and perimeter technique. Keep the values in the external archive set.

While c < CG do

a) Order the individuals in the whole swarm based on their fitness value

b) Split the whole swarm into swarm_1 and swarm_2

c) For i = 1 to Nsa, do

d) The Self-Adaptive Technique determines the ratio of individuals r

e) Produce fresh individuals in swarm_1 by using Butterfly Migration Operator

Based on the Greedy Technique, fresh individuals with better fitness value will be included in swarm_1 End For

For i = 1 to Nsb, do Produce fresh individuals in swarm_2 by using Butterfly Adjustment Operator End For

Merge fresh individuals decided for swarm_1 and swarm_2 as the whole swarm

Assess the individuals against fitness function. Order the individuals in the whole swarm derived from the ef-dominance method and perimeter technique. Keep the values in the external archive set.

Increase the iteration counter c by one

Return Solutions in the External Archive set as Output

Apart from the essential components of MBO, the proposed algorithm contains the following additional components:

5.2.1 Representation of Solution by MOIMBO

To enhance the task scheduling problem using MOIMBO in the cloud environment, the population requires to map a different solution. Each individual represents Task-Resource mapping, which maps each task into a relevant resource in the cloud. Task-Resource mapping produces m*n matrix, where m is the number of available resources and n is the number of tasks shown in Tab. 1.

5.2.2 Enhancement of Elite Archive

Elite archive method [20] in multi-objective optimization problem is utilized to maintain best non-dominated solutions in elite archive set. Initially, SN numbers of solutions are stored in the archive set. In each iteration, solutions from the present iteration and the solutions from the archive set of prior iterations are combined, and 2*SN solutions are arranged using Epsilon-fuzzy values. If numerous solutions hold similar Epsilon-fuzzy dominance values, then the perimeter I (.) value is calculated using (12), and the solution with the most significant perimeter value is preferred. Hence, the leading SN solutions modify the archive set from 2*SN solutions based on Epsilon-fuzzy dominance and perimeter.

6  Experimental Evaluation

Cloudsim toolkit [25] simulates the task scheduling problem and evaluates the proposed approach in the data center. Cloudsim is a java based toolkit that permits modeling and simulation of resources and task scheduling in the cloud data center. The cloudsim toolkit models the components such as data centers, resource provisioning policies, and virtual machines (VMs).

The simulation design for the proposed algorithm consists of two data centers with three hosts. The first host has a 2-core processor, and the next two hosts consist of 4-core processors. Let us consider each host consists of 16 GB RAM and an 800 GB hard disk capacity. Each host consists of 5 VMs. The speed of the VMs can be measured by Million Instructions Per Second (MIPS). Two data sets, such as HPC2N data set [26] and Braun’s data set [27], are considered to evaluate the proposed algorithm in the cloud environment. HPC2N data set is the popular parallel workload of the high-performance computing center. This data set consists of related details about 527,371 tasks. In another way, Braun’s data set represents the uniform distribution of data, consistency types (consistent, inconsistent, or semi-consistent) of data, and heterogeneity nature of resources and tasks. With this data collection, simulation is conducted in cloudsim to test the proposed algorithm.

This division demonstrates the accomplishment of the suggested MOIMBO algorithm for multi-objective task scheduling problems by comparing with highly competitive techniques: GA-based non-dominated sort genetic algorithm (NSGA-II), Weight-based Multi-objective Particle Swarm Optimization (MOPSO) algorithm. Parameters used in the MOIMBO, NSGA-II, and MOPSO are given below, which helps fine-tune the algorithms to produce the best performance. The parameters are assigned for MOIMBO: swmax = 1.0, mp = 1.2, v = 5/12, α=5/12, CG = 200, Nsa= 21, Nsb= 29; NSGA-II: Population size = 25, mutation rate= 0.4, Crossover rate = 0.9;MOPSO: Population size = 25, c1 = 0.5 and c2 = 0.5, ω= 0.1 to 0.9; failure rate of resource (λ_(j ))=0.0001 to 0.0005.The proposed algorithm’s efficiency is evaluated with test suits drawn from the data mentioned in the above sets.

6.1 Performance Metrics

The proposed multi-objective task scheduling algorithm is evaluated by the following metrics [28] (1) Generation Distance(GD) is the metric that measures th3e distance between true Pareto Optimal Solutions (acquired by combining the non-dominated solutions over ten runs) and Pareto front produced at termination stage of the algorithm. (2) A spacing metric(SM) is used to measure the spacing between solutions in the Pareto front. Generation Distance and Spacing metrics can be represented as follows:

For Generation Distance,

di=minj=1|Q|∑i=1F(Si(k)-Si(j))2(26)

GD=∑i=1|Q|di|Q|(27)

where F is the amount of objective functions, Si is the fitness value for objective i, and di is the Euclidean distance between true Pareto front solutions Q and nearer Pareto front solutions. The average of di is used to calculate GD.

For Spacing metrics,

di=minj=1|Q|[∑i=1F|Si(k)-Si(j)|](28)

SM=∑i=1F(d̄-di)2F-1(29)

di is the interval between the solution and its adjacent solution in the Pareto front solutions. It is distinct from Euclidean distance. d is the average value of the di. The lowest rate of GD and SM are advisable for heuristics algorithms.

6.2 Best Compromise Solution

To choose the most acceptable compromised solution among the non-dominated solutions in the Pareto optimal set, the following simple linear membership function [28] acts as decision-maker,

μi={1,Fi≤FiminFimax-FiFimax-Fimin,Fimin≤Fi≤Fimax0,Fi≥Fimax}(30)

LetFimax and Fimin are the extreme and most negligible value of the ith objective function in the Pareto set. The normalized membership function μk for the kth non-dominated solution is defined as

μk=∑i=1Fμik∑k=1Q∑i=1Fμik(31)

where Q is the quantity of non-dominated solutions in the Pareto Group and F is the number of objective functions in the multi-objective optimization problem. The best-compromised solution is the solution which is having the highest membership function value.

6.3 Evaluation of Proposed Approach

6.3.1 Test Suit 1

First test suits have been taken from the above mentioned High-performance computing center workload to evaluate the proposed approach, The proposed multi-objective approach, makespan, reliability, and load balancing index are examined to analyze the MOIMBO algorithm’s characteristics. The simulation results are presented and analyzed by using tables and graphs, as shown below. Initially, individual objectives are examined, and then multiple objectives are considered. Fig. 1 shows the makespan of three algorithms based on ten virtual machines with different task sets. The proposed MOIMBO algorithm provides better results when compared to the other two methods NSGA-II and MOPSO. For small datasets, the makespan of the MOIMBO algorithm is relatively closer to the other two algorithms. However, as the quantity of tasks improves, the suggested approach has a higher chance to reduce the makespan by 9–11% compared to NSGA-II and 17–18% compared to MOPSO because the MOIMBO algorithm can avoid the premature convergence by using the composite mutation techniques.

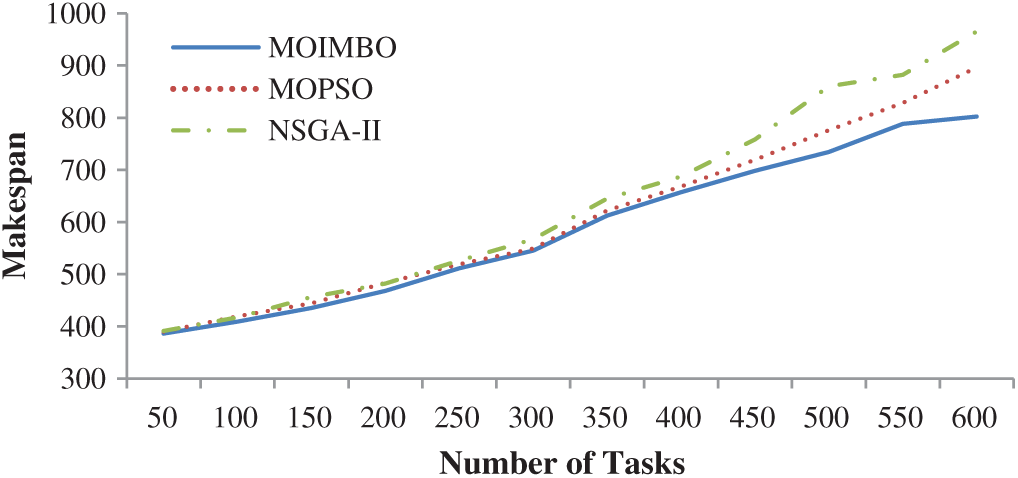
Figure 1: Measure of makespan using ten resources

Fig. 2 shows the Failure probability rates of the different resources with the same workload. It expresses that the failure probability rate reduces as the quantity of resources improves. It explicitly illustrates that scheduling algorithms have more options for assigning tasks to resources when the number of resources is increased. Apart from that, MOIMBO with a fast local search algorithm provides better results when compared to the other two algorithms. However, if the number of resources and tasks are high simultaneously, it increases failure probability due to longer scheduling length.

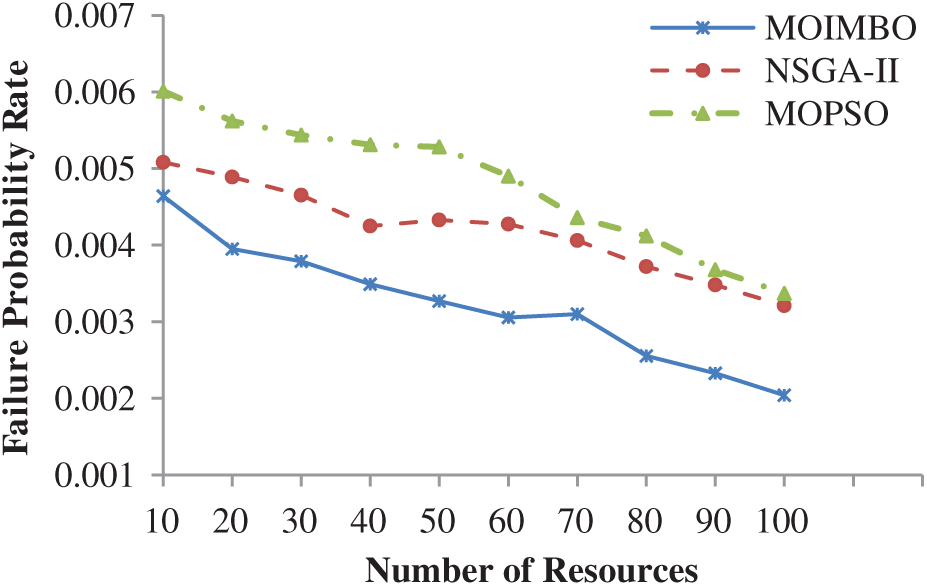
Figure 2: Measure of failure probability for different resources

According to Fig. 3, when the number of tasks increases, the failure probability of tasks also increases because computational resources take a long time to complete a large number of tasks [29]. It gives more chance to increase the failure probability of resources which causes the increment in failure probability of tasks. The failure probability rate and makespan are considered together in the multi-objective task scheduling problem, as shown below. The Pareto optimal solutions are analyzed and generated by MOIMBO, NSGA-II, and MOPSO, as well as the best compromise solution (using (30) and (31)) among Pareto solutions, are obtained with the help of fuzzy approach as shown in Fig. 4.

Even though NSGA-II and MOPSO were used to generate non-dominated solutions at each iteration, the level of non-domination between solutions was not measured, so the solutions are not closer to the Pareto front when compared to the MOIMBO algorithm. Since the usage of perimeter operator and Epsilon-fuzzy dominance in the proposed approach, it selects the solutions near to Pareto front and shows that the deviation of the Pareto optimal solutions of the MOIMBO is more suitable than other two algorithms. The finest compromise solution among 25 Pareto front solutions for different task sets was shown in Tab. 2.

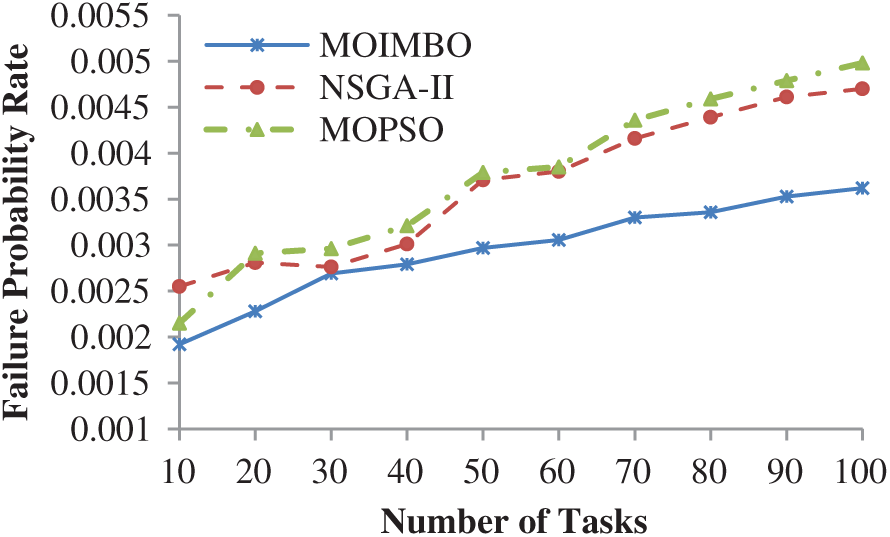
Figure 3: Measure of failure probability for different tasks

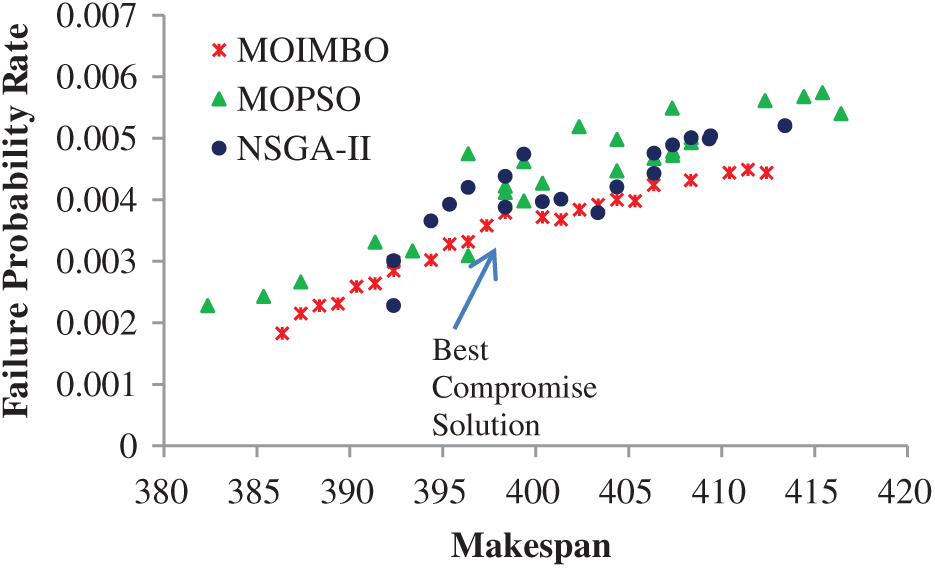
Figure 4: Pareto front and performance of algorithms for ten resources and 20 tasks

These different sets of tasks were run using ten resources. When the number of tasks increased, then the execution time, failure probability, and load metrics values began to increase. The results generated by (taking the average of 20 runs) the three algorithms based on GD and Spacing metrics were compared in Tab. 3. Since the Epsilon-fuzzy dominance sort technique in the proposed approach is selected as the better solution for the next iteration, the Pareto solution set was very nearer to the Pareto front, which causes the smaller value of GD for the proposed algorithm. The lower value of the spacing metric of the proposed approach represented that there is a uniform spacing between solutions in the Pareto optimal set.

Fig. 5 demonstrates that makespan is reduced when the amount of iterations is increased. Since epsilon-fuzzy dominance sorting selects the Pareto front solutions, the quality algorithm improves at each iteration is shown. However, NSGA-II and MOPSO were getting stuck into the local optimum. However, composite mutation strategies and fast local search algorithm in MOIMBO provide a better and quicker convergence as well as reduce the makespan as compared to the other two algorithms.

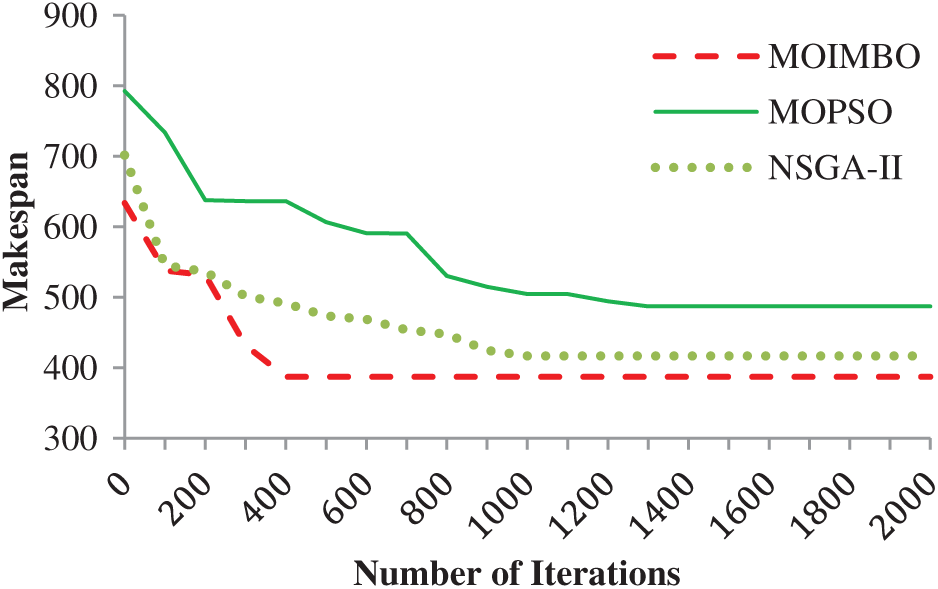
Figure 5: Convergence analysis for makespan

6.3.2 Test Suit 2

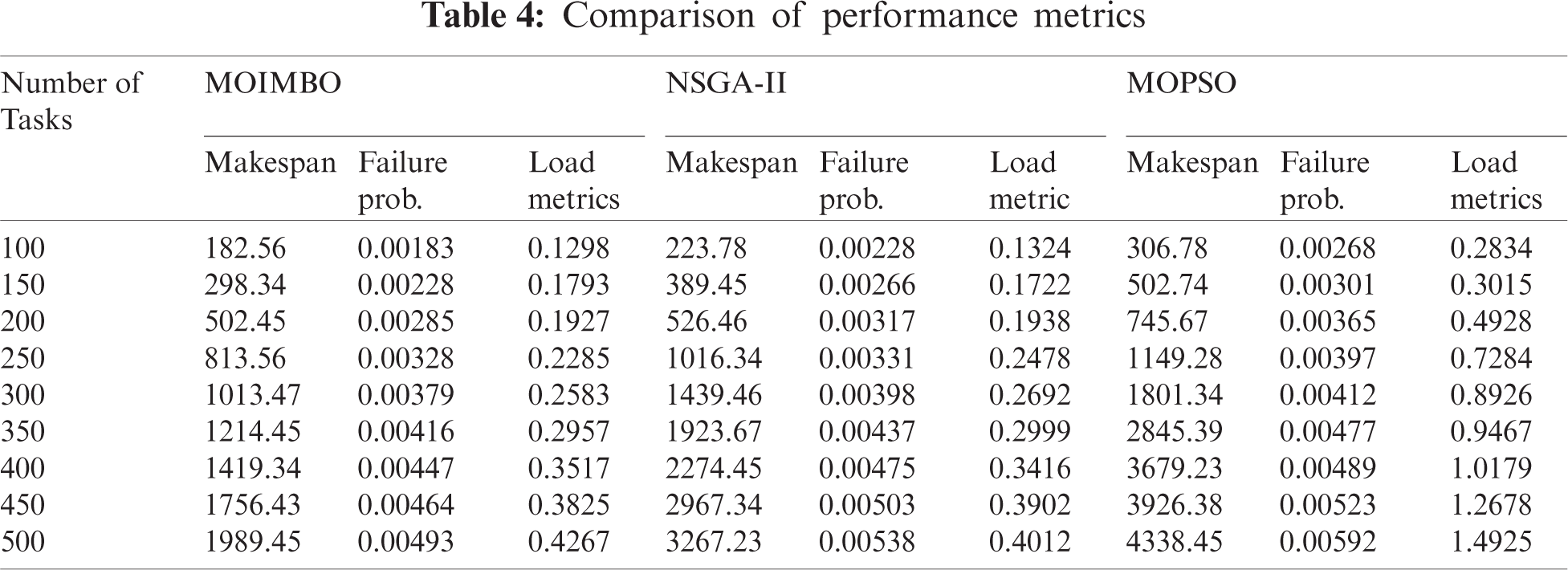
For the evaluation of the proposed approach, Braun’s data set has been taken as a second test suit. The data set considered for the second test suit consists of 16 cloud resources with 512 tasks. Twelve different instances are available in this data set. To explicitly compare the proposed MOIMBO algorithm with NSGA-II and MOPSO algorithms, the different tables are used to show the above-stated algorithms’ accomplishment. Tab. 4 depicts the performance of MOIMBO, NSGA-II, and MOPSO algorithms with the help of the following metrics such as makespan, failure probability rate, and load metrics. The best compromise solution produced by the proposed algorithm using Test suit2 was shown in Tab. 5.

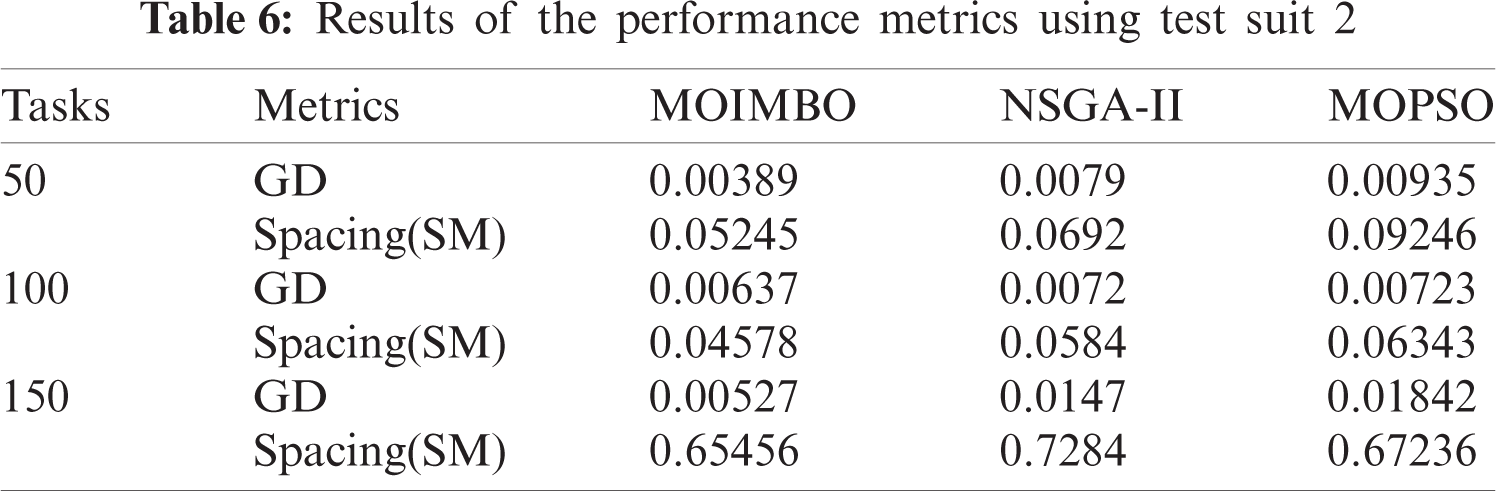
Tab. 6 demonstrates the assessment results of the three algorithms concerning GD and spacing. It shows that the proposed MOIMBO algorithm provides uniform spacing when compared to the other two algorithms. The above experiment results show that MOIMBO is a better approach for multi-objective task scheduling problem in the data center.

7  Conclusions

The multi-objective task scheduling problem in the data center is solved with the Epsilon-fuzzy dominance sort-based CABC algorithm. The proposed approach emphasizes on three contradictory objectives like Makespan, Reliability, and Average load balancing index while solving the task scheduling problem. The Self-adaptive and Greedy methods in the MOIMBO algorithm provide an excellent weighing scale between global exploration and local exploitation capabilities, enhancing convergence speed and quality of the solution. The simulation results show that the MOIMBO approach produces better results than NSGA-II and MOPSO in terms of convergence towards the Pareto front set. Uniform space between solutions in the Pareto set reduces the computation overhead with the Epsilon-fuzzy dominance sorting method and perimeter operator. The best-compromised solution among the Pareto optimal solutions is generated using the linear membership function. The load among heterogeneous cloud computing systems is balanced better than NSGA-II and MOPSO. In future research, the Hybrid heuristics approach will be used to schedule tasks which will consider task priorities and extend the problem to minimize energy consumption.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. D. Dikaiakos, D. Katsaros, P. Mehra, G. Pallis and A. Vakali, “Cloud computing: Distributed internet computing for IT and scientific research,” IEEE Internet Computing, vol. 13, no. 5, pp. 10–11, 2009. [Google Scholar]

 2.  P. Kumar and A. Verma, “Scheduling using improved genetic algorithm in cloud computing for independent tasks,” in Proc. ICACCI Series, Chennai, India, pp. 137–142, 2012. [Google Scholar]

 3.  X. Zuo, G. Zhang and W. Tan, “Self-adaptive learning PSO-based deadline constrained task scheduling for hybrid IAAS cloud,” IEEE Transactions on Automation Science and Engineering, vol. 11, no. 2, pp. 564–573, 2014. [Google Scholar]

 4.  A. Dogan and F. Özgüner, “Matching and scheduling algorithms for minimizing execution time and failure probability of applications in heterogeneous computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 13, no. 3, pp. 308–323, 2002. [Google Scholar]

 5.  A. S. Sofia and P. G. Kumar, “Multi-objective task scheduling to minimize energy consumption and makespan of cloud computing using NSGA-II,” Journal of Network and Systems Management, vol. 26, no. 2, pp. 463–485, 2018. [Google Scholar]

 6.  E. S. Alkayal, N. R. Jennings and M. F. Abulkhair, “Efficient task scheduling multi-objective particle swarm optimization in cloud computing,” in Proc. LCN, Dubai, pp. 17–24, 2016. [Google Scholar]

 7.  X. Tang, K. Li, R. Li and B. Veeravalli, “Reliability-aware scheduling strategy for heterogeneous distributed computing systems,” Journal of Parallel and Distributed Computing, vol. 70, no. 9, pp. 941–952, 2010. [Google Scholar]

 8.  L. Zhang, K. Li, Y. Xu, J. Mei, F. Zhang et al., “Maximizing reliability with energy conservation for parallel task scheduling in a heterogeneous cluster,” Information Sciences, vol. 319, pp. 113–131, 2015. [Google Scholar]

 9.  J. Wang, W. Bao, X. Zhu, L. T. Yang, and Y. Xiang, “FESTAL: Fault-tolerant elastic scheduling algorithm for real-time tasks in virtualized clouds,” IEEE Transactions on Computers, vol. 64, no. 9, pp. 2545–2558, 2015. [Google Scholar]

10. G. Xie, H. Peng, Z. Li, J. Song, Y. Xie et al., “Reliability enhancement toward functional safety goal assurance in energy-aware automotive cyber-physical systems,” IEEE Transactions on Industrial Informatics, vol. 14, no. 12, pp. 5447–5462, 2018. [Google Scholar]

11. Y. Sharma, W. Si, D. Sun and B. Javadi, “Failure-aware energy-efficient VM consolidation in cloud computing systems,” Future Generation Computer Systems, vol. 94, pp. 620–633, 2019. [Google Scholar]

12. M. A. Ardakan and M. T. Rezvan, “Multi-objective optimization of reliability–redundancy allocation problem with cold-standby strategy using NSGA-iI,” Reliability Engineering & System Safety, vol. 172, pp. 225–238, 2018. [Google Scholar]

13. P. Guo, M. Liu, J. Wu, Z. Xue and X. He, “Energy-efficient fault-tolerant scheduling algorithm for real-time tasks in cloud-based 5G networks,” IEEE Access, vol. 6, pp. 53671–53683, 2018. [Google Scholar]

14. H. Wang and Y. Wang, “Maximizing reliability and performance with reliability-driven task scheduling in heterogeneous distributed computing systems,” Journal of Ambient Intelligence and Humanized Computing, vol. 9, pp. 1–11, 2018. [Google Scholar]

15. H. Xu, R. Li, C. Pan, and K. Li, “Minimizing energy consumption with reliability goal on heterogeneous embedded systems,” Journal of Parallel and Distributed Computing, vol. 127, pp. 44–57, 2019. [Google Scholar]

16. S. Dehnavi, H. R. Faragardi, M. Kargahi, and T. Fahringer, “A reliability-aware resource provisioning scheme for real-time industrial applications in a fog-integrated smart factory,” Microprocessors and Microsystems, vol. 70, pp. 1–14, 2019. [Google Scholar]

17. B. Gomathi and K. krishnasamy, “A task scheduling based on hybrid self-organizing migrating algorithm in cloud environment,” Asian Journal of Information Technology, vol. 15, pp. 3703–3707, 2016. [Google Scholar]

18. A. Girault, É. Saule and D. Trystram, “Reliability versus performance for critical applications,” Journal of Parallel and Distributed Computing, vol. 69, no. 3, pp. 326–336, 2009. [Google Scholar]

19. B. Kruekaew and W. Kimpan, “Virtual machine scheduling management on cloud computing using artificial bee colony,” Lecture Notes in Engineering and Computer Science, vol. 2209, pp. 18–22, 2014. [Google Scholar]

20. K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multi objective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. [Google Scholar]

21.  K. Deb, Multi-Objective Optimization Using Evolutionary Algorithms: An Introduction, Accessed, USA: John Wiley & Son, 2011 [Online]. Available: http://www.iitk.ac.in/kangal/deb.htm. [Google Scholar]

22. P. Koduru, Z. Dong, S. Das, S. M. Welch, J. L. Roe et al., “A multiobjective evolutionary-simplex hybrid approach for the optimization of differential equation models of gene networks,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 5, pp. 572–590, 2008. [Google Scholar]

23. G. G. Wang, S. Deb and Z. Cui, “Monarch butterfly optimization,” Neural Computing and Applications, vol. 31, no. 7, pp. 1995–2014, 2019. [Google Scholar]

24. H. Hu, Z. Cai, S. Hu, Y. Cai, J. Chen et al., “Improving monarch butterfly optimization algorithm with self-adaptive population,” Algorithms, vol. 11, no. 5, pp. 71–90, 2018. [Google Scholar]

25. R. N. Calheiros, R. Ranjan, C. A. F. De Rose, and R. Buyya, CloudSim: A Novel Framework for Modeling and Simulation of Cloud Computing Infrastructures and Services, Technical Report GRIDS-TR-20091, Grid Computing and Distributed Systems Laboratory, The University of Melbourne, 2009. [Online]. Available: http://arxiv.org/abs/0903.2525. [Google Scholar]

26. M. Sivaram, V. Porkodi, A. S. Mohammed, V. Manikandan and N. Yuvaraj, “Retransmission DBTMA protocol with fast retransmission strategy to improve the performance of MANETs,” IEEE Access, vol. 7, pp. 85098–85109, 2019. [Google Scholar]

27. M. Sivaram, D. Yuvaraj, A. S. Mohammed, V. Manikandan, V. Porkodi et al., “Improved enhanced DBTMA with contention-aware admission control to improve the network performance in MANETS,” computers, Materials & Continua, vol. 60, no. 2, pp. 435–454, 2019. [Google Scholar]

28. V. Manikandan, M. Sivaram, A. S. Mohammed and V. Porkodi, “Nature inspired improved firefly algorithm for node clustering in WSNs,” computers, Materials & Continua, vol. 64, no. 2, pp. 753–776, 2020. [Google Scholar]

29. C. A. Coello, G. T. Pulido and M. S. Lechuga, “Handling multiple objectives with particle swarm optimization,” IEEE Transactions on Evolutionary Computation, vol. 8, no. 3, pp. 256–279, 2004. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.