DOI:10.32604/cmc.2021.017697

| Computers, Materials & Continua DOI:10.32604/cmc.2021.017697 |  |
| Article |
FastAFLGo: Toward a Directed Greybox Fuzzing
1School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
2Department of Computer Science, University of Illinois Springfield, Springfield, 62703, IL, USA
3Civil Aviation Management Institute of China, Beijing, 100102, China
*Corresponding Author: Yanhui Guo. Email: yguo56@uis.edu
Received: 07 February 2021; Accepted: 26 April 2021
Abstract: While the size and complexity of software are rapidly increasing, not only is the number of vulnerabilities increasing, but their forms are diversifying. Vulnerability has become an important factor in network attack and defense. Therefore, automatic vulnerability discovery has become critical to ensure software security. Fuzzing is one of the most important methods of vulnerability discovery. It is based on the initial input, i.e., a seed, to generate mutated test cases as new inputs of a tested program in the next execution loop. By monitoring the path coverage, fuzzing can choose high-value test cases for inclusion in the new seed set and capture crashes used for triggering vulnerabilities. Although there have been remarkable achievements in terms of the number of discovered vulnerabilities, the reduction of time cost is still inadequate. This paper proposes a fast directed greybox fuzzing model, FastAFLGo. A fast convergence formula of temperature is designed, and the energy scheduling scheme can quickly determine the best seed to make the program execute toward the target basic blocks. Experimental results show that FastAFLGo can discover more vulnerabilities than the traditional fuzzing method in the same execution time.
Keywords: Directed; greybox; fuzzing; power schedule
With the proliferation of network applications related to people’s work and lives [1], the threat of network attack is becoming severe; the confrontations between network attack and defense are frequent [2–5]. Attackers use vulnerabilities to implement network penetration attacks. According to data from Cvedetails [6], more than 10000 vulnerabilities were exposed each year from 2017 to 2019 (see Fig. 1). Not only is the number of vulnerabilities increasing rapidly, but the degree of harm presents an upward trend. With the increase in software logic complexity and the proliferation of code size, automatic vulnerability fuzzing has become a popular research topic.
Using the characteristics of the tested program and input data, with the help of various dynamic and static program analysis technologies, automatic vulnerability fuzzing aims to find the balance between the coverage and efficiency of the analysis of a tested program and to alleviate the problems of low path coverage and poor scalability, improve the efficiency of vulnerability fuzzing, and discover more or deeper vulnerabilities in a shorter time. Software vulnerability fuzzing technologies include binary comparison, model detection, static analysis, taint analysis, fuzzing, and symbol execution. With homology analysis on software code blocks, artificial intelligence technology has been recently introduced to vulnerability fuzzing research.
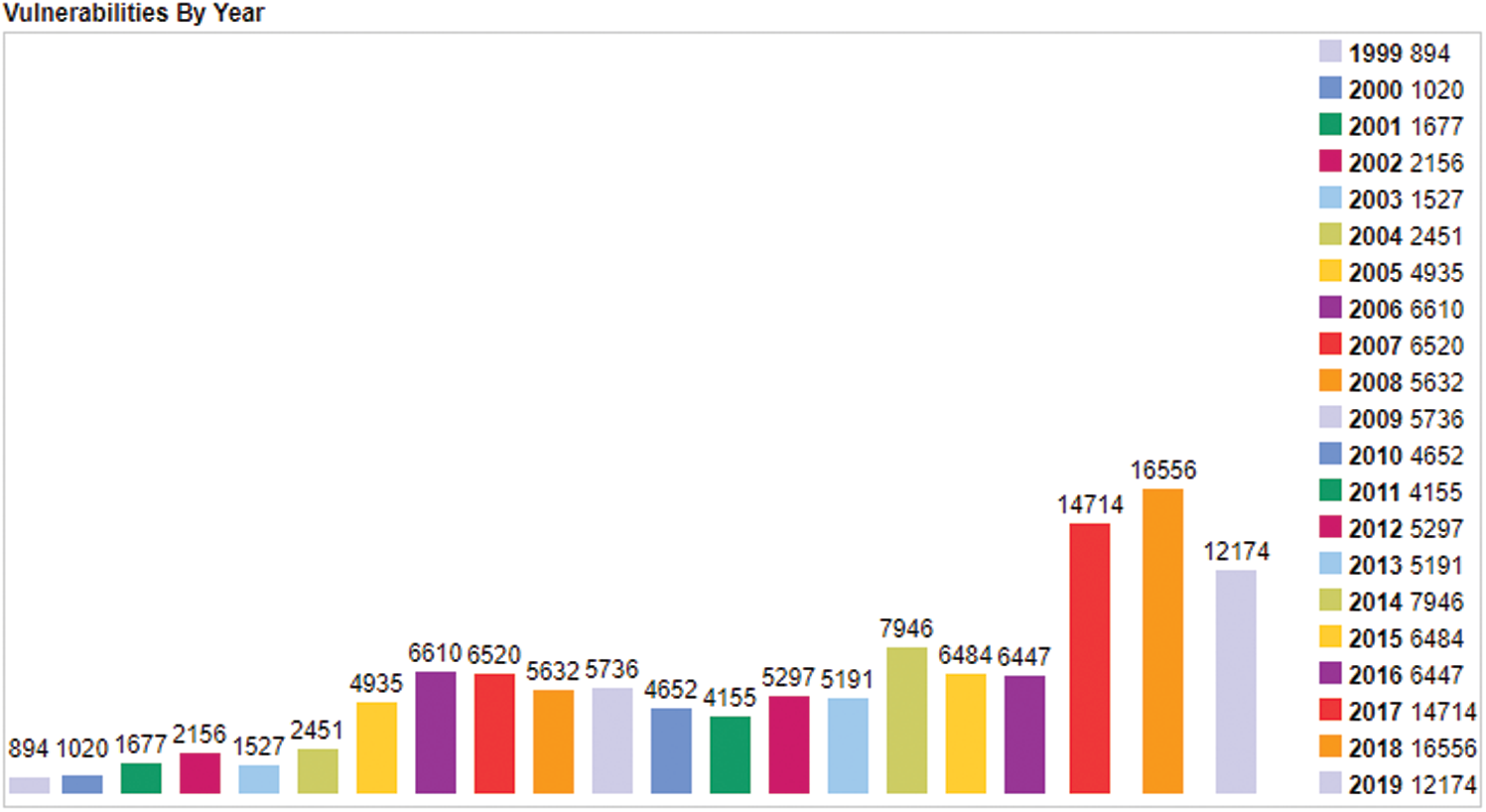
Figure 1: Number of vulnerabilities exposed by year
Fuzzing is an important automatic vulnerability discovery method, whose core idea is to discover potential vulnerabilities of a program by constructing irregular data as the input and to determine whether a program will crash when processing it. By tracking the processing in which inputs trigger the tested program to crash, the researcher analyzes the cause and develops an exploitation code. Once a crash occurs, the code blocks concerned with the crash can become vulnerabilities.
The advantage of fuzzing is that it can quickly generate a large number of test cases as input for the tested program to execute, and can automatically capture the crashes. However, the test cases are randomly generated based on some mutated strategies. When test cases must cover a specific path of the program or pass some verification requested by it, a large number of invalid test cases will reduce the efficiency of vulnerability fuzzing. Hence to improve the efficiency of the fuzzing is an important challenge.
This paper makes the following contributions:
(1) A directed fuzzing model, FastAFLGo, is proposed based on AFLGo [7], the efficiency of which is enhanced by assigning high energy to seeds closer to the target basic blocks.
(2) A new cooling schedule is proposed in which the temperature can drop rapidly to enter the exploitation phase under the condition of ensuring sufficient time for the exploration phase.
(3) Comparisons with several typical fuzzing models on the LAVA-M dataset show that FastAFLGo improves the efficiency of vulnerability fuzzing without increasing time consumption.
Fuzzing methods include whitebox, greybox, and blackbox. Whitebox fuzzing can get the tested program source code and then analyze it. Based on fully understanding the internal logic structure of the tested program, whitebox fuzzing can generate more accurate test cases; correspondingly, due to lack of source code, blackbox fuzzing does not analyze the tested program at all and arbitrarily generates a large number of test cases for the tested program to execute. Tested programs usually include some magic bytes to verify the input; hence, the efficiency of blackbox fuzzing is very low, and this method is almost no longer used in actual vulnerability fuzzing. Greybox fuzzing is a method in between. Since greybox fuzzing cannot get the source code of the tested program, it can only analyze the binary code to obtain information for use as knowledge to generate test cases. The execution states of the tested program are analyzed, and the input test cases are modified accordingly.
Fuzzing methods can also be divided, according to the strategies of new test case generation, as mutation-based fuzzing, generation-based fuzzing, hybrid fuzzing, and symbolic execution.
Mutation-based fuzzing, which is based on the static and dynamic analysis of the tested program and execution information, continually generates test cases mutated from seeds. Representative seed-selection algorithms include AFL [8], Honggfuzz [9], LibFuzzer [10], CollAFL [11], and VUzzer [12]. To reduce the generation of invalid test cases is an important goal. AFL aims to improve the path coverage rate. By monitoring the execution of the path, new paths are found or low-frequency paths are executed, and corresponding test cases are included in the seed set. Because the size of the bitmap file used to record the execution times of the path is only 64K bytes, there is a hash collision problem. To solve this problem, CollAFL uses an improved hash approach and increases the size of the bitmap file, which reduces the possibility of collision and improves the statistical effect of path coverage. To explore more paths and reduce the excessive execution of high-frequency paths, AFLFast [13] selects seeds by gravitating toward low-frequency paths in a Markov chain. VUzzer regards the basic blocks within deep paths as the primary targets. Based on the static analysis of the control flow of the tested program, the key constant string is identified and extracted to reduce the number of invalid test cases. At the same time, the weights of these basic blocks are calculated. During fuzzing, the test cases corresponding to the execution path with the highest weight are selected as the seed.
Unlike the above fuzzing models, which focus on control flow characteristics, GREYONE [14] focuses on data flow characteristics, infers the tainted variables by changing the input bytes, and monitors the changes in variable values during the fuzzing process. The evolution direction of the fuzzing is adjusted according to the distance between the tainted variable and the expected value of the untouched branch. Steelix [15] extracts magic bytes of the tested program through light-weight static analysis and binary instrumentation, and generates test cases through verification of the magic byte.
AFLGo, Hawkeye [16], and AFLPro [17] adopt the guided fuzzing strategy that approaches the target basic blocks. AFLGo optimizes the seed by using the energy schedule based on a simulated annealing algorithm to assign more energy to test cases closer to the target basic blocks. Hawkeye precisely collects some important information, such as a called graph, the distance between different functions and the target basic blocks. It generates dynamic metrics for the seed’s energy schedule and adaptive mutation. AFLPro proposes a strategy of direction-sensitive fuzzing. It improves the validity of selected seeds based on basic block aggregation (BBA), achieves {fine-grained} seeds by using a multi-dimensional oriented selection strategy, and optimizes genetic variation to ensure the diversity of the seed. TortoiseFuzz [18] is a fuzzing method for detecting memory corruption vulnerabilities, which employs a coverage-guided fuzzer with coverage accounting for prioritization of test cases. The coverage accounting concerns three metrics consisting of functions, loops, and basic blocks. Current greybox fuzzing does not consider the thread interleavings that affect the execution states in a multi-threaded program. MUZZ [19] uses three thread-aware instrumentations, i.e., coverage-oriented, thread-context, and schedule-intervention. These create feedback in runtime, which can be used in dynamic seed selection.
Based on format information and grammar knowledge of the tested program, fuzzing can automatically generate highly structured test cases. Peach [20] writes a configuration file to constrain the format of test cases. Langfuzz [21] utilizes code fragments in the grammar learning test set and recombines these to generate a new test case. Because generation-based fuzzing relies heavily on the generated model or grammar training, traditional generation-based fuzzing is less efficient than mutation-based fuzzing. Machine learning has recently been introduced to fuzzing. Machine learning technology is used to analyze and learn massive numbers of test cases to guide the generation of higher-quality test cases. For instance, Learn & Fuzz [22] transforms the problem of high structured test case generation to that of text generation in the natural language processing (NLP) domain. The use of a training dataset and statistical machine learning technology can automatically generate test cases that conform to grammar. NEUZZ [23] uses a surrogate neural network to incrementally learn smooth approximations of the tested program’s branch behaviors and guides the generation of test cases through gradient-guided input-generation schemes.
2.3 Hybrid Fuzzing and Symbolic Execution
When fuzzing cannot cover more branches during execution, or when it is difficult to generate test cases that can cover a certain target basic block, fuzzing, and symbolic execution are combined to generate test cases to execute new paths. Symbolic execution, such as S2E [24] and Angr [25], builds branch constraints through symbolization analysis and can generate test cases for each path with the help of a constraint solver. Because symbolic execution consists of rigorous logical reasoning under constraints, the biggest problems are path explosion and difficulty in constraint solving. Driller [26] combines AFL and Angr to explore the execution path of the tested program alternately by fuzzing and symbolic execution. This can determine how to generate a test case that can make the tested program to execute a new testing path of deeper basic blocks when the path coverage of the tested program is growing slowly, and it directly avoids path explosion due to symbolic execution. Similarly, Munch [27] combines symbolic execution and fuzzing to improve deeper path coverage. The difference between Munch and Driller is that Munch uses a guided strategy.
Böhme [7,13] showed that coverage-based greybox fuzzing can be modeled as a Markov chain. A power schedule decides how many test cases are generated by fuzzing the seed in each state. How to assign the power on each seed becomes a key question. Power schedule strategies yield different priorities of paths to be executed. One of our research goals is to discover the vulnerability of the tested program as much as possible, and another is to discover more vulnerabilities within a limited time. For example, if we request some memory overflow vulnerabilities, we must execute a power schedule strategy on the preferred basic blocks, including a large number of memory operations as soon as possible. If we want to discover vulnerabilities in specific areas, such as in patch code, we can guide the power schedule by assigning more energy to seeds that are closer to the target locations. AFL uses a constant power schedule by which a fairly high amount of energy is assigned to the seeds. AFLFast adopts an exponential power schedule to gravitate the fuzzer toward low-frequency paths in each Markov state. The seeds are assigned very little energy the first time, but when constantly chosen, they will be assigned more energy. AFLGo adopts the simulated annealing-based Markov Chain Monte Carlo (MCMC) power schedule. The closer to the target locations, the more energy assigned to the seed.
AFLFast evaluates six kinds of power schedules: the exploitation-based constant schedule (EXPLOIT), exploration-based constant schedule (EXPLOIT), cut-off exponential schedule (COE), exponential schedule (FAST), linear schedule (LINEAR), and quadratic schedule (QUAD). AFLGo’s framework [28] implements four kinds of energy scheduling: EXPLORE, LOG, LINEAR, and QUAD. AFLGo slowly transitions from the exploration phase to the exploitation phase, according to the annealing function implemented as a power schedule. A seed’s assigned energy is inversely proportional to the temperature. Although the energy is locally assigned to each seed, the temperature is global to all seeds in the simulated annealing-based power schedule. The cooling schedule, which controls the convergence rate of temperature, decides the timing of entering the exploitation phase from the exploration phase. Therefore, how to accelerate the convergence rate of temperature while maintaining sufficient exploration time is an important focus in this paper.
The formulas for the temperature T in the cooling schedules of EXPLORE, LOG, LINEAR, and QUAD are shown, in order, as follows [7,28]:
where x is the ratio of execution time to exploration time.
The cooling curve of the temperature T is shown in Fig. 2, where the abscissa is the above parameter x, and the ordinate is T.
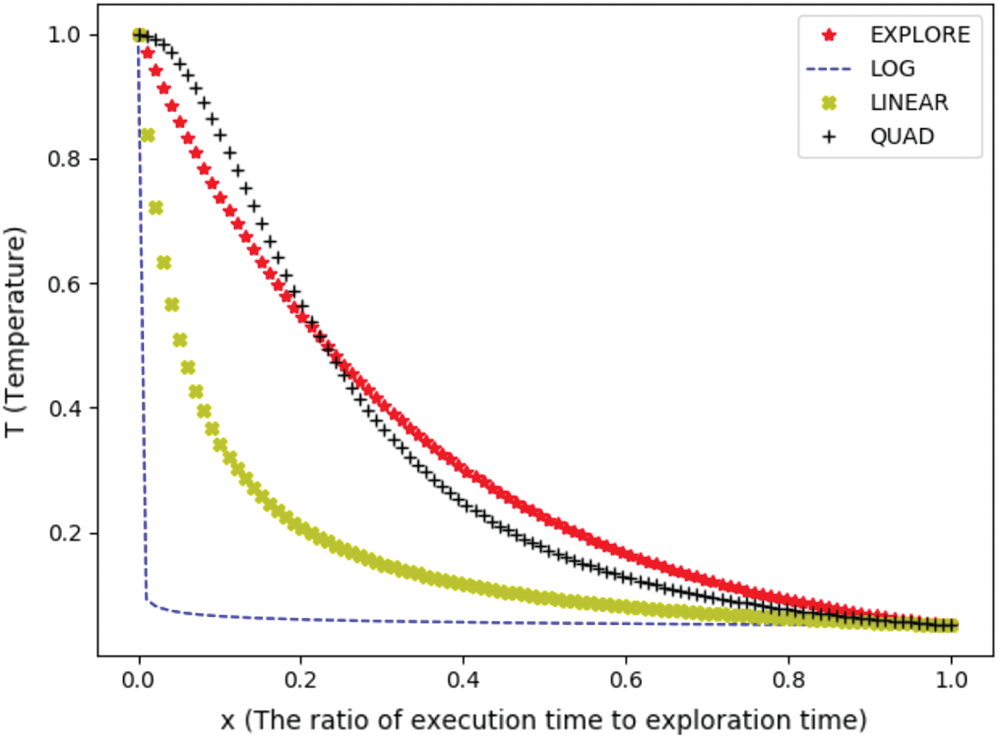
Figure 2: Cooling schedule of AFLGo
It can be seen that the convergence rate of T is significantly different, and it decreases more obviously in the range (0, 0.5) than other ranges. At the same time, the exploration phase must be allowed sufficient time. Although the curve of the power schedule LOG has the highest value of convergence, it does not leave sufficient time for exploration. Therefore, how a better convergence formula for T can be obtained and the time at which the cooling schedule is to be triggered have become interesting research topics.
We adopt the same value of temperature T in AFLGo and use it to trigger the fuzzing procedure from the exploration phase into the exploitation phase, i.e., the cooling schedule enters the exploitation phase when T is less than or equal to 0.05. The exploration time is preset by users. When the ratio of execution time to exploration time is 1, T is 0.05. Once the execution time matches the exploration time, the simulated annealing process is comparable to a classical greedy search algorithm.
To make the temperature T rapidly fall below 0.05, we proposed a new cooling schedule formula that has better convergence in the open interval (0, 1),
where x is the ratio of execution time to exploration time.
Because exploration time is constant and preset, the execution time is proportional to x. Furthermore, the temperature T is proportional to execution time, and thus we can express the relationship between temperature T and execution time by x. This means that the smaller is x when the temperature T drops to 0.05, the shorter is the execution time. Finally, we can shorten the time of fuzzing.
As shown in Fig. 3, compared with the cooling schedules of EXPLORE, LOG, LINEAR, and QUAD, the proposed new cooling schedule first cools the temperature T to 0.05 so that we can make the cooling schedule enter the exploitation phase earlier. Therefore, the new cooling schedule can help reduce the execution time of the annealing-based power schedule in each round.
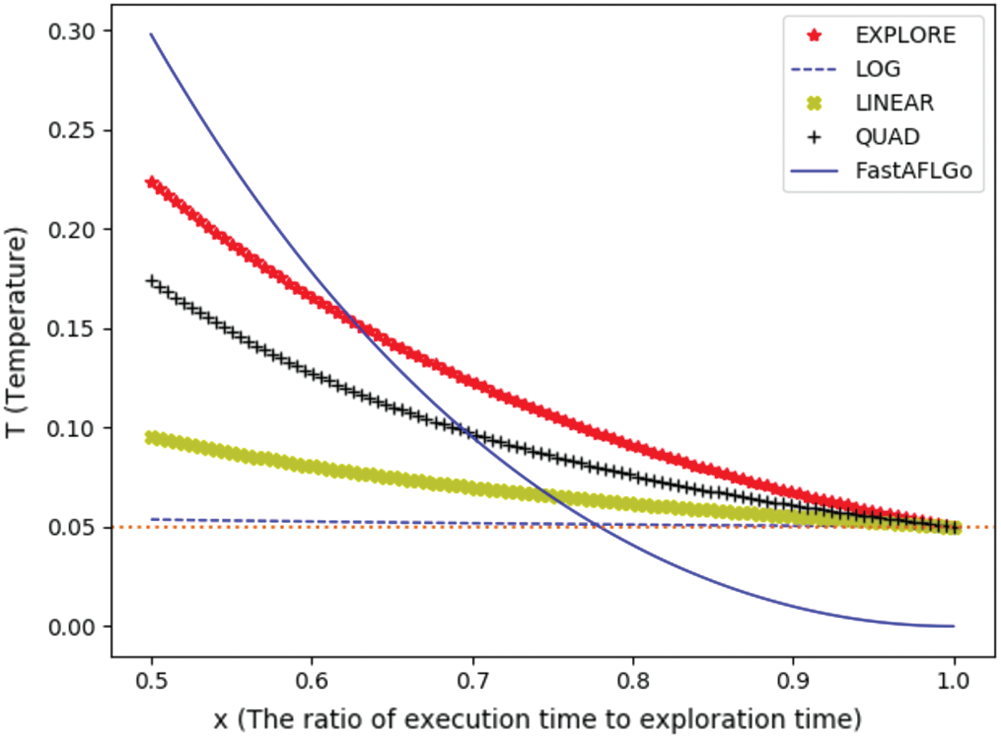
Figure 3: Comparison of cooling schedules
3.3 Annealing-Based Power Schedules
We follow and maintain the annealing-based power schedules in AFLGo, which assigns more energy to seeds that are closer to the target locations and reduces that of seeds that are farther away. Therefore, the distance of a seed to a target basic block is important. The formula of annealing-based power schedules is shown as follow [7,28]:
where:
(1) s is a seed;
(2) BBb is target basic block b;
(3) T is the temperature in the cooling schedule;
(4) Dsb is the distance of seed s to BBb.
We develop an improved directed greybox fuzzing model, FastAFLGo, as shown in Fig. 4.
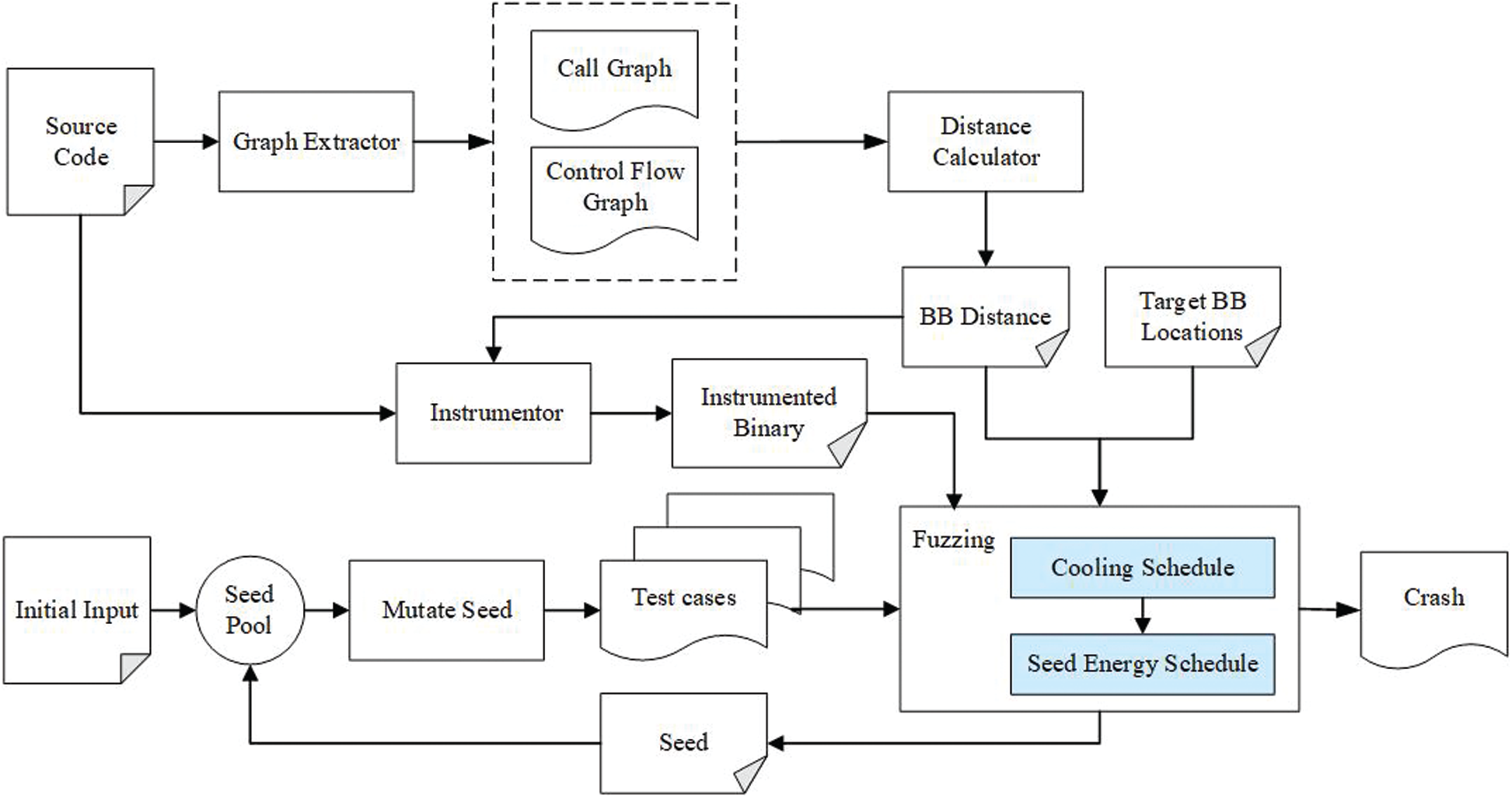
Figure 4: FastAFLGo model
Before starting the fuzzing of the tested program, we must do the same work as AFLGo to obtain the distance between basic blocks and assign energy to each candidate seed. The process is as follows.
(1) Based on the component of the graph extractor, the call graph (CG) and control flow graph (CFG) are extracted.
(2) Based on the CG and CFG, the inter-procedural distances are computed by the component of the distance calculator.
(3) The distance information is instrumented in each basic block in the target binary by the component of the instrumentor. The information provided by the instrumented binary is not only about coverage but about the seed distance.
The guidance information is now ready. Algorithm 1 describes the process of directed greybox fuzzing. In the FastAFLGo model, AssignEnergy is replaced with our proposed new energy schedule to assign candidate seeds to different energy.

A set of seed inputs S is provided to the Fuzzer, which chooses seed s from S and determines the number of new inputs by AssignEnergy. The Fuzzer generates e new test cases by mutating seed s. If test case s′ is important, e.g., it covers a new branch of the tested program, then it is added to S. If the generated test case s′ leads the tested program to crash, then it is added to the CrashSet.
We used the LAVA-A dataset, which includes the programs base64, who, uniq, and md5sum, as the unified test set. A large number of vulnerabilities are present in each of these programs. We regard the number of discovered vulnerabilities in a test cycle as an evaluation criterion. We used seven days as a test cycle.
Experiments were performed on a computer with an Intel Xeon E5-2650 V4 CPU, 16 GB memory, a 1-TB hard disk, and a Ubuntu 16.04 operating system.
The experimental results are shown in Tabs. 1 and 2, which show the total number of crashes and number of unique crashes, respectively, of VUzzer, AFLGo and FastAFLGo.


The results in Tabs. 1 and 2 show that FastAFLGo is significantly more effective than AFLGo and VUzzer with the same time cost.
Due to the complexity of software and the growing amount of code, automatic vulnerability discovery has become a research hotspot. Coverage-based fuzzing is an important method of vulnerability discovery. AFLGo is a good method for directed greybox fuzzing. We analyzed its annealing-based power schedule and redesigned cooling schedule corresponding to temperature. Experimental results show that FastAFLGo can discover more vulnerabilities with the time consumption remaining the same. In our future work, we plan to introduce artificial intelligence approaches to identify basic blocks similar to the blocks that confirmed vulnerabilities.
Funding Statement : This work was supported by the Natural Science Foundation of China (Grant No. 61702013), National Key Research and Development Plan (Grant Nos. 2018YFB1800302 and 2019YFA0706404), Beijing Natural Science Foundation (Grant Nos. KZ201810009011, 4202020, and 19L2021), and Science and Technology Innovation Project of North China University of Technology (19XN108).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Su, Z. Tian, S. Liang, S. Li, S. Du et al., “A reputation management scheme for efficient malicious vehicle identification over 5G networks,” IEEE Wireless Communications, vol. 27, no. 3, pp. 46–52, 2020. [Google Scholar]
2. J. Qiu, Z. Tian, C. Du, Q. Zuo, S. Su et al., “A survey on access control in the age of internet of things,” IEEE Internet of Things Journal, vol. 7, no. 6, pp. 4682–4696, 2020. [Google Scholar]
3. C. Du, S. Liu, L. Si, Y. Guo and T. Jin, “Using object detection network for malware detection and identification in network traffic packets,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1785–1796, 2020. [Google Scholar]
4. S. Su, Z. Tian, J. Qiu, Y. Jiang, Y. Sun et al., “Evaluating the topology coverage of BGP monitors,” Computers, Materials & Continua, vol. 62, no. 3, pp. 1397–1412, 2020. [Google Scholar]
5. X. Yu, Z. Tian, J. Qiu, S. Su and X. Yan, “An intrusion detection algorithm based on feature graph,” Computers, Materials & Continua, vol. 61, no. 1, pp. 255–273, 2019. [Google Scholar]
6. Mitre, “Cve details,“ 2021. [Online]. Available: https://www.cvedetails.com/browse-by-date.php. [Google Scholar]
7. M. Böhme, V. T. Pham, M. D. Nguyen and A. Roychoudhury, “Directed greybox fuzzing,” in Proc. CCS, Dallas, TX, USA, pp. 2329–2344, 2017. [Google Scholar]
8. M. Zalewski, “American fuzzy lop,” 2021. [Online]. Available: https://lcamtuf.coredump.cx/afl. [Google Scholar]
9. Google, “Honggfuzz,” 2021. [Online]. Available: https://github.com/google/honggfuzz. [Google Scholar]
10. Llvm, “libFuzzer,” 2021. [Online]. Available: https://www.llvm.org/docs/LibFuzzer.html. [Google Scholar]
11. S. Gan, C. Zhang, X. Qin, X. Tu, K. Li et al., “CollAFL: Path sensitive fuzzing,” in Proc. S&P, San Francisco, CA, USA, pp. 679–696, 2018. [Google Scholar]
12. S. Rawat, V. Jain, A. Kumar, L. Cojocar, C. Giuffrida et al., “VUzzer: Application-aware evolutionary fuzzing,” in Proc. NDSS, San Diego, CA, USA, pp. 1–14, 2017. [Google Scholar]
13. M. Böhme, V. T. Pham and A. Roychoudhury, “Coverage-based greybox fuzzing as markov chain,” IEEE Transactions on Software Engineering, vol. 45, no. 5, pp. 489–506, 2019. [Google Scholar]
14. S. Gan, C. Zhang, P. Chen, B. Zhao, X. Qin et al., “GREYONE: Data flow sensitive fuzzing,” in Proc. USENIX Security, Boston, MA, USA, pp. 2577–2594, 2020. [Google Scholar]
15. Y. Li, B. Chen, M. Chandramohan, S. Lin, Y. Liu et al., “Steelix: Program-state based binary fuzzing,” in Proc. ESEC/FSE, Paderborn, Germany, pp. 627–637, 2017. [Google Scholar]
16. H. Chen, Y. Xue, Y. Li, B. Chen, X. Xie et al., “Hawkeye: Towards a desired directed grey-box fuzzer,” in Proc. CCS, Toronto, Canada, pp. 2095–2108, 2018. [Google Scholar]
17. T. Ji, Z. Wang, Z. Tian, B. Fang, Q. Ruan et al., “AFLPro: Direction sensitive fuzzing,” Journal of Information Security and Applications, vol. 54, pp. 1–14, 2020. [Google Scholar]
18. Y. Wang, X. Jia, Y. Liu, K. Zeng, T. Bao et al., “Not all coverage measurements are equal: Fuzzing by coverage accounting for input prioritization,” in Proc. NDSS, San Diego, CA, USA, pp. 1–17, 2020. [Google Scholar]
19. H. Chen, S. Guo, Y. Xue, Y. Sui, C. Zhang et al., “MUZZ: Thread-aware grey-box fuzzing for effective bug hunting in multithreaded programs,” in Proc. USENIX Security, Boston, MA, USA, pp. 2325–2342, 2020. [Google Scholar]
20. Gitlab, “Peach-fuzzer-community,” 2021. [Online]. Available: https://gitlab.com/peachtech/peach-fuzzer-community. [Google Scholar]
21. C. Holler, K. Herzig and A. Zeller, “Fuzzing with code fragments,” in Proc. USENIX Security, Bellevue, WA, USA, pp. 445–458, 2012. [Google Scholar]
22. P. Godefroid, H. Peleg and R. Singh, “Learn&Fuzz: machine learning for input fuzzing,” in Proc. ASE, Urbana, IL, USA, pp. 50–59, 2017. [Google Scholar]
23. D. She, K. Pei, D. Epstein, J. Yang, B. Ray et al., “NEUZZ: Efficient fuzzing with neural program smoothing,” in Proc. S & P, San Francisco, CA, USA, pp. 803–817, 2019. [Google Scholar]
24. V. Chipounov, V. Kuznetsov and G. Candea, “S2E: A platform for in-vivo multi-path analysis of software systems,” in Proc. ASPLOS, Newport Beach, CA, USA, pp. 265–278, 2011. [Google Scholar]
25. Y. Shoshitaishvili, R. Wang, C. Salls, N. Stephens, M. Polino et al., “SOK: (State of) the art of war: Offensive techniques in binary analysis,” in Proc. S & P, San Jose, CA, USA, pp. 138–157, 2016. [Google Scholar]
26. N. Stephens, J. Grosen, C. Salls, A. Dutcher, R. Wang et al., “Driller: Augmenting fuzzing through selective symbolic execution,” in Proc. NDSS, San Diego, CA, USA, pp. 1–16, 2016. [Google Scholar]
27. S. Ognawala, T. Hutzelmann, E. Psallida and A. Pretschner, “Improving function coverage with munch: A hybrid fuzzing and directed symbolic execution approach,” in Proc. SAC, Pau, France, pp. 1475–1482, 2018. [Google Scholar]
28. M. Böhme, V. T. Pham, M. D. Nguyen and A. Roychoudhury, “Aflgo,” 2021. [Online]. Available: https://github.com/aflgo/aflgo. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |