Computers, Materials & Continua DOI:10.32604/cmc.2021.016218
Article

An Efficient Scheme for Interference Mitigation in 6G-IoT Wireless Networks

Fahd N. Al-Wesabi1,*, Imran Khan2, Nadhem Nemri3, Mohammed A. Al-Hagery4, Huda G. Iskander5, Quang Ngoc Nguyen6, Babar Shah7 and Ki-Il Kim8

1Department of Computer Science, King Khalid University, Muhayel Aseer, KSA
2Department of Electrical Engineering, University of Engineering and Technology, Peshawar, Pakistan
3Department of Information Systems, King Khalid University, Mayahel Aseer, KSA
4Department of Computer Science, College of Computer, Qassim University, Saudi Arabia
5Faculty of Computer and IT, Sana'a University, Sana'a, Yemen
6Department of Communications and Computer Engineering, Faculty of Science and Engineering, Waseda University, Shinjuku-ku, Tokyo, 169-0051, Japan
7College of Technological Innovation, Zayed University, Abu Dhabi, UAE
8Department of Computer Science and Engineering, Chungnam National University, Daejeon, 34134, Korea
*Corresponding Author: Fahd N. Al-Wesabi. Email: falwesabi@kku.edu.sa
Received: 27 December 2020; Accepted: 03 March 2021

Abstract: The Internet of Things (IoT) is the fourth technological revolution in the global information industry after computers, the Internet, and mobile communication networks. It combines radio-frequency identification devices, infrared sensors, global positioning systems, and various other technologies. Information sensing equipment is connected via the Internet, thus forming a vast network. When these physical devices are connected to the Internet, the user terminal can be extended and expanded to exchange information, communicate with anything, and carry out identification, positioning, tracking, monitoring, and triggering of corresponding events on each device in the network. In real life, the IoT has a wide range of applications, covering many fields, such as smart homes, smart logistics, fine agriculture and animal husbandry, national defense, and military. One of the most significant factors in wireless channels is interference, which degrades the system performance. Although the existing QR decomposition-based signal detection method is an emerging topic because of its low complexity, it does not solve the problem of poor detection performance. Therefore, this study proposes a maximum-likelihood-based QR decomposition algorithm. The main idea is to estimate the initial level of detection using the maximum likelihood principle, and then the other layer is detected using a reliable decision. The optimal candidate is selected from the feedback by deploying the candidate points in an unreliable scenario. Simulation results show that the proposed algorithm effectively reduces the interference and propagation error compared with the algorithms reported in the literature.

Keywords: 6G networks; internet of things; resource allocation; optimization

1  Introduction

The sixth generation (6G) aims to provide a 1000× factor of transmission capacity increase, at least 100 billion Internet-of-Things (IoT) device connections, a transmission rate of up to 10 Gbit/s, and an ultra-low latency user experience in the range of ms [1–5]. In addition to human-to-human communication, the next-generation mobile Internet will establish zero-distance connections between humans and machines, and between machines and machines. Wireless technology will promote future economic and social development in a new way. Therefore, ultra-low latency transmission is regarded as one of the main technical features of 6G systems [6–8]. Its goal is to achieve an end-to-end transmission delay below 1 ms, thereby supporting human-to-machine and machine-to-machine real-time communication and remote control applications. In addition to addressing higher requirements in terms of transmission delay, reliability, and throughput, 6G has also been developed to introduce major changes in the next-generation mobile Internet architecture. Software-defined networking and network function virtualization (NFV) technologies, as emerging technologies from the 5G/B5G network architecture, enable the infrastructure network to be divided into several logical networks, allowing multiple differentiated applications to share the same physical network and resources; this is the so-called network slicing technology {[9–12]}. Each independent slice can call a virtual network function running on the public network infrastructure, and configure and adjust its communication and computing resources as needed to meet the specific business needs of specific network slice applications [13,14]. For instance, a notable recent study proposed an integrated content delivery service using information-centric networking and content delivery network slices employing NFV technology; their design and testbed implementation results were reported in [15,16]. In addition, each tenant usually signs a service level agreement with the infrastructure provider. Therefore, through custom slicing applications and functions, and dynamic allocation of resources of custom slicing, public mobile networks can support specific emergency IoT slicing and ensure the coexistence and safe isolation of slicing and another mobile network slicing [17].

In IoT communications, anti-interference of the wireless channel is still affected by various factors [18,19]. Multi-antenna systems have been widely used for improving the quality of wireless channels in recent years. In practical applications, owing to the high complexity of the maximum-likelihood detection algorithm, when the number of antennas increases, the complexity grows exponentially. Therefore, the application of multiple-antenna systems is difficult to achieve [20]; consequently, the application of wireless communication for the Internet is impacted. To solve this practical application problem, researchers from various countries have made many achievements in recent years [21]. The QR decomposition detection algorithm has attracted the attention of researchers owing to its low complexity and the use of serial interference cancellation characteristics. The authors in [22] introduced an improved SQRD algorithm that maximizes the diversity gain based on the serial interference cancellation SQRD, ensuring that the signal power of the first detection layer is the largest in each detection; thus, the maximum detection layer can be obtained. Diversity gain, while using serial interference cancellation, reduces the complexity of the algorithm, but improving the performance is not ensured. The authors in [23] introduced a detection algorithm based on MMSE-SQRD, using a sort-free QRD-M algorithm to avoid the delay caused by sorting the detection phase, reduce the sorting complexity of the path search process, and improve the system performance. The researchers also found that the accuracy of the first detection layer of the QR algorithm is critical. The authors in [24] introduced a simplified QRM-MLD algorithm that uses QR decomposition with the M algorithm to reduce the system complexity while maintaining the system performance. It was proposed to use the estimated noise variance threshold method to reduce the complexity of the QRM-MLD. It can be concluded from the simulation results that, in contrast with adding MLD, the proposed method achieved a 10× reduction in the complexity. The authors in [25] introduced an adaptive candidate scheme in the QRM-MLD algorithm for multi-antenna detection. QRM-MLD is a near-ML detection algorithm that can achieve a trade-off between BER performance and computational complexity in a multi-antenna system. Using adaptive candidate schemes to enter QRM-MLD, similar to the traditional QRM-MLD, the proposed detection application with multi-branch optimization can achieve near-ML performance. The study in [26] introduced a signal selection scheme suitable for the QRM-MLD algorithm. The numerical results obtained by computer simulation showed that even if the number of candidates in QRM-MLD is relatively small, the proposed scheme can provide a diversity performance equal to N signal candidate points. In addition, owing to the low computational complexity, the proposed scheme is feasible for implementation.

Aiming at solving the problem of poor detection of the conventional QR method in multi-antenna systems, this study proposes a QR decomposition scheme based on ML criteria and a candidate mechanism. This algorithm greatly improves the performance while featuring low complexity.

2  Antenna System Model

A multi-antenna system is shown in Fig. 1; it is assumed that the system has M transmitting antennas and N receiving antennas, and N≥M is satisfied. The wireless propagation channel experiences quasi-static flat fading and is in a strong scattering environment, that is, the channel fading experienced between each transmitting antenna and receiving antenna can be regarded as mutually independent [27].

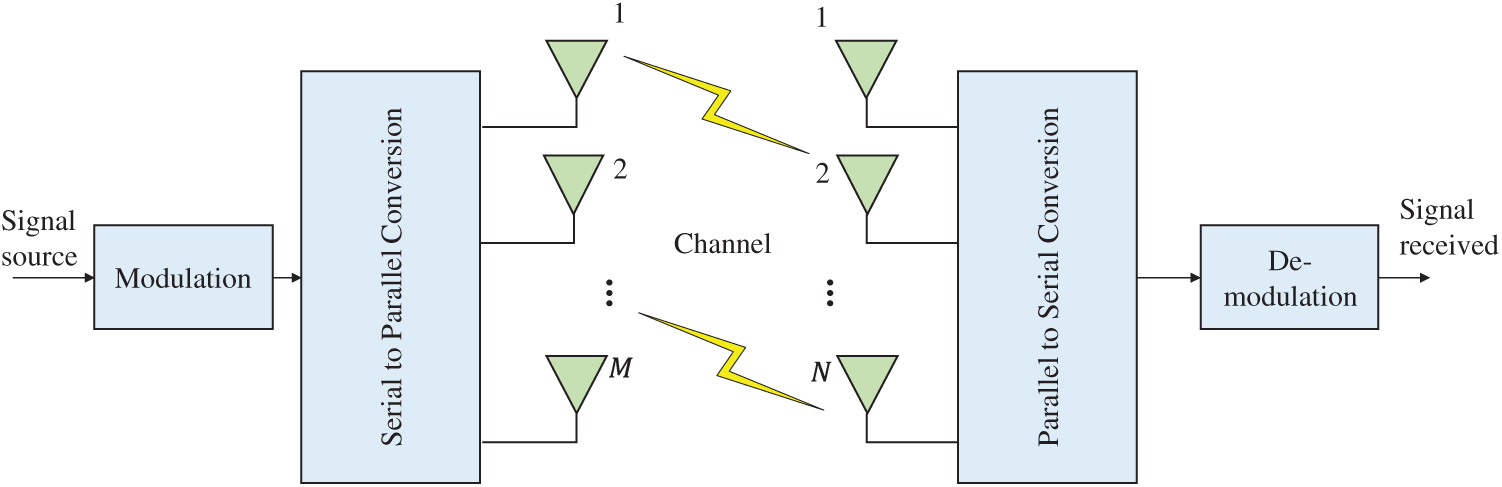
Figure 1: Proposed system model

The received signal can be expressed as follows:

r(i)=∑k=1Mhksk(i)+n(i),(1)

The vector form can be expressed as follows:

r=Hs+n(2)

where r(i) is an N×1 dimensional vector that represents the received signal; s(i) represents the M×1 dimensional vector, i.e., the transmitted signal; and the kth element sk(i) represents the signal transmitted by the kth antenna. Each element of s(i) is independently and identically distributed (i.i.d.), and the mean value of the transmitted signal is zero. The covariance is expressed as follows:

E[s(i)sH(i)]=σs2I(3)

where E[⋅] represents the signal digital expectation; (⋅)H represents the Hermitian operation; σs2 represents the signal power; I represents the identity matrix; hk represents the N×1 dimensional channel coefficient; and H represents the N×M dimensional matrix. This is a matrix of all channel vectors and represents the channel fading coefficient from each transmitting antenna to each receiving antenna. Note also that n(i) is an N×1 dimensional vector representing Gaussian white noise whose power is σs2 and mean is zero; it has independent and imaginary parts with equal variances. The covariance matrix is expressed as follows:

E[n(i)nH(i)]=σn2I(4)

3  Basic Principle of the Proposed Algorithm

3.1 Traditional QR Decomposition Algorithm

The core idea of the QR decomposition algorithm is to decompose the channel matrix to obtain an upper triangular matrix and an orthogonal matrix, and then use the correlation properties of the matrix to detect the received signal. Compared with the MMSE and ZF algorithms, the QR decomposition algorithm avoids the calculation of the channel matrix inversion and effectively reduces the computational complexity of the detection algorithm [28,29].

When the number of antennas at the receiving end is not less than the number of antennas at the transmitting end, QR decomposition is performed on channel H to obtain the following expression:

H=QR(5)

where Q is a unitary matrix, R is an upper triangular matrix, and the received signal r is left-multiplied by the conjugate transpose of the matrix Q to obtain sufficient statistics of the transmitted vector s:

r^=QTr=QTHs+QTn(6)

Simplifying, we obtain:

r^=Rs+u(7)

u=QTn(8)

where u represents the noise vector after orthogonal transformation of the noise vector. Eq. (8) expands as follows:

[r^1r^2r^3⋮r^NT]=[r1100⋮0r12r220⋮0………⋮…r1,NTr2,NTr3,NT⋮rNT,NT][s1s2s3⋮sNT]+[u1u2u3⋮uNT](9)

Note that the received signal of the last antenna is not interfered by other signals. Thus, the signal of this layer can be s elected to be detected first, and then the transmitted signal can be estimated in sequence:

s^i=Q(r^i−∑j=i+1NT⁡rijs^jrii),i=NT−1,NT−2,…,1(10)

The QR decomposition algorithm detects layer by layer, and inevitably there is error propagation between two adjacent detection layers, leading to system performance degradation. If there is an error in the signal estimation of the first detection layer, it will affect the signal estimation of all subsequent layers. Therefore, the order of detection is critical for the QR algorithm, and the performance of the entire system largely depends on the first detection layer [30].

3.2 Proposed Algorithm

For QR decomposition detection algorithms, the correctness of the initial detection layer directly affects the signals of other detection layers. Ensuring the correctness of the first detection layer can effectively reduce the error propagation. The framework of the proposed ML-QR algorithm implementation is shown in Fig. 2.

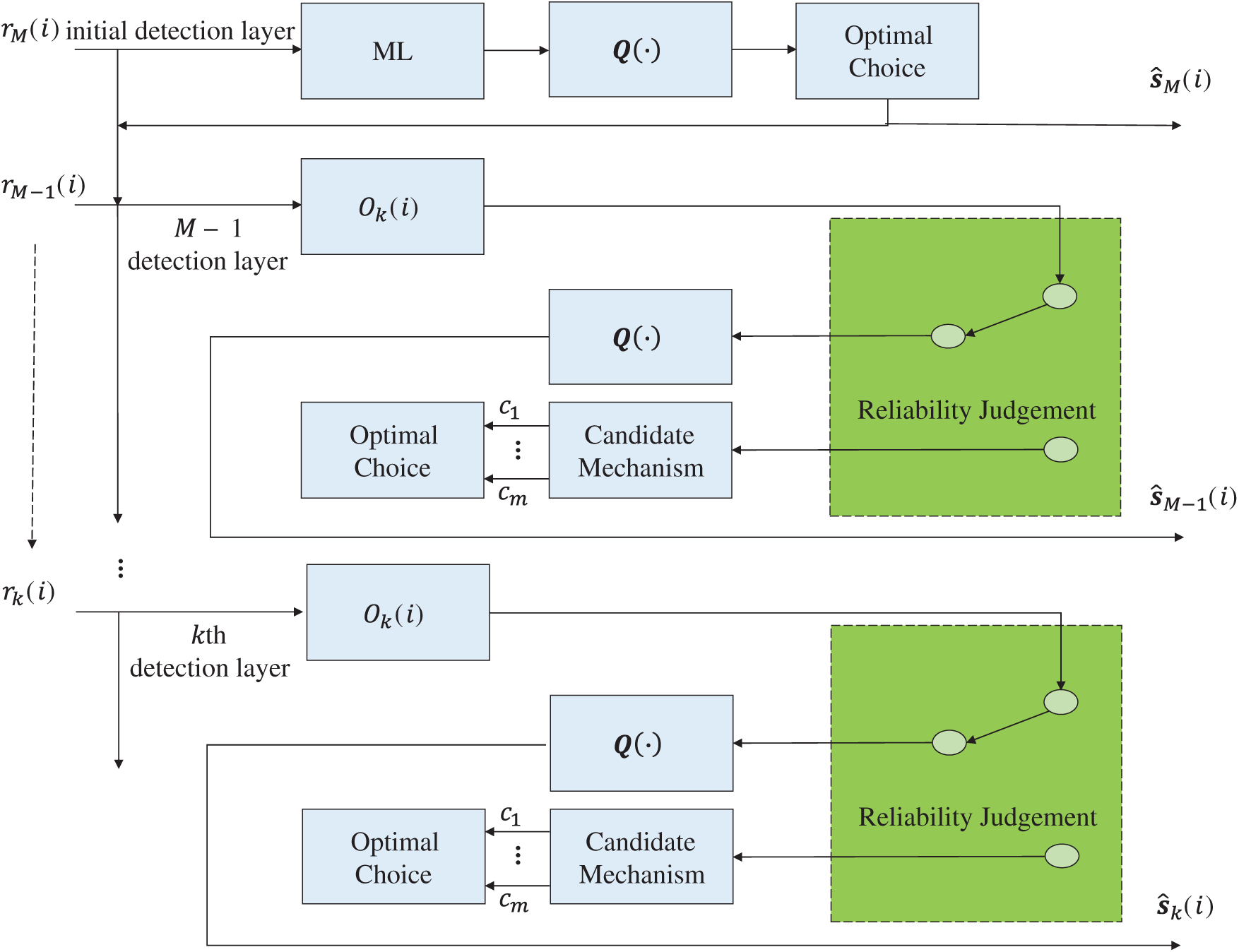
Figure 2: Implementation framework of the proposed ML-QR algorithm

The ML criterion is applied to the initial detection layer of the QR detection algorithm, that is, the modulation constellation points are sequentially used as the estimated model of the first layer, and then the QR detection algorithm is performed on the remaining layers. The optimal constellation point among the constellation points is selected for feedback as the initial detection layer estimation signal. After the initial layer signal is determined, the reliability of the soft estimation of the remaining layers is judged, and if the judgment is reliable, the candidate point is selected for optimal feedback [31].

The reliability decision scheme is shown in Fig. 3. Judging the reliability of the soft decision based on the location of the soft decision point can improve the performance of the algorithm, avoid the redundant tree process, and greatly reduce the computational complexity. In the scheme, the inner circle area represents the reliable area, the center of the circle is the constellation point coordinates, and the unreliable area is represented by the shaded region. The QR decomposition algorithm calculates the soft estimation signal of the transmitted signal hierarchically. If the soft estimation point is located in the shadow area, then it will result in an unreliable soft decision. Conversely, if the soft estimation is located in the white area of the constellation diagram, then the soft estimation is reliable. The candidate mechanism uses the m minimum distances estimated by the near soft estimation as candidate points, and then select the best candidate point from those m candidate points [32].

Figure 3: Reliability decision method using QPSK

First, the modulation constellation points, ς=[c1,c2,…,cL], are successively used as the estimated points of the first detection layer of the QR method. Then, the conventional QR decomposition algorithm is carried out separately, that is, cl is respectively taken from Eq. (10) to obtain the estimated signal pl(i) of the L group, where pl(i)=[cl,sM−1l(i),…,s1l(i)].

If Eq. (11) is satisfied, then ct is the optimal detection of the initial detection layer, and it is also selected as the best feedback symbol of the next layer:

t=arg⁡min1≤l≤L‖r−Hpl(i)‖2(11)

In addition to the initial detection layer, the subsequent detection layer uses OM−1=r^M−1/rM−1,M−1 to obtain the soft estimate of the M−1 layer, and then detects layer by layer to obtain k=M−2,…,1 through layer soft estimation. The reliability of soft estimation is judged by dk. The mathematical expressions for dk and Ok(i) are as follows:

dk=|Ok(i)−af|(12)

Ok(i)=(r^i−∑j=i+1M⁡rijs^j)/rii(13)

where af represents the constellation point closest to the soft estimate Ok(i) of the kth layer.

If the constellation point is represented by A, then af can be described as follows:

af=af∈Aargmin{|Ok(i)−af|}(14)

If dk≥d (d represents the range of reliability), then the soft estimate Ok(i) is present in the shadow region, resulting in an unreliable soft decision of the kth layer. Conversely, if dk≤d, then the soft estimate Ok(i) is located in the reliable area of the constellation diagram, and the soft decision of the kth layer is reliable [27]. When the soft decision is reliable, the soft decision Ok(i) is the reliable point, and the conventional QR decomposition scheme is implemented. The kth layer symbol estimation s^k(i) is obtained by the hard decision s^k(i)=Q[Ok(i)].

The soft decision Ok(i) is an unreliable point, and the candidate points ς=[c1,c2,…,cn,…,cN] will be generated, where N denotes that the candidate-point distance of soft estimation renders Ok(i) as the nearest constellation point. The unreliable decision Q[Ok(i)] is replaced by s^k(i)=cmopt, where cmopt is the best candidate from ς=[c1,c2,…,cn,…,cN].

The process of obtaining optimal feedback candidate points is described next.

To determine the best candidate point, we define the selection vector [b1,b2,…,bn,…,bN], where N is equal to the number of constellation candidates in ς=[c1,c2,…,cn,…,cN]; the vector bn is selected as an M×1 dimensional vector. When the soft estimation of the kth layer is unreliable, the M-layer elements of bn are composed as follows:

•   The previously detected symbols [ct,s^M−1(i),…,s^k+1(i)] range from the Mth layer to the (k + 1)th layer;

•   The kth layer is an unreliable decision Q[Ok(i)] candidate cn selected from the constellation points;

•   The symbols from the k − 1 to the first layer belong to the traditional QR decomposition algorithm

Thus, the following expression can be obtained:

bn(i)=[ct,…,s^k−1,cn,bk+1n,…,bqn(i),…,bMN(i)]T(15)

where bqn(i) is a potential decision:

bqn(i)=Q[(r^q−∑l=q+1Mrq,lb^ln)/rqq],(16)

where q is the index of a certain layer, ranging from k − 1 to 1.

mopt=1≤n≤Nargminr−Hbn(i)2(17)

If the above conditions are met, cmopt is currently the best character for a more reliable user decision, and it is chosen as the best symbol for the next step. The pseudocode of the algorithm is shown in Algorithm 1.

4  Complexity Analysis

4.1 Initial Layer Detection Signal Estimation

The first inspection layer with constellation points is in turn replaced, and a QR decomposition algorithm is in turn performed. The complexity of QR decomposition is mainly based on the decomposition of Q and R, and its computational complexity is {\cal O}(n3). The algorithm proposed in this study is performed after the decomposition algorithm of Q and R. Only Eq. (10) is calculated. The complexity is L{\cal O}(n3), where L is the number of modulation bits.

4.2 Other Detection Layers

The soft judgment reliability judgment is denoted by p. A reliable decision occurs when p=0, whereas p=1 denotes an unreliable decision. The computational complexity calculation is approximately 2M2+pNM2. Note from Figs. 4 and 5 that at 25 dB and 30 dB, the reliability probability of the algorithm detection is very low. The complexity of the QR decomposition detection algorithm is the lowest in the current detection complexity, so it is compared with SIC (computational complexity). For some non-linear detection approaches such as o({\cal O}(n4)), the complexity of the algorithm proposed in this study does not increase significantly, and according to the simulations, the performance of the proposed QR detection algorithm based on the ML criterion is improved notably.

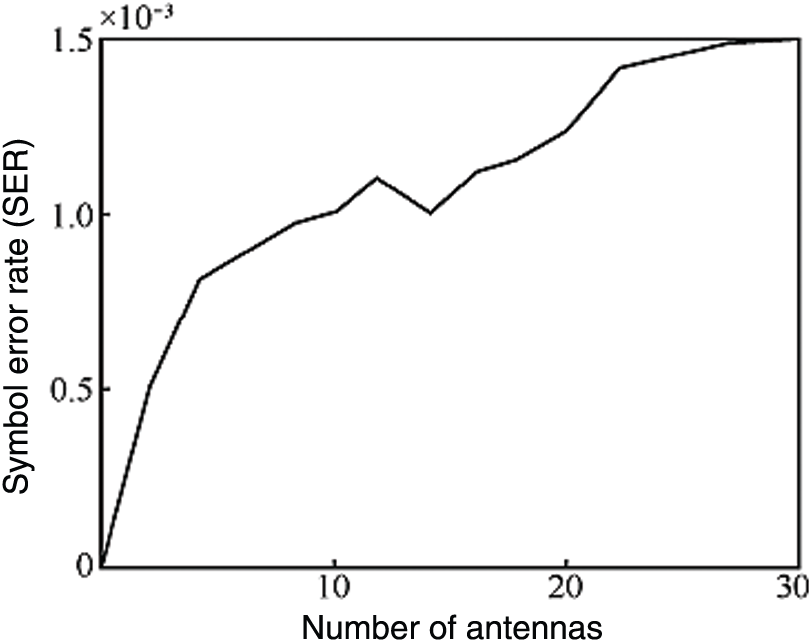
Figure 4: Comparison of the SER vs. number of antennas at SNR = 25 dB

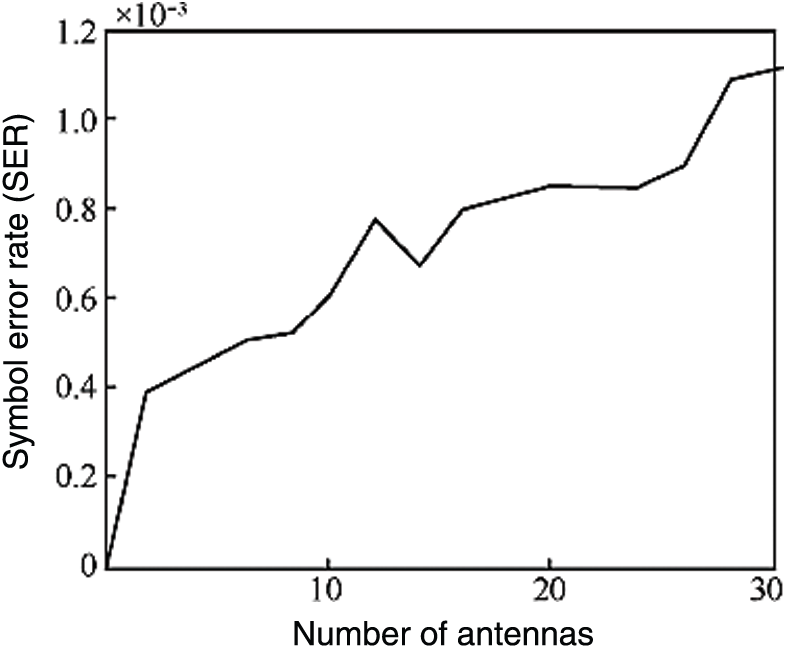
Figure 5: Comparison of the SER vs. number of antennas at SNR = 30 dB

5  Simulation Results and Discussion

Let us assume that under flat Rayleigh fading channel in a multi-antenna system, the data sent by the transmitting antennas are mutually independent, the data frame length is 20,000, the unwoven system and QPSK modulation mode are used, and the algorithm performance is measured by the bit error rate [27].

Fig. 6 shows the performance curve of QR decomposition, the ML-QR algorithm, and the ML detection algorithm assuming an arrangement of 4 × 4 transceiver antennas. The reliable radius d was set to 0.4, and four candidate points were selected. As shown in Fig. 6, the proposed algorithm shows better performance than the conventional QR method. When the BER is 10−2, the proposed method is 10 dB better than the conventional QR method. When the BER is 10−3, the proposed ML-QR algorithm is 15 dB better than the QR decomposition algorithm. Note from Fig. 6 that with the continuous increase in SNR, the BER of the proposed ML-QR algorithm decreases linearly, becoming much lower than that of the traditional QR decomposition algorithm. This shows that for the QR algorithm, the detection sequence is critical, and the performance of the entire system largely depends on the first detection layer. In addition, it is clear from these results that the performance of the proposed algorithm is also close to the performance of the optimal detection algorithm.

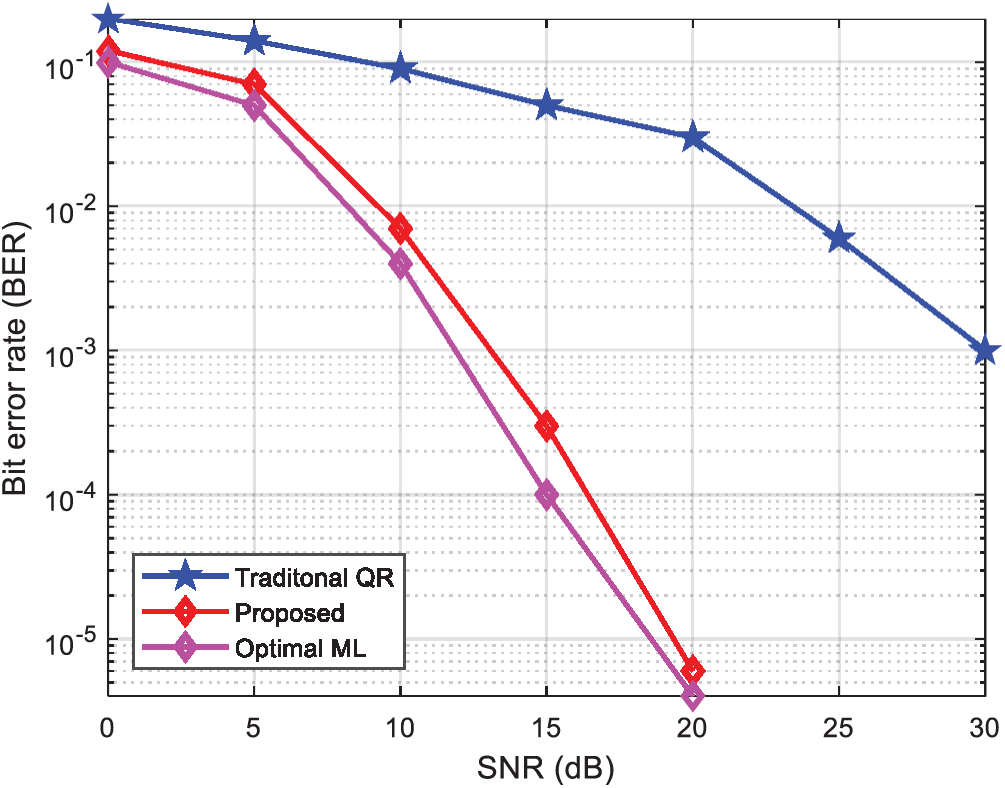
Figure 6: Comparison of the BER for three different algorithms with a 4 × 4 antenna arrangement and QPSK modulation

In Fig. 7 the BER of the proposed method is compared with different numbers of candidates points and thresholds. The Tx-Rx antennas were set in a 4 × 4 arrangement. Note that the BER of the proposed method is better for smaller thresholds. The BER is improved with increasing candidate points. The proposed algorithm mitigates the propagation of false judgments in the entire process of detection, and greatly improves the system performance.

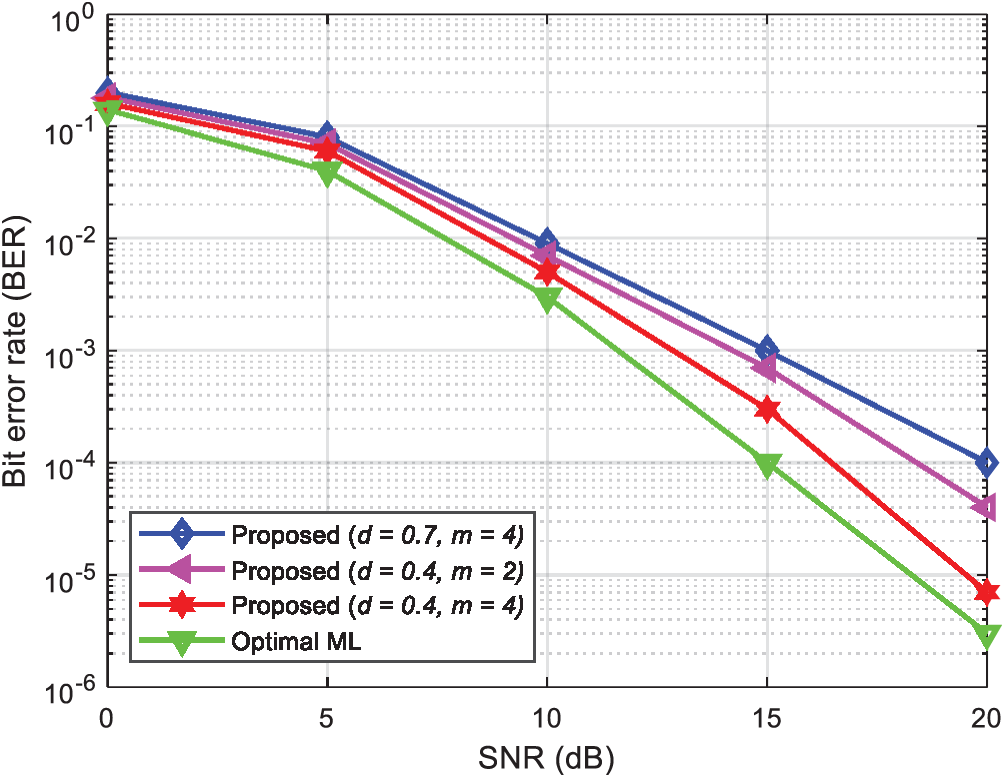
Figure 7: Comparison of the BER under different parameters with a 4 × 4 antenna arrangement and QPSK modulation

Fig. 8 shows the traditional QR decomposition, the proposed algorithm, and optimal ML algorithm performance curves with the optimal threshold of 0.4, four candidate points, and 6 × 6 arrangement of Tx-Rx antennas. Note from Fig. 8 that the proposed algorithm improves the BER by 9.5 dB over the conventional QR method. When the BER is 10−3, the proposed method improves the performance by 15 dB vs. the conventional QR method.

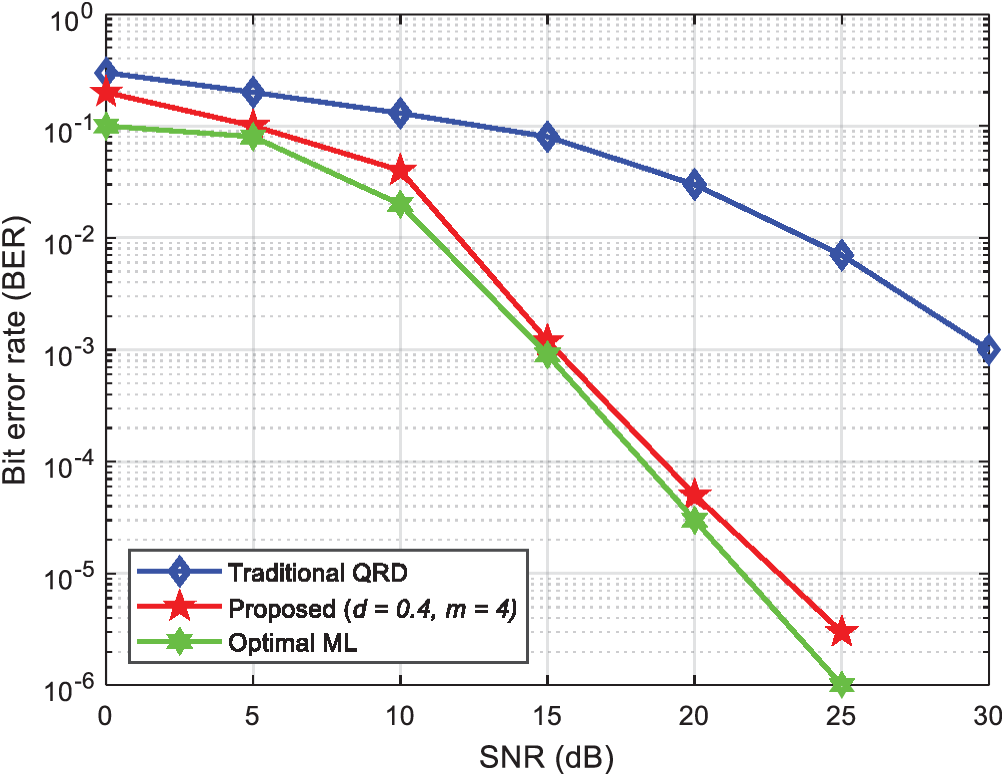
Figure 8: Comparison of the BER for three different algorithms with a 6 × 6 antenna arrangement and QPSK modulation

Fig. 9 shows the performance curves of different reliability radii and candidate points under the condition that the arrangement of transmitting and receiving antennas is 6 × 6. Note that when the candidate points coincide, the smaller the reliability threshold, the better the performance. Likewise, the greater the number of candidate points, the better the performance. Compared with Fig. 5, when the antenna arrangement is 4 × 4, the system performance with a 6 × 6 antenna arrangement decreases, indicating that as the number of antennas increases, the error propagation between antennas increases, resulting in a decrease in system performance.

Overall, the proposed detection algorithm can significantly improve the system performance with a certain degree of complexity. Simultaneously, it can effectively control the performance and complexity of the system through the threshold and the number of candidate points, thereby achieving a balanced compromise between the performance and complexity of the detection algorithm. The ideological response has a positive effect on reducing the cost of IoT communication and improving its reliability.

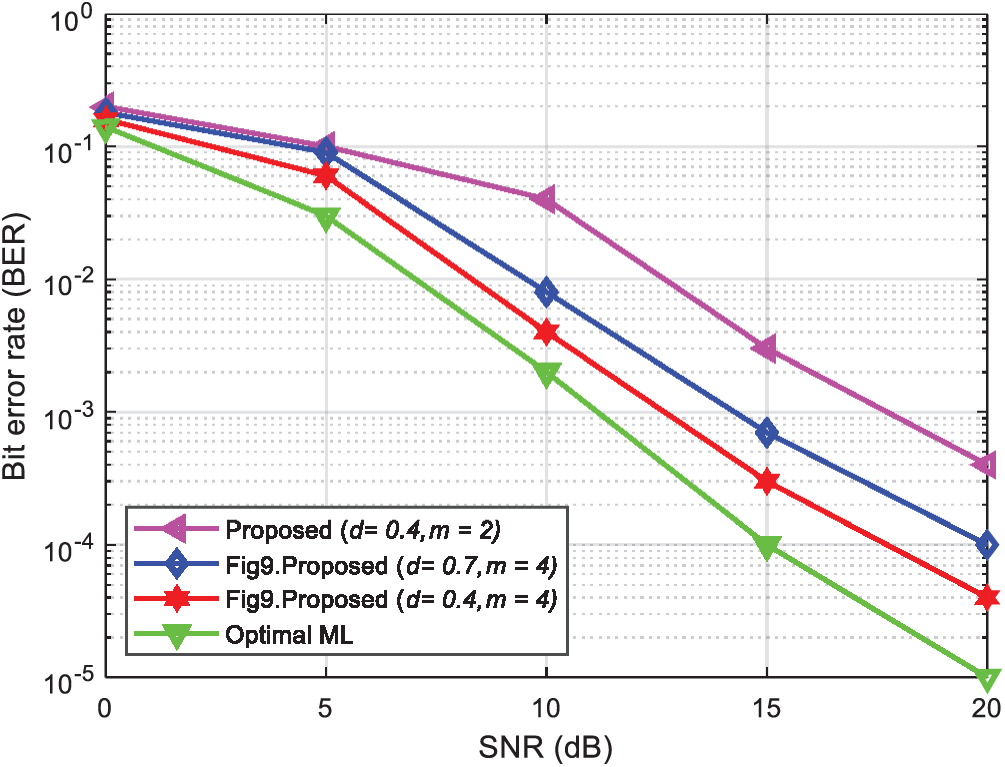
Figure 9: Comparison of the BER under different parameters with a 6 × 6 antenna arrangement and QPSK modulation

6  Conclusion

An effective error detection algorithm can greatly improve the communication performance of the IoT. The proposed algorithm can accurately estimate the initial detection layer signal through the principle of the ML criterion algorithm. Specifically, the proposed system model uses the shadow area constraint to enhance the interference cancelation and effectively reduces the impact of error propagation. In addition, it can ensure that the complexity caused by unreliability is reduced, and the candidate mechanism can be used to suppress the propagation of false judgments in the entire detection process effectively and improve the system performance. According to MATLAB simulations of the system, it is shown that the algorithm can greatly improve the system performance and effectively save the signal-to-noise ratio. In addition, the proposed algorithm can control the computational complexity and improve the system performance according to the threshold and number of candidate points, thereby achieving a good balance between detection performance and complexity. A potential future study could consider the mean square error and throughput analysis.

Acknowledgement: The author extends his appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP.2/23/42), Received by Fahd N. Al-Wesabi. https://www.kku.edu.sa.

Funding Statement: This study is supported by Fujitsu-Waseda Digital Annealer FWDA Research Project and Fujitsu Co-Creation Research Laboratory at Waseda University (Joint Research between Waseda University and Fujitsu Lab). The study was also partly supported by the School of Fundamental Science and Engineering, Faculty of Science and Engineering, Waseda University, Japan. This study was supported by the Institute for Information & Communications Technology Planning & Evaluation (IITP) Grant funded by the Korean government (MSIT) (No.2019-0-01343, Training Key Talents in Industrial Convergence Security) and Research Cluster Project, R20143, by the Zayed University Research Office.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Sun, J. Liu, J. Wang, Y. Cao and N. Kato, “When machine learning meets privacy in 6G: A survey,” IEEE Communications Surveys & Tutorials, vol. 22, no. 4, pp. 2694–2724, 2020. [Google Scholar]

 2.  T. Huang, W. Yang, J. Wu, J. Ma, X. Zhang et al., “A survey on green 6G network: Architecture and technologies,” IEEE Access, vol. 7, pp. 175758–175768, 2019. [Google Scholar]

 3.  A. A. Fuqaha, M. Guizani, M. Mohammadi, M. Aledhari and M. Ayyash, “Internet of things: A survey on enabling technologies, protocols, and applications,” IEEE Communications Surveys & Tutorials, vol. 17, no. 4, pp. 2347–2376, 2015. [Google Scholar]

 4.  M. A. Garadi, A. Mohammed, A. K. Ali, X. Du, I. Ali et al., “A survey of machine and deep learning methods for internet of things (IoT) security,” IEEE Communications Surveys & Tutorials, vol. 22, no. 3, pp. 1646–1685, 2020. [Google Scholar]

 5.  F. Qamar, M. U. A. Siddiqui, M. N. Hindia, R. Hassan and Q. N. Nguyen, “Issues, challenges, and research trends in spectrum management: A comprehensive overview and new vision for designing 6G networks,” Electronics, vol. 9, no. 9, pp. 1–39, 2020. [Google Scholar]

 6.  J. Gojal, E. Monteiro and J. S. Silva, “Security for the internet of things: A survey of existing protocols and open research issues,” IEEE Communications Surveys & Tutorials, vol. 17, no. 3, pp. 1294–1312, 2015. [Google Scholar]

 7.  K. Tange, M. D. Donno, X. Fafoutis and N. Dragoni, “A systematic survey of industrial internet of things security: Requirements and foq computing opportunities,” IEEE Communications Surveys & Tutorials, vol. 22, no. 4, pp. 2489–2520, 2020. [Google Scholar]

 8.  S. Bashir, M. H. Alsharif, I. Khan, M. A. Albreem, A. Sali et al., “MIMO-Terahertz in 6G nano-communications: Channel modeling and analysis,” Computers, Materials & Continua, vol. 66, no. 1, pp. 263–274, 2020. [Google Scholar]

 9.  A. Silva, S. Teodore, R. Dinis and A. Gameiro, “Iterative frequency-domain detection for IA-precoded MC-cDMA systems,” IEEE Transactions on Communications, vol. 62, no. 4, pp. 1240–1248, 2014. [Google Scholar]

10. A. Silva, J. Assucao, R. Dinis and A. Gameiro, “Performance evaluation of IB-dFE based strategies for SC-fDMA systems,” EURASIP Journal on Wireless Communications and Networking, vol. 13, pp. 1–10, 2013. [Google Scholar]

11. D. Castanheira, A. Silva, R. Dinis and A. Gameiro, “Efficient transmitter and receiver designs for SC-fDMA based heterogeneous networks,” IEEE Transactions on Communications, vol. 63, no. 7, pp. 2500–2510, 2015. [Google Scholar]

12. D. Castanheira, A. Silva and A. Gameiro, “Set optimization for efficient interference alignment in heterogeneous networks,” IEEE Transactions on Wireless Communications, vol. 13, no. 10, pp. 5648–5660, 2014. [Google Scholar]

13. S. Teodoro, A. Silva, R. Dinis, F. Barradas, P. M. Cabral and A. Gameiro, “Theoretical analysis of nonlinear amplification effects in massive MIMO systems,” IEEE Access, vol. 7, pp. 172277–172289, 2019. [Google Scholar]

14. F. Jameel, T. Ristaniemi, I. Khan and B. M. Lee, “Simultaneous harvest-and-transmit ambient backscatter communications under Rayleigh fading,” EURASIP Journal on Wireless Communications and Networking, vol. 19, no. 1, pp. 1–9, 2019. [Google Scholar]

15. I. Benkacem, M. Bagaa, T. Taleb, Q. Nguyen, T. Toshitaka and T. Sato, “Integrated ICN and CDN slice as a service,” in IEEE Global Communications Conf., Abu Dhabi, United Arab Emirates, pp. 1–7, 2018. [Google Scholar]

16. Yan C., Q. N. Nguyen, I. Benkacem, D. Okabe, A. Nakao et al., “Design and implementation of integrated ICN and CDN as a video streaming service,” in Int. Conf. on Wired/Wireless Internet Communication, Bologna, Italy, pp. 194–206, 2019. [Google Scholar]

17. W. Shahjehan, S. Bashir, S. L. Mohammed, A. B. Fakhri, A. A. Isaiah et al., “Efficient modulation scheme for intermediate relay-aided IoT networks,” Applied Sciences, vol. 10, no. 6, pp. 1–12, 2020. [Google Scholar]

18. A. M. Mustafa, Q. N. Nguyen, G. I., Ohta and T. Sato, “The design and performance evaluation of 4-sSB using hilbert transform with SISO turbo and shadow equalizer toward 5G communication networks and beyond,” Proc. of Fifth Int. Congress on Information and Communication Technology, Singapore, vol. 1183, pp. 355–363, 2020. [Google Scholar]

19. M. M. Alhasani, Q. N. Nguyen, G. I. Ohta and T. Sato, “A novel four single-sideband M-QAM modulation scheme using a shadow equalizer for MIMO system toward 5G communications,” Sensors, vol. 19, no. 8, pp. 1–20, 2019. [Google Scholar]

20. O. A. Saraereh, A. Alsaraira, I. Khan and B. J. Choi, “A hybrid energy harvesting design for on-body internet-of-things (IoT) networks,” Sensors, vol. 20, no. 2, pp. 1–14, 2020. [Google Scholar]

21. T. Jabeen, Z. Ali, W. U. Khan, F. Jameel, I. Khan et al., “Joint power allocation and link selection for multi-carrier buffer aided relay network,” Electronics, vol. 8, no. 6, pp. 1–15, 2019. [Google Scholar]

22. R. A. Pitaval and B. M. Popovic, “Linea receivers for spectrally-precoded MIMO-OFDM,” IEEE Communication Letters, vol. 21, no. 6, pp. 1269–1272, 2017. [Google Scholar]

23. J. H. Ro, J. K. Kim, Y. H. You and H. K. Song, “Linear approximation signal detection scheme in MIMO-oFDM systems,” Applied Sciences, vol. 8, no. 1, pp. 1–12, 2017. [Google Scholar]

24. T. H. Liu, “Two efficient and stable MMSE detection algorithms for the V-bLAST system,” International Journal of Communication Systems, vol. 26, no. 2, pp. 236–249, 2013. [Google Scholar]

25. B. S. Kim, S. D. Kim, D. Na and K. Choi, “A very complexity QRD-M MIMO detection based on adaptive search area,” Electronics, vol. 9, no. 5, pp. 1–15, 2020. [Google Scholar]

26. N. Murokawa, Y. Ida, T. Mastumoto and S. Mastufuji, “Cr-qrm-mld for sd-sm hybrid MIMO systems,” Transactions on Emerging Telecommunications Technologies, vol. 31, no. 8, pp. 1–19, 2020. [Google Scholar]

27. S. Li, L. Li, B. Xu, Y. Feng and H. Zhou, “Research of a reliable constraint algorithm on MIMO signal detection,” International Journal of Embedded Systems, vol. 12, no. 2, pp. 1–13, 2020. [Google Scholar]

28. A. A. Nimrat, M. Smadi, O. A. Saraereh and I. Khan, “An efficient channel estimation scheme for mmWave massive MIMO systems,” in IEEE Int. Conf. on Communications, Networks and Satellite, Makassar, Indonesia, pp. 1–8, 2019. [Google Scholar]

29. S. Tanabe, A. D. Shigyo and K. Ishibashi, “Not-so-large MIMO signal detection based on damped QR-decomposed belief propagation,” in IEEE Int. Sym. Information Theory and Its Applications, Monterey, CA, pp. 463–467, 2016. [Google Scholar]

30. S. Alemaishat, O. A. Saraereh, I. Khan, S. H. Affes, X. Li et al., “An efficient precoding scheme for millimeter-wave massive MIMO systems,” Electronics, vol. 8, no. 9, pp. 1–16, 2019. [Google Scholar]

31. S. J. Choi, S. J. Shim, Y. H. You, J. Cha and H. K. Song, “Novel mimo detection with improved complexity for near-mL detection in mimo-ofdm systems,” IEEE Access, vol. 7, pp. 60389–60398, 2019. [Google Scholar]

32. C. M. Chen, C. H. Lin and P. Y. Tsai, “Multi-mode sorted QR decomposition for 4 × 4 and 8 × 8 single-user/multi-user MIMO precoding,” in IEEE Int. Sym. on Circuits and Systems, Lisbon, Portugal, pp. 2980–2983, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.