Computers, Materials & Continua DOI:10.32604/cmc.2021.016187
Article

Dynamic Resource Pricing and Allocation in Multilayer Satellite Network

Yuan Li1,7, Jiaxuan Xie1, Mu Xia2, Qianqian Li3, Meng Li4, Lei Guo5,* and Zhen Zhang6

1Tsinghua University, Beijing, 100084, China
2School of Automation, Northwestern Polytechnical University, Xi’an, 710129, China
3University of Science and Technology Beijing, Beijing, 100083, China
4Beijing University of Posts and Telecommunications, Beijing, 100876, China
5Systems Engineering Institute AMS, Beijing, 100071, China
6Audio Analytic, 2 Quayside, Cambridge, CB5 8AB, UK
7Beijing Commsat Technology Development Co., Ltd., Beijing, 100089, China
*Corresponding Author: Lei Guo. Email: guolei_jk@163.com
Received: 26 December 2020; Accepted: 07 April 2021

Abstract: The goal of delivering high-quality service has spurred research of 6G satellite communication networks. The limited resource-allocation problem has been addressed by next-generation satellite communication networks, especially multilayer networks with multiple low-Earth-orbit (LEO) and non-low-Earth-orbit (NLEO) satellites. In this study, the resource-allocation problem of a multilayer satellite network consisting of one NLEO and multiple LEO satellites is solved. The NLEO satellite is the authorized user of spectrum resources and the LEO satellites are unauthorized users. The resource allocation and dynamic pricing problems are combined, and a dynamic game-based resource pricing and allocation model is proposed to maximize the market advantage of LEO satellites and reduce interference between LEO and NLEO satellites. In the proposed model, the resource price is formulated as the dynamic state of the LEO satellites, using the resource allocation strategy as the control variable. Based on the proposed dynamic game model, an open-loop Nash equilibrium is analyzed, and an algorithm is proposed for the resource pricing and allocation problem. Numerical simulations validate the model and algorithm.

Keywords: Resource pricing; resource allocation; satellite network; LEO; dynamic game; Nash equilibrium

1  Introduction

Research of 6G mobile communication has become a major direction for the upgrade of satellite networks for next-generation mobile communication [1]. This integrated space-air-ground network includes satellite and ground communication. Satellite networks facilitate global communication services and enhance network accessibility in areas inaccessible to ground communication networks [2–5].

Many companies have launched low-Earth-orbit (LEO) satellites, the next generation in satellite communication [6], for commercial reasons [7]. Telesat launched 28 innovative LEO satellites integrated with a data network. SpaceX and Commsat plan to launch tens of thousands of LEO satellites to build a global satellite Internet. However, the deployment of LEO satellites can affect satellites already in orbit, especially regarding spectrum resource efficiency. Traditional non-low-Earth-orbit (NLEO) satellites are authorized users with priority to use spectrum resources, and LEO satellites are unauthorized. The use of spectrum resources by LEO satellites interferes with NLEO satellites. Optimum allocation of spectrum resources will help LEO satellites balance user service requirements and address interference problems. The allocation of resources and management of NLEO satellite interference are challenging problems that must be addressed, and research on spectrum resource allocation in satellite communication networks is critically needed [8,9].

Many studies [10–13] have explored the resource allocation of satellite communication networks. A Stackelberg-game-based resource allocation scheme was proposed to divide satellites into two groups based on their priorities [10]. In another study [11], a beam-hopping scheme was used to maximize the network throughput of a cognitive satellite network. Heuristic algorithms were proposed to solve the spectrum distribution problems. Deep reinforcement learning (DRL) was used to dynamically allocate resources in satellite communication networks [12]. A joint power and sub-channel allocation problem was solved using a novel optimization model [13] to address the interference between primary and secondary networks.

To solve resource allocation problems, a dynamic game-based resource allocation scheme in multilayer satellite communication networks, using resource pricing as the main control variable, is proposed. The contributions of this study follow.

1) A dynamic game-based resource pricing and allocation model for LEO satellites, to control service price and resources for mobile users, is proposed.

2) The resource price is formulated as the dynamic state of the LEO satellites, the variation of which is affected by the resource allocation strategy.

3) Each satellite controls the resource allocation based on the Nash equilibrium solution for the proposed model. The optimal strategy is obtained for each satellite.

The rest of this paper is organized as follows. In Section 2, a system model for the research of a multilayer satellite communication network is provided and the resource pricing and allocation problem formulated. In Section 3, the proposed model is analyzed. Numerical simulations and their results are discussed in Section 4. Section 5 concludes the paper.

2  System Model and Problem Formulation

2.1 System Model

Fig. 1 shows a multilayer satellite system, multiple mobile users, multiple LEO satellites, and one NLEO satellite. The NLEO satellite is the authorized user, with the right to use the spectrum resources. The LEO satellites are unauthorized users that cannot use the spectrum resources. They only have access to the spectrum resources if the NLEO satellite is not using them. The satellites are running in orbits, and when an LEO satellite moves into the NLEO satellite coverage area, it shuts down communication to allocate spectrum resources to the NLEO satellite. When not in the NLEO satellite coverage area, LEO satellites can use the spectrum resources. In the proposed multilayer satellite system, the movement of the LEO satellites and periodic usage of spectrum resources cause interference in the NLEO satellite network. Thus, controlling the LEO satellite equipment is crucial to managing their service time. This is an effective solution to the interference problem when LEO satellites are in the NLEO satellite coverage area.

However, the shutdown of LEO satellites will interrupt connected mobile users and increase the waiting time for service. This reduces the quality of service (QoS) and decreases revenue from mobile users. Users whose services are interrupted must be placed in a waiting queue for service recovery, and time in the queue is controlled by LEO satellite service strategies, which are critical to balance QoS and stop interference due to a NLEO satellite.

The multilayer satellite system is formulated herein as a dynamic game system using a dynamic variable state and control variables to optimally allocate the LEO satellites. Fig. 1 shows the multilayer satellite system. LEO satellites should control service prices and times to balance the service and interference due to a NLEO satellite.

Figure 1: System model

2.2 Problem Formulation

It is assumed that N LEO satellites are in the proposed multilayer satellite system. After paying for spectrum resources, the LEO satellites provide mobile services. The communication load of mobile users on LEO satellite i at time t is denoted mi(t), and the resource allocated by the satellite is ri(t). The service latency time is si=mi(t)ri(t), ui is the unit cost of service time, and the cost brought by latency is

ci=uisi=uimi(t)ri(t). (1)

The service price provided by LEO satellite i is denoted pi(t), with i = 1, 2,…, N. LEO satellites charge users a constant price c, which is their minimum operation cost, where pi(t)≥c. Given the service price, LEO satellites earn a profit of

Fi(t)=pi(t)ri(t). (2)

LEO satellites control their pricing strategies, which are considered state variables of the proposed satellite system. The resource allocation strategies are the main criteria used to define resource-pricing strategies because the allocation strategies can affect latency performance [14]. If LEO satellites allocate more resources, then communication service requirements are better satisfied, improving latency performance and lowering the resource price. If the allocated resources for mobile users decrease, then latency performance will be worse, which raises the resource price. When service resources increase, LEO satellites should increase the service price. The relationship between the service price and allocated resources is expressed as

dpi(t)dt=δipi(t)+αimi(t)−βiri(t), (3)

where δi, αi, and βi are weighted parameters.

Spectrum resources are unavailable when LEO satellites are in a NLEO satellite coverage area, and mobile users are placed in a queue. Assuming the arrival rate of a NLEO satellite is λ, following a Poisson distribution, then the probability that the LEO satellites are in a NLEO satellite coverage area is

Prob=λe−λ. (4)

The objective of each LEO satellite is to maximize the revenue earned from mobile users,

Ji(ri,pi)=∫0T[pi(t)ri(t)−uimi(t)ri(t)](1−λe−λ)dt, (5)

subject to

dpi(t)dt=δipi(t)+αimi(t)−βiri(t). (6)

The resource pricing and allocation problem in the multilayer satellite system is formulated as a dynamic game, as follows:

•   The LEO satellites are the players.

•   The system state is the resource price.

•   The strategy of each LEO satellite consists of the allocated resources for mobile users.

3  Game Analysis

The optimal strategies for the proposed problem are now discussed. Based on the system model and problem formulation, a dynamic resource pricing and allocation model is provided, as shown in Fig. 2.

Figure 2: Pricing and allocation model

The Bellman dynamic programming technique is used to solve the proposed dynamic game model. As the resource-pricing strategy is formulated as the system state and the resource allocation strategy is the control variable, the optimal pricing strategy is achieved once the optimal resource allocation strategy for each LEO satellite is obtained. The following definitions must be developed before obtaining the optimal strategies.

Definition 1 The resource allocation strategy ri∗(t) is the optimal strategy for each LEO satellite, which, for all strategies ri(t)≠ri∗(t), satisfies

Ji(t, ri∗(t))≥Ji(t, ri(t)). (7)

To obtain the resource allocation strategy for each LEO satellite, a Hamiltonian function is constructed for the proposed dynamic game model. This is a key component of the Bellman dynamic programming technique [15], and is defined as follows.

Definition 2 The Hamiltonian function of LEO satellite i is

Hi=[pi(t)ri(t)−uimi(t)ri(t)](1−λe−λ)+Λidpi(t)dt, (8)

where Λi(t) is the co-state function, which satisfies

dΛi(t)dt=−∂Hi∂pi(t). (9)

From the Hamiltonian function above, the first derivative is calculated to find the optimal resource allocation strategy for each LEO satellite, as explained by the following theorem.

Theorem 1 The optimal resource allocation strategy ri∗(t) is obtained based on the open-loop Nash equilibrium of the proposed dynamic game in (5) and (6), where pi∗(t) is the corresponding optimal resource pricing strategy if there is a constant function Λi(t) for LEO satellite i that satisfies

ri∗(t)=arg⁡maxri(t)Hi=arg⁡maxri(t){[pi(t)ri(t)−uimi(t)ri(t)](1−λe−λ)+Λi(t)dpi(t)dt}. (10)

Considering the optimal resource allocation and pricing problem given by (3) and (4), based on Pontryagin’s maximum principle, the Nash equilibrium solution is achieved for each LEO satellite, as given in the following theorem.

Theorem 2 There is a unique open-loop Nash equilibrium for each LEO satellite in the resource pricing and allocation problem, with optimal resource allocation strategy

ri∗(t)=[uimi(t)(1−λe−λ)Λiβi−pi(t)(1−λe−λ)]12, (11)

where [pi(t),Λi(t)] are the solutions to the following equations:

dpi(t)dt=δipi(t)+αimi(t)−βi[uimi(t)(1−λe−λ)Λiβi−pi(t)(1−λe−λ)]12, (12)

dΛi(t)dt=−[uimi(t)(1−λe−λ)Λiβi−pi(t)(1−λe−λ)]12(1−λe−λ)−δiΛi(t). (13)

Proof: The partial derivative of the Hamiltonian function given in (8) is calculated, giving

∂Hi∂ri(t)=[pi(t)ri(t)+uimi(t)ri2(t)](1−λe−λ)−Λiβi. (14)

Setting the partial derivative to zero,

ri∗(t)=[uimi(t)(1−λe−λ)Λiβi−pi(t)(1−λe−λ)]12, (15)

where ri∗(t) is the optimal resource allocation strategy for LEO satellite i. Λi(t) is the co-state function, which satisfies

dΛi(t)dt=−∂Hi∂pi(t)=−[uimi(t)(1−λe−λ)Λiβi−pi(t)(1−λe−λ)]12(1−λe−λ)e−ρt−δiΛi(t). (16)

Taking the optimal resource allocation strategy of LEO satellite i into the various functions of the service price,

dpi(t)dt=δipi(t)+αimi(t)−βi[uimi(t)(1−λe−λ)Λiβi−pi(t)(1−λe−λ)]12. (17)

The algorithm to obtain the optimal resource allocation strategy for a LEO satellite is expressed as Algorithm 1.

Based on the proposed algorithm and the Nash equilibrium solutions of the proposed dynamic game, each satellite controls the resource allocation strategy and optimizes the objective function. An optimal pricing strategy is obtained for each satellite. As the differential game-based model is non-cooperative, satellites do not require cooperation. To optimize their objective functions, the satellites non-cooperatively control their resource allocation strategies.

4  Numerical Simulations

Numerical simulations of the optimal pricing strategies and resource allocation strategies of LEO satellites were conducted using one NLEO satellite, which is the authorized user of spectrum resources, and three LEO satellites. When the LEO satellites are in the coverage area of the NLEO satellite, their spectrum resources are retrieved. Tab. 1 provides parameters for the simulations.

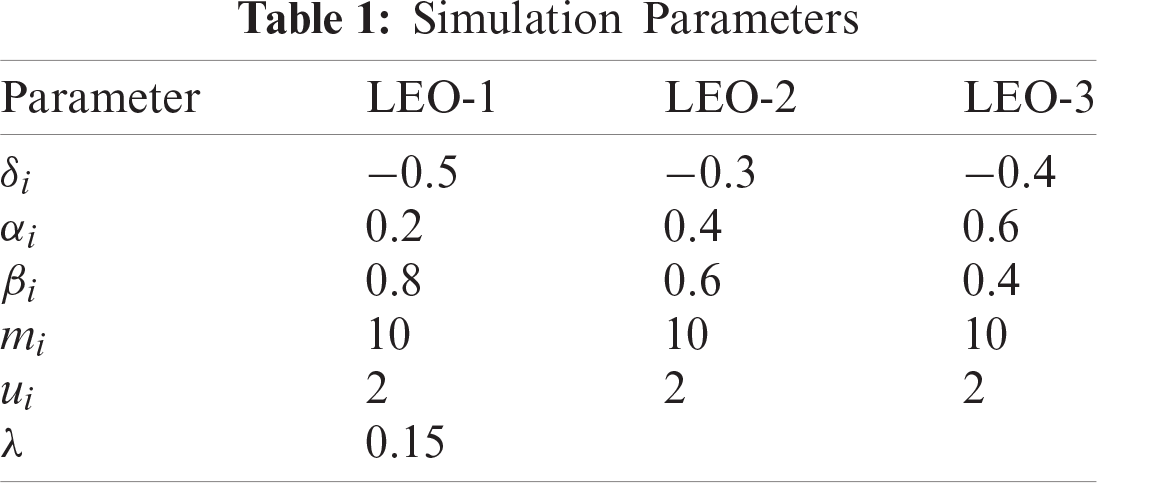
Fig. 3 provides the optimal resource allocation strategies for LEO satellites when the arrival rate of the NLEO satellite is 0.15. The LEO satellites allocate more resources at the beginning of the game to attract mobile users and provide satisfactory service. After approximately five iterations, each LEO satellite decreases the allocated resources to reduce the interference caused by the NLEO satellite. When the resource allocation strategies of the LEO satellites converge, LEO-2 has the most allocated resources and LEO-1 has the least; however, LEO-1 has the fastest convergence rate. Before the resource allocation strategies converge, LEO-3 has the largest value of allocated resources.

Figure 3: Resource allocation strategies when λ = 0.5

The LEO satellite's optimal resource allocation strategies when the arrival rate of the NLEO satellite is changed were also simulated, as shown in Figs. 4a and 4b. The arrival rates of the NLEO satellite in Figs. 4a and 4b are 0.5 and 0.85, respectively. It is shown that the LEO satellites increase the allocated resources at the beginning of the game. After five iterations, the LEO satellites decrease their allocated resources. Comparing the resource allocation strategies in Figs. 4a and 4b with that in Fig. 3, it is observed that the allocated resources decrease with the increase of the NLEO satellite’s arrival rate.

Figure 4: Resource allocation strategies (a) λ=0.5 (b) λ=0.85

Fig. 5 shows the optimal resource-pricing strategies for LEO satellites when the arrival rate of the NLEO satellite is 0.15. The resource-pricing strategy converges to a stable value after five iterations, which is fast. Based on the resource allocation strategies, LEO-2 and LEO-3 will increase their resource price and LEO-1 will decrease its price. LEO-3 has the highest resource price and LEO-1 has the lowest.

Figure 5: Resource pricing strategies when λ = 0.15

5  Conclusions

The resource allocation problem of a multilayer satellite system was investigated and a dynamic game-based resource pricing and allocation model, using differential equations to formulate the resource-pricing strategy of each LEO satellite, proposed. Utility maximization based on an objective function was proposed for each LEO satellite, with the resource allocation strategy as the control variable. Bellman dynamic programming was used to maximize the objective function, and the Nash equilibrium solution of resource allocation of each LEO satellite was obtained. An algorithm was developed for the resource pricing and allocation model, and numerical simulations demonstrated its accuracy.

Funding Statement: This work is supported by the National Natural Science Foundation of China (Grant No. 61971032) and Fundamental Research Funds for the Central Universities (Grant No. FRF-TP-18-008A3).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Peng, T. Dong, R. Gu, Q. Guo, J. Yin et al., “A review of dynamic resource allocation in integrated satellite and terrestrial networks,” in Int. Conf. on Networking and Network Applications, Xi’an, China, pp. 127–132, 2018. [Google Scholar]

 2.  C. Gong, F. Lin, X. Zhou and X. Lü, “Amygdala-inspired affective computing: To realize personalized intracranial emotions with accurately observed external emotions,” China Communications, vol. 16, no. 8, pp. 115–129, 2019. [Google Scholar]

 3.  C. Gong, F. Lin, X. Gong and Y. Lu, “Intelligent cooperative edge computing in internet of things,” IEEE Internet of Things Journal, vol. 7, no. 10, pp. 9372–9382, 2020. [Google Scholar]

 4.  C. Guo, C. Gong, J. Guo, Z. Wei, Y. Han et al., “Software-defined space-air-ground integrated network architecture with the multi-layer satellite backbone network,” Computers, Materials & Continua, vol. 64, no. 1, pp. 527–540, 2020. [Google Scholar]

 5.  L. He, H. Bai, D. Ouyang, C. Wang, C. Wang et al., “Satellite cloud-derived wind inversion algorithm using GPU,” Computers, Materials & Continua, vol. 60, no. 2, pp. 599–613, 2019. [Google Scholar]

 6.  A. Ivanov, M. Stoliarenko, S. Kruglik, S. Novichkov and A. Savinov, “Dynamic resource allocation in LEO satellite,” in 15th Int. Wireless Communications & Mobile Computing Conf., Tangier, Morocco, pp. 930–935, 2019. [Google Scholar]

 7.  S. Xu, X. Wang and M. Huang, “Proportional fairness-based resources allocation algorithm for LEO satellite networks,” in 14th Int. Symp. on Distributed Computing and Applications for Business Engineering and Science, Guiyang, 2015. [Google Scholar]

 8.  H. Wang, A. J. Liu, X. F. Pan and L. L. Jia, “Optimal bandwidth allocation for multi-spot-beam satellite communication systems,” in Proc. 2013 Int. Conf. on Mechatronic Sciences, Electric Engineering and Computer, Shengyang, pp. 2794–2798, 2013. [Google Scholar]

 9.  F. Chiti, R. Fantacci and F. Marangoni, “Advanced dynamic resource allocation schemes for satellite systems,” in IEEE Int. Conf. on Communications, 2005, Seoul, vol. 3, pp. 1469–1472, 2005. [Google Scholar]

10. J. Su, S. Yang, H. Xu and X. Zhou, “A stackelberg differential game-based bandwidth allocation in satellite communication network,” China Communications, vol. 15, no. 8, pp. 205–214, 2018. [Google Scholar]

11. P. Zuo, T. Peng, W. Linghu and W. Wang, “Resource allocation for cognitive satellite communications downlink,” IEEE Access, vol. 6, pp. 75192–75205, 2018. [Google Scholar]

12. X. Hu, S. Liu, R. Chen, W. Wang and C. Wang, “A deep reinforcement learning-based framework for dynamic resource allocation in multibeam satellite systems,” IEEE Communications Letters, vol. 22, no. 8, pp. 1612–1615, 2018. [Google Scholar]

13. Z. Chen, D. Guo, K. An, B. Zhang, X. Zhang et al., “Efficient and fair resource allocation scheme for cognitive satellite-terrestrial networks,” IEEE Access, vol. 7, pp. 145124–145133, 2019. [Google Scholar]

14. H. Li, H. Xu, C. Zhou, X. Lü and Z. Han, “Joint optimization strategy of computation offloading and resource allocation in multi-access edge computing environment,” IEEE Transactions on Vehicular Technology, vol. 69, no. 9, pp. 10214–10226, 2020. [Google Scholar]

15. M. Wang, H. Xu, S. Yang, L. Yang, R. Duan et al., “Non-cooperative differential game based energy consumption control for dynamic demand response in smart grid,” China Communications, vol. 16, no. 8, pp. 107–114, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.