DOI:10.32604/cmc.2021.014759

| Computers, Materials & Continua DOI:10.32604/cmc.2021.014759 |  |
| Article |
An Optimized Convolutional Neural Network Architecture Based on Evolutionary Ensemble Learning
1College of Physical Education and Sports Sciences, University of Kirkuk, Kirkuk, 36001, Iraq
2College of Administration & Economics, University of Kirkuk, Kirkuk, 36001, Iraq
3Department of Information Technology, Institute of Graduate Studies and Research, Alexandria University, Alexandria, Egypt
4Department of Computer Engineering, Alexandria Higher Institute of Engineering & Technology (AIET), Alexandria, Egypt
*Corresponding Author: Saad Darwish. Email: saad.darwish@alexu.edu.eg
Received: 14 October 2020; Accepted: 15 April 2021
Abstract: Convolutional Neural Networks (CNNs) models succeed in vast domains. CNNs are available in a variety of topologies and sizes. The challenge in this area is to develop the optimal CNN architecture for a particular issue in order to achieve high results by using minimal computational resources to train the architecture. Our proposed framework to automated design is aimed at resolving this problem. The proposed framework is focused on a genetic algorithm that develops a population of CNN models in order to find the architecture that is the best fit. In comparison to the co-authored work, our proposed framework is concerned with creating lightweight architectures with a limited number of parameters while retaining a high degree of validity accuracy utilizing an ensemble learning technique. This architecture is intended to operate on low-resource machines, rendering it ideal for implementation in a number of environments. Four common benchmark image datasets are used to test the proposed framework, and it is compared to peer competitors’ work utilizing a range of parameters, including accuracy, the number of model parameters used, the number of GPUs used, and the number of GPU days needed to complete the method. Our experimental findings demonstrated a significant advantage in terms of GPU days, accuracy, and the number of parameters in the discovered model.
Keywords: Convolutional neural networks; genetic algorithm; automatic model design; ensemble learning
Convolutional Neural Networks (CNNs) design has become a rapidly growing area, requiring significant effort on the part of researchers [1]. Numerous common state-of-the-art CNN architectures, such as ResNet [2] and GoogleNet [3], are generated manually by experts. These methods are mostly iterative in nature and necessitate a thorough understanding of the architecture dimensions of CNN models. To address this issue, a research path is taken that focuses on the automation of CNN design through artificial intelligence techniques. The approaches to automated CNN programming are classified into a variety of methodologies, the majority of which are focused on Evolutionary Algorithms (EAs), such as Particle Swarm Optimization (PSO) or Reinforcement Learning (RL) [4]. For RL-based methods, such as those described in [5–10], these methods rely heavily on recurrent networks to serve as the controller for model generation. This approach consumes a significant number of computational power. For instance, in Neural Architecture Search (NAS) [5], the process requires 800 Graphical Processing Units (GPUs) over a three-week span. The successor researchers attempted to reduce computation costs by efficiency enhancements, as described in [6–10], but the RL methods still need a massive computational overhead, ranging from 400 GPUs for 4 days to more than 30 GPUs for 3 days.
For the PSO-based methods described in [11–13], the researchers must discretize the naive PSO, as architecture design is a discrete optimization problem and PSO is continuous in nature [14]. Additionally, the binary PSO inherits certain limitations, one of which is its poor convergence rate [15]. As a consequence, the PSO must be changed to account for the fact that it demands additional work overhead in addition to its high computational expense, which is particularly visible for broad image datasets [16]. EA-based methods are paradigmatic to natural selection [17]. Parallelism is enabled by EAs, which assists in preventing local optima. Genetic Algorithms (GAs) are the most often used EA technique [18]. GAs have been applied in a broad variety of domains and have demonstrated their ability to solve a variety of optimization problems, especially multi-objective problems [19]. In the CNN automated design domain, GA-based methods such as those described in [20] achieved approximately the same efficiency as RL-based methods thus using significantly less resources and time.
When developing lightweight architectures, the designer must take into account the number of parameters, as in MobileNet [21] and SqueezeNet [22]. MobileNet and SqueezeNet have used a mix of basic filters to reduce the architecture’s trainable parameters, thus speeding up training [23]. The issue is that since accuracy is proportional to the number of parameters in the model, the designer must prioritize model size while maintaining accuracy, which is deemed a difficult task [24]. Additionally, manually constructing these models is a difficult challenge due to the designer’s need to handle the various forms of layers and their parameters.
To create our proposed paradigm, we considered the following hypotheses: (1) manually designing CNNs is a time-consuming process that results in suboptimal topologies; (2) using lightweight CNN building blocks will result in a reduction in the number of parameters in discovered models; (3) produced structures would outperform manually designed structures. We consider introducing an automated GA-driven paradigm based on these working hypotheses. The proposed structure is novel in that it completely automates the process of defining lightweight CNN architectures that better match the defined domain dataset in terms of validation accuracy and parameter count.
The achievements estimated to make the study effective and have an effect on the science domain are grouped into three major categories in this proposed work: (1) Architecture Search Method: Introducing an encoding method for variable-length multi-level chromosomes that denotes the CNN model topology that can be used by a specified evolutionary algorithm approach; (2) Architecture Building Elements: Dealing with lightweight building blocks to customize the proposed framework in order to generate CNN topologies with a small number of parameters with predefined parameters; and (3) Ensemble Learning: Build a tailored ensemble at the completion of our system to improve the performance of a committee of the best generated CNN architectures obtained via the proposed framework’s search mechanism.
This section would discuss similar work on automated CNN design methods that use GA. In [20] the authors addressed a technique named Genetic CNN “GeNet” for optimizing CNN architectures by the use of GA. It is based on graph evolution and operates by connecting various convolutional layer nodes. Since the chromosomes are set in duration in this encoding process, the number of CNN nodes and stages must be predefined, preventing the exploration of several different CNN structures. Additionally, since the GeNet method only encodes layer connections, it does not accept other hyperparameters such as the number of generated feature maps, kernel size, dropout rates, or layer pooling.
In [25], a system dubbed “EDEN” was proposed that utilizes GA with two genes chromosomes reflecting the learning rate and a CNN structure. The learning rate gene encodes the value used to train each produced structure. The structure gene specifies the order of the CNN layers and the sort of operations performed by each layer. However, this method of encoding chromosomes with a fixed size results in shallow CNN-generated topologies; additionally, this method does not support skip connections or layer pooling. In [26], the authors addressed a completely automated approach-based GA named “AE-CNN” that evolves CNN topologies using blocks from ResNet and DenseNet. The developers asserted that their algorithm does not need any predefined expert experience to operate efficiently. This strategy needs several GPU days to complete. The authors of [27] suggested a methodology dubbed “CGP-CNN” that employs Cartesian Genetic Programming (CGP) for CNN topology generation. This strategy considers six distinct layers. Due to the predefined matrix dimension, CGP-CNN can only explore a finite number of CNN constructs. According to their experiments, the cost of CGP-CNN calculation is extremely high due to the time-consuming nature of the CNN fitness assessment method.
In addition to the majority voting ensemble, the authors in [28] utilized pre-trained CNN models in the initial population. However, since the produced models are based on basic building elements, the performance accuracy is poor. Recent work in [4] developed a completely automated design algorithm dubbed “CNN-GA” for generating a chromosome based on real numbers. The primary disadvantage is that the chromosome number is predetermined. Additionally, they neglected to account for the completely linked layers that would be encoded inside the created chromosome. We assume that the following gaps exist between the above associated approaches: (1) The majority of similar methods are impractical since they need a large amount of computational power and time to operate; (2) The design of lightweight CNN topologies was not contemplated in these approaches; and (3) The majority of methods did not address the possibility of integrating the generated models within an ensemble structure.
The proposed framework’s overall workflow is depicted in Fig. 1, and it is divided into three major phases: (1) it begins with the generation of an initial random CNN population for use in the GA search process; (2) it uses the GA-based search algorithm to navigate the solution space; and (3) it uses the customized stack ensemble technique to improve the overall output validation accuracy from the GA search process. In the following sub-sections, we describe each part in depth to demonstrate how it works.
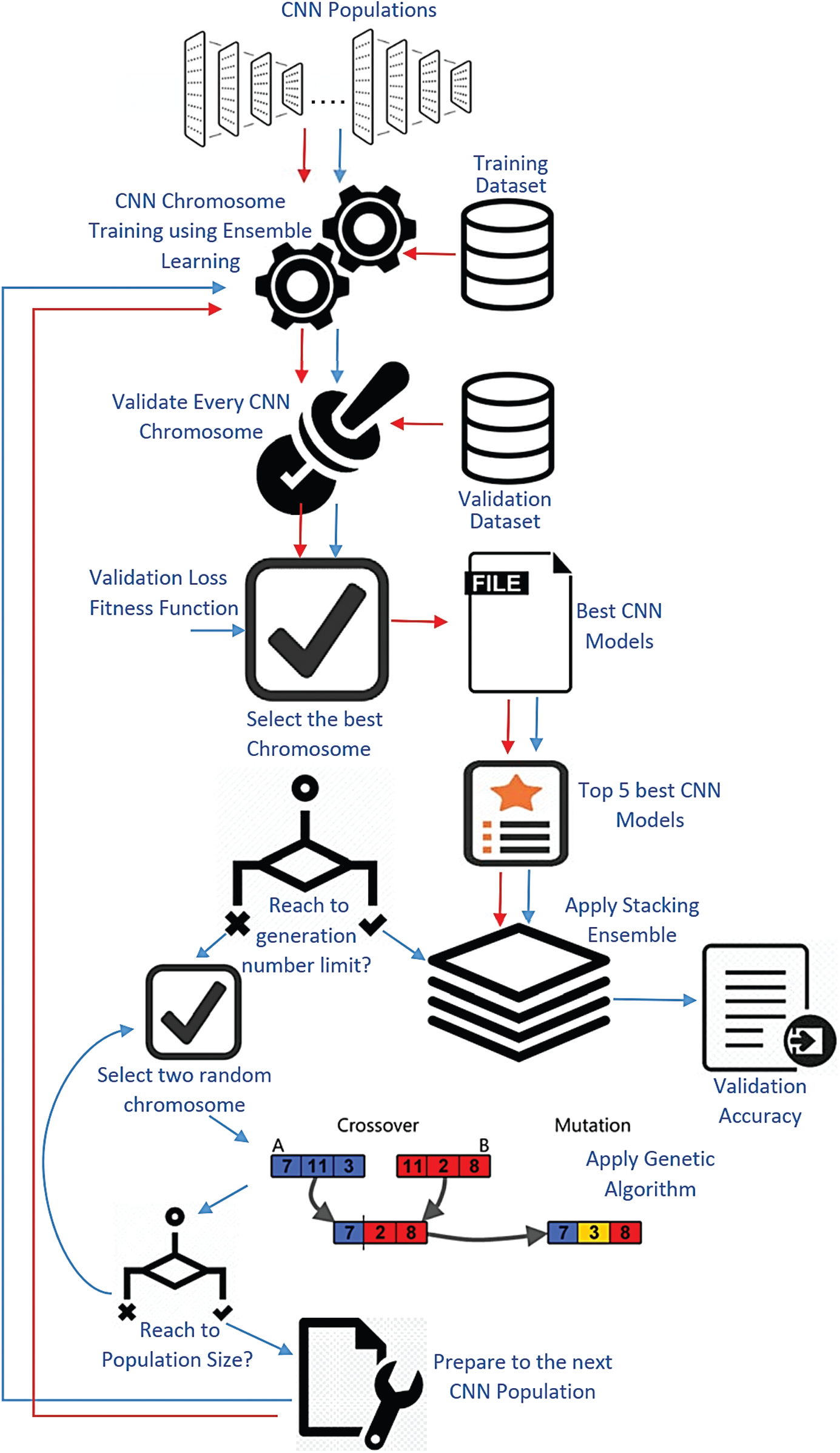
Figure 1: The proposed framework
The proposed framework employs an encoding technique to construct the GA chromosomes that describe the created CNN architectures. Unlike the GeNet method, which is based on a one-dimensional fixed binary encoded chromosome, we suggested a variable multi-level chromosome that encodes CNN parameters using real strings. The following are the benefits of using a multi-level encoding scheme for our chromosomes: (1) It supports a variety of data types; (2) The chromosomes may be expanded in terms of layers inside each block. This chromosome represents a set of blocks; the suggested encoding procedure arbitrarily initializes the number of blocks. Each block is composed of many layers that are randomly initialized. The layer is composed of CNN components.
These components are stored in the components list Lc, which allows the encoding algorithm to choose one or more elements from which to build the layer inside the block. The convolutional module (F), the ReLU activation function (R) [29], batch normalization (B) [30], and dropout units (D) [31] are the layer components. The convolutional module can be Normal Convolution (NC), Depth-Wise Separable Convolution (DSC), or squeeze net fire. The use of various types of convolution, particularly the second and third, enables us to meet the requirement for a lightweight CNN architecture. The method specifies the output (Out) for each block in the produced chromosome. At the end of the chromosome, there is a final block that indicates the existence or absence of fully connected layers in the created CNN model.
3.2 Architecture Search Framework
The central component of our proposed system is the GA-based search approach [32]. The proposed framework begins by initializing some of GA’s primary parameters. A random population of initial CNN architectures is produced using the proposed technique of encoding the CNN chromosomes as nested layers inside sequential blocks. The proposed structure procedure is based on a central iteration loop that regulates evolution through generation. The learning rate is known to be the most critical hyperparameters to tune while training deep CNNs. The Cyclic Learning Rate (CLR) [33] is used in our case since it practically eliminates the need to find the optimal values and schedule for global learning rates experimentally. Early Stopping (ES) is another technique that is used during the training phase [34] and it is a well-known strategy for reducing overfitting during training. This technique significantly reduces training time, as we are training a large number of different created architectures in our case.
The trained CNN is then validated using the given validation dataset in the second stage. The third operation is an assessment process that involves computing the CNN chromosome’s fitness, which in this case is the validation accuracy. The system then selects a predefined number of fittest validated CNN chromosomes and saves them in a list that includes the GA Elitism chromosomes [35]. It mitigates genetic drift by ensuring that the right chromosomes pass on their characteristics across generations. This technique enables the GA to rapidly converge [36]. The GA selection procedure is based on the “Roulette Wheel” strategy of selection [37]. A two-dimensional array is constructed that includes the index of each chromosome, its fitness value, and its probability of selection value. Various operations are performed on the list during the framework process, such as inserting or deleting individuals based on their fitness, as the chromosomes may be substituted by the fittest component of each generation. Additionally, the list is iteratively sorted after each generation. The individual’s fitness function fi is determined as follows:
where TP “True Positives” is the class instances number that is recognized correctly, TN “True Negatives” is the class instances number that is recognized correctly which do not belong to the class, “False Positives” FP is the class instances number that the instances were mistakenly assigned to the class, and “False Negatives” FN is the class instances number that the instances were not recognized within the class instances.
To produce new offspring, the mechanism employs crossover and mutation at predefined rates that are initialized at the algorithm’s outset. The framework must expand its search space to include different regions in order to increase the consistency of solutions, prevent premature convergence, and maintain chromosome diversity; the framework then enters a loop to verify chromosome similarity. The following two Equations describe the relation of two CNN chromosomes ci and cj:
These similarity equations are influenced by the one used in [38], but as previously mentioned, the suggested encoding scheme relies on blocks to build the CNN chromosome, and each block has its own layers. Thus, we must first evaluate the number of blocks nB in the ci and cj to ensure that the blocks are identical in size, and then the number of layers nL inside each block to determine the size of the specified block in one chromosome Bik compared to the corresponding block in the other chromosome Bjk. If they are of similar scale, the system verifies that they share common components such as the ReLU activation function, batch normalization, and dropout units. The suggested framework prevents duplications by repairing the population of CNN entities by mutation.
The new generation is created by combining the existing generation’s descendants with the elite list. Prior to progressing to the next generation, the framework saves the CNN individual with the highest validity accuracy in a list called “Top Global” TG list, which includes the Top-1 CNN architectures from each generation. The key loop iterates until the predefined limit number of generations has been reached. Each CNN in the TG list has a retraining step that optimizes the weights of these CNN architectures over a predefined number of epochs. The proposed framework’s final step makes use of the stacked ensemble, in which each CNN individual with its qualified weights in the global list is combined into the stack ensemble model. To obtain the overall prediction accuracy, the ensemble model is learned and validated.
3.3 The Customized Stack Ensemble
Finally, we add a customized stacking ensemble to the suggested structure [39]. The stacking ensemble approach blends several first-level classifiers by feeding their outputs to a higher-level second-level classifier (meta-classifier). The meta-level classifier is regarded as the ensemble committee’s master classifier. This committee is made up of a variety of base classifiers. Each member of the committee receives unique training in order to obtain varying degrees of classification accuracy. Thus, the best CNN architectures saved in the TG list are used as the base classifiers, while the meta-classifier is chosen to be a completely linked neural network that concatenates the output classification weights from each trained CNN base model’s final layer. To obtain new validation accuracy, the meta-classifier is trained and tested on the benchmark dataset.
3.4 Architecture Building Elements
The lightweight CNN models rely heavily on convolutional modules, which have a small number of trainable parameters in comparison to the standard convolutional module. As a result, we proposed that the layers within the created CNN chromosome blocks be constructed using a modified squeeze fire module. The updated fire module is constructed using Depth-wise Separable Convolution (DSC fire Module) rather than Squeeze Net’s initial fire module, which is constructed using natural convolution (NC fire Module). As opposed to the initial NC fire module, this module reduces the amount of parameters by 68.34 percent [40]. The number of parameters (PFIRE−DSC) is calculated according to:
where I denotes the number of layer input channels, OS denotes the number of channels of squeeze layer output, OE denotes the number of channels of the expand layer output, and SK is the size of the kernel. The skip connection is a structural feature [41]. It functions as shortcuts through the layers, allowing the system to bypass one or more layer. The following explanations justify the usage of skip connections in our work: (1) Skip connections mitigate the effect of vanishing gradients and allow the training of very deep models; (2) They simplify the model during the early stages of training, accelerating the learning process by reusing activations from previous layers [42]; (3) As in [43], skip connections resolve the singularities problem by breaking the neural network nodes permutation symmetries.
4 Experimental Settings and Results
MNIST [44], CIFAR-10 [45], CIFAR-100 [45], and ImageNet [46] were used as benchmark datasets in this study. They are often used datasets by researchers to evaluate various machine learning and image recognition techniques. The significant feature of these datasets is that the item in the sample image often occupies a variety of positions and areas and is not consistent across images. Additionally, they require limited formatting and preprocessing steps.
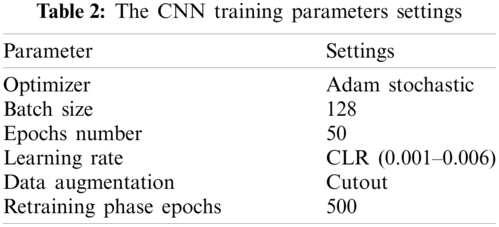
In this subsection, we will demonstrate how to set up experiments, which is a critical part of reproducible research. In our case, the experiment configuration consists primarily of GA parameter settings (as shown in Tab. 1) and CNN training parameter settings (as shown in Tab. 2). To define the maximum number of generations and population size, we must strike a compromise between obtaining the optimal solution and minimizing the time required by GA to perform the search. We found that when the GA reaches 20 generations, there is no improvement; although this calculation does not often guarantee convergence, it is considered a reasonable trade-off for reducing the search time for the method. As in [47,48], the crossover and mutation frequencies are set at 0.9 and 0.03 respectively. For training parameters, we chose to train each produced CNN for 50 epochs with 128 sample batch sizes using the optimizer “Adam stochastic optimization” algorithm [49]. The CLR system is used, with a base learning rate of 0.001 and a maximum learning rate of 0.006. During training, the cutout data augmentation technique [50] is used to prevent overfitting by randomly erasing neighboring pixels in the images to be applied as changed data samples to the dataset. After the GA method is complete, the best architectures are retrained to optimize their weights for 500 epochs.

The proposed architecture is implemented in Python 3 and trained using the Keras framework with a TensorFlow backend. The computer machine used in the experiment has an Intel core-i7-8700K 3.7 GHz CPU and 16 GB of RAM, and all the produced CNN models are trained and validated on a single GPU with the model form “NVIDIA GeForce GTX 1080.”
This subsection would discuss the experimental results obtained for the proposed framework in order to evaluate its success under various configurations of usable architectural building components.
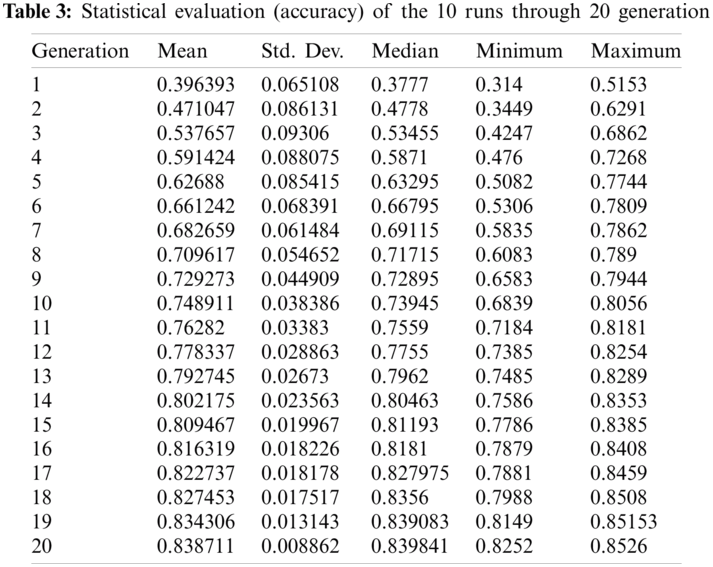
We investigated the impact of four different configurations on the created CNN architectures in terms of performance validation accuracy and parameter number. Normal convolution (NC), depth-wise separable convolution (DSC), NC fire module, and DSC fire module are the four configurations where each configuration is designed to be the primary convolution module for the framework’s CNN model generation. We replicated the experiments ten times on each design on the four datasets chosen to determine the degree of outcome uncertainty. Tab. 3 provides a statistical evaluation of the validation accuracy for the NC fire module configuration for the ImageNet dataset using these ten runs of twenty generations in terms of mean, median, standard deviation, minimum, and maximum. Fig. 2 illustrates the plot of ten runs of this configuration through twenty GA generations in terms of maximal validity accuracy. The plot depicts the search evolution mechanism for feasible validation accuracies in different runs of the proposed framework, which continues to converge over generations. The results in Tabs. 4 and 5 show the performance of the proposed model concerning validity accuracy (Val. Acc.) for the fewest CNN model trainable parameters (Param. #) for the four configurations (see Tab. 4) along with its GPU days needed and stack ensemble overall accuracy (See Tab. 5).
As seen in Tab. 4, when we ran our experiments using the four configurations as the architecture building blocks inside the created CNN chromosomes, we discovered that using the NC fire module or DSC fire module results in an increase in model accuracy and a decrease in parameter number. As a general observation, the configuration that performs the highest in terms of validation accuracy is often the produced CNN models based on the NC Fire Module, while the configuration with the fewest parameters is the generated CNN models based on DSC convolution. Meanwhile, we see that the DSC fire module configuration is superior in these two respects because it enables us to achieve an acceptable level of validation precision with a small number of model trainable parameters, which has a direct effect on the time required for the proposed framework’s GA search operation. The results indicate that the number of parameters in several models, especially DSC-based CNN models, is less than one million trainable parameters, except for ImageNet.
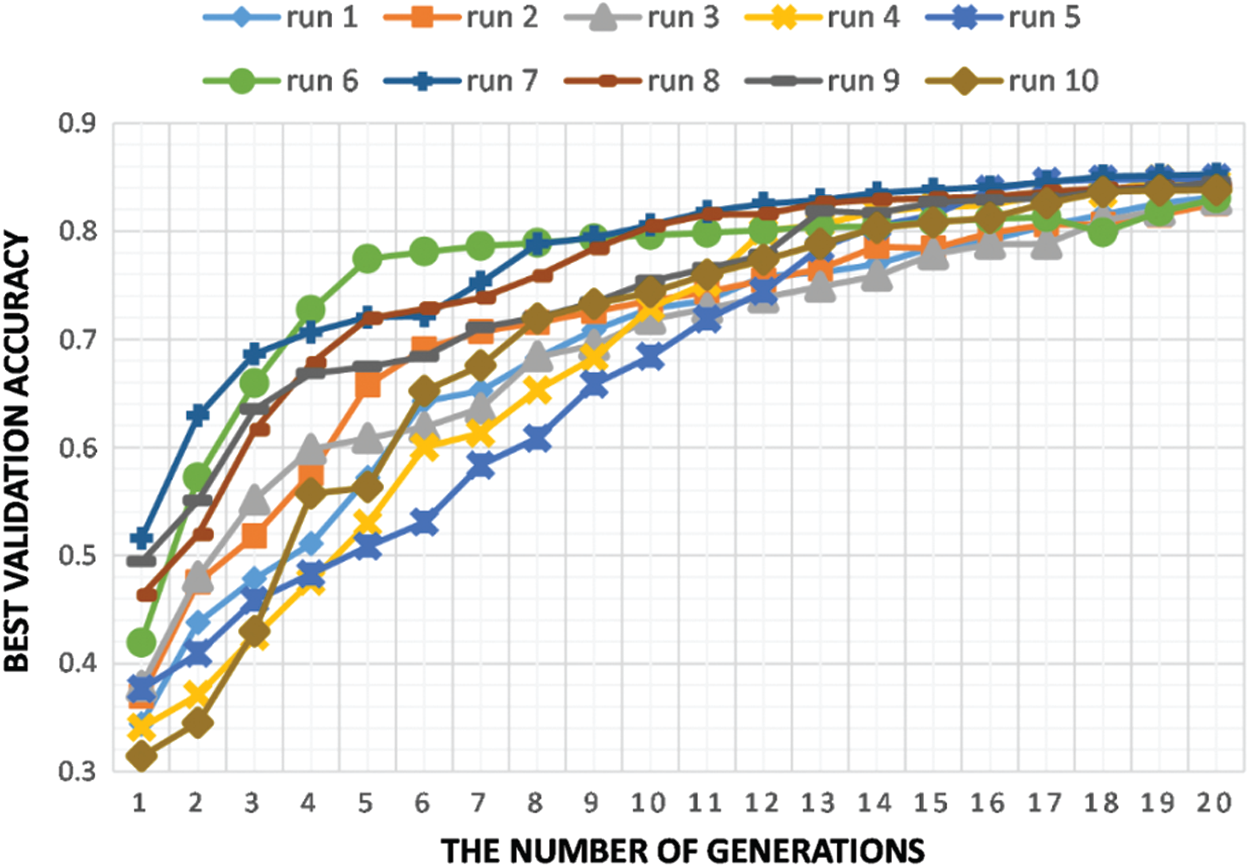
Figure 2: Ten runs of NC fire module configuration on ImageNet
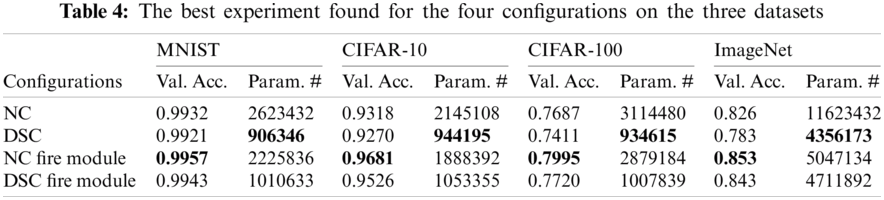
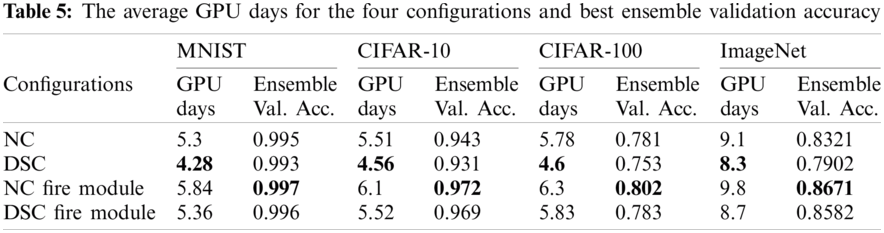
We observed that, on average, the fire modules deepen the produced models without significantly increasing the number of parameters. As shown in Tab. 5, when applied to different datasets, the customized stack ensemble technique improves overall validation accuracy by 0.4 percent to 1.7 percent in the case of the CIFAR-10 dataset and by 0.3% to 1.6% in the case of the CIFAR-100 dataset. In MNIST, the average validity performance improves by 0.09 to 0.18% following stack ensemble. When compared to other datasets, the increase in accuracy due to the stack ensemble process is small in the case of MNIST. This is because the top CNN models trained on MNIST reached nearly slope accuracy prior to entering the stack ensemble process. From a time perspective, the system completed the process in a range of 4.28 to 6.3 GPU days for the three datasets, which is deemed low in comparison to similar work.
4.4.2 Comparison with Related Work
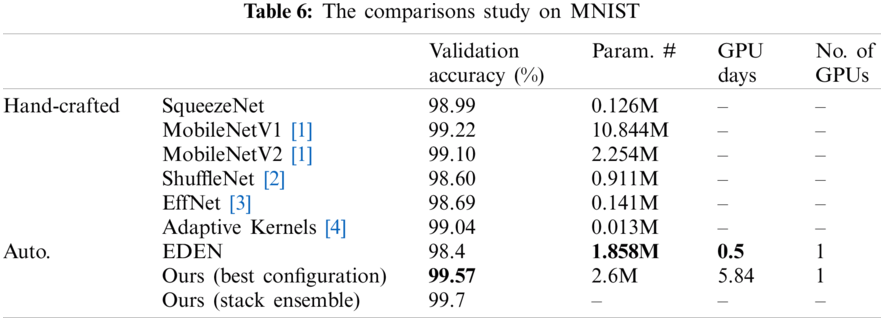
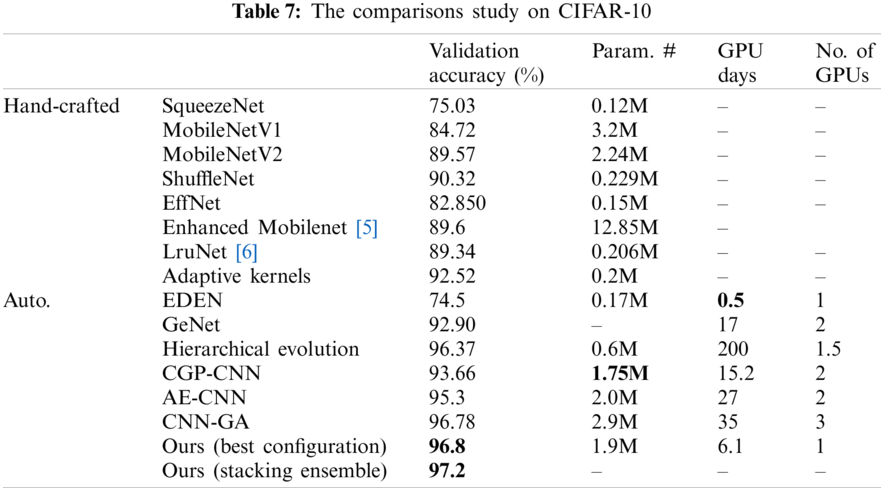
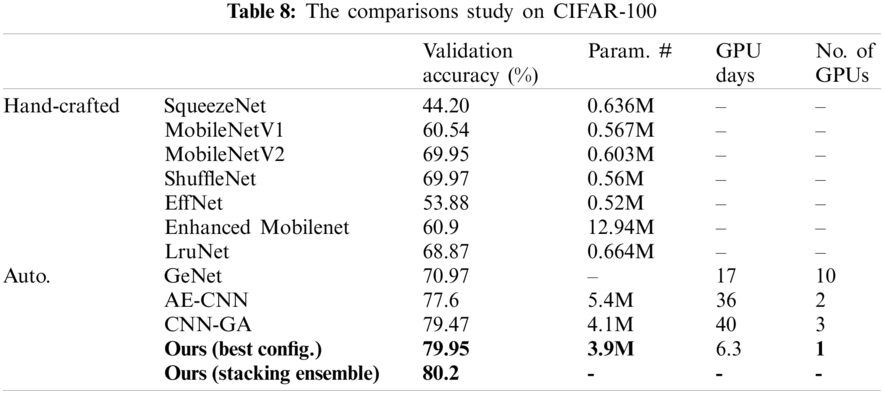
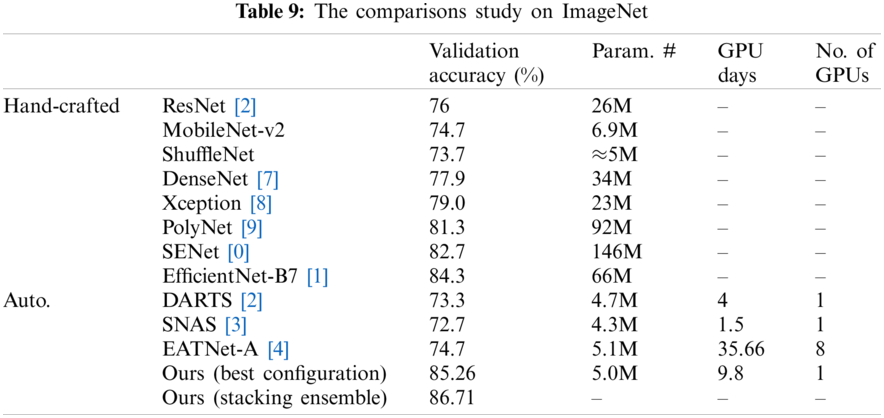
To verify our proposed methodology, we compared it to other related work approaches that make use of the same benchmark datasets using the validation accuracy metric. Additionally, since we concentrated on lightweight and resource-constrained models, we compared the model trainable parameters (Param. #), the GPU days, and the amount (no.) of GPUs used, as seen in Tabs. 6–9. In Tab. 6, we test the proposed framework on the MNIST dataset against EDEN [25]. The suggested framework achieved 1.182% more than their validation accuracy; however, they have a smaller number of parameters for their model and fewer GPU days. As seen in Tab. 7, our validation accuracy beats the best-related peer competitor CNN-GA by 0.02%. While this is a tiny amount, we achieve this precision by reducing the number of parameters by 41% in a CNN model of 1.9 million parameters. As seen in Tab. 8, we achieved a 0.6% increase over CNN-GA by reducing the number of parameters by 5%. In the case of ImageNet in Tab. 9, the ideal configuration improves validation accuracy by 13.2% as opposed to the automated solution EATNet and reduces the number of parameters by 1.98%. Meanwhile, in the hand-crafted domain, the proposed model outperforms EfficientNet by 1.13% in accuracy and significantly reduces the number of parameters.
In this article, we suggested a method for finding lightweight CNN models that is built on a genetic algorithm. To create and reflect CNN models, the proposed architecture employs a novel encoding process. This encoding method is used by the framework search process to describe the created CNN models as solutions in order to construct the solution search space. Validation of the system is performed using a variety of image benchmark datasets. It outperformed competitors in terms of validation precision, GPU days, and model parameter count. Additionally, a stack ensemble approach was adapted for our challenge, and the experiments demonstrate that it outperformed the single best-generated model. Future research would concentrate on reducing the amount of time spent on the search method by proposing and implementing increasingly sophisticated search algorithms. These search algorithms will incorporate multiple-objective fitness requirements in order to handle various facets of the CNN architecture. Another potential enhancement is the addition of new layer elements such as Long-Short Time Memory units or some other kind of layer element capable of accommodating non-sequential models in order to provide a more flexible architecture capable of handling any configuration topology.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Gu, Z. Wang, J. Kuen, L. Ma., A. Shahroudy et al., “Recent advances in convolutional neural networks,” Pattern Recognition, vol. 77, no. 11, pp. 354–377, 2018. [Google Scholar]
2. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Las Vegas, USA, pp. 770–778, 2016. [Google Scholar]
3. C. Szegedy, “Going deeper with convolutions,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 1–9, 2015. [Google Scholar]
4. Y. Sun, B. Xue, M. Zhang, G. Yen and J. Lv, “Automatically designing CNN architectures using the genetic algorithm for image classification,” IEEE Transactions on Cybernetics, vol. 50, no. 9, pp. 3840–3854, 2020. [Google Scholar]
5. B. Zoph and Q. V. Le, “Neural architecture search with reinforcement learning,” in Proc. Int. Conf. on Learning Representations, Toulon, France, pp. 1–16, 2017. [Google Scholar]
6. B. Zoph, V. Vasudevan, J. Shlens and V. Q. Le, “Learning transferable architectures for scalable image recognition,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Salt Lake City, Utah, USA, pp. 8697–8710, 2018. [Google Scholar]
7. Z. Zhong, J. Yan and C. L. Liu, “Practical block-wise neural network architecture generation,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Salt Lake City, Utah, USA, pp. 2423–2432, 2018. [Google Scholar]
8. B. Baker, O. Gupta, N. Naik and R. Raskar, “Designing neural network architectures using reinforcement learning,” in Proc. Int. Conf. on Learning Representations, Toulon, France, pp. 1–18, 2017. [Google Scholar]
9. H. Cai, T. Chen, W. Zhang, Y. Yu and J. Wang, “Efficient architecture search by network transformation,” in Proc. AAAI Conf. on Artificial Intelligence, Louisiana, USA, pp. 2787–2794, 2018. [Google Scholar]
10. H. Pham, M. Guan, B. Zoph, Q. Le and J. Dean, “Efficient neural architecture search via parameter sharing,” in Proc. Int. Conf. on Machine Learning, Sweden, pp. 4092–4101, 2018. [Google Scholar]
11. B. Wang, Y. Sun, B. Xue and M. Zhang, “Evolving deep convolutional neural networks by variable-length particle swarm optimization for image classification,” arXiv: 1803.06492, pp. 1–8, 2018. [Google Scholar]
12. B. Wang, Y. Sun, B. Xue and M. Zhang, “A hybrid differential evolution approach to designing deep convolutional neural networks for image classification,” in Proc. Int. Joint Conf. on Artificial Intelligence, Wellington, New Zealand, pp. 237–250, 2018. [Google Scholar]
13. B. Fielding and L. Zhang, “Evolving image classification architectures with enhanced particle swarm optimization,” IEEE Access, vol. 6, pp. 68560–68575, 2018. [Google Scholar]
14. R. Hassan, B. Cohanim, O. Weck and G. Venter, “A comparison of particle swarm optimization and the genetic algorithm,” in Proc. AIAA Structural Dynamics, and Materials Conf., Texas, pp. 1–13, 2005. [Google Scholar]
15. Z. Beheshti and S. Shamsuddin, “A review of population-based meta-heuristic algorithms,” International Journal of Soft Computing and Its Applications, vol. 5, no. 1, pp. 1–35, 2013. [Google Scholar]
16. A. Darwish, A. E. Hassanien and S. Das, “A survey of swarm and evolutionary computing approaches for deep learning,” Artificial Intelligence Review, vol. 53, no. 3, pp. 1767–1812, 2020. [Google Scholar]
17. K. O. Stanley, J. Clune, J. Lehman and R. Miikkulainen, “Designing neural networks through neuro-evolution,” Nature Machine Intelligence, vol. 1, no. 1, pp. 24–35, 2019. [Google Scholar]
18. A. Dastanpour and R. Mahmood, “Feature selection based on genetic algorithm and support vector machine for intrusion detection system,” in Proc. Int. Conf. on Informatics Engineering and Information Science, Kuala Lumpur, Malaysia, pp. 169–181, 2013. [Google Scholar]
19. Y. Sun, G. Yen and Z. Yi, “IGD indicator-based evolutionary algorithm for many-objective optimization problems,” IEEE Transactions on Evolutionary Computation, vol. 23, no. 2, pp. 173–187, 2019. [Google Scholar]
20. L. Xie and A. Yuille, “Genetic CNN,” in Proc. Int. Conf. on Computer Vision, Venice, pp. 1388–1397, 2017. [Google Scholar]
21. A. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang et al., “Mobilenets: Efficient convolutional neural networks for mobile vision applications,” arXiv: 1704.04861, pp. 1–9, 2017. [Google Scholar]
22. F. N. Iandola, S. Han, M. W. Moskewic, K. Ashraf, W. J. Dally et al., “Squeezenet: Alexnet-level accuracy with 50
23. J. Zhou, H. N. Dai and H. Wang, “Lightweight convolution neural networks for mobile edge computing in transportation cyber physical systems,” ACM Transactions on Intelligent Systems and Technology, vol. 10, no. 6, pp. 1–20, 2019. [Google Scholar]
24. Y. Huang, Y. Cheng, A. Bapna, O. Firat, D. Chen et al., “Gpipe: Efficient training of giant neural networks using pipeline parallelism,” in Proc. Advances in Neural Information Processing Systems Conf., Vancouver, Canada, pp. 103–112, 2019. [Google Scholar]
25. E. Dufourq and B. Bassett, “A EDEN: Evolutionary deep networks for efficient machine learning,” in Proc. Robotics and Mechatronics Conf., Bloemfontein, South Africa, pp. 110–115, 2017. [Google Scholar]
26. Y. Sun, B. Xue, M. Zhang and G. G. Yen, “Completely automated CNN architecture design based on blocks,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 4, pp. 1242–1254, 2019. [Google Scholar]
27. M. Suganuma, S. Shirakawa and T. Nagao, “A genetic programming approach to designing convolutional neural network architectures,” in Proc. Genetic and Evolutionary Computation Conf., Berlin, Germany, pp. 497–504, 2017. [Google Scholar]
28. A. A. Ahmed, S. Darwish and M. M. El-Sherbiny, “A novel automatic CNN architecture design approach based on genetic algorithm,” in Proc. Int. Conf. on Advanced Intelligent Systems, Cairo, Egypt, pp. 473–482, 2019. [Google Scholar]
29. V. Nair and G. E. Hinton, “Rectified linear units improve restricted Boltzmann machines,” in Proc. Int. Conf. on Machine Learning, Haifa, Israel, pp. 807–814, 2010. [Google Scholar]
30. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. Int. Conf. Machine Learning, Lille, France, pp. 448–456, 2015. [Google Scholar]
31. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, “Dropout: A simple way to prevent neural networks from overfitting,” Journal of Machine Learning Research, vol. 15, pp. 1929– 1958, 2014. [Google Scholar]
32. D. Lin and C. Lee, “A multi-level GA search with application to the resource-constrained re-entrant flow shop scheduling problem,” World Academy of Science, Engineering and Technology, vol. 6, pp. 788–792, 2012. [Google Scholar]
33. L. N. Smith, “Cyclical learning rates for training neural networks,” in Proc. Workshop on Applications of Computer Vision, Santa Rosa, California, pp. 464–472, 2017. [Google Scholar]
34. L. Prechelt, “Early stopping–-but when?,” in Lecture Notes in Computer Science. vol. 1524. Berlin, Heidelberg: Springer, pp. 53–67, 2012. [Google Scholar]
35. C. Ahn and R. Ramakrishna, “Elitism-based compact genetic algorithms,” IEEE Transactions on Evolutionary Computation, vol. 7, no. 4, pp. 367–385, 2003. [Google Scholar]
36. H. Du, Z. Wang, W. Zhan and J. Guo, “Elitism and distance strategy for selection of evolutionary algorithms,” IEEE Access, vol. 6, pp. 44531–44541, 2018. [Google Scholar]
37. P. Esfahanian and M. Akhavan, “GACNN: Training deep convolutional neural networks with genetic algorithm,” arXiv: 1909.13354, pp. 1–17, 2019. [Google Scholar]
38. A. Baldominos, Y. Saez and P. Isasi, “Evolutionary convolutional neural networks: An application to handwriting recognition,” Neurocomputing, vol. 283, no. 3, pp. 38–52, 2018. [Google Scholar]
39. J. Thorne, M. Chen, G. Myrianthous, J. Pu, X. Wang et al., “Fake news stance detection using stacked ensemble of classifiers,” in Proc. EMNLP Workshop: Natural Language Processing Meets Journalism, Copenhagen, Denmark, pp. 80–83, 2017. [Google Scholar]
40. A. Santos, C. de Souza, C. Zanchettin, D. Macedo, A. L. Oliveira et al., “Reducing squeezenet storage size with depthwise separable convolutions,” in Proc. Int. Joint Conf. on Neural Networks, Rio de Janeiro, Brazil, pp. 1–6, 2018. [Google Scholar]
41. R. Srivastava, K. Greff and J. Schmidhuber, “Highway networks,” arXiv: 1505.00387, pp. 1–6, 2015. [Google Scholar]
42. A. Smith, B. Wyk and S. Du, “CNNs and transfer learning for lecture venue occupancy and student attention monitoring,” in Proc. Int. Symp. on Visual Computing, Lake Tahoe, NV, USA, pp. 383–393, 2019. [Google Scholar]
43. A. Orhan and X. Pitkow, “Skip connections eliminate singularities,” in Proc. Int. Conf. on Machine Learning, Stockholm, Sweden, pp. 1–22, 2018. [Google Scholar]
44. Y. LeCun, L. Bottou, Y. Bengio and P. Haffner, “Gradient based learning applied to document recognition,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. [Google Scholar]
45. A. Krizhevsky and G. Hinton, “Learning multiple layers of features from tiny images, vol. 1, Toronto, ON, Canada: University of Toronto, Technical Report, 2009. [Google Scholar]
46. J. Deng, W. Dong, R. Socher, L. Li, K. Li et al., “Imagenet: A large-scale hierarchical image database,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Miami, Florida, USA, pp. 248–255, 2009. [Google Scholar]
47. A. Hassanat, K. Almohammadi, E. Alkafaween, E. Abunawas, A. Hammouri et al., “Choosing mutation and crossover ratios for genetic algorithms–-A review with a new dynamic approach,” Information, vol. 10, no. 12, pp. 390, 2019. [Google Scholar]
48. D. L. Tong and R. Mintram, “Genetic algorithm-neural network (GANNA study of neural network activation functions and depth of genetic algorithm search applied to feature selection,” International Journal of Machine Learning and Cybernetics, vol. 1, no. 1, pp. 75–87, 2010. [Google Scholar]
49. D. Kingma and J. Ba, “Adam: A method for stochastic optimization,” in Proc. Int. Conf. on Learning Representations, San Diego, CA, USA, pp. 1–15, 2015. [Google Scholar]
50. T. DeVries and G. W. Taylor, “Improved regularization of convolutional neural networks with cutout,” arXiv: 1708.04552, pp. 1–8, 2017. [Google Scholar]
51. M. Sandler, A. Howard, M. Zhu, A. Zhmoginov and L. C. Chen, “Mobilenetv2: Inverted residuals and linear bottlenecks,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, Utah, USA, pp. 4510–4520, 2018. [Google Scholar]
52. X. Zhang, X. Zhou, M. Lin and J. Sun, “ShuffleNet: An extremely efficient convolutional neural network for mobile devices,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Salt Lake City, Utah, USA, pp. 6848–6856, 2018. [Google Scholar]
53. I. Freeman, L. Roese-Koerner and A. Kummert, “Effnet: An efficient structure for convolutional neural networks,” in Proc. Int. Conf. on Image Processing, Athens, Greece, pp. 6–10, 2018. [Google Scholar]
54. J. Esquivel, A. Vargas, P. Meyer and O. Tickoo, “Adaptive convolutional kernels,” in Proc. Int. Conf. on Computer Vision, Seoul, Korea, pp. 1998–2005, 2019. [Google Scholar]
55. H. Y. Chen and C. Y. Su, “An enhanced hybrid mobilenet,” in Proc. Int. Conf. on Awareness Science and Technology, Fukuoka, Japan, pp. 308–312, 2018. [Google Scholar]
56. O. Köpüklü, M. Babaee, S. Hörmann and G. Rigoll, “Convolutional neural networks with layer reuse,” in Proc. Int. Conf. on Image Processing, Taipei, Taiwan, pp. 345–349, 2019. [Google Scholar]
57. G. Huang, Z. Liu, L. V. D. Maaten and K. Q. Weinberger, “Densely connected convolutional networks,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Hawaii, USA, pp. 4700–4708, 2017. [Google Scholar]
58. F. Chollet, “Xception: Deep learning with depth-wise separable convolutions,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Hawaii, USA, pp. 1610–02357, 2017. [Google Scholar]
59. X. Zhang, Z. Li, C. Loy and D. Lin, “Polynet: A pursuit of structural diversity in very deep networks,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, pp. 3900–3908, 2017. [Google Scholar]
60. J. Hu, L. Shen and G. Sun, “Squeeze-and-excitation networks,” in Proc. Int. Conf. on Computer Vision and Pattern Recognition, Salt Lake City, Utah, USA, pp. 132–7141, 2018. [Google Scholar]
61. M. Tan and Q. V. Le, “Efficientnet: Rethinking model scaling for convolutional neural networks,” arXiv: 1905.11946, pp. 1–10, 2019. [Google Scholar]
62. H. Liu, K. Simonyan and Y. Yang, “DARTS: Differentiable architecture search,” in Proc. Int. Conf. on Learning Representations, New Orleans, USA, 2019. [Google Scholar]
63. S. Xie, H. Zheng, C. Liu and L. Lin, “SNAS: Stochastic neural architecture search,” in Proc. Int. Conf. on Learning Representations, Vancouver, Canada, 2018. [Google Scholar]
64. J. Fang, Y. Chen, X. Zhang, Q. Zhang, C. Huang et al., “EAT-NAS: Elastic architecture transfer for accelerating large-scale neural architecture search,” arXiv: 1901.05884, pp. 1–10, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |