Computers, Materials & Continua DOI:10.32604/cmc.2021.018052
Article

Image Authenticity Detection Using DWT and Circular Block-Based LTrP Features

Marriam Nawaz1, Zahid Mehmood2,*, Tahira Nazir1, Momina Masood1, Usman Tariq3, Asmaa Mahdi Munshi4, Awais Mehmood1 and Muhammad Rashid5

1Department of Computer Science, University of Engineering and Technology, Taxila, 47050, Pakistan
2Department of Computer Engineering, University of Engineering and Technology, Taxila, 47050, Pakistan
3College of Computer Engineering and Sciences, Prince Sattam bin Abdulaziz University, Al-Kharj, 11942, Saudi Arabia
4College of Computer Science and Engineering, University of Jeddah, Jeddah, 21577, Saudi Arabia
5Department of Computer Engineering, Umm Al-Qura University, Makkah, 21421, Saudi Arabia
*Corresponding Author: Zahid Mehmood. Email: zahid.mehmood@uettaxila.edu.pk
Received: 23 February 2021; Accepted: 19 April 2021

Abstract: Copy-move forgery is the most common type of digital image manipulation, in which the content from the same image is used to forge it. Such manipulations are performed to hide the desired information. Therefore, forgery detection methods are required to identify forged areas. We have introduced a novel method for features computation by employing a circular block-based method through local tetra pattern (LTrP) features to detect the single and multiple copy-move attacks from the images. The proposed method is applied over the circular blocks to efficiently and effectively deal with the post-processing operations. It also uses discrete wavelet transform (DWT) for dimension reduction. The obtained approximate image is distributed into circular blocks on which the LTrP algorithm is employed to calculate the feature vector as the LTrP provides detailed information about the image content by utilizing the direction-based relation of central pixel to its neighborhoods. Finally, Jeffreys and Matusita distance is used for similarity measurement. For the evaluation of the results, three datasets are used, namely MICC-F220, MICC-F2000, and CoMoFoD. Both the qualitative and quantitative analysis shows that the proposed method exhibits state-of-the-art performance under the presence of post-processing operations and can accurately locate single and multiple copy-move forgery attacks on the images.

Keywords: Copy-move forgery; discrete wavelet transform; LTrP features; image forensic; circular blocks

1  Introduction

In this digital era, digital devices’ economic prices have enabled people to keep using a variety of smart devices like cell phones, digital cameras, tabs, and laptops, etc. People usually buy these devices to perform their daily tasks. However, these gadgets also allow them to save their memories in digital format such as in the form of images and videos [1]. At the same time, it is also very easy for them to acquire apps and tools that can easily alter this digital data and change the information conveyed through them [2,3]. Although the availability of such tools and apps can help people to make their data more appealing and delighting. At the same time, it can also make the conveyed information unreliable and untrusted especially, in such scenarios where these images and videos are used in investigating a criminal case or processing legal claims. The method of forging image information is known as digital image forgery. The approaches used to identify the forensic changes made are known as forgery detection (FD) techniques. These approaches have been categorized into two classes namely the active and passive methods [4]. Active methods are only workable for those scenarios where the information of the source images like watermarks or digital signatures is available [5,6]. Therefore, mostly passive techniques are employed to identify the two types of image manipulations, namely the copy-move forgery (CMF) and the splicing [7]. In the case of generating a spliced forged image, the contents of different images are merged [8]. While for CMF, the information of the same image is used to manipulate its content. CMF is more challenging as the overall properties of the image are not altered. Fig. 1 is representing an example of CMF.

Figure 1: An example of CMF. (a) Original image, (b) Copy-move attack (dublicated object highlighted)

The FD methods are categorized into two types namely: i) the block-based FD techniques ii) the keypoints-based FD methods [9]. In the block-based FD approaches, the suspected image is divided into overlapping blocks where FD techniques are applied on each block. These approaches usually suffer from high computational costs. In contrast, keypoints-based FD methods work by computing the key features of the whole suspected image. These approaches are computationally robust and exhibit better detection performance for the high textured forged images [10]. As generating CMF content does not require special skills, so, in daily life scenarios, it is very easy for a person to manipulate image content. Therefore, the need of the hour is to introduce such techniques that can efficiently detect these forensic changes. Although, until now, several techniques have been introduced in the field of copy-move forgery detection (CMFD), there is no generalized method that can give a promising performance under the presence of various post-processing attacks like scaling, rotation, noise and JPEG compression, etc.

In the proposed method, we have introduced a novel technique for the CMFD. First, the input image is converted into a grey-scale image, on which the DWT approach is applied for dimension reduction. The obtained approximate image sub-band is then converted into circular blocks. Next, the local tetra pattern (LTrP) algorithm is applied over overlapped circular blocks to calculate each block’s feature vector. Finally, the Jeffreys and Matusita distance is computed to determine the similarity among the data points. We have evaluated the proposed method over the different post-processing image operations like scaling, rotation, blurring, brightness reduction, and compression. Experimental results indicate that the proposed method exhibits a state-of-the-art performance while compared with its competitor's methods.

The following are the main contributions of the proposed method:

•   The light encoded features enable the proposed method to identify copied regions from the input forged image accurately, even under the presence of post-processing attacks like angle and scale, intensity and chrominance variations, etc.

•   The proposed method employs LTrP features over circular blocks to generate the rotation-invariant feature vector, enabling the efficient and effective localization of regular and irregular-shaped manipulated areas and minimizes the false detection rate.

•   The proposed method can locate single and multiple CMF attacks effectively, even from tiny and exceptionally flat areas of an altered sample.

•   The circular blocks, lightweight feature descriptor, and RANSAC enhance the identification performance of the proposed method as well as its identification performance and increase the robustness by faster detection of the optimum key points deduction of false matches over the manipulated content.

The remaining sections of this article are arranged as follows: related work is discussed in Section 2. Comprehensive details of the proposed method are given in Section 3. The performance evaluation parameters and experimental results are discussed in Section 4, and finally, the conclusion is presented in Section 5.

2  Literature Review

Form the last decades, numerous approaches have been introduced to detect the manipulations made within digital images. It is quite a challenging task to identify the CMF because the content from the same image is used to alter its information. So, the major attributes of an image such as the light effects, resolution, and brightness, etc. remain the same. Several methods have been employed by the researchers to deal with the complexities of the CMF. Bilal et al. [11] proposed a technique to detect the forensic charges of digital images. First, the dynamic histogram equalization (DHE) technique was used to adjust the input image's contrast. Then, the SURF descriptor was employed to calculate the feature vector of the adjusted image. Finally, the mDBSCAN clustering algorithm was used to localize the forged area in a given image. The approach [11] is robust to CMFD. However, this technique is unable to detect the forensic changes made in the flat regions. Roy et al. [12] presented a framework to detect the forgeries of digital images. First, the SURF descriptor was used to identify the features of an input image. Then, the Rotated Local Binary Pattern (RLBP) approach was applied to extract the features from the obtained SURF keypoints. Next, the generalized two Nearest Neighborhood (g2NN) method was used to compute the similarity among the extracted keypoints, and finally, the Hierarchical Clustering [13] scheme was used to cluster the manipulated portion of an input image. This approach is robust to detect the forgeries against the occurrence of rotational changes, blurring, and compression operations applied in the forged images. However, the detection accuracy of [12] is affected over the low-quality input samples. Lin et al. [14] introduced a novel method for CMFD. The hybrid features were estimated from the input image by applying the SIFT and LIOP feature extraction algorithm. The g2NN method was applied to perform the feature matching and then transitive matching was used to improve the matching results. Finally, the RANSAC algorithm was employed to reduce the false matching. The technique [14] has shown better results in CMFD as compared to the latest techniques. However, this work is suffering from a high computational rate.

Agarwal et al. [15] introduced a deep learning-based technique to identify the forensic changes made within the digital images. First, an input image was segmented into various parts by using the Simple Linear Iterative Clustering (SLIC) technique. A convolutional neural network namely the VGGNet (Visual Geometry Group-net) was applied to the individual segments to extract the key points from the input sample. Finally, the adaptive patch matching (APM) method was applied to measure the pixels resemblance to show the forged content from the input sample. This method is robust to various image transformation attacks such as blurring, rotation, and compression. However, the approach in [15] is computationally expensive. Alkawaz et al. [16] performed CMFD by dividing an input image into overlapping blocks. Then the discrete cosine transform (DCT) was applied to each block to compute the DCT coefficients. In the last step, the euclidian distance was computed to find the correspondence between the DCT coefficients. This framework shows better detection performance. However, the false choice of block size may lead to a reduction in forgery detection accuracy. A hybrid feature extraction-based CMFD methodology was proposed by Bilal et al. [17]. Initially, the DWT technique was applied to an input image to obtain the approximate sub-band. Then, SURF and BRISK feature extraction techniques were applied to the obtained sub-band to extract the features. Next, the hamming distance was computed to measure the similarity between the keypoints. Then, the DBSCAN clustering approach was employed to the matched features to localize the altered content. Finally, the RANSAC method was applied to remove the false matches. This approach is robust to image transformation operations. However, the intense image changes in scaling, brightness, and color reduction may degrade the detection performance. Bi et al. [18] presented a framework to detect altered information in digital images. The input image was categorized into non-overlapping blocks. Then, the SIFT descriptor was used to extract the keypoints from each block. To measure the similarity between the extracted features, the adaptive patch matching algorithm was employed. Finally, the identified doubtful patches were combined to show the final results. The technique in [18] shows better performance to CMFD; however, it is computationally complex. A block-based CMFDapproach was introduced by Chen et al. [19] that worked by dividing an input digital image into non-overlapping patches. The similarity between the blocks was computed by using the block sampled matching with the region growing (BSMRG) algorithm. Finally, the manipulated regions were shown by using a region growing step. The method in [19] is computationally robust, however, it is unable to define the block size automatically. Muzaffer et al. [20] proposed a SIFT descriptor-based approach for CMFD where binarized descriptors were employed to identify the manipulated regions. The technique [20] has reduced the search space. However, the detection accuracy is low as compared to a simple SIFT-based approach. Emam et al. [21] presented a novel method for CMFD that used the SIFT algorithm to extract the key features from the digital images texture area, and the Harris corner operator to measure the keypoints from the flat areas in the image. The keypoints from both descriptors were combined by using the Multi-support Region Order-based Gradient Histogram (MROGH) descriptor. The forged content was computed by measuring the similarity of fused key features. The technique [21] is robust to additive noise attacks, however shows a low recall rate.

3  Materials and Methods

This section presents the details of the method proposed for detecting the forensic changes made within digital images. The introduced technique works by applying the DWT approach together with the LTrP feature descriptor on the overlapped circular blocks of the image. The similarity of the content is computed by employing the Jeffreys and Matusita distance method. The complete workflow of the proposed method is presented in Fig. 2. The proposed method's experimental analysis shows that employing the DWT and the LTrP feature descriptor gives promising results for identifying the digital image forgeries due to their high robustness, accurate detection, and low computational cost.

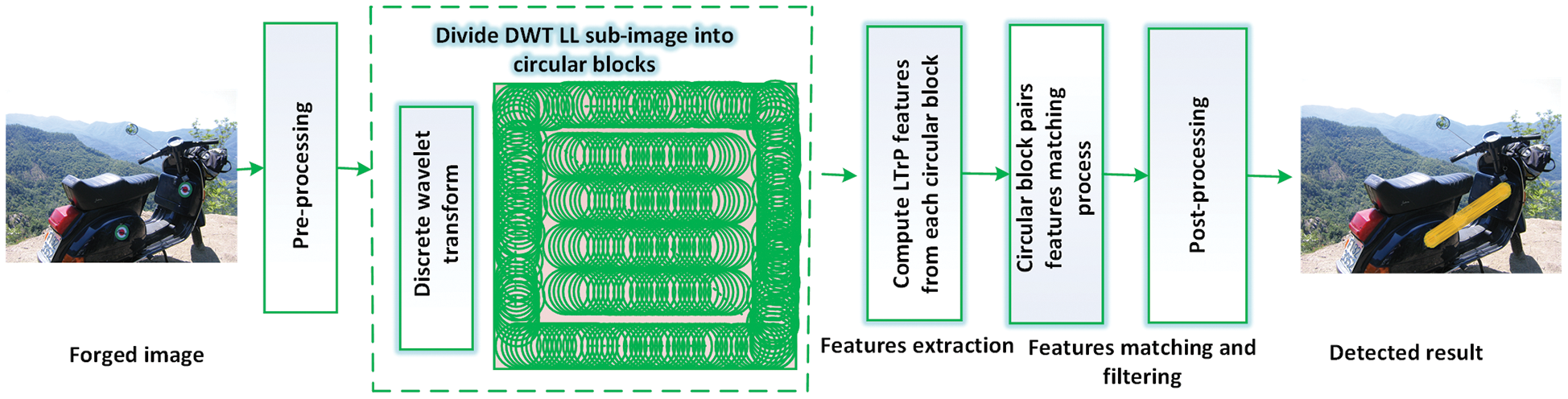
Figure 2: Workflow diagram of the proposed method

3.1 Pre-processing

Initially, the input color image is converted to a grey-scale image by employing the Eq. (1):

imggs=(0.299×rcom)+(0.587×gcom)+(0.114×bcom) (1)

Here imggs represents the grey-scale image, while rcom , gcom and bcom show the red, green, and blue components of the input image.

3.2 Dimension Reduction Using DWT

After the pre-processing step, we applied the DWT to the image for dimension reduction [22]. In DWT, the input image is shifted to the frequency domain, and its components are modified to acquire a more robust representation of the image. The DWT approach processes the image in a hierarchal manner, giving both the image’s spatial and frequency details [23]. It processes the input image in horizontal, vertical, and diagonal directions to compute its four components namely Low_Low (LL), High_Low (HL), Low_High (LH) and High_High (HH). Here, the first letter defines the type of frequency pass either as High or Low, while the second letter determines the type of filter employed on the image column [24]. In the proposed method, the DWT converts the image into a sequence of wavelet coefficients related to its spatio-frequency sub-bands. Suppose Imgiθ shows the image sub-band at i intensity level which is 2 in our case as we have applied the DWT approach up to level-2 while θ ∈ {LL, LH, HH, HL}. The LL component is known as the approximate image and has the lowest intensity level. Moreover, the LL sub-band contains more specific regional details of the original image, so, we have used it for further processing in the proposed method. The size of the LL component is only 1/4i of the original sample. While the HH , LH, and HL show the diagonal, horizontal, and vertical components of the input sample, respectively.

3.3 Division of the Image into Circular Blocks

After obtaining an approximate image Img2ll through the DWT, we have divided the image into circular blocks for further processing. The main reason to select the circular blocks over the square blocks is that in the case of the square blocks, the information is diverse particularly at the image’s corners. Therefore, the square blocks make the representation of manipulated blocks different which affects the correct identification of the forged blocks. Hence, employing rotational invariant keypoints set along with the circular blocks result in efficient forgery detection.

Suppose Img2ll is distributed into the square overlapped blocks with the dimensions of L × L. The elements of circular blocks Bj are computed by using the ratio of circular and matrix areas, say Ca, Ma, respectively which are given by Eqs. (2) and (3) with radius R.

Ca=πR2. (2)

Ma=4R2 (3)

and

Prc=CaMa 4)

where Prc is known as the circle parameter ratio, which is obtained by computing the ratio of circular and matrix areas. In our method, we have obtained the final representation of blocks Bj through a kernel window f given by Eq. (5) over each block Bj.

f=(--rSin(2πp /P),rCos(2πp/P)) (5)

where radius r = 1 and P denotes the number of nearest neighbors for each Bj with the value of 8 while j = 1, 2, 3, …, n and 2πp is the angular velocity. In our proposed technique, each circular block Bj has radius R = 8. So, the approximate image Img2ll of size x×y is divided into n = (x – 2R+ 1) × (y – 2R + 1) overlapping circular blocks.

3.4 Computing LTrP Features Over Circular Blocks

After the conversion of the approximate image Img2ll into the circular blocks n , the LTrP [25] is applied over them to compute the feature vector. The main reasons for selecting the LTrP over the LBP [26], local ternary pattern (LTP) [27], and the local directional pattern (LDP) [28] are as follows: i) The LBP, LTP, and LDP techniques work by representing an input image with two or three different values. While in comparison, the LTrP is capable of encoding the sample image with four different values. Therefore, the LTrP provides more detailed image information. ii) The LBP and LTP work by employing the simple relation of central pixel’s grey value to its neighbors, whereas the LTrP employs the direction-based relation of central pixel to its neighborhoods, therefore, it assists in computing efficient keypoints that are robust to scaling and rotation variations and help in proficiently locating the CMF.

We have obtained Bj overlapped circular blocks. So, for each block b∈Bj, the LTrP along its nth order will calculate the four different values at central pixel say gcom by computing the (n−1)th order derivatives along 0° and 90° through using the Eq. (6):

bDn−1(gcom)={1,b0on−1(gcom)≥0∧b90on−1(gcom)≥02,b0on−1(gcom)<0∧b90on−1(gcom)≥03,b0on−1(gcom)<0∧b90on−1(gcom)<04,b0on−1(gcom)≥0∧b90on−1(gcom)<0 (6)

After determining the direction of computed features, the nth order LTrP of the central pixel gcom along its 8 neighbors denoted as gp is given by Eq. (7):

f(bDn−1(gp),bDn−1(gcom)={0,if bDn−1(gp)=bDn−1(gcom)bDn−1(gp),else (7)

After computing the directions of features, the LTrP further employs three binary patterns. By assuming the directional orientation of the central feature to 1, the LTrP is computed by using Eq. (8):

LTrPPn(gcom)direction=Δ=∑n=1N2(n−1)∗f(LTrPPn(gcom))direction=Δ where Δ=2,3,4 (8)

And

f(LTrPPn(gcom))direction=Δ={1,ifLTrPPn(gcom)=Δ0,otherwise} (9)

After computing the three binary patterns, the fourth pattern known as magnitude pattern (mp) can be calculated by using the values of horizontal and vertical derivatives of eight neighborhood features, given by the Eq. (10):

mp=∑p=1P2p−1∗f(Mb(gp)−Mb(gcom))|P=8 (10)

where

Mb(gp)=(b00n−1(gp))2+(b900n−1(gp))2 (11)

These computed four patterns have been utilized to describe the feature vector vj of each block Bj which is sorted lexicographically to ease the process of CMFD as it makes similar features close together. The feature matrix F^ for the whole image is calculated by combining the vectors from all the blocks and defined in Eq. (12).

A visual representation of LTrP is given in Fig. 3 and more details about the LTrPs feature representation can be found in [25].

F^=[v1v2v3...vj] (12)

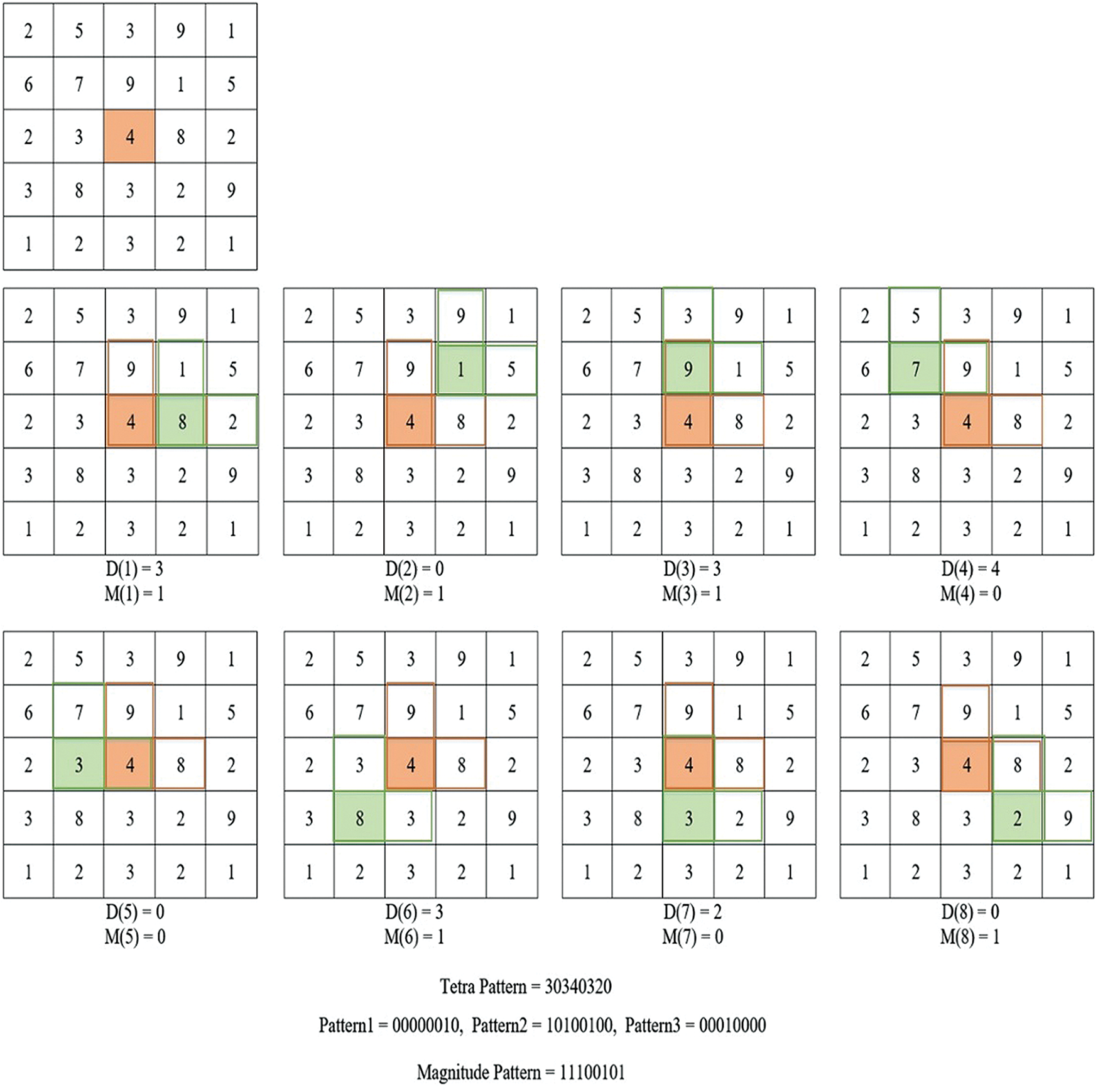
Figure 3: Methodology of computing the LTrP feature descriptors

3.5 Similarity Measurement

After performing the feature vector estimation, the next step is to compute the resemblance among them to check the image for CMF. If in the matching process, any similarities are found, then the image is marked as forged. In the proposed method, we have employed the Jeffreys and Matusita distance d [29] to measure the similarity between the detected data points. The main motivation of employing the Jeffreys and Matusita distance over Euclidian and Manhattan distance formulas is that it generalizes well to all sort of pixel distributions and works well for high dimensional feature space as compared to Euclidian and Manhattan distances.

For two features, say xi and xj are said to be similar, if the Jeffreys and Matusita distance dij defined in Eq. (13) is less than T. Here, T is the threshold value which is set as 0.5 for the proposed method.

dij=(xi−xj)2 (13)

3.6 Post-Processing

Finally, in the last step, to improve the effectiveness of the proposed method the RANSAC technique [30] is employed to eliminate the false matches from the computed results. The affine transformation matrix of the matched area is calculated by choosing the random points from it and is defined by the Eq. (14):

(ab)=[t1t3t2t4](xy)+(txty) (14)

where (a, b) and (x, y) show the corresponding copied and pasted region’s pixels in the image. While t1, t2, t3, t4, tx, and ty are the values of the affine transformation. Finally, a model is computed by employing the least square method, which categorized the matched data points into two sets namely inliers and outlier data points. To show the final results, the outliers are discarded, and inlier data points are utilized.

4  Results and Discussions

We have performed different experiments for the performance evaluation of the proposed method against post-processing attacks, i.e., noise, scaling, rotation, and JPEG compression. We have used MATLAB 2015b software with the Intel core I-7 machine, 32 GB RAM, and 250 GB hard drive for experiments.

4.1 Datasets

The evaluation experiments are performed by employing three databases namely MICC-F220 [31], MICC-F2000 [31], and CoMoFoD [32]. A detailed explanation of databases is given in Tab. 1. The MICC-F220 database comprises 220 samples, of which 110 samples are real, and the remaining 110 images are forged. The MICC-F2000 dataset contains 2000 images, in which 1300 images are real and 700 are forged images. While the CoMoFoD dataset consists of 260 forged samples. The images are distributed into 5 classes having applied manipulations i.e., rotation, translation, scaling, distortion, and combination. Fig. 4 shows the sample images of all the given datasets.

In Fig. 4, the first row shows images from the CoMoFod dataset while the next row shows images from the MICC-F220 dataset, and the last row shows images from the MICC-F2000 dataset. The first and third columns exhibit the original images, while the second and fourth columns show forged sample images.

4.2 Evaluation Metrics

We have used the different metrics i.e., precision (P), recall (R), and F1score for the performance evaluation of the proposed method. These metrics are defined mathematically by Eqs. (15)–(17), respectively:

P=TpTp+Fp (15)

R=TpTp+Fn (16)

F1score=2×P×RP+R (17)

where Tp presents the forged regions in the image identified as forged, while Fp presents the original area in the image identified as forged, and Fn represents those cases where the forged areas are identified as the original.

Figure 4: Sample of images from all employed datasets

4.3 Performance Testing

This section presents the proposed method's evaluation power under the simple attacks of the CMF strategy. Various tests are performed for the detection of a forged area in the suspected images. In this operation, the selected region is copied and pasted in the same image. The visual results are presented in Fig. 5, which shows that the proposed method achieves remarkable results.

Figure 5: Performance evaluation of the proposed method on different CMF datasets

In Fig. 5, the first column presents the original, fake, and the detected image results from the MICC-F220 dataset. While the second column shows the original, fake, and the detected results of the MICC-F2000 dataset and the last column contains the original, manipulated, and the detected results from the CoMoFoD dataset.

4.4 Robustness Testing

After testing the simple CMF strategy, the presented approach is tested against the post-processing attacks, i.e., rotation, scaling, additive noise, and JPEG compression. According to the obtained visual results, we can say that our method also performed well under post-processing manipulations.

4.4.1 Scaling Case

To analyze the proposed method's performance against scaling manipulation, where the tempered areas are scaled before pasting using the 10 different parameters of scaling, i.e., s = 91:109 with a step size of 2. Fig. 6, shows the proposed method's visual results against the scaling manipulation, which exhibits the robustness of the proposed methodology. In Fig. 6, the first column presents the visual results from MICC-F220, while the second column shows the results of MICC-F2000, and the last column exhibits the visual results of the CoMoFoD dataset.

Figure 6: Visual results of the proposed method on the scaling CMF attack

4.4.2 Rotational Case

The effectiveness of the introduced method is also tested under the condition of rotational manipulation, where the forged portion of the image is rotated to different angles (θ = 0:10 with step 2). The visual results are presented in Fig. 7, which shows that the presented approach outperforms and effectively detects the forgery under rotation manipulations. In Fig. 7, the first, second, and third columns show results of the proposed method on the sample images of MICC-F220, MICC-F2000, and CoMoFoD datasets, respectively.

4.4.3 JPEG Compression Case

The proposed method is also evaluated against the JPEG compression attacks with a quality factor of 70 and 80 and achieved good results. The visual results are presented in Fig. 8, which shows the proposed method's capability to identify the forensic changes under JPEG compression attacks.

Figure 7: Visual results of the proposed method on the rotational CMF attack

Figure 8: Visual results of the proposed method on the JPEG compression attack

In Fig. 8, the visual results of the proposed method on the samples from the MICC-F220, MICC-F2000, and CoMoFoD datasets are shown in the first, second, and third columns, respectively.

4.4.4 Additive Noise Case

The robustness of the presented method is tested under additive noise operation as well. The proposed method’s visual results are presented in Fig. 9, in which images contain the Gaussian noise with zero mean and varying values of the standard deviation. According to the visual results shown in Fig. 9, it can be concluded that the proposed method can effectively detect forgery under the additive noise attack.

Figure 9: Visual results of the proposed method in the presence of additive noise CMF attack

In Fig. 9, the visual results of the proposed method on the samples from the MICC-F220, MICC-F2000, and CoMoFoD datasets are reported in the first, second, and third columns, respectively.

4.4.5 Multiple CMF Case

After the robustness testing, we have analyzed the proposed method’s performance on multiple CMF where when one region is copied and pasted on multiple places of an image. The multiple forged region results are presented in Fig. 10, which demonstrates that the proposed method can precisely identify the images of multiple forged areas.

Figure 10: Visual results of the proposed method in the presence of multiple-CMF attacks

4.5 Comparisons and Discussions

The experimental results of the proposed method against various post-processing operations are presented in Sections 4.3 and 4.4 that confirmed the efficacy of the proposed method. In this section, we have evaluated the performance of the presented technique against the state-of-the-art approaches. For the CoMoFod dataset, we have compared the proposed method's performance with [33–35]. Similarly, for the MICC-F2000 dataset, the proposed method’s performance is evaluated with the latest techniques in [36–38], and for the MICC-F220 dataset, we have compared the performance of the proposed method with [39–41]. The performance comparison of the proposed method with the state-of-the-art techniques on all the datasets is reported in Tab. 2. The reported results show that the proposed method exhibits better detection accuracy than the techniques in [33–41] as the method in [33] works well for rotational variations, however, exhibits lower detection accuracy for other post-processing operations. While the methods in [34,35] are robust to the CMDF under the presence of noise and compression in input samples. However, not perform well for rotational and scale variations in the input image. The frameworks in [36–38] lack the detection performance under resizing, rotation, and illumination changes attacks. Moreover, the methods in [39–41] show less CMFD accuracy under the additive noise, scaling, and light variations post-processing attacks. While the proposed method achieved promising performance under the presence of all post-processing attacks in comparison to the other CMFD methods. The main reason for the robust performance of the presented approach is due to the accurate detection and localization of circular block-based image features computed using the LTrP descriptor. Moreover, the proposed method is more proficient against post-processing operations as compared to comparative approaches, as using LTrP along with circular blocks enables to generate the rotation and scale-invariant feature vector. Additionally, features computed by LTrP exhibits more detailed image information by utilizing the direction-based relation of central pixel to its neighborhoods. Therefore, the proposed method outperforms the rest of the comparative CMFD methods.

5  Conclusion

In this article, we have proposed a block-based approach based on the DWT along with the LTrP features to detect the forensic changes from the digital images. First, a low approximation image sub-band is obtained through the DWT from the suspected image, which is further divided into circular blocks. Then, the LTrP descriptor is applied over each circular block to obtain the final feature matrix. After that, the Jeffreys and Matusita distance formula is applied over each block's computed features to measure the similarity. Finally, RANSAC is used to remove the false matches. The proposed method exhibits promising results as compared to the state-of-the-art forgery detection methods under the occurrence of different post-processing attacks such as rotational changes, scale variations, compression, additive noise, and intensity changes. The experimental results of the proposed method also demonstrate that it performs better than other CMFD methods in terms of precision, recall, and F1-score. As the proposed method can effectively detect the single and multiple copy-move forgeries in the presence of different post-processing attacks on images. It can play a vital role in image forensics-based applications.

Compliance with Ethical Standards

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Bohn, V. Coroamă, M. Langheinrich, F. Mattern and M. Rohs, “Living in a world of smart everyday objects—social, economic, and ethical implications,” Human Ecological Risk Assessment, vol. 10, no. 5, pp. 763–785, 2004. [Google Scholar]

 2.  W. Chen, L. Lin, M. Wu and J. Newman, “Tackling android stego apps in the wild,” in 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conf., IEEE, pp. 1564–1573, 2018. [Google Scholar]

 3.  L. Lin, W. Chen, S. Reinder, M. Wu and J. Newman, “A wild manhunt for stego images created by mobile apps,” in Proc. of the 2020 American Academy of Forensic Sciences, Anaheim, CA, 2020. [Google Scholar]

 4.  N. K. Gill, R. Garg and E. A. Doegar, “A review paper on digital image forgery detection techniques,” in 2017 8th Int. Conf. on Computing, Communication and Networking Technologies, IEEE, pp. 1–7, 2017. [Google Scholar]

 5.  G. K. Birajdar and V. H. Mankar, “Digital image forgery detection using passive techniques: A survey,” Digital Investigation, vol. 10, no. 3, pp. 226–245, 2013. [Google Scholar]

 6.  C. I. Podilchuk and E. J. Delp, “Digital watermarking: Algorithms and applications,” IEEE Signal Processing Magazine, vol. 18, no. 4, pp. 33–46, 2001. [Google Scholar]

 7.  J. Li, X. Li, B. Yang and X. Sun, “Segmentation-based image copy-move forgery detection scheme,” IEEE Transactions on Information Forensics Security, vol. 10, no. 3, pp. 507–518, 2014. [Google Scholar]

 8.  E. S. M. El-Alfy and M. A. Qureshi, “Combining spatial and DCT based Markov features for enhanced blind detection of image splicing,” Pattern Analysis Applications, vol. 18, no. 3, pp. 713–723, 2015. [Google Scholar]

 9.  T. K. Huynh, K. V. Huynh, T. Le-Tien and S. C. Nguyen, “A survey on image forgery detection techniques,” in 2015 IEEE RIVF Int. Conf. on Computing & Communication Technologies-Research, Innovation, and Vision for Future, Can Tho, Vietnam, IEEE, pp. 71–76, 2015. [Google Scholar]

10. M. A. Qureshi and M. Deriche, “A bibliography of pixel-based blind image forgery detection techniques,” Signal Processing: Image Communication, vol. 39, no. 1, pp. 46–74, 2015. [Google Scholar]

11. M. Bilal, H. A. Habib, Z. Mehmood, R. M. Yousaf, T. Saba et al., “A robust technique for copy-move forgery detection from small and extremely smooth tampered regions based on the DHE-SURF features and mDBSCAN clustering,” Australian Journal of Forensic Sciences, vol. 6, no. 3, pp. 1–24, 2020. [Google Scholar]

12. A. Roy, R. Dixit, R. Naskar and R. S. Chakraborty, “Copy-move forgery detection with similar but genuine objects,” in Digital Image Forensics. Singapore: Springer, pp. 65–77, 2020. [Google Scholar]

13. J. Friedman, T. Hastie and R. Tibshirani, The Elements of Statistical Learning. Series in statistics, vol. 1. New York: Springer, 2001. [Google Scholar]

14. C. Lin, W. Lu, X. Huang, K. Liu, W. Sun et al., “Copy-move forgery detection using combined features and transitive matching,” Multimedia Tools Applications, vol. 78, no. 21, pp. 30081–30096, 2019. [Google Scholar]

15. R. Agarwal and O. P. Verma, “An efficient copy move forgery detection using deep learning feature extraction and matching algorithm,” Multimedia Tools Applications, vol. 79, no. 11-12, pp. 1–22, 2019. [Google Scholar]

16. M. H. Alkawaz, G. Sulong, T. Saba and A. Rehman, “Detection of copy-move image forgery based on discrete cosine transform,” Neural Computing Applications, vol. 30, no. 1, pp. 183–192, 2018. [Google Scholar]

17. M. Bilal, H. A. Habib, Z. Mehmood, T. Saba and M. Rashid, “Single and multiple copy-move forgery detection and localization in digital images based on the sparsely encoded distinctive features and DBSCAN clustering,” Arabian Journal for Science Engineering, vol. 45, no. 4, pp. 1–18, 2019. [Google Scholar]

18. X. Bi, C.-M. Pun and X.-C. Yuan, “Multi-scale feature extraction and adaptive matching for copy-move forgery detection,” Multimedia Tools Applications, vol. 77, no. 1, pp. 363–385, 2018. [Google Scholar]

19. C.-C. Chen, L.-Y. Chen and Y.-J. Lin, “Block sampled matching with region growing for detecting copy-move forgery duplicated regions,” Inf. Hiding Multimed Signal Process, vol. 8, no. 1, pp. 86–96, 2017. [Google Scholar]

20. G. Muzaffer and G. Ulutas, “A fast and effective digital image copy move forgery detection with binarized SIFT,” in 2017 40th Int. Conf. on Telecommunications and Signal Processing, Barcelona, Spain, IEEE, pp. 595–598, 2017. [Google Scholar]

21. M. Emam, Q. Han and H. Zhang, “Two-stage keypoint detection scheme for region duplication forgery detection in digital images,” Journal of Forensic Sciences, vol. 63, no. 1, pp. 102–111, 2018. [Google Scholar]

22. L. Quan and A. Qingsong, “A combination of DCT-based and SVD-based watermarking scheme,” in Proc. 7th Int. Conf. on Signal Processing, Beijing, China, IEEE, pp. 873–876, 2004. [Google Scholar]

23. X.-F. Shen and X.-H. Ma, “Watermarking algorithm for digital image based on DCT and SVD,” Journal of Nantong University (Natural Science), vol. 3, pp. 1–11, 2006. [Google Scholar]

24. E. E. Abdallah, A. B. Hamza and P. Bhattacharya, “A robust block-based image watermarking scheme using fast Hadamard transform and singular value decomposition,” in 18th Int. Conf. on Pattern Recognition, Hong Kong, China, IEEE, pp. 673–676, 2006. [Google Scholar]

25. S. Murala, R. Maheshwari and R. Balasubramanian, “Local tetra patterns: A new feature descriptor for content-based image retrieval,” IEEE Transactions on Image Processing, vol. 21, no. 5, pp. 2874–2886, 2012. [Google Scholar]

26. G. Zhang, X. Huang, S. Z. Li, Y. Wang and X. Wu, “Boosting local binary pattern (LBP)-based face recognition,” in Chinese Conf. on Biometric Recognition, Berlin: Springer, pp. 179–186, 2004. [Google Scholar]

27. W.-H. Liao, “Region description using extended local ternary patterns,” in 2010 20th Int. Conf. on Pattern Recognition, Istanbul, Turkey, IEEE, pp. 1003–1006, 2010. [Google Scholar]

28. T. Jabid, M. H. Kabir and O. Chae, “Local directional pattern (LDP) for face recognition,” in 2010 Digest of Technical Papers Int. Conf.on Consumer Electronics,, Las Vegas, NV, USA, IEEE, pp. 329–330, 2010. [Google Scholar]

29. P.-E. Danielsson, “Euclidean distance mapping,” Computer Graphics Image Processing, vol. 14, no. 3, pp. 227–248, 1980. [Google Scholar]

30. O. Chum, J. Matas and J. Kittler, “Locally optimized RANSAC,” in Joint Pattern Recognition Symp., Springer, pp. 236–243, 2003. [Google Scholar]

31. I. Amerini, L. Ballan, R. Caldelli, A. Del Bimbo and G. Serra, “A sift-based forensic method for copy-move attack detection and transformation recovery,” IEEE Transactions on Information Forensics and Security, vol. 6, no. 3, pp. 1099–1110, 2011. [Google Scholar]

32. D. Tralic, I. Zupancic, S. Grgic and M. Grgic, “CoMoFoD—New database for copy-move forgery detection,” in Proc. ELMAR-2013, Zadar, Croatia, IEEE, pp. 49–54, 2013. [Google Scholar]

33. S.-J. Ryu, M. Kirchner, M.-J. Lee and H.-K. Lee, “Rotation invariant localization of duplicated image regions based on Zernike moments,” IEEE Transactions on Information Forensics Security, vol. 8, no. 8, pp. 1355–1370, 2013. [Google Scholar]

34. Y. Lai, T. Huang, J. Lin and H. Lu, “An improved block-based matching algorithm of copy-move forgery detection,” Multimedia Tools Applications, vol. 77, no. 12, pp. 15093–15110, 2018. [Google Scholar]

35. O. M. Al-Qershi and B. E. Khoo, “Enhanced block-based copy-move forgery detection using k-means clustering,” Multidimensional Systems Signal Processing, vol. 30, no. 4, pp. 1671–1695, 2019. [Google Scholar]

36. M. Zandi, A. Mahmoudi-Aznaveh and A. Talebpour, “Iterative copy-move forgery detection based on a new interest point detector,” IEEE Transactions on Information ForensicsSecurity, vol. 11, no. 11, pp. 2499–2512, 2016. [Google Scholar]

37. I. Amerini, L. Ballan, R. Caldelli, A. Del Bimbo, L. Del Tongo et al., “Copy-move forgery detection and localization by means of robust clustering with J-Linkage,” Signal Processing: Image Communication, vol. 28, no. 6, pp. 659–669, 2013. [Google Scholar]

38. D. M. Uliyan and M. T. Alshammari, “Investigation of image forgery based on multiscale retinex under illumination variations,” Forensic Imaging, vol. 22, pp. 200385, 2020. [Google Scholar]

39. C.-M. Pun, X.-C. Yuan and X.-L. Bi, “Security image forgery detection using adaptive oversegmentation and feature point matching,” IEEE Transactions on Information Forensics, vol. 10, no. 8, pp. 1705–1716, 2015. [Google Scholar]

40. J. Zhong, Y. Gan, J. Young, L. Huang and P. Lin, “A new block-based method for copy move forgery detection under image geometric transforms,” Multimedia Tools Applications, vol. 76, no. 13, pp. 14887–14903, 2017. [Google Scholar]

41. D. Cozzolino, G. Poggi and L. Verdoliva, “Efficient dense-field copy-move forgery detection,” IEEE Transactions on Information Forensics Security, vol. 10, no. 11, pp. 2284–2297, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.