DOI:10.32604/cmc.2021.018017

| Computers, Materials & Continua DOI:10.32604/cmc.2021.018017 |  |
| Article |
Neutrosophic Rule-Based Identity Verification System Based on Handwritten Dynamic Signature Analysis
1Department of Mathematics, Faculty of Science, Cairo University, Giza, 12613, Egypt
2Faculty of Computers and Information, Cairo University, Giza, 12613, Egypt
*Corresponding Author: Sameh H. Basha. Email: SamehBasha@sci.cu.edu.eg
Received: 22 February 2021; Accepted: 25 March 2021
Abstract: Identity verification using authenticity evaluation of handwritten signatures is an important issue. There have been several approaches for the verification of signatures using dynamics of the signing process. Most of these approaches extract only global characteristics. With the aim of capturing both dynamic global and local features, this paper introduces a novel model for verifying handwritten dynamic signatures using neutrosophic rule-based verification system (NRVS) and Genetic NRVS (GNRVS) models. The neutrosophic Logic is structured to reflect multiple types of knowledge and relations among all features using three values: truth, indeterminacy, and falsity. These three values are determined by neutrosophic membership functions. The proposed model also is able to deal with all features without the need to select from them. In the GNRVS model, the neutrosophic rules are automatically chosen by Genetic Algorithms. The performance of the proposed system is tested on the MCYT-Signature-100 dataset. In terms of the accuracy, average error rate, false acceptance rate, and false rejection rate, the experimental results indicate that the proposed model has a significant advantage compared to different well-known models.
Keywords: Biometrics; online signature verification; neutrosophic rule-based verification system
Biometrics is a wide research field that addresses distinguishing people according to recognizing some measurable anatomical or behavioral characteristics. Biometrics have been gradually replacing traditional methods that recognize people according to what they own, such as cards or keys, or what they know, such as passwords [1]. Iris, face, odor, fingerprint, ear structure, and hand geometry are examples of anatomical characteristics, while voice, walking manner, or signature are behavioral characteristics [2,3]. These biometric modalities should be worldwide, unchangeable, exclusive, and attainable. However, each biometric modality does not need to meet these criteria. Each modality has its pros and cons, so what makes a biometric suitable or not is the application, the biometric itself and its collected-in circumstances. Signature biometric is also not ideal for all cases, but it is very specific for state, civil and commercial transactions.
Signature verification is the process where the biometric algorithm aims to validate a person’s stated identity by matching the signature sample submitted to one or more reference signatures previously entered [4]. Predominantly, due to the time and effort needed to verify the manual signature, there is no verification where a signature is needed. Automating the process of signature verification focuses on improving the existing situation and avoiding forgery [5]. Automatic signature verification has two main research areas; online and offline signature verification; based on how signatures are collected. In verifying offline signature, the signature is scanned to depict the digital image. In contrast, the online signature verification uses a digitizing tablet to capture pen motions when signing [6]. Even though online signatures are still far from normal, the dynamics of writing that are not available in the 2-D representation of the signature are captured in addition to the form of the signature. Therefore, the online signature is hard to hack; more attention is given to online signature over the corresponding offline. Many methods have been employed for verification techniques such as probabilistic classifiers, dynamic time warping, deep neural networks [7], hidden Markov models, and nearest neighbor classifiers [5,8,9].
In signature verification, rule-based verification/classification approaches are widely used. Any classification system that uses the IF-THEN rules for verification/classification purposes can be referred to as a rule-based verification/classification system. Typically, any IF-THEN rule is a term on the left-hand side (LHS) and right-hand side (RHS) where LHS is a series of satisfying conditions to derive RHS-represented conclusion. For rule-based verification/classification, the LHS of the rule predominantly consists of a conjunction of attribute checks, while its RHS is a class label (Genuine or forgery). Fuzzy sets and fuzzy logic are used in the Fuzzy Rule-based Classification system (FRBCs) to represent and model various types of information about the problem at hand, which is online signature verification in our case. FRBCs have received significant attention among biometric researchers due to the good behavior in the real-time datasets and have been applied effectively to a wide variety of problems in multiple domains [10,11]. The nonlinearity of fuzzy rule-based classifiers helps reduce possible verification errors. Compared with other classifiers, like neural network and support vector machine, FRBCs have the more significant benefit of offering consistency and avoiding learning time. Consequently, FRBCs have been applied in online signature verification and achieved promising results [11].
This paper presents Neutrosophic rule-based verification/classification system (NRVS) to verify online-signature.
NRVS extends the fuzzy rule-based verification/classification by defining each logical variable using its degrees of truth, indeterminacy, and falsity. Instead of fuzzy Logic, the antecedents and descendants of the rules are composed of neutrosophical logic arguments. To the best of our knowledge, Neutrosophic logic was never used in the identity verification of online signatures. Further, for improving our NRVS model’s verification performance, the genetic algorithm is employed for refining and optimizing the neutrosophic “IF-THEN” rules. Further, the proposed model is capable to treat global and regional features as well as vague features that cannot be categorized as global or regional features. The strength in the NRVS is due to usage of the indeterminacy term introduced by the neutrosophic logic.
The rest of the paper is structured as follows: A summary of the previous work is introduced in Section 2. In Section 3, theoretical background about Neutrosophic Logic and Neutrosophic Set is introduced. Further, the proposed NRVS model and its hybridization with Genetic Algorithms, GNRVS are introduced in Section 4. In Section 5, the experimental results and discussions are introduced. Finally, some concluding remarks and future directions are given in Section 6.
In studying online signature, one has to address the following concepts: registration and acquisition of data, preprocessing, feature selection and extraction, classification, and verification [12]. There are two perspectives in the registration and data collection phases, reference-based and model-based. Depending on the signature structures stored in the database, a set of models is generated for each signer or statistical model, respectively. Most perspectives do some preprocessing in the preprocessing phase before extracting signature features such as stroke concatenation, resampling, smoothing, and normalization [4].
There are three strategies in the extraction of features: extraction based on features that rely on global features as in [13–15], function-based extraction which relies on local features as in [16], and regional approach extraction as in [11]. Several methods proposed mixture of all perspectives. Online signature is a dynamic multi-dimensional signal which synthesis all approaches and has attained good results. Some approaches pay more attention to one element such as signal, while other methods focus on another issue such as time [17].
In classification and verification phase, researchers proposed strategies that calculate a signature similarity score. They match the score with a global or user-dependent tolerance to achieve the verification outcome. There exist three matching perspectives here: global [13], local [6,16,18] and a combination of local and global [14,15,18], based on the features used in the preceding phase. Dynamic Time Warping (DTW) [19–21] was the most popular and effective local form used during the verification process where the signatures are expressed by each signatory as a series of copies and was the champion of the first verification contest [22]. The authors in [19] replaced the Euclidean distance with the Mahalanobis distance to boost DTW-based verification efficiency. Like the Euclidean distance, the Mahalanobis distance measures can take the differences between different characteristics into account and place weights on various characteristics. Moreover, the Hidden Markov Model (HMM) [23,24] is a very popular and effective local method used in this phase for each signer to derive a statistical model.
In the literature, several strategies were proposed to choose the best features combination to mitigate the error in verification [6,25].
Experimentally, in [25], the authors have shown that the speed and the curvature change are the most valuable features, and the pressure does not significantly improve accuracy. On the other hand, in [6] the local features are combined with the pen pressure feature.
Many approaches have been suggested in the literature for approximating the time functions accompanying the signing procedure. The Fourier Transform was applied in [17], whereas the Wavelet Transform was introduced in [26,27]. In [6,12] Legendre Orthogonal Polynomials were used. In [17], a fixed-length approximation of the signatures is presented using the Fast Fourier Transform. Yanikoglu et al. used the Fourier domain in their ability to model a compact online signature using a certain number of signature coefficients to generate fast matching algorithms regardless of the size of the signature. Nevertheless, they revealed that much of the signature’s timing information is eliminated by sampling, which is usually used to normalize the signature size and that information loss decreases verification efficiency. Because of this regional feature-based viewpoint (Fourier descriptors), the same datasets’ error rates are more significant than function-based perspectives. The results experimentally demonstrated that combining this insight with the DTW method decreases the error rate.
Fuzzy logic approaches are used in online signature verification. For example, in [15], researchers selected a single feature set per signer. They determined weights of importance for features chosen in evolution. However, their approach did not take the number of users in the dataset into consideration, and they only used the values of global features. In [28], the metaheuristic gravitational search algorithm was employed for the discovery and tuning of fuzzy rule parameters for the appropriate features. In [11], researchers used signature partitioning that is formed by a combination of vertical and horizontal sections of the signature. They used the one-class neuro-fuzzy classifier, whose structure is decided for each user individually without using forgeries.
Neutrosophy has emerged strongly in the scientific world in the last few years. In [29], authors introduce Neutrosophic Rule-based Classification (NRBCS), which extends the fuzzy rule-based classification (FRBCS). Their model obtained results better than the Fuzzy Rule-Based Classification system. Moreover, in terms of computational time, NRBCS is faster than FRBCS because NRBCS does not require much preprocessing as FRBCS.
3 Neutrosophic Logic and Neutrosophic Set: Theoretical Background
The fuzzy set (FS) theory was developed by Zadeh in mid-1960s, to manage fuzzy, and vague data. It is defined by μA(x) ∈ [0, 1], a membership degree, for every element x in A [30,31]. FS theory received some extensions such as intuitionistic FS [32], interval-valued FS [33], and interval-valued intuitionistic FS. Every theory of them treats only one side of inexactness.
For example, the FS theory mismanages incompleteness and contradiction in the information. Therefore, the neutrosophic set theory was designed to manage incomplete and also incompatible data. Besides, the neutrosophic set theory is a massive framework that aims to generalize all sets’ principles, it is a generalization of the classic set theory, FS theory, FS with interval values, intuitionist FS, and intuitionist FS with interval values [34].
Smarandache introduced neutrosophy in 1995, which deals with the origin, scope, and nature of neutralities, as well as their experiences with specific mental visions [35]. The theory takes into account three concepts:
a) <A>, the idea.
b) <Anti–A>, its negation.
c) <Neut–A>, a wide range of “neutralities”, to support all ideas between the idea and its negation excluding these extremes.
Both <Neut–A> and <Anti–A> are shortened to <Non–A>, where each of <Anti–A> and <Non–A> is used in balancing <A> [35].
Smarandache proposed basic principles for the neutrosophic system in [36] and Salama et al. [37]. They have put a logical foundation as well as mathematically analyzed the neutrosophic phenomena to construct new branches of mathematics based on neutrosophic logic.
Mathematically, let the x(T, F, I) variable be an element in the set as follows: t is true in the set, f is false, and i is indeterminate in the set, where t, f, and i are real numbers elements in T, F, and I sets, respectively, with no limit to T, F, I, or their total n = t + f + i [36].
For a space of objects, X, let x ∈ X be a generic component. A neutrosophic subset A of X is distinguished by three membership functions: truth (TA), a falsity FA(x), and an indeterminacy (IA). TA(x), FA(x), and IA(x) are real intervals standard of non-standards over ]−0, 1+[ (i.e., TA, IA, FA(x) : X →]−0, 1+[). There is no limitation on the sum of TA(x), FA(x), and IA(x), so, −0 ≤ supTA(x) + supFA(x) + supIA(x) ≤ 3+.
Neutrosophic set operators can be created by more than one way [36]:
• Complement: The complement
for x ∈ X.
• Union: The union C = A ∪ B of two neutrosophic sets A and B is defined as follows [34–36]:
for x ∈ X.
• Intersection: The intersection C = A ∩ B of two neutrosophic sets is defined by [34–36]:
for x ∈ X.
• Containment: C = A ⊆ B, a neutrosophic set A is subset of another neutrosophic set B if and only if [35,36]:
for x ∈ X.
• Difference: The difference of two neutrosophic sets
for x ∈ X.
Neutrosophic logic has been constructed to serve mathematically building models containing uncertainty of many different types ambiguity or vagueness, inconsistency or contradiction, redundancy or incompleteness, and incompleteness [36,38]. Neutrosophica logic is constructed such that each hypothesis is assumed to have a proportion of the truth in the T subset, a proportion of the falsification in the F subset, and a proportion of the indeterminacy in the I subset, where T, F, I are real subsets of ]−0, 1+[, where supT = t_sup, infT = t_inf, supF = f_sup, infF = f_inf, supI = i_sup, infI = i_inf, n_sup = t_sup + f_sup + i_sup, and n_inf = t_inf + f_inf + i_inf [39–41].
T, F, and I are called the neutrosophic elements, and these elements refer to the values of the truth, falsehood, and indeterminacy respectively [42]. Standard real interval [0, 1] for T, I, and F is easy to use in practical applications than the nonstandard unit interval ]−0, 1+[ [39,43]. T, I, and F sets are not required to be intervals but can be either discrete or continuous subsets, whether finite or infinite, countable or uncountable, scalar or not, an intersection or union of various subsets [36,44]. In a static manner, the components T, F and I are subsets, but dynamically, these are set-valued vector functions/operators dependent on space, time, and other many parameters [36].
4 The Proposed Neutrosophic Rule-Based Verification System
Fig. 1 shows the architecture of the proposed model for verifying signatures, and it consists of four phases: feature extraction, Neutrosophic, creating rules, and verification phases. These phases and their characteristics along with the architecture of the proposed model are described in more details in the following sections.
4.1 Extracting Information Phase
Valuable information is collected, during this phase, in order to implement NRVS through input data and to extract the following information:
• Number of attributes used.
• The maximum and minimum value of each attribute.
• The number and names of classes.
Our proposed Neutrosophic Rule-based Verification System (NRVS) utilizes the Neutrosophic Logic to generalize the Fuzzy Rule-based Verification scheme. In NRVS, the origins and consequences of the “IF-THEN” principles are all neutrosophic logic statements. There are three phases on the NRVS:
a) Neutrosophication: Implementation of the knowledge base (KB) in neutrosophic logic by translating raw data using the three neutrosophic features: truthmembering, falsity-membering, and indeterminacy membering.
b) Inference Engine: To achieve a neutrosophic output, KB and the neutrosophic “IF-THEN” implication rules are implemented, and
c) Deneutrosophication: Use three functions similar to those used by neutrosophisation, transforms the neutrosophic output of the second phase to a crisp value.
The KB used above contains the available neutrosophic “IF-THEN” rules mode. After that, the knowledge base uses neutrosophic sets to collect the neutrosophic rule semantics.
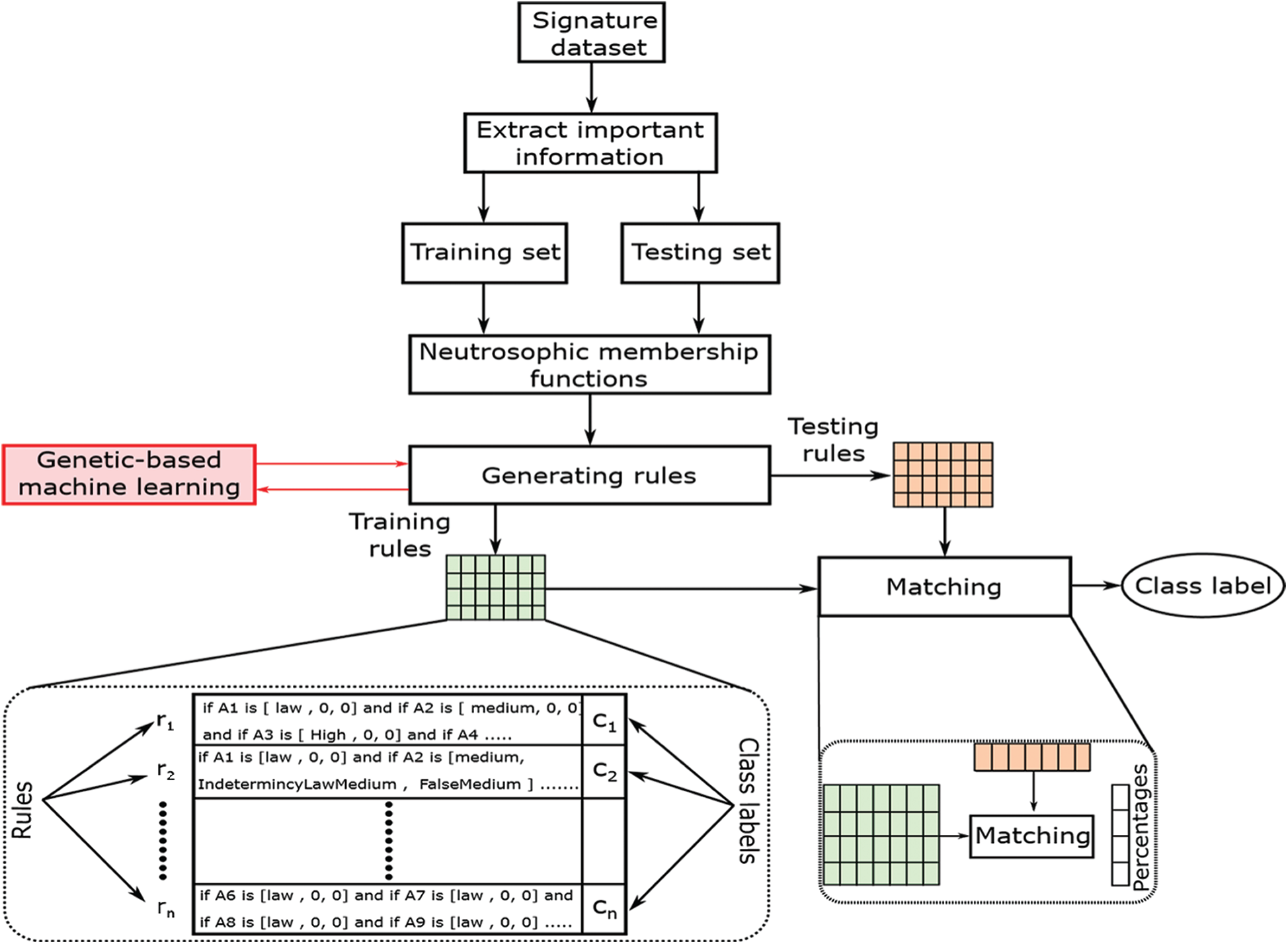
Figure 1: The architecture of the proposed neutrosophic rule-based verification system
The following membership functions are specified:
a) Truth membership function.
b) Falsity membership function.
c) Indeterminacy membership function.
Such membership functions will be drawn using the function of the Fuzzy Trapezoidal membership. In the neutrosophic type, three neutrosophic components are required to reflect each value for each feature. We applied three membership functions to each value in each attribute of the dataset in order to get those three components.
The aim, here, is to develop rules to be used predominantly during the verification phase. Suppose that the data is in the form X = x1, x2,…, xn, since xi is the ith instance and n is the overall count of instances. Every instance has just one class label denoting ci ∈ 1, 2,…, C, since C refers to the overall count of classes. The first step is to divide the dataset into training data (Xtraining) which has labelled instances and testing data (Xtesting) that have unlabelled instances. During this phase, the training and testing data produce exact neutrosophic rules. In NRVS, in each neutrosophic rule, each attribute has three components that define the three degrees of truth, indeterminacy, and falsehood.
The matrix of testing is built in this phase without class labelling. For each testing rule (xt ∈ Xtesting), the percentage of intersections between the test rule and other training rules should be determined (Xtraining) (see Fig. 1), and these percentages are denoted by P = p1, p2,…, pq, where q is the number of rules in the training set and pi is the matching percentage between xt and the training rule xi. The testing rule is assigned the training rule-class label, which has a maximum intersected percentage. When there is no overlap of at least 50% between the training rules and the existing testing rules (pi < 0.5, ∀ i = 1,…, q), the class label is determined from the exact rules set (i.e., annotated). Afterward, this testing rule is added to the training rules instead of testing rules.
(Xtraining = Xtraining ∪ xt). Finally, the test matrix that projected class labels is contrasted with the same matrix that currently carries class labels. To evaluate our model, the confusion matrix is computed. Different terms, such as True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN), can be computed from the confusion matrix.
An example of comparison with neutrosophic and fuzzy classifiers is given by Fig. 2. As shown, with two classes, the classes may be linearly and separable; this is clear in Fig. 2b, in which the fuzzy classifier output is 65 (i) in the range (0 and a) 100% is Class I, and (ii) in the range (b and c) 100% is Class II. Practically, there is an overlapping zone between classes, as illustrated in Fig. 2a (the zone with the gray color). In this region, where an indeterminacy degree is found, there are three potential outcomes: (i) Class I has a high membership value in (a and (a + b)/2) range, (ii) Class II has a high membership value in ((a + b)/2 and b) range, and (iii) Both Class I and Class II have the same membership value as (a + b)/2. Additionally, as shown in the overlapping area between the two classes, the membership function falls until it arrives at (a + b)/2 point where the membership function value is the same for the two classes. The membership function falls until it arrives at (a + b)/2 point where the membership function value is the same for the two classes. Fig. 2c depicts the neutrosophic class truth component, and the output is 100% belongingness to class I in (0 and a) range, and 100% belongingness to class II in (b and c) range, which is similar to the output of the fuzzy classifier. Further, in Fig. 2c, there is no overlapping belongs to the component of truth membership while the indeterminacy and falsity components exclusively cover the overlapping area of the neutrosophic classifier as shown in Figs. 2d and 2e, respectively. As a result, the fuzzy classifier is not concerned with the indeterminacy of the data. Conversely, two additional components of the neutrosophic classifier manage the overlap area between the two classes.
In this example, the steps of the NRVS model will be illustrated. Assume we have two classes (C1 and C2), each one has five instances, and each instance is represented by only two features f1 and f2 (see Tab. 1). As seen, for the first two attributes, the minimum is 10.0 and 4.0, respectively, and for the first two attributes, the maximum is 26.0 and 16.0, respectively. In Tab. 1, the testing data is written in red color, while the training part is in black.
All values in the dataset are converted into a neutrosophical space in the neutrosophication phase. Therefore, each value is expressed by three values (t, i, f) using the T, I, and F neutrosophcal membership functions. After converting it to neutrosophical space, as shown in Tab. 2 each crisp value is converted to neutrosophic as follows: <tlow, tMedium, tHigh>, <iLow, iMedium>, <fLow, fMedium, fHigh>. As an example the crisp value 16.0 is converted to <0.0, 0.5, 0.0>, <0.5, 0.0>, <0.25, 0.75, 1.0>.
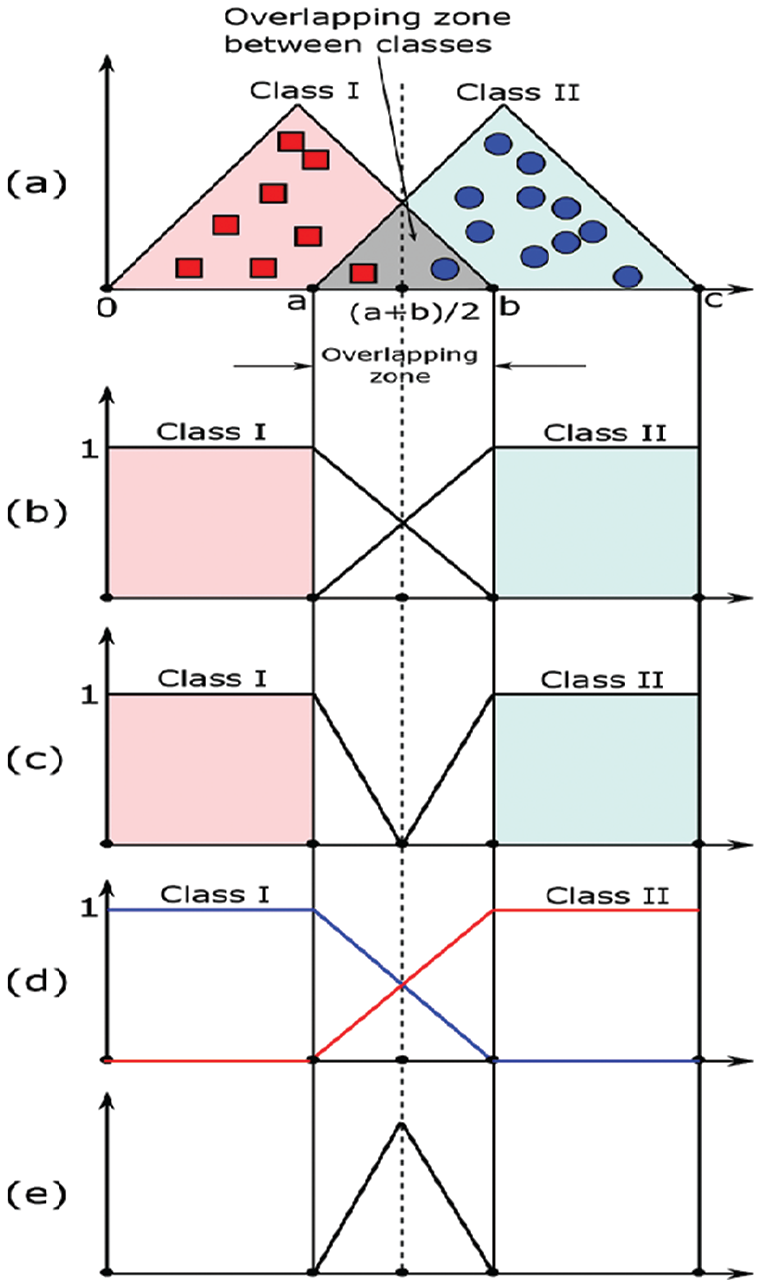
Figure 2: A comparison between NRVS and fuzzy verification. (a) The triangular fuzzy membership function of classes I, II; (b) A fuzzy verification; (c), (d), and (e) Represent the neutrosophical truth, falsity, and indeterminacy parts, respectively


The rules of training and test data are obtained in the neutrosophic space in the 3rd phase (i.e., rules generation phase) (see Tab. 2). The training rules are employed for verifying/classifying testing data.
Samples of the training rules are as follows:
where the rule [3, 5, 8][3, 5, 8] → class C2 means: if f1 is [High, 0, 0] and f2 is [Low, 0, 0] then the class label is C2. The testing rules are as follows:
Lastly, in the verification/classification phase of the NRVS model, all training rules will be applied to match each rule in the test data. (see Fig. 1). To do this matching, we used the Euclidean distance. The testing rule is allocated to the class which has the smallest distance from the testing rule by the training rule. Hence the class label of the first and second testing rules are C1, and as shown, four instances are correctly classified, and only the first testing instance is misclassified.
4.6 GNRVS: Hybrid Verification System Depending on Genetic Algorithm and Neutrosophic Logic
The proposed GNRVS combines the Genetic Algorithm (GA) and NRVS model. The GA is used in the NRVS model to refine the neutrosophic “IF-THEN” rules [45]. Then a new phase is introduced in this model, and it is called the Michigan-based Genetic-based Machine Learning Phase. The rules are automatically generated in this phase, and those rules may have redundant rules. Consequently, GA is used to search the space for rules and determine the most appropriate rules and delete obsolete rules.
The proposed GNRVS model has the same steps as the NRVS model, but a new phase is called the Genetic-based machine learning phase. In this phase, GA is used for refining linguistic rules in the KB. Algorithm 1 summarizes the steps of the GNRVS model.

5 Experimental Results and Discussions
Three experiments have been carried out in this paper. In the first (in Section 5.1), the proposed NRVS model is compared with conventional classifiers [46]. This section has two aims. The first aim is to verify the handwritten dynamic signature, without partitioning, by the proposed NRVS. The second aim is to test the capability of the proposed system to work with uncertain data with neither feature selection nor pre-processing tools. The second experiment (in Section 5.2) aims to evaluate the NRVS model by comparing its results with another rule-based classification system such as the Fuzzy Rule-based Verification System (FRVS) which is one of the most well-known rule-based verification/classification systems. The goal of the third experiment (Section 5.3), with the use of the hybrid verification method (GNRVS), is to enhance the results obtained from the first two experiments for the verification of handwritten signatures using dynamic features.
Experiments are carried out using Intel(R)_Core (TM)i7−4790_CPU@3.6 GHz Frequency, 32.0 GB ram, 2 TB Hard Disk Drive, and 64-bit Windows 10, and algorithms are self-coded and written in Python and Java programming languages.
In our experiments, we used the MCYT-Signature-100 dataset. This dataset includes ten-print fingerprint and online signature modes for each person registered in the dataset (330 persons). It contains many samples of each modality under various control levels to deal with the inevitable variability of each function during the registration process, as outlined below. The signatures were acquired using Device: WACOM Intuos (Inking pen) x, y, pressure, pen azimuth, and pen altitude signals at 100 samples per sec. This dataset has 16500 signatures: 8250 genuine signatures (each person has 25 signatures) and 8250 forgeries (each person has 25 signatures). Figs. 3a and 4a show an example from MCYT-Signature-100 dataset of a genuine signature and its corresponding forgery one, respectively. While Figs. 3b and 4b show some extracted attributes from the signatures in Figs. 3a and 4a, respectively.
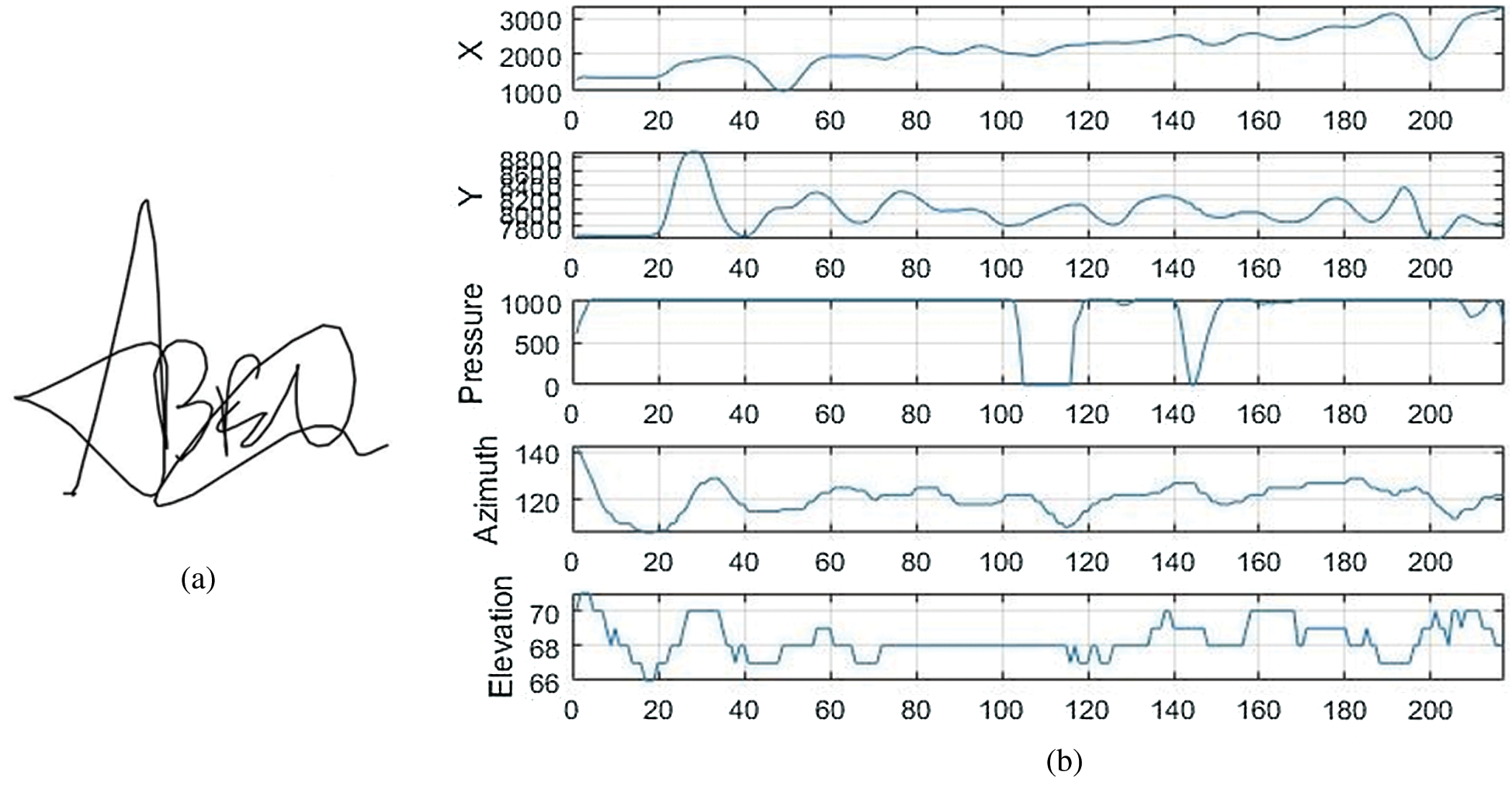
Figure 3: An example of signature shape and the extracted features of a genuine signature from MCYT. (a) A sample of a genuine signature shape (b) X, Y trajectories, pressure, azimuth and elevation attributes
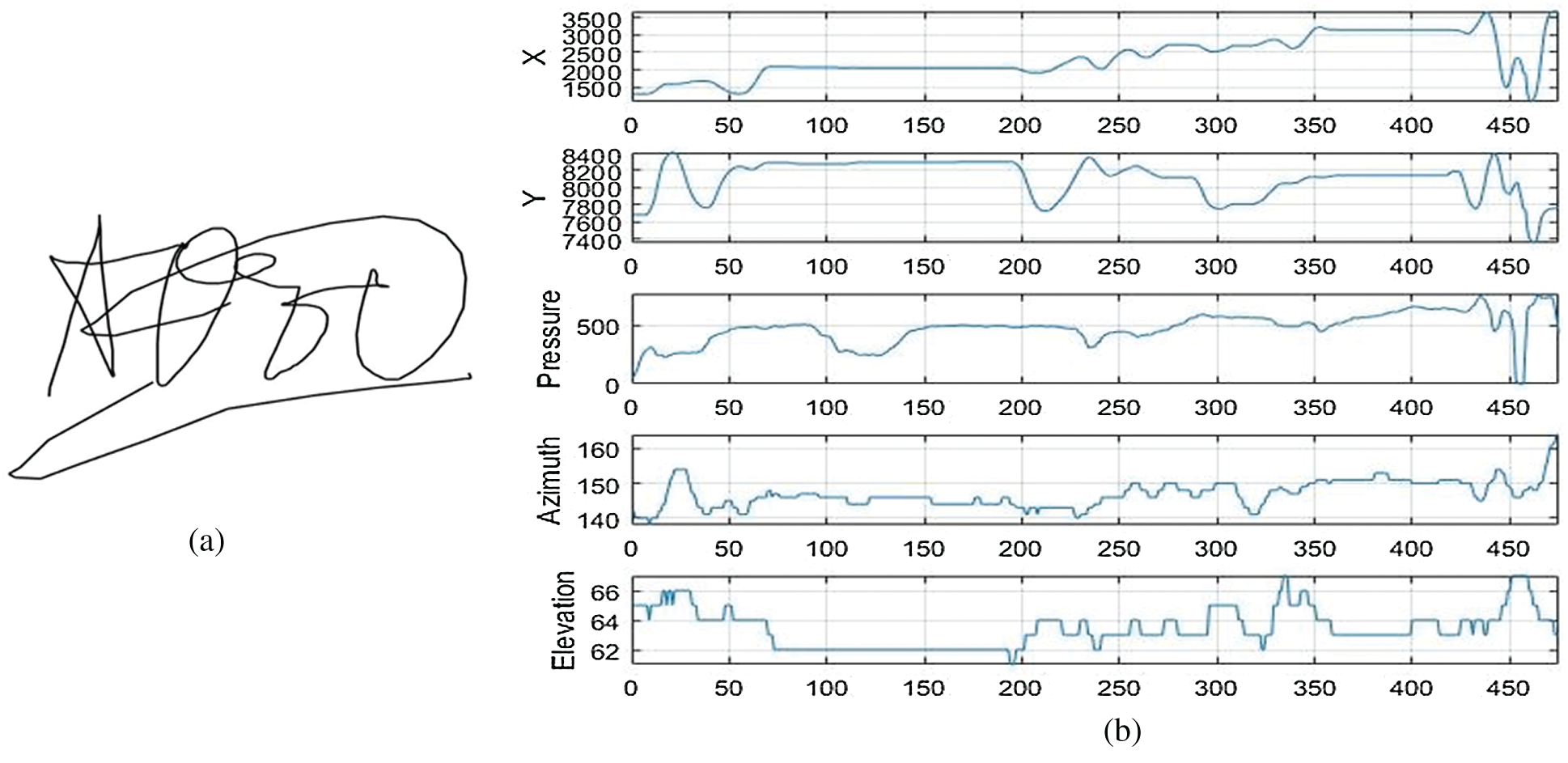
Figure 4: An example of signature shape and the extracted features of a forgery signature from MCYT. (a) A sample of a forgery signature shape (b) X, Y trajectories, pressure, azimuth and elevation attributes
The results of a 10 × 10-fold cross-validation were obtained in all experiments. The dataset samples were divided, in a random manner, into k subsets (k = 10) of the same lengths, and the experiment was performed ten times. One sub-set was used for each run for model evaluation and the other subsets were used for model training. This process has been replicated five times over. The average of these 10 × 10 experimental tests would yield the final results.
5.1 NRVS vs. Conventional Classifiers
In this experiment, the proposed NRVS model is evaluated by comparing the results of it with (i) six well-known learning algorithms, namely, Multilayer Perceptron (MLP) [47], Support Vector Machines (SVM) [48], Linear Discriminant Analysis (LDA) [49], Decision Tree (DT) [50], Naive Bayes (NB) [51], and Random Forest (RF) [51] classifiers, and (ii) one of the most related methods such as the proposed one in [46]. The method in [46] was based on getting the most insightful features. They used features such as extracting intersection points with adjacent intersection pixels centered in the central pixel. They used the classification of the signer independent form on the k-nearest neighbor (K-NN) classifier. This comparison aims to test the NRVS system by the imprecision, incomplete, inconsistency, and vagueness data without using any features selection techniques. The verification results of this experiment, according to many evaluation metrics, are summarized in Tab. 3. From Tab. 3, we can conclude that:
• In terms of the accuracy, all models obtained high accuracy, and the proposed NRVS obtained the second-best accuracy, while SVM and NB achieved the worst accuracies.
• In terms of specificity, the NRVS, k-NN, and SVM obtained the best specificity. Moreover, NRVS obtained competitive sensitivity results compared to the other models.
• The NRVS, k-NN, and SVM models outperform the other models in terms of the precision results.
• In terms of F1-Score, NRVS obtained competitive results compared to the other models.
To conclude, the proposed NRVS model achieved promising results compared to the mentioned conventional classifiers.

This experiment aims to compare the proposed NRVS model with one of the rulebased systems, such as the Fuzzy Rule-based Verification System (FRVS), which is one of the most well-known rule-based systems. This comparison aims to show that NRVS generalizes and outperforms the FRVS model. Many research proposed methods based on a fuzzy rule-based verification system such as [11,15]. In [11], they used a fuzzy system to measure the similarity of signatures divided into weighted partitions. However, in [15], they used a genetic-fuzzy hybrid approach based on global features only. Mamdani in Mamdani (1974) proposed the first type of fuzzy rule-based system by applying the fuzzy system to a control problem Cordón (2002).
The general structure of the fuzzy rule-based system [52,53] contains four components:
• Knowledge Base: this contains two parts: database and rule base. The dataBase part contains the dataset and the fuzzy membership functions used in the rulesbased system and will be used in the inference engine. The rule base part contains fuzzy rules in the form of “IF-THEN” rules.
• Fuzzifier: this component converts the crisp input to fuzzy input which input to the inference engine.
• Inference Engine: this component produces the results as the fuzzy output by using the fuzzy input and knowledge base.
• Defuzzifier: this converts the fuzzy output into the crisp output.
In this sub-experiment, we use the membership function proposed in Mahmood et al. (2013). The results of this experiment, according to different evaluation metrics are summarized in Tab. 4. Moreover, Tab. 5 summarizes the results in terms of False Acceptance Rate (FAR) and False Rejection Rate (FRR), where (i) the FAR is the ratio of the approved number of imposters to the total number of submitted forgeries (i.e., what percentage of times the system accepts for an invalid person), and (ii) The FRR is the ratio of the number of genuine test signatures rejected by the system to the total number of genuine test signatures submitted (i.e., the percentage of times a valid user is rejected by the system). These two metrics (i.e., FAR and FRR) are used for evaluating many handwritten signature recognition systems [54].
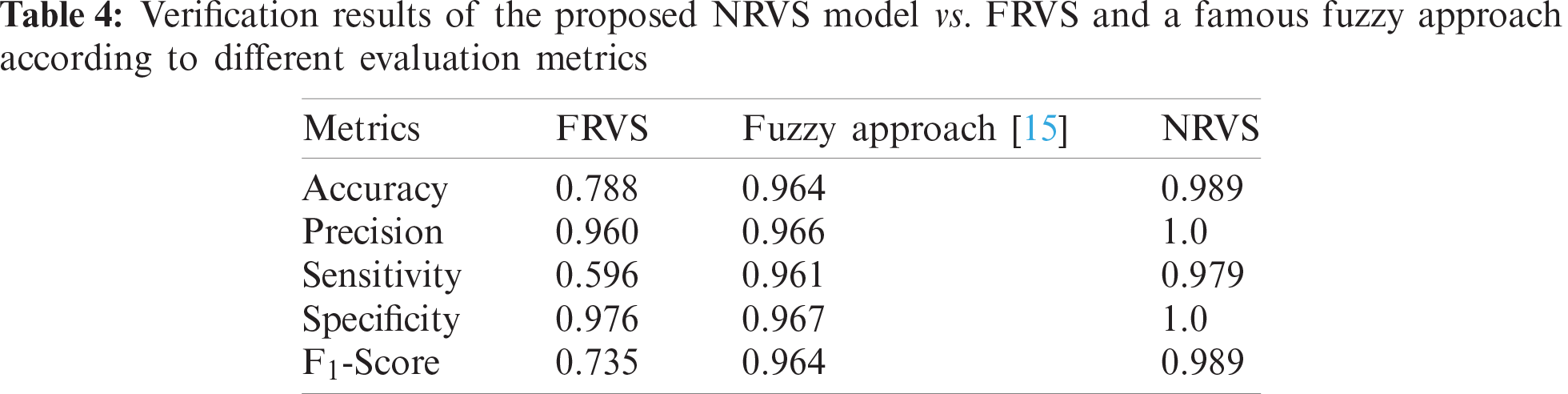

From Tabs. 4 and 5, it is clear that the proposed NRVS model significantly outperforms the other two fuzzy-based models. Using all assessment methods, the NRVS achieved the best results, and the FRVS obtained the worst results. In terms of FAR and FRR, as illustrated in Tab. 5, NRVS yielded zero FAR, while the Fuzzy approach obtained 3.29 FAR. Additionally, in terms of FRR, NRVS achieved FRR lower than the Fuzzy approach. These results proved that our NRVS model is significantly better than some state-of-the-art Fuzzy-based approaches.
This experiment is conducted to compare the proposed GNRVS verification system with the NRVS. In this experiment, as in the previous two experiments, we used all attributes, i.e., without a feature selection process. Besides, the results of this experiment are compared with the results of the Fuzzy-Genetic approach that was proposed in [15]. The results of this experiment are summarized in Tab. 6, which shows the results in terms of different evaluation metrics. Tab. 7 summarizes the results of this experiment in terms of FAR and FRR.


From the results in Tab. 6, we could conclude that:
• GNRVS improves NRVS in terms of all measures.
• GNRVS achieves better accuracy as RF, DT, and MLP.
• GNRVS as NRVS is better than the RF, DT, and MLP classifiers in terms of precision and Specificity measures.
• GNRVS improves the proposed NRVS model in terms of F1-Score to achieve the second-best results.
Additionally, from Tab. 7, we can conclude that GNRVS as NRVS can determine with complete accuracy the forgeries signatures (FAR = 0). Moreover, GNRVS determines genuine signatures more accurately than NRVS.
This paper proposes a novel model to verify online-signatures based on their dynamic characteristics using neutrosophic rule-based verification system (NRVS) that generalizes the fuzzy rule-based verification system. The proposed system has three primary stages: Firstly, stable features are derived from online signature data in the feature extraction process. Secondly, the proposed NRVS is used to classify signatures into authentic signatures and forgeries by generating neutrosophic “IF-THEN” rules. Thirdly, a hybridization of NRVS and Genertic Algorithms (GNRVS) is used to refine the neutrosophic “IF-THEN” rules generated in the previous stage. The MCYT-Signature-100 dataset, which has 8250 genuine signatures and 8250 forgery signatures, is used to test the proposed system. To evaluate the proposed model, various experiments were carried out and we obtained promising results. Overall, the observations of the proposed model show that it could be applied for handwritten signature verification. We plan to develop a hybrid framework between a neutrosophic, a rule-based system, and deep learning in future work.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Kaklauskas, E. Zavadskas, V. Pruskus, A. Vlasenko, L. Bartkiene et al., “Recommended biometric stress management system,” Expert Systems with Applications, vol. 38, no. 11, pp. 14011–14025, 2011. [Google Scholar]
2. A. Iorliam, A. T. Ho, A. Waller and X. Zhao, “Using benford’s law divergence and neural networks for classification and source identification of biometric images,” in Int. Workshop on Digital Watermarking, Cham: Springer, pp. 88–105, 2016. [Google Scholar]
3. G. Satapathy, G. Bhattacharya, N. B. Puhan and A. T. S. Ho, “Generalized Benford's law for fake fingerprint detection,” in 2020 IEEE Applied Signal Processing Conf., Kolkata, India, pp. 242–246, 2020. https://doi.org/10.1109/ASPCON49795.2020.9276660. [Google Scholar]
4. L. G. Hafemann, R. Sabourin and L. S. Oliveira, “Learning features for offline handwritten signature verification using deep convolutional neural networks,” Pattern Recognition, vol. 70, no. 1, pp. 163–176, 2017. [Google Scholar]
5. A. K. Jain, A. A. Ross and K. Nandakumar, Introduction to Biometrics. Boston, MA: Springer, pp. 1–49, 2011. [Google Scholar]
6. M. Parodi and J. C. Gómez, “Legendre polynomials based feature extraction for online signature verification. Consistency analysis of feature combinations,” Pattern Recognition, vol. 47, no. 1, pp. 128–140, 2014. [Google Scholar]
7. J. Kim, B. Rim, N. Sung and M. Hong, “Left or right hand classification from fingerprint images using a deep neural network,” Computers, Materials & Continua, vol. 63, no. 1, pp. 17–30, 2020. [Google Scholar]
8. T. Plötz and G. A. Fink, “Markov models for offline handwriting recognition: A survey,” International Journal on Document Analysis and Recognition, vol. 12, no. 4, pp. 269–298, 2009. [Google Scholar]
9. R. A. Naqvi, D. Hussain and W. Loh, “Artificial intelligence-based semantic segmentation of ocular regions for biometrics and healthcare applications,” Computers, Materials & Continua, vol. 66, no. 1, pp. 715–732, 2021. [Google Scholar]
10. M. Elkano, M. Galar, J. Sanz and H. Sola, “CHI-BD: A fuzzy rule-based classification system for big data classification problems,” Fuzzy Sets and Systems, vol. 348, no. 2, pp. 75–101, 2017. [Google Scholar]
11. K. Cpałka, M. Zalasinski and L. Rutkowski, “A new algorithm for identity verification based on the analysis of a handwritten dynamic signature,” Applied Soft Computing, vol. 43, pp. 47–56, 2016. [Google Scholar]
12. A. Hefny and M. Moustafa, “Online signature verification using deep learning and feature representation using legendre polynomial coefficients,” in Proc. AMLTA, Cairo, Egypt: Springer, pp. 689–697, 2019. [Google Scholar]
13. M. Zalasinski, K. Cpałka and Y. Hayashi, “New method for dynamic signature verification based on global features,” in Proc. ICAISC, Zakopane, Poland, pp. 231–245, 2014. [Google Scholar]
14. M. Zalasinski, K. Cpałka and E. Rakus-Andersson, “An idea of the dynamic’ signature verification based on a hybrid approach,” in Proc. ICAISC, Zakopane, Poland, pp. 232–246, 2016. [Google Scholar]
15. M. Zalasinski, K. Cpałka and L. Rutkowski, “Fuzzy-genetic approach to identity verification using a handwritten signature,” in Advances in Data Analysis with Computational Intelligence Methods, Cham: Springer International Publishing, pp. 375–394, 2018. [Google Scholar]
16. Y. Liu, Z. Yang and L. Yang, “Online signature verification based on DCT and sparse representation,” IEEE Transactions on Cybernetics, vol. 45, no. 11, pp. 2498–2511, 2015. [Google Scholar]
17. B. Yanikoglu and A. Kholmatov, “Online signature verification using fourier descriptors,” Eurasip Journal on Advances in Signal Processing, vol. 2009, no. 1, pp. 102, 2009. [Google Scholar]
18. V. Iranmanesh, S. M. S. Ahmad, W. A. W. Adnan, S. Yussof, O. A. Arigbabu et al., “Online handwritten signature verification using neural network classifier based on principal component analysis,” Scientific World Journal, vol. 2014, pp. 1–9, 2014. [Google Scholar]
19. Q. Yu, W. XingXing and X. Chunjing, “Learning mahalanobis distance for DTW based online signature verification,” in Proc. ICIA, Vienna, Austria, pp. 333–338, 2011. [Google Scholar]
20. J. Fernandes and N. Bhandarkar, “Enhanced online signature verification system,” International Journal of Emerging Trends and Technology in Computer Science, vol. 3, no. 6, pp. 205–209, 2014. [Google Scholar]
21. A. Sharma and S. Sundaram, “An enhanced contextual DTW based system for online signature verification using vector quantization,” Pattern Recognition Letters, vol. 84, no. 3, pp. 22–28, 2016. [Google Scholar]
22. D. Y. Yeung, H. Chang, Y. Xiong, S. George, R. Kashi et al., “SVC2004: First international signature verification competition,” in Proc. ICBA, Berlin, Heidelberg, Germany, pp. 16–22, 2004. [Google Scholar]
23. E. A. Rúa and J. L. A. Castro, “Online signature verification based on generative models,” IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 42, no. 4, pp. 1231–1242, 2012. [Google Scholar]
24. M. R. Kaur and M. P. Choudhary, “Handwritten signature verification based on surf features using HMM,” International Journal of Computer Science Trends and Technology, vol. 3, no. 1, pp. 187–195, 2015. [Google Scholar]
25. M. Khalil, M. Moustafa and H. Abbas, “Enhanced DTW based on-line signature verification,” in Proc. ICIP, Cairo, Egypt, pp. 2713–2716, 2009. [Google Scholar]
26. V. A. Bharadi and V. I. Singh, “Hybrid wavelets based feature vector generation from multidimensional data set for on-line handwritten signature recognition,” in Proc. Confluence, Noida, India, pp. 561–568, 2014. [Google Scholar]
27. H. Chang, D. Dai, P. Wang and Y. Xu, “Online signature verification using wavelet transform of feature,” Function Journal of Information & Computational Science, vol. 9, no. 11, pp. 3135–3142, 2012. [Google Scholar]
28. M. B. Bardamova, A. Konev, I. Hodashinsky and A. Shelupanov, “Gravitational search for designing a fuzzy rule-based classifier for handwritten signature verification,” Journal of Communications Software and Systems, vol. 15, no. 3, pp. 254–261, 2019. [Google Scholar]
29. S. H. Basha, A. Tharwat, A. Abdalla and A. E. Hassanien, “Neutrosophic rule-based prediction system for toxicity effects assessment of biotransformed hepatic drugs,” Expert Systems with Applications, vol. 121, no. 4, pp. 142–157, 2019. [Google Scholar]
30. L. A. Zadeh, “Fuzzy sets. In fuzzy sets, fuzzy logic, and fuzzy systems: Selected papers by lotfi a zadeh,” in Advances in Fussy Systems, Applications and Theory. vol. 6. Singapore: World Scientific, pp. 394–432, 1996. [Google Scholar]
31. Y. Wang, F. Subhan, S. Shamshirband, M. Z. Asghar, I. Ullah et al., “Fuzzy-based sentiment analysis system for analyzing student feedback and satisfaction,” Computers, Materials & Continua, vol. 62, no. 2, pp. 631–655, 2020. [Google Scholar]
32. K. T. Atanassov, “More on intuitionistic fuzzy sets,” Fuzzy Sets and Systems, vol. 33, no. 1, pp. 37–45, 1989. [Google Scholar]
33. I. B. Turksen, “Interval valued fuzzy sets based on normal forms,” Fuzzy Sets and Systems, vol. 20, no. 2, pp. 191–210, 1986. [Google Scholar]
34. M. Arora, R. Biswas and U. Pandy, “Neutrosophic relational database decomposition,” International Journal of Advanced Computer Science and Applications, vol. 2, no. 8, pp. 121–125, 2011. [Google Scholar]
35. H. Wang, F. Smarandache, R. Sunderraman and Y. Q. Zhang, “Interval neutrosophic sets and logic: Theory and applications in computing,” in Neutrosophic Book Series. vol. 5. Arizona, USA: Infinite Study, 2005. [Google Scholar]
36. F. Smarandache, A Unifying Field in Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability and Statistics, 4thed., Rehoboth, USA: American Research Press, 2003. [Google Scholar]
37. S. Alblowi, A. Salama and M. Eisa, “New concepts of neutrosophic sets,” International Journal of Mathematics and Computer Applications Research, vol. 3, no. 4, pp. 95–102, 2013. [Google Scholar]
38. A. E. Hassanien, S. H. Basha and A. S. Abdalla, “Generalization of fuzzy c-means based on neutrosophic logic,” Studies in Informatics and Control, vol. 27, no. 1, pp. 43–54, 2018. [Google Scholar]
39. A. Q. Ansari, R. Biswas and S. Aggarwal, “Neutrosophic classifier: An extension of fuzzy classifer,” Applied Soft Computing, vol. 13, no. 1, pp. 563–573, 2013. [Google Scholar]
40. A. Robinson, Non-standard analysis. In: Mathematical Logic in the 20th Century. Singapore: Singapore University Press and World Scientific, pp. 385–393, 2003. [Google Scholar]
41. F. Smarandache, S. Jha, G. P. Joshi, L. Nkenyereya and D. W. Kim, “A direct data-cluster analysis method based on neutrosophic set implication,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1203–1220, 2020. [Google Scholar]
42. C. Ashbacher, Introduction to Neutrosophic Logic. Rehoboth, USA: American Research Press, 2002. [Google Scholar]
43. S. Basha, A. Sahlol, S. El Baz and A. E. Hassanien, “Neutrosophic rule-based prediction system for assessment of pollution on benthic foraminifera in burullus lagoon,” in Proc. ICCES, Cairo, Egypt, pp. 663–668, 2017. [Google Scholar]
44. S. Basha, A. Abdalla and A. E. Hassanien, “Neutrosophic rule-based classification system,” in Proc. IntelliSys, London, United Kingdom, pp. 627–639, 2016. [Google Scholar]
45. A. Y. Hamed, M. H. Alkinani and M. R. Hassan, “A genetic algorithm to solve capacity assignment problem in a flow network,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1579–1586, 2020. [Google Scholar]
46. M. Houtinezhad and H. R. Ghaffary, “Writer-independent signature verification based on feature extraction fusion,” Multimedia Tools and Applications, vol. 79, pp. 6759–6779, 2019. [Google Scholar]
47. W. Yamany, A. Tharwat, M. F. Hassanin, T. Gaber, A. E. Hassanien et al., “A new multi-layer perceptrons trainer based on ant lion optimization algorithm,” in Proc. ISI, Busan, South Korea, pp. 40–45, 2015. [Google Scholar]
48. C. Gruber, T. Gruber, S. Krinninger and B. Sick, “Online signature verification with support vector machines based on LCSS kernel functions,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 40, no. 4, pp. 1088–1100, 2010. [Google Scholar]
49. A. Tharwat, “Linear vs. quadratic discriminant analysis classifier: A tutorial,” International Journal of Applied Pattern Recognition, vol. 3, no. 2, pp. 145–180, 2016. [Google Scholar]
50. J. Hu, Z. Guo, Z. Fan and Y. Chen, “Offline signature verification using local features and decision trees,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 31, no. 3, pp. 1753001:1–1753001:31, 2016. [Google Scholar]
51. S. Chandra, “Verification of dynamic signature using machine learning approach,” Neural Computing & Applications, vol. 32, no. 15, pp. 11875–11895, 2020. https://doi.org/10.1007/s00521-019-04669-w. [Google Scholar]
52. S. Sivanandam, S. Sumathi and S. N. Deepa, Introduction to Fuzzy Logic Using Matlab. vol. 1. Berlin Heidelberg: Springer-Verlag, 2007. [Google Scholar]
53. R. Alcalá, J. Casillas, O. Cordón, F. Herrera and S. J. I. Zwir, “Techniques for learning and tuning fuzzy rule-based systems for linguistic modeling and their application,” in Knowledge-Based Systems, C. Leondes (Eds.vol. 3. Cambridge, Massachusetts, United States: Academic Press, pp. 889–941, 2000. [Google Scholar]
54. M. Sivaram, D. Yuvaraj, G. Megala, V. Porkodi and M. Kandasamy, “Biometric security and performance metrics: FAR, FER, CER, FRR,” in Proc. ICCIKE, Dubai, United Arab Emirates, pp. 770–772, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |