DOI:10.32604/cmc.2021.018014

| Computers, Materials & Continua DOI:10.32604/cmc.2021.018014 |  |
| Article |
Automated Disassembly Sequence Prediction for Industry 4.0 Using Enhanced Genetic Algorithm
1Department of Mechanical Engineering, Industrial Robotics and Manufacturing Automation Laboratory, National Institute of Technology, Kariakal, 609609, India
2Department of Computer Science Engineering, National Institute of Technology, Kariakal, 609609, India
3Raytheon Chair for Systems Engineering, Advanced Manufacturing Institute, King Saud University, Riyadh, 11421, Saudi Arabia
4Industrial Engineering Department, College of Engineering, King Saud University, Riyadh, 11421, Saudi Arabia
*Corresponding Author: Mustufa Haider Abidi. Email: mabidi@ksu.edu.sa
Received: 21 February 2021; Accepted: 17 April 2021
Abstract: The evolution of Industry 4.0 made it essential to adopt the Internet of Things (IoT) and Cloud Computing (CC) technologies to perform activities in the new age of manufacturing. These technologies enable collecting, storing, and retrieving essential information from the manufacturing stage. Data collected at sites are shared with others where execution automatedly occurs. The obtained information must be validated at manufacturing to avoid undesirable data losses during the de-manufacturing process. However, information sharing from the assembly level at the manufacturing stage to disassembly at the product end-of-life state is a major concern. The current research validates the information optimally to offer a minimum set of activities to complete the disassembly process. An optimal disassembly sequence plan (DSP) can possess valid information to organize the necessary actions in manufacturing. However, finding an optimal DSP is complex because of its combinatorial nature. The genetic algorithm (GA) is a widely preferred artificial intelligence (AI) algorithm to obtain a near-optimal solution for the DSP problem. The converging nature at local optima is a limitation in the traditional GA. This study improvised the GA workability by integrating with the proposed priori crossover operator. An optimality function is defined to reduce disassembly effort by considering directional changes as parameters. The enhanced GA method is tested on a real-time product to evaluate the performance. The obtained results reveal that diversity control depends on the operators employed in the disassembly attributes. The proposed method’s solution can be stored in the cloud and shared through IoT devices for effective resource allocation and disassembly for maximum recovery of the product. The effectiveness of the proposed enhanced GA method is determined by making a comparative assessment with traditional GA and other AI methods at different population sizes.
Keywords: Automation; internet of things; disassembly sequence planning; priori cross over operator; enhanced GA; disassembly predicates
Industries are experiencing a paradigmatic shift from global manufacturing to agile manufacturing to achieve product variety in limited quantities according to customer desire [1]. Carlsonn et al. studied various manufacturing practices and opinioned that agile manufacturing can fulfill customer desire completely, but could cause severe raw material scarcity in the short term because of the practice of linear economy policies. It concentrated on production and the distribution of products instead of its takeback and turning into raw material for production in the future [2]. Industrial revolution 4.0 explored the possibility to perform manufacturing and de-manufacturing activities by smartly sharing information from one machine to another [3]. Wang et al. opinioned that agile manufacturing can be extended to meet the circular economy objectives by adopting cloud computing (CC) and Internet of Things (IoT) technologies because cloud computing technologies can support the storage and retrieval of the necessary information at manufacturing time, whereas IoT is essential for its use at de-manufacturing [4]. IoT can be used to create a potential interacting machine network for supporting the specified disassembly actions without human intervention at the manufacturing stage. It consists of a set of devices connected to a database to extract information and data processing units to execute them in the practical environment. The human–machine interaction can be avoided by supplying appropriate information with extensive validation before supplying it databased. Essential information about each activity in a production line must be collected and validated to avoid undesirable errors with their execution at different production lines [5–7].
An optimal disassembly sequence plan (DSP) can contain essential information at the product development stage because it has undergone extensive validation through various disassembly predicates because of its significance over the overall manufacturing process [8]. Traditionally, DSP is generated at the product development stage to organize various downstream activities in manufacturing [9]. Sharing an optimal DSP can supply valid and essential information from one production line to another. However, DSP is treated as a nondeterministic polynomial time (NP-hard) combinatorial problem because of multiple constraints in evaluating optimality [10–12]. The complexity of a DSP problem can be increased with an increase in the number of disassembly constraints and the total number of parts in a product [13]. Researchers have explored various methods for assembly/disassembly training, such as virtual reality [14–16].
AI methods are proven successful to solve the NP-hard and combinatorial optimization problems. Methods, such as artificial neural networks, genetic algorithm (GA), ant colony optimization (ACO), particle swarm optimization (PSO), and teaching and learning basic optimization (TLBO) are commonly applied AI techniques to solve the DSP problem [17–20]. However, these methods demand huge computational effort and space to generate high-quality solutions. Most research approaches have not considered necessary disassembly predicates to avoid computational complexities [21]. Disassembly predicates significantly affect presenting real-time conditions and are essential to evaluate the physical applicability of generated solutions.
Bahubalendruni et al. [22] extensively studied predicate consideration and observed that non-consideration of the predicate could reduce computational effort but adversely affect the quality of the solution. Abdullah et al. [23] observed that liaison and geometrical feasibility are preferred disassembly predicates for initial solution generation and implementing different criteria, such as time, directional changes, tool changes, and cost. Chakrabarty et al. [24] opinioned that as long as geometrical feasibility testing is confined to test principal axis directions such as
The proposed research generates an optimal solution for representing essential information in the manufacturing stage and the execution of the same for its management after the EoL. The method should offer necessary qualifying criteria and require minimum computation effort for solution generation. The article is organized as follows. Section 2 presents the reviewed literature, and Section 3 describes the necessary DSP attributes and their role in presenting real-time disassembly conditions. Section 4 presents the fitness value evaluation of the given disassembly sequence, and Section 5 explains the enriched GA and implementation on different case studies. Section 6 consists of detailed discussions on the working of the proposed method, and Section 7 concludes the article by proposing the future scope of research.
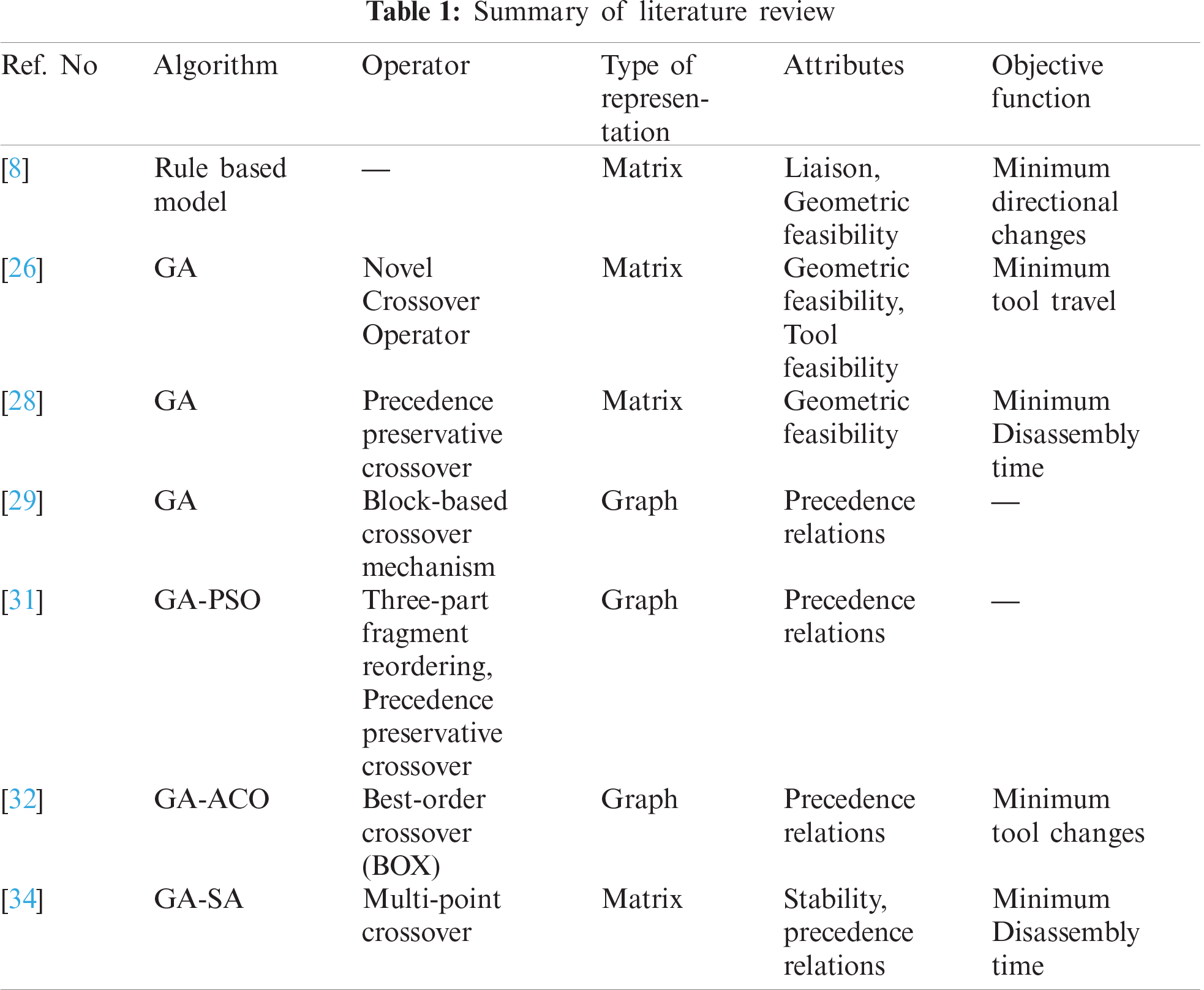
GA is a prominent and widely used AI method to solve the DSP problem under different objectives. Hui et al. originated the implementation of GA to solve the DSP problem by taking it as a complex combinatorial problem. A chromosome was made by representing each part of the product with a unique number, and a fitness function is developed to produce offspring after its evaluation [25]. Methods such as roulette wheel, tournament, and elitism selections are used to avoid the identified issue, and the roulette wheel selection was found effective [8]. Lazzerini and Marcelloni used partially matched crossover (PMX) and mutation operators to assess the generated disassembly plan [26]. Tian et al. applied GA to generate an optimal DSP based on environmental and economic constraints. The precedence of disassembly tasks was identified from the interference graphs [27]. The traditional GA was subjected to many limitations, such as premature convergence and heavy computational effort demand [28]. Researchers attempted to avoid the premature convergence problem by improving the crossover and mutation operator performance. Kongar and Gupta developed a priority preservative crossover (PPX) mechanism and stated that their mechanism could generate near-optimal solutions with fewer computations [29]. Giudice and Fargione used the PPX operator in GA and took the disassembly time, lifecycle cost parameters into the fitness function. Kheder et al. adopted the PPX mechanism developed by Kongar and Gupta to solve the DSP problem for maintenance [8]. Tseng et al. proposed a novel block-based GA to solve the premature convergence problem by modifying the selection process using the goal formula and score matrix [30]. Xing and Wang hybridized the GA with PSO to achieve an optimal solution for the DSP problem. PSO is used to remember the previously visited best position and record it for initial solution generation. Later, the formulated solution is optimized using the crossover operator of GA [31]. Researchers also attempted GA hybridization with other AI methods to overcome the limitations encountered with the traditional method [32–37]. Tab. 1 represents the summary of AI methods used to solve the DSP problem with different objectives.
The following research gaps were observed from the cited literature.
• The information sharing from assembly level at manufacturing stage to disassembly at product EoL stage is concerning, which is addressed in this article. The solution offered by the proposed method can be stored in the cloud and further shared through IoT devices for effective resource allocation and disassembly for maximum recovery of the product. Figs. 1 and 2 show the overall product cycle without and with cloud and IoT devices, respectively.
• A huge amount of computational effort is needed to produce a feasible solution for the disassembly sequence-planning problem.
• The necessary product information is not supplied prior because of the complexities of attribute representation.
• The generated solutions using existing methods lack optimality and practical feasibility in the de-manufacturing environment.

Figure 1: Product lifecycle without Cloud and IoT devices

Figure 2: Product life cycle with Cloud and IoT devices
3 Disassembly Attributes Representation and Conversion
Attributes are given importance in DSP formulation to represent conditions in an actual disassembly environment to achieve a practical solution. This study considers the disassembly direction of each part and subassembly stability during the disassembly process.
Geometrical feasibility is an attribute used to represent the feasible directions of a part regarding other parts to perform the necessary disassembly operations. The existing methods considered only principal axis directions, such as

Figure 3: Feasible directions that need human intervention to test geometric feasibility
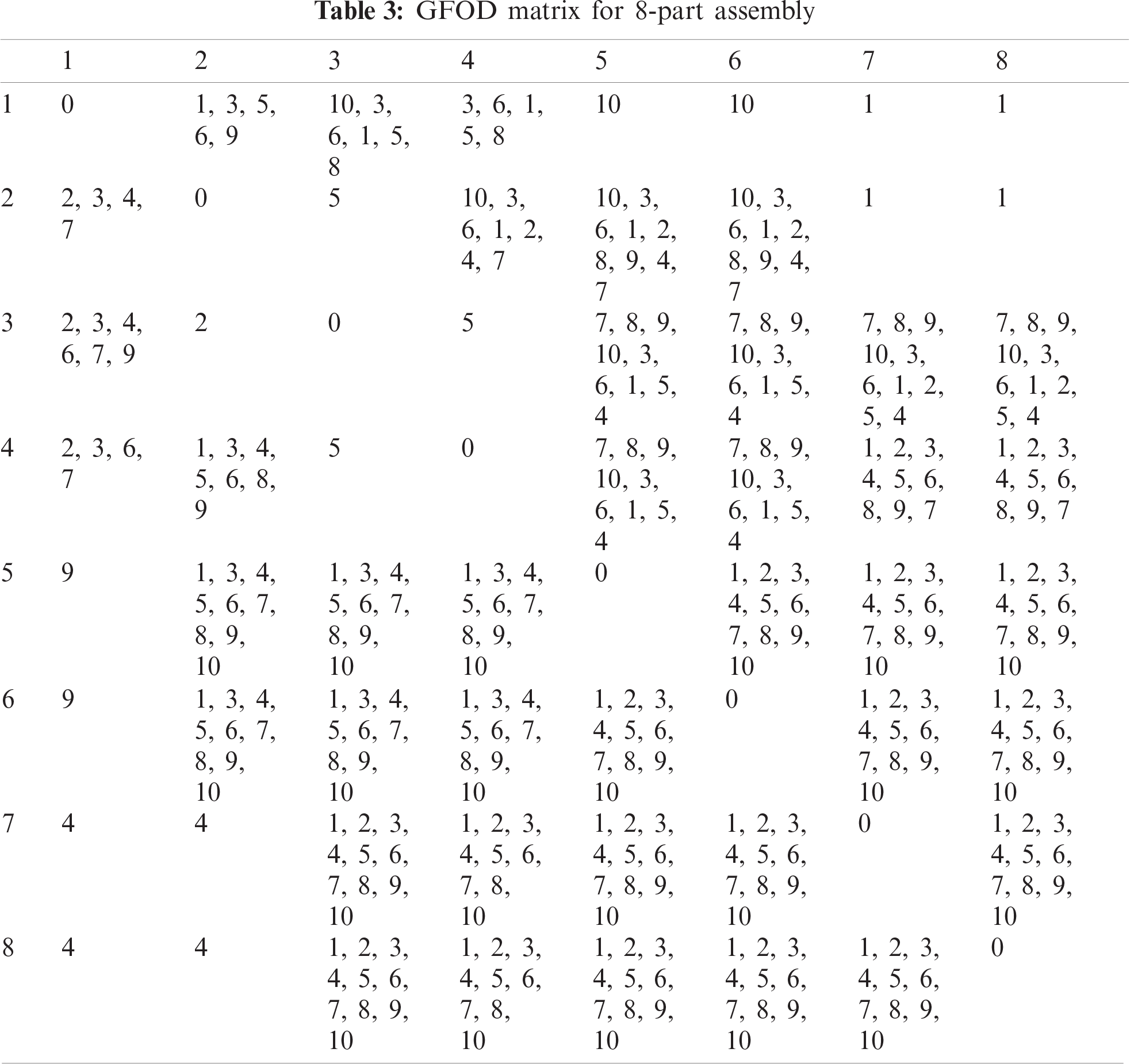
Bahubalendruni et al. proposed and developed a method to evaluate geometrical feasibility, other than principal axis directions; however, the method is intended to solve the exploded view generation problem in the computer-aided design (CAD) environment [38]. This research adopted the similarity in problem formulation and performed the necessary modifications to improve the encryption. An omnidirectional geometrical feasibility matrix is used to represent the conditions in the actual disassembly environment. The product represented in Fig. 4 is taken to demonstrate the concept of geometric feasibility and the corresponding representation in the matrix format.

Figure 4: 8-part assembly
The geometric feasibility omni-direction (GFOD) matrix is an
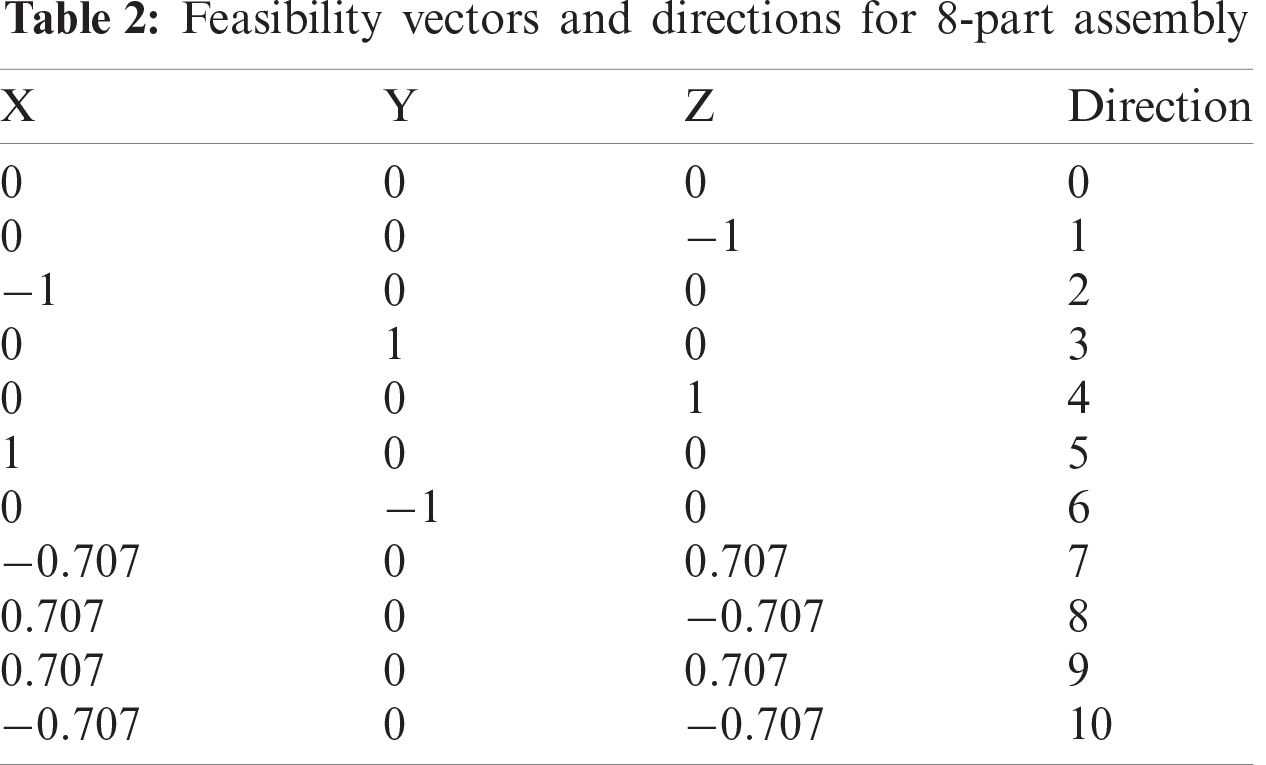
In GFOD, 0 represents the infeasibility to disassemble the column part in the present part given in the row, whereas 1 represents the feasibility to disassemble in the respective direction. For the product shown in Fig. 4, 11 normal directions of all parts exist, so the binary format will be width 11. Tab. 3 shows the GFOD matrix.
The stability between different parts of the product is referred to as the ability to maintain its contact, irrespective of the orientation. Bahubalendruni et al. classified various stability, such as partial, permanent, and enriched stability based on the contact, the relationship between the assembly products [38]. It is critical to examine the existence of stability between the parts of a product to avoid debacles in the disassembly environment. Fig. 5X represents the possibility of occurring debacles because of the non-coincidence of the center of gravity of two parts. Fig. 5Y represents the stability between two parts in which the bottom part should not be disassembled before the upper part, and Fig. 5Z represents the stability between two parts because of external connectors.

Figure 5: (X) Possibility of occurring debacles because of the non-coincidence of the center of gravity of two parts (Y) Stability between two parts in which the bottom part should not be disassembled before the upper part (Z) Stability between two parts because of external connectors
The stability matrix is an

Figure 6: Stability matrix
4 Disassembly Predicate Testing
Disassembly predicate testing is performed to verify whether the generated sequence is feasible or not. The working scheme of the geometrical feasibility and stability predicates is explained in 4.1 and 4.2, respectively.
4.1 Geometrical Feasibility Predicate Testing
A non-blocking direction to remove the desired part in the presence of other parts can be identified using the GFOD matrix. Binary AND operation is performed over GFOD values at (Si, Sj), where i < j < = n over the GFOD matrix. It results in all possible directions in which part Si can be removed. Algorithm 1 is used to evaluate the geometrical predicate testing.

The above procedure is to be repeated for all parts.
4.2 Stability Predicate Testing
For a part to be removed, it is verified from the stability matrix that any other existing part has contact with it or not. Algorithm 2 is used to evaluate the stability predicate testing.

The above procedure is to be repeated for all parts.

Figure 7: Fitness function flow chart
The fitness value of each sequence is computed from the geometric and stability checks. Fig. 7 depicts a flowchart in which the geometric feasibility of the sequence is first verified and promoted to the next level evaluating with the stability predicate. If the sequence fails to qualify the stability predicate, the process is initiated from the first step until the completion of all possible part combinations. If the sequence is geometrically feasible and stable, fitness is equal to the sum of the number of parts (N) and 1/(1+r), where r is the number of rotations. Eq. (2) is used as fitness
GA is an evolutionary method inspired by biological concepts to solve computationally complex problems. The solution is represented as a chromosome whose fitness value is evaluated using the feasibility and optimality criteria. The exchange of genetic information to produce a child is achieved using a crossover operation. A mutation operation is used to produce new genes absent in the parent chromosomes. For each iteration, crossover and mutation operations are applied on the present chromosomes to produce new offspring. After a certain number of iterations, the algorithm is prompted to converge and discover the best chromosome as an optimal solution.
5.1 Chromosome Representation and Process Initialization
For DSP, the chromosome is a sequence of numbers representing the order in which the parts are to be disassembled. Fig. 8 consists of individual chromosomes representing the possible solution for a selected 8-part assembly. The initial population is randomly initiated, and roulette wheel selection is used for the selection process.
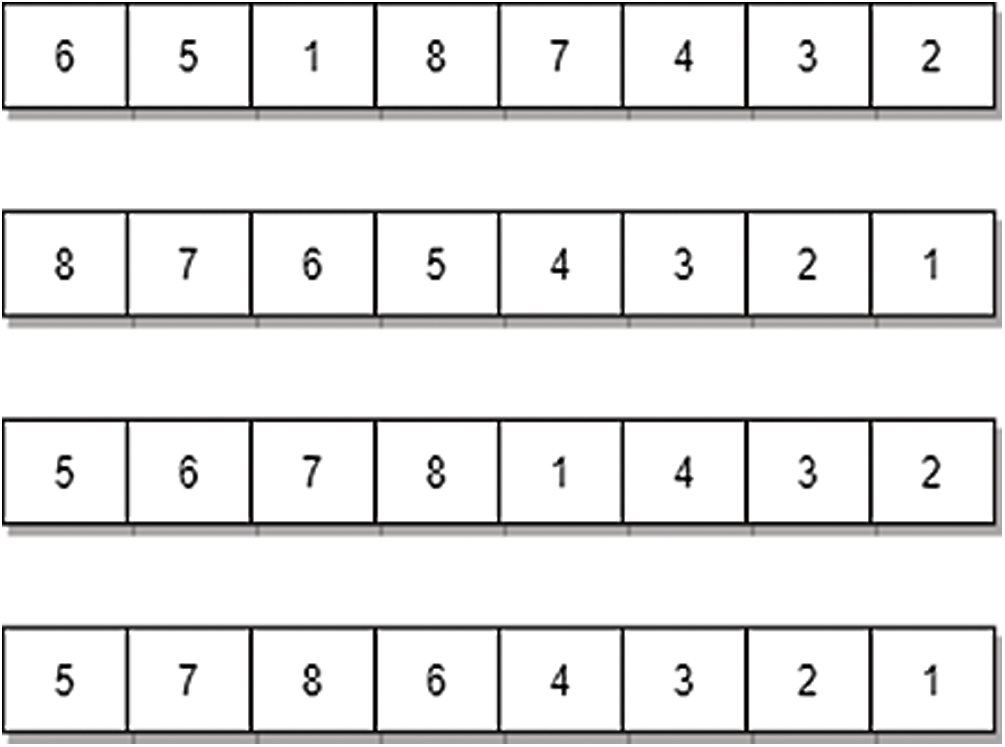
Figure 8: Chromosome representation
5.2 Crossover and Mutation Operators
Crossover operation is also called a recombination operation. The objective is to combine genetic information from parents to generate new offspring. The partially mapped crossover (PMX), cycle crossover (CX), order crossover operator (OX1), order-based crossover operator (OX2), position-based crossover operator, voting recombination crossover operator (VR), and alternating-position crossover operator (AP) are widely preferred crossover operators for combinatorial optimization problems [40]. This study proposes a novel crossover operator to solve the DSP problem.
Priori Operator
The proposed crossover operator has multiple parents, a master parent (M) and other parents (Pi). The working of this operator is as follows:
Step 1: Select master (M) and other parents (Pi)
Step 2: For each parent, compute partial sequence from 0 to fitness value
Step 3: Copy master to the child
Step 4: For each parent, identify the parts in its partial sequence but not in the master parent partial sequence. For each identified part, reposition it in the child chromosome, such that the prior part in both child and parent is the same.
The process shown in Fig. 9 assumed the number of parents set to 3. The fitness values of the master parent, parent A, and parent B are 3, 4, and 4, respectively.

Figure 9: Priori operator
For each iteration, a new population is generated based on the roulette wheel selection mechanism, priori crossover, and swap mutation. The function discussed in Section 4.3 is used to evaluate the feasibility and fitness of the sequence.
Termination
The evolutionary process of GA runs until the termination condition is satisfied. The terminating conditions implemented are
1. reach the maximum number of iterations
2. obtain a predefined fitness value
The enhanced GA will terminate immediately if any previously mentioned condition is true.
The developed algorithm is evaluated over different real-time product configurations by supplying the necessary data about disassembly attributes, such as geometrical feasibility and stability. It is implemented using Python programming language and tested on a Windows 10.0 operating system, 4 GB RAM, 1 TB ROM. The performance of the developed program was compared with other AI methods, such as traditional GA and PSO [24,29]. Parameters, such as computational time, iteration count, and efficiency were considered to compare its performance. Tab. 4 presents the performance of different AI methods and the proposed enriched GA method upon generating a solution for the product shown in Fig. 4.

Fig. 10 represents the comparison between the developed enriched GA and other algorithms of efficiency regarding population size. The developed enriched GA has a higher efficiency than other algorithms taken for the comparison. Generally, a product made with n number of parts might have more than n! possible representations. However, among all possible representations, only one solution can be optimal and practically feasible in the de-manufacturing environment. The efficiency of an algorithm underlies generating the population and identification of such an optimal solution by eliminating the infeasible solutions. All algorithms improve their efficiency with the increase in population size because of the elimination of such an infeasible solution for each increment in the population. The selection criteria chosen for the enriched GA worked efficiently to eliminate the infeasible solutions for further steps.

Figure 10: Efficiency % vs. Population size
Fig. 11 represents the comparison between the enriched GA and other methods for the no. of iterations taken to arrive at the optimal solution. As the population size rises, the number of iterations needed to arrive at optimal solutions gradually decreases because more possible solutions are explored as the population size grows at each iteration. The iteration needed for the enriched GA is lower than conventional GA and PSO because the proposed heuristic operator can find a viable sequence faster.

Figure 11: No. of Iterations vs. Population Size
Fig. 12 represents the comparison between the enriched GA and other methods for the computational time taken for the optimal solution generation. The traditional GA required a higher computational time because of the lack of an effective operator for the fitness value evaluation. PSO consumed less compared to the traditional GA because of recognition and remembrance of the best positions at the initial stages and using those positions for further stages might reduce the consumption. However, the fitness evaluation at the intermediate stages for optimal solution generation might demand more computation to arrive at the final solution. The proposed enriched GA facilitates the storing and reuse of higher fitness part combinations for further generations and significantly helped to reduce computational time.

Figure 12: Computational Time vs. Population Size
The limitation in the proposed operator is the overhead of setting the additional parameter, i.e., the number of parents and the diversification of chromosomes depend on the mutation operator similar to the traditional GA. Hence, the proposed algorithm could be converged at local optima with improperly specified parameters.
This research proposed a traditional AI method to enhance its performance in producing an optimal solution for validating information to be supplied for IoT and CC technologies. It can be used to create a potential network among machines from the product assembly stage to execute the disassembly actions at the de-manufacturing stage. The workability of the proposed enriched GA method was evaluated by applying it to a real-time product and the obtained results were compared with other methods. The following novelties were contributed and discussed in this paper.
• A novel priori crossover operator is developed, integrated into the versatile algorithm, and its efficiency was proven by applying it to a product.
• The developed operator can determine an operation path based on the fitness value of parents.
• Deterministic fitness functions were developed to evaluate the feasibility of a generated disassembly sequence.
The future scope of this research is to generalize the proposed method by inducing a heuristic mutation operator and incorporate various technologies, such as cybersecurity and image-based malware classification technologies for enhancing security in the developed system.
Funding Statement: The authors are grateful to the Raytheon Chair for Systems Engineering for funding.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. Krishnamurthy and J. Cecil, “A next-generation IoT-based collaborative framework for electronics assembly,” International Journal of Advanced Manufacturing Technology, vol. 96, no. 1–4, pp. 39–52, 2018. [Google Scholar]
2. I. L. Carlsson and H. Aronsson, “Investing in lean to improve basic capabilities: A strategy for system supply?,” Journal of Industrial Engineering and Management, vol. 10, no. 1, pp. 28–48, 2017. [Google Scholar]
3. W. S. Alaloul, M. S. Liew, N. A. W. A. Zawawi and I. B. Kennedy, “Industrial revolution 4.0 in the construction industry: Challenges and opportunities for stakeholders,” Ain Shams Engineering Journal, vol. 11, no. 1, pp. 225–230, 2020. [Google Scholar]
4. C. Wang, Z. Bi and L. Da Xu, “IoT and cloud computing in automation of assembly modeling systems,” IEEE Transactions on Industrial Informatics, vol. 10, no. 2, pp. 1426–1434, 2014. [Google Scholar]
5. P. K. R. Maddikunta, G. Srivastava, T. R. Gadekallu, N. Deepa and P. Boopathy, “Predictive model for battery life in IoT networks,” IET Intelligent Transport Systems, vol. 14, no. 11, pp. 1388–1395, 2020. [Google Scholar]
6. N. Deepa, B. Prabadevi, P. K. R. Maddikunta, T. R. Gadekallu, T. Baker et al. “An AI-based intelligent system for healthcare analysis using ridge-adaline stochastic gradient descent classifier,” Journal of Supercomputing, vol. 77, pp. 1998–2017, 2021. [Google Scholar]
7. N. Deepa, M. Z. Khan, B. Prabadevi, D. R. Vincent, P. K. R. Maddikunta et al., “Multiclass model for agriculture development using multivariate statistical method,” IEEE Access, vol. 8, pp. 183749–183758, 2020. [Google Scholar]
8. S. Smith, G. Smith and W. H. Chen, “Disassembly sequence structure graphs: An optimal approach for multiple-target selective disassembly sequence planning,” Advanced Engineering Informatics, vol. 26, no. 2, pp. 306–316, 2012. [Google Scholar]
9. M. Kheder, M. Trigui and N. Aifaoui, “Disassembly sequence planning based on a genetic algorithm,” Proceeding of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, vol. 229, no. 12, pp. 2281–2290, 2015. [Google Scholar]
10. K. Meng, P. Lou, X. Peng and V. Prybutok, “An improved co-evolutionary algorithm for green manufacturing by integration of recovery option selection and disassembly planning for end-of-life products,” International Journal of Production Research, vol. 54, no. 18, pp. 5567–5593, 2016. [Google Scholar]
11. M. V. A. R. Bahubalendruni and V. P. Varupala, “Disassembly sequence planning for safe disposal of end-of-life waste electric and electronic equipment,” National Academy of Science Letters, pp. 1–5, 2020. [Online]. Available: https://doi.org/10.1007/s40009-020-00994-0. [Google Scholar]
12. X. Liu, G. Peng, X. Liu and Y. Hou, “Disassembly sequence planning approach for product virtual maintenance based on improved max-min ant system,” International Journal of Advanced Manufacturing Technology, vol. 59, no. 5–8, pp. 829–839, 2012. [Google Scholar]
13. G. Tian, M. Zhou and J. Chu, “A chance constrained programming approach to determine the optimal disassembly sequence,” IEEE Transactions on Automation Science and Engineering, vol. 10, no. 4, pp. 1004–1013, 2013. [Google Scholar]
14. M. H. Abidi, A. M. Al-Ahmari, A. Ahmad, W. Ameen and H. Alkhalefah, “Assessment of virtual reality-based manufacturing assembly training system,” International Journal of Advanced Manufacturing Technology, vol. 105, no. 9, pp. 3743–3759, 2019. [Google Scholar]
15. A. M. Al-Ahmari, M. H. Abidi, A. Ahmad and S. Darmoul, “Development of a virtual manufacturing assembly simulation system,” Advances in Mechanical Engineering, vol. 8, no. 3, pp. 1–13, 2016. [Google Scholar]
16. M. H. Abidi, A. M. Al-Ahmari and A. Ahmad, “A systematic approach to parameter selection for CAD-virtual reality data translation using response surface methodology and mOGA-iI,” Plos One, vol. 13, no. 5, pp. e0197673, 2018. [Google Scholar]
17. B. Yu, E. Wu, C. Chen, Y. Yang, B. Z. Yao et al., “A general approach to optimize disassembly sequence planning based on disassembly network: A case study from automotive industry,” Advances in Production Engineering and Management, vol. 12, no. 4, pp. 305–320, 2017. [Google Scholar]
18. X. F. Zhang, G. Yu, Z. Y. Hu, C. H. Pei and G. Q. Ma, “Parallel disassembly sequence planning for complex products based on fuzzy-rough sets,” International Journal of Advanced Manufacturing Technology, vol. 72, no. 1–4, pp. 231–239, 2014. [Google Scholar]
19. B. M. Gunji, B. B. V. L. Deepak, M. V. A. R. Bahubalendruni and B. B. Biswal, “An optimal robotic assembly sequence planning by assembly subsets detection method using teaching learning-based optimization algorithm,” IEEE Transactions on Automation Science and Engineering, vol. 15, no. 3, pp. 1369–1385, 2018. [Google Scholar]
20. Z. Zhou, J. Liu, D. T. Pham, W. Xu and F. J. Ramirez, “Disassembly sequence planning: Recent developments and future trends,” Proceeding of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, vol. 233, no. 5, pp. 1450–1471, 2019. [Google Scholar]
21. M. V. A. R. Bahubalendruni and B. B. Biswal, “A review on assembly sequence generation and its automation,” Proceeding of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, vol. 230, no. 5, pp. 824–838, 2016. [Google Scholar]
22. M. V. A. R. Bahubalendruni, B. B. Biswal, M. Kumar and R. Nayak, “Influence of assembly predicate consideration on optimal assembly sequence generation,” Assembly Automation, vol. 35, no. 4, pp. 309–316, 2015. [Google Scholar]
23. M. A. Abdullah, M. F. F. Ab Rashid and Z. Ghazalli, “Optimization of assembly sequence planning using soft computing approaches: A review,” Archives on Computational Methods in Engineering, vol. 26, no. 2, pp. 461–474, 2019. [Google Scholar]
24. S. Chakrabarty and J. Wolter, “A structure-oriented approach to assembly sequence planning,” IEEE Transactions on Robotics and Automation, vol. 13, no. 1, pp. 14–29, 1997. [Google Scholar]
25. W. Hui, X. Dong and D. Guanghong, “A genetic algorithm for product disassembly sequence planning,” Neuro Computing, vol. 71, no. 13–15, pp. 2720–2726, 2008. [Google Scholar]
26. B. Lazzerini and F. Marcelloni, “A genetic algorithm for generating optimal assembly plans,” Artificial Intelligence in Engineering, vol. 14, no. 4, pp. 319–329, 2000. [Google Scholar]
27. Y. Tian, X. Zhang, Z. Liu, X. Jiang and J. Xue, “Product cooperative disassembly sequence and task planning based on genetic algorithm,” International Journal of Advanced Manufacturing Technology, vol. 105, no. 5, pp. 2103–2120, 2019. [Google Scholar]
28. J. R. Li, L. P. Khoo and S. B. Tor, “A novel representation scheme for disassembly sequence planning,” International Journal of Advanced Manufacturing Technology, vol. 20, no. 8, pp. 621–630, 2002. [Google Scholar]
29. E. Kongar and S. M. Gupta, “Genetic algorithm for disassembly process planning,” in Environmentally Conscious Manufacturing II, vol. 4569. Bellingham, USA: SPIE Digital Library, pp. 54–62, 2002. [Google Scholar]
30. H. E. Tseng, C. C. Chang, S. C. Lee and Y. M. Huang, “A block-based genetic algorithm for disassembly sequence planning,” Expert Systems and Applications, vol. 96, pp. 492–505, 2018. [Google Scholar]
31. Y. Xing and Y. Wang, “Assembly sequence planning based on a hybrid particle swarm optimisation and genetic algorithm,” International Journal of Production Research, vol. 50, no. 24, pp. 7303–7312, 2012. [Google Scholar]
32. C. B. Kalayci, O. Polat and S. M. Gupta, “A hybrid genetic algorithm for sequence-dependent disassembly line balancing problem,” Annals of Operation Research, vol. 242, no. 2, pp. 321–354, 2016. [Google Scholar]
33. F. Pistolesi, B. Lazzerini, M. Dalle Mura and G. Dini, “Emoga: A hybrid genetic algorithm with extremal optimization core for multiobjective disassembly line balancing,” IEEE Transactions on Industrial Informatics, vol. 14, no. 3, pp. 1089–1098, 2017. [Google Scholar]
34. W. Hao and Z. Hongfu, “Using genetic annealing simulated annealing algorithm to solve disassembly sequence planning,” Journal of Systems Engineering and Electronics, vol. 20, no. 4, pp. 906–912, 2009. [Google Scholar]
35. C. Ravi and N. Khare, “BGFS: Design and development of brain genetic fuzzy system for data classification,” Journal of Intelligent Systems, vol. 27, no. 2, pp. 231–247, 2018. [Google Scholar]
36. C. Ravi, “Fuzzy crow search algorithm-based deep lSTM for bitcoin prediction,” International Journal of Distributing Systems and Technology, vol. 11, no. 4, pp. 53–71, 2020. [Google Scholar]
37. C. Ravi and N. Khare, “BSFS: Design and development of exponential brainstorm fuzzy system for data classification,” International Journal of Uncertainty, Fuzziness Knowledge-Based Systems, vol. 25, no. 2, pp. 267–284, 2017. [Google Scholar]
38. M. V. A. R. Bahubalendruni, A. Gulivindala, M. Kumar, B. B. Biswal and L. N. Annepu, “A hybrid conjugated method for assembly sequence generation and explode view generation,” Assembly Automation, vol. 39, no. 1, pp. 211–225, 2019. [Google Scholar]
39. A. K. Gulivindala, M. V. A. R. Bahubalendruni, S. S. V. P. Varupala and K. Sankaranarayanasamy, “A heuristic method with a novel stability concept to perform parallel assembly sequence planning by subassembly detection,” Assembly Automation, vol. 40, no. 5, pp. 779–787, 2020. [Google Scholar]
40. P. Kora and P. Yadlapalli, “Crossover operators in genetic algorithms: A review,” International Journal of Computer Applications, vol. 162, no. 10, pp. 34–36, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |