Computers, Materials & Continua DOI:10.32604/cmc.2021.018481
Article

Adaptive Relay Selection Scheme for Minimization of the Transmission Time

Yu-Jin Na1, Ji-Sung Jung1, Young-Hwan You2 and Hyoung-Kyu Song1,*

1Department of Information and Communication Engineering, and Convergence for Intelligent Drone, Sejong University, Seoul, 05006, Korea
2Department of Computer Engineering, and Convergence for Intelligent Drone, Sejong University, Seoul, 05006, Korea
*Corresponding Author: Hyoung-Kyu Song. Email: songhk@sejong.ac.kr
Received: 09 March 2021; Accepted: 10 April 2021

Abstract: As the installation of small cells increases, the use of relay also increases. The relay operates as a base station as well as just an amplifier. As the roles and types of relays become more diverse, appropriate relay selection technology is an effective way to improve communication performance. Many researches for relay selection have been studied to secure the reliability of relay communication. In this paper, the relay selection scheme is proposed for a cooperative system using decode-and-forward (DF) relaying scheme in the mobile communication system. To maintain the transmission rate, the proposed scheme classifies a candidate group considering the outage probability of multiple relays. For the applicable candidate group, the proposed scheme selects the relay considering the amount of data allocated to each user. Therefore, the proposed scheme defines the unit transmission time through each user’s data and relay capacity. Finally, the proposed scheme selects a relay that minimizes the total transmission time through the relay transmission time that calculates the unit transmission time for all users. With this adaptive relay selection scheme, an optimal relay can be assigned for each user. For the same transmission rate and the amount of data, the proposed scheme improves the performance of transmission time and reliability. Simulation results show that the proposed scheme reduces the total transmission time for the same amount of data and signal to noise ratio (SNR).

Keywords: Relay selection; cooperative relay; MIMO; outage probability; transmission time

1  Introduction

In upcoming years, the usage of mobile traffic is expected to be massive, and throughput of communication is getting higher. As the usage of mobile data is increased, mobile network is needed to provide higher performance in terms of throughput, latency and reliability.

Current mobile network systems such as long-term evolution (LTE) and 5G new radio (NR) are deployed in a variety of ways to meet the actual needs and possibilities. Meanwhile, there are many cases where sufficient reliability and throughput are not guaranteed in the wireless communication system. For example, in the mmWave bands, although a shorter transmission time interval can be used because of low frequency selectivity, the cell coverage would be limited because of higher path loss, which would inevitably lead to the use of small cell sizes [1]. Also, cells are overloaded due to increased space density and mobile devices [2]. Therefore, the design of a new cell is required.

The future communication network may be a heterogeneous layer network consisting of macrocells, traditional micro/picocells, new local small cells, and relay and other low-power nodes [3]. Specifically, the relay system can be used in various ways in the future wireless mobile communication network. The relay system is one of the techniques to provide sufficient coverage and reliability in the wireless communication system. The relay is used to overcome poor wireless link conditions in a cooperative communication system. By implementing a relay node, the relay node handles and routes data traffic between source and destination. Therefore, the SNR and capacity can be increased. Also, relays can improve the topology, network robustness and power consumption of mobile communication systems. As the wireless backhaul secures sufficient capacity, the mobile station can be a solution for the mobile communication systems that can configure a mobile cell architecture [4–6]. The relay supports mobile group access and can provide new services by supporting access nodes in the Internet of things (IoT) network [3,7].

There are many researches related to relay technologies [8–10]. A relay node can assist a pair of users with one-way (OW) or two-way (TW) traffic patterns [11]. For the same data rate, two-way relaying protocol improves transmission power consumption and spectral than one-way relaying protocol [12]. For this reason, two-way relaying protocols have been studied actively to improve performance [13].

To enhance the capacity and reliability, the multiple-input multiple-output (MIMO) relay system can be considered. MIMO techniques provide higher capacity gain using diversity and multiplexing in a relay system.

This paper proposes the adaptive relay selection scheme to enhance the transmission time of the wireless system. The proposed scheme not only considers the link capacity but also the buffered data traffic of active users. Specifically, the proposed scheme classifies the available relay group and then considers the amount of data assigned to each user. Therefore, the proposed scheme reduces the transmission time while the transmission rate is maintained.

This paper is organized as follows. Section 2 introduces the system model. Section 3 explains the conventional schemes. Section 4 describes the algorithm and advantage of the proposed scheme. Simulation results are shown in Section 5. Finally, Section 6 gives the brief conclusions.

2  System Model

Fig. 1 shows the heterogeneous dense network consisting of multi-small cells. Fig. 2 is one of the small cells in Fig. 1. Also, Fig. 2 shows two-hop MIMO relay wireless system model in a wireless network. The system consists of one source node (S) node and each user UEm (m=1,…,M). Fig. 3 shows the buffers for UEm. The amount of data UEm can be changed, and the buffer size can be changed accordingly. Also, UEm requires different amount of data. The number of antennas on S and UEm is the same as Na. Furthermore, multiple relays exist in the system model. Each relay node is expressed as Rn (n=1,…,N). Rn has Nr antennas for the receiving and transmitting data. A set of Rn uses the decode-and-forward (DF) protocol. Since DF protocol demodulates received signal and re-encodes the signal before retransmission of the signal, the effect of noise can be reduced. Direct links (S→UEm) are assumed to be too weak and cannot support the transmission of high quality [13]. Therefore, direct links (S→UEm) are not considered. Non-direct links ((S→Rn) and (Rs→UEm)) are only available. In addition, it is assumed that each node operating as a transmitter knows channel state information (CSI) through feedback according to transmission of a pilot signal to the receiver node.

Figure 1: The heterogeneous network for multi-small cells

Figure 2: Two-hop MIMO relaying system

Figure 3: Assigned buffers for each user

System model uses two time slots for signal transmission. S transmits signal to Rn during the first time slot. The received signal at Rn is as follows,

yn=Hnx+nr,(1)

where x∈CNa is the transmitted signal vector from S. Hn is the Nr×Na channel between S and Rn.

Furthermore, Hn is modeled as Rayleigh fading. x is a signal transmitted from S. And nr∈CNr is an additive white Gaussian noise (AWGN) vector with zero mean and variance N0 at Rn.

During the second time slots, Rs transmits a signal to UEm. Rs (s=1,…,S) is selected as a relay among a set of Rn. The received signals at UEm are as follows,

ym=Gmsx^s+nd,(2)

where transmitted signal from a set of Rs is ym=[y1,…,ym]T. Gms is the Na×Nr compound channel between UEm and a set of Rs. A compound channel is a combination of channels between relays that can be used to transmit to the same destination. Furthermore, Gms=[gm1,…,gmS]T is modeled as Rayleigh fading. x^s=[x^1,…,x^S] is retransmitted signal from Rs. Na of UEm receives different signals. nd∈CNa is an AWGN vector.

3  The Conventional Relay Selection Schemes

This section describes two conventional relay selection schemes. Many researchers have studied for the methods to select relays in different communication environments [14–16]. In each research, there are various schemes for selecting relays, but eventually the relay with the best channel conditions is selected. In other words, the channel condition of R determines the communication performance. Accordingly, the most conventional schemes use channel magnitude from R. Among the conventional schemes, the relay selection schemes that provide the basis for other researches are as follows.

3.1 The Frobenius Norm-Based Selection Scheme

Norm usually uses the Frobenius norm, which is L2-norm, to indicate the distance from the origin. The Frobenius norm is defined for a channel matrix of R as follows,

‖R‖F=(∑i=1Nr∑j=1Na|aij|2)12,(3)

where ‖R‖F means the Frobenius norm of R. aij is an element of Hn consisting of Nr×Nr. aij with the absolute value is expressed as |aij|. The Frobenius norm of R is the square root of a sum of all |aij|2.

‖R‖F=tr(HnTHn)(4)

And the diagonal entry in HnTH is the sum of the squares of each column of Hn. Therefore, the sum of the diagonal entries of HnTH is equal to the total sum of |aij|2. Furthermore, it is same with the sum of an eigenvalue HnTH. σi2 means the square of the singular value of Hn. Eq. (5) presents the singular value decomposition (SVD) of Hn. Hn can be described as follows,

Hn=UΣVH,(5)

where U and V are unitary matrix. Σ is a diagonal matrix with the singular value. σi is a component of Σ. The sum of an eigenvalue HnTH is equal to the sum of σi2. In other words, the Frobenius norm depends on singular value. The Frobenius norm-based selection scheme calculates Eq. (3) for each candidate relay channel and selects the relay with the largest Frobenius norm.

3.2 The MIMO Capacity-Based Selection Scheme

Among the relay selection schemes, the scheme using MIMO relay channel capacity is frequently used [17–19]. The MIMO channel capacity of the k-th relay is as follows,

Cn=log2⁡(det(I+ρNaHnHnH)),(6)

where I denotes the identity matrix. ρ denotes average SNR at each antenna of the relay as PtN0. Pt is the transmitting power of the signal and N0 is noise power. HnH means the Hermitian conjugate transpose matrix of Hn. Therefore Eq. (6) can be approximated as follows,

Cn=∑i=1Nalog2⁡(1+σi2ρ).(7)

As a σi2 increases, available channel capacity also increases. The MIMO capacity-based selection scheme selects relay with the largest capacity using Eqs. (6) or (7).

4  The Proposed Selection Scheme

The relay selection scheme to reduce the total transmission time is proposed. The selection process consists of two selection steps. In the first step, the transmitter organizes a relay group by selecting qualified relays. According to the result of the first step, in the second step, relays for transmission are selected to minimize the total transmission time. The selection process is described in the following subsection.

4.1 Classification of Relay Candidate Group

For reliability of relaying, qualified Rn is selected. For the selection, S calculates probability that outage does not happen for each Rn based on reported CSI. Residual capacity of the links between S and each Rn is calculated as follows,

εn=max(Cn−β,0),(8)

where Cn denotes normalized channel capacity of Hn. β is the number of bits in x. εn is the residual capacity of the link between S and Rn. If outage happens, εn becomes zero. In other words, S decides that the link is valid when the Cn is greater than x. Among the Rn, the relay that meets the non-zero condition of Eq. (8) is defined as Rg (g=1,…,G). The group of the qualified relays is expressed as follows,

G={Rg∣εg>0}.(9)

The selection process is summarized as follows:

(1) Inputs:

β,Hn,n=1,…,N

(2) initialize:

Cn,εn,g←0

G←{}

(3) for n=1:N

(4) if εn>0then

(5) g←g+1

(6) Rg←Rn

(7) G←Rg

(8) end if

(9) end for

(10) if G<2then

(11) break

(12) Rn with largest Cn is selected as Rs

(13) else

(14) Go to the second process

(15) end if

The line of (10) explains processing for low SNR environment. The low SNR environment can make every εn zero and outage happens in all links. In this case, S can stop transmission until qualified link is detected.

However, to prevent waste of bandwidth, in proposed algorithm, S selects the most favorable relay as Rs in the coherence time. If any non-correctable errors occur, the relay should notify necessity of retransmission.

4.2 Relay Selection to Minimize the Transmission Time

In this section, the process to allocate relays to users is performed for minimization of the total transmission time. In this process, two cases are considered. The cases are determined according to G. If G is lower than two, the case is low SNR case. In the low SNR case, the most favorable relay is determined as Rs and the data of all users is transmitted through the selected relay. In other words, the transmission time is optimized only if the number of G is larger than one. In the low SNR case, the transmission time is as follows,

Ttot=∑m=1mBmCm,s,(10)

where Cm,s is normalized channel capacity between Rs and UEm.

In the other case, S optimizes the transmission time by using the CSI between the qualified relays and the users. The transmission time between Rg and UEm is defined as follows,

Tm,g=BmCm,g,(11)

where Bm (m=1,2,…,M) is the amount of data from UEm. The amount is considered as random variable and generally the distribution of Bm is modeled by Poisson distribution. Cm,g (g=1,2,…,G) denotes normalized channel capacity between Rg and UEm. According to Eq. (10), the total transmission time can be described as follows,

Ttot=∑m=1MTm,gm.(12)

In other words, Ttot is the total time required to transmit data of all users. To minimize Ttot, gm is determined as follows,

gm=arg maxRg∈G{Cm,g}.(13)

The detailed description is summarized as follows:

(1) Inputs:

G, Bm (m=1,…,M)

(2) Initialize:

Cm,0←0

(3) for m=1:M

(4) gm←0

(5) for g=1:G

(6) If Cm,g>Cm,g−1

(7) gm←g

(8) end for

(9) end for

The proposed scheme classifies a candidate relay group with non-outage. For a configured group of candidate relays, the relay with the minimum transmission time is selected. The proposed scheme can select a relay that reduces the transmission time while the BER performance through two steps is improved.

5  Simulation Results

Tab. 1 shows the simulation parameters. The proposed scheme is simulated with 64 symbols and a 7-path Rayleigh fading channel. Two different modulation schemes of QPSK and 16-QAM are used to analyze the performance according to the modulation order. The zero-forcing (ZF) scheme is used to simplify signal detection. Three distance ranges are used to compare the performance effect of distance and outage. The first distance range is divided into S to Rn and Rn to UEm based on 0.25. The second distance range is divided into S to Rn and Rn to UEm based on 0.5. The third distance range is divided into S to Rn and Rn to u based on 1. The maximum total distance of the first and second range is normalized to 1. The third distance range has a higher channel variation than the other distance ranges. Rn has a random distribution within each distance range. The number of users is two and uses single-user detection by ZF. The number of Rn is four and eight to compare the performance according to the number of relays. The number of all antennas is fixed as 2 to exclude the performance change according to the number of antennas. The simulations iterate 10,000 times for statistics on performance.

Table 1: Simulation parameters

The simulation graphs show the total transmission time and the maximum performance is normalized to 1. The proposed scheme is compared with the two conventional selection schemes, and the comparison schemes are mentioned in Section 3. The number of Rn is four in Figs. 4–6. When the number of Rn is eight, performance is shown in Figs. 7–9. Figs. 4 and 7 use 0.25 distance range and Figs. 5 and 7 use 0.5 distance range. Figs. 6 and 9 use 1 distance range. All simulation graphs show the performance of 16-QAM and QPSK modulation scheme. The proposed scheme improves the total transmission time than the capacity and Frobenius norm-based scheme. In the same parameter, the capacity and Frobenius norm-based scheme have the same performance.

In Fig. 4, the proposed scheme using QPSK modulation shows about 1.5 times faster performance at low SNR than the comparison scheme. At mid-SNR, the proposed scheme using QPSK modulation has about 1.3 times faster performance than the comparison scheme. As SNR increases, the occurrence of outages also decreases and the gain of time performance decreases. The proposed scheme using QAM modulation has about 1.5 times faster performance at low SNR. At mid-SNR, the proposed scheme using QAM modulation has about 1.3 times faster performance than the comparison scheme.

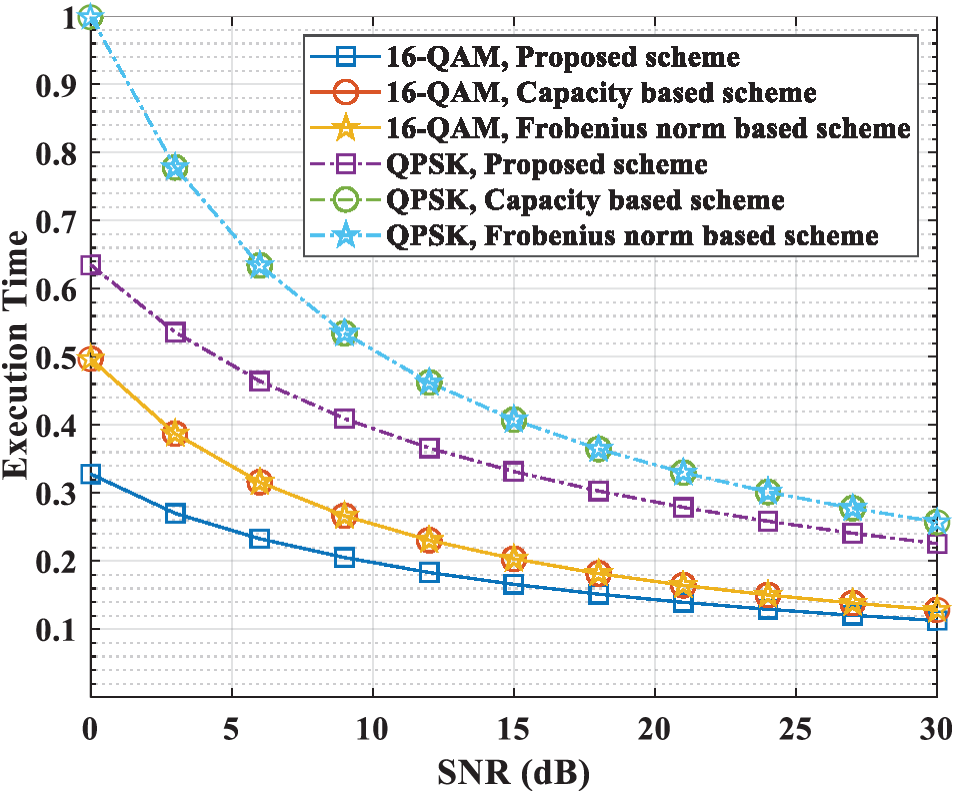
Figure 4: Total time performance (4 relays 0.25 distance)

In Fig. 5, the proposed scheme using QPSK modulation is about 1.3 times faster than the comparison scheme at low SNR. The proposed scheme using QAM modulation is about 1.15 times faster than the comparison scheme at low SNR. In the middle SNR, all performance gains are reduced between the proposed scheme and the comparison schemes. As the distance between the S and Rn is averaged, the performance gain of the proposed scheme is reduced.

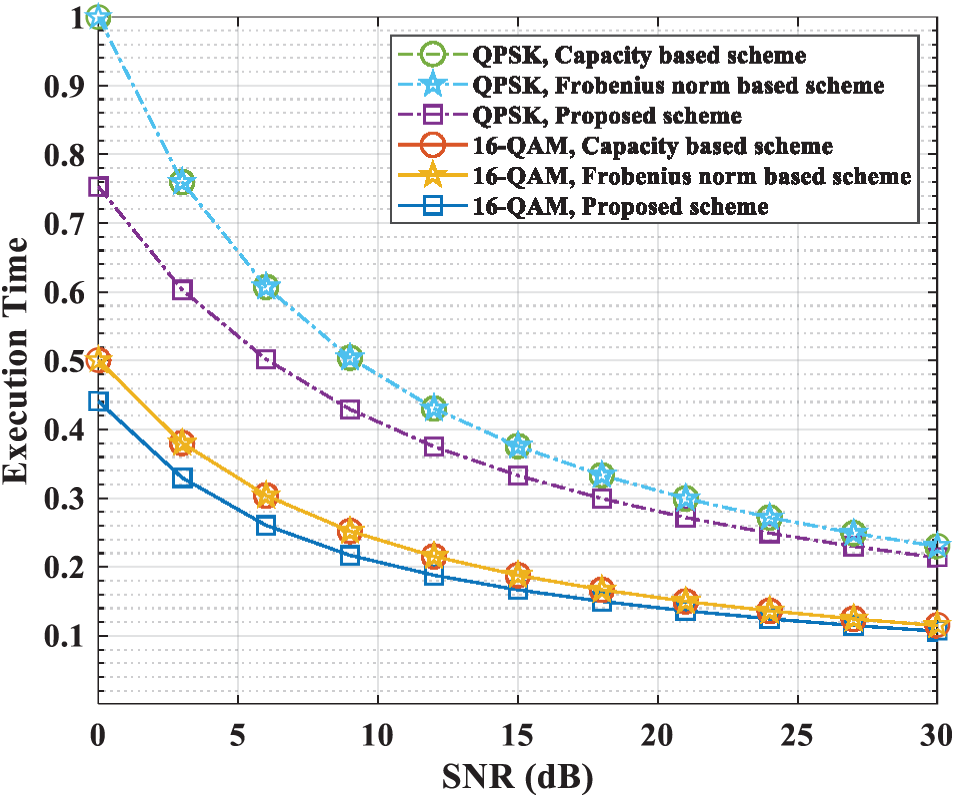
Figure 5: Total time performance (4 relays 0.5 distance)

Fig. 6 shows that the proposed scheme using QPSK modulation has 1.5 times faster performance gain than the comparison schemes of low SNR. At mid-SNR, the proposed scheme using QPSK modulation shows about 1.4 times faster than the comparison schemes. Compared to Fig. 5, the performance gain of the proposed scheme using QAM modulation is similar at low SNR, but increases at medium SNR. When a distance range is 1, the proposed scheme using QPSK modulation has performance improvement at low SNR.

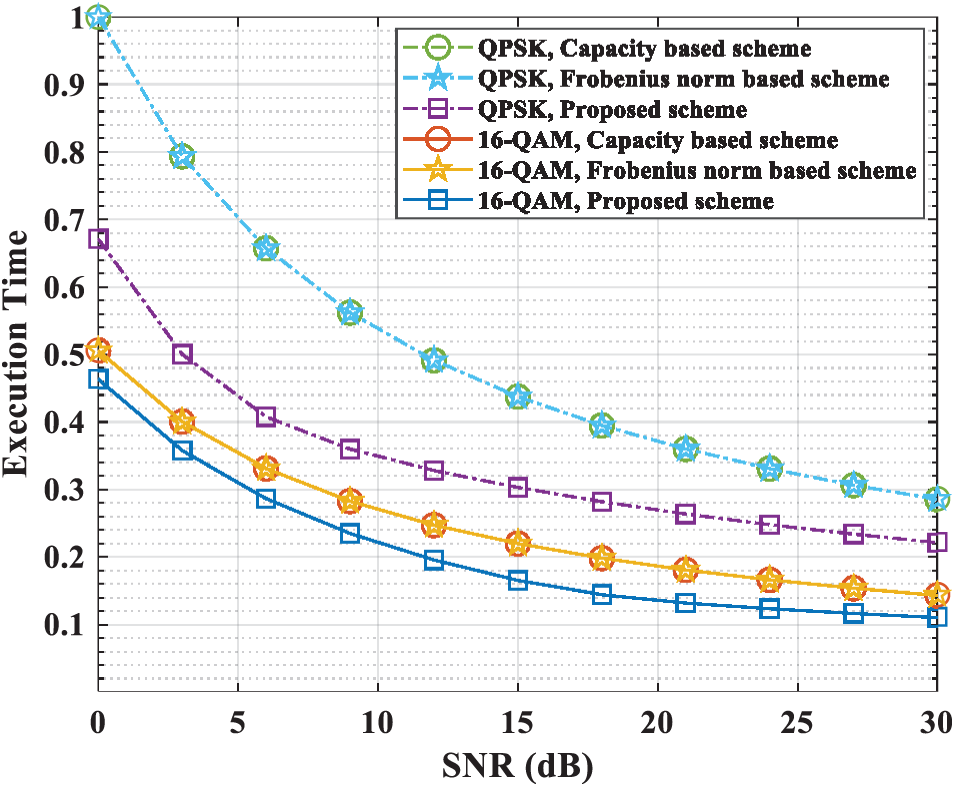
Figure 6: Total time performance (4 relays 1 distance)

All schemes in Figs. 4 and 7 have almost similar performance gain. Fig. 7 shows that the only proposed scheme has 1.2 times performance gain than the proposed scheme in Fig. 4. Although the number of Rn increases, the diversity gain is not linearly increased because the number of Rs is one. For the same reason, the performance of Fig. 8 is similar to Fig. 5.

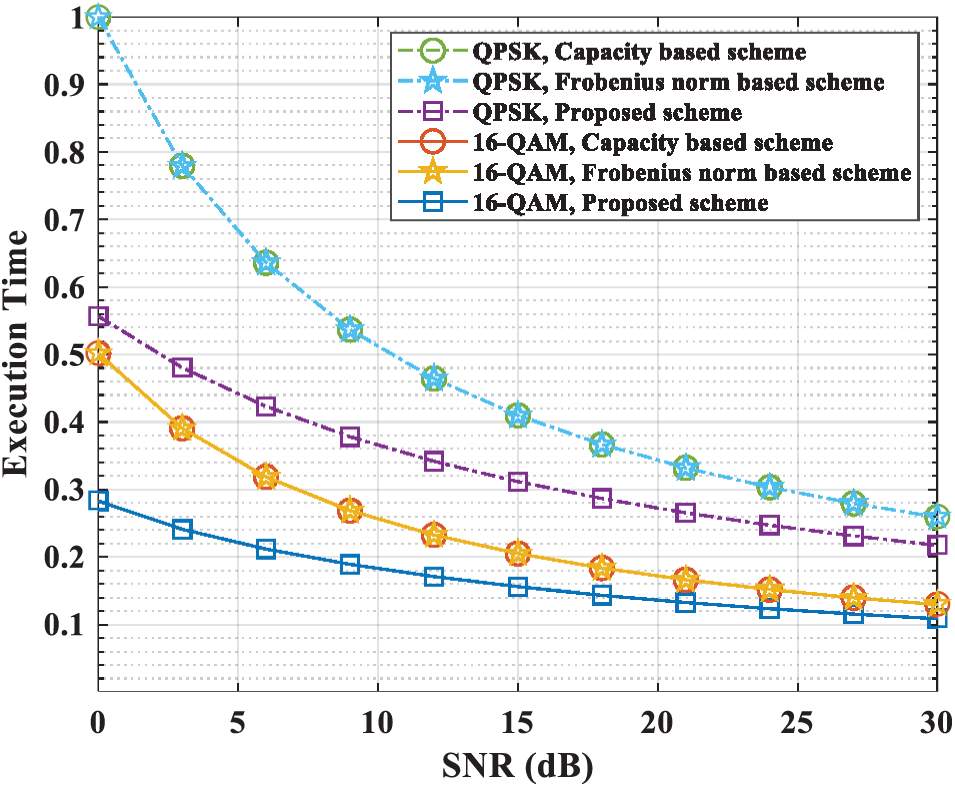
Figure 7: Total time performance (8 relays 0.25 distance)

In Fig. 9, the proposed scheme using QAM modulation is 1.3 times faster than the comparison schemes. The proposed scheme using QPSK modulation has 2 times performance improvement at low SNR than the comparison schemes. At mid-SNR, the proposed scheme using QPSK modulation has 1.8 times performance improvement at low SNR than the comparison schemes. The proposed scheme using QPSK modulation has 1.4 times performance improvement at low SNR compared to Fig. 6. At mid-SNR, the proposed scheme using QPSK modulation has 1.4 times performance improvement compared to Fig. 6. The performance of the proposed scheme using QAM modulation is similar to Fig. 6. The proposed scheme using QPSK modulation has a different form of performance gain than other Figures. With the QPSK modulation scheme, signal demodulation is easier than the QAM modulation scheme even when the outage occurs.

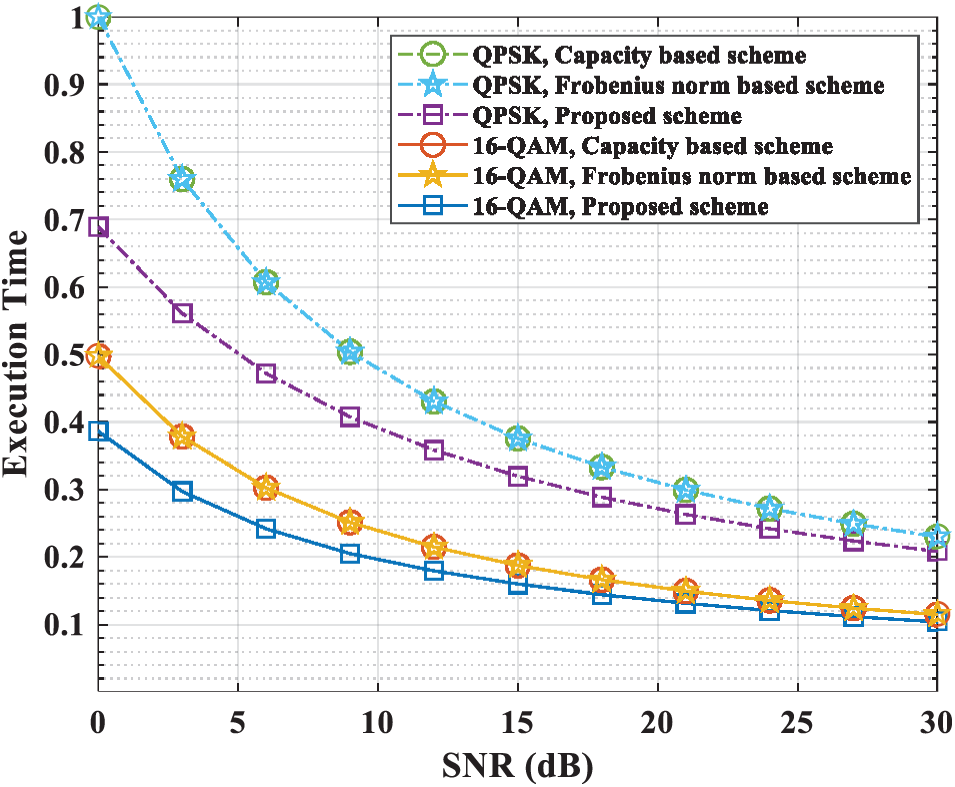
Figure 8: Total time performance (8 relays 5 distance)

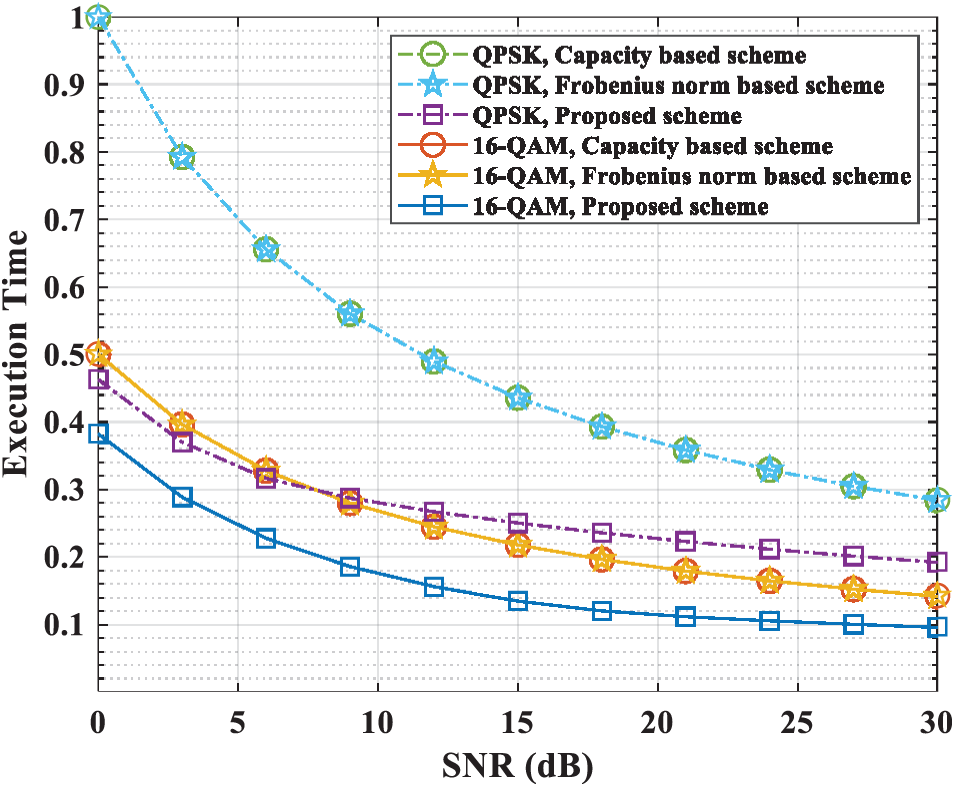
Figure 9: Total time performance (8 relays 1 distance)

The simulation results show that the proposed scheme reduces the performance of the total time than the comparison schemes. As the low SNR, the proposed scheme has higher performance gain. Depending on the distance range, the performance gain of the comparison schemes is same but the performance gain of the proposed scheme can be improved. Especially for distance ranges of 0.25 and 1, the proposed scheme has a performance gain. The performance gain can be increased with more users.

6  Conclusions

In this paper, a relay selection scheme is proposed for reducing the transmission time. The proposed scheme gets the performance gain from two steps. The available relays in the first step are classified as candidate relay group. According to the result of the first step, the second step is executed. When an applicable case exists, the second step determines a relay considering the transmission time of each user. Through this process, the proposed scheme shows that the total transmission time is improved even at low SNR. Simulation results show that the proposed scheme improves the total transmission time when the same data are transmitted.

Funding Statement: This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2019-2018-0-01423) supervised by the IITP (Institute for Information & communications Technology Promotion) and was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1A6A1A03038540).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Q. C. Li, H. Niu, A. T. Papathanassiou and G. Wu, “5G network capacity: Key elements and technologies,” IEEE Vehicular Technology Magazine, vol. 9, no. 1, pp. 71–78, 2014. [Google Scholar]

 2.  Liu, Y. Zhou, J. Yuan, W. Zhuang and Y. Wang, “Economically optimal MS association for multimedia content delivery in cache-enabled heterogeneous cloud radio access networks,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 7, pp. 1584–1593, 2019. [Google Scholar]

 3.  S. Chen and J. Zhao, “The requirements, challenges, and technologies for 5G of terrestrial mobile telecommunication,” IEEE Communications Magazine, vol. 52, no. 5, pp. 36–43, 2014. [Google Scholar]

 4.  A. Krendzel, “LTE-A mobile relay handling: Architecture aspects,” in European Wireless 2013; 19th European Wireless Conf., Guildford, UK, pp. 1–6, 2013. [Google Scholar]

 5.  M. Pan, T. Lin and W. Chen, “An enhanced handover scheme for mobile relays in LTE-A high-speed rail networks,” IEEE Transactions on Vehicular Technology, vol. 64, no. 2, pp. 743–756, 2015. [Google Scholar]

 6.  H. Yasuda, A. Kishida, J. Shen, Y. Morihiro, Y. Morioka et al., “A study on moving cell in 5G cellular system,” in IEEE 82nd Vehicular Technology Conf., Boston, MA, pp. 1–5, 2015. [Google Scholar]

 7.  W. Li and M. Dong, “Joint relay beamforming and receiver processing for multi-way multi-antenna relay networks,” IEEE Transactions on Communications, vol. 66, no. 2, pp. 576–588, 2018. [Google Scholar]

 8.  D. Jiang, H. Zheng, D. Tang and Y. Tang, “Relay selection and power allocation for cognitive energy harvesting two-way relaying networks,” in 2015 IEEE 5th Int. Conf. on Electronics Information and Emergency Communication, Beijing, China, pp. 163–166, 2015. [Google Scholar]

 9.  H. Wang and B. Yang, “A new residual energy based relay selection in two-way buffer-aided relay networks,” in Int. Conf. on Network and Information Systems for Computers, Shanghai, China, pp. 72–76, 2017. [Google Scholar]

10. Y. Li, T. Wang, Z. Zhao, M. Peng and W. Wang, “Relay mode selection and power allocation for hybrid one-way/two-way half-duplex/full-duplex relaying,” IEEE Communications Letters, vol. 19, no. 7, pp. 1217–1220, 2015. [Google Scholar]

11. L. R. Ximenes, “Unified joint symbol and channel estimation with interference subtraction for one-way and two-way MIMO relaying systems,” in IEEE 10th Latin-American Conf. on Communications, Guadalajara, pp. 1–6, 2018. [Google Scholar]

12. Y. Wang, K. Xu, A. Liu and X. Xia, “Hybrid one-way full-duplex/two-way half-duplex relaying scheme,” IEEE Access, vol. 5, pp. 7737–7745, 2017. [Google Scholar]

13. M. Wen, X. Cheng and L. Yang, Index Modulation for 5G Wireless Communications. Cham, Switzerland: Springer International Publishing AG, 2017. [Google Scholar]

14. H. S. Ryu, J. S. Lee and C. G. Kang, “Relay selection scheme for orthogonal amplify-and-forward relay-enhanced cellular system in a multi-cell environment,” in IEEE 71st Vehicular Technology Conf., Taipei, Taiwan, pp. 1–5, 2010. [Google Scholar]

15. R. Narasimhan, “Spatial multiplexing with transmit antenna and constellation selection for correlated MIMO fading channels,” IEEE Transactions on Signal Processing, vol. 51, no. 11, pp. 2829–2838, 2003. [Google Scholar]

16. V. N. Q. Bao, N. Linh-Trung and M. Debbah, “Relay selection schemes for dual-hop networks under security constraints with multiple eavesdroppers,” IEEE Transactions on Wireless Communications, vol. 12, no. 12, pp. 6076–6085, 2013. [Google Scholar]

17. O. Semiari, W. Saad, M. Bennis and Z. Dawy, “Inter-operator resource management for millimeter wave multi-hop backhaul networks,” IEEE Transactions on Wireless Communications, vol. 16, no. 8, pp. 5258–5272, 2017. [Google Scholar]

18. L. Bononi and M. di Felice, “A cross layered MAC and clustering scheme for efficient broadcast in VANETs,” in IEEE Int. Conf. on Mobile Adhoc and Sensor Systems, Pisa, Italy, pp. 1–8, 2007. [Google Scholar]

19. H. A. Suraweera, M. Soysa, C. Tellambura and H. K. Garg, “Performance analysis of partial relay selection with feedback delay,” IEEE Signal Processing Letters, vol. 17, no. 6, pp. 531–534, 2010. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.