DOI:10.32604/cmc.2021.018239

| Computers, Materials & Continua DOI:10.32604/cmc.2021.018239 |  |
| Article |
Integrated CWT-CNN for Epilepsy Detection Using Multiclass EEG Dataset
1Robotics and Machine Intelligence Engineering, School of Mechanical and Manufacturing Engineering, National University of Sciences and Technology (NUST), Islamabad, 44000, Pakistan
2National University of Sciences and Technology (NUST), Islamabad, 44000, Pakistan
3Department of Computer Science, HITEC University Taxila, Taxila, Pakistan
4Department of Computer Science and Engineering, Soonchunhyang University, Asan, Korea
*Corresponding Author: Yunyoung Nam. Email: ynam@sch.ac.kr
Received: 01 March 2021; Accepted: 02 April 2021
Abstract: Electroencephalography is a common clinical procedure to record brain signals generated by human activity. EEGs are useful in Brain controlled interfaces and other intelligent Neuroscience applications, but manual analysis of these brainwaves is complicated and time-consuming even for the experts of neuroscience. Various EEG analysis and classification techniques have been proposed to address this problem however, the conventional classification methods require identification and learning of specific EEG characteristics beforehand. Deep learning models can learn features from data without having in depth knowledge of data and prior feature identification. One of the great implementations of deep learning is Convolutional Neural Network (CNN) which has outperformed traditional neural networks in pattern recognition and image classification. Continuous Wavelet Transform (CWT) is an efficient signal analysis technique that presents the magnitude of EEG signals as time-related Frequency components. Existing deep learning architectures suffer from poor performance when classifying EEG signals in the Time-frequency domain. To improve classification accuracy, we propose an integrated CWT and CNN technique which classifies five types of EEG signals using. We compared the results of proposed integrated CWT and CNN method with existing deep learning models e.g., GoogleNet, VGG16, AlexNet. Furthermore, the accuracy and loss of the proposed integrated CWT and CNN method have been cross validated using Kfold cross validation. The average accuracy and loss of Kfold cross-validation for proposed integrated CWT and CNN method are, 76.12% and 56.02% respectively. This model produces results on a publicly available dataset: Epilepsy dataset by UCI (Machine Learning Repository).
Keywords: Deep learning; electroencephalography; epilepsy; continuous wavelet transform
Electroencephalography is an electrophysiological method to record neural activity generated by brain neurons. Electrodes are used to perform this method and record all brainwave patterns. These brain signals are helpful to analyze brain performance in different conditions since EEGs are formed of brainwaves caused by emotional changes, motor movements and motor movement imagery, tumor, epileptic Seizure, and many other systems of the human body [1,2]. Electroencephalography has been an important and well-researched topic over the past few years since it plays a significant role in the diagnosis of neural abnormalities. Moreover, these brain signals have been of great interest for Brain Computer Interfaces which are used to facilitate people who are suffering from Paraplegia, Quadriplegia, and Locked-In syndrome [3]. Because EEG has a huge impact on human life, it is imperative to design reliable classification algorithms which are cost efficient and have better diagnostic accuracy.
To perform common EEG inspection, brainwaves are compared with standard EEGs and the experts identify if there are any abnormalities by manual examination. Since it is difficult and time consuming to analyze EEG signals manually, various Source Localization techniques [4,5] have been proposed and widely used to analyze EEG signals. A wide range of statistical techniques has been developed to analyze EEG signals in temporal and spatial resolution [6]. There are many signal transformation techniques such as Fourier Transform, Short-Time Fourier Transform, Hilbert Huang Transform, and Wavelet-based Transform [7,8] which have been used for interpretation of brain signals and to detect anomalies.
Machine Learning (ML) has been of great interest for ML researchers [9,10] and data science practitioners due to its significance in the industrial sector and classification systems [11,12]. In recent years, many machine learning algorithms have been proposed and implemented for EEG classification such as Support Vector Machine [13], K-Nearest Neighbors [14], and Neural networks [15]. Conventional EEG classification methods require Prior knowledge of data and accurate feature selection for better classification accuracy [16,17]. Lately, with the success of Deep Learning (DL) models, researchers have overcome many classification challenges such as deep learning models do not require prior feature derivation and selection techniques [18,19]. Convolutional neural network (CNN), a subtype of Neural Networks, is considered best as compared to other machine learning techniques because it has end-to-end learning ability on raw data in terms of information extraction, online applications, usability, and classification accuracy [20].
Epilepsy is a recurring neural disease which can cause brain dysfunction due to unexpected occurrences of seizures. These Seizures can result in loss of consciousness, limb Tremors, behavioral disorders, and transient sensory disorders, etc. due to mental shocks caused by Seizures [21]. Brain tumors are also a major cause of Seizures, limb numbness, and behavioral disorders [22]. EEG can be a reliable source for the early detection of Seizures due to Epilepsy or Brain Tumors but, it tends to be contaminated by various physiological activities. Traditional EEG classification methods enforce prior feature engineering and their classification accuracy is solely dependent on correct feature selection. Therefore, it is imperative to design an efficient method which can separate the useful information from noisy characteristics of EEG. The application of Deep Learning in Neuroscience has been of great help in the detection of neural abnormalities because DL models can recognize complex EEG patterns without predefined feature engineering.
The classification of EEG signals using machine learning algorithms is solely dependent on the correct detection of distinctive EEG features. The categorization of EEG signals in time domain has been performed using a variety of classification methods [23]. The author of [24] implemented EEG classification in the frequency domain using CNN. Image-based EEG classification has also been proposed by the author of [25]. In [26], the author performed EEG classification using Continuous Wavelet transform and machine learning algorithms e.g., SVM and KNN. CNN was initially designed to classify images, but it has been successfully used to classify EEG data in the frequency domain. The binary classification of EEGs has been implemented in [27] using Radial Basis Function for feature extraction and a One Against One binary classifier.
In [24], the author proposed a 1D-CNN for epilepsy detection using the Butterworth filter to denoise raw data and then created a spectrograms matrix which has been used to train CNN for classification. Similarly, a fixed size overlapping window is also used in [28] to generate a collection of sub-signals of EEGs in the time domain whose plot images are used for binary and ternary classification using CNN. A 3D image reconstruction and classification method have been proposed in [29] which used a sliding window to divide time series data into 2D segments and then, 3D image reconstruction is performed to create images suitable for 3D CNN. The author of [30] proposed binary classification of the Epilepsy dataset using KNN, Logistic regression, Decision Tree, and Random Forest. Various machine learning methods are implemented and compared in [31] for binary classification of the Epilepsy dataset.
In the recent literature [26,28,30], multiclass EEG datasets have been used to perform the binary classification via K nearest neighbor, decision tree, random forest, and logistic regression. However, these techniques are dependent on the correct feature selection. Accuracy may also get affected by the inconsistency and non-abruptness of the EEG signals, along with other features extracted from the patient history. Many of the researchers have not included the spatial resolution feature. It is also challenging to select the appropriate window length when using time series data.
In this paper, a multiclass classification on Epilepsy dataset [32] is carried out by using Integrated CWT and CNN method, which classifies data into five different classes. The proposed Integrated CWT and CNN method aim to improve accuracy and loss results achieved by existing method. Lastly, a comparison of the results produced by proposed Integrated CWT and CNN method and the existing DL models is carried out to evaluate performance of our model. The performance of proposed Integrated CWT and CNN method is also evaluated using the K-Fold cross validation.
The proposed integrated CWT and CNN method uses CWT to create time-frequency images of the Epilepsy dataset. Then, the images created by CWT are used as input to the CNN model for feature learning and classification. The rest of the paper is organized as follows: Section 3 defines the techniques used in this paper; in Section 4, the proposed integrated CWT and CNN method is explained, Section 5 contains the description of the Epilepsy dataset used in this paper to generate results, in Section 6, we cross validated the performance of proposed integrated CWT and CNN method against existing deep learning models and K-Fold cross validation using K = 10 folds. Lastly, Section 7 consists of the conclusion derived from this research.
In this section, the working of Convolution Neural Network and Continuous Wavelet Transform is explained.
3.1 Continuous Wavelet Transform
In recent years, many signal transformation techniques have been useful to analyze signals such as Fast Fourier transforms (FFT) which provides frequency components of signals, and Short-Time Fourier Transform (STFT), which uses a sliding window to extract time-frequency components of a signal. However, STFT has the limitation of window size and it is suitable for signals that do not change the frequency over time. Empirical Mode Decomposition (EMD) also provides a time-frequency analysis of signals, but it has complex exhibition modes of data which are difficult to interpret. Wavelet transformation (WT) decomposes a signal into a set of frequency components and present their distribution in temporal and spectral domain by compressing, scaling, and shifting signals. Since all frequencies become apparent in WT, it is advantageous over other transformation techniques [33].
A Wavelet (
where
Through this transformation, a one-dimensional signal
where, the function
Morlet wavelet extract temporal features of a variety of signals and it can adapt to their time-frequency resolution. There is a criterion for selecting a scale which is based on the entropy of signals:
where E is the entropy of signal f whereas pi is the probability of k-th class in f.
3.2 Convolutional Neural Network
Deep learning has been of great interest for researchers in recent years and it has shown a great advantage to every aspect of life where it has been used. To name a few, denoising, Pattern recognition, fault, and motion detection image segmentation, high-resolution reconstruction, and classification [35] are advance deep learning applications [36,37]. The most prominent model of deep learning is Convolutional Neural Networks(CNN) which do not enforce prior selection of input features. CNN takes raw data as input and learns certain patterns in time and scale dimensions (i.e., scalograms) without any handcrafted filters. CNN has the adaptability to any kind of transformation e.g., linear, and non-linear transformation.
As shown in Fig. 1, a CNN architecture has two main layers, an input, and output layer where there can be a variable number of hidden layers between these two layers. The hidden layers are comprised of combinations of Convolution layer, pooling layer, batch normalization layers, Rectified Linear Unit Layer, and one or more fully connected layers. CNN is just like feed-forward neural networks which is composed of one or more layers with a variable number of neurons. The input passes through the network as linear combinations of input culminated by each neuron from each layer so that the network can learn highly non-linear features.
Convolution layer is the essence of CNN architectures because this layer is composed of feature maps which are generated by computing cross-correlation between the previous layer’s output and kernels in receptive neurons. Each neuron in the current layer is associated with a different region of the previous layer’s input to extract distinct elements from it [38]. Typically, due to internal covariation in training data, the distribution of feature maps changes due to the update of parameters. This phenomenon requires selecting a small learning rate and initialize parameters carefully. This problem seems to slow down the learning process and makes it harder to learn features with saturating nonlinearities. Therefore, each convolution layer is followed by a batch normalization (BN) layer to avoid overfitting and slow convergence while classification.
Fully connected (FC) layer takes the output of previous layers and combines them to generate a vector of probability scores. The output layer of CNN architecture assigns data to the respective classes based on computed probability scores. The classification accuracy and loss can be determined by using Eqs. (6) and (7).
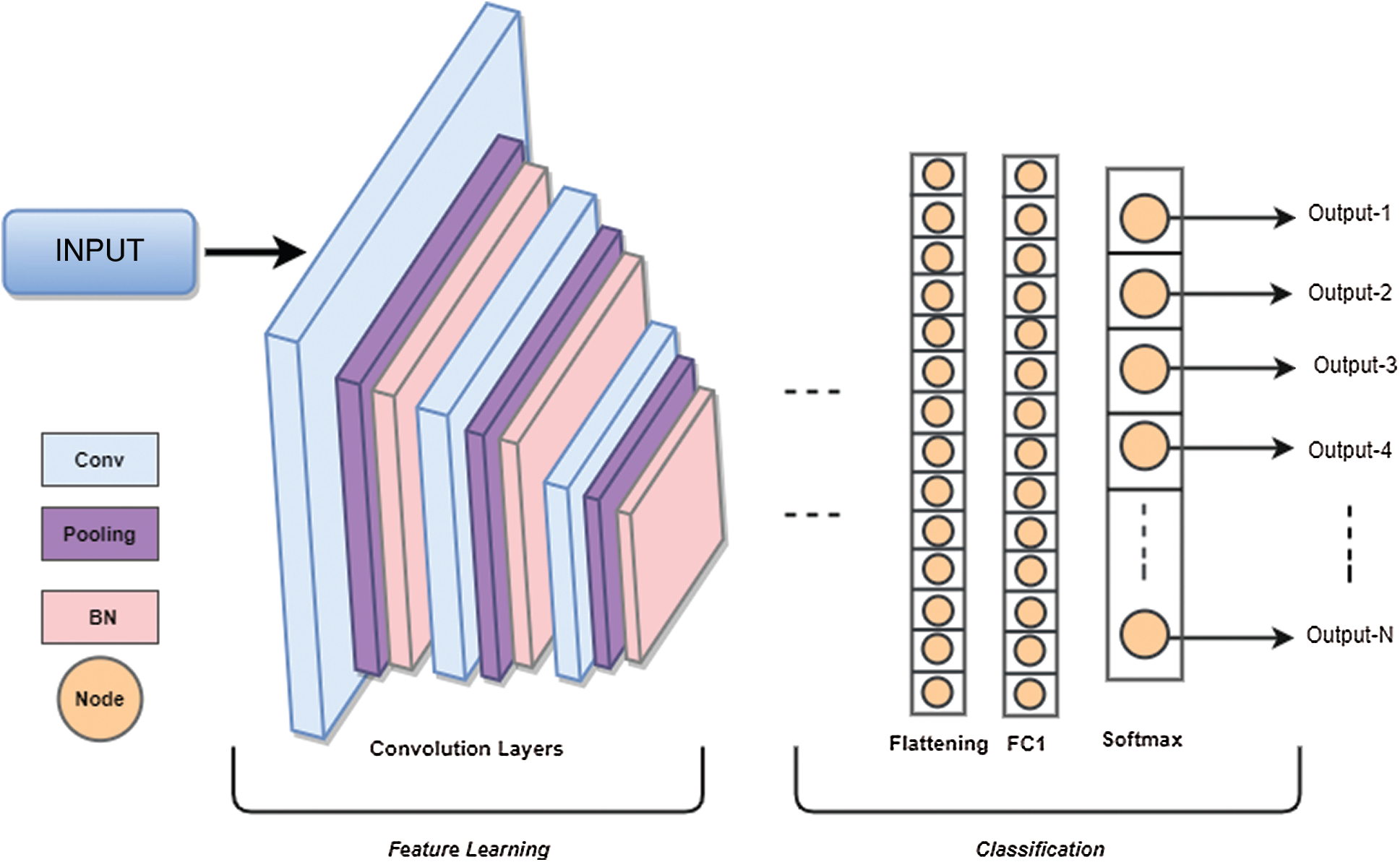
Figure 1: CNN architecture
4 Proposed Integrated CWT and CNN Method
Since the classification of Epilepsy Dataset can lead to early seizure detection, it is crucial to design a method which can achieve maximum classification accuracy to avoid adverse consequences of seizures. The maximum accuracy achieved by the author of [39] on Epilepsy Dataset using CNN is 72.49%. In this paper, we incorporated Continuous Wavelet Transformation with a new Convolutional Neural Network model to improve classification accuracy and performance of [39]. Initially, the dataset is shuffled randomly to make sure that samples from different classes are appearing in training, validation, and testing datasets equally. Furthermore, a standard scaler is used to normalize data with mean = 0 and standard deviation = 1. For reading the Epilepsy dataset and performing data normalization on the acquired dataset, we have divided the dataset using a splitting factor = 0.3 such that a) training dataset contains 8050 images b) validation and testing datasets contains 1725 images each. Then Continuous Wavelet transform is applied to generate 2D images of shape 128 × 128, and the images are reshaped to 128 × 128 × 1. Lastly, performing label encoding on label vectors e.g., Training_labels, Validation _labels, and Tesing_labels.
The continuous wavelet transformation is used to create two dimensional images using scale values 0 to 128. These time-frequency coefficients are then rescaled by 128 to create 128 × 128 dimension images. Furthermore, the collection of these images is then divided into training, validation, and testing datasets with a splitting factor of 0.3. The training dataset contains 8050 images where the validation and testing datasets have 1725 images each. The proposed integrated CWT and CNN method take these images as input to learn all possible features of attributes of Epilepsy Dataset, see Tab. 2. A flowchart of the proposed Integrated CWT and CNN method is presented in Fig. 2.
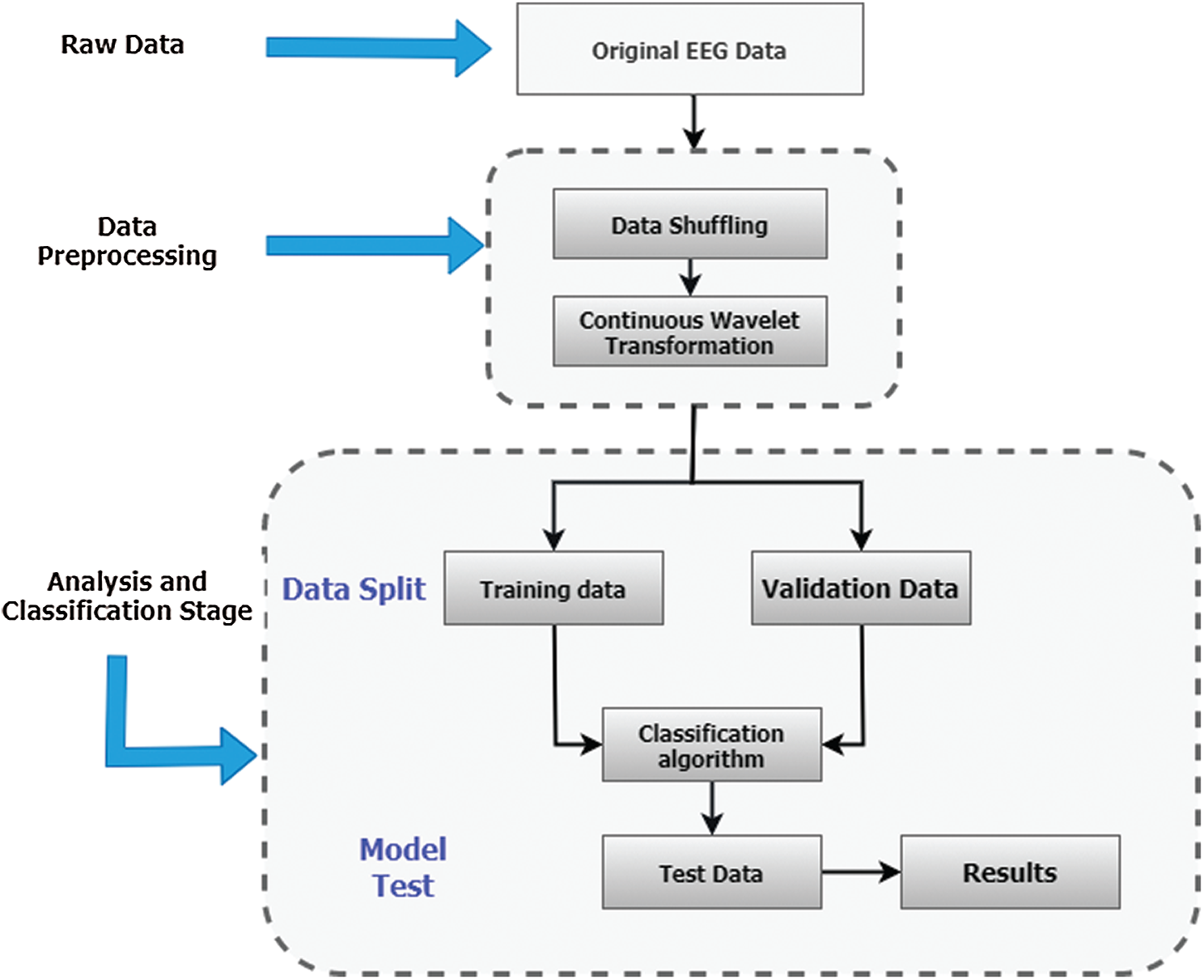
Figure 2: Proposed integrated CWT and CNN method flowchart
The proposed Integrated CWT and CNN method is broken down into feature detection and classification. The feature detection part has three convolutional (Conv) layers present in proposed architecture followed by a Batch normalization (BN) Layer. The convolution layers use ReLU function to activate neurons which contain linear combinations of data patterns learned by the network, whereas Batch Normalization is performed right after convolution layers.
For the classification part, the network consists of a flatten layer which converts all features into one dimensional data so that, the data can be forwarded to the fully connected layer. There are three fully connected layers in this part where the ReLU activation function is applied in the first two dense (FC) layers, and the Softmax activation function is used in classification layer. Essentially, the output layer has five nodes as it must classify five-class data. The architecture of proposed CWT and CNN method is presented in Fig. 3.
The proposed Integrated CWT and CNN method has input size of 128 × 128 pixels. The first convolutional layer has 128 filters of 7-by-7, the second layer has 256 filters of size 5-by-5, and the third layer has 128 filters of 5-by-5. Furthermore, the first convolution layer uses a stride of size 4, where the second and third convolution layers use strides of size 1. For the classification part, the first two FC layers contain 128, 50, and 5 nodes, respectively to classify data with respect to five attributes. The network is trained using the 18,430,257 parameters, however, the total number of parameters learned in this architecture are 18,431,281, and there are 1024 Non-trainable parameters due to BN and dropout layers. For a complete summary of our integrated CWT and CNN method, see Tab. 1.
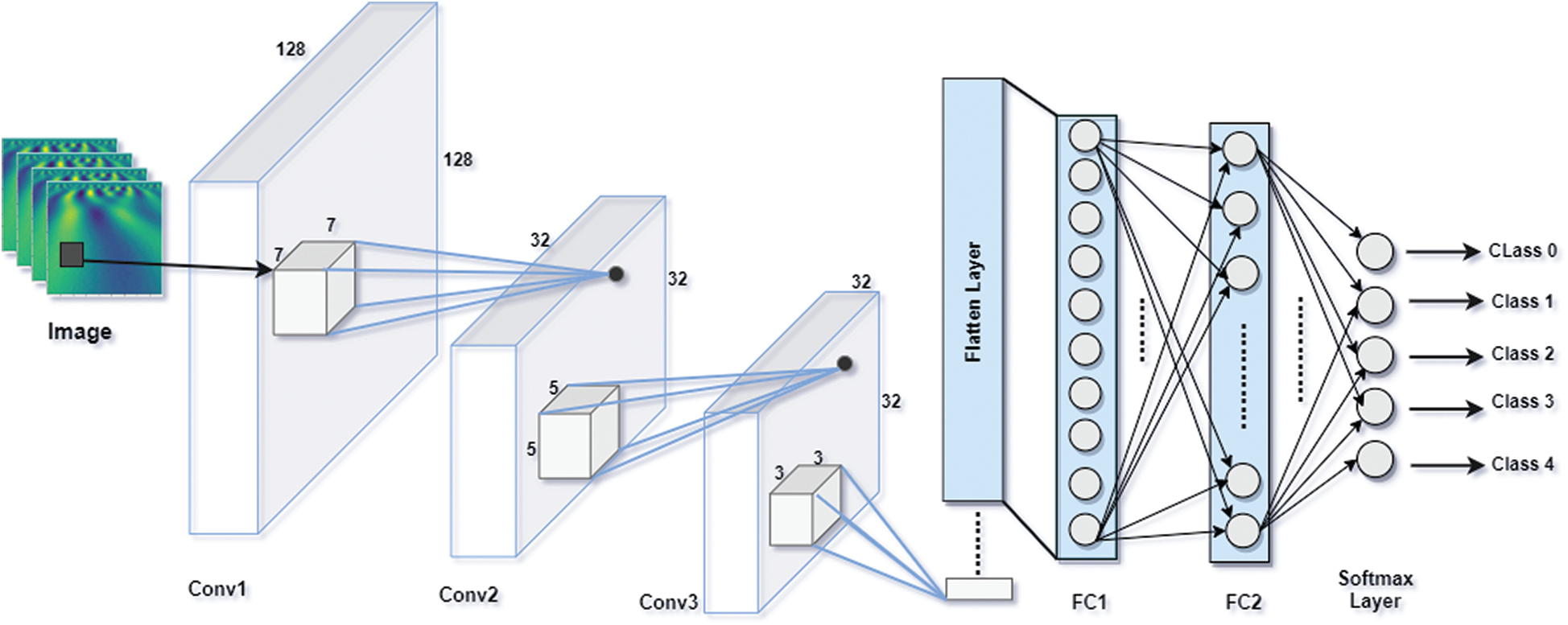
Figure 3: Architecture of proposed integrated CWT and CNN method
Table 1: Description of proposed integrated CWT and CNN method

RELU activation helps deep learning models to train faster on complex features than standard unit. Also, RELU does not suffer with the issue of vanishing gradients. The proposed Integrated CWT and CNN method use RELU activation for each convolution layer and hidden FC layers. The output layer is reserved for Softmax activation and it contains concluded probabilities for all classes. (See Eq.(8))
where, C is used for number of classes in an input vector I.
Loss functions evaluate the performance of deep learning model on the given data. There are two types of loss functions in deep learning: regression and classification. Since our work is based on Classification, we used the Cross-entropy loss (CEL) function. CEL is a log loss, which estimates the performance of a classification model whose output is a probability which always lies between 0 and 1. Eq. (9) can be used to define the cross-entropy loss function for multi-class data.
where, M and P are used for number of classes in the data and probability of a sample o in class c, respectively.
Adam Optimizer is useful in the training process to update weight parameters since it is adaptive to moment estimation and it overcame the problem of vanishing learning rates/moments. It is computationally effective because it requires very less memory.
Electroencephalography records non-invasive brain signals generated by neurons due to some neural activity. These signals can be used to track brain functions, but EEGs tend to be noisy due to epilepsy, brain tumors, muscle movements, movement imagery, and Alzheimer’s disease, etc. Usually, these noisy characteristics in the EEG signals make it challenging to separate the useful information from attributes of other classes with similar time-frequency patterns. For a precise identification and classification of multiclass EEG signals, machine learning models require a large amount of data since, the data will be divided, pooled, and normalized during the feature learning process.
The data used in proposed Integrated CWT and CNN method is an open-access dataset known as Epilepsy dataset which is available at UCI Machine Learning Repository and it was published by [32]. This data was recorded from 500 individuals with different health conditions such as healthy, epilepsy and tumor, etc. This dataset contains a collection of attributes of data from five different classes, see Tab. 2.
The original Epilepsy dataset contains five folders, where each folder contains EEG data recorded from 100 subjects. For each class, there are 4097 data points recorded for the duration of 23.6 s. To create a significant number of training images, each EEG recording is divided into a collection of small one second instances, where each instance contains 178 data points. The resulting dataset is comprised of 11500 information samples of one second. Additionally, the dataset is shuffled and reorganized to avoid biased classification of EEG data towards any class and, to make sure that the data points from each class get to be part of CNN training. Essentially, samples from each class have different characteristics from each other which are illustrated in Fig. 4.
Table 2: Attributes of EEG dataset

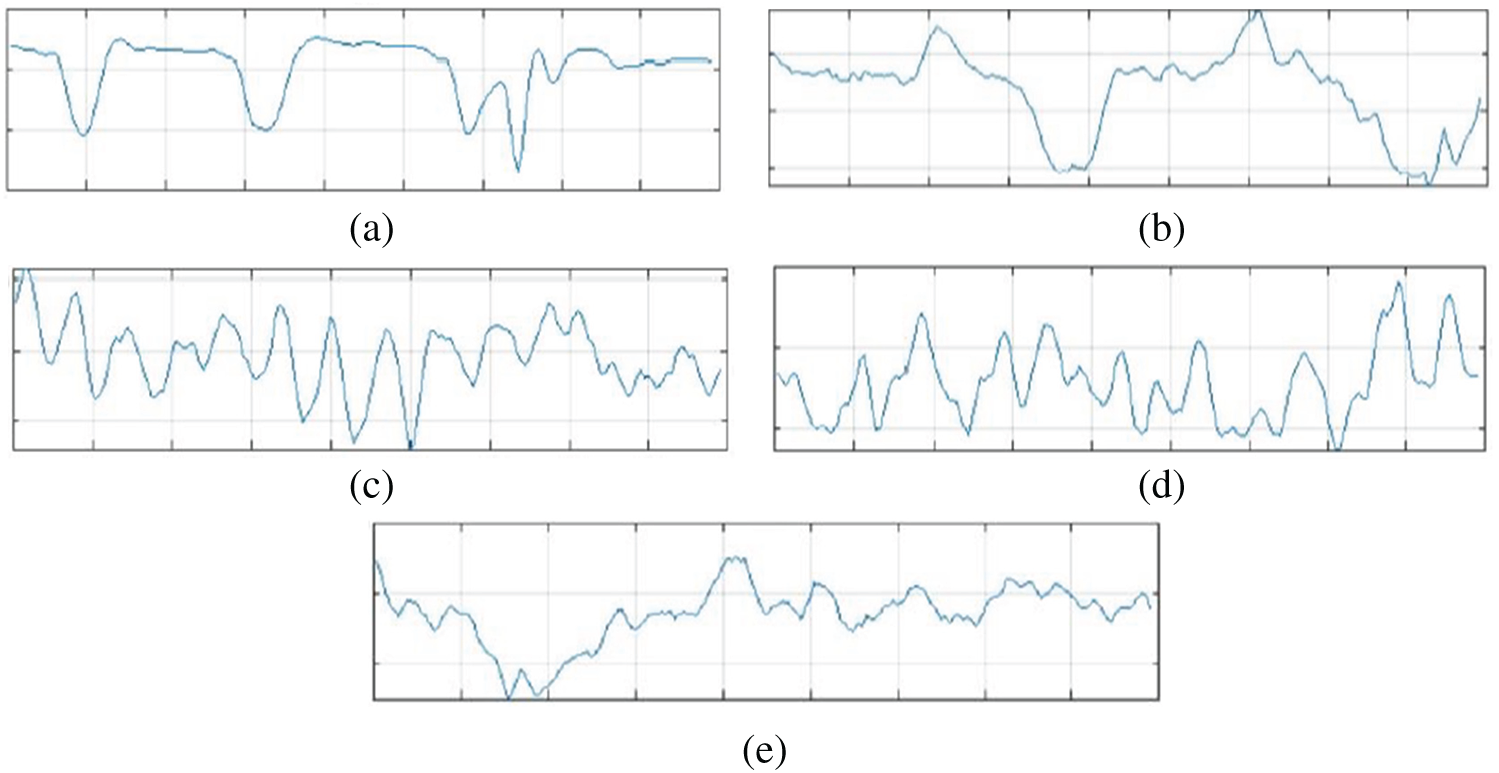
Figure 4: Attributes of dataset. (a): Epileptic (b): Tumor (c): Eyes closed (d): Eyes open (e): Healthy
We trained the proposed Integrated CWT and CNN method using Google Colaboratory, which is a cloud-computing based service to train deep learning models in Python environment. We implemented this method in Keras using Tensorflow at the backend. Multiple python libraries such as Pandas, Numpy, and sklearn etc., have been used for data processing and simulations. Famous deep learning (DL) models such as GoogleNet, VGG16, and AlexNet are also implemented so that comparison between the proposed Integrated CWT and CNN method and existing DL models could be performed. AlexNet architecture won ILSVRC-2012. AlexNet is trained for 150 epochs and the resulting accuracy and loss of AlexNet for EEG dataset classification can be seen in Fig. 5.
GoogleNet won ILSVRC—2014. This model is trained for 300 epochs and the resulting accuracy and loss graph of GoogleNet performance on the EEG dataset are shown in Fig. 6. VGG16 is also a famous deep learning architecture which is named after the Visual Geometry Group at Oxford. This model outperformed many previous generation models in ILSVRC-2012 and ILSVRC-2013 competitions. Fig. 7 presents the resulting accuracy and loss of VGG16 for 150 epochs.
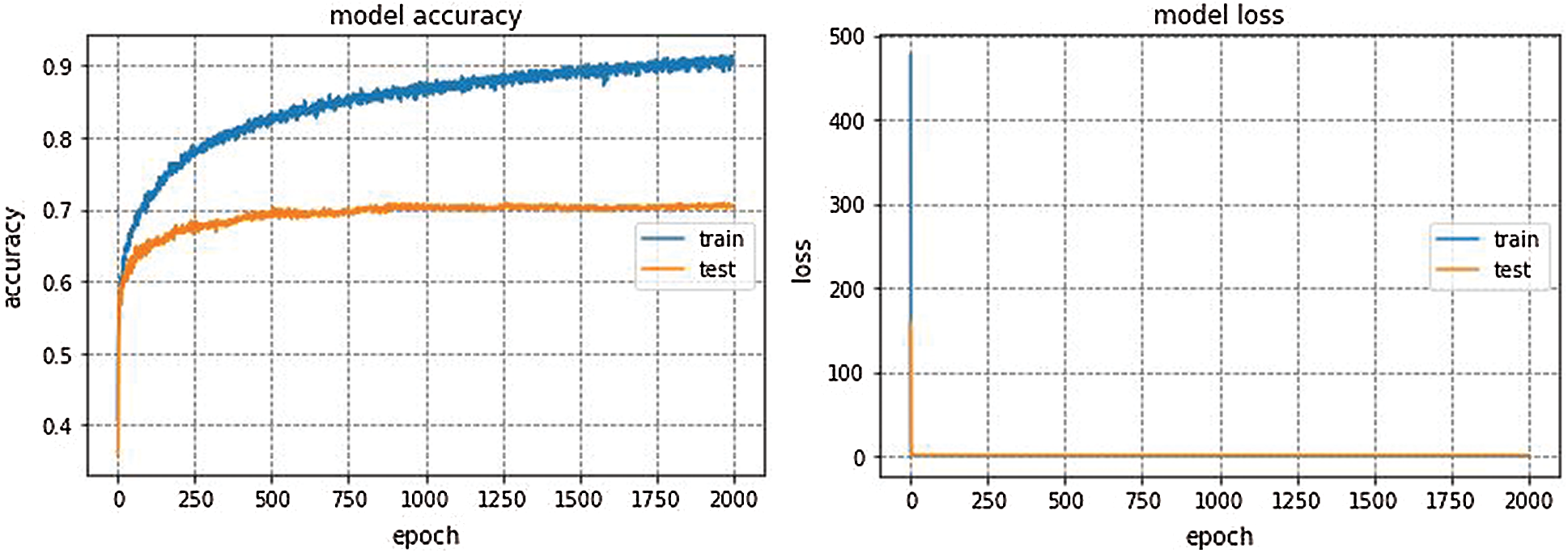
Figure 5: AlexNet performance
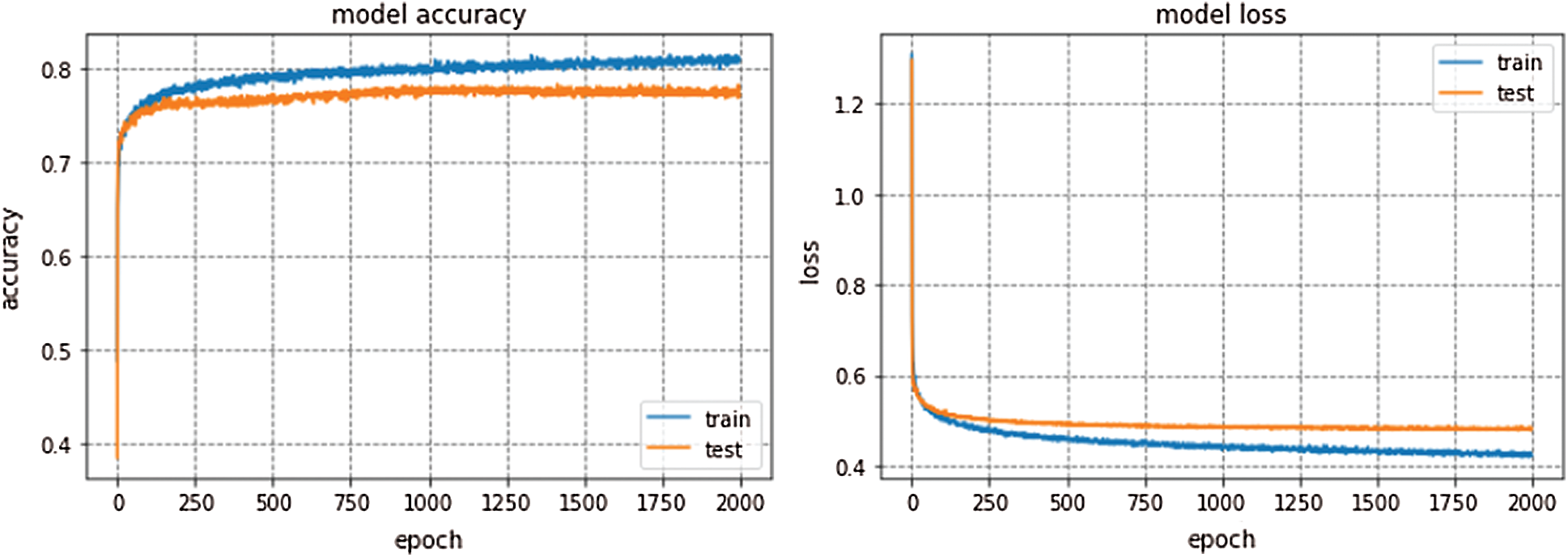
Figure 6: GoogleNet performance
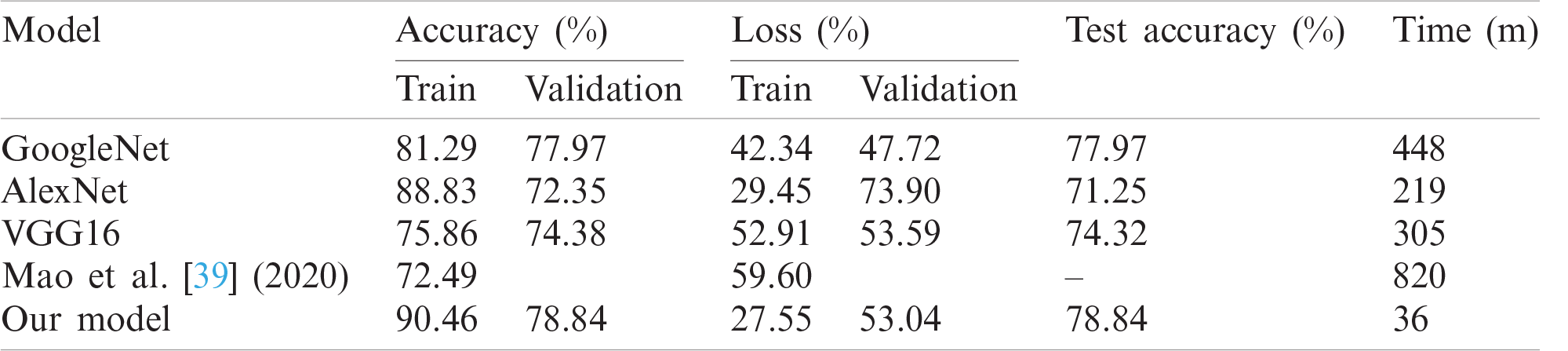
GoogleNet, VGG16, and AlexNet architectures seem to perform well on the Epilepsy dataset during training and validation steps whereas, these architectures suffer from overfitting while performing classification on test data which results in bad accuracy scores. The proposed Integrated CWT and CNN method seem to perform well on the same Epilepsy dataset and the results of proposed Integrated CWT and CNN method do not show a huge discrepancy in accuracy scores of training, validation, and testing phases. The results generated by all DL models and proposed Integrated CWT and CNN method for their performance assessment are presented in Tab. 3.
The results of proposed Integrated CWT and CNN method are also cross validated using K-Fold cross validation using 10 folds of Epilepsy dataset. K-Fold cross-validation method is useful to evaluate the performance of a trained model on unseen data from the original dataset. This cross-validation process makes sure that the model is not performing in a biased manner towards a specific class. In this process, each data point gets to be a part of the testing process at least once and the model gets to trains on this data on multiple times depending on the number of folds i.e., if we use k = 10 folds then each data point is used as a part of training for k − 1 times.
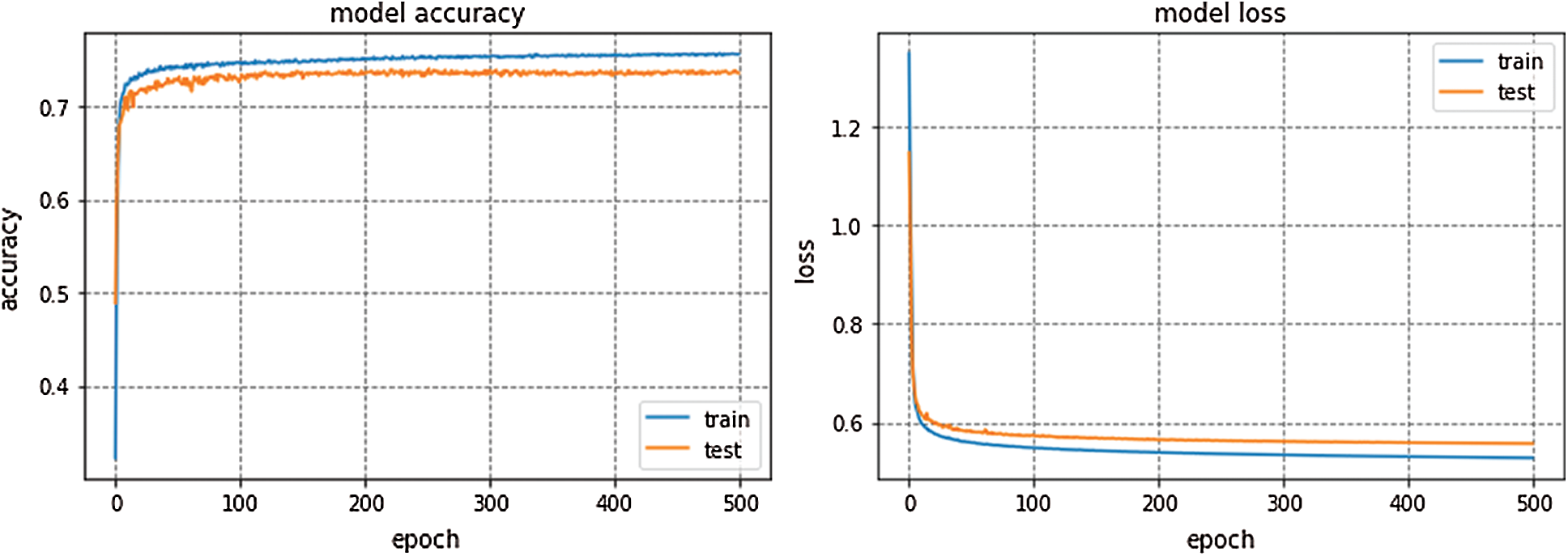
Figure 7: VGG16 performance
Table 3: Performance of proposed method vs. other DL architectures
The average accuracy achieved by Kfold cross validation for proposed Integrated CWT and CNN method is 76.02%. The overall Accuracy lies in the range of 74% to 79% and loss lies in the range of 50% to 57%. The proposed Integrated CWT and CNN method has improved classification accuracy by 6.35%, loss is reduced by 6.02% and the performance time of proposed Integrated CWT and CNN method is also efficient. Lastly, the performance of proposed Integrated CWT and CNN method can be observed in Fig. 8.
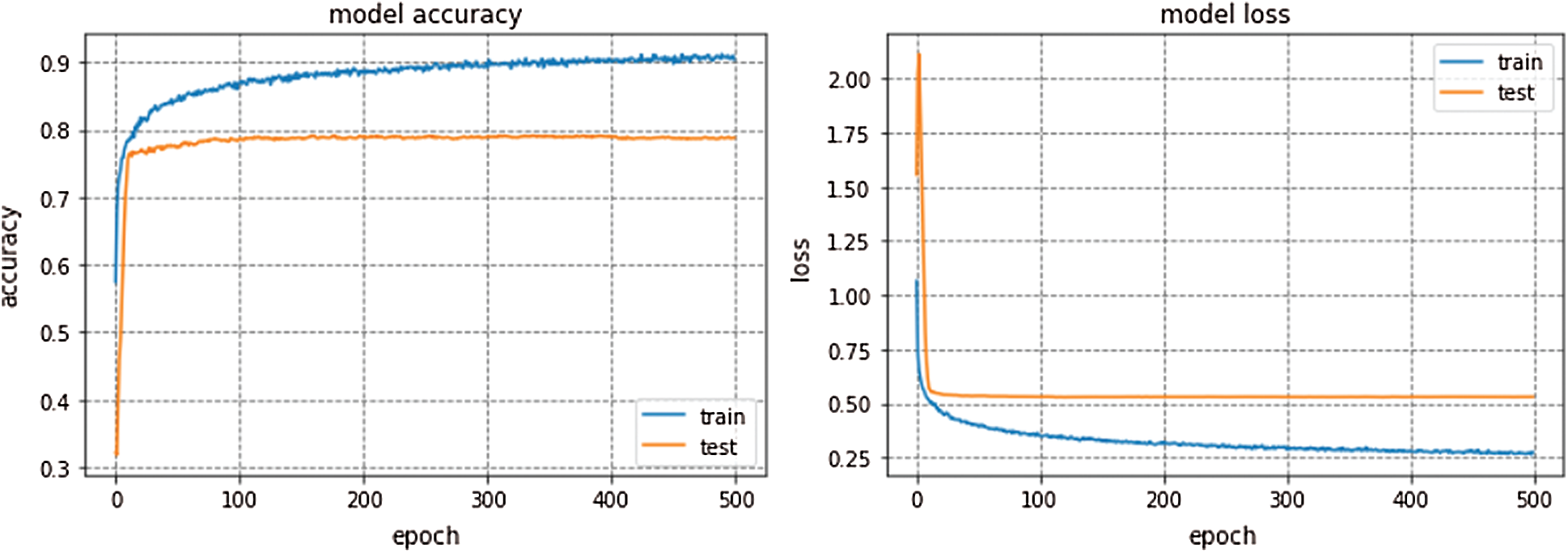
Figure 8: Performance of proposed integrated CWT and CNN method
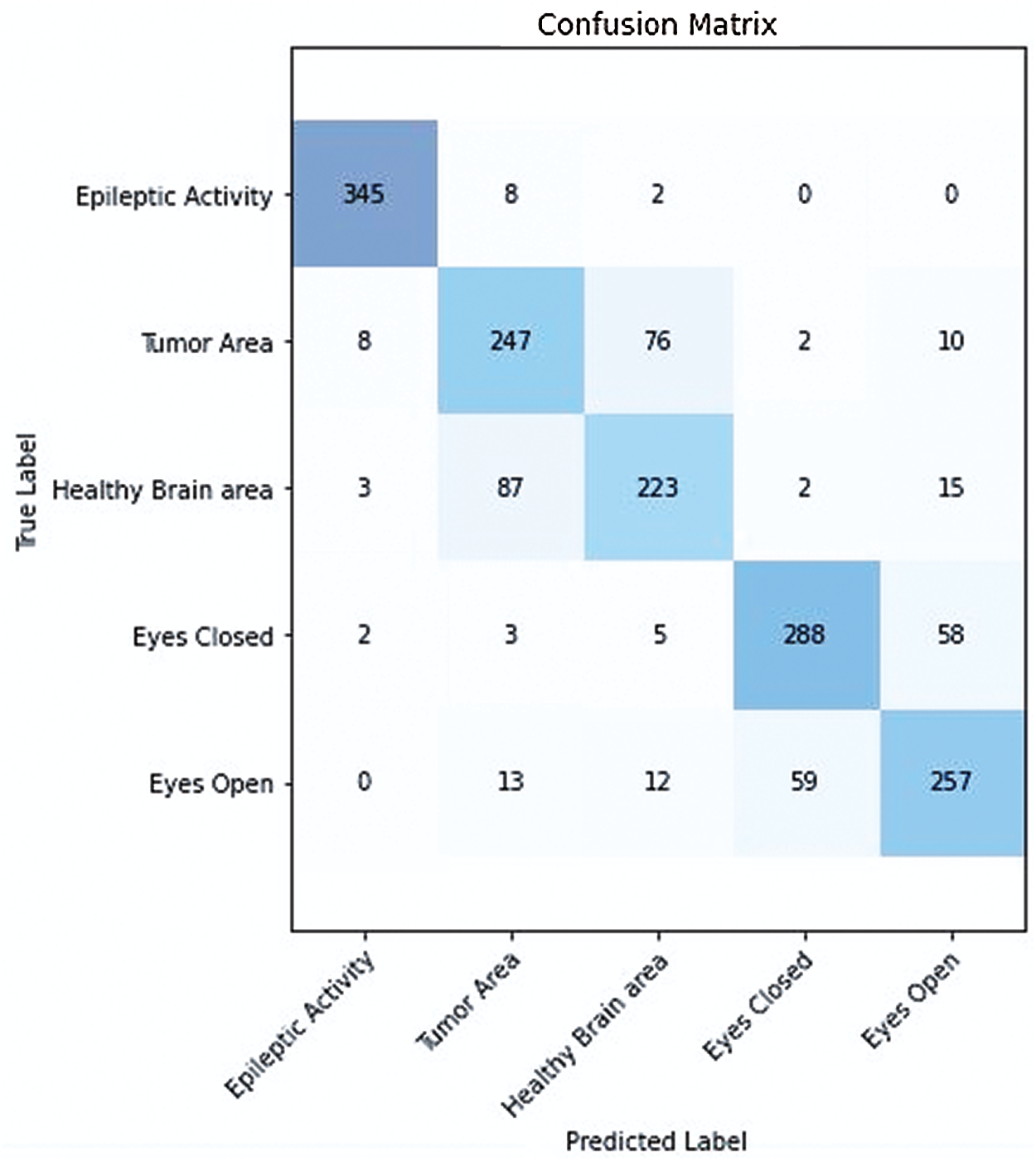
Figure 9: Confusion matrix of proposed integrated CWT and CNN method
In the proposed work, we demonstrated that Deep learning models are advantageous for EEG classification and timely prediction of epileptic seizures to avoid damage caused by recurrent seizure occurrences. We proposed an Integrated CWT and CNN method to classify EEG data and detect seizures caused by Epilepsy and Brain Tumors. The configurations of three existing Deep Learning models are experimented on Epilepsy Dataset [32] and their results are compared to the proposed Integrated CWT and CNN method.
The proposed CWT and CNN method generated better accuracy and loss results in a timely manner. As shown in Tab. 3, our program generated better loss and accuracy results than [39]. Specifically, the proposed Integrated CWT and CNN achieved better test accuracy than GoogleNet, VGG16, and AlexNet. Consequently, the proposed Integrated CWT and CNN method has better loss results than VGG16, AlexNet, and [39]. Moreover, the proposed Integrated CWT and CNN method has better learning time against GoogleNet, VGG16, AlexNet, and [39]. The proposed Integrated CWT and CNN is performing better for the EEG classification over other classification techniques due to their ability of end-to-end learning. We incorporated CWT and CNN successfully to classify EEG data without losing low or high frequencies.
In the proposed integrated CWT and CNN method, if the classification accuracy is improved, the loss score is increased as well for a certain amount of dataset, which may require further research. We hope to improve performance time, and accuracy of the proposed Integrated CWT and CNN method by adding more data, multiple feature selection, and refining the layered architecture of CNN. Additionally, we aim to reduce the number of false positives (See Fig. 9.) while performing EEG classification on Epilepsy Dataset. The research intents to utilize the proposed method in medical applications for early seizure and brain tumor detection in the future. Further study is required to refine the performance of the proposed Integrated CWT and CNN method and achieve maximum classification accuracy with minimum loss score.
Funding Statement: This research was supported by X-mind Corps program of National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT (No. 2019H1D8A1105622) and the Soonchunhyang University Research Fund.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Soufineyestani, D. Dowling and A. Khan, “Electroencephalography (EEG) technology applications and available devices,” Applied Sciences, vol. 10, pp. 7453, 2020. [Google Scholar]
2. M. Naz, J. H. Shah, M. Sharif, M. Raza and R. Damaševičius, “From ECG signals to images: A transformation based approach for deep learning,” PeerJ Computer Science, vol. 7, no. 1, pp. e386, 2021. [Google Scholar]
3. N. Padfield, J. Zabalza, H. Zhao, V. Masero and J. Ren, “EEG-based brain-computer interfaces using motor-imagery: Techniques and challenges,” Sensors, vol. 19, no. 6, pp. 1423, 2019. [Google Scholar]
4. S. Asadzadeh, T. Y. Rezaii, S. Beheshti, A. Delpak and S. Meshgini, “A systematic review of EEG source localization techniques and their applications on diagnosis of brain abnormalities,” Journal of Neuroscience Methods, vol. 339, pp. 108740, 2020. [Google Scholar]
5. C. M. Michel and D. Brunet, “EEG source imaging: A practical review of the analysis steps,” Frontiers in Neurology, vol. 10, pp. 325, 2019. [Google Scholar]
6. C.-T. Lin, C.-S. Huang, W.-Y. Yang, A. K. Singh and Y.-K. Wang, “Real-time EEG signal enhancement using canonical correlation analysis and gaussian mixture clustering,” Journal of Healthcare Engineering, vol. 2018, pp. 1–8, 2018. [Google Scholar]
7. K. Samiee, P. Kovacs and M. Gabbouj, “Epileptic seizure classification of EEG time-series using rational discrete short-time Fourier transform,” IEEE Transactions on Biomedical Engineering, vol. 62, no. 2, pp. 541–552, 2014. [Google Scholar]
8. S. Garg and R. Narvey, “Denoising & feature extraction of EEG signal using wavelet transform,” International Journal of Engineering Science and Technology, vol. 5, pp. 1249, 2013. [Google Scholar]
9. M. S. Sarfraz, M. Alhaisoni, A. A. Albesher, S. Wang and I. Ashraf, “StomachNet: Optimal deep learning features fusion for stomach abnormalities classification,” IEEE Access, vol. 8, pp. 197969–197981, 2020. [Google Scholar]
10. N. Hussain, A. Majid, M. Alhaisoni, S. A. C. Bukhari, S. Kadry et al., “Classification of positive COVID-19 CT scans using deep learning,” Computers, Materials and Continua, vol. 66, no. 3, pp. 1–15, 2021. [Google Scholar]
11. F. Afza, M. Sharif, M. Mittal and D. J. Hemanth, “A Hierarchical three-step superpixels and deep learning framework for skin lesion classification,” Methods, vol. 2, pp. 1–19, 2021. [Google Scholar]
12. Y.-D. Zhang and T. Akram, “Pixels to classes: Intelligent learning framework for multiclass skin lesion localization and classification,” Computers & Electrical Engineering, vol. 90, pp. 106956, 2021. [Google Scholar]
13. A. Subasi and M. I. Gursoy, “EEG signal classification using PCA, ICA, LDA and support vector machines,” Expert Systems with Applications, vol. 37, no. 12, pp. 8659–8666, 2010. [Google Scholar]
14. S. Siuly and Y. Li, “Designing a robust feature extraction method based on optimum allocation and principal component analysis for epileptic EEG signal classification,” Computer Methods and Programs in Biomedicine, vol. 119, no. 1, pp. 29–42, 2015. [Google Scholar]
15. M.-P. Hosseini, A. Hosseini and K. Ahi, “A review on machine learning for EEG signal processing in bioengineering,” IEEE Reviews in Biomedical Engineering, vol. 8, pp. 1–13, 2020. [Google Scholar]
16. A. Rehman, T. Saba, Z. Mehmood, U. Tariq and N. Ayesha, “Microscopic brain tumor detection and classification using 3D CNN and feature selection architecture,” Microscopy Research and Technique, vol. 84, no. 1, pp. 133–149, 2021. [Google Scholar]
17. M. Qasim, H. M. J. Lodhi, M. Nazir, K. Javed, S. Rubab et al., “Automated design for recognition of blood cells diseases from hematopathology using classical features selection and ELM,” Microscopy Research and Technique, vol. 84, no. 2, pp. 202–216, 2021. [Google Scholar]
18. I. Ashraf, M. Alhaisoni, R. Damaševičius, R. Scherer, A. Rehman et al., “Multimodal brain tumor classification using deep learning and robust feature selection: A machine learning application for radiologists,” Diagnostics, vol. 10, pp. 565, 2020. [Google Scholar]
19. A. Craik, Y. He and J. L. Contreras-Vidal, “Deep learning for electroencephalogram (EEG) classification tasks: A review,” Journal of Neural Engineering, vol. 16, no. 3, pp. 31001, 2019. [Google Scholar]
20. H. Arshad, M. I. Sharif, M. Yasmin, J. M. R. Tavares, Y. D. Zhang et al., “A multilevel paradigm for deep convolutional neural network features selection with an application to human gait recognition,” Expert Systems, vol. 11, pp. e12541, 2020. [Google Scholar]
21. Y. Gao, B. Gao, Q. Chen, J. Liu and Y. Zhang, “Deep convolutional neural network-based epileptic electroencephalogram (EEG) signal classification,” Frontiers in Neurology, vol. 11, pp. 1–17, 2020. [Google Scholar]
22. J. W. Lee, P. Y. Wen, S. Hurwitz, P. Black, S. Kesari et al., “Morphological characteristics of brain tumors causing seizures,” Archives of Neurology, vol. 67, pp. 336–342, 2010. [Google Scholar]
23. H. U. Amin, W. Mumtaz, A. R. Subhani, M. N. M. Saad and A. S. Malik, “Classification of EEG signals based on pattern recognition approach,” Frontiers in Computational Neuroscience, vol. 11, pp. 103, 2017. [Google Scholar]
24. G. C. Jana, R. Sharma and A. Agrawal, “A 1D-CNN-spectrogram based approach for seizure detection from EEG signal,” Procedia Computer Science, vol. 167, no. 3, pp. 403–412, 2020. [Google Scholar]
25. F. Li, F. He, F. Wang, D. Zhang and X. Li, “A novel simplified convolutional neural network classification algorithm of motor imagery EEG signals based on deep learning,” Applied Sciences, vol. 10, pp. 1605, 2020. [Google Scholar]
26. N. Kumar, K. Alam and A. H. Siddiqi, “Wavelet transform for classification of EEG signal using SVM and ANN,” Biomedical and Pharmacology Journal, vol. 10, no. 4, pp. 2061–2069, 2017. [Google Scholar]
27. D. Zhou and X. Li, “Epilepsy EEG signal classification algorithm based on Improved RBF,” Frontiers in Neuroscience, vol. 2, pp. 1–16, 2020. [Google Scholar]
28. I. Ullah, M. Hussain and H. Aboalsamh, “An automated system for epilepsy detection using EEG brain signals based on deep learning approach,” Expert Systems with Applications, vol. 107, no. 4, pp. 61–71, 2018. [Google Scholar]
29. X. Wei, L. Zhou, Z. Chen, L. Zhang and Y. Zhou, “Automatic seizure detection using three-dimensional CNN based on multi-channel EEG,” BMC Medical Informatics and Decision Making, vol. 18, no. 1, pp. 71–80, 2018. [Google Scholar]
30. K. M. Almustafa, “Classification of epileptic seizure dataset using different machine learning algorithms,” Informatics in Medicine Unlocked, vol. 21, no. 55, pp. 100444, 2020. [Google Scholar]
31. S. Shafique, S. Sarfraz, U. Q. Shaikh, A. Nadeem and Z. U. Rehman, “Comparative analysis of classifiers for prediction of epileptic seizures,” Pakistan Journal of Engineering and Technology, vol. 3, pp. 84–88, 2020. [Google Scholar]
32. R. G. Andrzejak, K. Lehnertz, F. Mormann, C. Rieke and C. E. Elger, “Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state,” Physical Review E, vol. 64, no. 6, pp. 61907, 2001. [Google Scholar]
33. Q. Li, C. Liu, Q. Li, S. P. Shashikumar, S. Nemati et al., “Ventricular ectopic beat detection using a wavelet transform and a convolutional neural network,” Physiological Measurement, vol. 40, no. 5, pp. 55002, 2019. [Google Scholar]
34. A. Briassouli, D. Matsiki and I. Kompatsiaris, “Continuous wavelet transform for time-varying motion extraction,” IET Image Processing, vol. 4, no. 4, pp. 271–282, 2010. [Google Scholar]
35. M. Rashid, M. Alhaisoni, S.-H. Wang, S. R. Naqvi, A. Rehman et al., “A sustainable deep learning framework for object recognition using multi-layers deep features fusion and selection,” Sustainability, vol. 12, pp. 5037, 2020. [Google Scholar]
36. Y.-D. Zhang, S. A. Khan, M. Attique, A. Rehman and S. Seo, “A resource conscious human action recognition framework using 26-layered deep convolutional neural network,” Multimedia Tools and Applications, vol. 8, pp. 1–23, 2020. [Google Scholar]
37. S. Kadry, M. Alhaisoni, Y. Nam, Y. Zhang, V. Rajinikanth et al., “Computer-aided gastrointestinal diseases analysis from wireless capsule endoscopy: A framework of best features selection,” IEEE Access, vol. 8, pp. 132850–132859, 2020. [Google Scholar]
38. E. Gómez-Luna, D. Silva, G. Aponte, J. Pleite and D. Hinestroza, “Obtaining the electrical impedance using wavelet transform from the time response,” IEEE Transactions on Power Delivery, vol. 28, no. 2, pp. 1242–1244, 2013. [Google Scholar]
39. W. Mao, H. Fathurrahman, Y. Lee and T. Chang, “EEG dataset classification using CNN method,” Journal of Physics, vol. 7, pp. 12017, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |