Computers, Materials & Continua DOI:10.32604/cmc.2021.018122
Article

A Joint Algorithm for Resource Allocation in D2D 5G Wireless Networks

Fahd N. Al-Wesabi1,2,*, Imran Khan3, Mohammad Alamgeer4, Ali M. Al-Sharafi5, Bong Jun Choi6, Abdallah Aldosary7 and Ehab Mahmoud Mohamed8,9

1Department of Computer Science, King Khalid University, Muhayel Aseer, KSA
2Faculty of Computer and IT, Sana’a University, Yemen
3Department of Electrical Engineering, University of Engineering and Technology, Peshawar, P.O.B 814, Pakistan
4Department of Information Systems, King Khalid University, Mayahel Aseer, KSA
5Department of Computer Science, College of Computers and Information Technology, University of Bisha, KSA
6School of Computer Science and Engineering, Soongsil University, South Korea
7Department of Computer Science, Prince Sattam bin Abdulaziz University, As Sulayyil, 11991, Saudi Arabia
8Electrical Engineering Department, College of Engineering, Prince Sattam Bin Abdulaziz University, Wadi Addwasir, 11991, Saudi Arabia
9Electrical Engineering Department, Faculty of Engineering, Aswan University, Aswan, 81542, Egypt
*Corresponding Author: Fahd N. Al-Wesabi. Email: falwesabi@kku.edu.sa
Received: 22 February 2021; Accepted: 26 March 2021

Abstract: With the rapid development of Internet technology, users have an increasing demand for data. The continuous popularization of traffic-intensive applications such as high-definition video, 3D visualization, and cloud computing has promoted the rapid evolution of the communications industry. In order to cope with the huge traffic demand of today’s users, 5G networks must be fast, flexible, reliable and sustainable. Based on these research backgrounds, the academic community has proposed D2D communication. The main feature of D2D communication is that it enables direct communication between devices, thereby effectively improve resource utilization and reduce the dependence on base stations, so it can effectively improve the throughput of multimedia data. One of the most considerable factor which affects the performance of D2D communication is the co-channel interference which results due to the multiplexing of multiple D2D user using the same channel resource of the cellular user. To solve this problem, this paper proposes a joint algorithm time scheduling and power control. The main idea is to effectively maximize the number of allocated resources in each scheduling period with satisfied quality of service requirements. The constraint problem is decomposed into time scheduling and power control subproblems. The power control subproblem has the characteristics of mixed-integer linear programming of NP-hard. Therefore, we proposed a gradual power control method. The time scheduling subproblem belongs to the NP-hard problem having convex-cordinality, therefore, we proposed a heuristic scheme to optimize resource allocation. Simulation results show that the proposed algorithm effectively improved the resource allocation and overcome the co-channel interference as compared with existing algorithms.

Keywords: 6G; wireless networks; mobile communication; linear programming

1  Introduction

Device-to-device (D2D) communication has been integrated into the cellular network as an innovation of next-generation communication [1–10]. This new type of wireless communication directly transmits data without being forwarded by the base station, so the spectrum utilization rate and data transmission rate are both Improved and reduced the burden of the load [11–21]. This communication method has become a research hotspot in the industry, and is committed to the solution of D2D communication solutions [22–25].

According to Cisco’s latest statistical results [26], multimedia streaming has become the mainstream business in wireless networks, and with the changes in people’s lifestyles, more and more multimedia streams are generated in neighboring areas. Communication between traditional base stations and equipment transmission efficiency of the mode in the above scenario is low. As a short-distance communication method, terminal direct communication enables data transmission links to be established directly between devices without forwarding through the base station. It can greatly improve the user’s quality-of-service (QoS) experience, improve the system frequency band utilization, and effectively reduce the load of the base station. Therefore, D2D communication has received extensive attention from academics and industry [27–29], and is regarded as one of the key technologies in 5G [30].

However, when multiple D2D links reuse the same resource, co-channel interference problems will occur. How to solve this problem becomes the key to D2D communication. The resource allocation can coordinate user interference and effectively alleviate the above problems [31–32]. In the existing literature, the authors [33] puts forward a channel selection strategy that maximizes the signal-to-interference-noise ratio in the single-link multiplexed single-channel scenario, with the system throughput as the goal, and observes that the system throughput is affected by the number of channels. In order to maximize the total transmission rate of the system, the authors in [34] proposed a reverse iterative combined auction mechanism for multi-link multiplexing single-channel scenarios, which reduced the algorithm complexity. The authors in [35] proposed a method for optimizing the power of D2D users from the perspective of power control in the single-link multiplexing single-channel scenario, and optimized the transmission rate. The authors in [36] optimizes the overall throughput of the system through channel allocation and greedy algorithm for the multi-user multiplexing single channel scenario. In [37], in order to optimize the spectrum utilization, in the single link multiplexing single channel scenario, power control and mode selection are combined to maximize spectrum utilization. In [38], in order to ensure the QoS of D2D users while minimizing the total energy consumption of the system, for the single-link multiplexing single-channel scenario, the joint mode selection, power control and channel allocation are optimized. The authors in [39] combined power control and resource allocation in the single-link multiplexing single-channel scenario, and proposed a resource allocation mechanism based on graph theory to ensure the quality of service for cellular users and D2D users. Minimize system energy consumption under the premise. Reference [40] aims at multi-user multiplexing single-channel resource scenarios, joint access control, power control and channel allocation to maximize the system throughput, and ensure the existing cellular link users and D2D users QoS. Reference [41] considers the best power allocation in the multi-link multiplexing single channel scenario and proposes a mechanism to maximize the system throughput under the premise of ensuring the QoS of D2D users. Reference [42] aims at the single-link multiplexing single-channel scenario, combined power control and mode selection, and uses an exhaustive search method to ensure the user transmission rate.

However, the literature [33–42] has the following defects: 1) The user’s QoS is not guaranteed with the user as the center, and the user’s communication quality cannot be guaranteed [33–41]; 2) Guaranteed D2D user’s QoS, but the scene a single D2D users can only reuse a single resource [37–39], and the scenario where a single D2D user reuses multiple channel resources has not been studied; 3) Without considering the joint optimization of multi-dimensional wireless resources, the optimization of system performance cannot be achieved [36–37]; 4) The algorithm is complex and difficult to implement [42].

Based on addressing the above problem, this paper proposes a user-centric resource allocation method. The original problem can be broken down into the following two parts: The power control part of the access control maximizes the number of D2D user’s resources that can reuse the same spectrum resource in a single time slot while ensuring the minimum bit error rate requirement. It belongs to a mixed integer linear programming problem, which is an NP-hard problem in a general sense. Therefore, a stepwise power control algorithm is proposed to achieve a compromise between algorithm performance and complexity. Based on the above results, the time scheduling part of the time domain is ensuring the transmission of user data. Based on the transmission rate, we determine the user’s scheduling times so as to maximize the number of D2D links. It is equivalent to the convex-cardinality problem, which also belongs to the NP-hard problem, and then proposes a low-complexity heuristic algorithm. The simulation results show that the method proposed in this paper is necessary for resource optimization, and verifies the effectiveness of the proposed algorithm.

2  System Model

2.1 Network Structure

This article considers the uplink of a single-cell cellular network and assumes that the interference between cells is effectively controlled. In addition, assuming that the system has set dedicated access resources for the D2D link, there is no problem of cellular user interference to D2D users, but the same resources can be reused between D2D users, and co-channel interference will occur at this time. The set of D2D users is D={1,2,…,M}, where the M represents the total number of D2D users. This article considers a system based on time division multiple access. The time slot structure is shown in Fig. 1a. The frame is the smallest scheduling period, and each frame contains several time slots. In each time slot, multiple links simultaneously reuse the same resources for communication, as shown in Fig. 1b.

For any time slot, the signal-to-interference and noise ratio SINR (Signal to Interference plus Noise Ratio) value is:

γiD=piDgiDNiD+∑l∈Dl≠iplDgi,lDD∀i∈D(1)

where piD represents the transmit power of the i-th D2D transmitter, giD represents the path gain from the i-th D2D transmitter to the receiver, gi,lDD represents the path gain from the l-th D2D transmitter to the i-th D2D receiver, and NiD represents the Gaussian white noise received by the i-th D2D receiver.

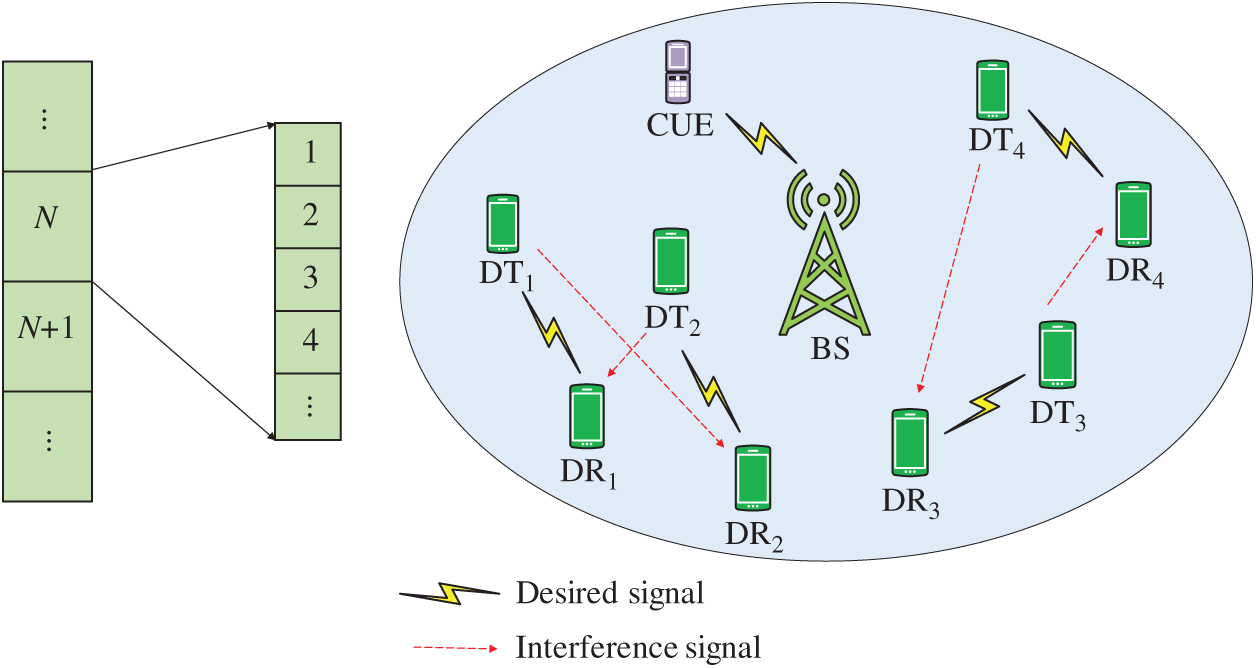
Figure 1: The proposed system model

2.2 User Demand Model

As shown in Fig. 1a, assume that the time domain width of each scheduling period is tf, and the frequency domain width is Sf. In addition, each scheduling period can be divided into time slots, and we denote the time slots as T1,T2,…,TNf. For the i-th D2D user, it is necessary to ensure that its transmission rate is greater than the transmission threshold during the entire scheduling period, so as to ensure the user’s QoS requirements. In a single time slot, the admission control part guarantees the lowest bit error rate, that is, the lowest SINR requirement, such as i-th D2D user. If the SINR threshold value is set to ΓiD, the number of times that the i-th D2D user access must meet the Eq. (2) in the scheduling period:

ωi=ceil(Ritf(tfNf)Sflog2⁡(1+ΓiD))∀i∈D(2)

Among them, the vector ω=[ωi]M×1 means that each D2D user needs to reuse the resources in the scheduling period to meet its transmission rate the minimum number of times; ceil(⋅) means the smallest positive integer not less than a. Fig. 2 shows a possible scheduling result, among them, DT1 and DR1, and DT2 and DR1 link access time slot T1, can guarantee the minimum of the above two links Bit error rate requirement (equivalent to minimum SINR threshold requirement). In the entire scheduling period, time-domain scheduling is performed according to the scheduling results to meet the user’s QoS.

2.3 Problem Description

Define the reuse pattern B={S⊆D∣γiD≥ΓiD,∀i∈S} represents the D2D set of resources that meet its minimum bit error rate in a certain time slot; set F is composed of multiplexing pattern B, which represents all D2D accesses. |F| represents the size of F, and G is the matrix form of F, where G represents the element in the i-th row and k-th column of G. If the i-th D2D link is connected in the k-th time slot, then Gi,k=1; Otherwise, Gi,k. For example, if D = \{1, 2, 3\}, F = 1 }, 1, 2 }, 1, 3 }, 2 }, 3 } }, then the corresponding G is:

GM×|F|=[111000101000101]3×5(3)

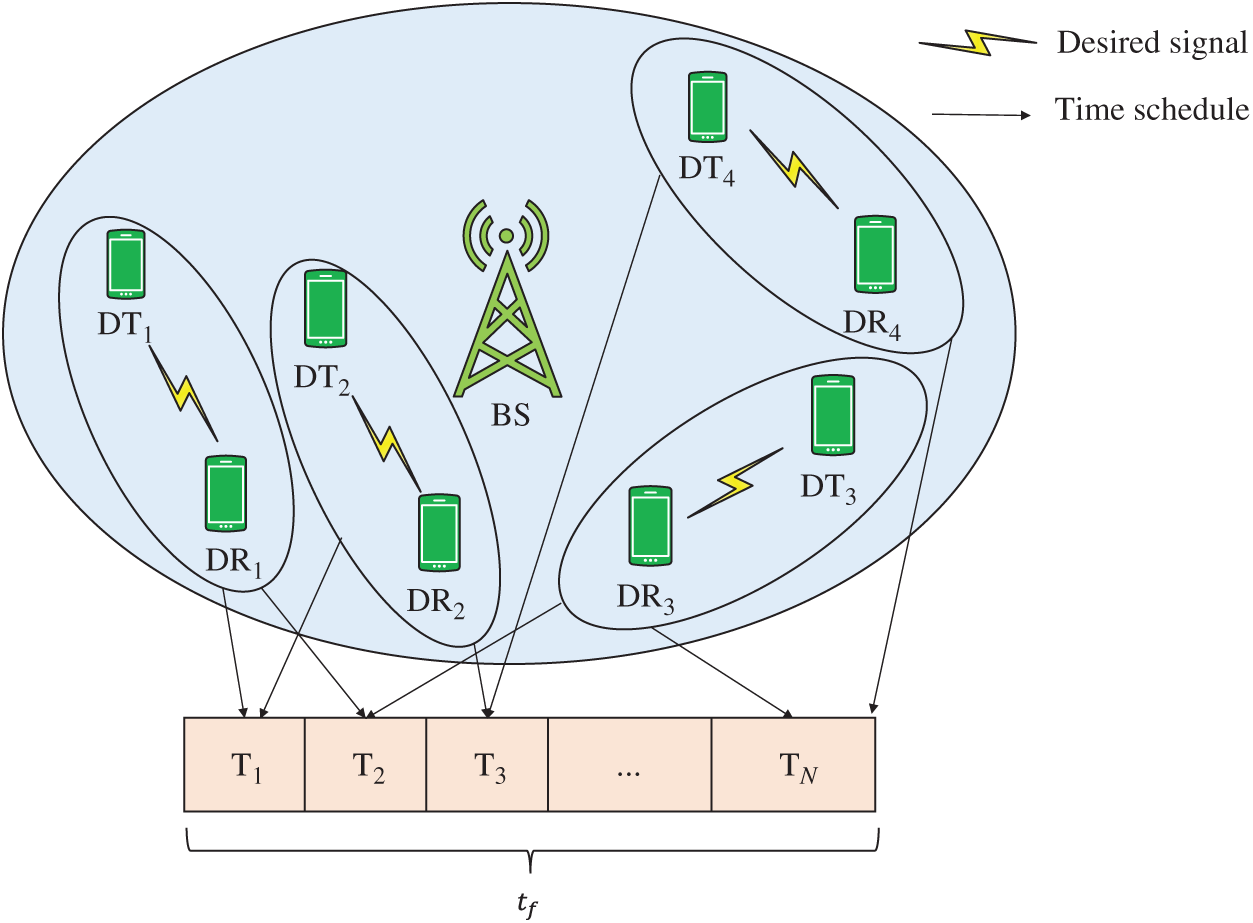
Figure 2: D2D user access scheduling in the time domain

Define the vector α=[αk]|F|×1 Represents the number of times that the multiplexing pattern is scheduled in the entire scheduling, then Gα represents the total number of multiplexing resources for each D2D users in the scheduling period. If ω−Gα≤0, it means that the rate requirement of the i-th D2D user is met in the entire scheduling period. Then ω−Gα>0 means the i-th D2D user rate requirement is not met. Therefore, the auxiliary variable q=[qi]M×1 is introduced, and ω−Gα≤q is introduced into the restriction condition. Among them, q=0 means the D2D user meets the speed requirement, and qi>0 means the D2D user does not meet the rate requirement. Therefore, maximizing the number of D2D users in any time slot is equivalent to minimizing the number of non-zeros in the variable q, and we can minimize the cardinality function card (q) as the optimization target value of this problem. In summary, the proposed algorithm can be described as Problem 1:

Problem 1:

minαk∈{0,1,2,…},qi∈{0,1,2,…}card(q)(4)

Subject to:

ω−Gα≤q(5)

11×|F|α≤Nf(6)

where 11×|F| represents the row vector with all elements l; Eq. (5) indicates that the rate requirement of the i-th D2D user is met within the scheduling period; Eq. (5) indicates that the total number of time slots cannot exceed Nf.

3  Joint Access Control and Time Domain Scheduling

In order to maximize the number of D2D users and minimize the number of multiplexed resources while ensuring user QoS, a joint resource allocation scheme is proposed. First, the admission control part determines the D2D user set that meets the minimum bit error rate condition in a single time slot, thereby determining the access matrix G; according to the result of admission. The time-scheduling part adjusts the resources of different time slots. In order to minimize the number of resources reused, the time-scheduling is the optimized result based on admission control.

3.1 Access Control

The purpose of the access control is to generate the multiplexing matrix G. According to the definition of the multiplexing pattern in Section 1.3, we can see that with as the number of D2D users increases, the dimension of G will grow exponentially. In addition, as shown in Eq. (3), compared to 1 }, 2 }, 3 }, the multiplexing patterns 1, 2 }, 1, 3 } can make full use of the resources of each time slot. Using it as the maximum multiplexing pattern is more conducive to maximizing the number of links meeting QoS requirements in the entire scheduling period. In order to better explain the nature of the specific reuse pattern in G, we first introduce the following definitions.

Definition: Maximum reuse pattern An, where n is the maximum number of multiplexing patterns, which meets the following two conditions:

Condition 1: i is the D2D user, i∈An;

Condition 2: For any D2D link set S∈{i∈D∣γiD≥ΓiD}, |S|≤|An| is satisfied. where |⋅| represents the collection size.

Satisfying condition 1 means that the D2D link i has the opportunity to access the system, and satisfying condition 2 means that each time slot resource is multiplexed by the maximum number of D-L, thereby creating the most multiplexing opportunities and ensuring the maximum number of D2D link can access the system. In order to solve An, We assume that the vector x=[xi]M×1 represents the D2D users that can be accessed in a certain time slot. If i-th D2D user is accessed in this time slot, xi=1; otherwise, xi=0. In order to optimize Problem 1, it is necessary to maximize the access of D2D users in any time slot. That is, maximize the sum of the elements of x. After obtaining x, it can be integrated into matrix G, so that Problem 1 can be further optimized. According to the single time slot, in order to guarantee D2D users, the QoS of D2D users and the maximum number of access resources can be described as Problem 2:

Problem 2:

maxpi,xi∑i∈Dxi(7)

Subject to:

0≤pi≤pimax,∀i∈D(8)

xiγiD≥xiΓiD,∀i∈D(9)

xi∈{0,1}, xj=1,∀i,j∈D(10)

Eq. (7) represents the i-th D2D user upper limit of the transmitting power; pimax represents the maximum transmitting power of the i-th D2D transmitting end. Eq. (8) represents the D2D user access resources QoS constraints; Eq. (9) indicates that the j-th D2D link has been connected to channel resources.

3.1.1 Traditional Algorithms and Drawbacks

It is easy to know that Problem 2 is a mixed integer linear programming problem, which belongs to the NP-hard problem. In the optimization theory, the branch and bound method (BB) can be used to obtain the optimal solution, but the above process requires a long calculation time [43]. If the number of nodes in the traversal tree when the optimal solution is found, the complexity of the BB algorithm is O(β(2M)3). The (2M)3 represents the average complexity of using the simplex method to solve the linear programming problem at any node on the traversal tree. With the increase of the problem dimension M, β will also increase to a certain extent, and there will be a situation of β→∞. However, in LTE-A, the actual deployment of the communication system, resource allocation needs to be completed in several time slots (millisecond level). Therefore, the traditional BB algorithm is not suitable for the problem considered in this article.

For the convenience of calculation, the optimization target variable of Problem 2 is transformed into the l0-norm function form that can be described as Problem 3:

Problem 3:

minpi,xicard(y)(11)

Subject to:

0≤pi≤pimax,∀i∈D(12)

xiγiD≥xiΓiD,∀i∈D(13)

0≤xi≤1, xj=1,∀i,j∈D(14)

where y=[yi]M×1, yi=1−xi. The above objective function is l0-norm that represents the number of non-zero elements in a vector. Problem 3 is a mixed integer linear programming problem, which can further transform the l0-norm function form the target variable into the l1-norm function form, which is described as Problem 4:

Problem 4:

minpi,xi∑i=1M|yi|(15)

Subject to:

(5−a); (5−b); (5−c)(16)

Problem 4 is a linear programming problem, which can be solved by the simplex method, but the solution result is quite different from the theoretical value.

3.1.2 Progressive Access Control Algorithm

Based on the shortcomings of traditional algorithms, this paper proposes a progressive access control algorithm to reduce complexity while ensuring system efficiency and solving Problem 2. The algorithm is divided into two parts: priority access and feasibility detection. The priority access goal is to maximize the number of access links on the premise of satisfying Eq. (8), and introduce the measured value of D2D link. The goal of feasibility detection is to satisfy the Eq. (7) in Problem 2, so as to solve Problem 2 with low complexity.

a) The first part is to give priority to receiving users. j represents the D2D received resource, Uj represents the D2D user collection of the received resource, Vj represents the remaining D2D sets, then Uj∪Vj=D. The main idea of this part is to calculate the measured value of the D2D link one by one, and select the D2D link with the smallest measured value. The measured value of the i-th D2D link is:

θiD=ΓiD(∑l∈Ujl≠izi,lDDplD∗+NiD)+∑j∈Ujj≠iΓiDzj,iDDpiD∗(17)

where zi,lDD means the i-th normalized path gain between l of the D2D user; plD∗ represents the optimal transmit power of the l-th D2D link; piD∗ represents the i-th item in the calculation of the received access measurement value D2D optimal transmit power. The first half of Eq. (17) indicates that the D2D user receives effective interference in the current time slot. The second half represents the effective interference caused by this D2D user to other in the current time slot. The smaller θiD it is, the smaller the interference between it and the connected link. Therefore, the i-th D2D link is considered to be connected to the resource first.

b) The second part is feasibility testing. First, find the optimal transmit power of D2D link that gives priority to access resources in the first part, and determine whether its optimal transmit power satisfies Eq. (6). Secondly, if it is satisfied, it is judged whether the minimum bit error rate is satisfied. For the constraint conditions of Eq. (8), it can be expressed as:

piDgiDNiD+∑l∈Dl≠iplDgi,lDD≥ΓiD,∀i∈Uj(18)

That is, piD−Γi∑l∈Ujl≠iplDgi,lDDgiDD≥ΓiNiDgiD. The corresponding matrix form is:

(E−ΓZ)p≥Γn(19)

where p represents the transmit power vector of D2D link; E represents the unit matrix modulo Uj of |Uj|;

Γ represents the diagonal matrix of the SINR threshold corresponding to the minimum QoS requirement of D2D link; Z represents the normalized path gain matrix between D2D users; n represent the normalized noise power vector. The specific definition is as follows:

p=[piD]|Uj|×1,i∈Uj(20)

n=[NiDgiD]|Uj|×1,i∈Uj(21)

Γ=[ΓiD]|Uj|×|Uj|={0i≠lΓiDi=li,l=Uj(22)

Z=[gi,lDDgiD]|Uj|×|Uj|={gi,lDDgiDi≠l0i=li,l=Uj(23)

From Eq. (20) to Eq. (23), it is positive and irreducible, Eq. (19) can meet the lowest QoS condition as (E−ΓZ)p≥Γn, namely:

p∗=(E−ΓZ)−1Γn(24)

If Eq. (24) makes sense, then p∗=(E−ΓZ)kΓn is meaningful, that is, when the matrix ΓZ maximum eigenvalue λ<1, there is a power vector p∗, when the i-th D2D is piD∗ transmit power during transmission, the lowest QoS is met, so it is deleted from one and added to Uj. When λ≥1, the i-th D2D link does not meet the access resource conditions and is deleted from Vj. Return to the first part until Vj=−80∅.

After each update of Uj, it is converted into matrix x (the process is similar to F to G), and x is stored in matrix G. If x⊂G, it is not stored. After traversing all j∈D, the final access matrix G is obtained.

In summary the main steps of the proposed algorithm are shown in Algorithm 1.

Algorithm 1 first determines the preferential access link under the premise of satisfying Eq. (8), and then uses feasibility detection to determine whether the Eq. (7) in Problem 2 is satisfied, so as to obtain the set Uj and x under the condition of low complexity, and then obtain G. The total complexity of the algorithm is O(M4+M(M2−1)/6), and the algorithm complexity of the priority access part is O(∑i=1Mi(M−i))=O(M(M2−1)/6), the feasibility detection part E−ΓZ, the complexity of the one-center matrix inversion algorithm is O(M3), and the number of algorithm iterations is about M, so the total complexity of the proposed algorithm is O(M4).

3.2 Time-Domain Scheduling

The above part is coordinated by power control and interference to solve D2D access problem in a single time slot access matrix G. According to this, how to solve Problem 1 under the condition of known G becomes the key. But Problem 1 is a mixed-integer linear programming problem, see Theorem 1, which is an NP-hard problem in the general sense.

Theorem 1: Given the matrix G, the optimization Problem 1 is a mixed integer linear programming problem.

Proof: Problem 1 can be rewritten as Problem 5:

Problem 5:

minαk∈{0,1,2,…},qi∈{0,1,2,…}∑i∈Dπi(25)

Subject to:

πili≤qi≤πiui,i∈D(26)

πi∈{0,1}(27)

ω−Gα≤q(28)

11×|F|α≤Nf(29)

where li is the minimum value of qi, and its value can be solved by Eq. (30), ui is the maximum value of qi, and its value can be solved by Eq. (31). When πi=0, qi=0; and when πi=1, li≤qi≤ui, so ∑i∈Dπi is minimized in the target variable. It is equal to maximizing the number of zero elements in q, that is, minimizing card(q). This problem is a mixed integer linear programming problem.

minαk∈{0,1,2,…},qi∈{0,1,2,…}qi(30)

Subject to:

(4−a)(4−b)(31)

maxαk∈{0,1,2,…},qi∈{0,1,2,…}qi(32)

Subject to:

(4−a)(4−b)(33)

It is known that Problem 1 is a mixed-integer linear programming problem, which is an NP-hard problem in the general sense. The optimal solution similar to Problems 4 and 5 can also be obtained using the BB algorithm, but requires a longer calculation time. Therefore, this paper proposes a heuristic algorithm. The main idea of the proposed algorithm is a process of selecting the largest multiplexing pattern step by step in the order of time slots. In the first time slot, traverse all the largest multiplexing patterns j, and select the smallest target value μ(j)=card(q) in Problem 1 and reuse pattern j, i.e., j∗=argminj⁡μ(j). Observe whether all D2D link multiplexing time slots are met. If they are met, the algorithm ends. Otherwise, continue to perform the above steps until all time slots are allocated to the largest pattern or all D2D user’s QoS requirements are all satisfied. Among them, in order to reduce the complexity of access, before the first time slot access by the D2D users, we start to delete some links with poor channel conditions, that is, delete the D2D users set of ω(i)−Nf>0, because even if all time slots are allocated to the above D2D users, their QoS requirements cannot be met, and α=[α(j)]|F|×1=0,j∈∅ is initialized.

The above algorithm is shown in Algorithm 2. The complexity of the initialization part is O(M), assuming that Ig is the number of time slots allocated for this part, and |An| is the number of D2D user that can receive the most access in a single time slot, so the algorithm is complicated and the complexity is O(|An|Ig), where |An|≤M, since there are at most Nf time slots, so Ig≤Nf. The total complexity of the time domain scheduling part of the proposed algorithm is O(|An|Ig+M), so the total complexity of the worst algorithm is O(M(Nf+1)). Therefore, the total complexity of the proposed joint algorithm is O(M5(Nf+1)).

4  Simulation Results

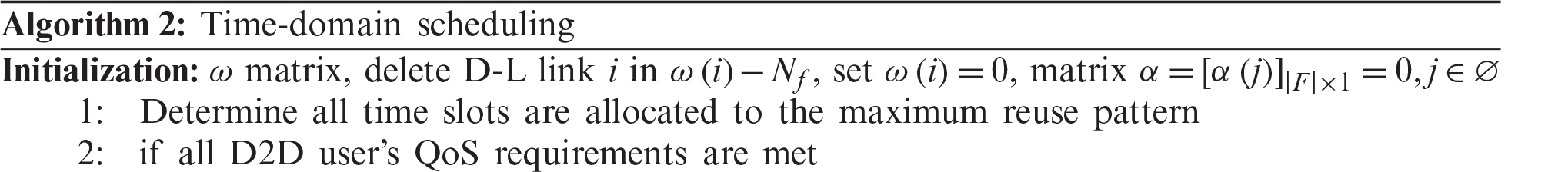
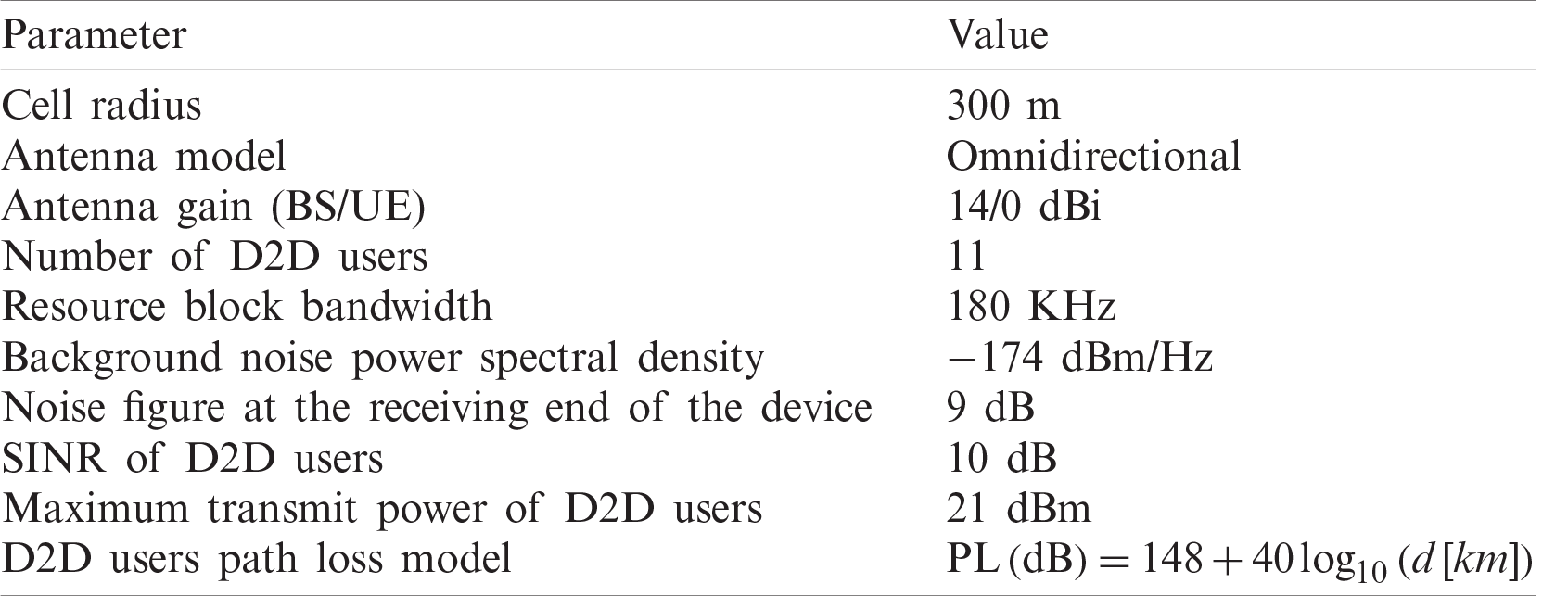
The simulation considers a single cell with a radius of 300 m. The base station is located in the center. All cellular users and DT are evenly distributed in the cell. DR is centered on DT to form a circular area with a radius of 10–50 m. The simulation part uses The main parameter description and settings are shown in Tab. 1. The entire time length is 1,000 time slots, and the MATLAB platform is used for simulation.

Table 1: Simulation parameters

4.1 Progressive Access Control

The algorithms involved in this part of the simulation include:

(1) The l1-norm algorithm: the algorithm has low complexity but insufficient performance.

(2) Traditional BB algorithm: The theoretical optimal solution can be obtained, but exponential complexity may appear, which is difficult to apply in actual situations.

(3) Proposed access control algorithm: Aiming at the access control problem of Problem l, using the step-by-step process, determine the maximum access resources in a single time slot while ensuring the user's lowest bit error rate. The complexity of the algorithms involved in the simulation is shown in Tab. 2.

Table 2: Analysis of algorithm complexity involved in simulation

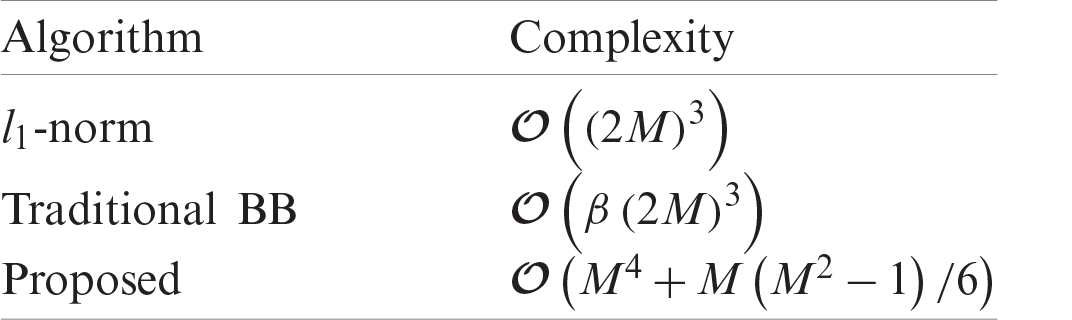
Fig. 3 shows the comparison of access resources when the number of D2D users in the cell changes from 20 to 30 under the condition of 1,000 iterations. The change in the ratio of the D2D link to the total link. As the number of D2D users increases, the ratio range decreases. Because the resources required for access remain unchanged, the increase of D2D users increases the interference between systems. It can be seen from the Fig. 3 that the proposed access control algorithm shows significantly better performance than l1-norm algorithm. The proposed algorithm increases the performance by 31.2l%, which is only 4.09% lower than the BB algorithm.

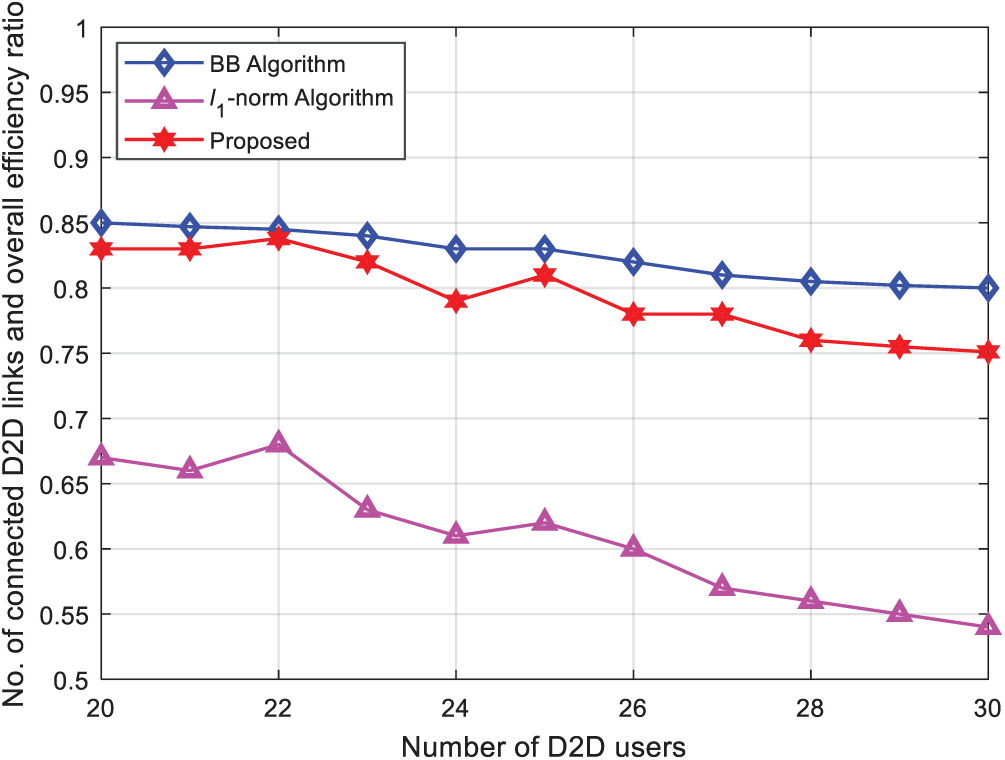
Figure 3: Performance comparison of access control algorithms

4.2 Joint Access Control and Time Domain Scheduling

The algorithms involved in this part of the simulation include:

(1) Random algorithm: based on the access control part mentioned in this article, it is solved by random method, with low complexity but insufficient performance;

(2) Traditional BB algorithm: The theoretical optimal solution can be obtained on the basis of the access control part mentioned in this article, but exponential complexity may appear;

(3) Proposed joint access control and time-scheduling algorithm: On the basis of the access control part proposed in this paper, the heuristic algorithm proposed in the time-scheduling stage is combined to solve Problem 1.

The algorithm complexity involved in the simulation is shown in Tab. 3.

Table 3: Analysis of algorithm complexity involved in simulation for Joint allocation

Fig. 4 shows the system performance when number of D2D users changes from 20 to 30. The change in the ratio of the D2D link to the total number of links. As the number of D2D users increases, the ratio range decreases. Because the interference between D2D user continues to increase, the number of D2D users that can be accessed continues to decrease, resulting in missed D2D link. The number of D2D users keeps increasing, and the system performance decreases. It can be seen from the Fig. 4 that the proposed joint resource allocation method is a heuristic algorithm that is close to the optimal, which is only 1.72% less than the optimal algorithm, but it is 13.03% better than the random algorithm, which reflects its effectiveness.

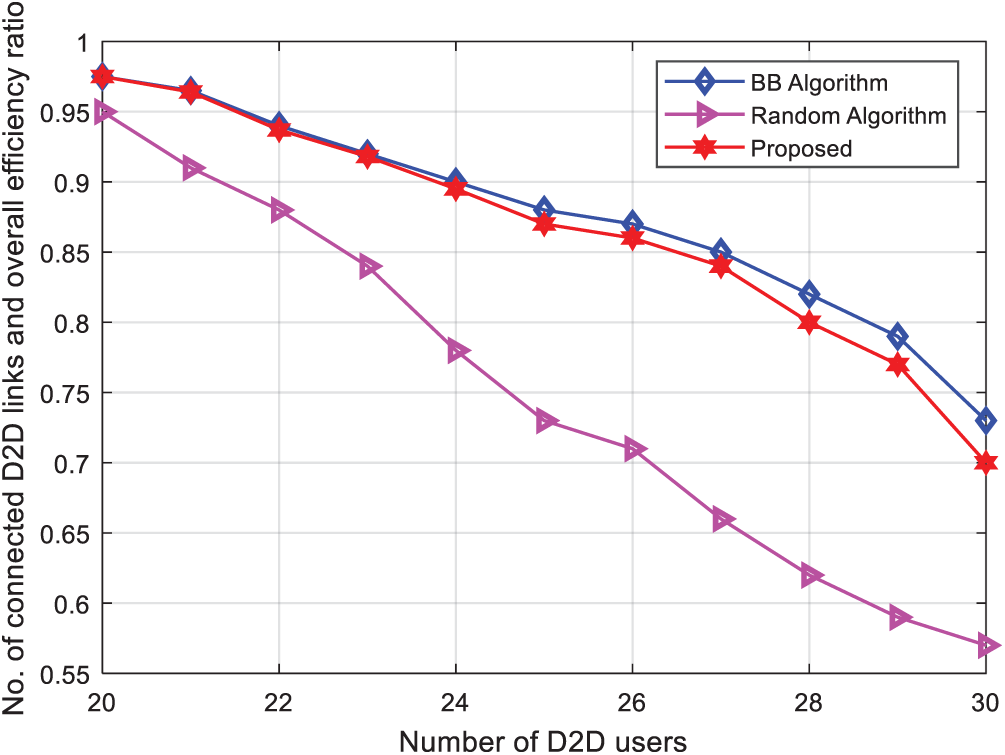
Figure 4: Performance comparison of the proposed joint resource allocation algorithm and existing algorithms with increasing number of D2D users

5  Conclusions and Future Recommendations

This paper analyzes the dense distribution of D2D links and proposes a user-centric joint access control and time-domain scheduling method, which solves the problem of maximizing the number of access links while ensuring the quality of D2D link service. The simulation shows that the algorithm in this paper is an approximate optimal algorithm, which achieves a compromise between algorithm performance and complexity. Further extension to this study is to consider the energy efficiency and integrate it with mmWave communication and evaluate the performance.

Acknowledgement: The author extends his appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under grant number (RGP.2/25/42), Received by Fahd N. Al-Wesabi. www.kku.edu.sa.

Funding Statement: The corresponding authors Bong Jun Choi and Ehab Mahmood Mohammad would like to thank their institutes (Soongsil University, South Korea & Aswan University, Egypt) for supporting this article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Waqas, Y. Niu, Y. Li, M. Ahmed, D. Jin et al., “A comprehensive survey on mobility-aware D2D communications: Principles, practice and challenges,” IEEE Communications Surveys & Tutorials, vol. 22, no. 3, pp. 1863–1886, 2020. [Google Scholar]

 2.  M. Ahmed, Y. Li, M. Waqas, M. Sheraz, D. Jin et al., “A survey on socially aware device-to-device communications,” IEEE Communications Surveys & Tutorials, vol. 20, no. 3, pp. 2169–2197, 2018. [Google Scholar]

 3.  F. S. Shaikh and R. Wismuller, “Routing in multi-hop cellular device-to-device (D2D) networks: A survey,” IEEE Communications Surveys & Tutorials, vol. 22, no. 3, pp. 2622–2657, 2018. [Google Scholar]

 4.  M. Haus, M. Waqas, A. Y. Ding, Y. Li, S. Tarkoma et al., “Security and privacy in device-to-device (D2D) communication: A review,” IEEE Communications Surveys & Tutorials, vol. 19, no. 2, pp. 1054–1079, 2017. [Google Scholar]

 5.  O. Hayat, R. Ngah, S. Z. M. Hashim, M. H. Dahri, R. F. Malik et al., “Device discovery in D2D communication: A survey,” IEEE Access, vol. 7, pp. 131114–131134, 2019. [Google Scholar]

 6.  A. Asadi, Q. Wang and V. Mancuso, “A survey on device-to-device communication in cellular networks,” IEEE Communications Surveys & Tutorials, vol. 16, no. 4, pp. 1801–1819, 2014. [Google Scholar]

 7.  B. M. Elhalawany, R. Ruby and K. Wu, “D2D communication for enabling internet-of-things: Outage probability,” IEEE Transactions on Vehicular Technology, vol. 68, no. 3, pp. 2332–2345, 2019. [Google Scholar]

 8.  I. Loannou, V. Vassiliou, C. Christophorou and A. Pitsillides, “Distributed artificial intelligence solution for D2D communication in 5G networks,” IEEE Systems Journal, vol. 14, no. 3, pp. 4232–4241, 2020. [Google Scholar]

 9.  P. Pawar, A. Trivedi and M. K. Mishra, “Outage and ASE analysis for power controlled D2D communication,” IEEE Systems Journal, vol. 14, no. 2, pp. 2269–2280, 2020. [Google Scholar]

10. F. Qamar, M. U. A. Siddiqui, M. H. D. Hinidia, R. Hassan and Q. N. Nguyen, “Issues, challenges, and research trends in spectrum management: A comprehensive overview and new vision for designing 6G networks,” Electronics, vol. 9, no. 9, pp. 1–124, 2019. [Google Scholar]

11. Y. R. B. Al-Mayouf, N. F. Abdullah, O. A. Mahdi, S. Khan, M. Ismail et al., “Real-time intersection-based segment aware routing algorithm for urban vehicular networks,” IEEE Transactions on Intelligent Transportation Systems, vol. 19, no. 7, pp. 2125–2141, 2018. [Google Scholar]

12. M. K. Hasan, M. M. Ahmad, A. H. A. Hashim, A. RAzzaque, S. Islam et al., “A novel artificial intelligence based timing synchronization scheme for smart grid applications,” Wireless Personal Communications, vol. 114, no. 2, pp. 1067–1087, 2019. [Google Scholar]

13. S. N. Makhadmeh, A. T. Khader, M. A. Al-Betar, S. Naim, A. K. Abasi et al., “A novel hybrid grey wolf optimizer with min-conflict algorithm for power scheduling problem in a smart home,” Swarm and Evolutionary Computation, vol. 60, no. 2, pp. 1–17, 2021. [Google Scholar]

14. N. Nurelmadina, M. K. Hasan, I. Memon, R. A. Saeed, K. A. Z. Ariffin et al., “A systematic review on cognitive radio in low power wide area network for industrial IoT applications,” Sustainability, vol. 13, no. 1, pp. 1–21, 2021. [Google Scholar]

15. S. Bashir, M. H. Alsharif, I. Khan, M. A. Albreem, A. Sali et al., “MIMO-Terahertz in 6G nano-communications: Channel modeling and analysis,” Computers, Materials & Continua, vol. 66, no. 1, pp. 263–274, 2020. [Google Scholar]

16. A. Amin, X. Liu, I. Khan, P. Uthansakul, M. Forsat et al., “A robust resource allocation scheme for device-to-device communications based on Q-learning,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1487–1505, 2020. [Google Scholar]

17. S. Alemaishat, O. A. Saraereh, I. Khan, S. H. Affes, X. Li et al., “An efficient precoding scheme for millimeter-wave massive MIMO systems,” Electronics, vol. 8, no. 9, pp. 1–15, 2019. [Google Scholar]

18. A. Al-Nimrat, M. Smadi, O. A. Saraereh and I. Khan, “An efficient channel estimation scheme for mmwave massive MIMO systems,” in Proc. IEEE Int. Conf. on Communication, Networks and Satellite, Makassar, Indonesia, pp. 1–8, 2019. [Google Scholar]

19. I. Khan and D. Singh, “Efficient compressive sensing based sparse channel estimation for 5G massive MIMO systems,” AEU-International Journal of Electronics and Communications, vol. 89, no. 2, pp. 181–190, 2018. [Google Scholar]

20. A. Amin, X. H. Liu, M. A. Saleem, S. Henna, T. Islam et al., “Collaborative wireless power transfer in wireless rechargeable sensor networks,” Wireless Communications and Mobile Computing, vol. 9701531, pp. 1–13, 2020. [Google Scholar]

21. F. Jameel, T. Ristaniemi, I. Khan and B. M. Lee, “Simultaneous harvest-and-transmit ambient backscatter communications under Rayleigh fading,” EURASIP Journal on Wireless Communications and Networking, vol. 19, no. 1, pp. 1–9, 2019. [Google Scholar]

22. W. Shahjehan, S. Bashir, S. L. Mohammed, A. B. Fakhri, A. A. Isaiah et al., “Efficient modulation scheme for intermediate relay-aided IoT networks,” Applied Sciences, vol. 10, no. 6, pp. 1–12, 2020. [Google Scholar]

23. O. A. Saraereh, A. Alsaraira, I. Khan and B. J. Choi, “A hybrid energy harvesting design for on-body internet-of-things (IoT) networks,” Sensors, vol. 20, no. 2, pp. 1–14, 2020. [Google Scholar]

24. T. Jabeen, Z. Ali, W. U. Khan, F. Jameel, I. Khan et al., “Joint power allocation and link selection for multi-carrier buffer aided relay network,” Electronics, vol. 8, no. 6, pp. 1–15, 2019. [Google Scholar]

25. S. Alemaishat, O. A. Saraereh, I. Khan and B. J. Choi, “An efficient resource allocation algorithm for D2D communications based on noma,” IEEE Access, vol. 7, pp. 120238–120247, 2019. [Google Scholar]

26. R. A. Alhameed, I. Elfergani and I. Rodriguez, “Recent technical developments in energy-efficient 5G mobile cells: Present and future,” Electronics, vol. 9, no. 4, pp. 1–4, 2020. [Google Scholar]

27. Z. Lin, H. Song and D. Pan, “A joint power and channel scheduling scheme for underlay D2D communications in the cellular network,” Sensors, vol. 19, no. 21, pp. 1–18, 2019. [Google Scholar]

28. P. Mach, Z. Beever and T. Vanek, “In-band device-to-device communication in OFDMA cellular networks: A survey and challenges,” IEEE Communication Surveys & Tutorials, vol. 17, no. 4, pp. 1885–1922, 2015. [Google Scholar]

29. R. Tang, J. H. Zhao, H. Qu, Z. Zhu and Y. Zhang, “Joint mode selection and resource allocation for mobile relay-aided device-to-device communication,” KSII Transactions on Internet and Information Systems, vol. 10, no. 3, pp. 950–975, 2016. [Google Scholar]

30. A. Imran and A. Zoha, “Challenges in 5G: How to empower SON with big data for enabling 5G,” IEEE Network, vol. 28, no. 6, pp. 27–33, 2014. [Google Scholar]

31. Q. Wang, C. Lai, Y. Dong, Y. Shu and X. Xu, “Joint user clustering and resource allocation for device-to-device communication underlaying mu-mimo cellular networks,” EURASIP Journal of Wireless Communications and Networking, vol. 145, pp. 1–17, 2015. [Google Scholar]

32. J. Li, G. Lei, G. Manogaran, G. Mastorakis and C. X. Mavromoustakis, “D2D communications mode selection and resource optimization algorithm with optimal throughput in 5G network,” IEEE Access, vol. 7, pp. 25263–25273, 2019. [Google Scholar]

33. S. Han, T. Kwon and J. W. Choi, “Analysis of D2D system performance with a maximal SINR channel selection strategy,” in IEEE Information and Communication Technology Convergence, Busan, South Korea, pp. 379–380, 2014. [Google Scholar]

34. C. Xu, L. Y. Song, Z. Han, Q. Zhao, X. Wang et al., “Efficient resource allocation for device-to-device underlay communication systems: A reverse iterative combinational auction based approach,” IEEE Journal on Selected Areas in Communications, vol. 31, no. 9, pp. 348–358, 2013. [Google Scholar]

35. G. P. Zhang, K. Yang, P. Liu and J. Wei, “Power allocation for full-duplex relaying-based D2D communication underlaying cellular networks,” IEEE Transactions on Vehicular Technology, vol. 64, no. 10, pp. 4911–4916, 2015. [Google Scholar]

36. M. Zulhasnin, C. Huang and A. Srinivasan, “Efficient resource allocation for device-to-device communication underlaying LTE network,” in IEEE Int. Conf. on Wireless and Mobile Computing, Networking and Communications, Niagara Falls, Canada, pp. 368–375, 2010. [Google Scholar]

37. C. H. Yu, K. Doppler, C. B. Ribeiro and O. Tirkkonen, “Resource sharing optimization for device-to-device communication underlaying cellular networks,” IEEE Transactions on Wireless Communications, vol. 10, no. 8, pp. 2752–2763, 2011. [Google Scholar]

38. C. Gao, X. Sheng, J. Tang, W. Zhang, S. Zou et al., “Joint mode selection, channel allocation and power assignment for green device-to-device communication,” in IEEE Int. Conf. on Communications, Sydney, Australia, pp. 178–183, 2014. [Google Scholar]

39. Z. Kuang, G. Li, L. Zhang, H. Zhou, C. Li et al., “Energy efficient mode selection, base station selection and resource allocation algorithm in D2D heterogeneous networks,” Peer-to-Peer Networking and Applications, vol. 13, no. 5, pp. 1814–1829, 2020. [Google Scholar]

40. X. Z. Xie, C. W. Li, S. G. Cheng, H. L. Yang and S. Tang, “Distributed beamforming algorithm based on game theory in device-to-device communications,” International Journal of Distributed Sensor Networks, vol. 14, no. 8, pp. 1–17, 2018. [Google Scholar]

41. W. C. Cheng, X. Zhang and H. L. Zhang, “Optimal power allocation with statistical QoS provisioning for D2D and cellular communications over underlaying wireless networks,” IEEE Journal on Selected Areas in Communications, vol. 34, no. 1, pp. 151–162, 2016. [Google Scholar]

42. J. Minchae, H. Kyuho and C. Sooyong, “Joint mode selection and power allocation with statistical QoS provisioning for D2D and cellular communications over underlaying wireless networks,” in IEEE 75th Vehicular Technology Conf. Spring, Yokohama, Japan, pp. 1–5, 2012. [Google Scholar]

43. B. Zhang, Y. Gao, X. Liu and X. Huang, “Output-space branch-and-bound reduction algorithm for a class of linear multiplicative programs,” Mathematics, vol. 8, no. 3, pp. 1–21, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.