Computers, Materials & Continua DOI:10.32604/cmc.2021.018061
Article

Two-Phase Bidirectional Dual-Relay Selection Strategy for Wireless Relay Networks

Samer Alabed*, Issam Maaz and Mohammad Al-Rabayah

College of Engineering and Technology, American University of the Middle East, Kuwait
*Corresponding Author: Samer Alabed. Email: samer.al-abed@aum.edu.kw
Received: 23 February 2021; Accepted: 29 March 2021

Abstract: In this article, we introduce a new bi-directional dual-relay selection strategy with its bit error rate (BER) performance analysis. During the first step of the proposed strategy, two relays out of a set of N relay-nodes are selected in a way to optimize the system performance in terms of BER, based on the suggested algorithm which checks if the selected relays using the max-min criterion are the best ones. In the second step, the chosen relay-nodes perform an orthogonal space-time coding scheme using the two-phase relaying protocol to establish a bi-directional communication between the communicating terminals, leading to a significant improvement in the achievable coding and diversity gain. To further improve the overall system performance, the selected relay-nodes apply also a digital network coding scheme. Furthermore, this paper discusses the analytical approximation of the BER performance of the proposed strategy, where we prove that the analytical results match almost perfectly the simulated ones. Finally, our simulation results show that the proposed strategy outperforms the current state-of-the-art ones.

Keywords: Two-way wireless relay networks; cooperative diversity techniques; distributed space-time coding; relay selection strategies; network coding schemes

1  Introduction

The new wireless communication systems such as 5G and beyond seek to increase the data rate, decrease the latency, reduce the complexity, and extend the coverage area. However, the performance of these wireless systems are badly affected by the multiuser interference, channel impairments, multipath propagation, and time-varying fading, leading to decrease the achievable data rate and increase the bit error rate [1–8]. Therefore, many multi-antenna techniques have been proposed in order to mitigate these challenges such as the use of relay selection techniques [9–14], distributed space-time-coding (STC) techniques [15,16], and distributed beamforming techniques [16–18]. Relay selection techniques have been applied on wireless communication systems in order to increase the achievable data rate, extend their coverage, as well as, to decrease the impact of channel impairments. As a result, the BER and data rate can be greatly enhanced using relaying techniques, which allow the user to receive different versions, i.e., different phases and amplitudes, of the same transmitted signal. These different versions are combined together in an efficient way in order to achieve a better performance.

A relay node is an intermediate entity between the transmitter and the receiver. It receives the signal from a source-node and then processes the data by employing advanced techniques to improve the received signal to noise ratio (SNR) and achievable data rate, and to minimize the overall BER. Increasing the number of relay nodes available between the transmitter and the receiver leads to a significant enhancement in the spatial diversity using one of the relaying schemes, i.e., one-way or two-way relaying schemes [1–5]. Many diversity techniques have been recently proposed assuming that the availability of the channel state information (CSI) is crucial at all nodes of the network with slow fading channels, whereas other techniques consider that CSI must be available only at the receiver side [2]. In addition, many techniques have been proposed in order to increase the diversity gain without needing CSI at any transmitting or receiving nodes such as non-coherent and differential diversity techniques [2–5]. Even though the latter techniques do not require any CSI at both the receiver and the transmitter sides, they suffer from high BER, high latency, and low spectral efficiency as compared to other techniques.

Other techniques such as bi-directional communication is proposed as a solution to improve the performance in terms of BER and spectral efficiency. Those systems consist of two terminals that communicate with each other through some in-between relay nodes that are randomly distributed between them [2–5]. Bi-directional schemes can be classified based on the number of phases needed to exchange the transmitted information between the communicating terminals into two-phase [2–3,6], three-phase [2,3], and four-phase [4,5] protocols. The number of phases can greatly affect the performance of the communication systems. More precisely, the spectral efficiency can be significantly improved by decreasing the number of needed time slots to exchange the messages between the transceivers from four-phase to three-phase or even to two-phase. As a result, the two-phase relaying systems offer a much better performance compared to the three phase and four phase relaying systems [2–4,11]. Furthermore, the relay nodes can process and encode the received signals using orthogonal or non-orthogonal coding techniques.

Some orthogonal techniques, such as STC, offer a full diversity gain with a low decoding complexity [2]. On the other hand, non-orthogonal coding techniques improve the overall system performance in terms of BER and achievable data rate and enjoy a full diversity with high coding gain. However, these techniques suffer from extremely high decoding complexity. Therefore, in order to achieve a full diversity gain and decrease the system complexity of the non-orthogonal relay selection techniques [6–12], many cooperative diversity techniques have recently been investigated with single and dual relay selection strategies [7–14].

In recent years, many relay selection techniques have adopted to select the best one or more relay nodes out of a group of intermediate relay-nodes. In [10–12], the authors proposed the max-min selection criterion that chooses the optimal relay out of a set of relay-nodes in a way to maximize either the SNR or the overall achievable data rate. The authors of [11] used the max-min method in order to choose the best two relay nodes offering a significant improvement in the system performance. The authors of [13,14] proposed a method based on dual-relay selection scheme. In their work, they have proved that dual-relay selection techniques offer higher coding gain than single relay selection ones. The authors of [19–21] introduced various downlink scheduling algorithms for 4G and 5G wireless communication systems that aim to address different traffic classes and balance the quality of service delivery with improvements to the overall system performance under channel and bandwidth constraints.

The motivation of this paper is that the current state-of-the-art articles are only considering the weakest or strongest channels to choose the best one or two relay-nodes, e.g., they select the relay-node among all available relay-nodes that owns the strongest forward or backward channel or they select two relays where one of them has the strongest forward channel and the other owns the strongest backward channel, while ignoring the differences among the close-value channels of the available relay-nodes. For instance, authors of [11–13] are selecting two relay-nodes using a certain criterion like the max-min criterion, considered as the optimal one for selecting only one relay. In this paper, the proposed algorithm, explained in Section 2, checks if the selected relays using the max-min criterion are the best ones before using them. Therefore, in this paper, we introduce a new two-relay selection strategy based on STC using the two-phase relaying protocol. In the suggested strategy, two relays out of N relay-nodes are chosen in a way to optimize the system performance in terms of BER. Additional improvement is achieved by performing a digital network coding scheme at the selected relay-nodes which reduces the power consumption via merging the symbols of the communicating terminals in a single symbol with the same constellation.

From our simulation results, we prove that our suggested strategy offers a better performance as compared to the existing relay selection strategies. This paper is summarized as follows: Section 2 discusses the system model. Section 3 explains the BER analysis. Section 4 and Section 5 demonstrate the performance analysis. The conclusion is drawn in Section 5.

2  System Model

Fig. 1 shows our system model where two terminal-nodes (T1 and T2) need to communicate with each other, but they cannot communicate directly because the distance between them is exceeding their transmission range. A group of N relay-nodes located randomly between T1 and T2 is used to facilitate this bi-directional communication. More specifically, two relay-nodes will be chosen based on a certain criterion to accomplish the required communication. We assume here that all the relay- and terminal-nodes have limited average transmit powers denoted as PTj, j=1,2 for terminal nodes and PRi, i=1,2,…,N for relay-nodes. Furthermore, all intermediate communication channels between terminal and relay-nodes are assumed to be reciprocal for transmissions, and are denoted as hi from T1 to relay-node i and gi from T2 to relay-node i. Finally, we use the following notations |.|,⌊.⌋,‖.‖, (.)*, [a]i, and E(.) to denote the absolute value, the floor function which rounds toward zero, the Frobenius norm, the complex conjugate, the ith element of the vector a, and the statistical expectation, respectively. In addition, the following abbreviations are used in this paper, BER: Bit error rate; bpcu: Bit per channel use; BPSK: Binary phase shift key; CSI: Channel state information; DF: Decode and forward; MGF: Moment generation function; ML: Maximum likelihood, SNR: Signal to noise ratio; STC: Space time coding; and QAM: Quadrature amplitude modulation.

In our proposed strategy all participating relay-nodes will be performing the decode-and-forward (DF) protocol [2,3]. During the first time slot, both terminal nodes T1 and T2 will transmit their data message vectors zT1 and zT2 simultaneously such that the rth relay-node Rr receives:

yRr=PT1hrzT1+PT2grzT2+nRr,(1)

Given that [zT1]i∈ZT1,[zT2]i∈ZT2, E{|[zT1]i|2}=1, E{|[zT2]i|2}=1, ZT1 and ZT2 are two, possibly different, constellations, and nRr is the noise vector at the first time-slot obtained by the rth relay-node Rr. The rth relay-node Rr will then use the maximum likelihood (ML) decoder to detect the two received message vectors z~T1,r and z~T2,r as follows:

argzT1,zT2⁡min‖yRr−PT1hrzT1−PT2grzT2‖,(2)

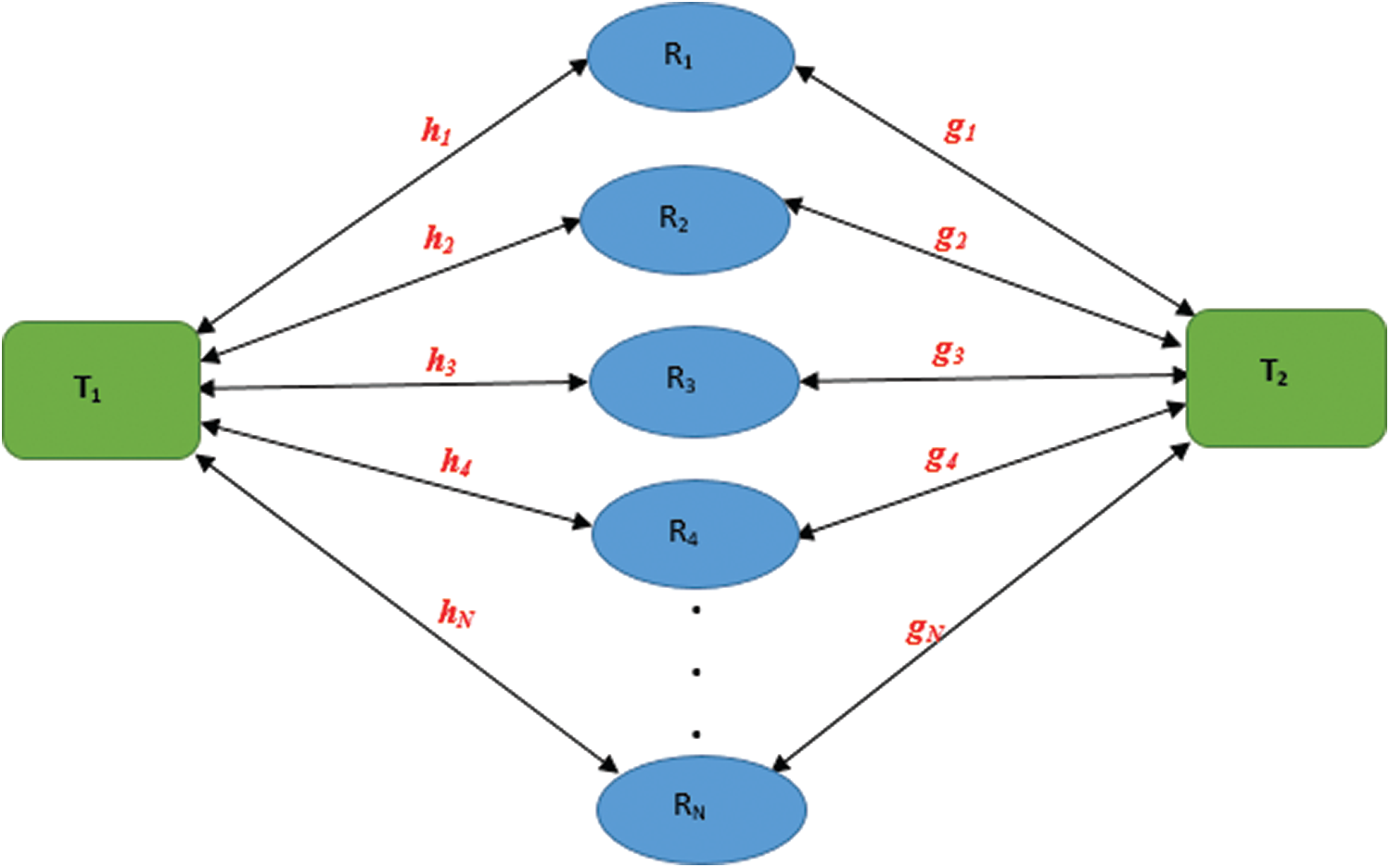
Figure 1: Bi-directional relay-nodes network

Note here that the relay-nodes are encountering a high decoding overhead. More specifically, the decoding complexity is increasing quadratically as the size of the constellation is getting larger, because the decoder needs to apply pairwise decoding to detect the received messages. After that, the rth relay node Rr will use a merging function to combine both received message vectors z~T1,r and z~T2,r to produce a new message vector, given by:

zR,r=F(z~T1,r,z~T2,r),(3)

where F(.,.) is a merging function used by the relay-node Rr to combine the two received message vectors. Recently, many merging functions have been suggested in the literature. For instance, the modular arithmetic [2], the XOR function [1,2], and the merging function suggested in [2] are some examples of the merging functions. Based on the proposed relay selection strategy, explained using the flowchart available in Fig. 2 below, two relay-nodes (Ra and Rb) will be chosen as follows:

Stage 1: The first relay-node Ra1 is chosen according to the max-min selection criterion, such that:

arga1max{min(|ha1|,|ga1|);∀a1={1,2,…,N}},(4a)

Stage 2: The next two relay nodes are chosen such as Rak,k={2,3} according to the max-min selection criterion again, such that:

argak⁡max{min(|hak|,|gak|)}∀ak={1,2,…,N},ak≠{ak−1,ak−2,…a1},(4b)

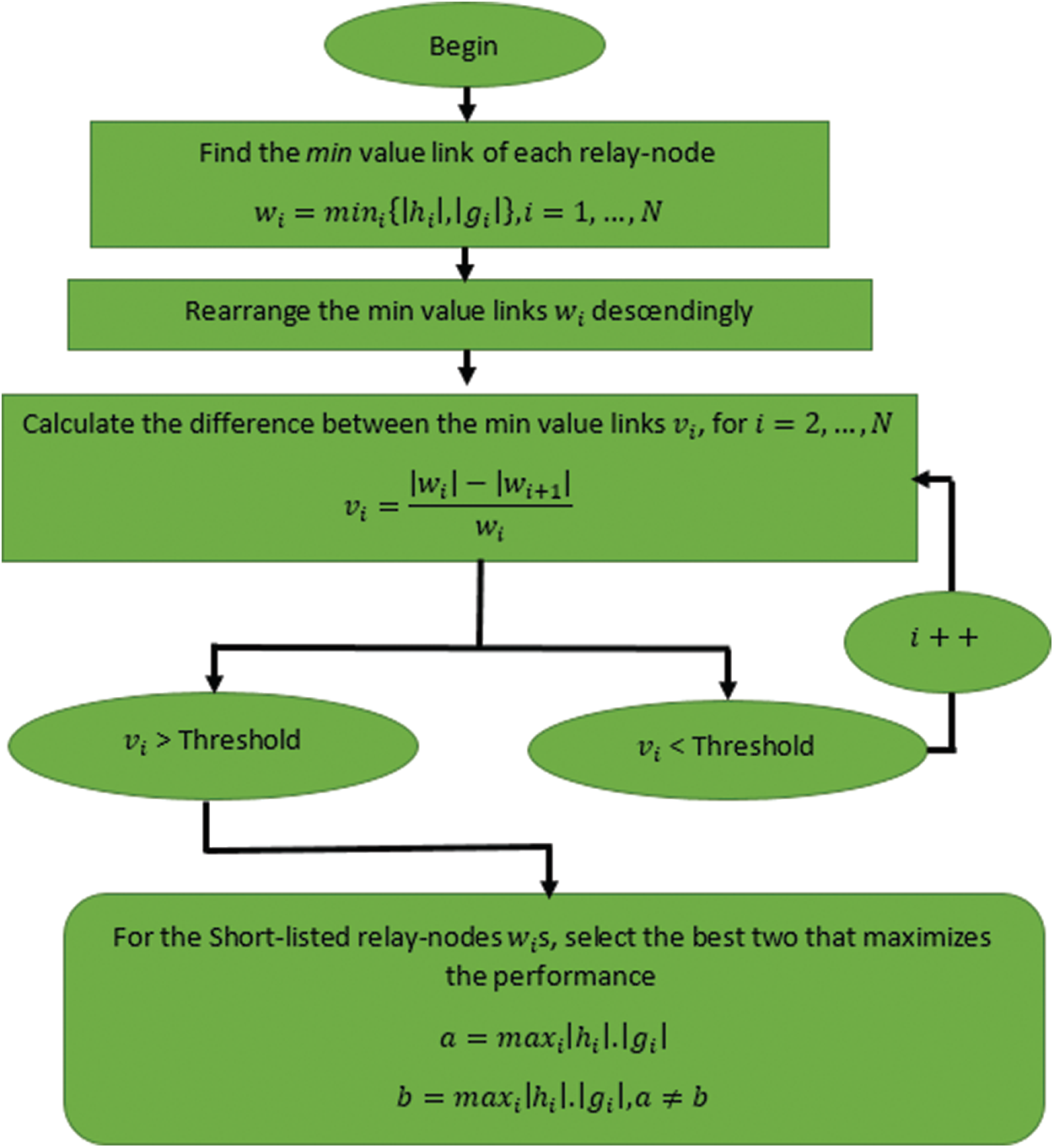
Figure 2: Flowchart of the proposed relay selection strategy

Stage 3: In the third stage of the proposed selection strategy, we select the minimum value channel between the forward channels, i.e., h, and the backward channels, i.e., g, of each relay node. Afterward, sort the results, i.e., the minimum value links of the relay-nodes, from largest down-ward to smallest in a certain quality vector ai=[a1,a2,…aN]. After that, the difference between the minimum channel of the second relay Ra2 and that of the third relay Ra3 will be calculated using the following equation with k=2, such that:

Diff=min(|hak−1|,|gak−1|)−min(|hak|,|gak|)min(|hak−1|,|gak−1|)×100%,(4c)

The two relays, Rak,k={1,2} if Diff > Threshold, will be selected as they own the best links between the two communicating terminals and offer the best performance in the whole network.

Stage 4: For the case of Diff < Threshold, Stages 2 and 3 will be repeated when k=4. Afterwards, if Diff > Threshold, then nk=3 else nk=4. The main point of this stage is to shortlist the available relay-nodes that have very close values, and it will be executed repeatedly as long as the Diff value is below the targeted threshold.

Stage 5: The expected performance of each shortlisted relay node will be calculated by multiplying its forward and backward channel. After that the best two relay-nodes that have the largest results will be chosen, such that:

Ra=maxak(|hak|×|gak|);ak={1,2,…nk}Rb=maxal(|hal|×|gal|);al={1,2,…nk;al≠a},(4d)

To enhance the overall system’s diversity and coding gain without adding extra decoding complexity, the two selected relay-nodes Ra and Rb, i.e., the ath relay and the bth relay, apply orthogonal STC technique using Alamouti scheme. In the second time slot, the two selected relay-nodes, i.e., Ra and Rb decode, combine, and then broadcast their message vectors toward the two-destination terminal-nodes. Thus, the second destination terminal receives:

yT2=PRahaAazR,a+PRbgbAb(zR,b)∗+nT2,(5)

given that Aa=[1001],Ab=[01−10], and nT2 represents the noise vector at the second terminal-node T2 received in the second time slot. To retrieve the received message vectors, the two terminals use a symbol-by-symbol decoder which enjoys a very low decoding complexity instead of the ML decoder whose complexity increases exponentially with the increase of the constellation size and the number of transmitted antennas. Note that the symbol-by-symbol decoder is feasible at the terminal nodes as they know their own transmitted messages, and they can apply the inverse of the combination function used by the relay nodes to enjoy a linear decoding complexity.

3  BER Performance Analysis

In this section, we propose the mathematical analysis of the BER for our relay selection strategy, which was explained in Section 2. In this analysis, we assume, without loss of generality, that the used modulation is the binary phase shift keying (BPSK). Moreover, we suppose that the used relay stations are ideal, similarly as in [13,14,18], and the noise is generated using independent distributed Gaussian random variables where its covariance matrix is σ2IT and its mean is set to zero. From (4a)–(4d) explained in Section 2, our relay selection strategy selects two relays, the ath and bth relay nodes, where the power distributed equally among all the relay nodes such that PRa=PRb=PN. Moreover, we assume that the SNR of the link between the relay station Rr and the destination terminal T1 is denoted by βrT1=β|hr|2, the SNR of the link between the relay station Rr and destination terminal T2 is denoted by βrT2=β|gr|2. In addition, we consider that β=PN/σ2 is the mean SNR at the rth relay station Rr. As a second step, we will increasingly sort βrTt,r=1,…,N,t=1,2 in a way that β1Tt≤β2Tt≤…≤βNTt and we suppose that w1Tt=β1Tt and wlTt=βlTt−β(l−1)Tt for l=2,…,N. It should be noted that the independent factors, wl for l=1,…,N, follow a probability distribution function given by the following expression [13,14,18]:

fwl(wl)=N−l−1βexp(−N−l−1βwl),(6)

In this proposed relaying strategy, out of N available relay stations, the ath relay station is chosen based on the criterion presented earlier in (4a)–(4d), where ga represents the link between the relay station Ra and the destination terminal T2 with βd1T2 and ha represents the link between the relay station Ra and the destination terminal T1 with βc1T1 where βc1T1≥β⌊N/2⌋T2, and c1 is any cth greater than d1. In the next stage, the bth relay station Rb is chosen out of the remaining (N−1) relays with gb represents the link between the relay station Rb and the destination terminal T2 with βd2T2, and hb represents the link between the relay station Rb and the destination terminal T1 with βc1T1≥βd2T2, and c2 is any cth greater than d2 and assuming that βd1T2≥βd2T2. As a result, the average BER of our dual-relay selection technique is depicted in the below expression:

D(β)=14E{Q(βd1T2+βd2T2)+Q(βc1T1+βc2T1)}+14E{Q(βd1T2+βc2T1)+Q(βd2T2+βc1T1)}=14(D1+D2+D3+D4),(7)

One can notice that the above expression consists of four terms where the part (βd1T2+βd2T2) available in the first term D1 can be expressed as:

Q1=βd1T2+βd2T2=∑i=1d2ωi+∑i=1d1ωi=2∑i=1d2ωi+∑i=d2+1d1ωi,(8)

Hence, the moment-generation function (MGF) of Q1 given in (8) can be written as [13,14,18]:

MQ1(s)=∫0∞…∫0∞(∏i=1Nfwl(wi))exp(sQ1)dω1…dωN=∏i=1N∫0∞fwi(wi)exp(2sωi)dωi×∏i=d2+1d1∫0∞fwi(wi)exp(sωi)dωi=d1!(−1)d12d2βd1∏i=1d21s−d1−i+12β∏i=d2+1d11s−d1−i+1β,(9)

The aforementioned expression, i.e., (9), can be simplified through the use of partial fraction method as shown below:

MQ1(s)=d1!(−1)d12d2βd1∑i=1d21(s−d1−i+12β)∏j=1j≠i⌊N2⌋(d1−i+12β−d1−j+12β)×∑p=d2+1d11(s−d1−p+1β)∏r=d2+1j≠pd1(d1−p+1β−d1−r+1β)=d1!(−1)d12β2∑i=1d2∑p=d2+1d11∏j=1j≠id2(j−i)∏r=d2+1r≠pd1(r−p)×1(s−d1−i+12β)(s−d1−p+1β),(10)

Thus, the term D1 can be written as [13,14,18]:

D1=12π∫0π2MQ1(−12sin2(φ))dφ,(11)

By combining (9)–(11), the term D1 can be expressed as shown below:

D1=d1!(−1)d14β2∑i=1d2∑p=d2+1d11∏j=1xj≠id2(j−i)∏r=d2+1r≠pd1(r−p)×1π∫0π21(12sin2(φ)+d1−i+12β)(12sin2(φ)+d1−p+1β)dφ(12)

In a similar way, D2, D3, and D4 expressed in (7) can be found by applying the same steps used to calculate the first part D1 as shown in the previous equations, i.e., (8)–(12).

D2=c1!(−1)c14β2∑i=1c2∑p=c2+1c11∏j=1j≠ic2(j−i)∏r=c2+1j≠pc1(r−p)×1π∫0π21(12sin2(φ)+c1−i+12β)(12sin2(φ)+c1−p+1β)dφ,(13)

D3=c2!(−1)c24β2∑i=1d1∑p=d1+1c21∏j=1j≠id1(j−i)∏r=d1+1r≠pc2(r−p)×1π∫0π21(12sin2(φ)+c2−i+12β)(12sin2(φ)+c2−p+1β)dφ,(14)

D4=c1!(−1)c14β2∑i=1d2∑p=d2+1c11∏j=1j≠id2(j−i)∏r=d2+1r≠pc1(r−p)×1π∫0π21(12sin2(φ)+c1−i+12β)(12sin2(φ)+c1−p+1β)dφ,(15)

Making use of the final expressions of D1, D2, D3, and D4 given in (12)–(15), the average BER of the proposed dual-relay selection strategy can be expressed as:

D(β)=14(D1+D2+D3+D4),(16)

In this step, we suppose that the Threshold value is equal to zero, then the ath relay station Ra is chosen from the N available relay stations based on the selection criterion explained earlier in Section 2 using the Eqs. (4a)–(4d) assuming that ga is the link between the relay station Ra and the destination terminal T2 with β⌊N/2⌋T2 and ha is the link between the relay station Ra and the terminal T1 with βc1T1 where βc1T1≥β⌊N/2⌋T2, and c1 is any cth greater than ⌊N/2⌋. Then, the bth relay station Rb is chosen in the same way, from the remaining (N−1) relay stations with gb representing the link between the relay station Rb and destination terminal T2 with β⌊(N−1)/2⌋T2, and hb is the link between the relay station Rb and the destination terminal T1 with βc2T1 where βc2T1≥β⌊(N−1)/2⌋T2 and c2 can be any cth greater than ⌊(N−1)/2⌋. Similar to (7), the average BER of the proposed dual-relay selection technique can be written as:

D(β)=14E{Q(β⌊N2⌋T2+β⌊(N−1)2⌋T2)+Q(βc1T1+βc2T1)}+14E{Q(β⌊N/2⌋T2+βc2T1)+Q(β⌊(N−1)/2⌋T2+βc1T1)}=14(D1+D2+D3+D4),(17)

where,

D1=⌊N/2⌋!(−1)⌊N/2⌋4β2∑i=1⌊(N−1)/2⌋∑p=⌊(N−1)/2⌋+1⌊N/2⌋1∏j=1j≠i⌊(N−1)/2⌋(j−i)∏r=⌊(N−1)/2⌋+1r≠p⌊N/2⌋(r−p)×1π∫0π21(12sin2(φ)−⌊N/2⌋−i+12β)(12sin2(φ)+⌊N/2⌋−p+1β)dφ,(18)

For the second part D2, we assume that c1≥c2 and use the MGF of Q2=βc1T1+βc2T1. Regarding the third part D3, we assume thatc2≥⌊N/2⌋ and use the MGF of Q3=βc2T1+β⌊N/2⌋T2. For the fourth part D4, we consider that c1≥⌊(N−1)/2⌋ and use the MGF of Q4=βc1T1+β⌊(N−1)/2⌋T2, then:

D2=c1!(−1)c14β2∑i=1c2∑p=c2+1c11∏j=1j≠ic2(j−i)∏r=c2+1r≠pc1(r−p)×1π∫0π21(12sin2(φ)−c1−i+12β)(12sin2(φ)+c1−p+1β)dφ,(19)

D3=c2!(−1)c24β2∑i=1⌊N/2⌋∑p=⌊N/2⌋+1c21∏j=1j≠i⌊N/2⌋(j−i)∏r=⌊N/2⌋+1r≠pc2(r−p)×1π∫0π21(12sin2(φ)−c2−i+12β)(12sin2(φ)+c2−p+1β)dφ,(20)

D4=c1!(−1)c14β2∑i=12⌊(N−1)2⌋∑p=⌊(N−1)2⌋+1c11∏j=12j≠i⌊(N−1)2⌋(j−i)∏r=⌊(N−1)2⌋+1r≠pc1(r−p)×1π∫0π21(12sin2(φ)−c1−i+12β)(12sin2(φ)+c1−p+1β)dφ,(21)

Using the final expressions of D1, D2, D3, and D4 given by (18)–(21), the average BER of the proposed dual-relay selection strategy, when the Threshold value is equal to zero, can be expressed as:

D(β)=14(D1+D2+D3+D4),(22)

4  Results and Discussion

In this section, we discuss the obtained results from both Monte Carlo simulations, as well as, analytical models discussed in Section 4. In the simulations, we have assumed a wireless relay network with two single-antenna relay nodes and independent flat Rayleigh fading channels where the power is distributed among the two terminals and relays similarly as in [11–13], the number of Monte Carlo runs is 1010, the number of relays available in the network varies between two to six, and the applied modulation technique is either BPSK or 4-QAM. For fair comparison of the BER performance of all techniques, the same total transmitted power and bit rate are used. Fig. 3 shows the BER performance with respect to the SNR of both the simulated proposed relay-selection strategy and the analytical results obtained from (22) in the presence of N = 2, 4, 6 } relay-nodes using BPSK modulation without direct links between the two communicating terminal-nodes T1 and T2. This figure shows a very close consistency between our simulations and the derived mathematical expression, i.e., (22).

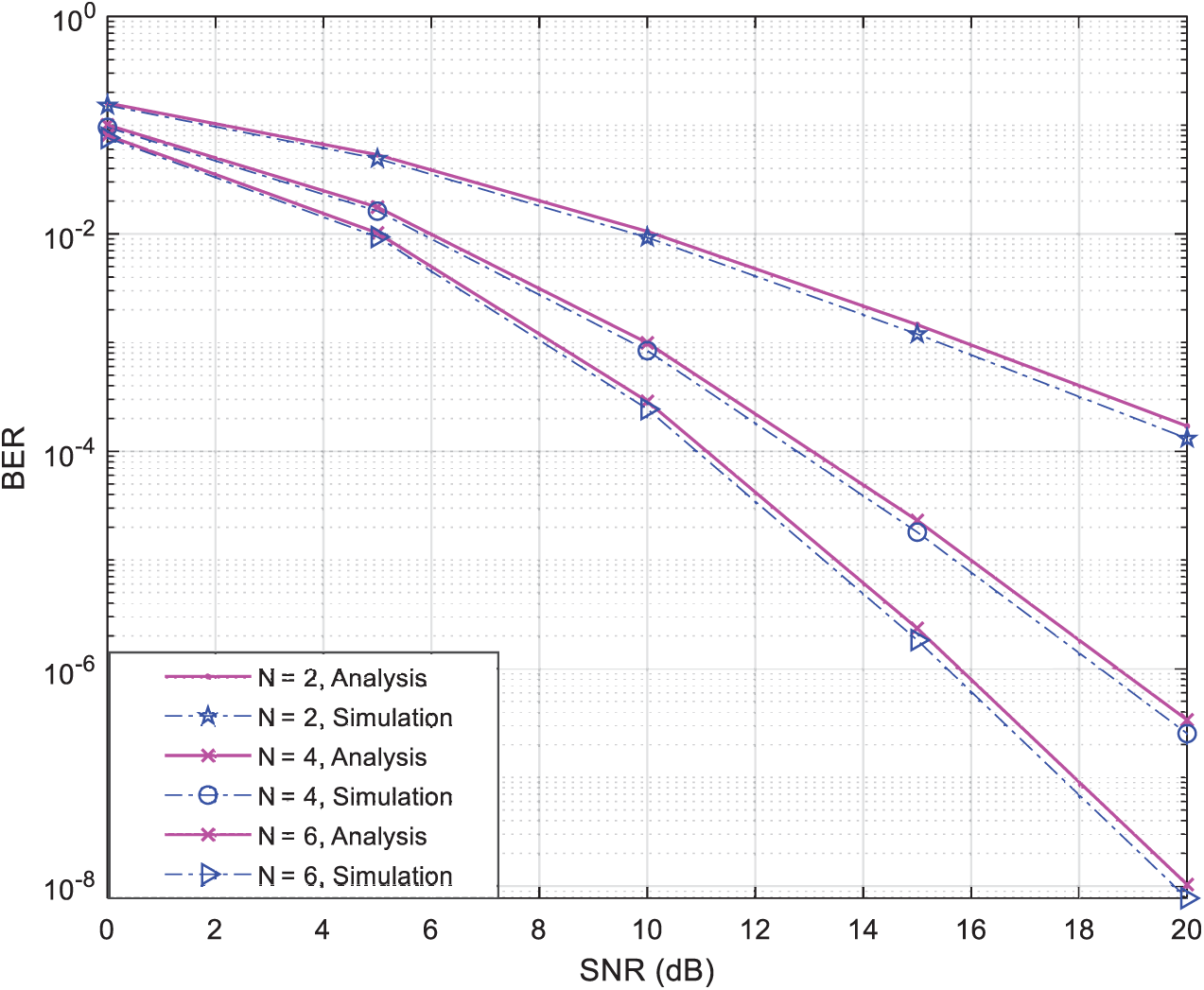
Figure 3: Theoretical and simulated BER performance vs. SNR

In Fig. 4, we show a comparison in terms of the BER performance with respect to the SNR between the proposed dual-relay selection strategy, the double-max technique available in [11], the max-min technique available in [12], and the dual-relay selection technique suggested in [13], in the presence of N = 2, 4 } relay-nodes using 4-QAM modulation and without direct links between the two terminal-nodes T1 and T2. We can clearly observe from Fig. 4 that the performance of our suggested relay selection strategy using the two-phase relaying protocol exceeds that of the current state-of-the-art strategies that perform the same relaying protocol and under the same assumptions explained in Section 2. In addition, Fig. 4 shows the BER performance of our proposed dual-relay selection strategy in the presence of four relay-nodes (N = 4) using 4-QAM modulation under different threshold values, i.e., threshold increases gradually from zero to five. It can be noticed that our suggested strategy with threshold value set to zero is equivalent to the selection strategy available in [14]. We can clearly notice from Fig. 4 that the best performance is achieved when the threshold value is three. To prove this finding, we have investigated in Fig. 5 the BER performance of our suggested relay selection strategy in the presence of four relay-nodes using 4-QAM modulation with SNR set to 20 dB under different threshold values. The results obtained in Fig. 5 clearly sustain with our findings in Fig. 4.

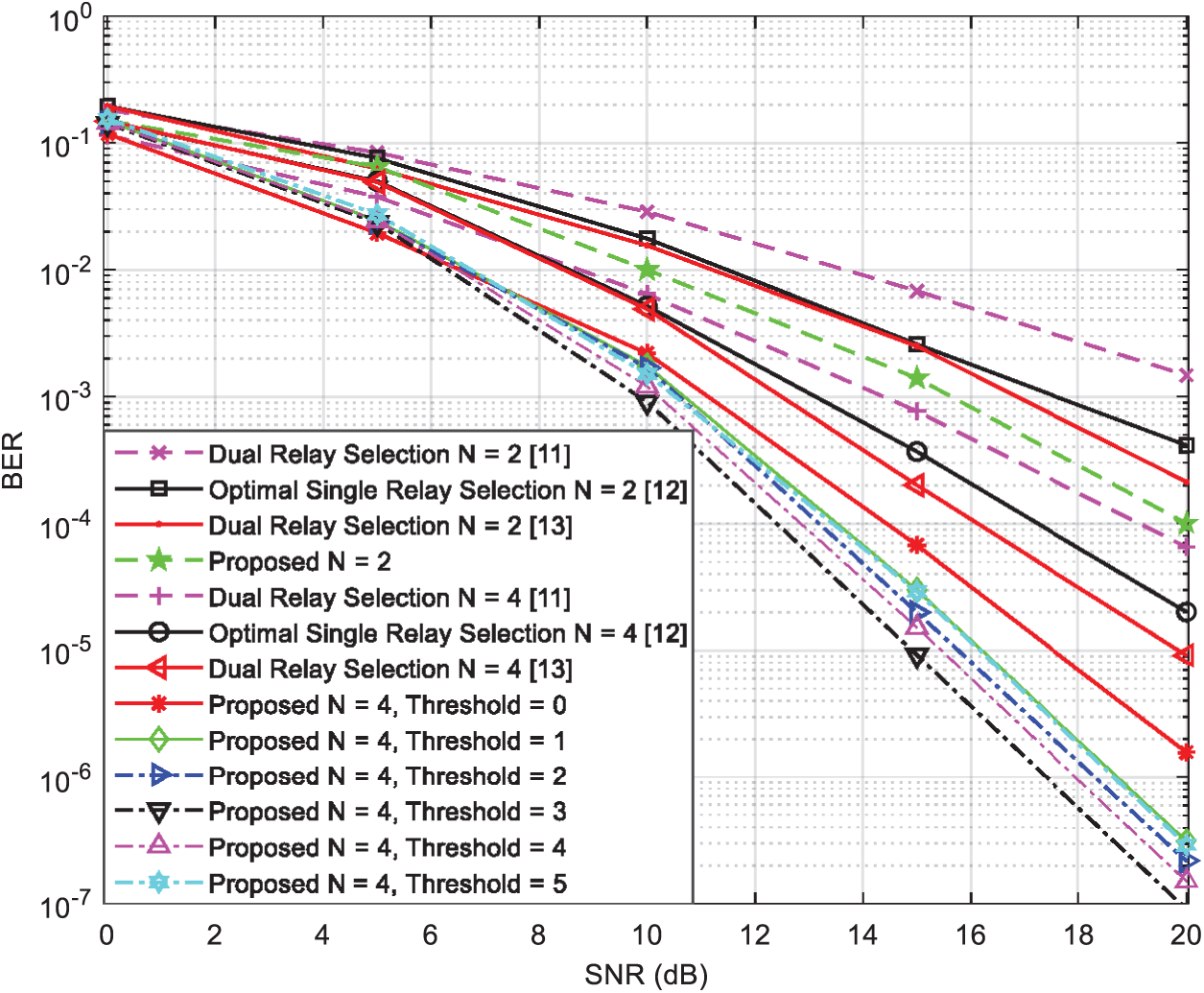
Figure 4: BER vs. SNR for several single and dual-relay selection techniques using the two-phase relaying protocol with N = 2, 4 } and 4-QAM modulation

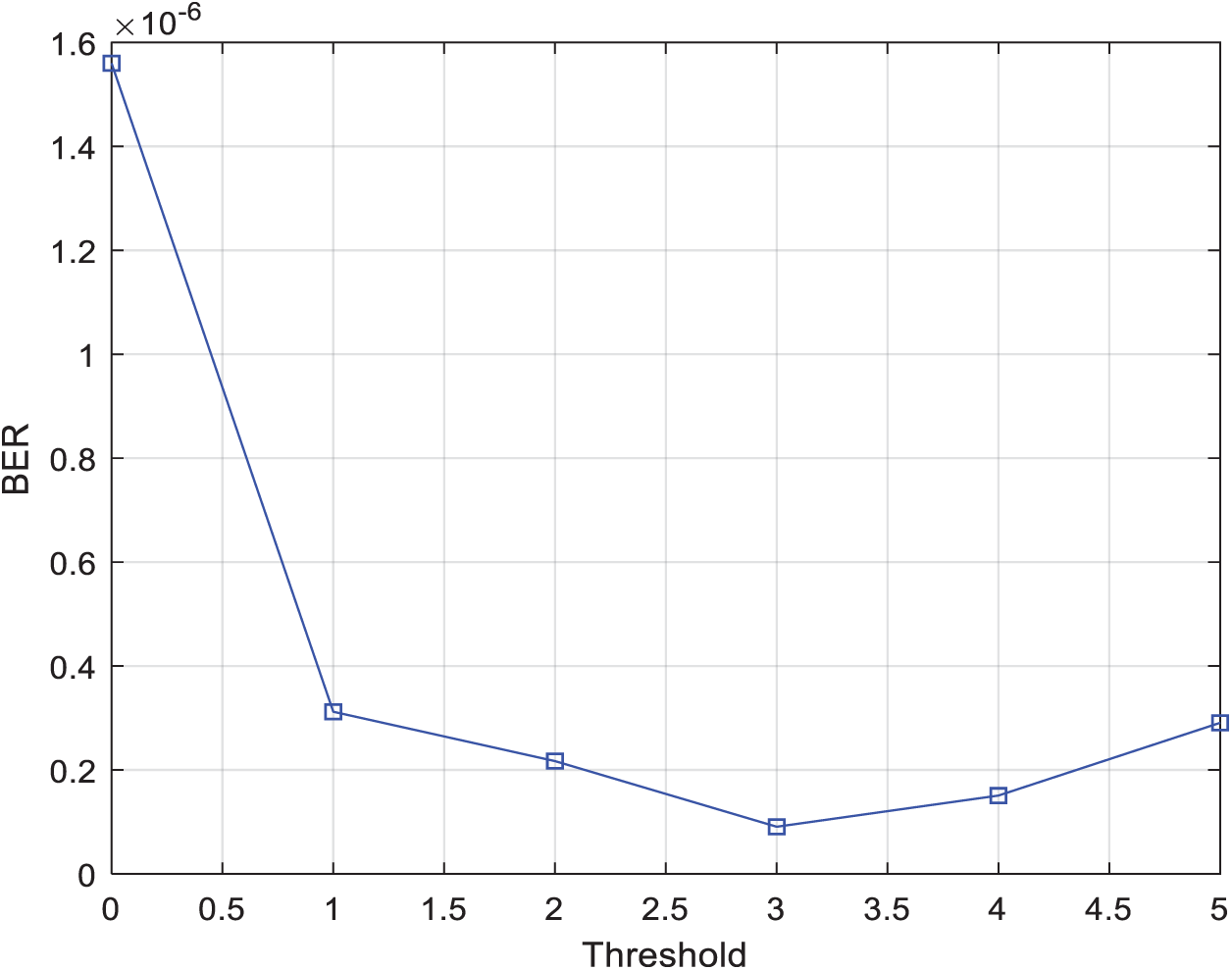
Figure 5: BER vs. Threshold for two-relay selection techniques using the two-phase protocol with 4-QAM modulation, N = 4, and SNR = 20 dB

Correspondingly, Fig. 6 shows the BER performance with respect to the SNR of our suggested dual-relay selection strategy in the presence of six relay-nodes (N = 6) using 4-QAM modulation under different threshold values, i.e., threshold increases gradually from zero to five. Again, this figure clearly shows that the best BER performance is obtained when the threshold value is between two and three.

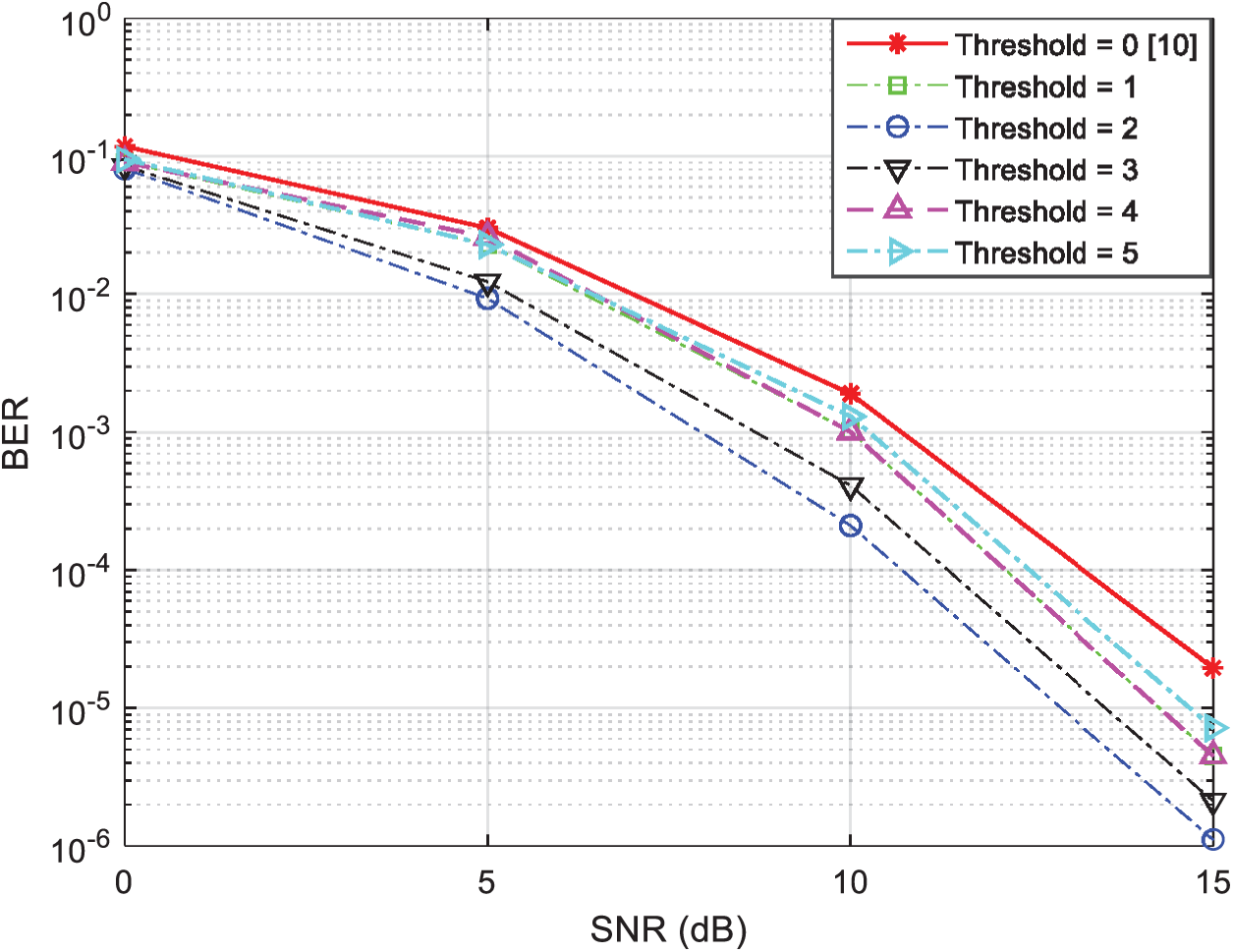
Figure 6: BER vs. SNR for two-relay selection techniques using the two-phase relaying protocol with 4-QAM modulation and N = 6

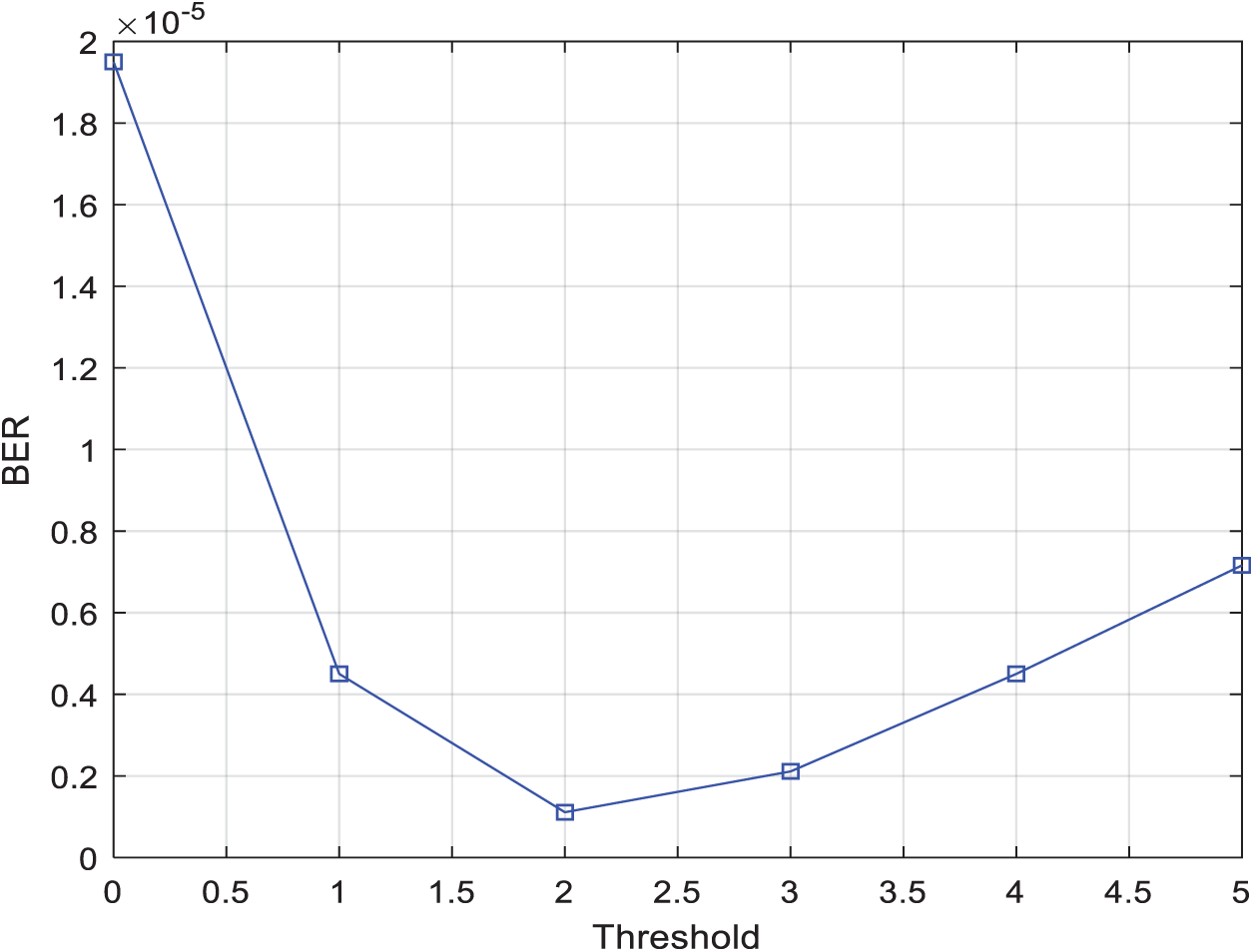
Figure 7: BER vs. Threshold for two relay selection techniques using the two-phase protocol with 4-QAM modulation, N = 6, and SNR = 15 dB

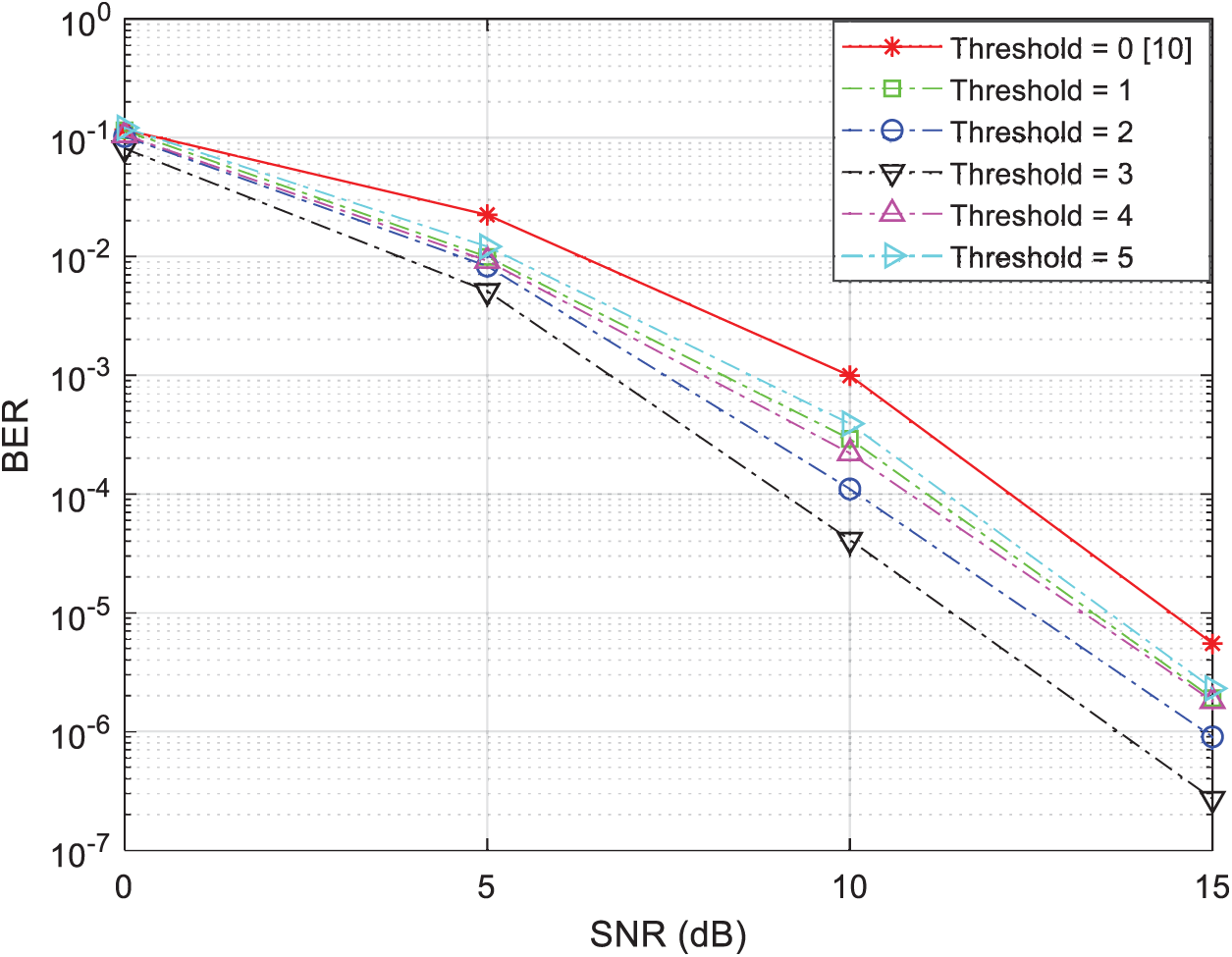
Figure 8: BER vs. SNR for two-relay selection techniques using the two-phase relaying protocol with 4-QAM modulation and N = 8

In Fig. 7, we show the BER results of our suggested relay selection strategy in the presence of six relay-nodes using 4-QAM modulation with SNR set to 15 dB under different threshold values. This figure clearly sustains our findings in Fig. 6 before.

In Fig. 8 we present the BER performance of our suggested relay selection strategy in the presence of eight relay-nodes (N = 8) using 4-QAM modulation under different threshold values, i.e., threshold increases gradually from zero to five. Again, the results obtained from this figure obviously concludes that the best performance is obtained when the threshold value is between two and three.

Fig. 9 shows the BER performance results of our suggested relay selection strategy using eight relay nodes with 4-QAM modulation and SNR set to 15 dB under different threshold values. This figure clearly sustains our findings in Fig. 8.

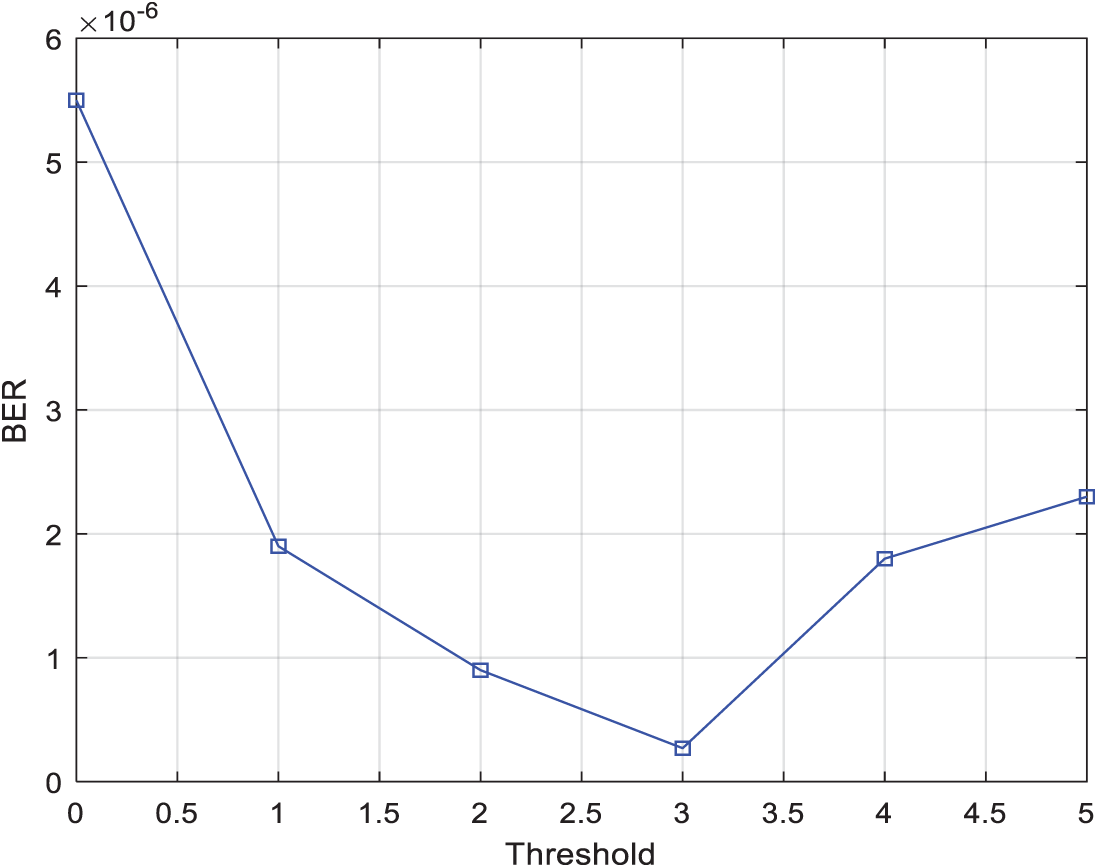
Figure 9: BER vs. Threshold for two-relay selection techniques using the two-phase protocol with 4-QAM modulation, N = 8, and SNR = 15 dB

In Fig. 10, we consider a wireless cooperative communication network with four, N = 4, relay nodes and no direct links between the two terminals. In Fig. 10, the performance in terms of BER at the first terminal is shown with respect to the SNR and with a bit rate of one bit per channel use (bpcu) where the introduced strategy that utilizes the two-phase relaying protocol using symbols drawn from 4-QAM modulation has been compared with the dual-relay selection strategy that utilizes the two- and the three-phase relaying protocol available in [11] using 4-QAM and 8-QAM constellation, respectively and the optimal single-relay selection strategy that utilizes the two- and the three-phase relaying protocol available in [12] using 4-QAM and 8-QAM constellation, respectively, and the dual-relay selection strategy that utilizes the two- and the three-phase relaying protocol available in [13] using 4-QAM and 8-QAM constellation. From Fig. 10, we can clearly see that the strategy that utilizes the two-phase relaying protocol outperforms those which utilize the three-phase relaying protocol due to the increase of the symbol rate [14]. We can also notice that the introduced strategy outperforms the current state-of-the-art two- and three-phase, single and dual-relay selection strategies by at least 2 dB compared to the work presented in [13], 3 dB compared to results provided in [12], and 8 dB compared to method proposed in [11]. The simulation results show that the proposed strategy outperforms the recent strategies as explained latter. At the same time, we have proved that the simulation results are very close to the theoretical analysis regarding to the proposed strategy as shown in Fig. 3 and given by the mathematical expression in (22). Therefore, we have proved using analytical and simulated results that the performance of the proposed strategy outperforms the recent strategies. Hence, we can observe the advantage of using the proposed strategy against the state-of-the-art strategies according to both analytical and simulated results.

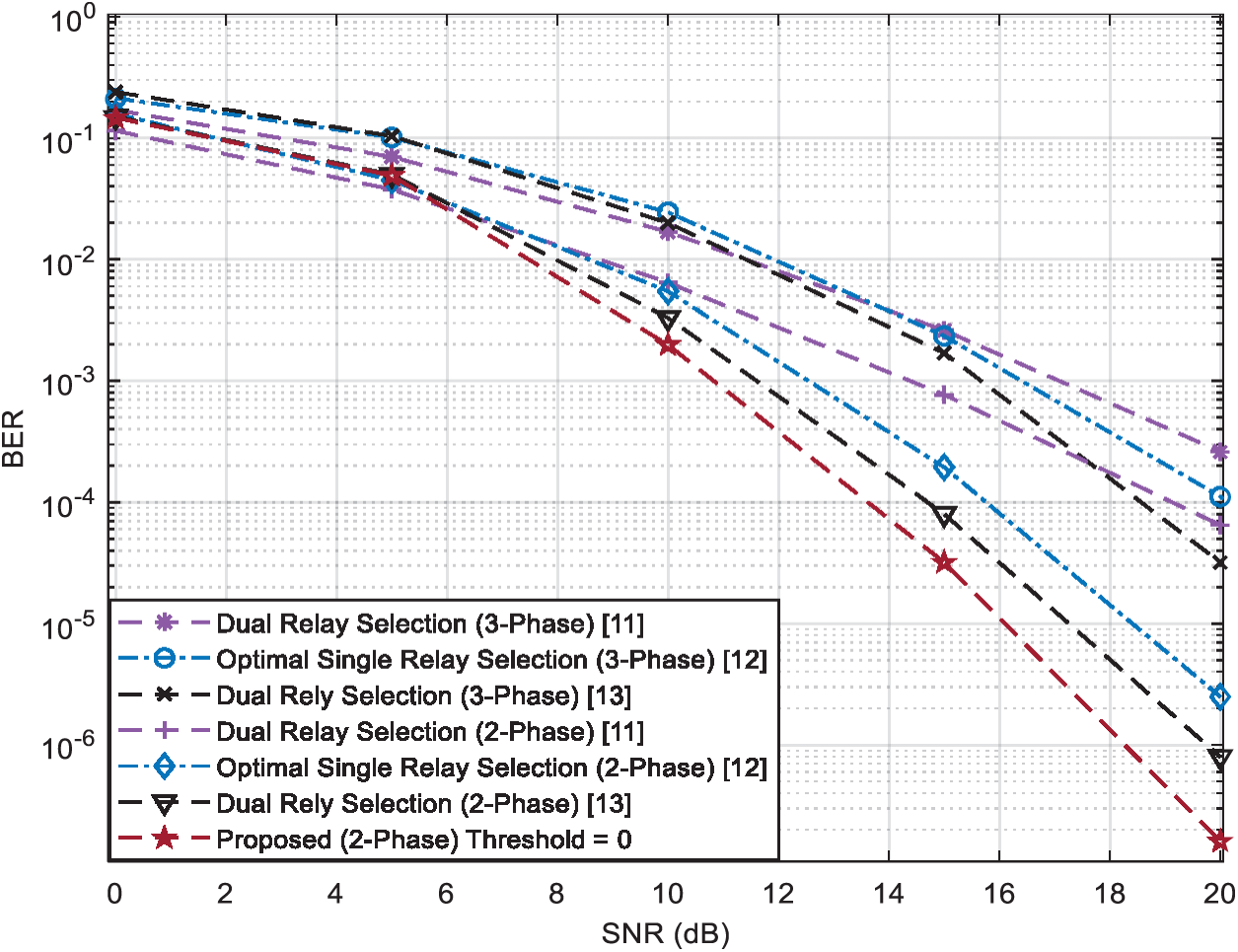
Figure 10: BER vs. SNR for several single and dual-relay selection strategies using the two and three-phase relaying protocol with a rate of 1 bpcu and N = 4

5  Conclusion

In this article, we introduced a new two-relay selection strategy using the two-phase protocol based on STC. Furthermore, this strategy is employing a digital network coding scheme at the selected relay-nodes in order to merge the symbols into one symbol with the same constellation to reduce the power consumption of sending redundant information. By doing this, additional coding gain is achieved. In addition to that, we have proposed the analytical BER of this novel strategy and compared it with our simulation results in order to validate the proposed BER expressions. We have further proved that the performance of our new strategy outperforms the most recent strategies.

Funding Statement: This work was supported by College of Engineering and Technology, the American University of the Middle East, Kuwait. Homepage: https://www.aum.edu.kw.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  P. Larsson, N. Johansson and K. Sunell, “Coded bi-directional relaying,” in Proc. IEEE Vehicular Technology Conf., Melbourne, VIC, Australia, vol. 2, pp. 851–855, 2006. [Google Scholar]

 2.  S. Alabed, J. Paredes and A. B. Gershman, “A simple distributed space-time coded strategy for two-way relay channels,” IEEE Transactions on Wireless Communications, vol. 11, no. 4, pp. 1260–1265, 2012. [Google Scholar]

 3.  S. Alabed, M. Pesavento and A. Klein, “Non-coherent distributed space-time coding techniques for two-way wireless relay networks,” EURASIP Special Issue on Sensor Array Processing, vol. 93, no. 12, pp. 3371–3381, 2013. [Google Scholar]

 4.  S. Alabed and M. Pesavento, “A simple distributed differential transmit beamforming technique for two-way wireless relay networks,” in 16th Int. IEEE/ITG Workshop on Smart Antennas, Dresden, Germany, pp. 243–247, 2012. [Google Scholar]

 5.  A. Schad, S. Alabed, H. Degenhardt and M. Pesavento, “Bi-directional differential beamforming for multi-antenna relaying,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, South Brisbane, QLD, Australia, pp. 2884–2888, 2015. [Google Scholar]

 6.  S. Alabed, M. Pesavento and A. Klein, “Relay selection based space-time coding for two-way wireless relay networks using digital network coding,” in Proc. of the 10th Int. Symp. on Wireless Communication Systems, Ilmenau, Germany, 2013. [Google Scholar]

 7.  S. Zhou, J. Xu and Z. Niu, “Interference-aware relay selection technique for two-hop relay networks with multiple source-destination pairs,” IEEE Trans. Veh. Technol., vol. 62, no. 5, pp. 2327–2338, 2013. [Google Scholar]

 8.  G. Cai, Y. Fang, G. Han, J. Xu and G. Chen, “Design and analysis of relay-selection strategies for two-way relay network-coded DCSK systems,” IEEE Trans. Veh. Technol., vol. 67, no. 2, pp. 1–13, 2017. [Google Scholar]

 9.  T. Nguyen, T. Minh, P. Tran, M. Voznak, T. Duy et al., “Performance enhancement for energy harvesting based two-way relay protocols in wireless ad-hoc networks with partial and full relay selection methods,” Ad Hoc Networks, vol. 84, no. 4, pp. 178–187, 2019. [Google Scholar]

10. Y. Li, R. Louie and B. Vucetic, “Relay selection with network coding in two-way relay channels,” IEEE Transactions on Vehicular Technology, vol. 59, no. 9, pp. 4489–4499, 2010. [Google Scholar]

11. G. Chen, Z. Tian, Y. Gong, Z. Chen and J. Chambers, “Max-ratio relay selection in secure buffer-aided cooperative wireless networks,” IEEE Trans. on Info. Forensics and Security, vol. 9, no. 4, pp. 719–729, 2014. [Google Scholar]

12. S. Atapattu, Y. Jing, H. Jiang and C. Tellambura, “Relay selection schemes and performance analysis approximations for two-way networks,” IEEE Trans. Commun., vol. 61, no. 3, pp. 987–998, 2012. [Google Scholar]

13. S. Alabed, I. Maaz and M. Al-Rabayah, “Improved two-way double-relay selection technique for cooperative wireless communications,” EURASIP Journal on Wireless Communications and Networking, vol. 2021, no. 57, 2021. https://doi.org/10.1186/s13638-020-018467. [Google Scholar]

14. S. Alabed, “Performance analysis of bi-directional relay selection strategy for wireless cooperative communications,” EURASIP Journal on Wireless Communications and Networking, vol. 2019, no. 97, 2019. https://doi.org/10.1186/s13638-019-1417-1. [Google Scholar]

15. D. Taleb, S. Alabed and M. Pesavento, “Optimal general-rank transmit beamforming technique for multicasting service in modern wireless networks using STTC,” in Proc. of the 19th Int. IEEE/ITG Workshop on Smart Antennas, Ilmenau, Germany, 2015. [Google Scholar]

16. X. Wen, K. Law, S. Alabed and M. Pesavento, “Rank-two beamforming for single-group multicasting networks using OSTBC,” in IEEE 7th Sensor Array and Multichannel Signal Processing Workshop, Hoboken, NJ, USA, Stevens Institute of Technology, June 17–20, pp. 65–68, 2012. [Google Scholar]

17. S. Alabed, “Performance analysis of differential beamforming in decentralized networks,” IEEE Canada, Canadian Journal of Electrical and Computer Engineering, vol. 8, no. 3, pp. 1692, 2020. [Google Scholar]

18. M. Simon and M. Alouini, Digital Communication Over Fading Channels: A Unified Approach to Performance Analysis. Hoboken, New Jersey, United States: Wiley, 2002. [Google Scholar]

19. H. A. Ramli, “A study on packet scheduling algorithms for healthcare contents over fifth generation (5G) mobile cellular network,” International Journal of Electronics and Telecommunications, vol. 66, no. 4, pp. 729–739, 2020. [Google Scholar]

20. M. M. Nasralla, “A hybrid downlink scheduling approach for multi-traffic classes in LTE wireless systems,” IEEE Access, vol. 8, pp. 82173–82186, 2020. [Google Scholar]

21. M. M. Nasralla, N. Khan and M. G. Martini, “Content-aware downlink scheduling for LTE wireless systems: A survey and performance comparison of key approaches,” Computer Communications, vol. 130, pp. 78–100, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.