Computers, Materials & Continua DOI:10.32604/cmc.2021.017968
Article

Probabilistic and Hierarchical Quantum Information Splitting Based on the Non-Maximally Entangled Cluster State

Gang Xu1, Rui-Ting Shan2, Xiu-Bo Chen2, Mianxiong Dong3 and Yu-Ling Chen4,*

1School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
2Information Security Center, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
3Muroran Institution of Technology, Muroran, 050-8585, Japan
4State Key Laboratory of Public Big Data, College of Computer Science and Technology, Guizhou University, Guiyang, 550025, China
*Corresponding Author: Yu-Ling Chen. Email: Ylchen3@gzu.edu.cn
Received: 19 February 2021; Accepted: 31 March 2021

Abstract: With the emergence of classical communication security problems, quantum communication has been studied more extensively. In this paper, a novel probabilistic hierarchical quantum information splitting protocol is designed by using a non-maximally entangled four-qubit cluster state. Firstly, the sender Alice splits and teleports an arbitrary one-qubit secret state invisibly to three remote agents Bob, Charlie, and David. One agent David is in high grade, the other two agents Bob and Charlie are in low grade. Secondly, the receiver in high grade needs the assistance of one agent in low grade, while the receiver in low grade needs the aid of all agents. While introducing an ancillary qubit, the receiver’s state can be inferred from the POVM measurement result of the ancillary qubit. Finally, with the help of other agents, the receiver can recover the secret state probabilistically by performing certain unitary operation on his own qubit. In addition, the security of the protocol under eavesdropping attacks is analyzed. In this proposed protocol, the agents need only single-qubit measurements to achieve probabilistic hierarchical quantum information splitting, which has appealing advantages in actual experiments. Such a probabilistic hierarchical quantum information splitting protocol hierarchical is expected to be more practical in multipartite quantum cryptography.

Keywords: Cluster state; hierarchical quantum information splitting; probabilistic; non-maximally entangled states

1  Introduction

Quantum information splitting, one of the core contents of quantum information science, means that secret information is split in some way and each sub-secret is managed by different agents. Only legal agents can work together to recover secret information. The concept of quantum information splitting and quantum state sharing [1,2] was first proposed by Hillery, Buzek & Berthiaume, who used the three-particle GHZ state and four-particle GHZ state to implement the information splitting scheme. Later, for the first time Cleve, Gottesman & Lo proposed (k, n) threshold quantum secret sharing scheme to distribute information. There are n agents in Gottesman’s scheme, and at least k agents are needed to recover the secret state. Quantum information splitting not only achieves absolute security in quantum communication, but also plays an extremely important role in protecting quantum information in the related region [3–8].

Quantum information splitting is possible if using a non-maximally entangled quantum source. In this condition, the success rate is probabilistic. Hence, this kind of protocol is referred to as probabilistic quantum information splitting protocol (PQIS). In the references [9–12], there have been some PQIS schemes with non-maximally entangled states. Besides, Gottesman pointed out a more general QIS protocol [13] in 2000, known as hierarchical quantum information splitting protocol (HQIS), which includes a hierarchy among agents in QIS protocol. That is to say, there is a hierarchy of the authorities for different agents. It has been shown that shares of the secret should be combined to recover the original secret state. In the references [14–16], Wang et al. had taken use of the |χ⟩ state, graph state and six-photon cluster state to implement HQIS. However, to recover the secret state, the receiver has to do high-dimensional projective measurement, which leads to complex experimental realization.

Researchers have focused on the diversity of feasible entangled states, which could realize probabilistic HQIS protocol, such as GHZ states [17], W states [18–19], six-qubit states [20], and so on. However, those states are maximally entangled states that are widely studied, while non-maximally entangled states that have relatively little research are more suitable and practical to achieve the protocol. In 2001, Raussendorf et al. [21] had proven a great use of a non-maximally four-qubit cluster state |C⟩1234=a(|0000⟩+|0110⟩)1234+b(|1001⟩−|1111⟩)1234 in one-way quantum computation, which is used as the quantum source in the paper. It has shown that this cluster state can be used for perfect teleportation and superdense coding [22–23]. The non-maximally entanglement of the cluster state enables the receiver to recover the secret state successfully with a certain probability. The symmetry of cluster states is conducive to the hierarchy of the protocol.

In this work, a novel probabilistic hierarchical quantum information splitting protocol (probabilistic HQIS) is designed to teleport an arbitrary one-qubit secret state |δ⟩x via a four-qubit non-maximally entangled cluster state |C⟩1234=a(|0000⟩+|0110⟩)1234+b(|1001⟩−|1111⟩)1234, where a and b are complex numbers. Each subscript refers to a particle which is owned by a certain agent. In the multiparty protocol, there is a sender (secret splitter) Alice, one agent Bob in high grade and two agents Charlie, David in low grade. The agents have different authorities to recover the secret state, i.e., their powers are hierarchical while recovering the original secret state. The agent in high grade needs the assistance of only one agent in low grade, while the agent in low grade needs the cooperation of all agents.

In the protocol, something needs to be noticed. First, the shared quantum source and secret state are both uncertain and probabilistic. So, the receiver can only recover the secret state probabilistically under the cooperation of other agents. Apart from sender Alice’s Bell measurement, the other agents Bob, Charlie and David only need to perform single-qubit measurement on his own qubit while one of them could recover the secret state. Second, for the sake of the secret state’s recovery, the receiver often needs to entangle one or more auxiliary qubits with the receiver’s qubits in the probabilistic schemes. In the protocol, after introducing one auxiliary qubit m, the receiver can infer the state of his own qubit through the measurement results of the auxiliary qubit m. As a result, the receiver could recover the secret state by performing appropriate unitary operations on his own particle. Finally, it is important to note that the states of qubit m are not orthogonal. Based on non-distinguishability of non-orthogonal states, if the two quantum states are nonorthogonal, they cannot be completely precisely distinguished. However, there exists a more general type of measurement than the projective measurements, which is known as positive operator-valued measure (POVM). POVM provides a useful way to distinguish between nonorthogonal states. Hence, it’s feasible and essential to introduce POVM to measure qubit m.

2  Probabilistic and Hierarchical Quantum Information Splitting via a Non-Maximally Entangled Four-Qubit Cluster State

We assume the particle 1, 2, 3 and 4 are entangled via a four-qubit cluster state owned by Alice, Bob, Charlie and David separately. Without loss of generality, if the high grade’s agent David wants to recover the original secret state, then he needs the aid of one agent in low grade. If Bob or Charlie informs David the measurement result of his own qubit through the classical channel, David would infer the state of his qubit by POVM and recover the secret state through appropriate unitary operations. However, when the low grade’s agent, let’s say Bob, he should obtain the cooperation of all other agents to recover the secret. Only if both Charlie and David informs their measurement results to Bob, can Bob recover the secret state through unitary operations on his own qubit.

Assume that the sender Alice wants to teleport an arbitrary one-qubit secret state

|δ⟩x=α|0⟩x+β|1⟩x(1)

where the coefficients α and β are both arbitrary complex numbers satisfying the normalized condition |α|2+|β|2=1. The four agents share a quantum source which is a non-maximally entangled four-qubit cluster state

|C⟩1234=a(|0000⟩+|0110⟩)1234+b(|1001⟩−|1111⟩)1234(2)

where the coefficients a and b are both arbitrary complex numbers satisfying |a|2+|b|2=1.

As shown in Fig. 1, Alice owns the secret qubit x and particle 1. Before teleporting the secret state, Alice splits the secret information into three pieces and distributes each piece to different agents so that any agent cannot recover the secret state alone.

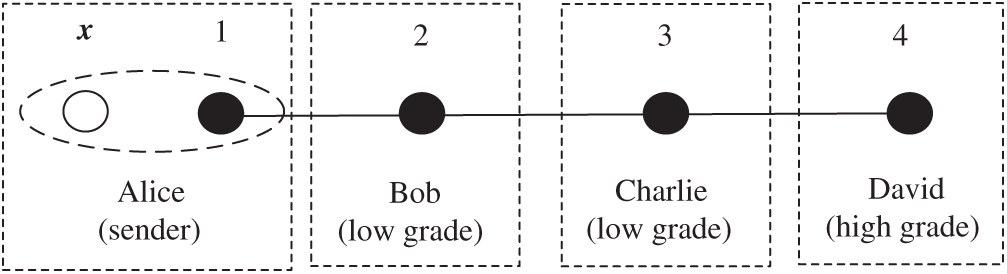
Figure 1: Four agents and their own particles, authorities

Then the whole system can be expressed as

|ϕ⟩x1234=|δ⟩x⊗|C⟩1234=αa(|00000⟩+|00110⟩)x1234+αb(|01001⟩−|01111⟩)x1234+βa(|10000⟩+|10110⟩)x1234+βb(|11001⟩−|11111⟩)x1234(3)

Now, Alice needs to perform a joint measurement on her particles x and 1 by using {Φ+,Φ−,Ψ+,Ψ−}, and then broadcasts the measurement result to every agent. The four states of Bell-basis can be given by

|Φ±⟩=12(|00⟩±|11⟩)(4)

|Ψ±⟩=12(|01⟩±|10⟩)(5)

After Alice informs her measurement result, the states of the other three would collapse into the following four possible outcomes:

x1⟨Φ±|ϕ⟩=12[αa(|000⟩+|110⟩)±βb(|001⟩−|111⟩)]234(6)

x1⟨Ψ±|ϕ⟩=12[αb(|001⟩−|111⟩)±βa(|000⟩+|110⟩)]234(7)

If the measurement result of Alice is |Φ+⟩=12(|00⟩+|11⟩), then the system would collapse into

x1⟨Φ+|ϕ⟩=12[αa(|000⟩+|110⟩)+βb(|001⟩−|111⟩)]234(8)

It’s important to note that only the authorized agent can recover the secret state |δ⟩x by a suitable local unitary operation on his own particle. According to the grade of the receiver, let us now consider the two cases of recovering the secret state.

2.1 High Grade’s Agent Recovers the Secret State

In the protocol, there is only one agent David in high grade. Suppose David is the receiver, we rewrite x1⟨Φ±|ϕ⟩ and x1⟨Ψ±|ϕ⟩ as follows:

x1〈ϕ±|ϕ〉=12[αa(〈|000+〈|110)±βb(〈|001−〈|111)]234=12[aα(〈|00+〈|11)23〈|04±bβ(〈|00−〈|11)23〈|14]=12[〈|0023(aα〈|0±bβ〈|1)4+〈|1123(aα〈|0∓bβ〈|1)4] (9)

x1〈ψ±|ϕ〉=12[αb(〈|001−〈|111)±βa(〈|000+〈|110)]234=12[bα(〈|00−〈|11)23〈|14±aβ(〈|00+〈|11)23〈|04]=12[〈|0023(bα〈|1±aβ〈|0)4−〈|1123(bα〈|1∓aβ〈|0)4] (10)

Next, Bob or Charlie needs to perform Z-basis measurement on their particle. No matter what Alice’s measurement result is, the measurement results of Bob and Charlie are always correlated. So only one agent is needed to perform single-qubit measurement. Hence, David can recover the secret state by certain unitary operation with the help of Bob or Charlie.

Suppose Alice and Bob’s measurement results are |ϕ1⟩4=12(aα|0⟩+bβ|1⟩)4 and |0⟩2, then the state of the whole system would collapse to

|ϕ1⟩4=12(aα|0⟩+bβ|1⟩)4(11)

At last, David performs a unitary operation Uj=I on his particle 4 so as to recover the original secret state, where Uj∈{I,σx,σz,iσy}, I is the identity operator, and σx,σy,σz are Pauli operators. As shown in Tab. 1, the corresponding unitary operations are listed.

Table 1: David’s unitary operations needed according to Alice’s and Bob’s measurement results

However, the state obtained by David is slightly different from the original secret state |δ⟩x=α|0⟩x+β|1⟩x. Therefore, David needs to introduce an auxiliary qubit in the initial state |0⟩m to help recover the original secret state. Now let us assume the state of the particle 4 is |ϕ1⟩4=12(aα|0⟩+bβ|1⟩)4, after the auxiliary qubit’s incorporation, the state of the particle 4 and m in David’s position is

|ϕ⟩4m=|ϕ1⟩4|0⟩m=12(aα|00⟩+bβ|10⟩)4m(12)

Then David needs to perform a controlled-NOT operation C4m on |ϕ⟩4m, in which particle 4 is the control qubit and particle m is the target qubit.

|ϕ|′⟩4m=C4m|ϕ⟩4m=C4m|ϕ1⟩4|0⟩m=12(aα|00⟩+bβ|11⟩)4m=122(|A⟩4⊗|B⟩m+|C⟩4⊗|D⟩m)(13)

where |A⟩4=α|0⟩4+β|1⟩4, |B⟩m=a|0⟩m+b|1⟩m, |C⟩4=α|0⟩4−b|1⟩4, |D⟩m=a|0⟩m−b|1⟩m. Especially, |A⟩4 and |C⟩4 are the forms of the secret state. If David knows the state of particle m, the state of particle 4 would be determined and David could perform appropriate unitary operations on particle 4 to recover the secret state. However, it is obvious that the states |B⟩m and |D⟩m are not orthogonal in fact.

Hence, they cannot be differentiated deterministically by usual projection measurement. To distinguish the two states of particle m with the certain success probability, David needs to perform an POVM on the auxiliary particle m. POVM provides the ability to distinguish non-orthogonal states. Just as its name implies, POVM consists of a set of positive operators denoted by O1, O2 and O3, where the subscripts are corresponding to three possible measurement results of particle m, respectively. The sum of the three positive operators should always be I. We denote [24]

O1=1ω|M1⟩⟨M1|,O2=1ω|M2⟩⟨M2|,O3=I−O2−O3(14)

where ω is a coefficient related with a and b

|M1⟩=1ε(1a|0⟩m+1b|1⟩m),|M2⟩=1ε(1a|0⟩m−1b|1⟩m),ε=1a2+1b2=12a2b2(15)

Note that O3 has to be a positive operator. According to the definition of the positive operator, the positive operator O3 should satisfy

⟨ψ|O3|ψ⟩≥0(16)

for all |ψ⟩∈C2. If the measurement result of particle m is O3, then David would not obtain any information about the state of the particle m. Only when the measurement result of particle m is O1 or O2, does David can successfully determine the state of the particle m is |B⟩m or |D⟩m respectively. At last, after applying POVM on the particle m, David can obtain the success probability of O1, O2 and O3.

The probabilities of obtaining the value of O1 and O2 are as follow:

Pr(O1)=4m⟨ϕ|′|O1|ϕ|′⟩4m=1(22)2m⟨B|O1|B⟩m=12ωε(17)

Similarly, Pr(O2) is equal to Pr(O1). And we can infer that

Pr(O3)=1−12ωε−12ωε=1−4ωε(18)

As shown above, David can obtain the state of qubit m with the probability 12ωε=a2b2ω via the value of O1 or O2. Based on the Eq. (18), the operator O3 could not identify the state of qubit m with the probability 1−4ωε.

Once the state of particle m is measured, the state of particle 4 is also determined. Consequently, David can get the secret state through appropriate local unitary operations on his particle 4. From Eq. (17), it is obvious that the state of David’s particle 4 is |A⟩4=α|0⟩4+β|1⟩4 with the probability a2b2ω when the state of particle m is |B⟩m=a|0⟩m+b|1⟩m. The state of David’s particle 4 is |C⟩4=α|0⟩4−b|1⟩4 with the probability a2b2ω when the state of particle m is |D⟩m=a|0⟩m−b|1⟩m. However, as proposed before, David cannot determine the state of particle m exactly when the measurement result is O3. In this situation, David cannot recover the secret state successfully.

Up to now, we only consider the success probability when Alice and Bob’s measurement results are |Φ+⟩=12(|00⟩+|11⟩)x1 and |0⟩2. However, the measurement result of Alice can be one of the other three. Bob’s measurement result can be the other. Tab. 2 shows all possible measurement results and their success probability.

Table 2: The success probability of the corresponding measurement results via POVM

2.2 Low Grade’s Agent Recovers the Secret State

Now, we consider the agent in low grade (Bob or Charlie) to recover the secret state. In this case, the agent in low grade needs the cooperation of all agents. Since Bob and Charlie have the same authority, they have the same recovery process. What follows is the process of Bob’s recovering the secret state |δ⟩x. We rewrite x1⟨Φ±|ϕ⟩ and x1⟨Ψ±|ϕ⟩ in the X-basis as follows:

x1〈ϕ±|ϕ〉=12[aα(|+++〉+|++−〉+|−−+〉+|−−−〉)±bβ(|+−+〉+|−++〉−|+−−〉−|−+−〉)]234=12[(aα|+〉±bβ|−〉)2|++〉34+(aα|+〉∓bβ|−〉)2|+−〉34+(aα|−〉±bβ|+〉)2|−+〉34+(aα|−〉∓bβ|+〉)2|−−〉34] (19)

x1〈ψ±|ϕ〉=12[bα(|+−+〉+|−++〉−|+−−〉−|−+−〉)±aβ(|+++〉+|++−〉+|−−+〉+|−−−〉)]234=12[(bα|+〉±aβ|−〉)2|−+〉34+(−bα|+〉±aβ|−〉)2|−−〉34+(bα|−〉±aβ|+〉)2|++〉34+(−bα|−〉±aβ|+〉)2|+−〉34] (20)

To help Bob recover the original secret state, Charlie and David need to measure their own particle in the X-basis. Then Bob can recover the secret state by certain unitary operation Uj, where Oj∈{I,σx,σz,iσy,H}. Ignoring the global factor, all possible measurement results of Charlie and David, Bob’s operation are listed in Tab. 3.

Table 3: Bob’s unitary operations needed according to others’ measurement results

As shown in Tab. 3, after performing operations on Bob’s particle 2, the states of the particle 2 can be aα|0⟩2+bβ|1⟩2 and bα|0⟩2+aβ|1⟩2. (Ignoring the global factor)

Just as proposed in case 1, Bob needs to introduce an auxiliary qubit m in state |0⟩ to recover the original secret state |δ⟩x=α|0⟩x+β|1⟩x. Assume the state of the particle 2 is |ϕ1⟩2=aα|0⟩2+bβ|1⟩2, after the qubit m’s incorporation, the state of the particle 2 and m in Bob’s position is

|ϕ⟩2m=|ϕ1⟩2|0⟩m=aα|00⟩2m+bβ|10⟩2m(21)

Then, Bob needs to perform a CNOT operation C2m on |ϕ⟩2m, in which particle 2 is the control qubit.

|ϕ|′⟩2m=C2m|ϕ⟩2m=C2m|ϕ1⟩2|0⟩m=aα|00⟩2m+bβ|11⟩2m=12(|A⟩2⊗|B⟩m+|C⟩2⊗|D⟩m)(22)

where |A⟩2=α|0⟩2+β|1⟩2, |B⟩m=a|0⟩m+b|1⟩m, |C⟩2=α|0⟩2−b|1⟩2, |D⟩m=a|0⟩m−b|1⟩m. As same as the situation in case 1, Bob performs POVM on particle m to determine the state of his own particle 2 so that Bob could perform appropriate unitary operations on particle 2 to recover the secret state. In summary, all possible measurement results of Alice’s particle (x, 1), Charlie’s particle 3, David’s particle 4, POVM’s positive operations and their corresponding success probability are listed in Tab. 4.

Because the permutation of Bob’s particle 2 and Charlie’s particle 3 cannot change the quantum source, Bob and Charlie are in |C⟩1234=a(|0000⟩+|0110⟩)1234+b(|1001⟩−|1111⟩)1234 the same low grade. Charlie has exactly the same authority as Bob. Without loss of generality, while assigning Charlie to recover the original secret state, the process and success probability are also the same as Bob’s.

Table 4: The success probability of the corresponding measurement results via POVM

3  Security Analysis

Assume there is an attacker named Eve, he attempts to steal the secret information from the four legitimate agents Alice, Bob, Charlie and David. So, there are two ways of eavesdropping: intercept-measure-resend attack and entanglement attack.

For the former, Eve would intercept and measure the qubits sent by Alice in a random basis. Then Eve resends fake qubits to the other legitimate agents to disturb the secret’s recovery. But Eve would introduce abnormal error rates of the process inevitably. Hence, the intercept-measure-resend attack can be detected, and the teleportation of the secret state should be aborted. If the quantum channel is noiseless, then the error rate is equal to 0. In this scenario, the state of Eve’s system and the original system is a simply separable state, or product state, which means there is neither quantum nor classical correlation between these two systems. Therefore, Eve cannot gain any information from the original quantum state.

For the latter, during the distribution of particle 2, 3, 4, Eve entangles an ancillary qubit e with the quantum source |C⟩1234 during the particle distribution process. Assume Eve’s attack happens, the detection process of Eve’s attack is described briefly as follows. Firstly, Alice performs a single-qubit measurement on her particle 1. The measurement basis is randomly selected, that is, the measurement basis of particle 1 can be {|+⟩,|−⟩} or {|0⟩,|1⟩}. Secondly, Alice informs the other three agents Bob, Charlie and David of her measurement basis across the classical channel. Thirdly, each of the other three agents performs a single-qubit measurement on his particle by using Alice’s measurement basis. They also inform the other agents of their measurement results. At last, compare their measurement results publicly. Their measurement results would be strongly correlated. If outside attack exists, these results cannot correlate strongly because of the disturbances caused by Eve. So, the current quantum source is not safe for teleporting the secret state. Obviously, outside attack can be detected and the protocol is safe from outside attack.

4  Conclusion

In summary, there are some merits in the paper. First of all, the shared quantum source, a non-maximally entangled four-qubit cluster state, is robust against quantum decoherence. It’s obvious that the generation and preservation of four-qubit non-maximally entangled states is easier than maximally six-qubit states, which has an attractive advantage in the experimental realization. The symmetry of cluster states helps the expansion of HQIS protocol. Then the secret state is arbitrary, which means the strong applicability and generality of the proposed protocol. What’s more, each agent has different grades so that there exists a hierarchy in the protocol. The receiver cannot recover the secret state successfully only if the cooperation of the other agents. Together with the non-maximally quantum source, the receiver could recover the secret state in a certain success probability. In other words, non-maximally quantum source and hierarchy of the protocol help expand the research scope of usual QIS protocols. In addition, only by single-qubit measurements can the receiver recover the secret state, which brings convenience to experimental realization.

Funding Statement: This work is supported by the NSFC (Grant Nos. 92046001, 61571024, 61671087, 61962009, 61971021), the Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant Nos. 2018BDKFJJ018, 2019BDKFJJ010, 2019BDKFJJ014), the Open Research Project of the State Key Laboratory of Media Convergence and Communication, Communication University of China, China (Grant No. SKLMCC2020KF006), the High-quality and Cutting-edge Disciplines Construction Project for Universities in Beijing (Internet Information, Communication University of China), and the Fundamental Research Funds for the Central Universities (Grant No. 2019XD-A02), the Scientific Research Foundation of North China University of Technology, the Fundamental Research Funds for the Beijing Municipal Education Commission and JSPS KAKENHI Grant Number JP20F20080.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Hillery, V. Bužek and A. Berthiaume, “Quantum secret sharing,” Physical Review A, vol. 59, no. 3, pp. 1829–1834, 1999. [Google Scholar]

 2.  R. Cleve, D. Gottesman and H. K. Lo, “How to share a quantum secret,” Physical Review Letters, vol. 83, no. 3, pp. 648–651, 1999. [Google Scholar]

 3.  G. Xu, K. Xiao, Z. Li, X. Niu and M. Ryan, “Controlled secure direct communication protocol via the three-qubit partially entangled set of states,” Computers, Materials & Continua, vol. 58, no. 3, pp. 809–827, 2019. [Google Scholar]

 4.  Z. Dou, G. Xu, X. Chen and K. Yuan, “Rational non-hierarchical quantum state sharing protocol,” Computers, Materials & Continua, vol. 58, no. 2, pp. 335–347, 2019. [Google Scholar]

 5.  Z. G. Qu, S. Y. Chen and X. J. Wang, “A secure controlled quantum image steganography algorithm,” Quantum Information Processing, vol. 19, no. 380, pp. 1–25, 2020. [Google Scholar]

 6.  Z. Qu, S. Wu, W. Liu and X. Wang, “Analysis and improvement of steganography protocol based on bell states in noise environment,” Computers, Materials & Continua, vol. 59, no. 2, pp. 607–624, 2019. [Google Scholar]

 7.  V. S. Naresh and S. Reddi, “Multiparty quantum key agreement with strong fairness property,” Computer Systems Science and Engineering, vol. 35, no. 6, pp. 457–465, 2020. [Google Scholar]

 8.  X. B. Chen, Y. R. Sun, G. Xu and Y. X. Yang, “Quantum homomorphic encryption scheme with flexible number of evaluator based on (k, n)-threshold quantum state sharing,” Information Sciences, vol. 501, no. 1, pp. 172–181, 2019. [Google Scholar]

 9.  G. Gordon and G. Rigolin, “Generalized quantum-state sharing,” Physical Review A, vol. 73, no. 6, pp. 062316, 2006. [Google Scholar]

10. C. M. Bai and Y. M. Li, “Probabilistic quantum information splitting based on the non-maximally entangled four-qubit state,” International Journal of Theoretical Physics, vol. 55, no. 3, pp. 1658–1667, 2016. [Google Scholar]

11. J. Wu, “Symmetric and probabilistic quantum state sharing via positive operator-valued measure,” International Journal of Theoretical Physics, vol. 49, no. 2, pp. 324–333, 2010. [Google Scholar]

12. J. Y. Peng and Z. W. Mo, “Hierarchical and probabilistic quantum state sharing with a nonmaximally four-qubit cluster state,” International Journal of Quantum Information, vol. 11, no. 1, pp. 1350004, 2013. [Google Scholar]

13. D. Gottesman, “Theory of quantum secret sharing,” Physical Review A, vol. 61, no. 4, pp. 313, 2000. [Google Scholar]

14. X. W. Wang, L. X. Xia, Z. Y. Wang and D. Y. Zhang, “Hierarchical quantum-information splitting,” Optics Communications, vol. 283, no. 6, pp. 1196–1199, 2010. [Google Scholar]

15. X. W. Wang, D. Y. Zhang, S. Q. Tang and L. J. Xie, “Multiparty hierarchical quantum-information splitting,” Journal of Physics B: Atomic, Molecular and Optical Physics, vol. 44, no. 3, pp. 35505, 2011. [Google Scholar]

16. X. W. Wang, D. Y. Zhang, S. Q. Tang, X. G. Zhan and K. M. You, “Hierarchical quantum information splitting with six-photon cluster states,” International Journal of Theoretical Physics, vol. 49, no. 11, pp. 2691–2697, 2010. [Google Scholar]

17. X. H. Li, P. Zhou, C. Y. Li, H. Y. Zhou and F. G. Deng, “Efficient symmetric multiparty quantum state sharing of an arbitrary m-qubit state,” Journal of Physics B: Atomic, Molecular and Optical Physics, vol. 39, no. 8, pp. 1975–1983, 2006. [Google Scholar]

18. H. Yuan, Y. M. Liu, W. Zhang and Z. J. Zhang, “Optimizing resource consumption, operation complexity and efficiency in quantum-state sharing,” Journal of Physics B: Atomic, Molecular and Optical Physics, vol. 41, no. 14, pp. 145506, 2008. [Google Scholar]

19. Z. Y. Xue, P. Dong, Y. M. Yi and Z. L. Cao, “Quantum state sharing via the GHZ state in cavity QED without joint measurement,” International Journal of Quantum Information, vol. 4, no. 5, pp. 749–759, 2006. [Google Scholar]

20. S. Choudhury, S. Muralidharan and P. K. Panigrahi, “Quantum teleportation and state sharing using a genuinely entangled six-qubit state,” Journal of Physics A: Mathematical and Theoretical, vol. 42, no. 11, pp. 115303, 2009. [Google Scholar]

21. R. Raussendorf and H. J. Briegel, “A one-way quantum computer,” Physical Review Letters, vol. 86, no. 22, pp. 5188–5191, 2001. [Google Scholar]

22. S. Muralidharan and P. K. Panigrahi, “Perfect teleportation, quantum-state sharing, and superdense coding through a genuinely entangled five-qubit state,” Physical Review A, vol. 77, no. 3, pp. 1, 2008. [Google Scholar]

23. P. Agrawal and B. Pradhan, “Task-oriented maximally entangled states,” Journal of Physics A: Mathematical and Theoretical, vol. 43, pp. 23, 2010. [Google Scholar]

24. M. Q. Bai and Z. W. Mo, “Hierarchical quantum information splitting with eight-qubit cluster states,” Quantum Information Processing, vol. 12, no. 2, pp. 1053–1064, 2013. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.