DOI:10.32604/cmc.2021.017647
| Computers, Materials & Continua DOI:10.32604/cmc.2021.017647 | |
| Article |
Design of an Efficient Cooperative Spectrum for Intra-Hospital Cognitive Radio Network
1Department of ECE, MNNIT Allahabad, Prayagraj, 211004, India
2Department of ECE, JECRC University, Jaipur, 303905, India
3Computer Science and Engineering, Lovely Professional University, Punjab, 144411, India
4Department of Computer Science, College of Computers and Information Technology, Taif University, P. O. Box 11099, Taif, 21944, Saudi Arabia
5Department of Computer Engineering, College of Computers and Information Technology, Taif University, P. O. Box 11099, Taif, 21944, Saudi Arabia
*Corresponding Author: Aman Singh. Email: amansingh.x@gmail.com
Received: 01 February 2021; Accepted: 05 March 2021
Abstract: This paper presents a new low delay centralized cooperative spectrum sensing method based on dynamic voting rule using multiple threshold level, for indoor hospital environment, where fading and direct path loss both are together responsible for variation in signal strength. In the proposed algorithm, weights of Cognitive Radios (CRs) in terms of assigned vote-count are estimated based on the sensed energy values with respect to multiple fixed threshold levels, so that the direct path loss can be dealt without further increasing the error, which occurs due to fading. For indoor hospital like environment, Rician fading model is more appropriate. Therefore, formulation, evaluation and analysis of various sensing performance parameters have been carried out considering Rician fading model. Comparative analysis and trade-off among three optimum parameters-energy threshold, total number of CRs participating in sensing and total error rate, are presented with respect to signal to noise ratio (SNR). Finally, the Monte Carlo simulation is designed and implemented considering the two conditions-only fading environment and fading along with direct path loss environment. It can be observed that in both cases, the proposed spectrum sensing rule outperforms the other contemporary rules.
Keywords: Cognitive radio; direct path loss; spectrum sensing; health care
E-healthcare is a very useful concept, which not only deals with uneven distribution of doctors, but also caters to quality healthcare services to the patients located in remote and rural areas. Rapid advancements in information and communication technologies (ICT) have enabled the design and implementation of newer telemedicine models to achieve better accessibility, availability, and affordability of the medical facilities. Evolution of wireless communication technologies such as 4G, 5G, Cognitive Radio (CR) etc. are going to make huge impact in the efficient delivery of services like e-governance, e-commerce, and e-healthcare. Wireless communication is a crucial mean to enhance effectiveness and system ability for various telemedicine practices, like consulting a patient at physically inaccessible (isolated) location, post-surgery monitoring (keeping patient at home) for any complication, and motorized clinic [1,2]. The vital physiological parameters obtained from medical sensors attached to patient for continuous monitoring, can be transferred to doctor’s end through many available technologies such as Zigbee, Bluetooth, infrared Wi-Fi, cellular, internet etc. [3,4]. With the emergence of heterogeneous wireless network access, modern e-healthcare services can exploit licensed as well as unlicensed bands together to meet excessive bandwidth demands of medical sensor nodes, for keeping a continuous record of patient health [5]. FCC has allotted a very low bandwidth of spectrum to be used for providing wireless telemedicine services, as a result, there is shortage of spectrum band to accommodate the upcoming advancements in wireless technologies for biomedical services and e-healthcare applications [6]. Therefore, uses of frequency band in opportunistic manner, through the implementation of dynamic spectrum assess (DSA) technique is desired for designing an efficient wireless telemedicine system. Medical devices operating in hospitals may not function properly due to interference of wireless communication devices active in hospitals premises [7]. Recently, many researchers have pointed out the problem of electromagnetic interference (EMI) and its effect on medical equipment’s occurred in hospitals during data transmission from wireless units [8,9]. When two or more units work in common frequency at same time in the locality, then EMI takes place and, in this situation, wireless medical instruments can fail to function normally, even if they are not nearby [10]. Generally, medical instruments are equipped with jammers, which can jam a particular frequency band, but the noise generated by the jammer may cause problems. Since, communication is significant part of E-healthcare system use of jammer is not a good option [11]. Wireless Ultra-wide band communication [12] technique can reduce the EMI up to very large extent in sort range communication. In addition to EMI, there are multiple factor which causes signal distortion in wireless communication have been be identified [13,14] and needed to be dealt with. Recently, many researchers have presented various scenarios of e-healthcare, based on Cognitive Radio (CR) communication. Cognitive Radio (CR) communication is based on dynamic resource allocation [15], which is administered by soft-ware defined radio [16]. Spectrum Sensing (SS), the fundamental block of Cognitive Radio (CR) has got lot of attention by researchers over last decade [17]. Energy Detection (ED), Matched Filter Receiver, Radio Identification and Cyclostationary detection etc., are the well-known methods of SS [18]. Energy detection-based method for Spectrum Sensing is the simplest of all available methods, which requires no prior knowledge about signal characteristic of PU [19]. The performance of energy detection technique has been analyzed using Neyman Pearson (NP) frame work [20]. Bayesian Framework is another method to analyses the ED based spectrum sensing, generally used in decentralized detection technique [21]. More details of the different methods of spectrum sensing and analysis have been discussed in [22]. The main objective of this paper is to propose a new centralized spectrum sensing scheme which also possess the benefits such as low delay and computational simplicity; the typical attributes of decentralized spectrum sensing technique. The objective will be achieved by applying optimum decision-making rule and reducing number of CRs participating in sensing; this will reduce the data sharing time required for making decision. The existing research challenges in the cooperative sensing of vacant spectrum band can be summarized as follows:
a) Proposing new and efficient fusion method or voting rule for identifying primary user.
b) Limiting the number of CRs participating in sensing, to avoid data over load at fusion center.
c) Threshold determination in given fading environment.
d) There is scope for proposing better spectrum sensing schemes by considering: computational simplicity and appropriate noise modelling the fading environment.
In the energy detection method of spectrum sensing, firstly, probability of false alarm is fixed, then by knowledge of channel response, energy threshold is calculated. Comparing the sensed energy with the computed threshold energy, decision about the channel availability is made by CR. Mathematically; spectrum sensing is a binary hypothesis problem which can be represented as:
H0: Primary User (PU) absent
H1: PU present
Let us assume that ith user receives signal from channel
Considering the AWGN channel, the probability of false alarm (pf, i), probability of detection (pd, i) and probability of miss detection (pm, i) for ith CR can be calculated as: [16]
Here,
where
Probability of false alarm is independent of fading and the can be observed in Eq. (2). This is because of the fact that, probability of false alarm is calculated in the absence of primary signal; only white noise is present in channel, irrespective of fading. Probability of detection
where parameters
Putting
Finally, the probability of detection in Rician fading channel can be approximated for time bandwidth product equals to one [24]:
In centralized cooperative spectrum sensing stage, multiple CRs are grouped together under single controller in decision making. The communication between controller and CRs is assumed to be error free. Final decision at fusion centre is made by following hypothesis testing:
Here Hf 0 and Hf 1 represent the decision made by controller. di can have value 0 or 1. ‘n’ is an integer threshold in final hypothesis testing, in which decision is made by “n out of K vote rule.” K is total number of votes, which can be greater than equal to actual number of CRs. Here, three main traditional decision-making rules are being used in cooperation sensing. First is “And Rule,” in which number of decisive votes are equal total number CRs participating in sensing (
First step of the proposed algorithm is to decide the decisive number of votes for any given threshold, used by each individual CR. This step is for K number of CRs sensing together with common fusion centre. CRs sense the energy value for given sensing duration and pass the information bit 0, if the sensed value is less than the threshold value and 1, if sensed value is greater than the threshold value. Now, for the given 1 vote per CR and “n out of K vote rule”; overall probability of false alarm and probability of detection can be represented by summation of probability error occurring due to each passible combination. Therefore, total probability of false alarm Pft is given by:
Further, probability of miss detection Pmt is given by:
The proposed algorithm works in two steps. Firstly, based on decision making we determine the optimal number of CRs desired to participate in voting minimum vote required, to decide the presence of PU and threshold (
2.1 Formulation of Decision-Making Rule Based on Static Vote Count and Single Energy Threshold for Spectrum Availability
This subsection attempts to determine the decisive number of CRs (n_d) out of total available CRs (Nc), for making decision about the availability of the spectrum, while keeping overall probability of error to minimum level. The overall probability of error is represented as
where, Pft, Pmt and Pdt represent the total probability of false alarm, overall probability of miss detection and overall probability of detection respectively.
Now minimization the (Pft + Pmt) can be achieved by minimizing the Eq. (14)
Differentiate Eq. (14) with respect to decisive number of votes n_d, we obtain:
Determine the value of n by equating Eq. (15) to zero, i.e.,
where
2.2 Determination of Optimum Energy Threshold
Once decision making rule is defined the total error rate can be reduced to minimum by differentiating the error function with respect to threshold value
L.H.S. of (19) contains two partial differentiation of two parameters.
First part is differential of total probability of false alarm with respect to threshold (
Second part of L.H.S. in Eq. (19) is differential of total probability of detection with respect to threshold (
Here, differentiation of individual level of probability of detection with respect to threshold
For AWGN channel differentiation of probability of detection with respect to energy threshold value is calculated from Eq. (3) using
For Rician channel differentiation of probability of detection with respect to energy threshold value is calculated from Eq. (7)
Using the Eqs. (16)–(22) value of threshold
2.3 Determination of Optimum Number of CRs
Spectrum sensing scheme will not be efficient, if there are large number of CRs participating in sensing process in a cognitive radio network. Therefore, it becomes crucial to determine the optimum number of CRs required for efficient sensing. This is achieved by defining an optimization problem for the given error rate bound [
If N_opt is minimum number of CRs required to achieve error bound
Now, let’s assume a function:
Here, n_dopt is minimum optimal vote and N_opt is minimum number of CRs participating in sensing to satisfy (
N_opt is point of zero crossing of function G (N_opt, n_dopt). It can be calculated from analysis of Fig. 6; determination optimum number of CRs (n_dopt) of Eqs. (25) and (26) is done on the basis of this figure.
2.4 Simulation Results and Comparative Analysis of Different Sensing Parameters in Fading Environment
The simulation results of the proposed cooperative spectrum-sensing scheme are presented in two parts. First part presents the performance evaluation of the proposed new voting rule based cooperative spectrum sensing scheme for different set of parameters such as error rate, energy threshold, number of CRs participating in sensing and SNR used by primary user. All the simulations have been performed using MATLAB 2011(b) installed in a desktop computer (Intel i7, 8 GB RAM, Windows 10). It is observed from Fig. 1 that under Rician fading condition, with a decrease in decisive number of CRs in the spectrum sensing procedure, the optimum threshold value increases for each fixed SNR value. In other word, CRs which are sensing higher energy values are more relevant in decision making as they can limit the error rate by themselves, irrespective of amount of energy sensed by others CRs.
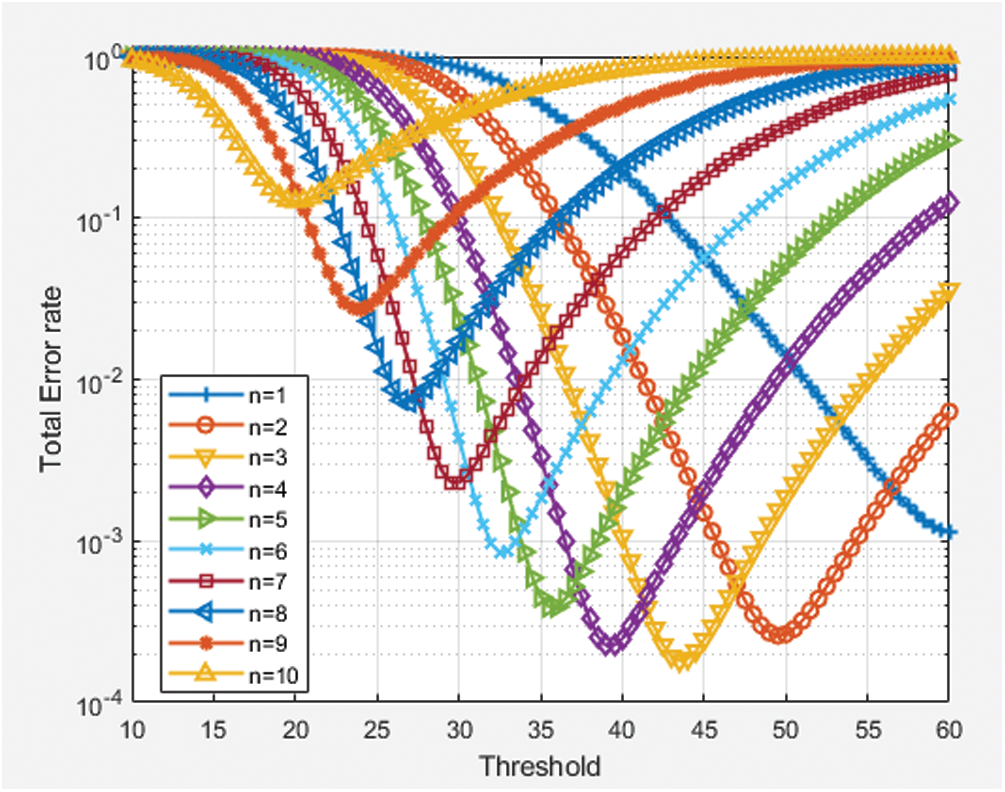
Figure 1: Total error rate corresponding to different number of decisive votes
In Fig. 2, variation of decisive number of votes (n_d) out of total votes to get minimum error rate at different levels of SNR values, are presented. Total number of votes considered in the simulation is 16. Following observations are made
a) At higher SNR value, larger numbers of decisive votes are needed for optimal decision regarding the vacancy of channel.
b) It is observed that, if the number of decisive votes (n_d) stays constant, then to minimize the error rate, threshold value has to increase with increase in SNR i.e., SNR value is directly proportional to the energy threshold value.
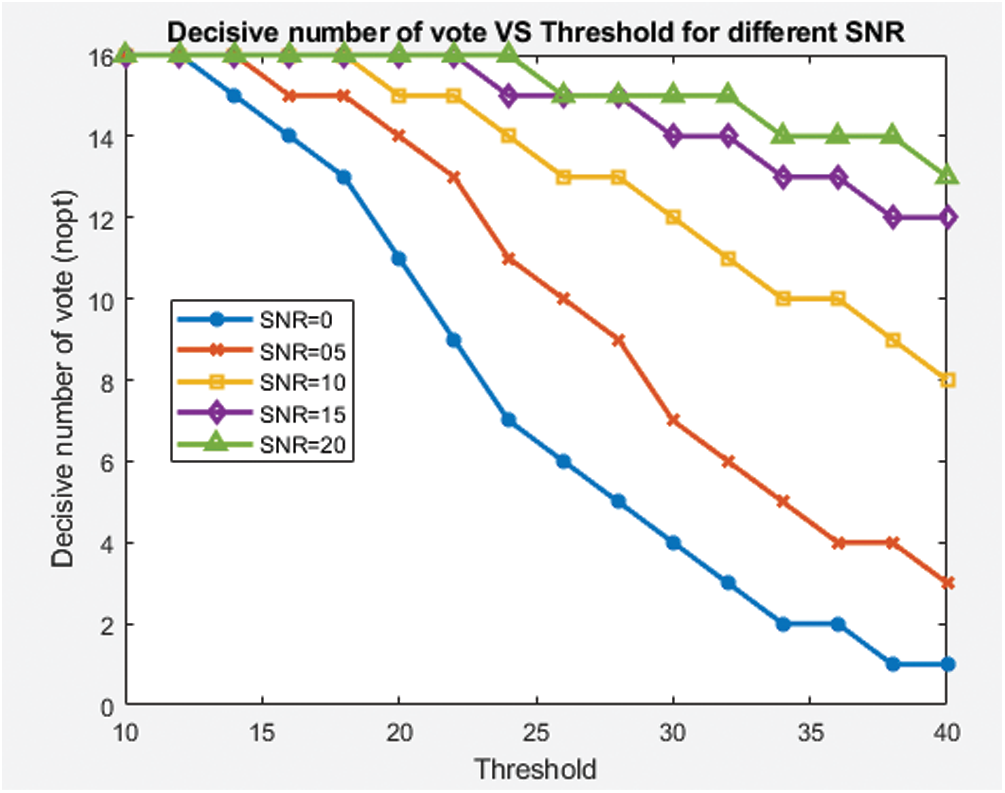
Figure 2: Effective number of CRs required at different thresholds for given SNR values in Rician fading environment
The main advantages of limiting the number of CRs participating in sensing is fast decision process regarding the spectrum vacancy, as the reduction in number of CRs participating in sensing, reduces the number of control packets shared between fusion centre and CRs. For different threshold values, error rate corresponding to total number of CRs participating in sensing, for the proposed new decision-making rule, is shown in Fig. 3.
The increase in SNR value always increases effectiveness of sensing for any number of CRs but high SNR value causes undesirable Electromagnetic Interference (EMI) effects in hospital environment. In the Rician fading environment, total error rate is calculated for varying number of CRs at fixed SNR value, which is shown in Fig. 4. From this figure, for given tolerance level (Error rate) and appropriate SNR (not high enough to cause EMI), the decision about number of CRs needed to group together in sensing process, can be made. Further, it can be observed that-higher SNR value produces lower error rate.
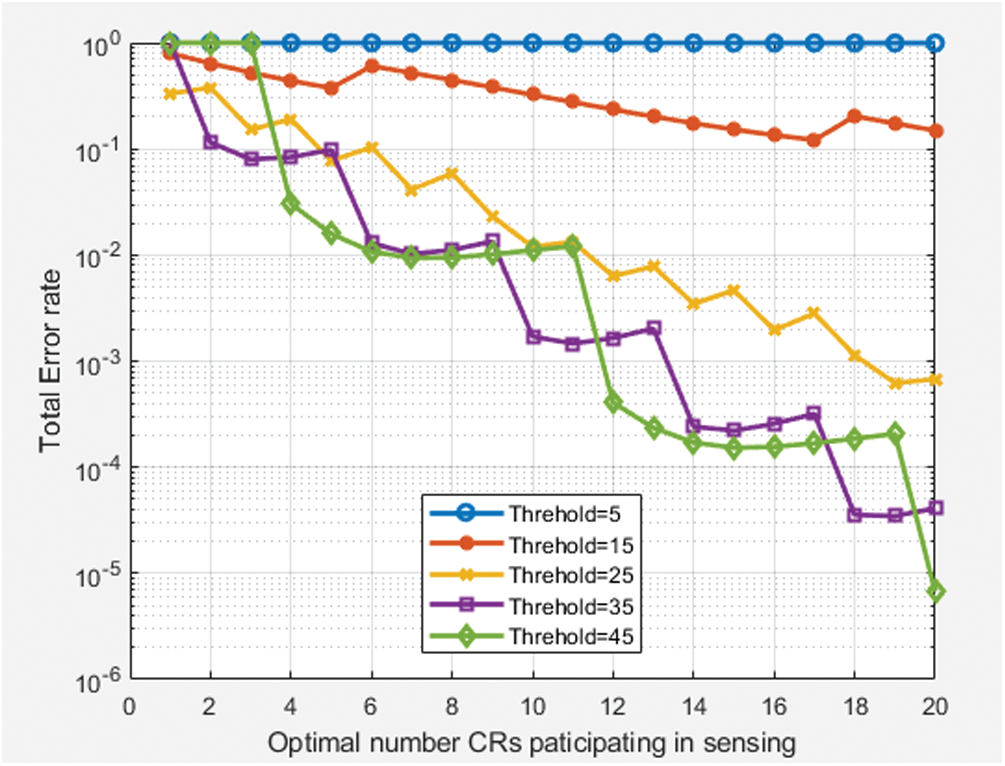
Figure 3: Variation the total error rate with total number of CRs in Rician fading environment
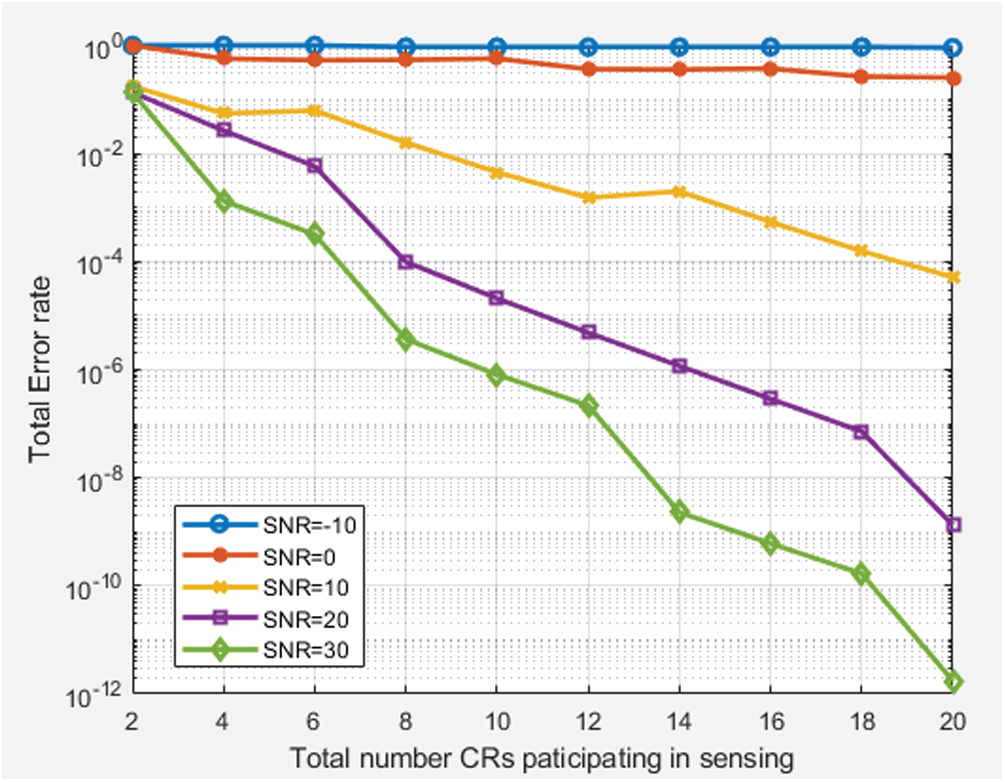
Figure 4: Total error rate for fixed SNR values with varying number of CRs in Rician fading environment
Sensing information in the proposed spectrum sensing scheme is represented using 2 bits, which is described in Tab. 1.
Table 1: Two-bit information corresponding to the sensed energy value passed to fusion centre by individual CR
The complete modified decision rule of cooperative spectrum sensing, which is based dynamic vote count and multiple energy thresholds, is given in Algorithm 2:
3 Result Comparison and Discussion
In this section, accuracy of proposed spectrum sensing scheme is tested against other available traditional schemes. A Monte Carlo simulation has been designed to represent the cognitive radio scenarios of fading environments with and without direct path loss. Fig. 5 shows the variation in the probability of detection at different values of the probability of false alarm at a given SNR value. The theoretical value of ‘probability of detection’ matches the probability of detection observed from designed Monte Carlo simulation for Rician fading environment, corresponding to the varying value of probability of false alarm. This indicates that designed simulation is accurate and can represent the practical environment with very high accuracy.
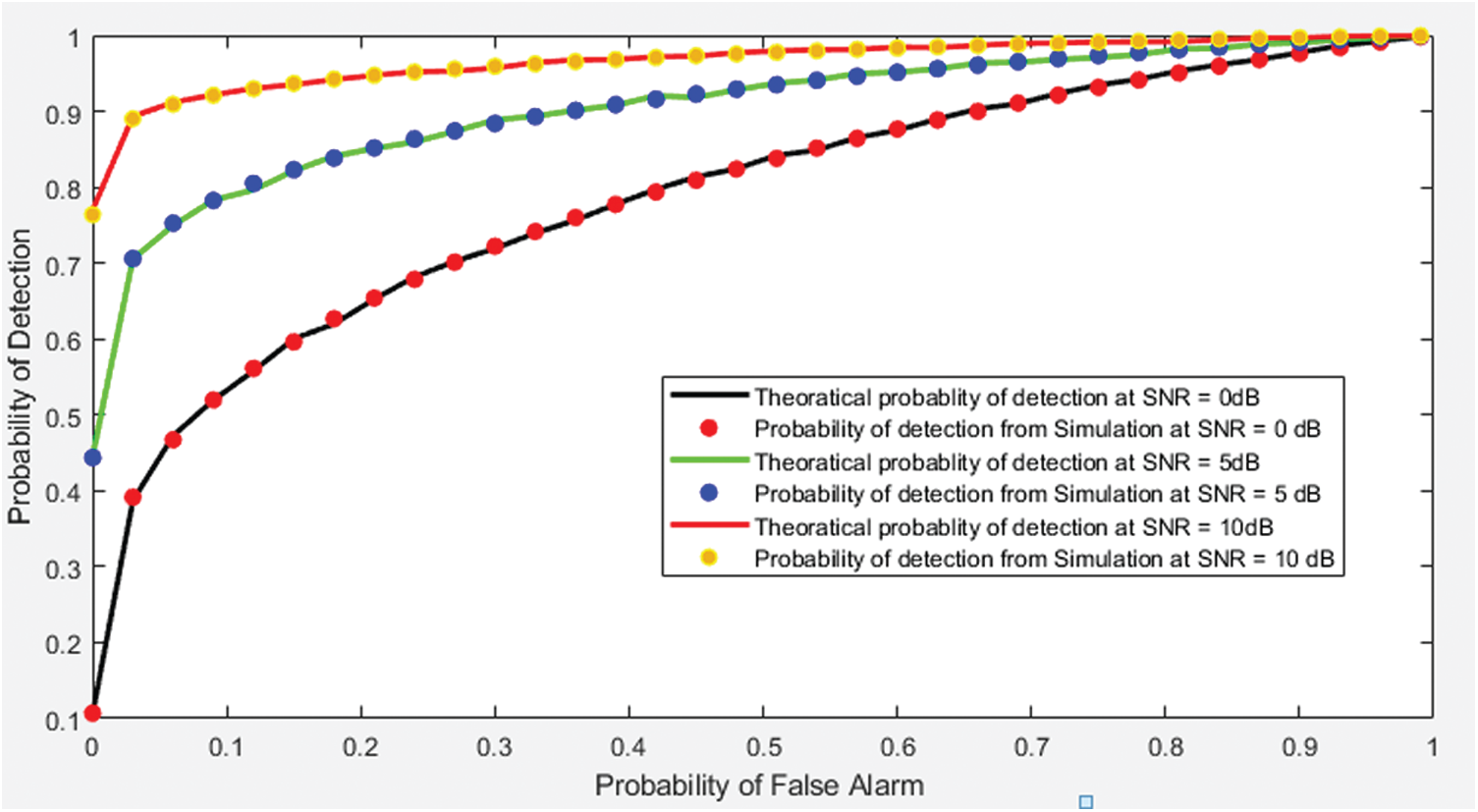
Figure 5: ROC curve for individual CR in Rician fading environment (Monte–Carlo simulation vs. theoretical value)
ROC curves of the different decision rules are shown in Fig. 6. Here, it can be observed that proposed rule gives maximum area under the curve with respect to other contemporary rules. Thus, it can be established that the proposed sensing rule out-performs other cooperative sensing rules under consideration, for given single threshold value, which is decided by individual level of probability of false alarm.
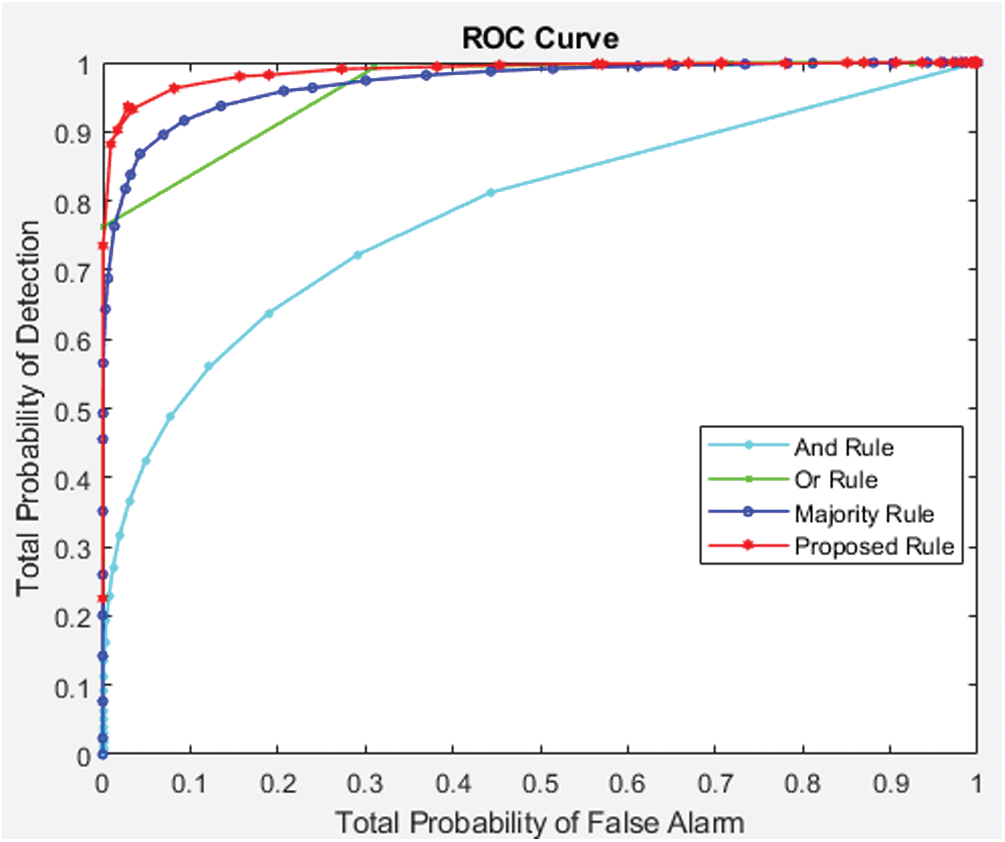
Figure 6: ROC curve for 20 number of CRs in Rician fading environment
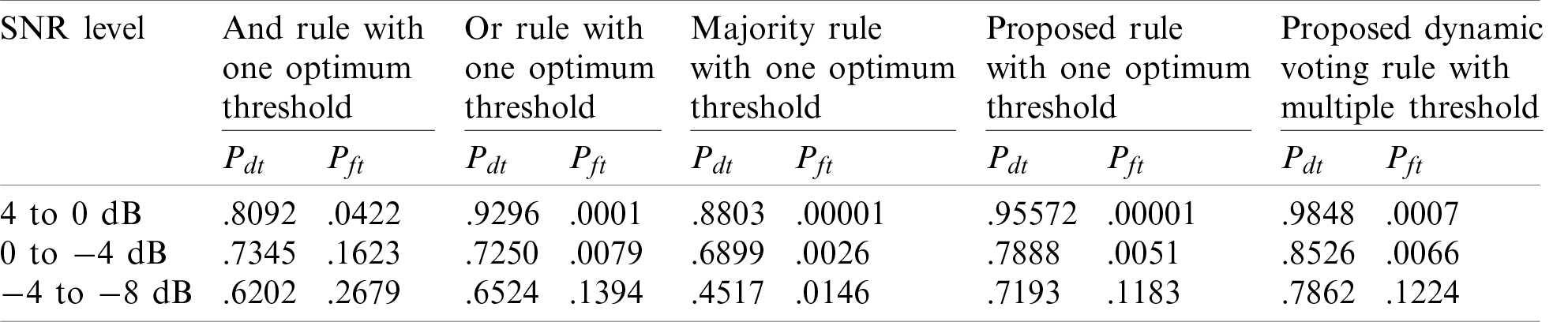
Tab. 2, it can be established that the proposed dynamic voting rule based on multiple threshold levels, outperforms other traditional rules as it achieves the highest total probability of detection for tolerable value of total probability of false alarm.
Table 2: Final result comparison between different rule with respect to 4 dB of direct path loss in term of total probability of false alarm (Pft) and total probability of detection (Pdt)
From Fig. 6, it can be visualized that the proposed decision-rule (i.e., optimum determination of decisive number of vote) for cooperative spectrum sensing, out-performs other decision rules (“AND” rule, “OR” rule and “Majority” rule) under consideration, for any given individual level of energy threshold. The overall process of sensing is shown in Fig. 7.
Figure 7: Steps involved in cooperative spectrum sensing
In the Fig. 8, four regions are shown corresponding to three thresholds. First region is below threshold 1, which represents absence of PU and other three regions represent presence of PU with different probabilities.
Figure 8: Regions to thresholds and corresponding bit sequence
This paper presented a cooperative spectrum-sensing algorithm based on dynamic vote count using multiple energy threshold levels and its analysis in intra-hospital environment defined by Rician fading. This paper used four steps to propose a new cooperative spectrum-sensing algorithm. The paper began with derivation of optimum decision rule, assuming equal weightage to each CRs. Firstly, applying mathematical approach, a decision making rule for cooperative spectrum sensing was defined for fixed energy threshold and SNR. In step second and third, the expression for other two main parameters for cooperative sensing, (1) optimum threshold value and (2) efficient number of cognitive radios needed to participate in sensing have been derived for different values of SNR. Error rates corresponding to different variables like SNR, threshold and number of participating CRs were calculated and demonstrated. In the fourth step, using the analysis of variation in error rate with respect to different sensing parameters, formulation of final cooperative sensing algorithm was done. In this algorithm, multiple threshold levels and dynamic vote count based on sensing values of CRs (unlike traditional equal weight vote count) was exploited to address the issue of direct path loss and fading, at the same time. The comparison of different cooperative sensing algorithms with the proposed algorithm, with respect to probability of false alarm at individual level was presented. The ROC curve analysis was done to show the efficiency of proposed rule against the other traditional rules. Finally, Monte Carlo simulation was performed to create a scenario where signal strength loss occurred due to both direct path loss as well as fading. The comparison results of this simulation, at different levels of SNR values were presented in a tabular form. It was established through result analysis that presented cooperative spectrum sensing algorithm based on dynamic voting rule, outperformed other traditional spectrum sensing algorithms such as “AND” rule, “OR” rule, “Majority” rule and initially proposed spectrum sensing algorithm based on single energy threshold. In other word, in a practical scenario where signal strength weakens due to direct path loss, the dynamic voting rule based on multiple threshold levels, performed better than the algorithms, which assigned equal weight to all CRs participating in sensing. In this paper, multiple energy threshold levels and corresponding vote assignment to CRs, done on basic analysis of tradeoff between various parameters, such as SNR, threshold value, number CRs participating in sensing and error rate. In the future work, the results corresponding to varying threshold levels will be analyzed and more appropriate optimization rule for determination of multiple energy threshold level based on complex statistical analysis will be presented. Further, for cognitive radio-based hospital environment, more suitable dynamic medium access protocol will be proposed taking into the account the varying node priorities. In near future, medical equipment in a healthcare center would utilize multimode functions and will deliver many services from single device. Some researchers have talked about spectrum sensing methods or algorithms to enhance performance of communication via their proposed architectures.
Acknowledgement: The authors would like to thanks the editors of CMC and anonymous reviewers for their time and reviewing this manuscript. Authors would like to acknowledge Research Scholarship scheme under Visvesvaraya Ph.D. programme of ministry of Electronics and Information Technology, Meity Government of India, for providing research grant.
Funding Statement: This research was supported by Taif University Researchers Supporting Project Number (TURSP-2020/214), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Stephen Berger and H. M. Gibson, “The wireless challenge, managing your hospital Rf spectrum,” Copyright AAMI 2013 Biomedical Instrumentation & Technology, 2013. [Online]. Available: https://meridian.allenpress.com/bit/article/47/3/193/142678/Managing-Your-Hospital-RF-Spectrum. [Google Scholar]
2. I. Ahmed, H. Karvonen, T. Kumpuniemi and M. Katz, “Wireless communications for the hospital of the future: Requirements, challenges and solutions,” International Journal of Wireless Information Networks, vol. 27, no. 1, pp. 4–17, 2020. [Google Scholar]
3. X. Liang, M. Barua, R. Lu and X. Shen, “Privacy preserving wireless data transmission for e-healthcare applications,” IEEE COMSOC MMTC E-Letter, vol. 6, no. 11, pp. 39–41, 2011. [Google Scholar]
4. Y. Lei, Q. Zheng and X. Fan, “RSPP: A reliable, searchable and privacy-preserving e-healthcare system for cloud-assisted body area networks,” in IEEE INFOCOM 2017-IEEE Conf. on Computer Communications, Atlanta, GA, USA, IEEE, pp. 1–9, 2017. [Google Scholar]
5. S. D. Baker and D. H. Hoglund, “Medical-grade, mission-critical wireless networks,” IEEE Engineering in Medicine and Biology Magazine, vol. 27, no. 2, pp. 86–95, 2008. [Google Scholar]
6. H. F. Rasvand, V. Traver Salcedo and D. llicscu, “Ubiquitous wireless telemedicine,” IET Communication, vol. 2, no. 2, pp. 237–264, 2008. [Google Scholar]
7. J. Feng, M. Ghosh Wang and K. Challapali, “Emerging cognitive radio applications: A survey,” IEEE Communications Magazine, vol. 49, no. 3, pp. 74–81, 2011. [Google Scholar]
8. L. Lu., X. Zhou, U. Onunkwo and G. Y. Li, “Ten years of research in spectrum sensing and sharing in cognitive radio,” Journal of Wireless Communication Network, vol. 28, no. 2012, pp. 1–16, 2012. [Google Scholar]
9. A. A. Mutlag, M. K. A. Ghania, N. A. Kumar, M. A. Mohammedad and O. Mohda, “Enabling technologies for fog computing in healthcare IOT systems,” Future Generation Computer Systems, vol. 90, no. 3, pp. 62–78, 2019. [Google Scholar]
10. M. Khaddar, H. Harroud, M. Boulmaif, M. Elkoutbi and A. Habbani, “Emerging wireless technology in e-health, trends, challenges, and framework design issues,” in ICMCS, Tangiers, Morocco, pp. 440–445, 2012. [Google Scholar]
11. S. J. Devaraj and K. Ezra, “Current trends and future challenges in wireless telemedicine system,” in 2011 3rd Int. Conf. on Electronics Computer Technology, Kanyakumari, pp. 417–421, 2011. [Google Scholar]
12. Y. A. Bryukhanov and Y. A. Lukashevich, “Nonlinear distortions caused by sigma–delta analog-digital conversion of signals,” Journal of Communications Technology and Electronics, vol. 62, no. 3, pp. 219–228, 2017. [Google Scholar]
13. O. Daoud, Q. Hamarsheh and A. Damati, “PAPR effect remedy in OFDM-based wireless systems,” Journal of Communications Technology and Electronics, vol. 62, no. 10, pp. 1122–1129, 2017. [Google Scholar]
14. K. V. Krishnan, R. M. Sajith and S. Khara, “Dynamic resource allocation in OFDM based cognitive radio system considering primary user Qos and secondary user proportional constraints,” Journal of Communications Technology and Electronics, vol. 60, no. 11, pp. 1269–1275, 2015. [Google Scholar]
15. D. V. Ivanov, V. A. Ivanov, N. V. Ryabova, A. A. Elsukov, M. I. Ryabova et al., “Software-defined radio technology in the problem concerning with the successive sounding of HF ionospheric communication channels,” Journal of Communications Technology and Electronics, vol. 61, no. 7, pp. 767–775, 2016. [Google Scholar]
16. S. N. Ohatkar and D. S. Bormane, “An optimization technique for efficient channel allocation in cellular network,” Journal of Communications Technology and Electronics, vol. 59, no. 11, pp. 1225–1233, 2014. [Google Scholar]
17. N. Sriranga, G. Kyatsandra, Nagananda, R. S. Blum, A. Saucan et al., “Energy-efficient decision fusion for distributed detection in wireless sensor networks,” in 2018 21st Int. Conf. on Information Fusion (FUSIONCambridge, UK, pp. 1541–1547, 2018. [Google Scholar]
18. A. Kumar and N. Kumar, “OFDM system with cyclostationary feature detection spectrum sensing,” ICT Express, vol. 5, no. 1, pp. 21–25, 2018. [Google Scholar]
19. A. Kumar and N. Kumar, “Analysis of OFDM system with energy detection spectrum sensing,” Indian Journal of Science & Technology, vol. 9, no. 16, pp. 1–6, 2016. [Google Scholar]
20. F. Penna and R. Garello, “Decentralized Neyman–Pearson test with belief propagation for peer-to-peer collaborative spectrum sensing,” IEEE Transactions on Wireless Communications, vol. 11, no. 5, pp. 1881–1891, 2012. [Google Scholar]
21. R. Couillet and M. Debbah, “A Bayesian framework for collaborative multi-source signal sensing,” IEEE Transactions on Signal Processing, vol. 58, no. 10, pp. 5186–5195, 2010. [Google Scholar]
22. S. Ziafat, W. Ejaz and H. Jamal, “Spectrum sensing techniques for cognitive radio networks: Performance analysis,” in 2011 IEEE MTT-S Int. Microwave Workshop Series on Intelligent Radio for Future Personal Terminals, Daejeon, pp. 1–4, 2011. [Google Scholar]
23. W. Lindsey, “Error probabilities for rician fading multichannel reception of binary and n-ary signals,” IEEE Transactions on Information Theory, vol. 10, no. 4, pp. 339–350, 1964. [Google Scholar]
24. S. S. Brkić and P. N. Ivanis, “Energy detector performance in Rician fading channel,” Serbian Journal of Electrical Engineering, vol. 10, no. 1, pp. 37–46, 2013. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |