DOI:10.32604/cmc.2021.016068

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016068 |  |
| Article |
An Identity-Based Secure and Optimal Authentication Scheme for the Cloud Computing Environment
Department of Information Technology, E. G. S. Pillay Engineering College, Nagapattinam, Tamilnadu, India.
*Corresponding Author: K. Raju. Email: profgkr@gmail.com
Received: 21 December 2020; Accepted: 04 April 2021
Abstract: Security is a critical issue in cloud computing (CC) because attackers can fabricate data by creating, copying, or deleting data with no user authorization. Most of the existing techniques make use of password-based authentication for encrypting data. Password-based schemes suffer from several issues and can be easily compromised. This paper presents a new concept of hybrid metaheuristic optimization as an identity-based secure and optimal authentication (HMO-ISOA) scheme for CC environments. The HMO-ISOA technique makes use of iris and fingerprint biometrics. Initially, the HMO-ISOA technique involves a directional local ternary quantized extrema pattern–based feature extraction process to extract features from the iris and fingerprint. Next, the features are fed into the hybrid social spider using the dragon fly algorithm to determine the optimal solution. This optimal solution acts as a key for an advanced encryption standard to encrypt and decrypt the data. A central benefit of determining the optimal value in this way is that the intruder cannot determine this value. The attacker also cannot work out which specific part of the fingerprint and iris feature values are acted upon as a key for the AES technique. Finally, the encrypted data can be saved in the cloud using a cloud simulator. Experimental analysis was performed on five fingerprint and iris images for a man-in-the-middle attack. The simulation outcome validated that the presented HMO-ISOA model achieved better results compared with other existing methods.
Keywords: Data security; authentication; identity-based authentication; optimal key generation; biometric
Data security is considered to be the major constraint in cloud computing (CC).Intruders can hack by using the man-in-the-middle (MIM) attack [1], where development, duplication, and elimination of data take place with no data authentication. Thus, the legal owner experiences a drastic loss because of unauthenticated actions. Confidential data has to be encrypted before sending it to the legitimate user to overcome these vulnerabilities. In the last few decades, password-based authorization has been applied to encrypt data. However, this approach has numerous short comings. The user may forget the password; security may be compromised when the password is known by a third party; and the system is easily hacked. Biometric-related authorization has been applied to overcome these issues, as it is stable, unique, and non-sharable. Most importantly, the concerned person has to be present for authorization, which means that without that person, it is impossible to retrieve the confidential data.
CC can provide superior service to end users through the internet; it plays an important role in daily life interms of software solutions. Most of the applications supported by CC require user, personal, and location details. This may create security and privacy problems. One of the recently developed areas of study for cloud services is security- and privacy-conserving authorization of users. Private details, such as economic data, health-based records, and personal information, are saved with basic security objectives. Therefore, authorization methods are essential to preserve sensitive data from adversaries in a CC platform. A defined number of users should have the rights to access cloud services at the same time; the authentication of user access should be effective; and the processing complexity has to be minimal. The privacy-aware access control model has relied on an attribute fuzzy grouping, named PriGuarder, to enhance data security in CC. Overall, authentication has not been that effective. A protocol for attribute-based signature outsourcing has also been used to ensure the security of the user in the cloud, but the processing complexity is higher.
Liu et al. [2] deployed a shared authority–based, privacy-preserving authentication protocol to overcome the security problems in CC. However, the number of clients was small. In the study by Zhou et al. [3], the researchers proposed an authorized accessible privacy model for enhancing the security and privacy of CC. However, the computational as well as communication burden were higher. The Identity-Based Remote Data Integrity Checking protocol reduce the difficulty and expense of public key validation. However, the Privacy-Preserving Rate (PPR) remains the same with no improvement even after using key homomorphic cryptographic methods. Cloud-based mutual authentication uses a privacy conservation protocol for achieving better security.
In the work by Rawal et al. [4], the secure disintegration protocol (SDP) was proposed to secure on-site privacy in the CC platform. However, private data integration could not be resolved. The two-factor data-security protection mechanism was proposed in an earlier work [5] for cloud storage. However, the time for user authentication in CC was also longer. In subsequent work, a Mutual Authentication Protocol was developed with the objective of securing elliptic curve cryptography (ECC) to reduce the costs of communication. However, the PPR was limited. Handoff authorization approaches have been used to provide user anonymity as well as untraceability in the cloud. A PPR three-factor authenticated key agreement protocol for securing data from diverse attacks ensured secrecy in the CC environment.
A new method has been described for conserving data privacy in on-demand CC services. Two server authentications and key agreement protocols have been deployed for accessing cloud services with maximum security. In a previous study [6], k-times attribute-based anonymous access control was proposed to authenticate the user in the cloud secretly. In another work [7], message digest–based authentication was deployed under the application of hashing for computing mutual authentication at the time of information retrieval from the cloud. Server-aided anonymous attribute–based security was established to retain the integrity of user data at reasonable expense [8]. The Privacy-Aware Authentication approach was developed for reducing the time consumed for authentication in the CC platform. In a study by Li et al. [9], a smart card–based validation approach was introduced to effectively secure CC communication. In [10], a key aggregate cryptosystem was developed to achieve secure data distribution from dynamic cloud storage. In further work [11], identity-based secure authentication technology was modeled with the support of quantum cryptography to find a loyal user. Effective user authentication was deployed to compute preserved data access in a CC environment.
Balakrishnan et al. [12] proposed a biometric leakage-resilient authenticated key exchange model to perform secure data distribution in a CC platform. A novel technique was developed for enhancing data transfer scheduling and optimization in the cloud. A Fountain code–based cloud storage approach was has been used to retrieve files with minimum delay and maximum efficiency [13]. Public-key cryptosystems have been developed to exchange data with one another in a protective manner. In a study by Xiong et al. [14], a secure re-encryption approach was introduced by applying EIGamal technology to report the security issues involved in a CC platform. An attribute-based encryption mechanism was proposed by Tameem & Cho [15] to enhance the integrity of cloud services. Other authentication schemes for the CC environment have been published [16–20].
This study presents a new concept of hybrid metaheuristic optimization for an identity-based secure and optimal authentication (HMO-ISOA) scheme for CC environments. The presented HMO-ISOA technique utilizes iris and fingerprint biometrics as identities. First, the HMO-ISOA technique involves a directional local ternary quantized extrema pattern(DLTerQEP)–based feature extraction process to extract the features from the iris and fingerprint. Next, the features are fed into the hybrid social spider dragonfly (HSSDF) algorithm to find the optimal solution. This solution serves as a key for advanced encryption standard (AES) for encryption and decryption of data. Finally, the encrypted data can be saved in the cloud using a cloud simulator. A set of simulations were carried out on five fingerprint and iris images for the case of MIM attack.
2 The Proposed HMO-ISOA Technique
The diagrammatic representation of the newly developed HMO-ISOA technique is shown in Fig. 1. The identities of the user (fingerprint and iris) are initially captured, and the feature extraction process is carried out using the DLTerQEP technique. Once the features are generated, they are provided to the HSSDF technique for optimal key generation. Subsequently, the AES algorithm encrypts the data using the generated optimal key, and the encrypted data are transmitted to the cloud environment.

Figure 1: Process involved in the proposed HMO-ISOA model
2.1 DLTerQEP-Based Feature Extraction
Once the input fingerprint and iris images are captured, the features in the images are extracted using the DLTerQEP model. Local binary patterns (LBP),local ternary patterns (LTP), and local quantized extrema patterns (LQEP) are part of the fundamental strategy for the local pattern (LP); they are employed to define DLTerQEP. DLTerQEP illustrates the spatial architecture of the local texture in patterns using the application of local extrema. It also illustratesthe directional geometric structures.
The local extrema are achieved in every direction from the newly developed DLTerQEP model by processing the local differences among the center pixel and neighbors and by indexing the patterns with pixel locations [21]. Next, the local directional extrema values (LDEV) for the LP neighborhoods of the image (I) are calculated as follows:
where k1 × k1 denotes the size of the input image. The directional local extrema measures in 0°, 45°, 90° and 135° directions are obtained from HVDA7 using the LDEV measures, as shown in Eq. (1). Four directional ternary extrema codings (DTEC) were collected on the basis off our directions under the application of the LTP. Hence, ternary coding patterns are obtained as follows:
where LDEV(g_ob)=LDEV at (a,b) position of a 7 × 7 grid, and gc implies the gray value of an intermediate pixel.
In the case of the upper LTP, DTECI is processed from Eq. (2) by accessing the value of
Likewise, from Eq. (2), the minimum LTP and DTEC2 are processed by accessing the value of
The DTEC is derived from Eqs. (2)–(4) as given by the following:
The DTEC coding is transformed as two binary codes. The Upper LTP code and Lower LTP code in LTP. Next, DLTerQEP enables four directional extrema for P = 12-bit (w = 0 … 11) string generation for all binary patterns of the LTP.
The combination of binomial weights in DTECLTP coding has exclusive DLTerQEP values from the special pattern (7 × 7) for classifying the spatial structure as shown in Eq. (6):
For the complete image, DTECLTP maps values from 0 to 4095 (0 to 2P−1).The entire DTECLTP map is developed with measures that range from (0 to (2(2P)) (-1)). The image is represented through a histogram of Eq. (7). One LP is predicted, and pattern (LBP or LTP or DTEC or DLTerQEP) values are obtained.
2.2 Optimal Key Generation Using the HSSDF Algorithm
The required features are generated and provided to the HSSDF technique for optimal key generation. The HSSDF technique integrates the merits of the Social-Spider Optimization (SSO) and the dragonfly (DF) algorithms to select the encryption key for AES proficiently.
In SSO, the search space is considered a communal spider web. The candidate solution in a population implies a spider. A spider obtains a weight based on the fitness value of a solution. It makes two search sets of evolutionary operators, which accelerates the distinct cooperative natures in a colony.
The main aim of this method is to resolve nonlinear global optimization issues using a box constraint, as formulated here:
where f:
Here, SSO applies the population S of N candidate solutions and resolves optimization issues. Population S is also classified into two search classes, namely Male (Ms) and Female (Fs). Count Nf are females to simulate a real spider colony. Nf is selected randomly from the greater extent of the whole population S, and the remaining Nm is assumed to be male individuals (Nm = S−Nf). Group Fs makes the collection of female individuals based on these constraints(Fs = fs1, fs2,…,fsNf }).Thus, the Ms group is male individuals (Ms = msl,ms2,…,msnm }), where S = Fs ∪ Ms (S = s1, s2, …, sN }).
Here, a spider is allocated a weight
where fiti implies fitness of the ith spider place; i∈1,…,N; and best as well as worst mean the optimal fitness value and worst fitness value, respectively, in the entire population S. fiti is accelerated by vibrations generated through the web. Therefore, the vibration of a spider is perceived from spider j and labeled as follows:
where wej indicates the weight of the jth spider, and di implies the distance between two spiders. A spider
where α,β, and δ denote arbitrary values from [0,1]; k implies the iteration value; and individuals sn and sb signify the closest spider with maximum weight compared with
The male spiders are characterized as two classes, namely Dominant (D) and Non-dominant (ND). Here, the D group is combined with a male spider in which the fitness values are optimal interms of the complete male set. In the optimization task, the male spiders
where α,δ, and rand indicate a random value from [0,1], and sf shows the closest female spider to the male individual j. In SSO, mating is carried out between a dominant male md and the female individuals within defined range r; as a result, a novel offspring snew is generated. Next, the weight of a spider describes the possibilities of a spider on snew; the high element has the maximum possibility of affecting a new individual snew. Fig. 2 shows the flow chart of the evolutionary operations.
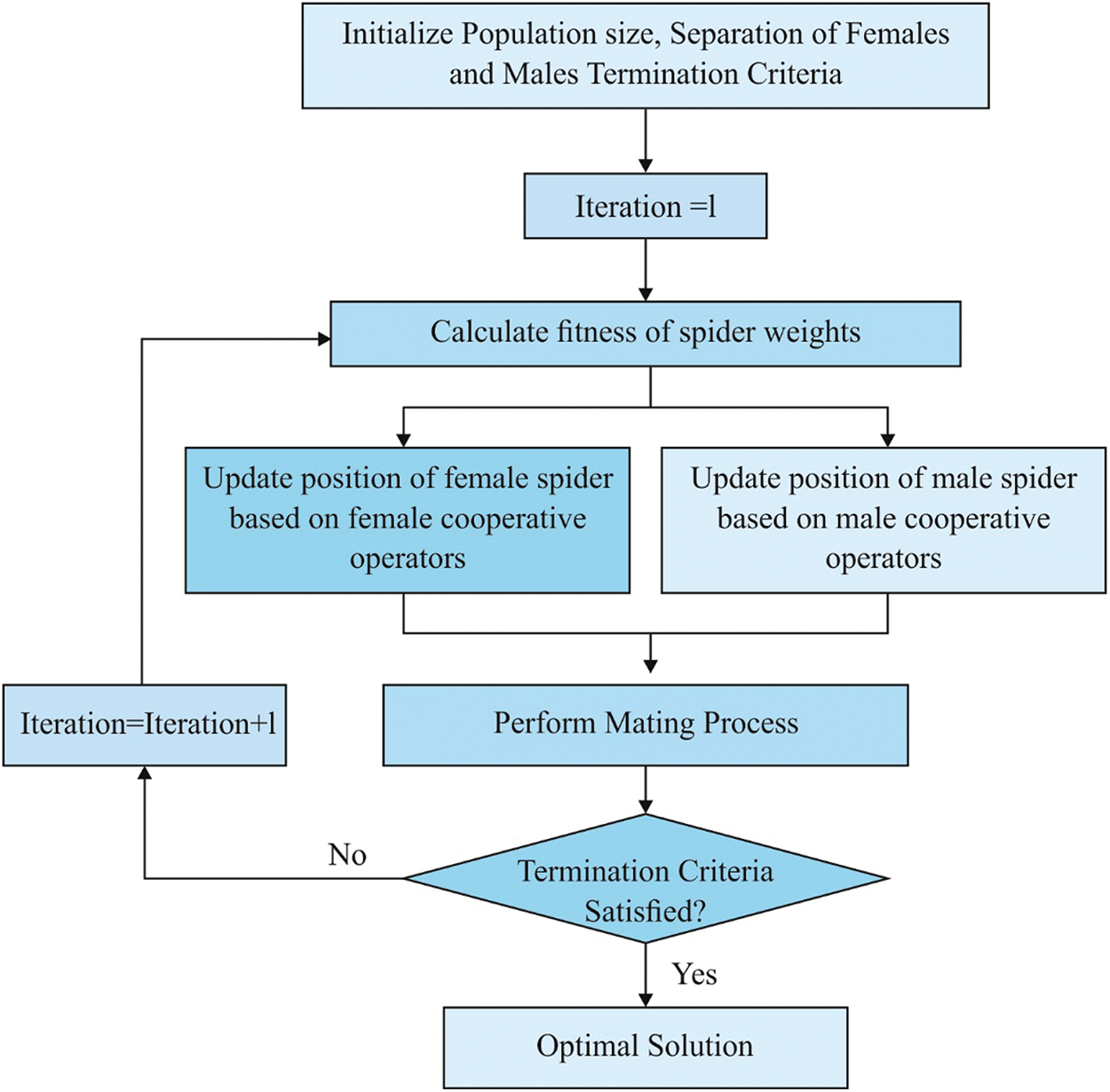
Figure 2: Flowchart of the SSO algorithm
The performance of SSO can be enhanced by using a hybridization of the SSO and DF algorithms. Recently, Mirjalili [23] developed the DF algorithm, which uses a population-based metaheuristic approach. This model was evolved from the behavior of hunting the named static swarm (feeding) and migration activities of DFs. Basically, DFs reside in tiny groups and discover food sources. This operation is named the hunting mechanism. Most of the DFs move in the same direction. This swarm traveling process is called the migration operation. Here, hunting and feeding are important tasks that contribute to this approach. They are depicted in Fig. 3.

Figure 3: Steps in the DF algorithm
The swarming nature of DFs is classified into five operators:
• Separation is a process that makes sure that search agents are placed away from one another within a neighborhood. Numerical modeling of a separation behavior is calculated through Eq. (13):
• Alignment defines the way of matching the velocity of a search agent with neighboring search agents. The arithmetical definition of alignment is as in Eq. (14):
where
• Cohesion refers to how individuals move from a nearby region to the center of mass. Cohesion behavior is represented in Eq. (15):
• Attraction implies how food sources bring flies toward them. The arithmetical calculation of this behavior is as in Eq. (16):
where
• Distraction means the potential of individuals to escape from the opponent or enemy. The distraction from the
where
In
The generic approach of the particle swarm optimization (PSO) method is applied by DF, as it applies two vectors for upgrading the position of the DF; hence, a step vector
The step vector (implied in Eq. (18)) is defined based on the action of DFs:
where
where
where implies
The position of the DF is upgraded per Eq. (22):
where referst refersrefers to the current step.
The optimal key values generated in the previous process are fed into the AES algorithm. In general, AES is meant to be an iterative method that is operated under four processes, namely Subbytes, Shiftrows, Mixcolumns, and key transformations (Add Round Key). Initially, the primary operation is performed by including a 128-bit first-round key along with 128-bit plain texts. Next, consecutive rounds are varied from others because of the absence of conversion in the mix column. The subsequent decryption task is the converse strategy of encryption.
Sub bytes conversion. This is defined as a nonlinear byte type that is computed on a byte that is independent of the substitution table (S- Box) [24].
Shift rows conversion. Here, rows are in a cyclic fashion that are moved to the left of the state matrix. Next, byte transformation is performed by shifting in the first row: 1-byte right shift in 2nd row; 2 bytes right as well as 3 bytes left shift in the 3rd and 4th rows.
Mix columns conversion. This is processed on an individual basis for each column. A column byte is matched to a new measure, assumed as the function of the above-mentioned bytes. Transformation is defined as a matrix multiplication on states that depend on Galois field multiplication.
Add round key. This is defined as an XOR (eXclusive OR) operation that happens among the state and round keys. It is obtained from the cipher key by the application of the key schedule.
AES key generation. Here, key generation is through expansion of words, which generates a linear array. Keys are saved from the first step and applied whenever they are essential.
In short, the overall steps involved in the presented algorithm are as follows:
Step 1: Add the fingerprint and iris feature extraction measures.
Step 2: Determine the feature values with the help of the fitness function (FF).
Step 3: Select an optimal value and upgrade the residual measure.
Step 4: Relate the added value and expanded value for estimating the FF value. This is also applied for generating the superior performance of the provided solution.
Here,
where F1 denotes the fitness; R1 depicts the reliability; and D1 indicates the distance.
Step 5: Follow the iteration until the optimal solution is found.
Step 6: Consequently, terminate the iteration. An optimal solution is referred to as a key to encrypt the data with the help of the AES method.
The performance of the HMO-ISOA algorithm was validated against a set of fingerprint and iris images. Some sample fingerprint and iris images are shown in Figs. 4 and 5.

Figure 4: Sample fingerprint images
Figure 5: Sample iris images
The results obtained by the HSSDF algorithm compared to the existing algorithms [25] with respect to the optimal solutions generated are shown in Tab. 1. The HSSDF algorithm obtained optimal solutions on all the applied images (Tab. 1). For instance, for FP_Image 1, the presented HSSDF algorithm attained the best solution compared with previous work [74,129], whereas the Hybrid Genetic Algorithm Particle Swarm Optimization (HGAPSO) [67,125] and Particle Swarm Optimization [62,34] algorithms performed worse. Similarly, for FP_Image2, the presented HSSDF algorithm achieved the best solution compared with other studies [168,21], whereas the HGAPSO [162,16] and PSO [95,87] algorithms were ineffective solutions. Likewise, for FP_Image3, the presented HSSDF algorithm obtainedthe best solution compared with other methods [109,102], whereas the HGAPSO [106,99] and PSO [20,43] algorithms achieved poor solutions. The results for the best solution attained by the HSSDF algorithm on the applied images compared with existing models are shown in Tab. 2. The findings for the best solution generated by HSSDF and other existing algorithms on the applied FP_Image 1 are shown in Fig. 6. The HSSDF algorithm generated an effective best solution of 129, whereas the HGAPSO and PSO algorithms failed to generate better results, attaining the least-best solutions of 125 and 62, respectively (Fig. 6).
Table 1: Optimal solutions obtained by the proposed HSSDF model

Table 2: Best solutions for fingerprint and corresponding Iris images

The best solution produced by HSSDF with existing systems for the applied FP_Image2 is shown in Fig. 7. The HSSDF algorithm gave an active best solution of 168, whereas the HGAPSO and PSO algorithms were unsuccessful in providing better results. They reached their best solutions with values of 162 and 95, respectively.
The best solution created by HSSDF with existing algorithms for the applied FP_Image 3 is shown in Fig. 8. The HSSDF algorithm gave a proficient best solution of 129, whereas the HGAPSO and PSO algorithms had poor performance with best solutions of 106 and 43, respectively. The performance of the HSSDF algorithm interms of the best solution under the presence of MIM attack is shown in Tab. 3 and Fig. 9. The PSO algorithm exhibited poor performance under the presence of MIM attack by attaining a higher best cost of 0.03989. The HGAPSO algorithm showed slightly better performance over the PSO algorithm with a moderate best cost of 0.01716, but it was not better than the presented HSSDF algorithm. Finally, the HSSDF algorithm showed effective performance compared with the other two models by achieving a least-best cost of 0.01043.
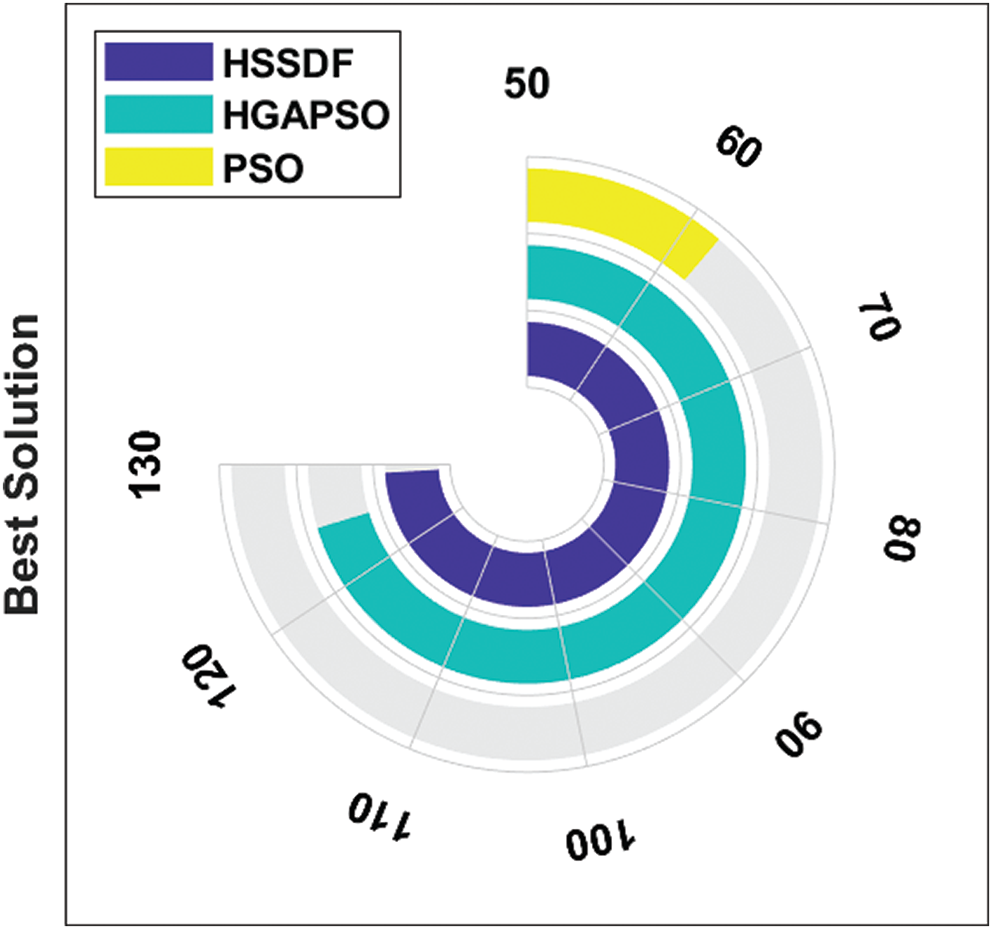
Figure 6: Best cost analysis of the HSSDF algorithm on FP_Image_1
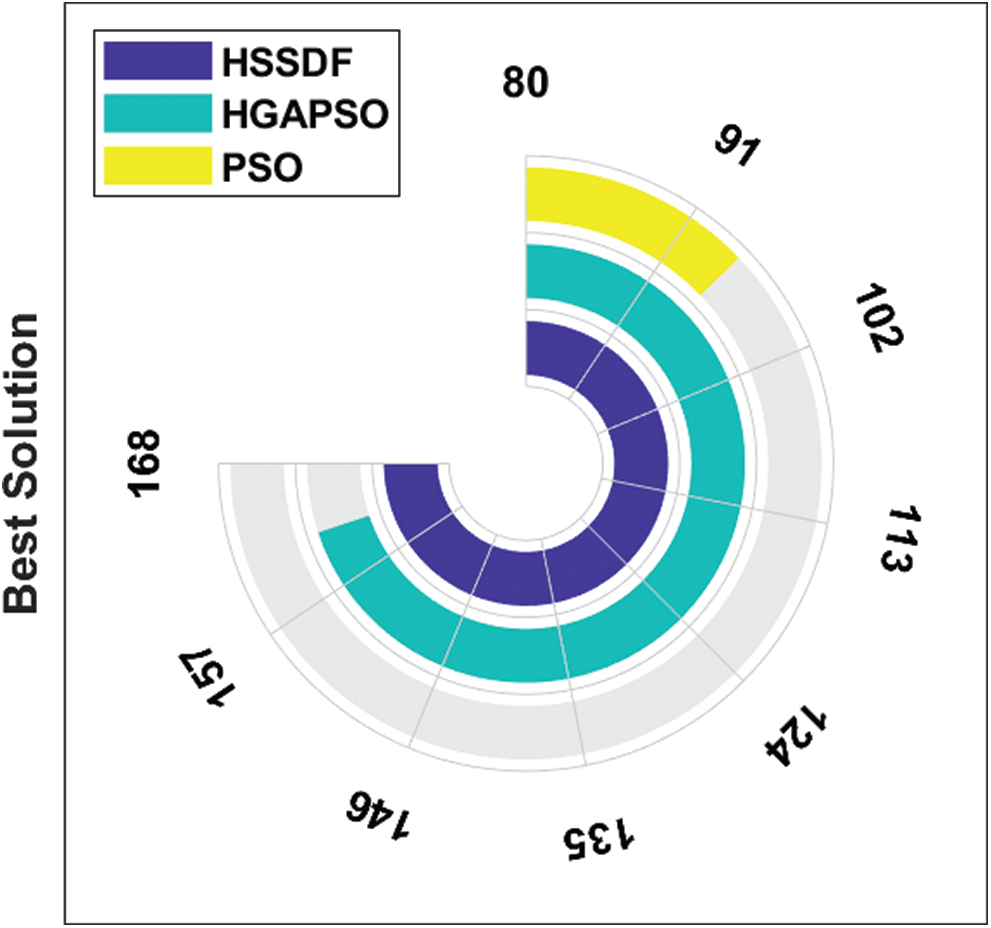
Figure 7: Best cost analysis of HSSDF algorithm on FP_Image_2
It is evident from the detailed experimental analysis that the HSSDF algorithm accomplishes better security compared with the HGAPSO and PSO algorithms even in the presence of MIM attacks. Therefore, the HSSDF algorithm can be employed as a proper model for the secure transmission of data in the cloud environment.
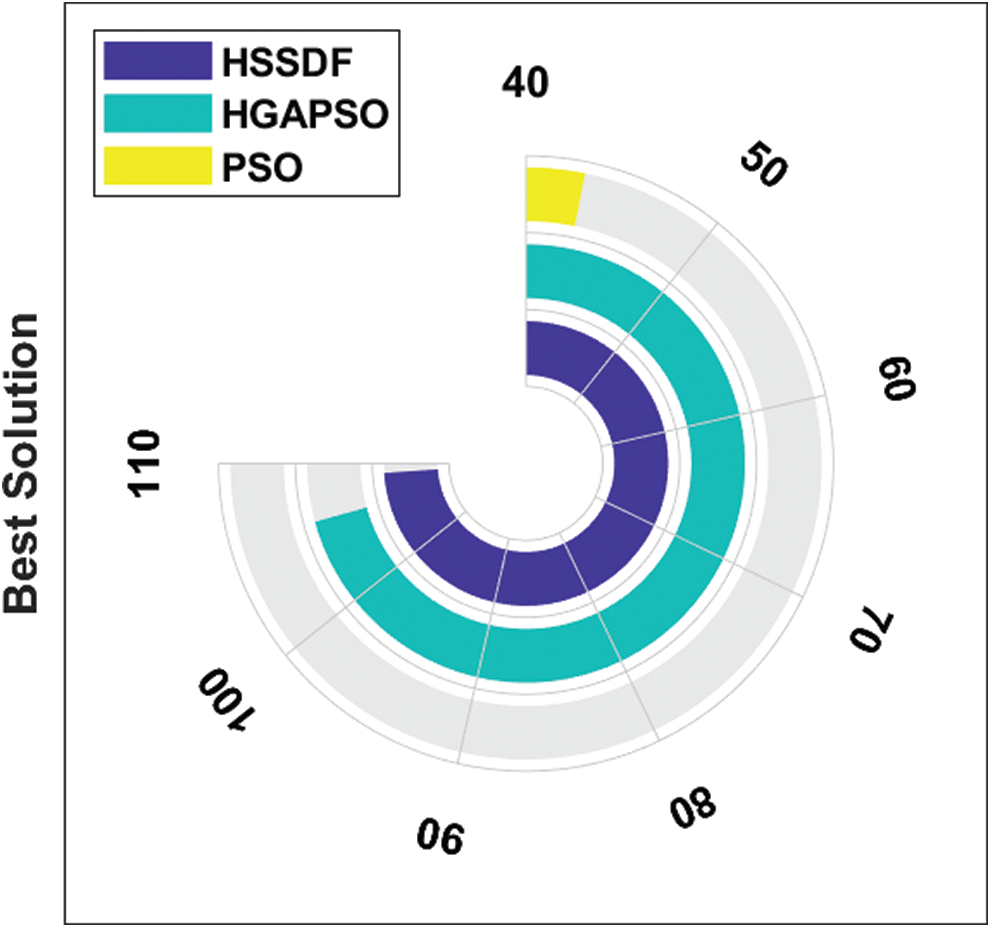
Figure 8: Best cost analysis of HSSDF algorithm on FP_Image_3
Table 3: Performance of MIM attack on existing algorithms and the proposed model


Figure 9: Results analysis of HSSDF under MIM attack
This paper describes a new HMO-ISOA scheme for CC environments. The presented HMO-ISOA technique makes use of iris and fingerprint biometrics. Primarily, the identities of the users (i.e., fingerprint and iris) are initially captured, and a feature extraction process is carried out using the DLTerQEP technique. Once the features are generated, they are provided to the HSSDF technique for optimal key generation. A central benefit of determining the optimal value in this way is that the intruder cannot determine it. In addition, the intruder cannot work out which specific part of the fingerprint or iris feature values are acted upon as a key for the AES technique. Subsequently, the AES algorithm encrypts the data using the optimal key that is generated, and the encrypted data is transmitted to the CC environment. Experimental analysis was performed on five fingerprint and iris images for the case of an MIM attack. The obtained results demonstrate the effectiveness of the HMO-ISOA technique compared with other existing methods interms of accuracy and best cost. In the future, the performance of the HMO-ISOA technique could be improved using compression models.
Acknowledgement: We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. B. Zhu and G. Gong, “Multidimensional meet-in-the-middle attack and its applications to KATAN32/48/64,” Cryptography and Communications, vol. 6, no. 4, pp. 1–15, 2014. [Google Scholar]
2. H. Liu, H. Ning, Q. Xiong and L. T. Yang, “Shared authority based privacy-preserving authentication protocol in cloud computing,” IEEE Transaction on Parallel and Distributed Systems, vol. 26, no. 1, pp. 241–251, 2015. [Google Scholar]
3. J. Zhou, X. Lin, X. Dong and C. Zhenfu, “PSMPA: Patient selfcontrollable and multi-level privacy-preserving cooperative authentication in distributed m-healthcare cloud computing system,” IEEE Transactions on Parallel and Distributed Systems, vol. 26, no. 6, pp. 1693–1703, 2015. [Google Scholar]
4. B. S. Rawal, V. Vijayakumar, G. Manogaran, R. Varatharajan and N. Chilamkurti, “Secure disintegration protocol for privacy preserving cloud storage,” Wireless Personal Communication, vol. 103, pp. 1–17, 2018. [Google Scholar]
5. L. Joseph, K. Liang, W. Susilo, J. Liu and Y. Xiang, “Two-factor data security protection mechanism for cloud storage system,” IEEE Transactions on Computers, vol. 65, no. 6, pp. 1992–2004, 2016. [Google Scholar]
6. T. H. Yuen, J. K. Liu, M. H. Au, X. Huang, W. Susilo et al., “K-times attribute-based anonymous access control for cloud computing,” IEEE Transactions on Computers, vol. 64, no. 9, pp. 2595–2608, 2015. [Google Scholar]
7. S. Dey, S. Sampalli and Q. Ye, “MDA: Message digest-based authentication for mobile cloud computing,” Journal of Cloud Computing: Advances, Systems and Applications, vol. 5, no. 18, pp. 1–13, 2018. [Google Scholar]
8. Z. Liu, H. Yan and Z. Li, “Server-aided anonymous attribute-based authentication in cloud computing,” Future Generation Computer Systems, vol. 52, pp. 61–66, 2015. [Google Scholar]
9. X. Li, J. Niu, M. K. Khan and J. Liao, “An enhanced smart card based remote user password authentication scheme,” Journal of Network and Computer Applications, vol. 36, pp. 1365–1371, 2013. [Google Scholar]
10. C. Guo, N. Luo, M. Z. A. Bhuiyan, Y. Jie, Y. Chen et al., “Key-aggregate authentication cryptosystem for data sharing in dynamic cloud storage,” Future Generation Computer Systems, vol. 84, pp. 190–199, 2018. [Google Scholar]
11. G. Sharma and S. Kalra, “Identity-based secure authentication scheme based on quantum key distribution for cloud computing,” Peer-to-Peer Networking and Applications, vol. 11, pp. 1–15, 2016. [Google Scholar]
12. S. Balakrishnan, J. Janet and K. N. Sivabalan, “Secure data sharing in a cloud environment by using biometric leakage resilient authenticated key exchange,” Pakistan Journal of Biotechnology, vol. 15, no. 2, pp. 293–297, 2018. [Google Scholar]
13. J. Janet, S. Balakrishnan and K. Somasekhara, “Fountain code based cloud storage mechanism for optimal file retrieval delay,” in 2016 Int. Conf. on Information Communication and Embedded Systems, Chennai, pp. 1–4, 2016. [Google Scholar]
14. L. Xiong, Z. Xu and Y. Xu, “A secure re-encryption scheme for data services in a cloud computing environment,” Concurrency and Computation: Practice and Experience, vol. 27, no. 17, pp. 4573–4585, 2015. [Google Scholar]
15. E. Tameem and G. Cho, “Providing privacy and access control in cloud storage services using a KPABE system with secret attributes,” Arabian Journal for Science and Engineering, vol. 39, no. 11, pp. 7877–7884, 2014. [Google Scholar]
16. F. Wang, G. Xu, G. Xu, Y. Wang and J. Peng, “A robust IoT-based three-factor authentication scheme for cloud computing resistant to session key exposure,” Wireless Communications and Mobile Computing, vol. 2020, no. 3805058, pp. 1–15, 2020. [Google Scholar]
17. A. Irshad, S. A. Chaudhry, O. A. Alomari, K. Yahya and N. Kumar, “A novel pairing-free lightweight authentication protocol for mobile cloud computing framework,” IEEE Systems Journal, pp. 1–9, Early Access, 2020. [Google Scholar]
18. V. Kumar, M. Ahmad, D. Mishra, S. Kumari and M. K. Khan, “RSEAP: RFID based secure and efficient authentication protocol for vehicular cloud computing,” Vehicular Communications, vol. 22, pp. 100213, 2020. [Google Scholar]
19. L. Xiong, F. Li, M. He, Z. Liu and T. Peng, “An efficient privacy-aware authentication scheme with hierarchical access control for mobile cloud computing services,” IEEE Transactions on Cloud Computing, pp. 1–10, Early Access, 2020. [Google Scholar]
20. S. Jain, C. Nandhini and R. Doriya, “ECC-based authentication scheme for cloud-based robots,” Wireless Personal Communications, pp. 1–20, Early Access, 2020. [Google Scholar]
21. G. Deep, L. Kaur and S. Gupta, “Directional local ternary quantized extrema pattern: A new descriptor for biomedical image indexing and retrieval,” Engineering Science and Technology, An International Journal, vol. 19, no. 4, pp. 1895–1909, 2016. [Google Scholar]
22. A. L. Chang, E. Cuevas, F. Fausto, D. Zaldivar and M. Perez, “Social spider optimization algorithm: Modifications, applications, and perspectives,” Mathematical Problems in Engineering, vol. 2018, no. 6843923, pp. 1–30, 2018. [Google Scholar]
23. S. Mirjalili, “Dragonfly algorithm: A new meta-heuristic optimization technique for 611 solving single-objective, discrete, and multi-objective problems,” Neural Computing and Applications, vol. 27, pp. 1053–1073, 2016. [Google Scholar]
24. R. L. B. Ambika and V. Burkpalli, “Encryption-based steganography of images by multiobjective whale optimal pixel selection,” International Journal of Computers and Applications, vol. 1, pp. 1–10, 2019. [Google Scholar]
25. P. Selvarani, A. Suresh and N. Malarvizhi, “Secure and optimal authentication framework for cloud management using HGAPSO algorithm,” Cluster Computing, vol. 22, no. 2, pp. 4007–4016, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |