Computers, Materials & Continua DOI:10.32604/cmc.2021.017643
Article

Hybrid Nanofluid Flow with Homogeneous-Heterogeneous Reactions

Iskandar Waini1,2, Anuar Ishak2,*and Ioan Pop3

1Fakulti Teknologi Kejuruteraan Mekanikal dan Pembuatan, Universiti Teknikal Malaysia Melaka, Hang Tuah Jaya, 76100, Durian Tunggal, Melaka, Malaysia
2Department of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, 43600, UKM Bangi, Selangor, Malaysia
3Department of Mathematics, Babeş-Bolyai University, 400084, Cluj-Napoca, Romania
*Corresponding Author: Anuar Ishak. Email: anuar_mi@ukm.edu.my
Received: 05 February 2021; Accepted: 11 March 2021

Abstract: This study examines the stagnation point flow over a stretching/shrinking sheet in a hybrid nanofluid with homogeneous-heterogeneous reactions. The hybrid nanofluid consists of copper (Cu) and alumina (Al2O3) nanoparticles which are added into water to form Cu-Al2O3/water hybrid nanofluid. The similarity equations are obtained using a similarity transformation. Then, the function bvp4c in MATLAB is utilised to obtain the numerical results. The dual solutions are found for limited values of the stretching/shrinking parameter. Also, the turning point arises in the shrinking region (λ<0). Besides, the presence of hybrid nanoparticles enhances the heat transfer rate, skin friction coefficient, and the concentration gradient. In addition, the concentration gradient is intensified with the heterogeneous reaction but the effect is opposite for the homogeneous reaction. Furthermore, the velocity and the concentration increase, whereas the temperature decreases for higher compositions of hybrid nanoparticles. Moreover, the concentration decreases for larger values of homogeneous and heterogeneous reactions. It is consistent with the fact that higher reaction rate cause a reduction in the rate of diffusion. However, the velocity and the temperature are not affected by these parameters. From these observations, it can be concluded that the effect of the homogeneous and heterogeneous reactions is dominant on the concentration profiles. Two solutions are obtained for a single value of parameter. The temporal stability analysis shows that only one of these solutions is stable and thus physically reliable over time.

Keywords: Homogeneous-heterogeneous reactions; stagnation point; hybrid nanofluid; shrinking sheet; dual solutions; stability analysis

1  Introduction

Boundary layer flow produced by the stretching or shrinking surface was introduced by researchers many years ago. The pioneered work of the problems can be found in the literature [1–4]. On the other hand, Hiemenz [5] was the first researcher to consider the boundary layer flow of a stagnation point over a rigid surface. Then, Homann [6] extended the problem to the axisymmetric flow, while Wang [7] considered the flow on a shrinking sheet. Furthermore, homogeneous (bulk) and heterogeneous (surface) reactions on the stagnation point flow were examined by Chaudhary and Merkin [8,9]. A simple of these reactions with equal and different diffusivities for autocatalyst and reactant was introduced in their studies. Then, Merkin [10] extended the problem to the Blasius flow. The homogeneous and heterogeneous reactions have significant applications in the biochemical, catalysis, and combustion systems. Inspired by these studies, Khan and Pop [11] examined these effects on the flow towards a permeable surface. They noticed that dual solutions exist in the injection region but a unique solution is observed in the suction region. Besides, Kameswaran et al. [12] studied a similar problem by considering the magnetic field effects. They discovered that the skin friction coefficient and the concentration gradient increased with increasing of the magnetic parameter. Apart from that, several studies [13–15] involving homogeneous and heterogeneous reactions have been reported in the literature.

In 1995, Choi and Eastman [16] introduced nanofluid, which is a mixture of the base fluid and a single type of nanoparticles, to enhance the thermal conductivity. Some works on such fluids can be found in [17–23]. Recently, some studies found that advanced nanofluid which consists of another type of nanoparticles and the regular nanofluid could improve its thermal properties, and this mixture is termed as ‘hybrid nanofluid’. The prior experimental works using the hybrid nanoparticles have been done by several researchers [24–26]. Besides, the numerical studies on the flow of hybrid nanofluids were studied by Takabi and Salehi [27]. Moreover, the dual solutions of the hybrid nanofluid flow were examined by Waini et al. [28–30]. Other physical aspects were considered by several authors [31–38]. Also, the review papers can be found in [39–44].

Motivated by the above mentioned studies, this paper considers the homogeneous-heterogeneous reactions on hybrid nanofluid flow with Al2O3-Cu hybrid nanoparticles. Different from the work reported by Ramesh et al. [33], the present study considers the stagnation point flow towards a stretching/shrinking sheet. Most importantly, in this study, two solutions are discovered for a single value of parameter, and the stability of these solutions over time is tested.

2  Mathematical Model

The stagnation point flow triggered by a stretching/shrinking sheet in Al2O3-Cu/water hybrid nanofluid is considered. In Fig. 1, the free stream and the surface velocities are given as ue(x)=cx and uw(x)=dx, respectively, with c>0, whereas d<0 and d>0 indicate the shrinking and stretching sheets, respectively, and d=0 indicates the static sheet. Meanwhile, the ambient and the surface temperatures are given by T∞ and Tw, respectively, and both are constants. The homogeneous-heterogeneous reactions are also taking into consideration.

Following Chaudhary and Merkin [8] and Merkin [10], a simple homogeneous reaction and the first order of heterogeneous reaction can respectively be written as

A+2B→3B,rates=k1ab2 (1)

A→B,rates=ksa (2)

where these processes are assumed to be isothermal. Here, a and b are the chemical concentrations for species A and B, respectively, with the rate constants k1 and ks. Thus, the equations that govern the hybrid nanofluid flow are [8,33]:

∂u∂x+∂v∂y=0 (3)

u∂u∂x+v∂u∂y=ueduedx+μhnfρhnf∂2u∂y2 (4)

u∂T∂x+v∂T∂y=khnf(ρCp)hnf∂2T∂y2 (5)

u∂a∂x+v∂a∂y=DA∂2a∂y2−k1ab2 (6)

u∂b∂x+v∂b∂y=DB∂2b∂y2+k1ab2 (7)

subject to:

v=0,u=uw(x),T=Tw,DA∂a∂y=ksa,DB∂b∂y=−ksa a y=0

u→ue(x),T→T∞,a→a0,b→0 as y→∞ (8)

where the coordinates (x,y) with corresponding velocities (u,v) are measured along the x- and y-axes, and T represents the temperature. Besides, DA and DB are the corresponding diffusion coefficients of species A and B, and a0>0. Further, the thermophysical properties can be referred to in Tabs. 1 and 2. Note that φ1 (Al2O3) and φ2 (Cu) are the nanoparticles volume fractions where φhnf=φ1+φ2, and the subscripts n1 and n2 correspond to their solid components, while the subscripts hnf and f signify the hybrid nanofluid and the base fluid, respectively.

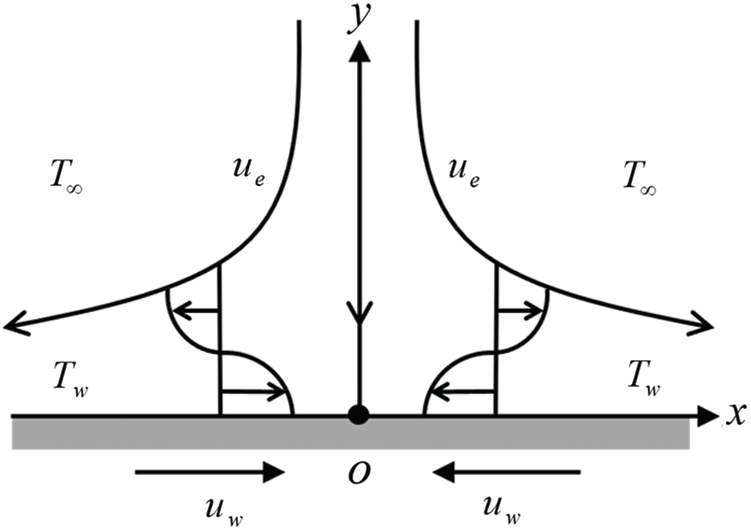
Figure 1: Flow configuration model

To obtain similarity solution, the following variables are employed [33]:

ψ=cνfxf(η),η=yc/νf,θ(η)=(T−T∞)/(Tw−T∞),

a=a0g(η),b=a0h(η) (9)

where ψ is the stream function defined as u=∂ψ/∂y and v=−∂ψ/∂x. Then one obtains

u=cxf′(η),v=−cνff(η). (10)

It is noted that the continuity Eq. (3) is identically satisfied.

Table 1: Thermophysical properties of nanoparticles and water [19]

Table 2: Thermophysical properties of hybrid nanofluid [27]

Now, Eqs. (4) to (7) respectively reduce to:

μhnf/μfρhnf/ρff‴+ff″−f′2+1=0 (11)

1Prkhnf/kf(ρCp)hnf/(ρCp)fθ″+fθ′=0 (12)

1Scg″+fg′−Kgh2=0 (13)

δSch″+fh′+Kgh2=0 (14)

subject to:

f(0)=0,f′(0)=λ,θ(0)=1,g′(0)=Ksg(0),δh′(0)=Ksg(0),

f′(η)→1,θ(η)→0,g(η)→1,h(η)→0as η→∞, (15)

where primes denote the differentiation with respect to η. The physical parameters appear in Eqs. (12) to (15) are the Prandtl number Pr, the Schmidt number Sc, the ratio of the diffusion coefficients δ, the strength of the homogeneous K and the heterogeneous Ks reactions, and the stretching/shrinking parameter λ, and they are given as:

Pr=(μCp)fkf,Sc=νfDA,δ=DBDA,K=k1a02c,Ks=ksDAc/νf,λ=dc (16)

Note that, λ<0 and λ>0 are for the shrinking and stretching sheets, respectively, while λ=0 designates the static sheet. As discussed by Chaudhary and Merkin [8], both diffusion coefficients (DA and DB) are of comparable sizes, thus, these coefficients are assumed to be equal by taking δ=1. Hence, one gets:

g(η)+h(η)=1. (17)

Using Eq. (17), Eqs. (13) and (14) become:

1Scg″+fg′−Kg(1−g)2=0 (18)

subject to:

g′(0)=Ksg(0),g(η)→1as η→∞ (19)

The skin friction coefficient Cf and the local Nusselt number Nux are defined as:

Cf=μhnfρfue2(∂u∂y)y=0,Nux=−xkhnfkf(Tw−T∞)(∂T∂y)y=0. (20)

Using the similarity variables (9), one obtains

Rex1/2Cf=μhnfμff″(0),Rex−1/2Nux=−khnfkfθ′(0) (21)

where Rex=uex/νf is the local Reynolds number.

3  Temporal Stability Analysis

The stability of the dual solutions over time is studied. This analysis was first introduced by Merkin [45] and then followed by Weidman et al. [46]. Firstly, consider the new variables as follows:

ψ=cνfxf(η,τ),η=yc/νf,θ(η,τ)=(T−T∞)/(Tw−T∞),

a=a0g(η,τ),b=a0h(η,τ),τ=ct (22)

Now, consider the unsteady form of Eqs. (4) to (7) while Eq. (3) remains unchanged. On using (22), one obtains:

μhnf/μfρhnf/ρf∂3f∂η3+f∂2f∂η2−(∂f∂η)2+1−∂2f∂η∂τ=0 (23)

1Prkhnf/kf(ρCp)hnf/(ρCp)f∂2θ∂η2+f∂θ∂η−∂θ∂τ=0 (24)

1Sc∂2g∂η2+f∂g∂η−Kg(1−g)2−∂g∂τ=0 (25)

subject to:

f(0,τ)=0,f′(0,τ)=λ,θ(0,τ)=1,g′(0,τ)=Ksg(0,τ),

f′(η,τ)→1,θ(η,τ)→0,g(η,τ)→1as η→∞ (26)

Then, the disturbance is applied to the steady solutions f=f0(η), θ=θ0(η), and g=g0(η) of Eqs. (11), (12) and (18) by employing the following relations [46]:

f(η,τ)=f0(η)+e−γτF(η),θ(η,τ)=θ0(η)+e−γτH(η),

g(η,τ)=g0(η)+e−γτG(η) (27)

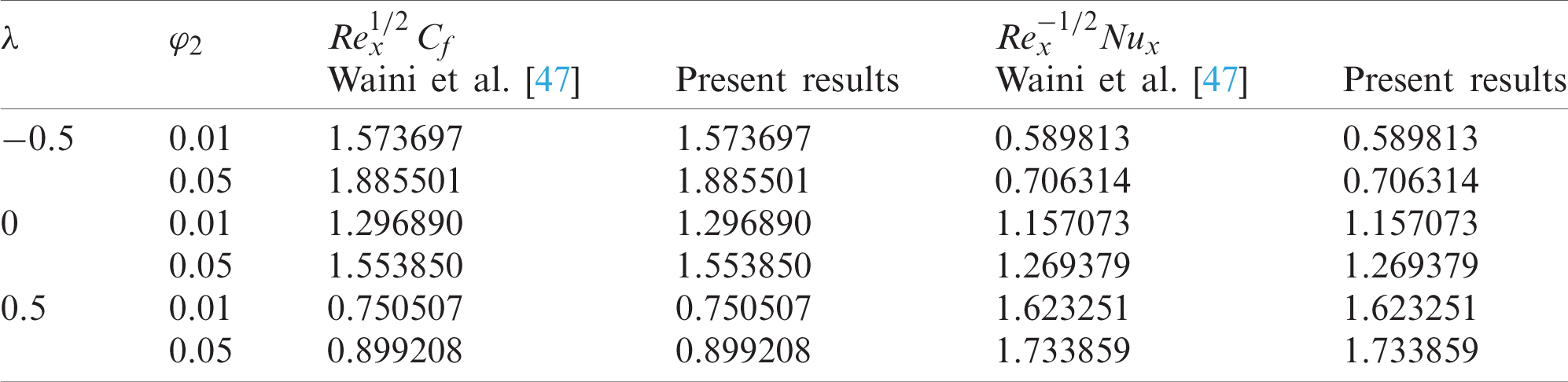
Table 3: Values of g(0) for various values of K and Ks when φhnf = 0 (regular fluid), Sc = 1, and λ = 0 (static sheet)

Table 4: Values of Rex1/2Cf and Rex−1/2Nux for different values of λ and φ2 when Pr=6.2 and φ1=0 (Cu/water)

The sign (positive or negative) of the eigenvalue γ determines the stability of the solutions. Also, F(η), H(η), and G(η) are relatively small compared to f0(η), θ0(η), and g0(η). On using Eq. (27), and after linearization, Eqs. (23) to (25) become:

μhnf/μfρhnf/ρfF‴+f0F″+f0″F−2f0′F′+γF′=0 (28)

1Prkhnf/kf(ρCp)hnf/(ρCp)fH″+f0H′+θ0′F+γH=0 (29)

1ScG″+f0G′+g0′F−K(1−4g0+3g02)G+γG=0 (30)

subject to:

F(0)=0,F′(0)=0,H(0)=0,G′(0)=KsG(0)

F′(η)→0,H(η)→0,G(η)→0as η→∞ (31)

The quantity F″(0) is fixed in order to obtain γ in Eqs. (28) to (30). Without loss of generality we take F″(0)=1, see also [48].

Table 5: Values of Rex1/2Cf, Rex−1/2Nux, and g′(0) for Al2O3-Cu/water with various values of parameters when Sc=1 and Pr=6.2

4  Results and Discussion

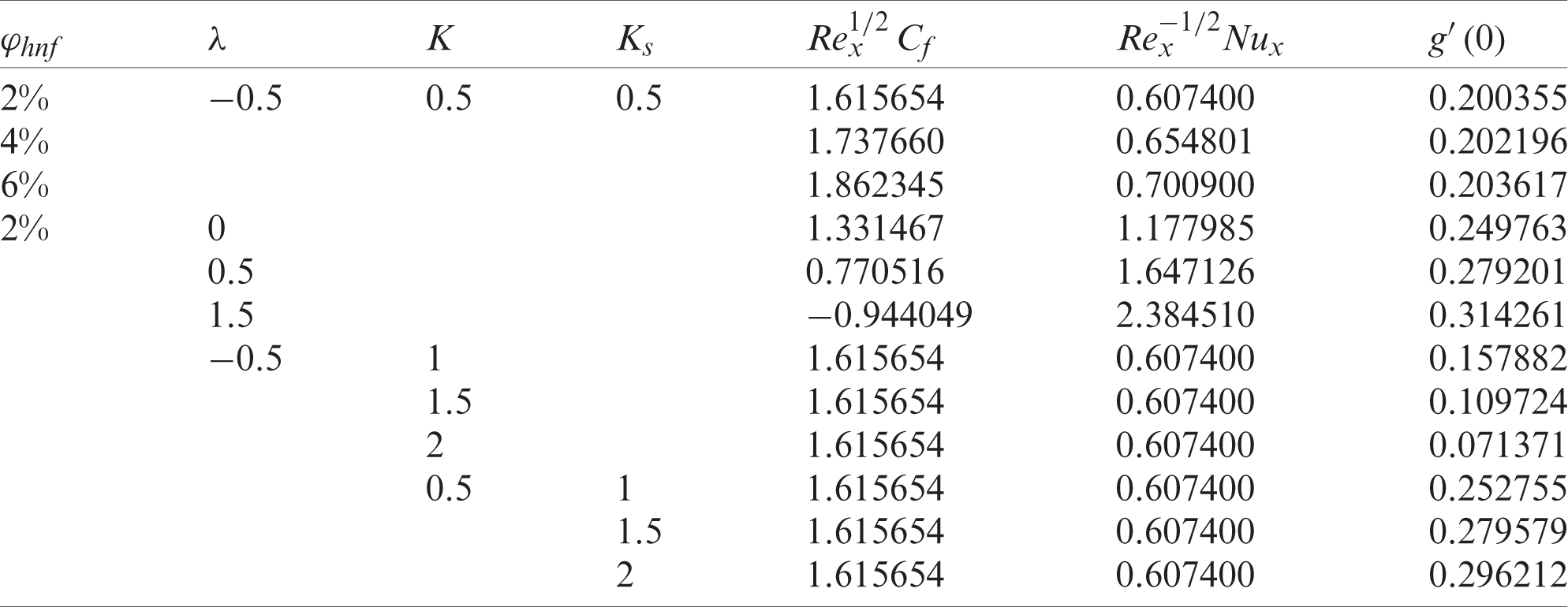
By utilising the package bvp4c in MATLAB software, Eqs. (11), (12), and (18) subjected to Eqs. (15) and (19) are solved numerically. In particular, bvp4c is a finite-difference code that implements the three-stage Lobatto IIIa formula [49]. This is a collocation formula that provides a continuous solution with fourth-order accuracy. Mesh selection and error control are based on the residual of the continuous solution. The effectiveness of this solver ultimately counts on our ability to provide the algorithm with an initial guess for the solution. Because the present problem may have multiple (dual) solutions, the bvp4c function requires an initial guess of the solution for Eqs. (11), (12), and (18). Using this guess value, the velocity, temperature and the concentration profiles must satisfy the boundary conditions (15)and (19)asymptotically. Determining an initial guess for the first solution is not difficult because the bvp4c method will converge to the first solution even for poor guesses. However, it is rather difficult to determine a sufficiently good guess for the second solution of Eqs. (11), (12), and (18). Also, this convergence issue is influenced by the value of the selected parameters. In this study, the relative tolerance was set to 10−10. Tosolve this boundary value problem, it is necessary to first reduce the equations to a system of first-order ordinary differential equations. Further, the effect of several physical parameters on flow behaviour is examined. The total composition of Al2O3 and Cu volume fractions are applied in a one-to-one ratio. For instance, 1% of Al2O3 (φ1=1%) and 1% of Cu (φ2=1%) are mixed to produce 2% of Al2O3-Cu hybrid nanoparticles volume fractions, i.e., φhnf=2%.

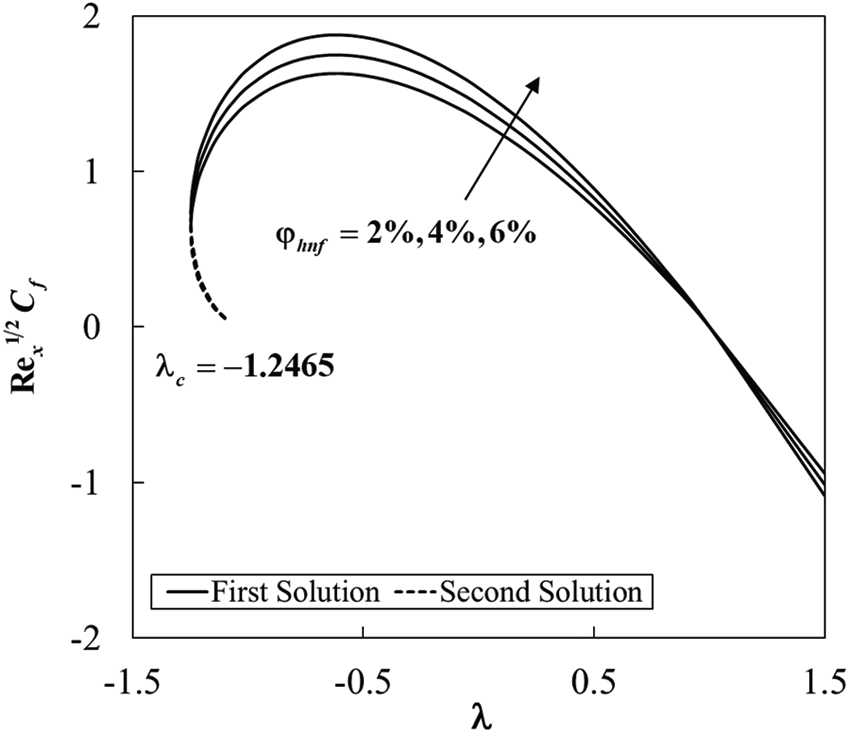
Figure 2: Variation of the skin friction Rex1/2Cf against λ for different values of φhnf

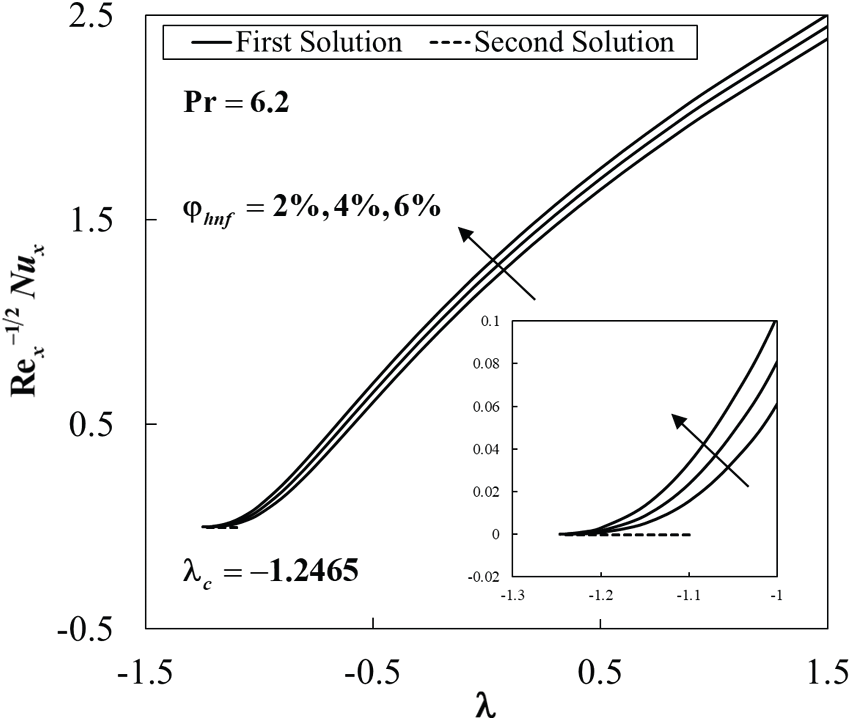
Figure 3: Variation of the local Nusselt number Rex−1/2Nux against λ for different values of φhnf

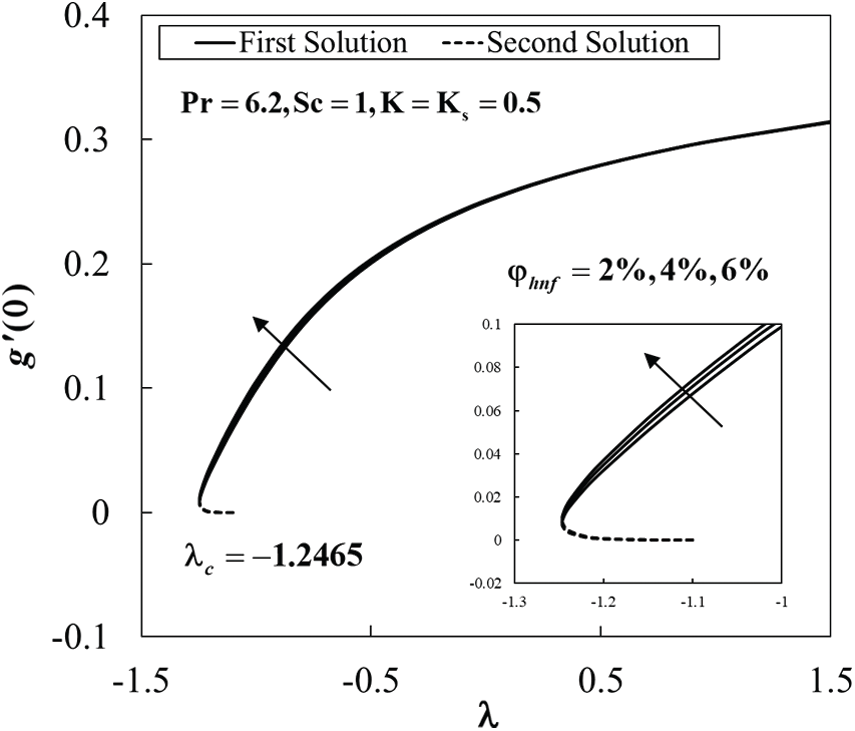
Figure 4: The concentration gradient at the surface g′(0) against λ for various values of φhnf

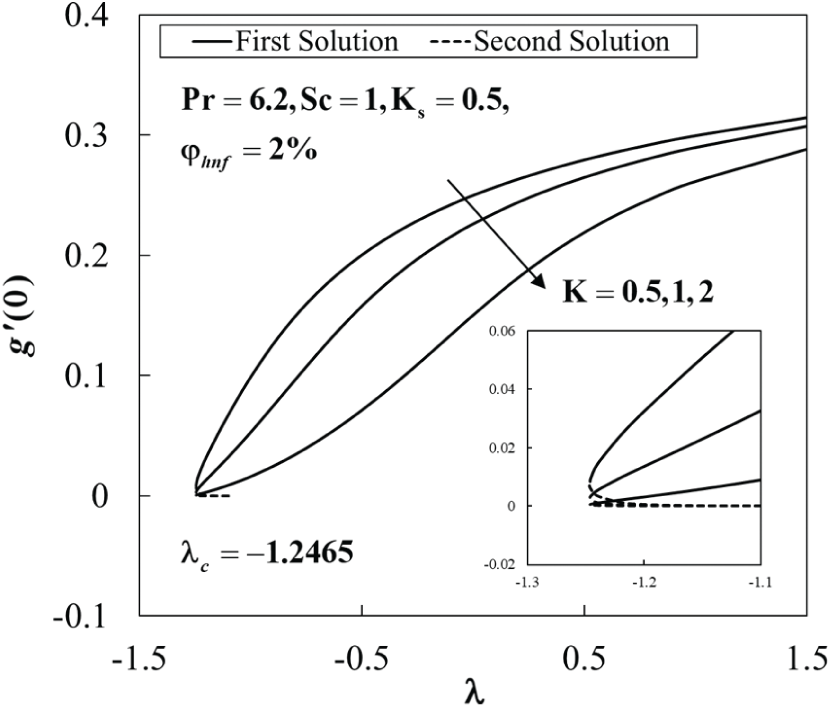
Figure 5: The concentration gradient at the surface g′(0) against λ for various values of K

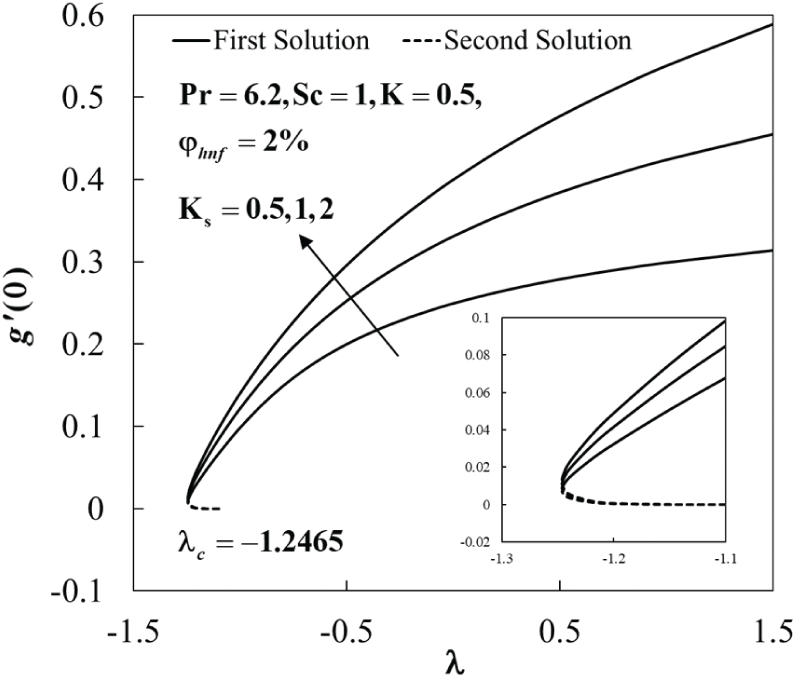
Figure 6: The concentration gradient at the surface g′(0) against λ for various values of Ks

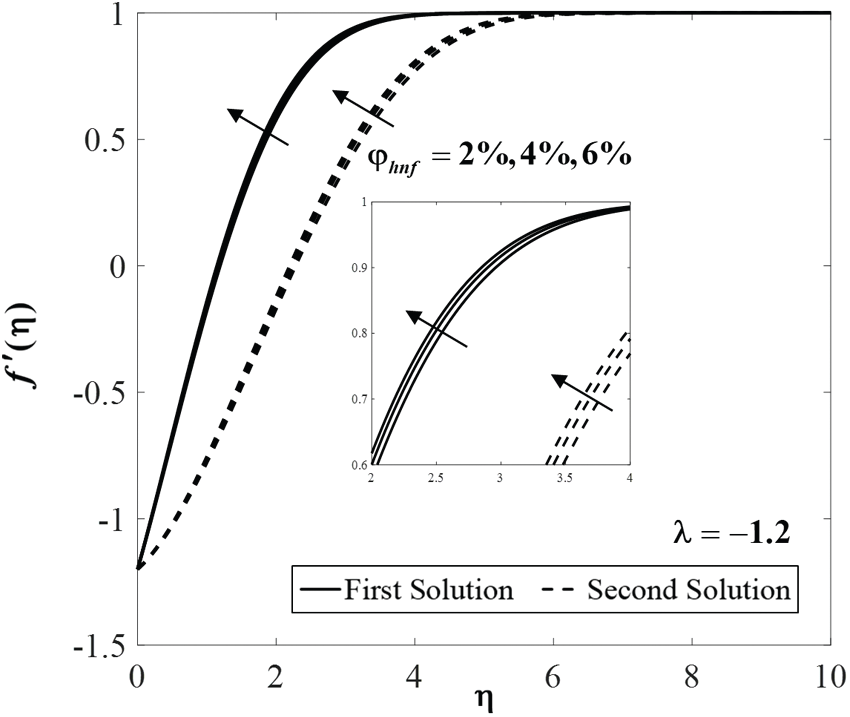
Figure 7: Velocity profiles f′(η) for various values of φhnf

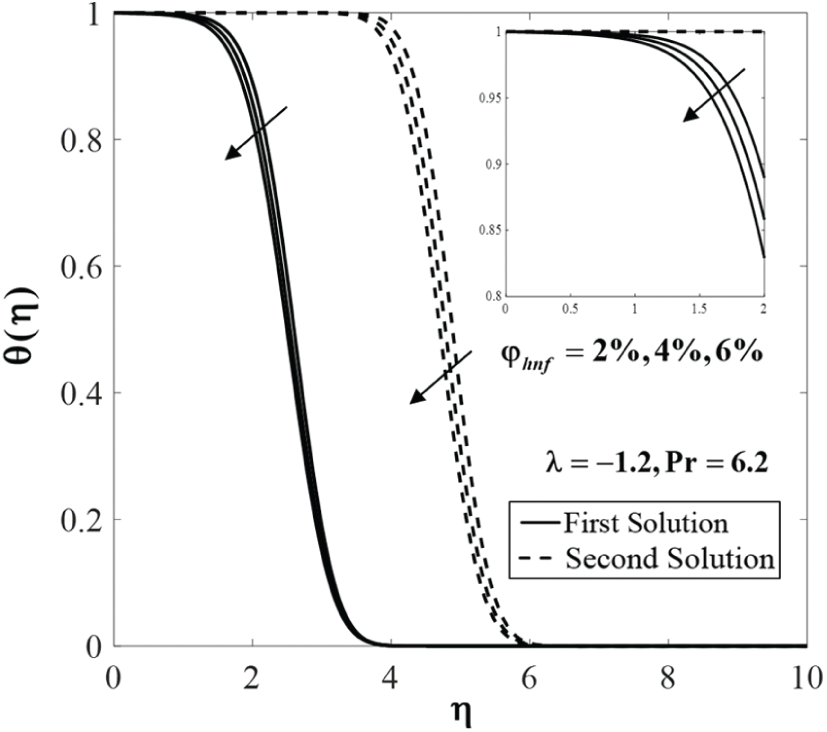
Figure 8: Temperature profiles θ(η) for various values of φhnf

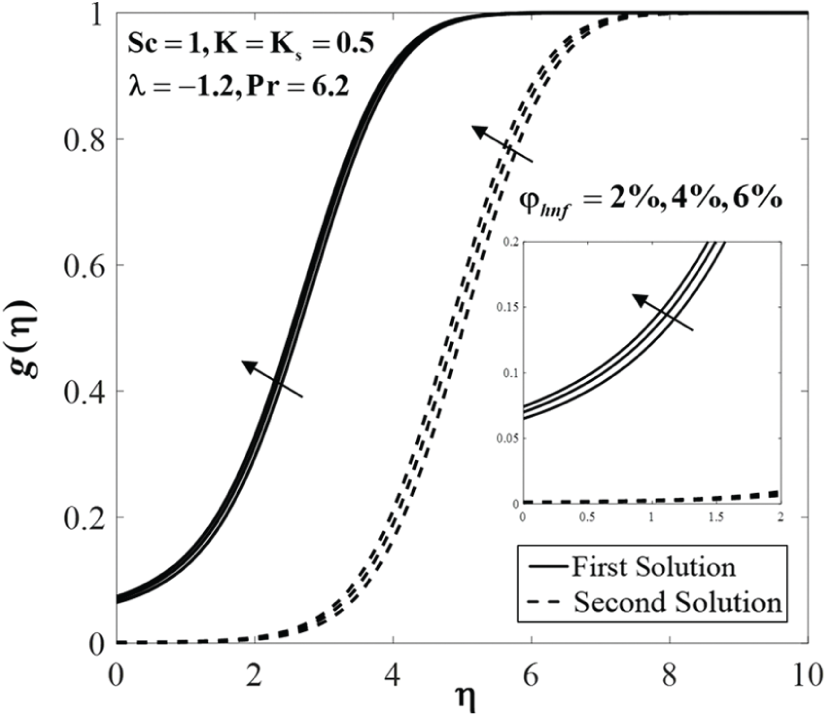
Figure 9: Concentration profiles g(η) for various values of φhnf

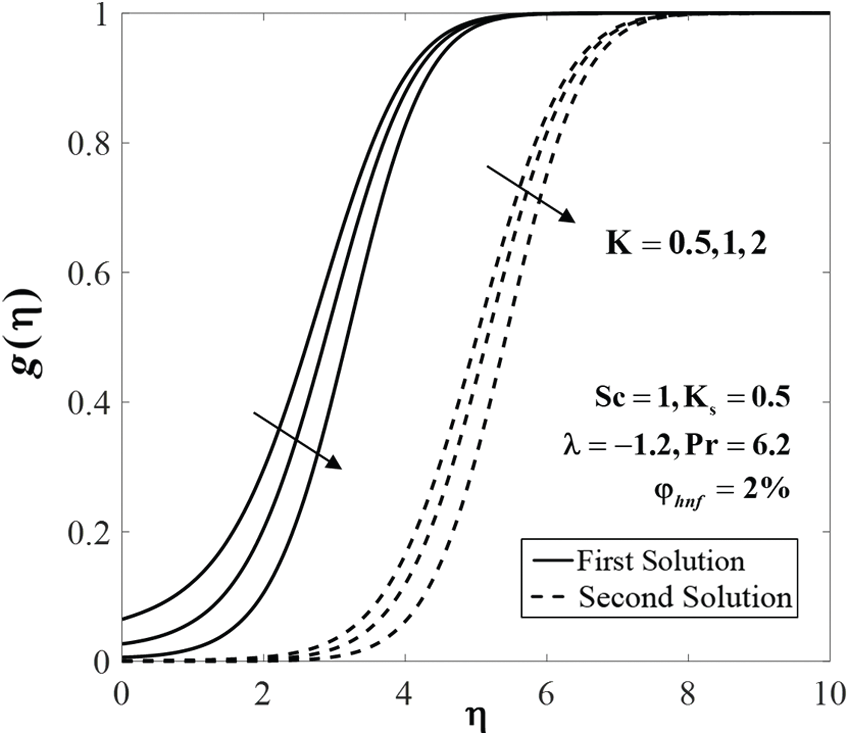
Figure 10: Concentration profiles g(η) for various values of K

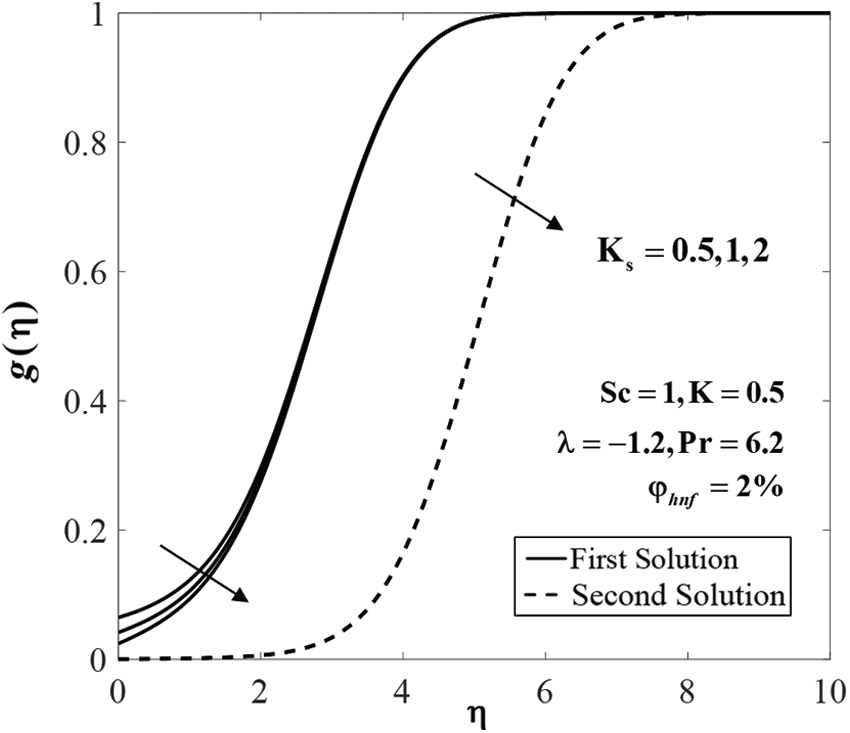
Figure 11: Concentration profiles g(η) for various values of Ks

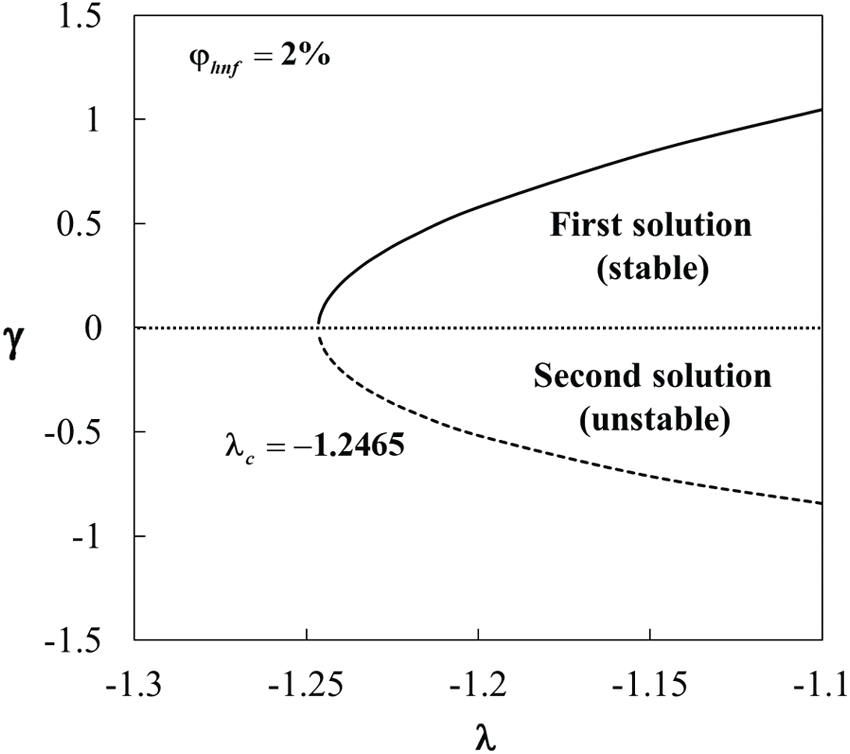
Figure 12: Eigenvalues γ against λ

The values of species concentration on the surface g(0) are compared with Khan and Pop [11] for various values of K and Ks when φhnf=0 (regular fluid), Sc=1, and λ=0 (static sheet). It is found that the results are comparable for each K and Ks considered, as shown in Tab. 3. Also, Tab. 4 shows the comparison of Rex1/2Cf and Rex−1/2Nux with Waini et al. [47] when Pr=6.2 for different values of λ and φ2 for Cu/water (φ1=0). It is noted that the present results are comparable with that mentioned literature. Next, Tab. 5 displays the values of Rex1/2Cf, Rex−1/2Nux and g′(0) for Al2O3-Cu/water with various values of parameters when Sc=1 and Pr=6.2. The rising of φhnf tends to upsurge the values of these physical quantities. These behaviours also can be seen in Figs. 2 to 4. This finding is consistent with the fact that the added hybrid nanoparticles improve the heat transfer rate due to synergistic effects as discussed by Sarkar et al. [39]. Besides, the increasing of λ leads to enhance the values of Rex−1/2Nux and g′(0), but the values of Rex1/2Cf is declining with λ. Also, the rise of K declines the values of g′(0), whereas the effect of larger Ks is to enhance the values of g′(0). However, the values of Rex1/2Cf and Rex−1/2Nux are not affected by these parameters. At the same time, Figs. 5 and 6 show the variations of g′(0) against λ with the effect of K and Ks. On the other hand, dual solutions are obtained for a limited range of λ as shown in Figs. 2 to 6. The bifurcation of the solutions occurs at λc=−1.2465 for all considered parameters.

Further, Figs. 7 to 9 display the effect of φhnf on f′(η), θ(η) and g(η) when λ=−1.2,6.2,Sc=1, and K=Ks=0.5. It is seen that both branch solutions of f′(η) and g(η) show an increasing pattern for higher compositions of φhnf. Meanwhile, the temperature θ(η) declines for both branch solutions. Physically, the addition of the nanoparticles increases the viscosity of the fluid and thus slowing down the fluid motion. Also, the added nanoparticles dissipate energy in the form of heat and consequently exert more energy which enhances the temperature.

The effects of K and Ks on the concentration g(η) when λ=−1.2,Pr=6.2,Sc=1 and φhnf=2% are depicted in Figs. 10 and 11, respectively. The decreasing pattern of concentration on both branch solutions is observed. It is consistent with the fact that the reaction rate increases as the values of K and Ks increase, which cause the reduction in the diffusion rate.

The variations of the eigenvalues γ against λ when φhnf=2% are portrayed in Fig. 12. For the positive values of γ, it is noted that e−γτ→0 as time evolves (τ→∞). In contrast, for the negative values of γ, e−γτ→∞, which shows an increasing of disturbance over time. These behaviours show that the first solution is stable and physically reliable, while the second solution is unstable in the long run.

5  Conclusion

The stagnation point flow of Al2O3-Cu/water hybrid nanofluid over a stretching/shrinking sheet was studied. Both homogeneous and heterogeneous reactions were considered. Findings revealed that dual solutions appeared for some ranges of the shrinking strength λ. The solutions were obtained up to a certain critical value of λ(<0), in the shrinking region. The increment of the skin friction coefficient Rex1/2Cf, local Nusselt number Rex−1/2Nux, and the concentration gradient at the surface g′(0) were observed with the rise of the nanoparticles volume fractions φhnf. The values of g′(0) decreased for larger values of K, but increased with the rise of Ks. Finally, it was discovered that two solutions were obtained for a single value of parameter. Further analysis showed that only one of these solutions is stable and thus physically reliable over time.

Acknowledgement: We acknowledge the Universiti Teknikal Malaysia Melaka and the Universiti Kebangsaan Malaysia (DIP-2020-001) for financial supports.

Funding Statement: This research was funded by Universiti Kebangsaan Malaysia (Project Code: DIP-2020-001).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. J. Crane, “Flow Past a stretching plate,” Zeitschrift Für Angewandte Mathematik Und Physik ZAMP, vol. 21, no. 4, pp. 645–647, 1970. [Google Scholar]

 2.  S. Goldstein, “On backward boundary layers and flow in converging passages,” Journal of Fluid Mechanics, vol. 21, no. 1, pp. 33–45, 1965. [Google Scholar]

 3.  C. Y. Wang, “Liquid film on an unsteady stretching surface,” Quarterly of Applied Mathematics, vol. 48, no. 4, pp. 601–610, 1990. [Google Scholar]

 4.  M. Miklavčič and C. Y. Wang, “Viscous flow due to a shrinking sheet,” Quarterly of Applied Mathematics, vol. 64, no. 2, pp. 283–290, 2006. [Google Scholar]

 5.  K. Hiemenz, “Die grenzschicht an einem in den gleichförmigen flüssigkeitsstrom eingetauchten geraden kreiszylinder,” Dinglers Polytechnisches Journal, vol. 326, pp. 321–410, 1911. [Google Scholar]

 6.  F. Homann, “Der Einflub Grober Zähigkeit Bei Der Strömung Um Den Zylinder Und Um Die Kugel,” Zeitschrift für Angewandte Mathematik und Mechanik, vol. 16, no. 3, pp. 153–164, 1936. [Google Scholar]

 7.  C. Y. Wang, “Stagnation flow towards a shrinking sheet,” International Journal of Non-Linear Mechanics, vol. 43, no. 5, pp. 377–382, 2008. [Google Scholar]

 8.  M. A. Chaudhary and J. H. Merkin, “A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. I equal diffusivities,” Fluid Dynamics Research, vol. 16, no. 6, pp. 311–333, 1995. [Google Scholar]

 9.  M. A. Chaudhary and J. H. Merkin, “A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. II Different diffusivities for reactant and autocatalyst,” Fluid Dynamics Research, vol. 16, no. 6, pp. 335–359, 1995. [Google Scholar]

10. J. H. Merkin, “A Model for isothermal homogeneous-heterogeneous reactions in boundary-layer flow,” Mathematical and Computer Modelling, vol. 24, no. 8, pp. 125–136, 1996. [Google Scholar]

11. W. A. Khan and I. Pop, “Flow near the two-dimensional stagnation-point on an infinite permeable wall with a homogeneous-heterogeneous reaction,” Communications in Nonlinear Science and Numerical Simulation, vol. 15, no. 11, pp. 3435–3443, 2010. [Google Scholar]

12. P. K. Kameswaran, P. Sibanda, C. R. Reddy and P. Vsn Murthy, “Dual solutions of stagnation-point flow of a nanofluid over a stretching surface,” Boundary Value Problems, vol. 2013, no. 1, pp. 1–12, 2013. [Google Scholar]

13. N. Bachok, A. Ishak and I. Pop, “On the stagnation-point flow towards a stretching sheet with homogeneous-heterogeneous reactions effects,” Communication in Nonlinear Science and Numerical Simulation, vol. 16, no. 11, pp. 4296– 4302, 2011. [Google Scholar]

14. N. S. Anuar, N. Bachok, N. M. Arifin and H. Rosali, “Stagnation point flow and heat transfer over an exponentially stretching/shrinking sheet in CNT with homogeneous-heterogeneous reaction: Stability analysis,” Symmetry, vol. 11, no. 4, pp. 522, 2019. [Google Scholar]

15. N. Xu and H. Xu, “A modified model for isothermal homogeneous and heterogeneous reactions in the boundary-layer flow of a nanofluid,” Applied Mathematics and Mechanics, vol. 41, no. 3, pp. 479–490, 2020. [Google Scholar]

16. S. U. S. Choi and J. A. Eastman, “Enhancing thermal conductivity of fluids with nanoparticles,” Proc. of the 1995 ASME Int. Mechanical Engineering Congress and Exposition, FED 231/MD, vol. 66, pp. 99–105, 1995. [Google Scholar]

17. K. Khanafer, K. Vafai and M. Lightstone, “Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids,” International Journal of Heat and Mass Transfer, vol. 46, no. 19, pp. 3639–3653, 2003. [Google Scholar]

18. R. K. Tiwari and M. K. Das, “Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids,” International Journal of Heat and Mass Transfer, vol. 50, no. 9–10, pp. 2002–2018, 2007. [Google Scholar]

19. H. F. Oztop and E. Abu-Nada, “Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids,” International Journal of Heat and Fluid Flow, vol. 29, no. 5, pp. 1326–1336, 2008. [Google Scholar]

20. M. A. A. Hamad, “Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field,” International Communications in Heat and Mass Transfer, vol. 38, no. 4, pp. 487–492, 2011. [Google Scholar]

21. U. Khan, A. Zaib, I. Khan and K. S. Nisar, “Activation energy on MHD flow of titanium alloy (Ti6Al4V) nanoparticle along with a cross flow and streamwise direction with binary chemical reaction and non-linear radiation,” Dual solutions, Journal of Materials Research and Technology, vol. 9, no. 1, pp. 188–199, 2020. [Google Scholar]

22. M. I. Khan, F. Alzahrani and A. Hobiny, “Simulation and modeling of second order velocity slip flow of micropolar ferrofluid with Darcy–Forchheimer porous medium,” Journal of Materials Research and Technology, vol. 9, no. 4, pp. 7335–7340, 2020. [Google Scholar]

23. R. Ellahi, S. M. Sait, N. Shehzad and Z. Ayaz, “A hybrid investigation on numerical and analytical solutions of electro-magnetohydrodynamics flow of nanofluid through porous media with entropy generation,” International Journal of Numerical Methods for Heat & Fluid Flow, vol. 30, no. 2, pp. 834–854, 2020. [Google Scholar]

24. R. Turcu, A. Darabont, A. Nan, N. Aldea, D. Macovei et al., “New polypyrrole-multiwall carbon nanotubes hybrid materials,” Journal of Optoelectronics and Advanced Materials, vol. 8, no. 2, pp. 643–647, 2006. [Google Scholar]

25. S. Jana, A. Salehi-Khojin and W. H. Zhong, “Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives,” Thermochimica Acta, vol. 462, no. 1–2, pp. 45–55, 2007. [Google Scholar]

26. S. Suresh, K. P. Venkitaraj, P. Selvakumar and M. Chandrasekar, “Synthesis of Al2O3-Cu/water hybrid nanofluids using two step method and its thermo physical properties,” Colloids and Surfaces A: Physicochemical and Engineering Aspects, vol. 388, no. 1–3, pp. 41–48, 2011. [Google Scholar]

27. B. Takabi and S. Salehi, “Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid,” Advances in Mechanical Engineering, vol. 6, no. 4, pp. 147059, 2014. [Google Scholar]

28. I. Waini, A. Ishak and I. Pop, “Squeezed hybrid nanofluid flow over a permeable sensor surface,” Mathematics, vol. 8, no. 6, pp. 898, 2020. [Google Scholar]

29. I. Waini, A. Ishak and I. Pop, “Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid,” Alexandria Engineering Journal, vol. 59, no. 3, pp. 1881–1891, 2020. [Google Scholar]

30. I. Waini, A. Ishak and I. Pop, “Hybrid nanofluid flow towards a stagnation point on an exponentially stretching/shrinking vertical sheet with buoyancy effects,” International Journal of Numerical Methods for Heat & Fluid Flow, vol. 31, no. 1, pp. 216–235, 2021. [Google Scholar]

31. N. S. Khashi’ie, I. Waini, N. A. Zainal and K. Hamzah, “Hybrid nanofluid flow past a shrinking cylinder with prescribed surface heat flux,” Symmetry, vol. 12, no. 9, pp. 1493, 2020. [Google Scholar]

32. U. Khan, A. Zaib, I. Khan, D. Baleanu and K. S. Nisar, “Enhanced heat transfer in moderately ionized liquid due to hybrid MoS2/SiO2 nanofluids exposed by nonlinear radiation: Stability analysis,” Crystals, vol. 10, no. 2, pp. 142, 2020. [Google Scholar]

33. G. K. Ramesh, S. Manjunatha and B. J. Gireesha, “Impact of homogeneous-heterogeneous reactions in a hybrid nanoliquid flow due to porous medium,” Heat Transfer, Asian Research, vol. 48, no. 8, pp. 3866–3884, 2019. [Google Scholar]

34. L. A. Lund, Z. Omar, I. Khan and E. S. M. Sherif, “Dual branches of MHD three-dimensional rotating flow of hybrid nanofluid on nonlinear shrinking sheet,” Computers, Materials and Continua, vol. 66, no. 1, pp. 127–139, 2021. [Google Scholar]

35. L. A. Lund, Z. Omar, S. Dero, Y. Chu, I. Khan et al., “Temporal stability analysis of magnetized hybrid nanofluid propagating through an unsteady shrinking sheet: Partial slip conditions,” Computers, Materials and Continua, vol. 66, no. 2, pp. 1963–1975, 2021. [Google Scholar]

36. M. Bilal, I. Khan, T. Gul, A. Tassaddiq, W. Alghamdi et al., “Darcy-forchheimer hybrid nano fluid flow with mixed convection past an inclined cylinder,” Computers, Materials and Continua, vol. 66, no. 2, pp. 2025–2039, 2021. [Google Scholar]

37. M. Hassan, M. Marin, R. Ellahi and S. Z. Alamri, “Exploration of convective heat transfer and flow characteristics synthesis by Cu-Ag/water hybrid-nanofluids,” Heat Transfer Research, vol. 49, no. 18, pp. 1837–1848, 2018. [Google Scholar]

38. A. Riaz, R. Ellahi and S. M. Sait, “Role of hybrid nanoparticles in thermal performance of peristaltic flow of Eyring-Powell fluid model,” Journal of Thermal Analysis and Calorimetry, vol. 143, no. 2, pp. 1021–1035, 2021. [Google Scholar]

39. J. Sarkar, P. Ghosh and A. Adil, “A Review on hybrid nanofluids: Recent research, development and applications,” Renewable and Sustainable Energy Reviews, vol. 43, no. 5, pp. 164–177, 2015. [Google Scholar]

40. N. A. C. Sidik, I. M. Adamu, M. M. Jamil, G. H. R. Kefayati, R. Mamat et al., “Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review,” International Communications in Heat and Mass Transfer, vol. 78, no. 1, pp. 68–79, 2016. [Google Scholar]

41. J. A. R. Babu, K. K. Kumar and S. S. Rao, “State-of-Art review on hybrid nanofluids,” Renewable and Sustainable Energy Reviews, vol. 77, pp. 551–565, 2017. [Google Scholar]

42. M. U. Sajid and H. M. Ali, “Thermal conductivity of hybrid nanofluids: A critical review,” International Journal of Heat and Mass Transfer, vol. 126, no. 21015, pp. 211–234, 2018. [Google Scholar]

43. G. Huminic and A. Huminic, “Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review,” Journal of Molecular Liquids, vol. 302, pp. 112533, 2020. [Google Scholar]

44. L. Yang, W. Ji, M. Mao and J. Huang, “An updated review on the properties, fabrication and application of hybrid-nanofluids along with their environmental effects,” Journal of Cleaner Production, vol. 257, no. 4, pp. 120408, 2020. [Google Scholar]

45. J. H. Merkin, “On dual solutions occurring in mixed convection in a porous medium,” Journal of Engineering Mathematics, vol. 20, no. 2, pp. 171–179, 1986. [Google Scholar]

46. P. D. Weidman, D. G. Kubitschek and A. M. J. Davis, “The effect of transpiration on self-similar boundary layer flow over moving surfaces,” International Journal of Engineering Science, vol. 44, no. 11–12, pp. 730–737, 2006. [Google Scholar]

47. I. Waini, A. Ishak and I. Pop, “MHD flow and heat transfer of a hybrid nanofluid past a permeable stretching/shrinking wedge,” Applied Mathematics and Mechanics (English Edition), vol. 41, no. 3, pp. 507–520, 2020. [Google Scholar]

48. S. D. Harris, D. B. Ingham and I. Pop, “Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip,” Transport in Porous Media, vol. 77, no. 2, pp. 267–285, 2009. [Google Scholar]

49. L. F. Shampine, I. Gladwell and S. Thompson, Solving ODEs with MATLAB. Cambridge: Cambridge University Press, 2003. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.