Computers, Materials & Continua DOI:10.32604/cmc.2021.014857
Article

Ergodic Capacity Evaluation of Multi-Hop Decode-and-Forward MIMO-OFDM Relaying Network

Latif Jan1, Mohammad Haseeb Zafar1, Abdul Waheed2, Mahdi Zareei3 and Faisal Alanazi*,4

1Department of Electrical Engineering, University of Engineering & Technology, Peshawar, 25120, Pakistan
2Department of Information Technology, Hazara University, Mansehra, 21120, Pakistan
3Tecnologico de Monterrey, School of Engineering and Sciences, Zapopan, 45201, Mexico
4Department of Electrical Engineering, Prince Sattam Bin Abdulaziz University, College of Engineering, Al Kharj, 16278, Saudi Arabia
*Corresponding Author: Faisal Alanazi. Email: faisal.alanazi@psau.edu.sa
Received: 22 October 2020; Accepted: 02 March 2021

Abstract: Spatial diversity plays a significant role in wireless communication systems, including the Fourth Generation (4G) and Fifth Generation (5G) systems, and it is expected to be a fundamental part of the future wireless communication systems as well. The Multiple-Input Multiple-Output (MIMO) technology, which is included in the IEEE 802.16j standard, still holds the most crucial position in the 4G spectrum as it promises to improve the throughput, capacity, spectral, and energy efficiency of wireless communication systems in the 2020s. This makes MIMO a viable technology for delay constrained medical and health care facilities. This paper presents an approximate closed-form expression of the ergodic capacity for the Decode-and-Forward (DF) protocol MIMO-Orthogonal Frequency Division Multiplexing (OFDM) relaying network. Although MIMO-OFDM is highly valuable for modern high-speed wireless communication systems, especially in the medical sciences, its performance degrades in multi-hop relay networks. Therefore, in this paper, an approximate closed-form expression is derived for an end-to-end ergodic capacity of multi-hop DF MIMO-OFDM wireless communication system has been presented. Monte-Carlo simulations are conducted to verify the performance of the presented analysis regarding the capacity (bits/s/Hz) for different SNR-dB values for single, 2×2, 4×4, and multi-hop DF MIMO-OFDM systems. The presented results provide useful insights for the research on the end-to-end ergodic capacity evaluation.

Keywords: Multiple-input multiple-output system; decode-and-forward protocol; orthogonal frequency division multiplexing; ergodic capacity

1  Introduction

The Multiple-Input Multiple-Output (MIMO) technology as persisting on the Physical Layer (PHY-L) still holds the Promising Primary Position (PPP) in the current Fifth Generation (5G) technology, and it is expected to remain if the Massive MIMO with envisioned protocols takes its place in the future. The MIMO technology prevails and contributes to the Fourth Generation (4G) and 5G contemporary technologies. In MIMO technology, the foremost guidelines pre-dominantly strengthen the performance of the irregularities, but there are some major challenges that need to be addressed. At the same time, due to the overcoming multipath fading, to achieve higher throughput and high data rate improvement in its spectral efficiency, it is necessary to improve the existing infrastructure for future networks [1,2]. Likewise, deploying a multi-hop transmission strategy at the transmitter side can improve the performance of a wireless system. Currently, the multi-hop transmission, i.e., relaying communication systems, represents a promising solution to meet the requirements of the next-generation broadband wireless services, including range extension, power saving, and connectivity. Therefore, both 5G and future Sixth Generation (6G) systems include relaying technology in their architectures [3,4]. Communication systems are equipped with relays to realize a long-distance propagation of signals from between transmitter and receiver. Namely, in order to achieve successful communication between the transmitter and receiver, relays, such as Decode-and-Forward (DF) or Amplify-and-Forward (AF) protocols, have been widely used to boost the performance of the overall system [5]. In a DF relaying system, the relay node decodes the received signal, regenerates, and re-transmits it to the next hop, and in an AF relaying system, the relay node amplifies the received signal and transmits it to the next hop. Due to the numerous advantages of relaying, there has been extensive research on relaying protocols for wireless communication systems. For instance, a three-terminal-channel-based multi-hop protocol was presented in [6]. The performance of the dual-hop relay using an AF protocol for an end-to-end system was examined in [7], where the authors presented the tight lower bounds and derived expressions for the closed form of the statistical harmonic mean of two independent distinctions for the error rate behavior of the system. In [8–11], the multi-hop relaying in fading channels was investigated to determine the outage probability and error rate, while the capacity for the upper bounds of a Gaussian relay channel was analyzed in [12]. In [13–15], the capacity of both single-and multi-relay channels and their power constraints of the AF-OFDM-based relay networks with additive white Gaussian noise (AWGN) were evaluated. The ergodic capacity due to hopping loss of MIMO-DF cooperative relaying network was obtained in [16] while the capacity of the multi-hop non-linear MIMO-OFDM relaying network was derived in [17]. The existing 4G wireless communication systems and an OFDM comprehensive analysis were discussed in [18]. A thorough analysis of MIMO-OFDM in a cooperative frequency selective fading channel was conducted in [19]. Recently, the Doppler effect was studied for the cyclic delay diversity scheme in the MIMO-OFDM-based system [20]. Also, it should be noted that the application of MIMO-OFDM in UAV communication systems has undoubtedly been an emerging area of research targeted by many authors [21]. An approach for exploiting an AF and DF mixed concept for non-orthogonal multiple access (NOMA) using an application for device-to-device networks was presented in [22]. Motivated by the previous studies on MIMO-OFDM and DF relaying protocols, in this work, the closed-form of expressions is derived using a simplified integral summation approach.

To the best of the authors’ knowledge, the performance analysis of DF relaying in MIMO-OFDM systems has been an interesting research problem that can be further extended to 5G technologies depending on the problem’s applicability. Therefore, this paper examines the problem of DF relaying in MIMO-OFDM systems by deriving approximate closed-form expressions of the ergodic capacity A MATLAB simulator is used to generate the Monte-Carlo (MC) simulations. The analytical expressions are validated by the MC simulations.

2  Materials and Methods

This section analyzes the derived closed-form expressions of the ergodic capacity for an end-to-end system using a multi-hop DF MIMO-OFDM relaying network.

2.1 System Model

This paper considers a K-hop wireless relaying network, as shown in Fig. 1. In the considered network, source node S transmits data to a destination node D via R relay nodes. Also, this work considers a MIMO-OFDM communication model that employs n sub-carriers per OFDM symbol. The number of transmitting antennas is denoted as M, whereas the number of receiving antennas is denoted as L. It is also considered that all M transmitting antennas transmit different symbols simultaneously and operate at the same frequency band. Hence, the considered model is a conventional L×M MIMO-multiplexing relaying model. Moreover, it is assumed that at each time slot, only one node transmits, and that only the receiver end has the channel state information (CSI) available.

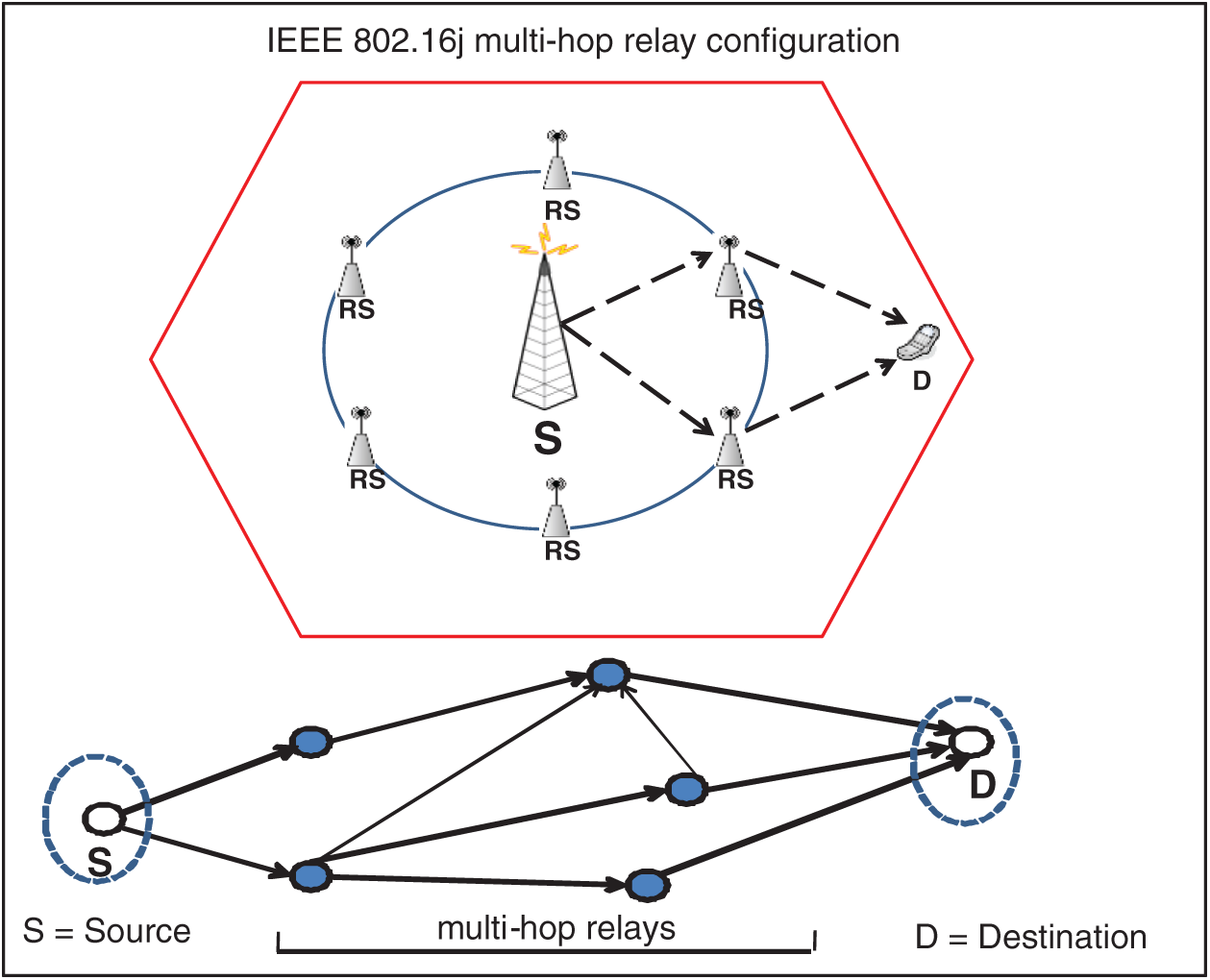
Figure 1: Broadband wireless using a multi-hop MIMO multiplexing relay network

Based on this system model, the MIMO’s channel transmission matrix at the ith hop is an nL×mM diagonal matrix, whose H[k]i diagonal elements are denoted as H[k]i where H[k]i represents the fading of the kth OFDM subcarrier, which is modeled as an independent and identically distributed (IID) random variable that obeys complex zero-mean Gaussian random distribution. The gains of relay channels H0,H1,H2,…,HR are independent of each other and follow the DF relaying scheme. The signal received at the ith relay node is given by:

yi=Hixi-1+nii=0,1,…,R,(1)

where xi-1 denotes an mM×1 vector that represents the transmitted signal, while ni is an nL×1 complex additive noise vector at the ith node modeled as an IID with a zero-mean, circular symmetry, and complex Gaussian random vector with the variance σk2. The transmitted signal xi from the ith relay node in a DF multi-hop relaying communication system is taken from the transmitted signal xo from the source node.

2.2 Multi-Hop DF Relaying System Capacity

The ergodic capacity of a multi-hop DF MIMO-OFDM relaying system is given by:

CDF= min{C1,C2,…,CR+1},(2)

where Ci=1,2,…,R+1 represents the ith hop’s capacity and is given by:

Ci=1n∑k=0n-1EH[k]i[log2{det[IL+ρiH[k]iH[k]iT]}],(3)

where E[.] denotes the expectation operator, IL is an L×L identity matrix, ρi=PinMσ02, and Pi, i=0,1,…,R.

In this work, Pi denotes the total transmitted power of the nodes, including both the source node and relay nodes, at the transmitter end. Let us define Nmin= min(M,L), Nmax= max(M,L), and δ=Nmax-Nmin. To express the ergodic capacity, it is necessary to use the expressions in terms of eigenvalues λ1k,i,λ2k,i,…,λNmink,i of H[k]iH[k]iT, where i=0,1,…,R, which can be written as:

Ci=1n∑k=0n-1∑m=1NminEλmk,i[log2(1+ρλmk,i)].(4)

The above-mentioned equation can be simplified as follows:

Ci=Nminn∑k=0n-1Eλk,i[log2(1+ρλk,i)],(5)

where λk,i is obtained by a random selection from the set of eigenvalues of H[k]iH[k]iT, which is denoted as {λ1k,i,λ2k,i,…,λNmink,i}.

The probability density function (PDF) of λk,i can be expressed as:

fλk,i(λ)=1Nmin∑k=0Nmin-1∑j=0j∑l=02j(-1)l(2j)!22k-lj!l!(δ+j)(2k-2jk-j)⋅(2j+2δ2j-l)λδ+le-λ.(6)

Then, the cumulative distribution function (CDF) of λk,i can be calculated by integrating the PDF, which is expressed as:

Fλk,i(λ)=∫0λfλk,i(x)dx=1Nmin[∑k=0Nmin-1∑j=0k∑l=02j(-1)l(2j)!22k-lj!l!(δ+j)(2k-2jk-j)(2j+2δ2j-l)∫0λxδ+le-xdx].(7)

Using ∫0uxne-μxdx=n!μn+1-e-uμ∑m=0nn!m!umμn-m+1, the following expression can be obtained:

Fλk,i(λ)=1Nmin[∑k=0Nmin-1∑j=0k∑l=02j(-1)l(2j)!22k-lj!l!(δ+j)(2k-2jk-j)(2j+2δ2j-l){(δ+l)!-e-λ∑m=0δ+l(δ+l)!m!λm}].(8)

To the best of the authors’ knowledge, the closed-form expression of Eq. (8) has not been reported in the related literature, even for a two-hop relaying system. Therefore, this paper presents the closed-form expressions for the CDF in Eq. (8) and the ergodic capacity of a multi-hop DF relaying system. Using Eq. (3), the ergodic capacity can be expressed as:

CDF=1n∑k=0n-1EH̃[k][log2{det[IL+ρH̃[k]H̃[k]T]}],(9)

where H̃[k]= min{H[k]0,H[k]1,…,H[k]R}. Similarly, by expressing the ergodic capacity using eigenvalues {λ̃1k,λ̃2k,…,λ̃Nmink} for H̃[k]i of H̃[k]iT i=0,1,…,R, we get:

CDF=1n∑k=0n-1∑m=1NminEλ̃m[log2(1+ρλ̃mk)],=Nminn∑k=0n-1Eλ̃[log2(1+ρλ̃k)].(10)

where λ̃k is selected from the eigenvalue set of {λ̃1k,λ̃2k,…,λ̃Nmink} for H̃[k]i of H̃[k]iT. To find the PDF of λ̃k, i.e., fλ̃k(λ), it is assumed that the fading per hop is IID. Let {Xj}j=1n denote the IID random variables using the order statistics (X1:n<X2:n…<Xn:n), then the PDF of the ranked random variable (in ascending order) Xj: n (1≤j≤n) is given by:

fj:n(x)=1B(j,n-j+1){F(x)}j-1{1-F(x)}n-jf(x),(11)

where F(x) represents the CDF, f(x) represents the PDF, and B(a,b)=∫01ta-1(1-t)b-1dt denotes a beta function, and it can be expressed as:

B(i,n-i+1)=(i-1)!1!(n-i)!n!.(12)

Using Eqs. (11) and (12), the PDF of the smallest random variable (i.e., f1:n(x)) is given by:

f1:n(x)=n{1-F(x)}n-1f(x).(13)

Thus, the PDF of λ̃k can be expressed as a combination of CDF and PDF of λk,i, which is given by:

fλ̃k(λ)=(R+1){1-Fλk,i(λ)}Rfλk,i(λ),(14)

where fλk,i(λ) and Fλk,i(λ) represent the PDF and CDF of λk,i given by Eqs. (6) and (7), respectively, and R represents the number of relay stations. Using a binomial expansion, a general expression of Eq. (14) valid for any of relay hops R can be written as:

fλ̃k(λ)=(R+1)fλk,i(λ)∑n=0∞(-1)n(Rn){Fλk,i(λ)}n=(R+1)fλk,i(λ)[1-RFλk,i(λ)+R(R-1)2!{Fλk,i(λ)}2-R(R-2)(R-3)3!{Fλk,i(λ)}3+…].(15)

For instance, for R = 1, Eq. (15) becomes:

fλ̃k(λ)=2fλk,i(λ){1-Fλk,i(λ)}.(16)

By substituting Eqs. (6) and (7) into Eq. (16), the PDF of λ̃k is obtained as:

fλ̃k(λ)=2[1Nmin∑s=0Nmin-1∑t=0s∑u=02t(-1)u(2t)!22s-ut!u!(Δ+p)(2s-2ts-t)(2t+2Δ2t-u)λΔ+ue-λ]-2[{1Nmin∑m=0N-1∑n=0s∑p=02n(-1)p(2n)!22s-mp!q!(Δ+n)(2m-2nm-n)(2n+2Δ2n-p)(Δ+p)!}×{1Nmin∑s=0Nmin-1∑t=0s∑u=02t(-1)u(2t)!22s-ut!u!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)λΔ+ue-λ}]+2[{1Nmin∑m=0N-1∑n=0s∑p=02n(-1)p(2n)!22s-mn!p!(Δ+n)(2m-2nm-n)(2n+2Δ2n-p)∑m=0Δ+p(Δ+p)!m!e-λλm}×{1Nmin∑s=0Nmin-1∑t=0s∑u=02t(-1)q(2t)!22s-ut!u!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)uλΔ+ue-λ}].(17)

After extensive simplification, the ergodic capacity of a multi-hop DF protocol-based MIMO-OFDM relaying system given by Eq. (10) can be obtained as:

CDF=Nminn∑k=0n-1∫0∞[log2(1+ρλk)]fλ̃k(λk)dλ,=Nminn∑k=0n-1[I1[k]-I2[k]+I3[k]].(18)

where

I1[k]=2Nmin∫0∞log2(1+eλk)[∑s=0Nmin-1∑t=0s∑u=02t(-1)u(2t)!22s-ut!u!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)(λk)Δ+qe-λk]dλk,(19)

I2[k]=2Nmin2∫0∞log2(1+eλk)[{∑m=0N-1∑n=0s∑p=02n(-1)p(2n)!22s-mn!p!(Δ+n)(2m-2nm-n)(2n+2Δ2n-l)(Δ+p)!}×{∑s=0Nmin-1∑t=0s∑u=02t(-1)u(2t)!22s-ut!u!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)(λk)Δ+qe-λk}]dλk, (20)

I3[k]=2Nmin2∫0∞log2(1+eλk)[{∑m=0N-1∑n=0s∑p=02n(-1)p(2n)!22s-mn!p!(Δ+n)(2m-2nm-n)(2n+2Δ2n-l)}×{∑s=0Nmin-1∑t=0s∑u=02t(-1)t(2u)!22s-ut!u!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)(λk)Δ+ue-λk}]dλk. (21)

The integrals in Eqs. (19)–(21) can be solved using the following approximation:

∫0∞log2(1+aλ)λl1+l2e-λdλ≈(l1+l2)![ln(a)-δ+∑ψ=1l1+l21ψ],(22)

where δ≈0.577. Using the above approximation, Eqs. (19)–(21) can be further expressed in the approximate closed-form, which is given by:

I1=2Nmin∑s=0Nmin-1∑t=0s∑u=02t(-1)u(2t)!22s-uu!t!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)(Δ+q)![ln(e)-Δ+∑ψ=1Δ+q1ψ],(23)

I2=2Nmin2∑m=0N-1∑n=0s∑p=02n(-1)p(2n)!22s-mn!p!(Δ+n)(2m-2nm-n)(2n+2Δ2n-l)(Δ+p)!×∑s=0Nmin-1∑t=0s∑u=02t(-1)u(2t)!22s-uu!t!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)(Δ+q)![ln(e)-Δ+∑ψ=1Δ+q1ψ], (24)

I3=2Nmin2∑m=0N-1∑n=0s∑p=02n(-1)p(2n)!22s-mn!p!(Δ+n)(2m-2nm-n)(2n+2Δ2n-l)×∑s=0Nmin-1∑t=0s∑u=02t(-1)t(2u)!22s-uu!t!(Δ+t)(2s-2ts-t)(2t+2Δ2t-u)(Δ+u)![ln(e)-Δ+∑ψ=1Δ+u1ψ]. (25)

Finally, by substituting Eqs. (23)–(25) into Eq. (18) and conducting some mathematical manipulations, the expression for the anticipated ergodic capacity in its approximate closed-form of a multi-hop DF relay protocol for a MIMO-OFDM system can be derived as:

CDF≈2Nmin∑a=0N-1∑b=0a∑c=02b(-1)c(2b)!22a-cb!c!(Δ+b)(2a-2ba-b)(2b+2Δ2b-c)∑m=0Δ(Δ)!m!∑s=0Nmin-1∑t=0s∑u=02t×(-1)u(2t)!22s-uu!t!(Δ+t)(2s-2ts-t)×(2t+2Δ2t-u)(12)Δ+s+t+u(Δ+u+m)![ln(e)-Δ+∑ψ=1Δ+u+m1ψ].(26)

As a special case, when Δ≈0.557 in the above expressions, and R = 0 in Eq. (15), then by solving the integral in Eq. (18), the anticipated ergodic capacity in its approximate closed-form of a single-hop DF relay protocol for a MIMO-OFDM system can be derived as:

CDF≈∑a=0N-1∑b=0a∑c=02b(-1)c(2b)!22a-cb!c!(Δ+b)(2a-2ba-b)(2b+2Δ2b-c)(Δ+q)![ln(ρ)-δ+∑ψ=1Δ+q1ψ].(27)

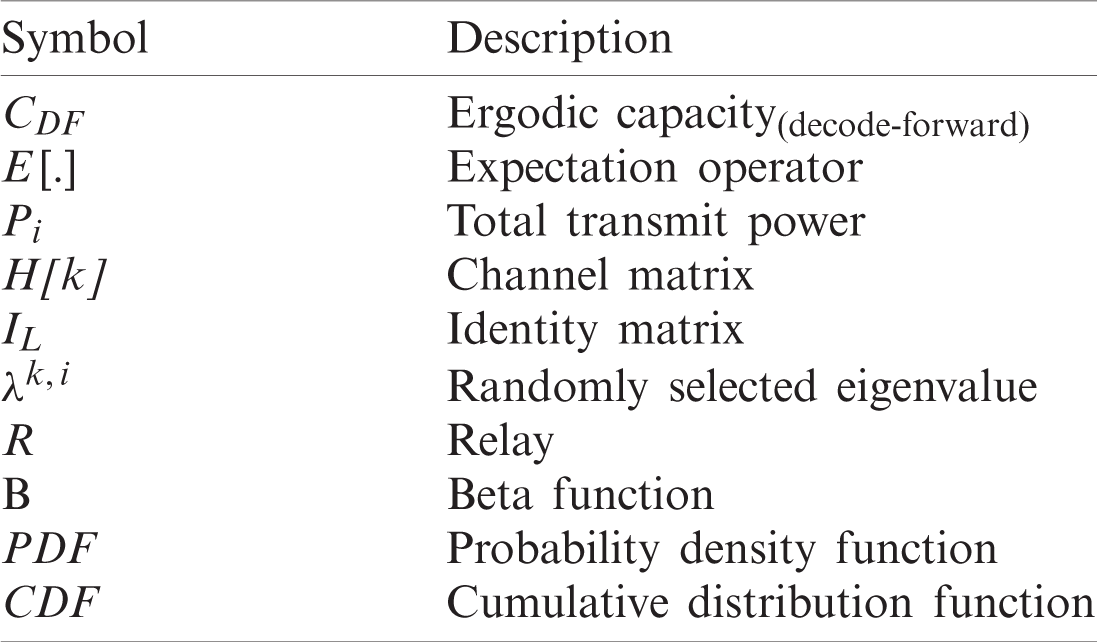
Table 1: Symbols with descriptions

2.3 Graphical Results and Analytical Expressions

All figures presented in this paper are obtained using MATLAB software. The analytical work is validated using MC simulations. Analytical expressions defining some symbols with descriptions are provided in Tab. 1.

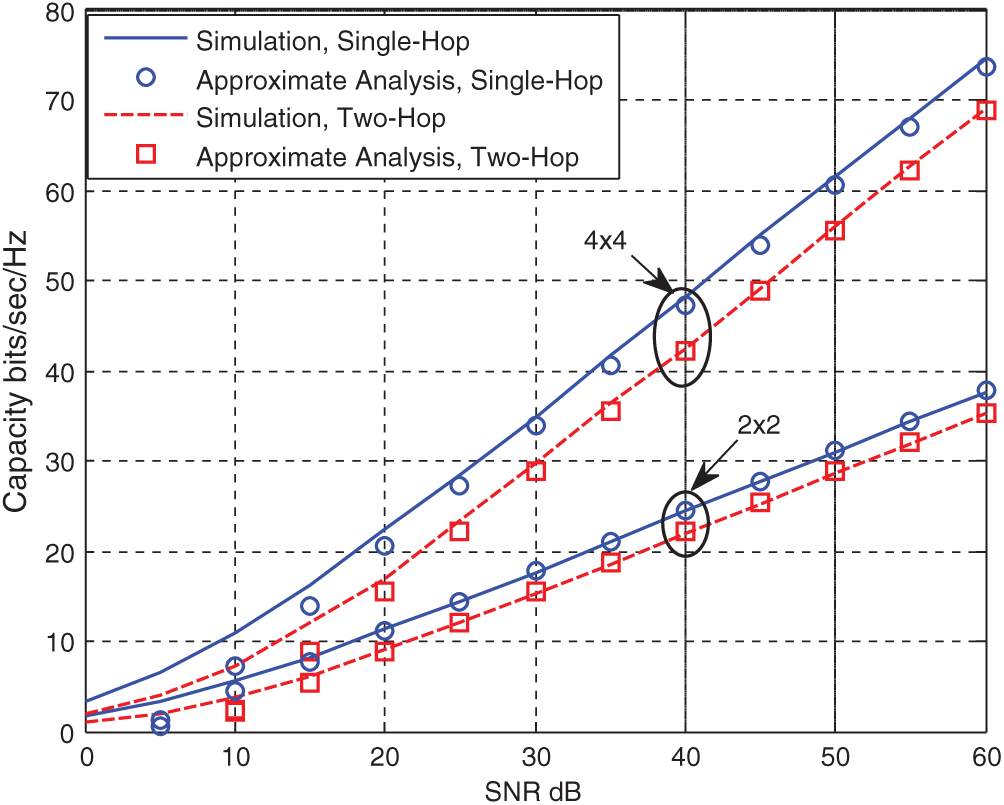
Figure 2: Simulation-based numerical results of the single- and dual-hop DF capacity of an IEEE 802.16j system

3  Simulation Results

This section presents the numerical and simulation results to verify the proposed system’s analytical findings of Fig. 1. The comparison of the numerical and theoretical results for the 2×2 and 4×4 MIMO multiplexing systems conforming to the IEEE 802.16j standard regarding the two-hop DF capacity performance is presented in Fig. 2. The results were obtained using the number of antennas and considering the high value of the SNR region. The results in Fig. 2 show that the capacity of the DF MIMO multiplexing relaying network decreased compared with the network that did not include relays, i.e., when R = 0. The simulation results of the capacity of 2×2 and 4×4 multi-hop DF MIMO relaying configurations are presented in Figs. 3 and 4, respectively, are compared with the theoretical results. As shown in Figs. 3 and 4, higher losses in capacity were caused by the increase in the order of the MIMO-DF relaying network configuration. Furthermore, the derived expressions were evaluated for different multi-hop DF relaying MIMO-OFDM systems. The results of different OFDM systems having different numbers of carriers, including the single- and multi-carrier configurations, are displayed in Fig. 5. The performances of the single-carrier, 256-OFDM, and 1024-OFDM systems were evaluated with 2×2 MIMO multiplexing using the DF protocol. The relaying approach has been envisioned in the sub-plots of Fig. 5 considering two setups, i.e., single-hop and three hops, where R = 0 and R = 2, respectively. As shown in Figs. 5a and 5b, for the same SNR value, the capacity was reduced when relaying was used. For the single-carrier OFDM, the capacity was reduced by 3.82 bits/s/Hz; for the 256-OFDM carrier, the decrease was 3.91 bits/s/Hz; and for 1024-OFDM, the decrease was 3.9 bits/s/Hz. Thus, based on the simulation result, it can be concluded that there is a hopping loss in MIMO-OFDM even if the number of relays exceeds one. Consequently, the presented results highlight the importance of the proposed expressions that have been derived through rigorous analysis and validated by MC simulations.

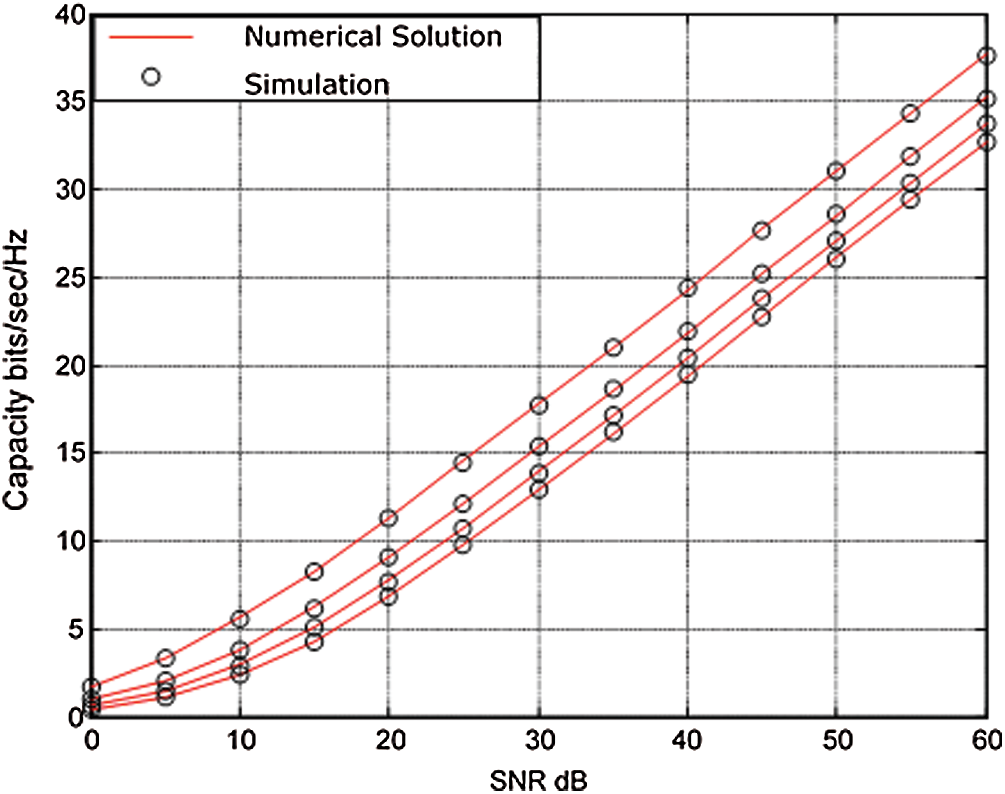
Figure 3: Simulation-based numerical results of a multi-hop DF capacity for a 2×2 MIMO multiplexer

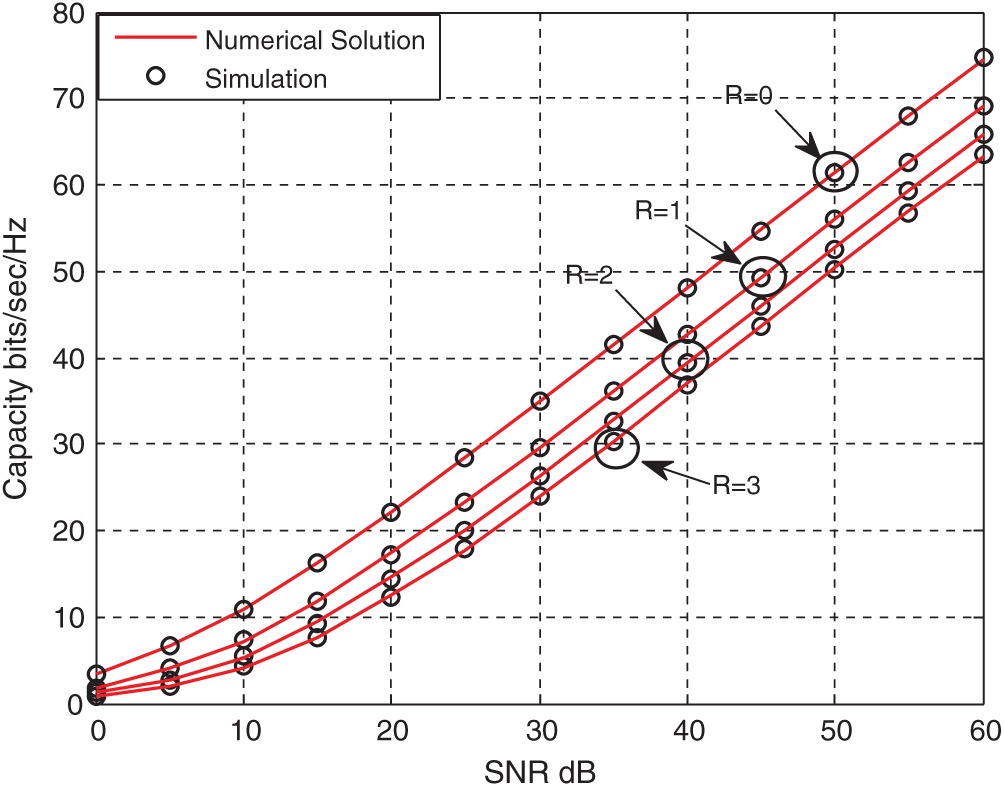
Figure 4: Simulation-based numerical results of a multi-hop DF capacity for a 4×4 MIMO multiplexer

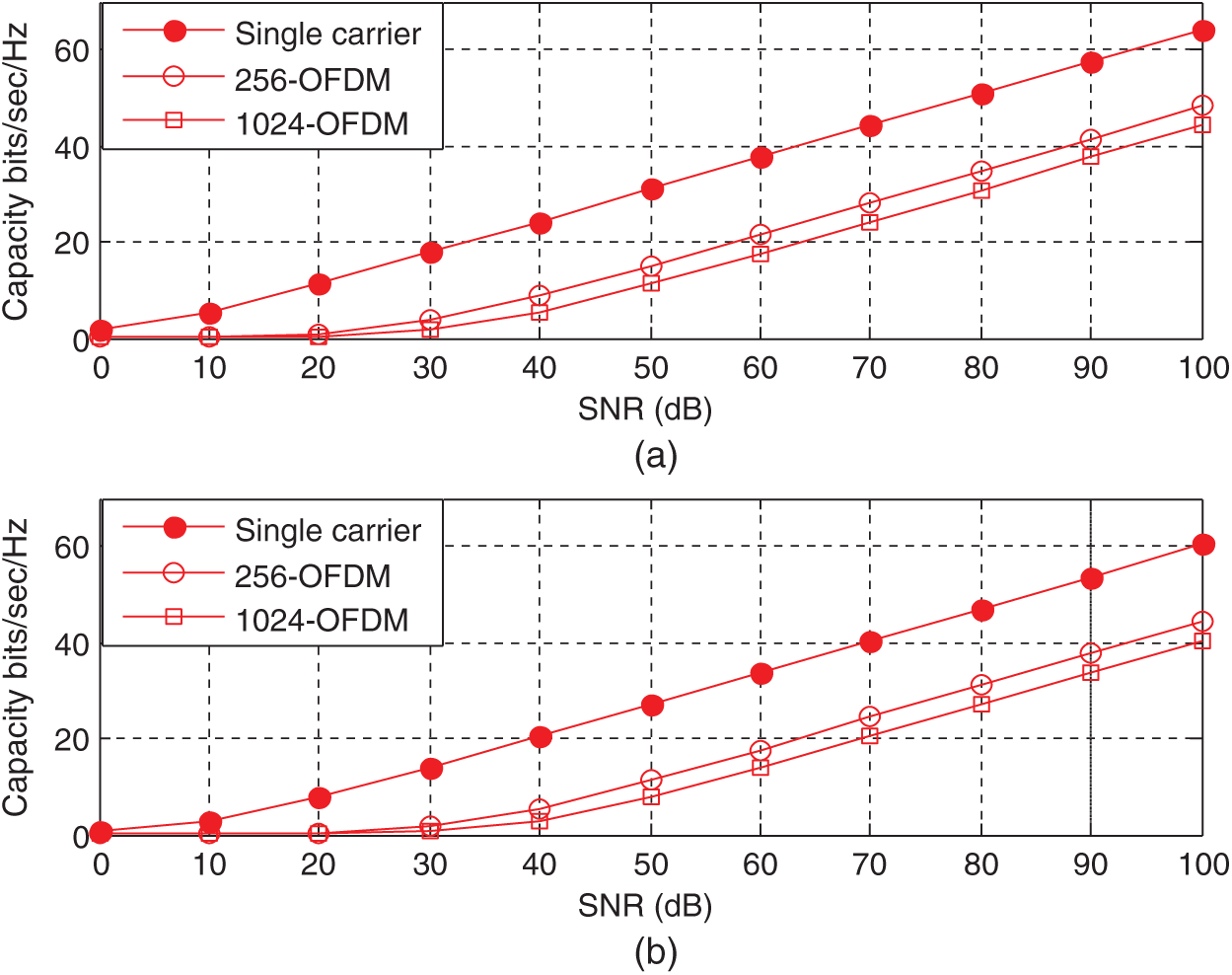
Figure 5: Capacity of a multi-hop DF-MIMO system using three different OFDM carriers. (a): No relaying R=0, (b): 3-hops relaying R=2

4  Conclusions

This paper presents the closed-form expressions of the ergodic capacity of a single- and multi-hop DF-based MIMO-OFDM relaying systems. The derived expressions are validated using a numerical method. The presented results provide many useful insights, such as the end-to-end ergodic capacity of the considered system model, which degrades with the increasing number of hops. It is also shown that the ergodic capacity of a higher-order MIMO is reduced when the number of hops increases. Moreover, the presented results reveal that the capacity loss of relay-based MIMO-OFDM is approximately constant for all the OFDM subcarriers. A future research direction would be to extend our derived results to a massive MIMO multi-hop relaying system based on the findings presented in this study.

Funding Statement: The author(s) received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. K. Simon and M. Alouini, “Fading channel characterization and modeling,” in Digital Communication Over Fading Channels, 2nd ed. Hoboken, NJ, USA: John Wiley & Sons, pp. 17–43, 2005. [Google Scholar]

 2.  L. Yang, “On the capacity of MIMO rayleigh fading channels with lognormal shadowing,” in Proc. Int. Congress on Image and Signal Processing, Sanya, China, pp. 479–482, 2008. [Google Scholar]

 3.  H. S. Nguyen, D. T. Do and M. Voznak, “Two-way relaying networks in green communications for 5G: Optimal throughput and the tradeoff between relay distance on power splitting-based and time switching-based relaying SWIPT,” AEU-International Journal of Electronics and Communications, vol. 70, no. 12, pp. 1637–1644, 2016. [Google Scholar]

 4.  T. M. Hoang, X. N. Tran, N. Thanh and L. T. Dung, “Performance analysis of MIMO SWIPT relay network with imperfect CSI,” Mobile Networks and Applications, vol. 24, no. 2, pp. 630–642, 2019. [Google Scholar]

 5.  A. I. Sulyman, G. Takahara, H. S. Hassanein and M. Kousa, “Multi-hop capacity of MIMO-multiplexing relaying in WiMAX mesh networks,” in Proc. IEEE Int. Conf. on Communications, Dresden, Germany, pp. 4545–4549, 2009. [Google Scholar]

 6.  G. Bakhshi, M. F. Sabahi and K. Shahtalebi, “A full-three-dimensional reference model for wideband MIMO mobile-to-mobile communication channels,” Wireless Personal Communications, vol. 85, no. 3, pp. 1351–1365, 2015. [Google Scholar]

 7.  M. O. Hasna and M. Alouini, “End-to-end performance of transmission systems with relays over Rayleigh-fading channels,” IEEE Transactions on Wireless Communications, vol. 2, no. 6, pp. 1126–1131, 2003. [Google Scholar]

 8.  G. K. Karagiannidis, “Performance bounds of multi-hop wireless communications with blind relays over generalized fading channels,” IEEE Transactions on Wireless Communications, vol. 5, no. 3, pp. 498–503, 2006. [Google Scholar]

 9.  N. C. Beaulieu and J. Hu, “A closed-form expression for the outage probability of decode-and-forward relaying in dissimilar rayleigh fading channels,” IEEE Communications Letters, vol. 10, no. 12, pp. 813–815, 2006. [Google Scholar]

10. C. Song, K. Lee and I. Lee, “Performance analysis of MMSE-based amplify and forward spatial multiplexing mimo relaying systems,” IEEE Transactions on Communications, vol. 59, no. 12, pp. 3452–3462, 2011. [Google Scholar]

11. K. Tourki, H. Yang and M. Alouini, “Error-rate performance analysis of incremental decode-and-forward opportunistic relaying,” IEEE Transactions on Communications, vol. 59, no. 6, pp. 1519–1524, 2011. [Google Scholar]

12. R. Tandon and H. V. Poor, “On the capacity region of multiple-access relay channels,” in Proc. 45th Annual Conf. on Information Sciences and Systems, Baltimore, MD, USA, pp. 1–5, 2011. [Google Scholar]

13. L. Jan, M. H. Zafar, I. Ahmad and M. I. Babar, “HPA nonlinearities mitigation by joint predistorter and constellation rotation using MIMO communication systems,” in Proc. Wireless Telecommunications Symp., Washington, DC, USA, pp. 1–6, 2014. [Google Scholar]

14. J. Liao, M. R. A. Khandaker and K. Wong, “Energy harvesting enabled MIMO relaying through power splitting,” in Proc. IEEE 17th Int. Workshop on Signal Processing Advances in Wireless Communications, Edinburgh, UK, pp. 1–5, 2016. [Google Scholar]

15. D. E. Simmons and J. P. Coon, “Capacity scaling laws for power constrained amplify-and-forward OFDM-based relay networks,” in Proc. IEEE Int. Conf. on Communications, Paris, France, pp. 1–6, 2017. [Google Scholar]

16. I. Ahmad, K. D. Nguyen, N. Letzepis and A. Pollok, “On the hopping loss in MIMO decode-and-forward cooperative relaying,” IEEE Transactions on Communications, vol. 66, no. 1, pp. 54–63, 2017. [Google Scholar]

17. I. Ahmad, A. I. Sulyman, K. A. Abuhasel, S. A. Alshebeili and A. K. Al-Asmari, “Ergodic capacity of nonlinear MIMO-OFDM relaying channels,” Wireless Personal Communications, vol. 81, no. 1, pp. 207–224, 2014. [Google Scholar]

18. S. Dixit and H. Katiyar, “OFDM for 4G wireless communications: A comprehensive analysis,” International Journal of Interdisciplinary Telecommunications and Networking, vol. 10, no. 1, pp. 63–84, 2018. [Google Scholar]

19. S. Dixit, H. Katiyar and A. K. Singh, “MIMO-OFDM in a cooperative frequency selective fading channel: An analysis,” Journal of Computer Networks and Communications, vol. 2019, no. 4, pp. 1–7, 2019. [Google Scholar]

20. S. Ghazi-Maghrebi and B. Akbarian, “Improved performance of alamouti scheme using cyclic delay diversity and doppler diversity for MIMO systems-based,” Wireless Personal Communications, vol. 116, pp. 1971–1992, 2021. [Google Scholar]

21. X. Tan, S. Su, X. Guo and X. Sun, “Application of MIMO-OFDM technology in UAV communication network,” in Proc. 2nd World Symp. on Artificial Intelligence, Guangzhou, China, pp. 1–4, 2020. [Google Scholar]

22. H. P. Dang, M. S. Nguyen and D. T. Do, “Exploiting hybrid decode-and-forward - amplify-and-forward in NOMA: An application to device-to-device networks,” International Journal of Communication Networks and Distributed System, vol. 25, no. 2, pp. 145–163, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.