Computers, Materials & Continua DOI:10.32604/cmc.2021.017237
Article

Grey Wolf Optimization Based Tuning of Terminal Sliding Mode Controllers for a Quadrotor

Rabii Fessi1, Hegazy Rezk2,3,*and Soufiene Bouallègue1,4

1Research Laboratory in Automatic Control (LARA), National Engineering School of Tunis (ENIT), University of Tunis EL MANAR, Tunis, 1002, Tunisia
2College of Engineering at Wadi Addawaser, Prince Sattam Bin Abdulaziz University, Al-Kharj, 11911, Saudi Arabia
3Department of Electrical Engineering, Faculty of Engineering, Minia University, Minia, 61517, Egypt
4High Institute of Industrial Systems of Gabès (ISSIG), University of Gabès, Gabès, 6011, Tunisia
*Corresponding Author: Hegazy Rezk. Email: hr.hussien@psau.edu.sa
Received: 23 January 2021; Accepted: 25 February 2021

Abstract: The research on Unmanned Aerial Vehicles (UAV) has intensified considerably thanks to the recent growth in the fields of advanced automatic control, artificial intelligence, and miniaturization. In this paper, a Grey Wolf Optimization (GWO) algorithm is proposed and successfully applied to tune all effective parameters of Fast Terminal Sliding Mode (FTSM) controllers for a quadrotor UAV. A full control scheme is first established to deal with the coupled and underactuated dynamics of the drone. Controllers for altitude, attitude, and position dynamics become separately designed and tuned. To work around the repetitive and time-consuming trial-error-based procedures, all FTSM controllers’ parameters for only altitude and attitude dynamics are systematically tuned thanks to the proposed GWO metaheuristic. Such a hard and complex tuning task is formulated as a nonlinear optimization problem under operational constraints. The performance and robustness of the GWO-based control strategy are compared to those based on homologous metaheuristics and standard terminal sliding mode approaches. Numerical simulations are carried out to show the effectiveness and superiority of the proposed GWO-tuned FTSM controllers for the altitude and attitude dynamics’ stabilization and tracking. Nonparametric statistical analyses revealed that the GWO algorithm is more competitive with high performance in terms of fastness, non-premature convergence, and research exploration/ exploitation capabilities.

Keywords: Quadrotor; cascade control; fast terminal sliding mode control; grey wolf optimizer; nonparametric Friedman analysis

1  Introduction

The quadrotor is one of the most popular architectures of UAV which is widely used in large areas of engineering and civilian applications [1,2]. Such an aerial robot can perform various missions with autonomous and/or half-autonomous modes as the prevention of forest fires, an inspection of borders and dams, spying and read the war maps, and so on [3,4]. Given the complexity of these aerial vehicles, i.e., underactuated and nonlinear dynamics, external disturbances, and model uncertainties, the design and tuning of robust flight controllers with a systematic and low time-consuming procedure become an increased need and obsessive concern.

Recently, advanced nonlinear control strategies have been especially proposed for quadrotors UAV. The Terminal Sliding Mode Control (TSMC) and Fast Terminal Sliding Mode Control (FTSMC) approaches are the most powerful and robust used ones [5–7]. In [8], a TSMC approach has been proposed for a quadrotor aircraft to reduce and eliminate the undesirable chattering phenomenon on altitude and attitude dynamics caused by the switching control action. Authors in [9] have proposed a global fast dynamic terminal sliding mode control-based technique for performing the finite-time position and attitude tracking of a small quadrotor UAV. The stability of the controlled system is demonstrated by the Lyapunov theory in the presence of external disturbances. In [10], a modified nonsingular FTSM guidance law has been computed to solve the problem of ground moving target tracking but for a fixed-wing UAV. The singularity in such a control law is avoided by using a modified saturation function. Demonstrative results are performed with three different motion states in comparison with the conventional sliding mode control method. Robust nonsingular terminal control is proposed to solve the strong coupling and underactuated problems. The works investigate the position and attitude tracking control problem. Compared with conventional sliding mode methods with sign functions, the chattering phenomenon is well attenuated and control performances are improved. In [11], the authors proposed a finite-time FTSM-based fault-tolerant control scheme for quadrotor UAV under actuator partial loss-of-effectiveness.

All the above described TSM and FTSM control methods have shown high performance and robustness improvements in the quadrotors’ stabilization and tracking framework. Unfortunately, they claim the selection and tuning of a large-scale of effective control parameters, i.e., the coefficients of manifolds and sign functions of switching control laws, which make the difficult, non-systematic, and time-consuming procedure of the controllers’ design. Indeed, these effective control parameters are often selected by repetitive trials-errors based methods. To overcome this drawback, various attempts have been proposed in the literature. In [12], a neural network-based terminal sliding mode control scheme has been designed for robotic manipulators including actuator dynamics. The nonlinear functions of the TSM manifold are approximated thanks to the proposed RBF neural network. In [13], the authors proposed an improved TSM-based time delay control strategy for an underwater vehicle-manipulator system. Fuzzy rules have been used to adaptively tuning the main parameters of the sliding mode controllers. In [14], a TSM control approach with a self-tuning gains algorithm has been proposed for the synchronization of the coronary artery system under model uncertainties. The introduced self-tuning mechanism further achieves better robustness and adaptation against unmodeled dynamics and external disturbances. A high-order TSM controller with adaptive laws for its manifold’s coefficients’ selection has been proposed and successfully applied for robotic manipulators with Backlash hysteresis [15]. In [16], a tuning method based on a fuzzy gains-scheduling supervisor has been proposed for the integral sliding mode control of a quadrotor UAV. All coefficients of the manifolds and switching laws have been adaptively updated as time-varying gains. Other recent and interesting optimization-based methods of TSM controllers tuning have been investigated. In [17], the parameters of the TSM controllers for a class of nonholonomic systems, i.e., wheeled mobile robot, have been tuned using various evolutionary algorithms such as differential evolution, bat optimization, cuckoo optimization, and bacterial foraging optimization. The tracking error reaches zero in a short and finite time and the chattering phenomenon is significantly reduced. In [18], the authors proposed a kidney-inspired algorithm to tune the TSM controller’s parameters for an active suspension system.

Tuning the effective parameters of the TSM control approach through optimization methods seems a promising solution for complex and large-scale systems. The metaheuristics theory gives a variety of global optimization algorithms and can be used to solve such a design and tuning problem [19]. Recently, several metaheuristics have been proposed in the literature and received much interest in dealing with hard optimization problems. Initially proposed by Mirjalili et al. [20], the Grey Wolf Optimizer (GWO) is one of the powerful and interesting metaheuristics compared to other ones [21,22]. Such a stochastic and free-parameters algorithm, which has been inspired by the social leadership hierarchy and intelligent behavior of grey wolves, is used in this work to deal with the FTSM parameters tuning problem for a quadrotor UAV. In this framework, the wolf position in the pack while encircling, hunting, and attacking the prey presents a potential solution to the optimization problem in the sense of the cost function. So, the selection and tuning of all effective FTSM parameters are formulated as an optimization problem under time-domain operational constraints for a quadrotor UAV. The hard and large-scale optimization problem is efficiently solved thanks to a stochastic GWO algorithm. Several performance criteria such as Integral Absolute Error (IAE), Integral Time-weighted Absolute Error (ITAE), Integral Square Error (ISE), Integral Time-weighted Square Error (ITSE) and Mean Square Error (MSE) are used as cost functions for the formulated hard and non-convex problem. The main contributions of this work are summarized as follows: 1) A full control scheme for a quadrotor UAV has been given to deal with the underactuated and coupled flight dynamics. 2) A systematic and intelligent tuning method of all effective parameters of altitude and attitude controllers has been proposed and successfully applied. 3) A free-parameters GWO metaheuristic has been investigated to deal with the tedious and time-consuming trials-errors based methods of tuning that often lead to local solutions for the problem. 4) A nonparametric statistical analysis method has been proposed to compare all reported solvers for the complex tuning problem.

The remainder of this paper is organized as follows. In Section 2, the problem of FTSM parameters’ tuning is stated and then formulated as a constrained optimization problem. A nonlinear dynamical model of the studied quadrotor is established and a full control scheme (attitude, altitude, and position) is given to deal with the coupled and underactuated drone’s dynamics. In Section 3, the proposed GWO algorithm is described and a pseudo-code for its implementation is given. Section 4 presents all simulations and demonstrative results for the proposed GWO-based sliding mode control strategy. Nonparametric statistical analysis based on Friedman and post-hoc tests is investigated to show the superiority and effectiveness of the proposed free-parameters GWO metaheuristic vs. other reported algorithms. Conclusions and perspectives of further works are drawn in Section 5.

2  Control Problem Formulation

2.1 Quadrotor Dynamic Model

A quadrotor is an unmanned aerial vehicle that has four motors and detailed with their body-frame RB(O,xb,yb,zb) and earth-frame RE(o,ex,ey,ez) as depicted in Fig. 1. Let us consider m and l the mass and the distance from each motor to the center, respectively. The drone is presented with its translational ζ=(x,y,z) and rotational η=(ϕ,θ,ψ) coordinates where -π/2≤ϕ≤π/2, -π/2≤θ≤π/2, and -π≤ψ≤π are the Euler roll, pitch, and yaw angles, respectively.

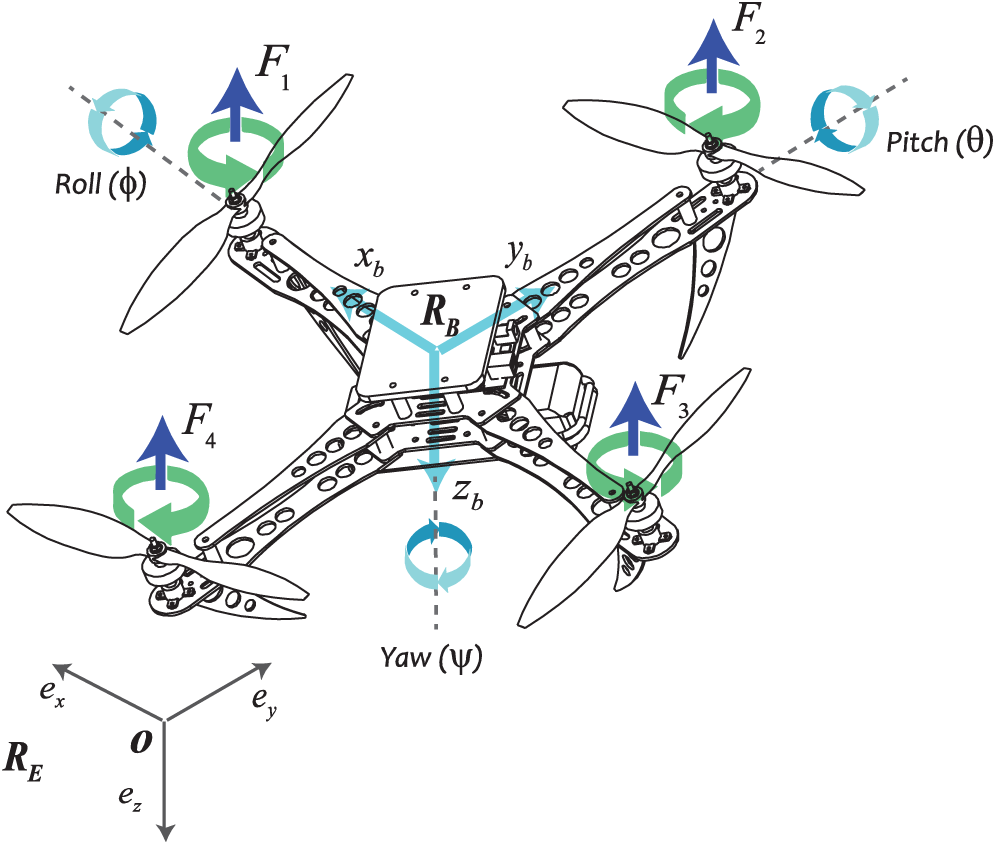
Figure 1: Mechanical structure and frames of the quadrotor UAV

Let a vector ϑ=(p,q,r) denotes the angular velocity of the drone in the body-frame RB and defined in the fixed-frame by the following transformation:

ϑ=(10- sinθ0cosϕsinϕcosθ0- sinϕcosϕcosθ)(ϕ̇θ̇ψ̇)(1)

By using the Newton–Euler formalism [23,24], nonlinear models for translational and rotational sub-systems are obtained respectively as follows:

{x¨=1m(cosϕcosψsinθ+ sinϕsinψ)u1-κ1mẋy¨=1m(cosϕsinψsinθ- sinϕcosψ)u1-κ2mẏz¨=1m cosϕcosθu1-g-κ3mż (2)

{ṗ=qrJy-JzJx-JrJxωrq-κ4Jxp+1Jxu2q̇=prJz-JxJy+JrJyωrp-κ5Jyq+1Jyu3ṙ=pqJx-JyJz-κ6Jzr+1Jzu4 (3)

where κ1,2,…,6 denote the drag and aerodynamic friction coefficients, Jr is the z-axis inertia of the propellers and Jx, Jy, and Jz are the body inertias, ωr is the overall residual rotor angular speed, and u1, u2, u3, and u4 are the control inputs of the drone given as:

(u1u2u3u4)=(μμμμ0-lμ0lμ-lμ0lμ0χ-χχ-χ)(ω12ω22ω32ω42)(4)

where ω1,2,3,4 are the angular speeds of motors, μ and χ are the lift and drag coefficients, respectively.

2.2 Problem Statement

Based on the established nonlinear model (2)–(3), one can see that the hovering dynamics are nonlinear, underactuated, and strongly coupled. Face to such a model complexity, our proposed control approach aims firstly to decouple the rotational variables from the translational ones. Such difficulty in the controllers’ design is circumvented using the proposed full control scheme of Fig. 2.

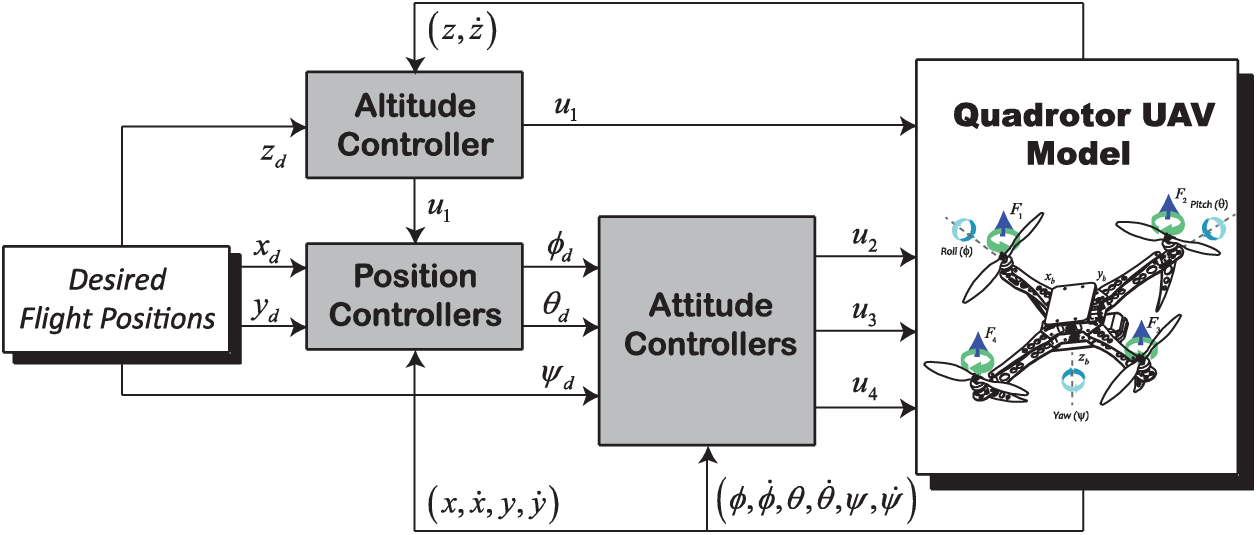
Figure 2: Block diagram of the proposed controllers’ design

Two cascade control loops are investigated to independently drive all flight dynamics of the drone, i.e., an inner control loop to ensure the attitude and heading’s stabilization and/or tracking, and outer loops for the positions (x,y) and altitude z. The desired trajectories for the attitude variables ϕd and θd are generated from Eqs. (5) and (6) shown as virtual control laws for the translational dynamics [25]:

ux=(cosϕcosψsinθ+ sinϕsinψ) (5)

uy=(cosϕsinψsinθ- sinϕcosψ) (6)

Solving Eqs. (5) and (6) for a given yaw angle ψ leads to the desired roll and pitch angles’ formula respectively given as follows:

ϕd= arctan(uxsinψ-uycosψ(1-ux 2sin2ψ+2uxuycos ψsin ψ+uy 2sin2ψ-uy 2)) (7)

θd= arcsin(uxcosψ+uysinψ(1-ux 2sin2ψ+2uxuycos ψsin ψ+uy 2sin2ψ-uy 2)) (8)

In Eqs. (7) and (8), the given virtual control laws ux and uy can be derived using any feedback control technique from the literature, i.e., PID, SMC, TSMC, or Integral Backstepping method as shown for a similar aerial vehicle in our previous work [25]. Since the proposed full control scheme of Fig. 2 makes computing and tuning separately of each flight control loop, only the dynamics of altitude and attitude are retained in this work to be controlled based on an improved FTSM control approach.

In the FTSM control framework, let consider the following model of a given uncertain second-order nonlinear system [11,26]:

{ξ̇1=ξ2ξ̇2=Φ(ξ)+Ψ(ξ)u+d(ξ)(9)

where ξ=(ξ1,ξ2)T∈ℝ2 is the system state vector, Φ(ξ) and Ψ(ξ)≠0 are two smooth nonlinear functions of ξ, u is the control input and d(ξ) represents the uncertainties and external disturbances that satisfied ∥d(ξ)∥≤Δ where Δ>0 is a constant.

Since the task of FTSM control is to design a control law u(t) to stabilize system (9) and improve the convergence speed of the sliding mode, a sliding manifold can be selected in the form:

s(ξ,t)=ξ2+αξ1+βξ1v/w(10)

where α>0 and β>0 are two design parameters, v and w are positive odd integers 1 < w/v < 2.

Such a choice of the sliding manifold leads to the following control law of the uncertain system (9):

u=-1Ψ(ξ)(Φ(ξ)+αξ2+βvwξ2ξ1v/w-1+λs+γsv/w)(11)

where λ>0 and γ>0 are two design constants and Ψ(ξ)≠0.

While considering the altitude and attitude dynamics’ models of Eqs. (2)–(3), the related fast sliding mode control laws of the quadrotor, with the same form of Eq. (11), are designed respectively as follows:

u1=mcosϕcosθ(g+αzż+βzvzwzżzvz/wz-1+λzsz+γzszvz/wz) (12)

u2=Jx(Jy-JzJxqr+αϕϕ̇+βϕvϕwϕϕ̇ϕvϕ/wϕ-1+λϕsϕ+γϕsϕvϕ/wϕ) (13)

u3=Jy(Jz-JxJypr+αθθ̇+βθvθwθθ̇θvθ/wθ-1+λθsθ+γθsθvθ/wθ) (14)

u4=Jz(Jx-JyJzpq+αψψ̇+βψvψwψψ̇ψvψ/wψ-1+λψsψ+γψsψvψ/wψ) (15)

where (αi,βi,λi,γi)∈ℝ+,∀i∈{z,ϕ,θ,ψ} are the effective design parameters of the fast terminal sliding mode controllers (12)–(15) of the drone attitude dynamics.

2.3 Tuning Problem Formulation

As depicted in Eqs. (12)–(15), the design of FTSM controllers involves the tuning of a set of unknown parameters(αi,βi,λi,γi)∈ℝ+ as shown in Fig. 3. The selection of these effective parameters is a hard and time-consuming problem. Since the iterative trials-errors procedures become ineffective, such a tuning problem is formulated as a constrained optimization program as follows:

{Minimizefi(x,t)x=(αi,βi,λi,γi)T∈S⊆ℝ+16,i∈{z,ϕ,θ,ψ}Subjectto:g1(x,t)=δz-δzmax≤0;g2(x,t)=δϕ-δϕmax≤0;g3(x,t)=δθ-δθmax≤0;g4(x,t)=δψ-δψmax≤0(16)

where x∈S⊆ℝ+16 are the decision variables, S={x∈ℝ+16,xlow≤x≤xup} denotes the bounded search space, fi:ℝ16→ℝ,i∈{z,ϕ,θ,ψ} are the cost functions to be minimized under operational constraints gj(.),j=1,2,…,4 on the responses overshoots δz, δϕ, δθ and δψ.

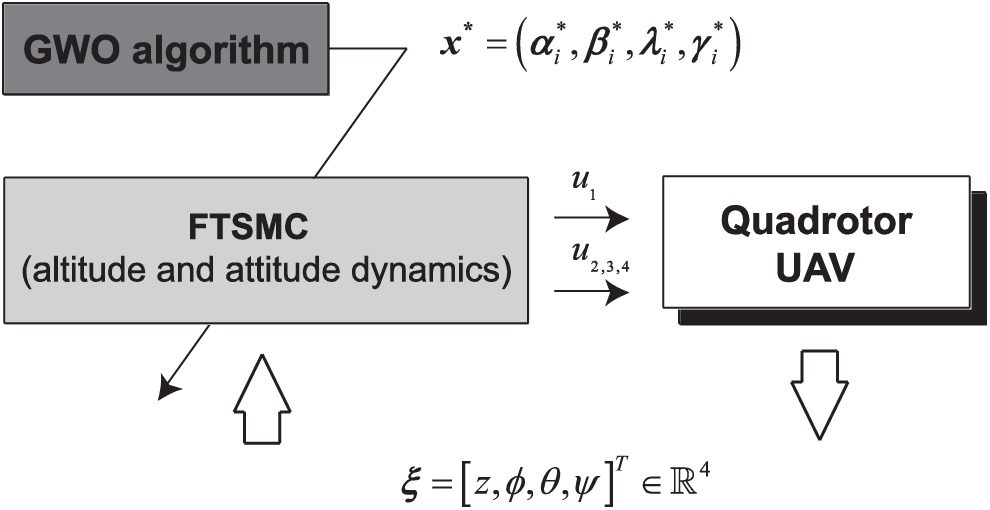
Figure 3: Optimization-based tuning of the FTSM controller for the quadrotor

Cost functions of the problem (16) are chosen as IAE, IATE, ISE, ISTE, and MSE performance criteria [23,27]. To handle the nonlinear constraints, a static penalty function used as follows:

Θi(x,t)=fi(x,t)+∑q=14Λq max{0,gq(x,t)}2(17)

where Λq are the prescribed scaling penalty parameters.

3  Grey Wolf Optimization Algorithm

The social hierarchy of the grey wolves is defined by four types of agents such as alpha (α), beta (β), delta (δ), and omega (ω) that guide the hunting process [20–22]. In a d -dimensional search space, each wolf in the pack is characterized by its position xki=(xk,1i,xk,2i,…,xk,di). The prey position is denoted as xkp=(xk,1p,xk,2p,…,xk,dp). In terms of optimization, the fittest solution is the position of α wolf in the search space. The second and third best solutions are β and δ, respectively. Other wolves, including ω ones, update their positions randomly around the prey. Since the best search agents α, β and δ have better knowledge about the potential location of prey as the problem optimum, the first three best solutions, i.e., xkbest,1, xkbest,2 and xkbest,3, are saved to oblige the other search agents, including the ω wolves, to update their positions according to the following motion equations:

xk+1i=xkbest,1+xkbest,2+xkbest,33,i≠α,β,δ(18)

where xkbest,1=xkα-Δkαϑ1,k, xkbest,2=xkβ-Δkβϑ2,k and xkbest,3=xkδ-Δkδϑ3,k. The vectors ϑ1,k, ϑ2,k and ϑ3,k as well as the terms Δkα, Δkβ, and Δkδ are computed as follows:

{ϑ1,k=2υ1,kU(0,1)-υ1,k;ϑ2,k=2υ2,kU(0,1)-υ2,k;ϑ3,k=2υ3,kU(0,1)-υ3,kΔkα=|λ1,kxkα-xki|;Δkβ=|λ2,kxkβ-xki|;ΔkΔ=|λ3,kxkΔ-xki|(19)

where υj,k, j∈{1,2,3}, are linearly decreased from 2 to 0 over the course of iterations and λj,ki are random numbers between 2 and 0, U{0,1} is a uniformly random number in the interval [0, 1].

Finally, the steps of the basic GWO pseudo-code are summarized as follows [20,21]:

•    Step 1: Randomly initialize the grey wolves population x0i, i=1,2,…,npop.

•    Step 2: Initialize ϑj,0, υj,0, and λj,0i.

•    Step 3: Calculate the fitness of each search agent and select x0α, x0β, and x0δ.

•    Step 4: Update the position of the current search agent by Eqs. (18)–(19).

•    Step 5: Update ϑj,k, υj,k, and λj,ki then calculate the fitness of all search agents.

•    Step 6: Update the positions xkα, xkβ, and xkδ.

•    Step 7: Check the termination criterion and repeat iterations. Return xkα as the best solution.

4  Results and Discussion

In this section, the proposed GWO is applied to solve the formulated tuning problem (16). The physical parameters of the studied quadrotor used are given in our previous works [23,24].

4.1 Algorithms Execution and Optimization Results

All reported algorithms are independently run 20 times on a PC with i7 Core 2 Duo-2.67 GHz CPU and 6.00 GB RAM. The termination criterion is set as a maximum number of iteration reached nGen = 100 for a population size of npop = 30. The control parameters of all optimizers are set in Tab. 1.

Table 1: Control parameters of the reported optimizers

Tab. 2 gives the optimization results attained by all algorithms for the problem (16). It can be clearly observed that the proposed GWO produces very competitive solutions with the reported algorithms especially in terms of solutions quality and convergence fastness, i.e., the standard deviation STD and the elapsed time ET are always minimal in the case of the GWO metaheuristic.

Table 2: Optimization results of the problem (16)

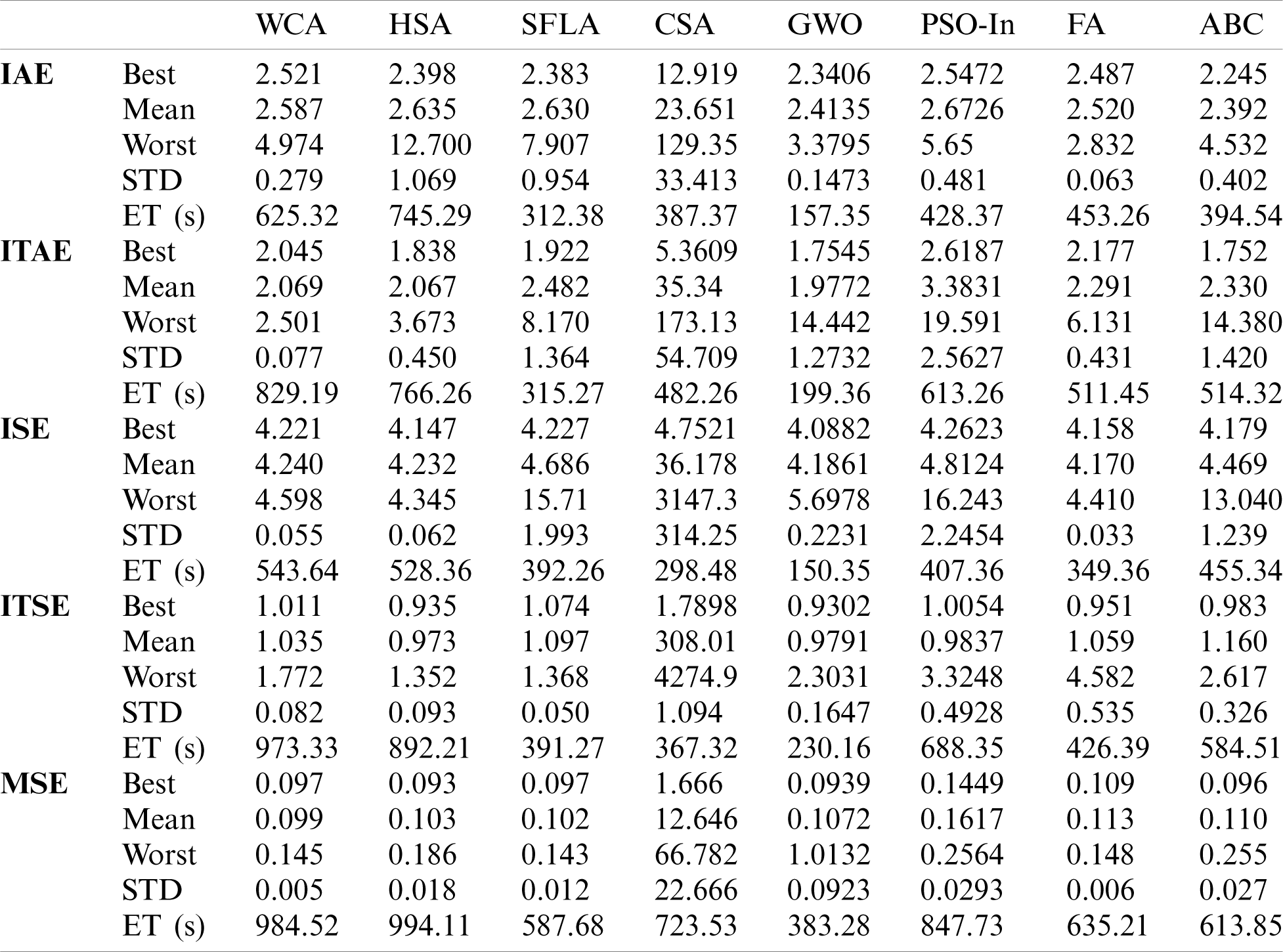
Fig. 4 shows the convergence histories related to the IAE, ITAE, ISE, ITSE, and MSE test problems. It is shown that the proposed GWO often outperforms the other reported methods in terms of fastness and non-premature convergences. Efficient exploration of the search space is guaranteed and the algorithm is able to escape from stagnation in local solutions. During the last iterations, the exploitation capabilities are better than the other methods which further improve the quality of the found global solutions.

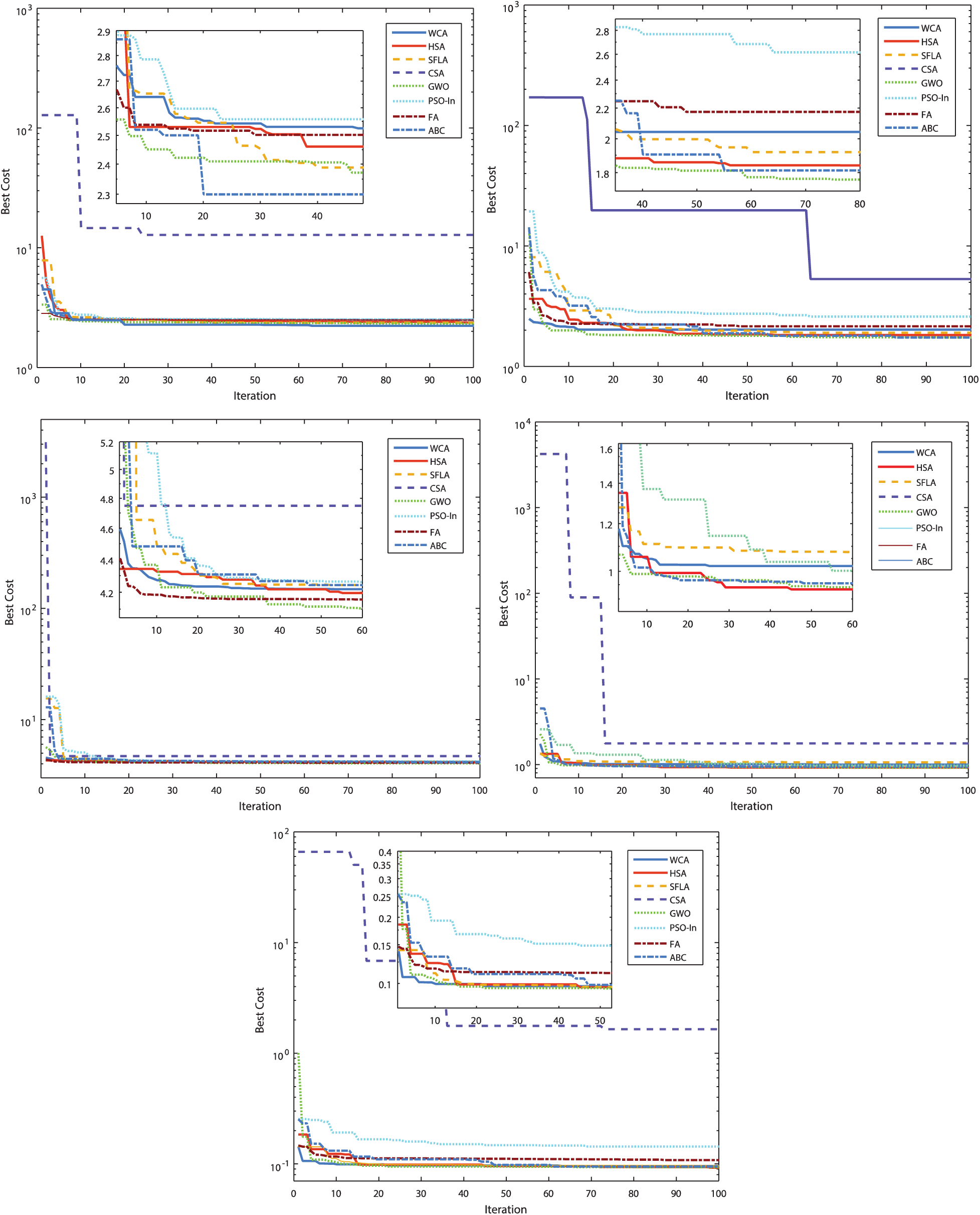
Figure 4: Algorithms performances comparison for the problem (16): (a) IAE criterion case, (b) ITAE criterion case, (c) ISE criterion case, (d) ITSE criterion case, (e) MSE criterion case

The time-domain performances of the controlled dynamics are shown in Fig. 5. The aim is to show the difference between the classical tuning methods and the GWO-tuned ones. Referring to these curves, the GWO-tuned FTSM controller indicates high performance in comparison with the other reported methods. The transient responses are further damped, and the steady-state is quickly reached. Fig. 6 shows the control signals for GWO-tuned FTSMC, standard TSMC, and FTSMC methods.

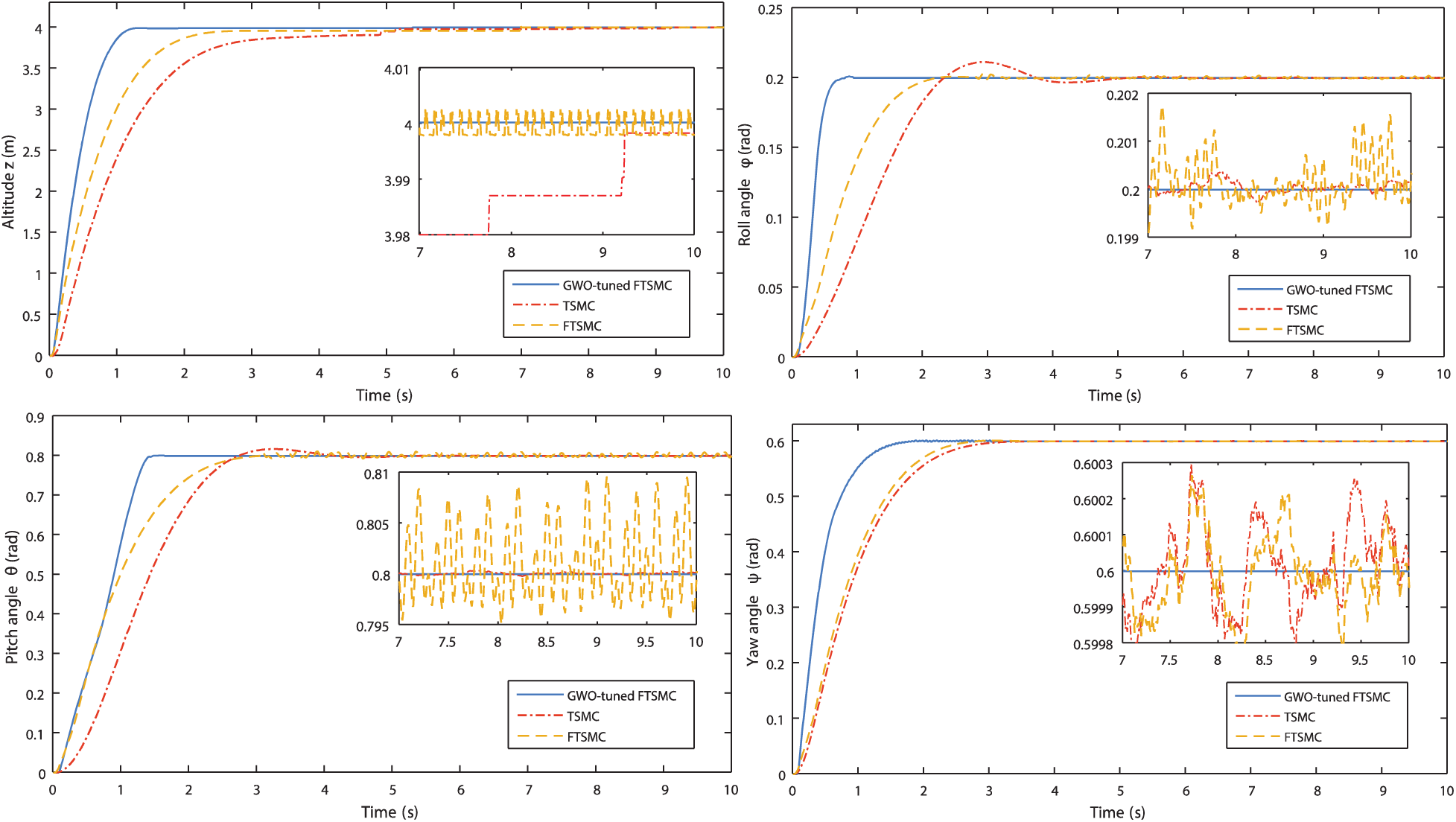
Figure 5: Step responses comparison of the controlled dynamics

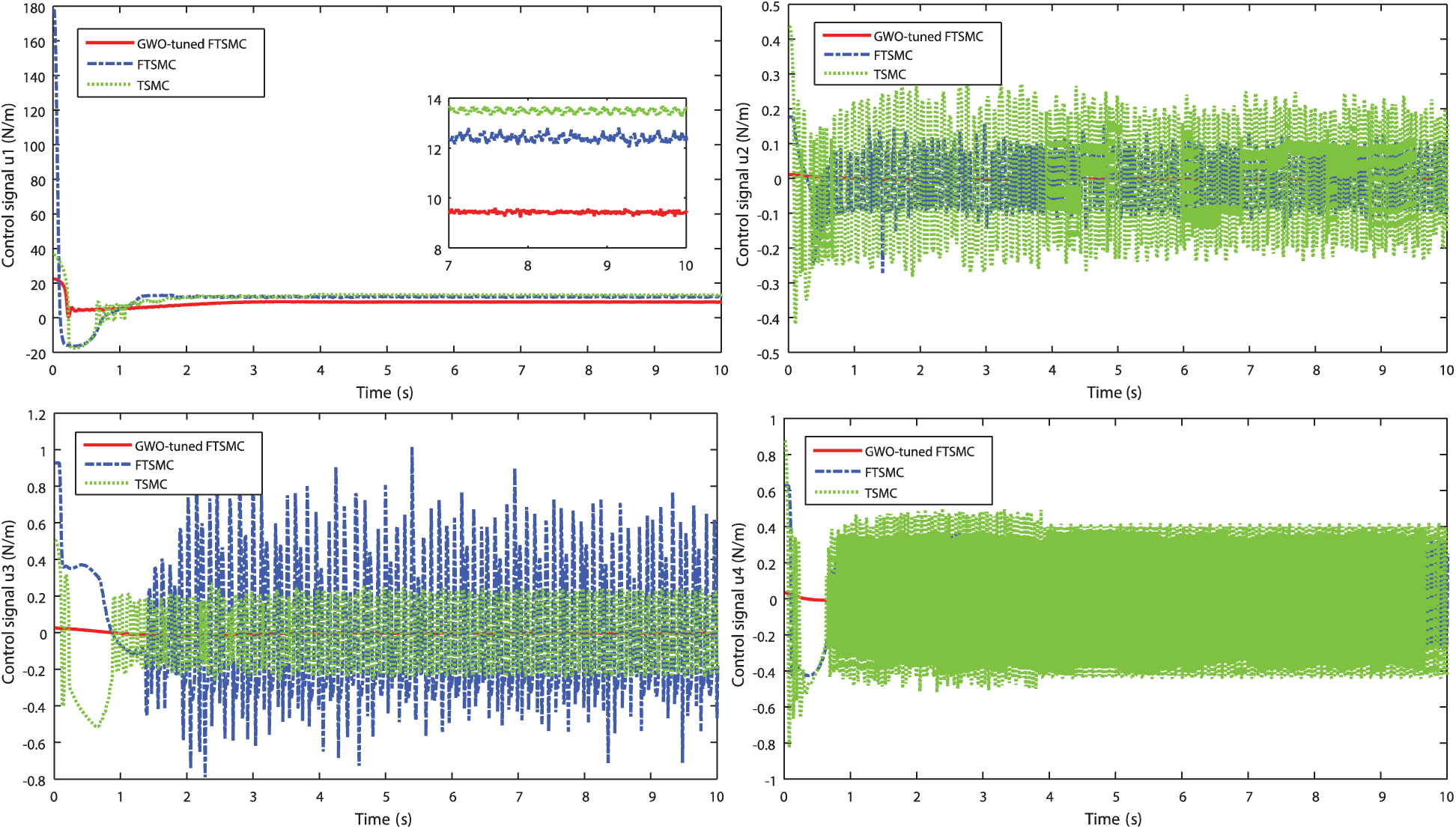
Figure 6: Control signals variations for the altitude and attitude dynamics

From these demonstrative results, one can observe the superiority of the proposed control approach to reduce the undesirable chattering phenomenon in comparison with the standard TSMC approach. The control amplitude of each flight dynamic is moderated and further reduced. Large transient oscillations and amplitudes are recorded for the reported FTSMC and TSMC cases.

Tabs. 3–6 give a quantitative comparison of all designed methods based on several time-domain indexes for a unit step response, i.e., rise time (s), settling time (s), steady-state error, and first overshoot (%). It can be shown that the performances of the GWO-tuned controllers often outperform the other reported methods.

Table 3: Time-domain performance of the controlled altitude dynamics

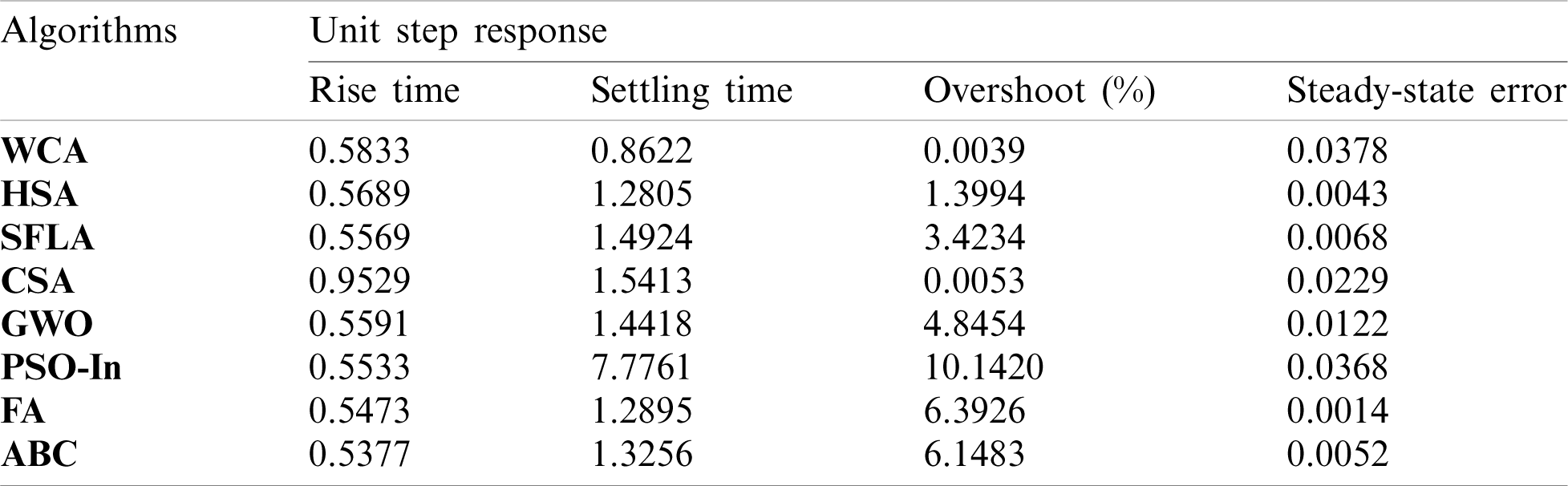
Table 4: Time-domain performance of the controlled roll dynamics

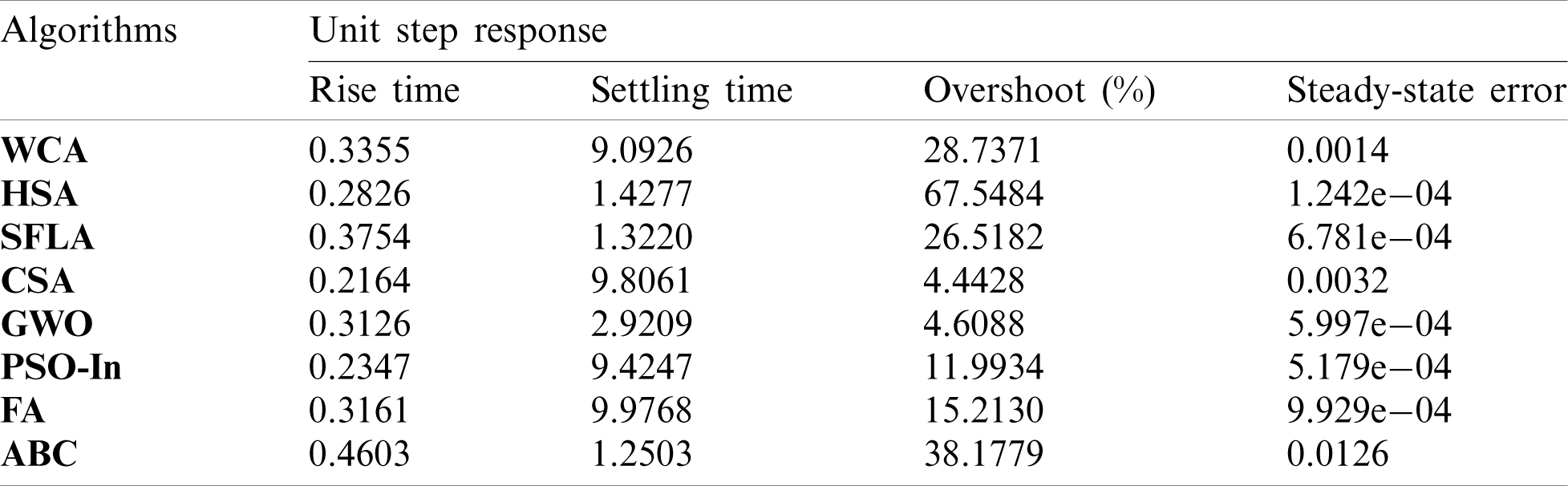
Table 5: Time-domain performance of the controlled pitch dynamics

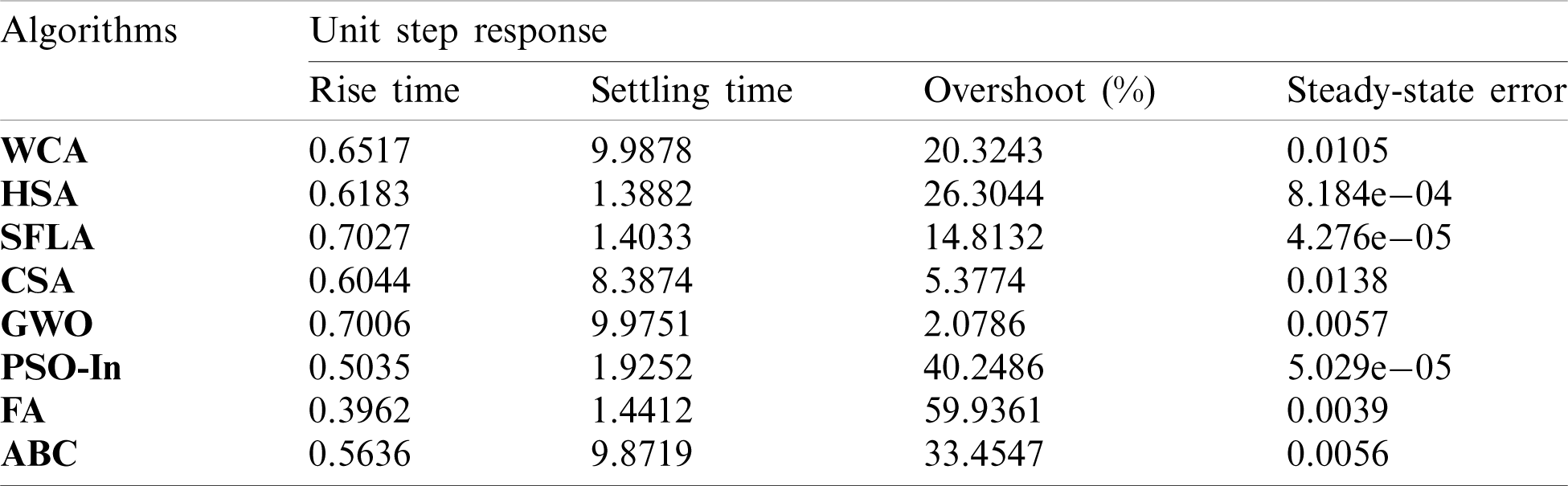
Table 6: Time-domain performance of the controlled yaw dynamics

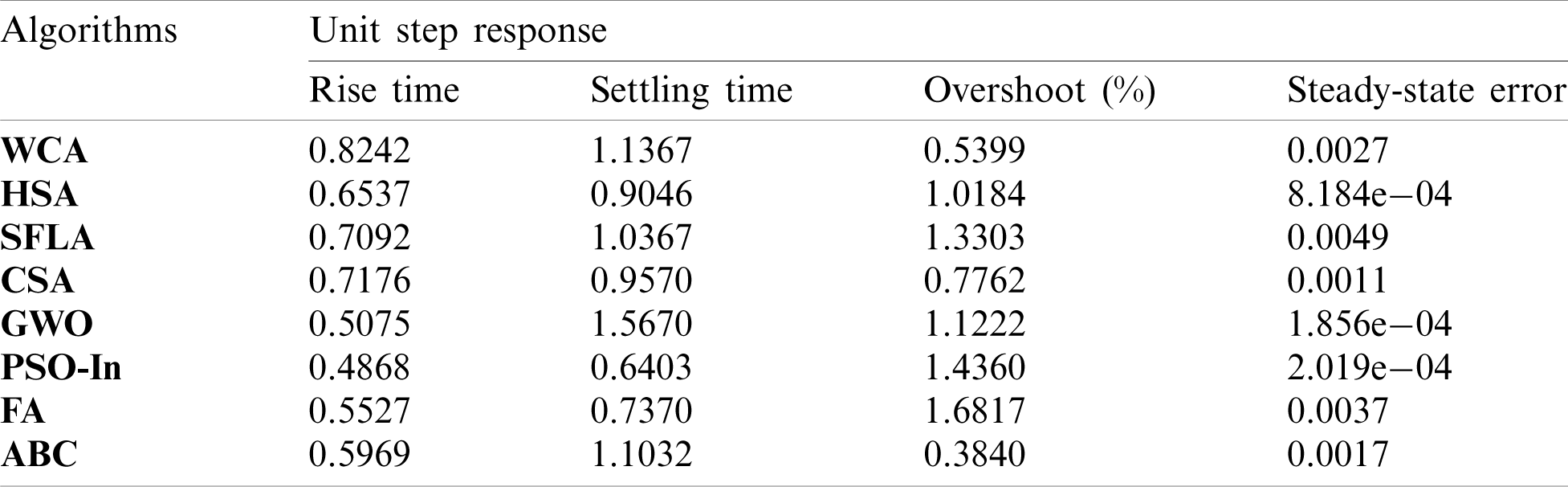
Figs. 7 and 8 show respectively the robustness and tracking performance of the proposed GWO-tuned FTSMC strategy in comparison with standard TSMC and Non-singular variant (NTSMC) [5,8,11]. External disturbances on flight dynamics are well rejected and the defined circular 3D trajectory is well tracked with the fastness and damped response of the GWO-TSMC controller. In terms of tracking performance analysis, a circular trajectory is investigated in a 3D flight space as shown in Fig. 8. Such a desired path is planned as xd(t)=2sin(t), yd(t)=2cos(t), and zd(t)=5. The quadrotor is initially located at the origin, i.e., ζ0=(0,0,0). Fig. 8 shows that the drone’s trajectories converge to the reference path without deviations or changes of direction for both NTSMC and GWO-FTSMC approaches. As shown in Fig. 8, the response of the proposed GWO-tuned FTSMC technique (dashed red line) first reaches the reference trajectory in comparison with that of NTSMC one (solid blue line). The transient behavior of the GWO-based FTSM controller, i.e., a small change of direction against the NTSMC curve, has the aim to reach as quickly as possible the desired trajectory. This further proves the superiority of such an optimized variant of TSMC in terms of fastness and tracking precision. The GWO-based controlled UAV follows the desired circular path closely and manages to accurately track the flight reference with fast and accurate responses.

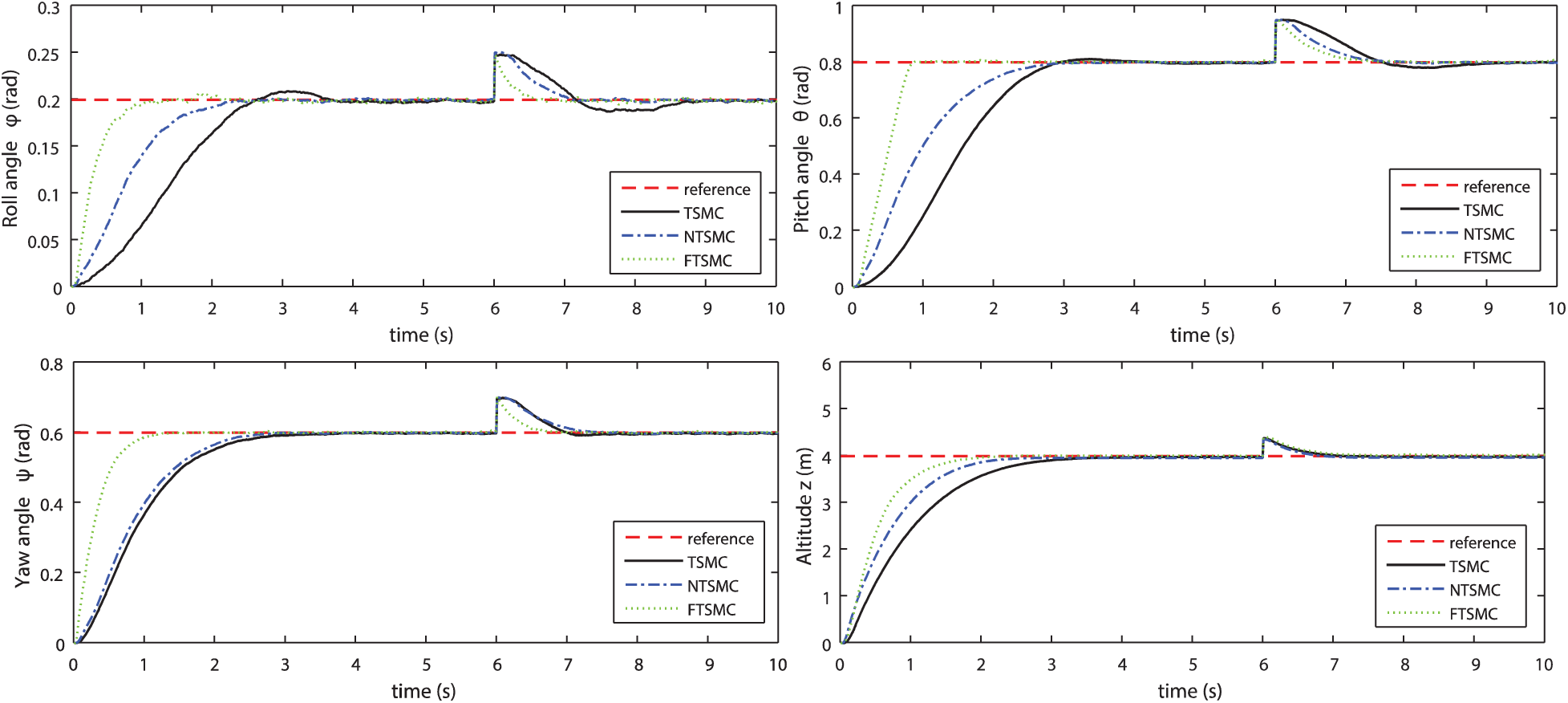
Figure 7: External disturbances’ rejection of the proposed GWO-tuned FTSMC approach

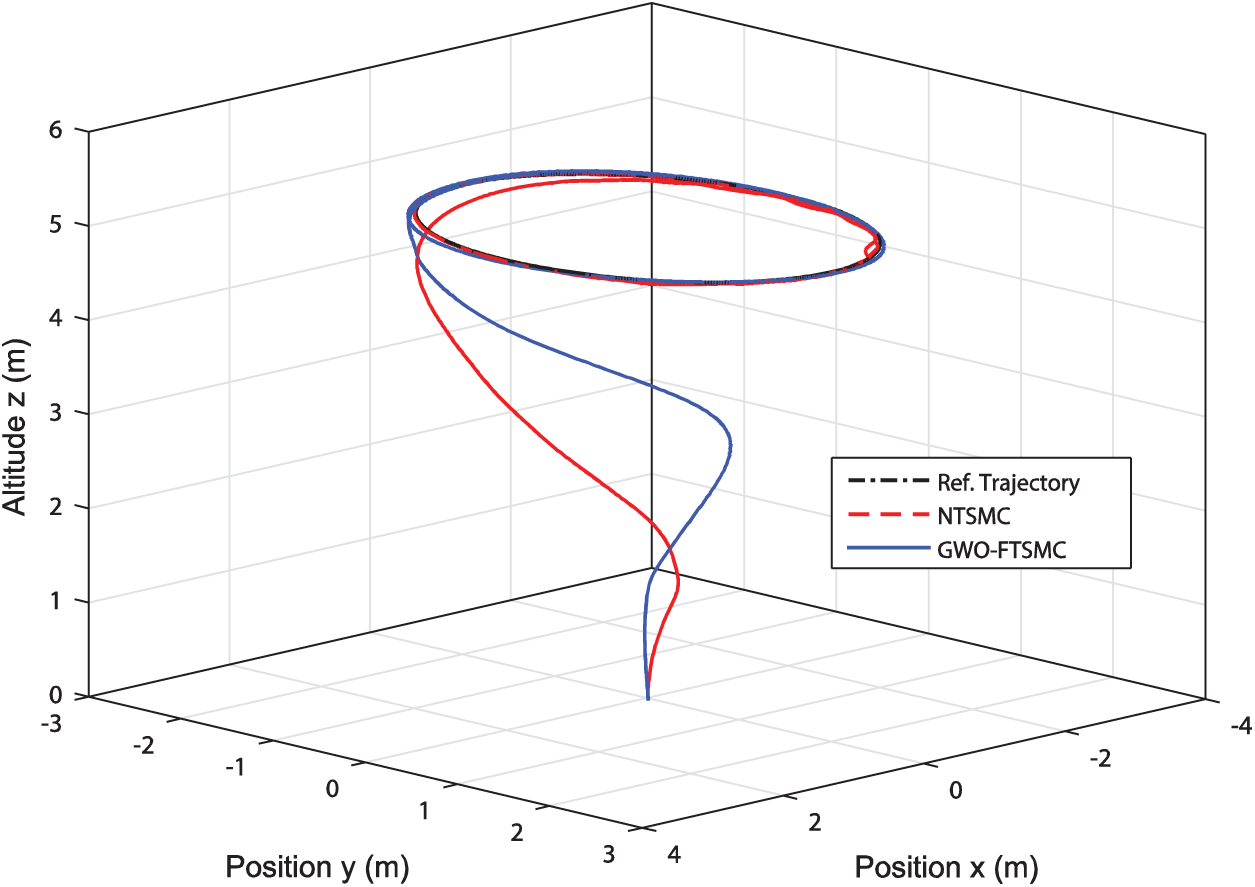
Figure 8: Flight tracking performance of the proposed GWO-tuned FTSMC approach

4.2 Statistical Analysis and Comparisons

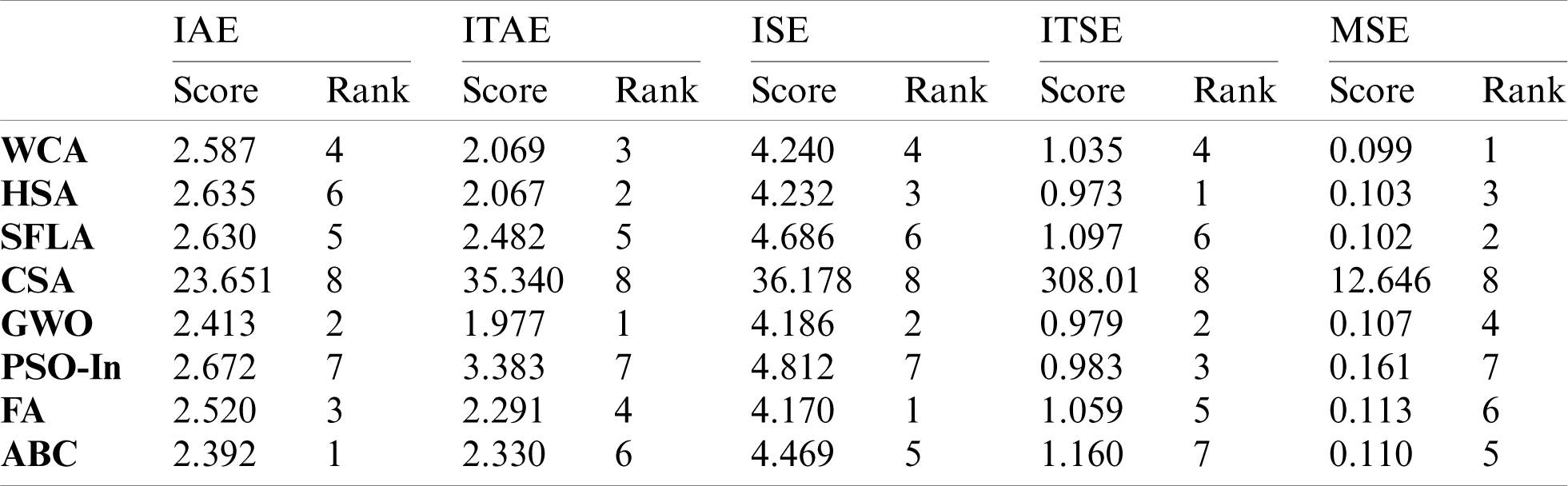
Nonparametric statistical comparison of the proposed metaheuristics is carried out based on the Friedman and pair-wise post hoc tests within the mean optimization case [35]. All algorithms are ranked and summarized in Tabs. 7 and 8. In Friedman ranking, the algorithm attains the best mean value ranks the lowest, while the one that has the worst mean value is given the highest rank. Roughly, the GWO has worthily attained the lowest average ranks compared to the remaining algorithms.

Table 7: Friedman ranking of algorithms for means performances

Based on the results of Tab. 8, the Friedman test for eight algorithms and five test problems provides the F-score of 7.200. Using a table of the F distribution with a level of significance of 99%, the F-statistics value is about 3.360. Since the computed F-score is greater than the F-statistics value, the null hypothesis is rejected and it can be deduced that the performances of the algorithms are statistically different. Hence, post hoc paired comparisons should be performed to express such a difference. Tab. 9 gives the absolute differences of the individual rank’s summation. Underlined values indicate that the metaheuristics are different. The computed critical difference in the summation ranks at 99% of the significance level is 14.299 for a t0.995 = 2.763 value of the t-distribution with 28 degrees of freedom.

Table 8: Nonparametric statistics test computation

Table 9: Paired comparisons of the proposed metaheuristics

From these results, it can be clearly deduced that the GWO metaheuristic has the same performance in solving the optimization problem (16) as other WCA, HSA, SFLA, FA, and ABC methods. The performance of the proposed GWO algorithm is clearly superior to the CSA and PSO-In ones. This verdict further justifies the use of this global metaheuristic for the efficient and less complex tuning of the designed fast terminal sliding mode controllers for drone dynamics stabilization.

5  Conclusions

In this work, a systematic and intelligent tuning method of all effective parameters of fast sliding mode controllers is proposed and successfully applied for a quadrotor UAV. The gains of sliding manifolds and switching functions of the FTSM control laws are selected thanks to the proposed free-parameters GWO algorithm. For such a hard and large-scale tuning problem, the tedious and time-consuming trials-errors based methods are no longer used, and the design time is further reduced. A full control scheme for the studied quadrotor UAV is first given to deal with the underactuated and coupled flight dynamics. Only the dynamics of altitude and attitude are considered for the optimization-based tuning process using the proposed GWO algorithm compared to other homologous methods. Demonstrative results in terms of optimization capabilities and time-domain performance are carried out to show the effectiveness of the proposed GWO-based tuning method. In comparison with the reported optimizers, the mean values of STD and elapsed time obtained for the proposed GWO algorithm are minimal and equal to 0.38012 and 224.1 s, respectively. This finding further encourages the use of such a free-parameters metaheuristic in real-world and online optimization scenarios. Regarding the chattering attenuation, the proposed GWO-tuned controllers succeeded to damp and cancel severe oscillations on control signals with the amplitude of 1.6 N/m for the no optimized FTSMC technique and 0.8 N/m for the classical TSMC approach. The performance metrics in terms of rising and settling times as well as the first overshoots are further improved by a reduction to 50% of their values in the cases without GWO-based tuning, i.e., classical TSMC, FTSMC, and NTSMC approaches. The superiority of the proposed GWO-tuned FTSMC in terms of stabilization and tracking is clearly shown. Nonparametric statistical analyses, i.e., using the Friedman and post-hoc tests, show that the proposed free-parameters GWO metaheuristic outperforms the reported algorithms retained as comparison tools.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Austin, Unmanned Aircraft Systems: UAVs Design, Development and Deployment, 1 st ed. London, UK: John Wiley & Sons, 2010. [Google Scholar]

 2.  Y. Bestaoui Sebbane, Smart Autonomous Aircraft: Flight Control and Planning for UAV, 1 st ed. New York, USA: CRC Press, Taylor & Francis Group, 2016. [Google Scholar]

 3.  R. Lozano, Unmanned Aerial Vehicles: Embedded Control, 1 st ed. New York, USA: John Wiley & Sons, 2010. [Google Scholar]

 4.  K. P. Valavanis and G. J. Vachtsevanos, Handbook of Unmanned Aerial Vehicles, 1 st ed. Dordrecht Netherlands: Springer-Netherlands, 2015. [Google Scholar]

 5.  J. Liu and X. Wang, “Chapter 1: Terminal sliding mode control,” In: J. Liu, X. Wang (Eds.) Advanced Sliding Mode Control for Mechanical Systems: Design, Analysis and MATLAB Simulation, 1 st ed. Berlin, Germany: Springer-Verlag, pp. 150–165, 2012. [Google Scholar]

 6.  D. Qian and J. Yi, Hierarchical Sliding Mode Control for Under-actuated Cranes: Design, Analysis and Simulation, 1 st ed. Berlin, Germany: Springer-Verlag, 2015. [Google Scholar]

 7.  S. Yu, X. Yu and M. Zhihong, “Robust global terminal sliding mode control of SISO nonlinear uncertain systems,” in Proc. of the 39th IEEE CDC, Sydney, NSW, Australia, pp. 2198–2203, 2000. [Google Scholar]

 8.  R. Fessi, S. Bouallègue, J. Haggège and S. Vaidyanathan, “Chapter 4: Terminal sliding mode controller design for a quadrotor unmanned aerial vehicle,” In: S. Vaidyanathan, C. H. Lien (Eds.) Applications of Sliding Mode Control in Science and Engineering, 1st ed. Berlin, Germany: Springer-Verlag, pp. 81–98, 2017. [Google Scholar]

 9.  J. J. Xion and G. B. Zhang, “Global fast dynamic terminal sliding mode control for a quadrotor UAV,” ISA Transactions, vol. 66, no. 1, pp. 233–240, 2017. [Google Scholar]

10. K. Wu, Z. Cai, J. Zhao and Y. Wang, “Target tracking based on a nonsingular fast terminal sliding mode guidance law by fixed-wing UAV,” Applied Sciences, vol. 7, no. 333, pp. 1–18, 2017. [Google Scholar]

11. J. Wang, Z. Zhao and Y. Zheng, “NFTSM-based fault tolerant control for quadrotor unmanned aerial vehicle with finite-time convergence,” IFAC-PapersOnLine, vol. 51, no. 24, pp. 441–446, 2018. [Google Scholar]

12. L. Wang, T. Chai and L. Zhai, “Neural-network-based terminal sliding-mode control of robotic manipulators including actuator dynamics,” IEEE Transactions on Industrial Electronics, vol. 56, no. 9, pp. 3296–3304, 2009. [Google Scholar]

13. H. N. Esfahani, V. Azimirad and M. Danesh, “A time delay controller included terminal sliding mode and fuzzy gain tuning for underwater vehicle-manipulator systems,” Ocean Engineering, vol. 107, no. 1, pp. 97–107, 2015. [Google Scholar]

14. Z. Zhao, X. Li, J. Zhang and Y. Pei, “Terminal sliding mode control with self-tuning for coronary artery system synchronization,” International Journal of Biomathematics, vol. 10, no. 3, pp. 1–14, 2017. [Google Scholar]

15. S. Ahmed, Wang and Y. Tian, “Adaptive high-order terminal sliding mode control based on time delay estimation for the robotic manipulators with Backlash hysteresis,” IEEE Transactions on Systems, Man and Cybernetics: Systems, vol. 51, no. 2, pp. 1–10, 2019. [Google Scholar]

16. N. Ben Ammar, S. Bouallègue and J. Haggège, “Fuzzy gains-scheduling of an integral sliding mode controller for a quadrotor unmanned aerial vehicle,” International Journal of Advanced Computer Science and Applications, vol. 9, no. 3, pp. 132–141, 2018. [Google Scholar]

17. H. Ghasemi, B. Rezaie and Z. Rahmani, “Terminal sliding mode control with evolutionary algorithms for finite-time robust tracking of nonholonomic systems,” Journal of Information Technology and Control, vol. 47, no. 1, pp. 26–44, 2018. [Google Scholar]

18. M. Du, D. Zhao, B. Yang and L. Wang, “Terminal sliding mode control for full vehicle active suspension systems,” Journal of Mechanical Science and Technology, vol. 32, no. 6, pp. 2851–2866, 2018. [Google Scholar]

19. M. Gendreau and J. Y. Potvin, Handbook of Metaheuristics, 3 rd ed. Gewerbestrasse, Switzerland: Springer International Publishing AG, 2019. [Google Scholar]

20. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, no. 1, pp. 46–61, 2014. [Google Scholar]

21. S. Gupta and K. Deep, “A novel random walk grey wolf optimizer,” Swarm and Evolutionary Computation, vol. 44, no. 1, pp. 101–112, 2019. [Google Scholar]

22. M. Kohli and S. Arora, “Chaotic grey wolf optimization algorithm for constrained optimization problems,” Journal of Computational Design and Engineering, vol. 5, no. 4, pp. 458–472, 2018. [Google Scholar]

23. R. Fessi and S. Bouallègue, “LQG controller design for a quadrotor UAV based on particle swarm optimization,” International Journal of Automation and Control, vol. 13, no. 5, pp. 569–594, 2019. [Google Scholar]

24. S. Bouallègue and R. Fessi, “Modelling and hardware co-simulation of a quadrotor unmanned aerial vehicle,” International Journal of Simulation and Process Modelling, vol. 13, no. 1, pp. 3–14, 2018. [Google Scholar]

25. S. Bouallègue and K. Ben Khoud, “Integral backstepping control prototyping for a quad tilt wing unmanned aerial vehicle,” International Review of Aerospace Engineering, vol. 9, no. 5, pp. 152–161, 2016. [Google Scholar]

26. X. Yu and M. Zhihong, “Fast terminal sliding-mode control design for nonlinear dynamical systems,” IEEE Transactions on Circuits and Systems, vol. 49, no. 2, pp. 261–264, 2002. [Google Scholar]

27. F. M’zoughi, I. Garrido, S. Bouallègue, M. Ayadi and A. J. Garrido, “Intelligent airflow controls for a stalling-free operation of an oscillating water column-based wave power generation plant,” Electronics, Section: Artificial Intelligence, vol. 8, no. 1, pp. 1–26, 2019. [Google Scholar]

28. D. Karaboga and B. Basturk, “On the performance of artificial bee colony (ABC) algorithm,” Applied Soft Computing, vol. 8, no. 1, pp. 687–697, 2008. [Google Scholar]

29. A. Askarzadeh, “A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm,” Computers and Structures, vol. 169, no. 1, pp. 1–12, 2016. [Google Scholar]

30. X. Z. Gao, V. Govindasamy, H. Xu, X. Wang and K. Zenger, “Harmony search method: Theory and applications,” Computational Intelligence and Neuroscience, vol. 2015, no. 258491, pp. 1–10, 2015. [Google Scholar]

31. H. Eskandar, A. Sadollah, A. Bahreininejad and M. Hamdi, “Water cycle algorithm: A novel metaheuristic optimization method for solving constrained engineering optimization problems,” Computers & Structures, vol. 111, no. 1, pp. 151–166, 2012. [Google Scholar]

32. J. Luo and M. R. Chen, “Improved shuffled frog leaping algorithm and its multi-phase model for multi-depot vehicle routing problem,” Expert Systems with Applications, vol. 41, no. 5, pp. 2535–2545, 2014. [Google Scholar]

33. M. Clerc and J. Kennedy, “The particle swarm: Explosion, stability, and convergence in a multidimensional complex space,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 1, pp. 58–73, 2002. [Google Scholar]

34. I. Fister, I. Fister Jr., X. S. Yang and J. Brest, “A comprehensive review of firefly algorithms,” Swarm and Evolutionary Computation, vol. 13, no. 1, pp. 34–46, 2013. [Google Scholar]

35. W. J. Conover, Practical Nonparametric Statistics, 3 rd ed. New York, USA: John Wiley & Sons, 1999. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.