DOI:10.32604/cmc.2021.016851

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016851 |  |
| Article |
Multi-Head Attention Graph Network for Few Shot Learning
1School of Computer Science and Technology, Huazhong University of Science and Technology, Wuhan, 430074, China
2School of Electronics, Electrical Engineering and Computer Science, Queens University, Belfast, BT7 1NN, UK
*Corresponding Author: Hefei Ling. Email: lhefei@hust.edu.cn
Received: 12 January 2021; Accepted: 13 February 2021
Abstract: The majority of existing graph-network-based few-shot models focus on a node-similarity update mode. The lack of adequate information intensifies the risk of overtraining. In this paper, we propose a novel Multi-head Attention Graph Network to excavate discriminative relation and fulfill effective information propagation. For edge update, the node-level attention is used to evaluate the similarities between the two nodes and the distribution-level attention extracts more in-deep global relation. The cooperation between those two parts provides a discriminative and comprehensive expression for edge feature. For node update, we embrace the label-level attention to soften the noise of irrelevant nodes and optimize the update direction. Our proposed model is verified through extensive experiments on two few-shot benchmark MiniImageNet and CIFAR-FS dataset. The results suggest that our method has a strong capability of noise immunity and quick convergence. The classification accuracy outperforms most state-of-the-art approaches.
Keywords: Few shot learning; attention; graph network
The past decade has seen the remarkable development of deep learning in a broad spectrum of Computer Vision field, including Image classification [1], Object Detection [2–4], Person re-identification [5–8], Face Recognition [9], etc. Such progress cannot be divorced from vast amounts of labeled data. Nevertheless, the performance can be adversely affected by the data-hungry condition. Thus, there is an urgent need to enable learning systems to efficiently resolve new tasks with few labeled data, which is termed as few-shot learning (FSL).
The origin of FSL can be traced back to 2000, E. G. Miller et al. investigated Congealing algorithm to learn the common features from a few examples and accomplished the matching of specific images [10]. Since then, considerable literature has grown up around the theme of few-shot learning [11]. The vast majority of existing implementation methodologies belong to meta-learning (ML), which implements an episodic training strategy to learn the task-agnostic knowledge from abundant meta-train tasks. Multifarious ML approaches fall into three major groups: learn-to-measure methods provide explicit criteria across different tasks to assess the similarity between labeled and unlabeled data [12,13]; learn-to-model methods generate and update parameters through collaborating with proven networks [14,15]; learn-to-optimize methods suggest to fine-tune a base learner for fast adaptation [16]. Despite its diversity and efficacy, mainstream meta-learning models mostly pay attention to generalize to the unseen task with transferable knowledge, but few explore inherent structured relation and regularity [17].
To remedy the drawback above, another line of work has focused on Graph Network, which adopted structural representation to support relational reasoning for few-shot learning [17]. The early work constructed a complete graph to represent each task, where label information was propagated by updating node features from neighborhood aggregation [18]. Thereafter, more and more graph methods have been devoted to few-shot learning. Such as edge-labeling framework EGNN [19], transductive inference methods TPN [20], distribution propagation methods DPGN [21], etc. With various features involved in the graph update, limited label information has been converted to multiple forms, and then double-counting and aggregation, entailing many otherwise unnecessary costs [22]. Consequently, how to find the discriminable information and realize effective propagation is a problem that desperately needs to be settled.
In this paper, we propose a novel multi-head attention Graph Network (MAGN) to address the problem stated above, which is shown in Fig. 1. In the process of updating the graph network, different weights are assigned to different neighbor nodes. Compared to the node-similarity based weight of existing methods, we provide new insights into multi-level fusion similarity mechanism with distribution feature and label information to improve discriminative performance. More specifically, for node update, we treat the label information as an initial adjacency matrix to soften the noise of irrelevant nodes, thereby providing a constraint for the update direction. For edge update, we excavate the distribution feature by calculating the edge-level similarity of overall samples, as a feedback of global information, it reveals more in-depth relations. Collocating with the regular node-level attention, more valuable and discriminable relations would be involved in the process of knowledge transfer. Furthermore, we verify the effectiveness of our methods through extensive experiments on the MiniImagenet and CIFAR-FS datasets. The results show that MAGN exceeds comparable performance in quick convergence, robustness at the same time keeps the property of accuracy.
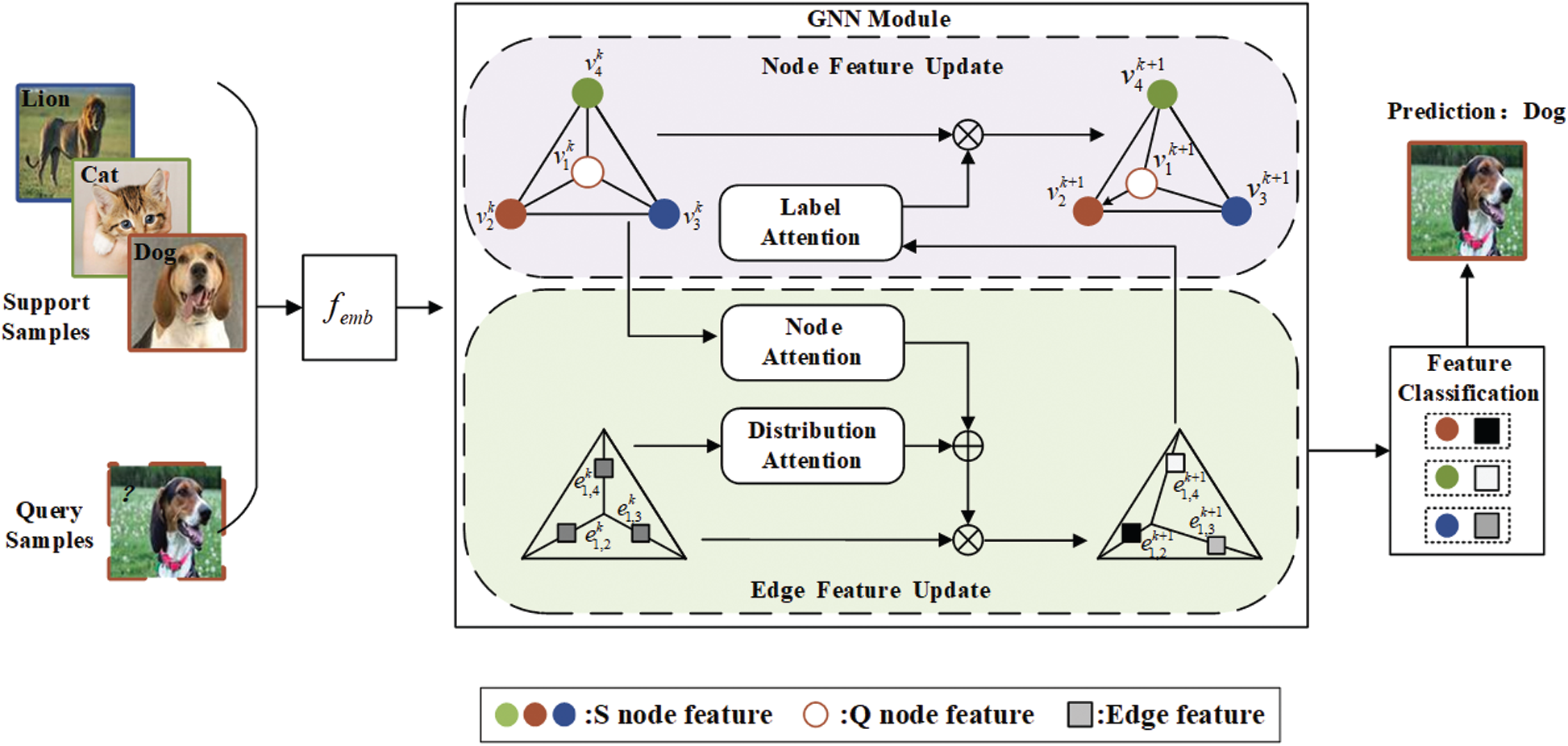
Figure 1: The overall framework of the MAGN model. In this figure, we present a 3-way 1-shot problem as an example. After Feature Embedding Module femb (details in Section 4.2.1), samples and their relations generate the initial graph. There are L generations in the GNN module (we show one of them for simplicity). Each generation consists of node feature update and edge feature update, with cooperation among the node-attention, distribution-attention and label-attention. The solid circle represents support samples and the hollow circle represents the query samples. The square indicates the edge feature and the darkness of color denotes the value. The darker the color, the larger the value. The detailed process is described in Section 3
Meta-learning, also known as “learn to learn,” plays an essential role in addressing the issue of few-shot learning. According to the different content in the learning systems, it can be divided into three categories: learn-to-measure methods, which based on metric learning, employs an attention nearest neighbor classifier with the similarity between labeled and unlabeled data. Matching networks adopts a cosine similarity [15], Prototypical network [12] establishes a prototype for each class and utilize Euclidean distance as a metric. Differ from above, Relation Net [13] devises a CNN-based relation metric network. Learn-to-optimize methods suggest to fine-tuning a base learner for fast adaptation. MAML [16] is a typical approach that learns a good initialization parameter for rapid generalization. Thereafter, various models derived from MAML, such as first-order gradients methods Reptile [23], task-agnostic method TAML [24], Bayes based method BMAML [25], etc. Learn-to-model methods generate and update parameters on the basis of the proven networks. Meta-LSTM [26] embraces the LSTM network to update the meta-learner parameters. VERSA [27] builds a probabilistic amortization network to obtain softmax layer weights. In order to predict weights, MetaOpt Net [28] advocates SVM, R2-D2 adopts ridge regression layer [29], while Dynamic Net [30] uses a memory module.
The attention mechanism is essential for a wide range of technologies, such as sequence learning, feature extraction, signal enhancement and so on [31]. The core objective is to select the information that is more critical to the current task objective from the numerous information. The early GCN works have been limited by the Fourier transform derivation, which was challenging to deal with a directed graph with indiscriminate equal weight [32]. Given that, Yoshua Bengio equipped the graph network with a masked self-attention mechanism [33]. During information propagation, it assigns different weights to each node according to the neighbor distribution. Benefited from this strategy, GAT can filter noise neighbor and improve the performance of the graph Framework. Such an idea was adopted and enhanced by GAAN [34]. It combined these two mechanisms, the multi-head attention to extract various information, likewise the self-attention to gather them.
In this section, we first summarize the preliminaries of few-shot classification following previous work and then describe our method in more technical detail.
Few-shot learning: The goal of FSL is to train a reliable model with the capability of learning and generalizing from few samples. A common setting is N -way K -shot classification task. Clearly, each task
Meta-Learning: One of the main obstacles in the FSL is overfitting caused by limited labeled data. Meta-learning adopts episodic training strategy to make up for this, which increase generalization ability through extensive training on similar tasks. Given train date set
Graph Neural Networks: In this section, we describe the overall framework of our proposed GNN, as shown in Fig. 1. Firstly, we utilize an embedding module to extract feature (detail in Section 4.2.1), after that each task is expressed as a fully-connected graph. Through L layers Graph Update, the GNN realizes information transfer and relational reasoning. Specifically, the task
Initial graph feature: In the graph
The majority of existing few-shot graph-models focus on a node-attention update mode, which adopts the node similarity to control neighborhood aggregation. This mode ignores the inherent relationships between the samples, which may lead to the risk of overtraining. Therefore, we propose a multi-head attention mechanism with distribution feature and label information to enhance the model capability.
Like some existing methods as EGNN and DPGN, the node-level attention is based on the similarity between the two nodes. Since each node has a different neighborhood, we use normalization operation for nodes in the same neighborhood to get more discriminative and comparable results. We employ node-level attention with node-similarity defined as follows:
In detail, given nodes
3.3.2 Distribution-Level Attention
The node-level attention relies on the local relationships of node similarity, while the global relationship has not yet been fully investigated. To mine more discriminative information, we extract the global distribution feature by aggregating the edge features of overall samples and then evaluate the similarity of distribution feature, with definitions as Eqs. (4) and (5).
where
In the previous work, though the aggregation scope is the neighborhood of each node, it extends beyond the same class. Furthermore, the update of graph network is a process of information interaction and fusion, therefore increasing the noise of nodes from diverse classes. We set an adjacency matrix to filter irrelevant information and constraint update direction as shown in Eq. (6).
where Ak is the adjacency matrix at the k-th layer. A is the label adjacency matrix, the element ai, j is equal to one when vi and vj have the same label and zero otherwise. Ek is the matrix of edge feature. It combines long-term label information with short-term updated edge features in a Recurrent Neural Network. Such operation prunes useless information from inter-class samples and distills useful intra-class samples.
Information transmission has been facilitated through the alternate update of node features and edge features. In particular, the update of node feature depends on neighborhood aggregation, where edge features cooperate with label information to control the relation transformation. While the edge features of MAGN subject to node-similarity and neighborhood distribution.
Based on the above update rule, the edge features at the
where
The node vectors at the
where
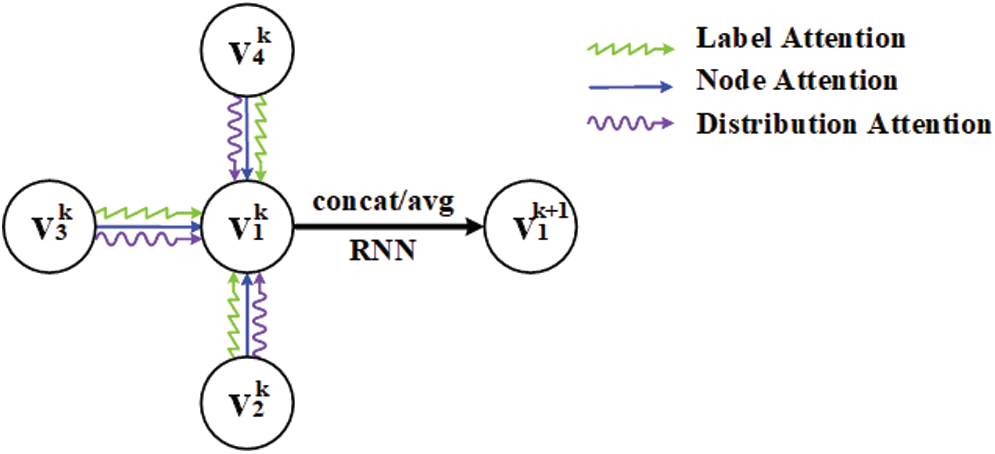
Figure 2: Multi-head attention
Over L layers update of node and edge feature, the classification results of node xi can be obtained from a prediction probability of corresponding edge feature at the final layer
In Eq. (9),
During the episodic training, the parameters of proposed GNN are trained in an end-to-end manner. The final objective is to minimize the total loss function computed in all layers as shown in Eq. (10):
where
For a fair comparison, we conduct our method on two standard few-shot learning datasets following the proposed experimental settings of EGNN and make contrast experiments with state-of-the-art approaches.
MiniImageNet is a typical benchmark few-shot dataset. As a subset of the ImageNet, it is composed of 60,000 images uniformly distributed over 100 classes. All of the images are RGB colored, the size is 84 * 84 * 3. Following the setting provided by [26], we randomly select 64 classes for training, 16 classes for validation, and 20 classes for testing.
CIFAR-FS is derived from CIFAR-100 dataset. The same as MiniImageNet, it is formed of 100 classes and each class contains 600 images, which splits 64, 16, 20 for training, validation, and testing. In particular, the main obstacles of low resolution (32 * 32) and high inter-class similarity make classification task technically challenging.
Before training, both datasets have been endured data augmentation with transformation as horizontal flip, random crop, and color jitter (brightness, contrast, and saturation).
We adopt ConvNet and ResNet12 for the backbone embedding module. Following the same setting used in [19,23], the ConvNet architecture contains four convolutional blocks, each block is composed of 3 * 3 convolutions, a batch normalization, a 2 * 2 max-pooling and a LeakyReLU activation. Similar to ConvNet, ResNet12 also has four blocks, one of which is replaced by a residual block.
We evaluate MAGN in 5-way 1-shot and 5-shot classification task on both benchmarks. There are three layers in the proposed GNN model. In the meta-train stage, each batch consists of 60 tasks. While in the meta-test step, each batch obtains ten tasks. During training, we adopt the Adam optimizer with an initial learning rate of 5 * 10−4 and a weight decay of 10−6. The dropout rate is set as 0.3, and the loss coefficient is 1. The results of our proposed model are obtained through 100k iterations on MiniImageNet and CIFAR-FS.
We compare our approach with recent state-of-the-art models. The main results are listed in Tabs. 1 and 2. According to diverse embedding architectures, the backbone can be divided into ConvNet, ResNet12, ResNet18, and WRN28. The major difference is the number of residual blocks. In addition, GNN-based methods are listed separately for the sake of intuition. Extensive results show that our MAGN yields better performance on both datasets. For example, among all the Convnet-architecture methods, The MAGN is substantially better than others. Although the results are slightly lower than DPGN, we still obtain the second place with a narrow gap of both backbones. Nevertheless, some common graph network methods like EGNN, DPGN adopt training and testing with labels in a consistent order, such as the label in the 5-way 1-shot task is from support set (0, 1, 2, 3, 4) to the query set (0, 1, 2, 3, 4). The learning system may learn the order of task rather than the relation of samples. To avoid this effect, we disrupt the label order of support set and query set. This setup makes our results less than optimal, but it is more in line with the reality of the scene. The proposed MAGN acquires a robust result that would not be biased by the noise of label order.
Table 1: Classification accuracy on CIFAR-FS

Table 2: Classification accuracies on MiniImageNet

Effect of Data shuffling mode: There are three ways to scramble data: shuffle the support set, shuffle the query set and shuffle both sets. We conduct a 5-way 1-shot trial with label-node attention in MiniImagenet. The comparative result is shown in the Tab. 3. As we can see, the use of data shuffling mode has little effect on the accuracy rate, while it makes a difference to the time of convergence. It is consistent with the essence of random selection. To further explore the convergence performance of the model, the default setting is shuffling the order of both sets.
Table 3: 5-way 1-shot results on MiniImagenet with different data shuffling mode

Effect of Different Attention: The major ablation results of different attention components are shown in Fig. 3. All variants are performed on the 5-way 1-shot classification task of MiniImageNet. The baseline adopts only node attention (“NodeAtt”). On this basis, the variant “DisNode” adds distribution-level attention to assist edge update. For samples in the same class, their surrounding neighborhood would follow a similar distribution. Thus the “DisNode” model can mine more discriminable relationship between the two nodes and obtain an enhancement in accuracy. Besides, the performance of concatenating aggregation is superior to average aggregation. This advantage extends to the final state of three attentions with a slight rise from 0.49 (“CatDisNode”-“AveDisNode”) to 0.85 (“Cat3Att”-“Ave3Att”). The variant “LabNode” equips node update with label-level attention, leading to a considerable improvement in convergent iteration from 89k to 63k. We attribute this to the filtering capability of label adjacency matrix, which constrains update direction and realizes fast convergence.
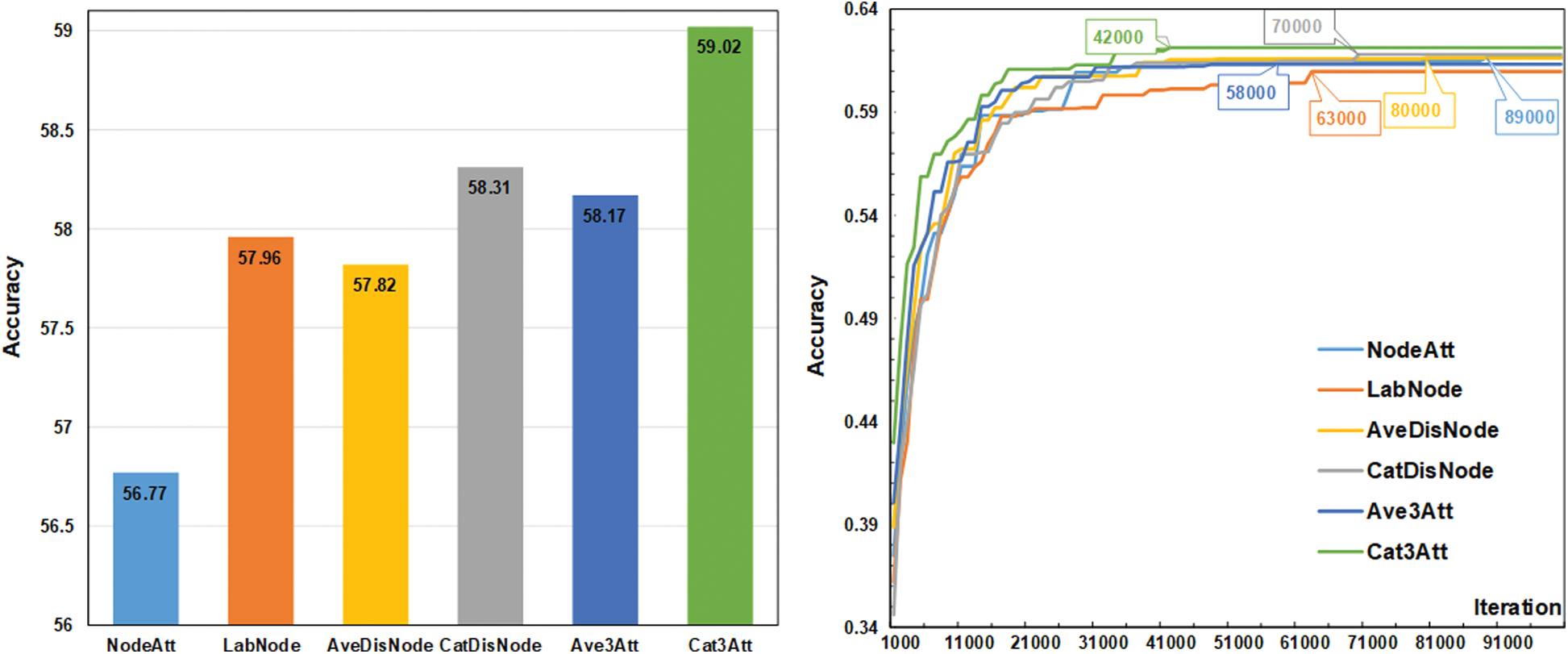
Figure 3: Effect of different attention. The left part shows the accuracy of variants with different attention components, the right part describes the convergence process of those variants
Effect of Layers: In GNN, the depth of the network has some influence on feature extraction and information transmission. To explore this problem, we perform 5-way 1-shot experiments with different numbers of layers. As shown in Tab. 4, accuracy rate and convergence times are improved steadily with the network deepens. To manage the trade-off between convergence and accuracy, a 3-layers GNN is configured for our models.
Table 4: 5-way 1-shot results on MiniImagenet with different layers

In this paper, we propose a multi-head attention Graph Network for few-shot learning. The multiple attention mechanism including three parts: node-level attention explores the similarities between the two nodes, and distribution-level attention extracts more in-deep global relation. The cooperation between those two parts provides a discriminative expression for edge feature. While the label-level attention, served as a filtration, weakens the noise of some inter-class information during node update and accelerates the convergence process. Furthermore, we scramble the training data of support set and query set to guarantee to transfer order-agnostic knowledge. Extensive experiments on few-shot benchmark datasets validate the accuracy and efficiency of the proposed method.
Funding Statement: This work was supported in part by the Natural Science Foundation of China under Grant 61972169 and U1536203, in part by the National key research and development program of China (2016QY01W0200), in part by the Major Scientific and Technological Project of Hubei Province (2018AAA068 and 2019AAA051).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. X. Ou, H. Ling, H. Yu, P. Li, F. Zou et al., “Adult image and video recognition by a deep multi context network and fine-to-coarse strategy,” ACM Transactions on Intelligent Systems and Technology, vol. 8, no. 5, pp. 1–25, 2017. [Google Scholar]
2. L. Wu, H. Ling, P. Li, J. Chen, Y. Fang et al., “Deep supervised hashing based on stable distribution,” IEEE Access, vol. 7, no. 1, pp. 36489–36499, 2019. [Google Scholar]
3. H. Ling, Y. Fang and L. Wu, “Balanced Deep Supervised Hashing,” Computers, Materials & Continua, vol. 58, no. 2, pp. 85–100, 2019. [Google Scholar]
4. L. Wu, Y. Fang, H. Ling, J. Chen and P. Li, “Robust mutual learning hashing,” in IEEE Int. Conf. on Image Processing, Taipei, Taiwan, pp. 2219–2223, 2019. [Google Scholar]
5. Y. Shi, Z. Wei, H. Ling, Z. Wang, J. Shen et al., “Person retrieval in surveillance videos via deep attribute mining and reasoning,” IEEE Transactions on Multimedia, Early Access, pp. 99, 2020. [Google Scholar]
6. Y. Shi, H. Ling, L. Wu, J. Shen and P. Li, “Learning refined attribute-aligned network with attribute selection for person re-identification,” Neurocomputing, vol. 402, pp. 22071, 2020. [Google Scholar]
7. H. Ling, Z. Wang, P. Li, Y. Shi, J. Chen et al., “Improving person re-identification by multi-task learning,” Neurocomputing, vol. 347, no. 6–7, pp. 109–118, 2019. [Google Scholar]
8. Y. Shi, Z. Wei, H. Ling, Z. Wang, P. Zhu et al., “Adaptive and robust partition learning for person retrieval with policy gradient,” IEEE Transactions on Multimedia, vol. 99, pp. 1, 2020. [Google Scholar]
9. J. Lei, B. Y. Zhang and H. F. Ling, “Deep learning face representation by fixed erasing in facial landmarks,” Multimedia Tools and Applications, vol. 78, no. 4, pp. 27703–27718, 2019. [Google Scholar]
10. E. G. Miller, N. E. Matsakis and P. A. Viola, “Learning from one example through shared densities on transforms,” in IEEE Conf. on Computer Vision and Pattern Recognition, Hilton Head, SC, USA, pp. 1464–1471, 2000. [Google Scholar]
11. H. J. Ye, H. Hu, D. C. Zhan and F. Sha, “Few-shot learning via embedding adaptation with set-to-set functions,” in IEEE Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 8805–8814, 2020. [Google Scholar]
12. J. Snell, K. Swersky and R. S. Zemel, “Prototypical networks for few-shot learning,” in Conf. on Neural Information Processing Systems, Long Beach, CA, USA, pp. 4077–4087, 2017. [Google Scholar]
13. F. Sung, Y. Yang, L. Zhang, T. Xiang, P. H. S. Torr et al., “Learning to compare: Relation network for few-shot learning,” in IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 1199–1208, 2018. [Google Scholar]
14. S. Gidaris and N. Komodakis, “Dynamic few-shot visual learning without forgetting,” in IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 4367–4375, 2018. [Google Scholar]
15. O. Vinyals, C. Blundell, T. Lillicrap, K. Kavukcuoglu and D. Wierstra, “Matching networks for one shot learning,” in Conf. on Neural Information Processing Systems, Barcelona, Spain, pp. 3630–3638, 2016. [Google Scholar]
16. C. Finn, P. Abbeel and S. Levine, “Model-agnostic meta-learning for fast adaptation of deep networks,” 34th Int. Conf. on Machine Learning, vol. 70, pp. 1126–1135, 2017. [Google Scholar]
17. P. Battaglia, B. Hamrick, V. Bapst, A. Sanchez, V. Zambaldi et al., “Relational inductive biases, deep learning, and graph networks,” arXiv preprint, 2018. [Google Scholar]
18. V. G. Satorras and J. B. Estrach, “Few-shot learning with graph neural networks,” in 6th Int. Conf. on Learning Representations, Vancouver, BC, Canada, 2018. [Google Scholar]
19. J. Kim, T. Kim, S. Kim and C. D. Yoo, “Edge-labeling graph neural network for few-shot learning,” in IEEE Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 11–20, 2019. [Google Scholar]
20. Y. Liu, J. Lee, M. Park, S. Kim, E. Yang et al., “Learning to propagate labels: Transductive propagation network for few-shot learning,” in 7th Int. Conf. on Learning Representations, New Orleans, LA, USA, 2019. [Google Scholar]
21. L. Yang, L. Li, Z. Zhang, X. Zhou, E. Zhou et al., “DPGN: Distribution propagation graph network for few-shot learning,” in IEEE Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 13387–13396, 2020. [Google Scholar]
22. A. Li, T. Luo, T. Xiang, W. Huang and L. Wang, “Few-shot learning with global class representations,” in IEEE Int. Conf. on Computer Vision, Seoul, South Korea, pp. 9714–9723, 2019. [Google Scholar]
23. A. Nichol, J. Achiam and J. Schulman, “On first-order meta-learning algorithms,” arXiv preprint, 2018. [Google Scholar]
24. M. A. Jamal and G. Qi, “Task agnostic meta-learning for few-shot learning,” in IEEE Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 11719–11727, 2019. [Google Scholar]
25. J. Yoon, T. Kim, O. Dia, S. Kim, Y. Bengio et al., “Bayesian model-agnostic meta-learning,” in Conf. on Neural Information Processing Systems, Montréal, Canada, pp. 7343–7353, 2018. [Google Scholar]
26. S. Ravi and H. Larochelle, “Optimization as a model for few-shot learning,” in 5th Int. Conf. on Learning Representations, Toulon, France, 2017. [Google Scholar]
27. J. Gordon, J. Bronskill, M. Bauer, S. Nowozin and R. E. Turner, “Meta-learning probabilistic inference for prediction,” in 7th Int. Conf. on Learning Representations, New Orleans, LA, USA, 2019. [Google Scholar]
28. S. Qiao, C. Liu, W. Shen and A. L. Yuille, “Few-shot image recognition by predicting parameters from activations,” in IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 7229–7238, 2018. [Google Scholar]
29. L. Bertinetto, Henriques, P. H. S. Torr and A. Vedaldi, “Meta-learning with differentiable closed form solvers,” in 7th Int. Conf. on Learning Representations, New Orleans, LA, USA, 2019. [Google Scholar]
30. S. Gidaris and N. Komodakis, “Dynamic few-shot visual learning without forgetting,” in IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 4367–4375, 2018. [Google Scholar]
31. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones et al., “Attention is all you need,” in Conf. on Neural Information Processing Systems, Long Beach, CA, USA, pp. 5998–6008, 2017. [Google Scholar]
32. Y. Li, D. Tarlow, M. Brockschmidt and R. Zemel, “Gated graph sequence neural networks,” in 4th Int. Conf. on Learning Representations, San Juan, Puerto Rico, 2016. [Google Scholar]
33. P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio et al., “Graph attention networks,” in 6th Int. Conf. on Learning Representations, Vancouver, BC, Canada, 2018. [Google Scholar]
34. J. Zhang, X. Shi, J. Xie, H. Ma, I. King et al., “Gaan: Gated attention networks for learning on large and spatiotemporal graphs,” in Proc. of the Thirty-Fourth Conf. on Uncertainty in Artificial Intelligence, Monterey, California, USA, pp. 339–349, 2018. [Google Scholar]
35. A. Ravichandran, R. Bhotika and S. Soatto, “Few-shot learning with embedded class models and shot-free meta training,” in IEEE Int. Conf. on Computer Vision, Seoul, South Korea, pp. 331–339, 2019. [Google Scholar]
36. K. Lee, S. Maji, A. Ravichandran and S. Soatto, “Meta-learning with differentiable convex optimization,” in IEEE Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 10657–10665, 2019. [Google Scholar]
37. S. Gidaris, A. Bursuc and N. Komodakis, “Boosting few-shot visual learning with self-supervision,” in IEEE Int. Conf. on Computer Vision, Seoul, Korea (Southpp. 8058–8067, 2019. [Google Scholar]
38. Z. Li, F. Zhou, F. Chen and H. Li, “Meta-SGD: Learning to learn quickly for few shot learning,” arXiv preprint, 2017. [Google Scholar]
39. W. Li, J. Xu, J. Huo, L. Wang and Y. Gao, “Distribution consistency based covariance metric networks for few-shot learning,” in 33rd AAAI Conf. on Artificial Intelligence, Honolulu, Hawaii, USA, pp. 8642–8649, 2019. [Google Scholar]
40. A. A. Rusu, D. Rao, J. Sygnowski, O. Vinyals, R. Pascanu et al., “Meta learning with latent embedding optimization,” in 7th Int. Conf. on Learning Representations, New Orleans, LA, USA, 2019. [Google Scholar]
41. N. Mishra, M. Rohaninejad, X. Chen and P. Abbeel, “A simple neural attentive meta-learner,” in 7th Int. Conf. on Learning Representations, New Orleans, LA, USA, 2019. [Google Scholar]
42. H. Ye, H. Hu, D. Zhan and F. Sha, “Learning embedding adaptation for few-shot learning,” arXiv preprint, 2018. [Google Scholar]
43. W. Chen, Y. Liu, Z. Kira, Y. F. Wang and J. Huang, “A closer look at few-shot classification,” in 7th Int. Conf. on Learning Representations, New Orleans, LA, USA, 2019. [Google Scholar]
44. H. Li, D. Eigen, S. Dodge, M. Zeiler and X. Wang, “Finding task-relevant features for few-shot learning by category traversal,” in IEEE Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 1–10, 2019. [Google Scholar]
45. S. Gidaris and N. Komodakis, “Generating classification weights with gnn denoising autoencoders for few-shot learning,” in IEEE Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 21–30, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |