DOI:10.32604/cmc.2021.016721

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016721 |  |
| Article |
Transmitter-Receiver Path Selection for Cell Range Extension Using Multi-Hop D2D
1Department of Electrical Engineering, International Islamic University, Islamabad, 44000, Pakistan
2Department of CIT, FAS, King Abdulaziz University, Jeddah, 21551, Saudi Arabia
3Department of Electrical Engineering, Air University, Islamabad, 44000, Pakistan
4Department of Computer Science, Bahria University, Islamabad, 44000, Pakistan
*Corresponding Author: Kiran Sultan. Email: kkhan2@kau.edu.sa
Received: 09 January 2021; Accepted: 17 February 2021
Abstract: Conventional approach of dealing with more users per coverage area in cellular networks implies densifying the amount of (Access Point) AP which will eventually result in a larger carbon footprint. In this paper, we propose a base station off-loading and cell range extension (CRE) scheme based on multi-hop device-to-device (MHD2D) path selection between transmitter and receiver node. The paper also provides derivations of upper and lower bounds for energy efficiency, capacity, and transmit power. The proposed path selection scheme is inspired by the foraging behavior of honey bees. We present the algorithm as a modified variant of the artificial bee colony algorithm (MVABC). The proposed optimization problem is modeled as a minimization problem where we optimize the Energy Efficiency (EE). The proposed path selection MVABC is compared with the Genetic Algorithm (GA) and also with classical artificial bee colony (ABC) through simulations and statistical analysis. The student’s t-test, p-value, and standard error of means (SEM) clearly show that MVABC based path selection out-performs the GA and classical ABC schemes. MVABC based approach is 66% more efficient when compared with classic ABC and about 62% efficient when compared with GA based scheme.
Keywords: Multi-hop; ultra-dense; D2D; path-selection; ABC; GA
Conventional cellular networks provide coverage to a user by having a direct connection established between a user and the base station. Although the scheme provides communication with less delay, the recent trend of increased wireless data users and devices makes it difficult for the conventional scheme to fulfill the QoS (Quality of Service) requirements [1]. This apparent increase in the data requirement or increase in the number of users reduces network reliability and efficiency when it is not able to cater to new users or provide dependable services to the edge users. Hence, the effect is similar to having a cell with reduced coverage. Increasing the number of BS in a cell may solve this issue but at the expense of increased BS and equipment installation charges along with an overall increase in power consumption. D2D communication promises to provide an alternative to this problem by allowing mobile devices to communicate directly with each other using low power in quite possibly the same band being used by some other cellular device [2]. This concept is based on space division multiple access.
From 3GPP (third generation global partnership project) LTE (long term evolution) release 12 and onwards, it is quite apparent that a MHD2D network is set to become a necessary part of 5G networks. Standards for D2D communication along with two-hop communication are already part of the latest release [3]. Moreover, the cell range of base stations can be extended by utilizing MHD2D relay nodes. To ensure that the cell range extension (CRE) offered by D2D links meet the required QoS demand, the energy efficiency (EE) metric is commonly used [4] which is generally defined as:
MHD2D is an emerging technology capable of providing service to user-driven demand. Catering for the similar user demand, the authors in [5] developed an algorithm for long-range D2D links which is done through multi-hop communication. However, the study lacks any insight regarding optimal path selection. In [6] the authors developed an algorithm for power control and routing in MHD2D where Dijkstra shortest path algorithm is used for routing. A drone-based D2D aided multi-hop network for emergency services is proposed in [7] where stochastic geometry is used for link coverage probability to minimize delay, however, the path selected for emergency message transmission is not considered in this paper.
A standard Dijkstra shortest path-based routing algorithm is developed in [8] for D2D for multi-hop communication in the Internet of Things (IoT) application. D2D based solution for offloading traffic in a cellular network is proposed in [9], the proposed framework offers a multi-hop routing scheme for different types of data transmissions. In [10] a MHD2D energy-efficient routing protocol is proposed to perform resource allocation while improving throughput and packet delivery ratio. MHD2D routing for the millimeter-wave network is proposed in [11] where received signal strength (RSS) is measured for relay nodes and an algorithm is designed to select a route based on the probability of route selection as generated by their RSS values.
Interference aware D2D routing is discussed in [12] where an adaptive algorithm is proposed which selects a route based on node location and amount of interference at next hop. Optimum path selection for 5G vehicular networks based on mmWave D2D links is discussed in [13] where the optimum path is found based on vehicular information rather than link quality. The authors in [14] investigate multi-hop data transfer between D2D transmitter and receiver by scheduling cellular resource blocks for optimizing transmission power which is done by maximizing the number of relay-based paths. In [15] a greedy algorithm is proposed for MHD2D relay selection. The algorithm works on a distributed local search.
The above-presented literature review on path selection, routing, or relay selection in MHD2D network clearly shows a lack of heuristic approach towards problem-solving, this gap is largely addressed in the proposed research. Literature provides evidence of using an ABC (artificial bee colony) based algorithm for optimization. ABC based scheduling is proposed in [16] where modified ABC is implemented for reducing travel distance and waiting time for a manufacturing workshop. The authors in [17] utilized ABC for the vehicle-to-vehicle emergency information dissemination by using the algorithm minimum route selection from source to destination. In [18] the ABC algorithm is implemented for intrabody nanonetwork where it is used for optimal selection of biosensors along the transmission path. The low energy reliable routing protocol problem is presented as an NP-hard problem in [19] which is solved using an ABC algorithm.
The literature survey supports the argument that heuristic approaches can be applied for optimum path selection, at the same time application for same in CRE for MHD2D remains unaddressed.
The major contributions of the research are:
• An MHD2D link-based cell range extension scheme is proposed.
• Single antenna transmit power and capacity upper and lower bounds calculations for the network without interference are derived.
• Upper and lower bounds of single antenna energy efficiency for a system without interference are calculated are derived.
• Transmit power and capacity upper and lower bound calculations for single antenna network with interference are derived.
• Energy efficiency upper and lower bound calculations for a network with interference derived.
• MVABC proposed for source-destination path selection in a MHD2D based link for CRE.
• Comparison between MVABC and genetic algorithm (GA) based path selection for MHD2D link between the source and destination node through simulation over a large data set of 30 runs of 200 iterations each is presented.
• Comparison between MVABC and classic ABC based path selection for MHD2D link between the source and destination node through simulation over a large data set of 30 runs of 200 iterations each is presented.
• Statistical analysis of simulation results using student’s t-test, p-value, and SEM (standard error of means).
Section 2 describes the system model and assumptions. In Section 3 we provide detailed derivations for transmitting power, capacity, and energy efficiency for two cases i.e., case one provides derivations without interference while case two provides derivations while considering the effects of interference in a single antenna network. Section 4 gives the mathematical formulation of the problem. In Section 5 we describe MVABC based path selection for MHD2D, which is followed by simulation and results with discussion in Section 6, and the paper is concluded in Section 7.
2 System Model and Assumptions
We consider a single input single output system without interference. The mobile users are distributed around the Macro Base Station (MBS) as Homogeneous Poisson Point Process (HPPP) and downlink communication from MBS to a far-off destination node is considered. A ‘far-off’ node is a node that lies just outside the cell range of MBS. Since the destination node D is located outside the coverage area of MBS, MHD2D links are used for CRE. It is also assumed that nodes independently decide about their willingness to participate in relaying between source and destination. The decision is based on the incentives offered to mobile relay nodes from the service providers. Fig. 1 shows that MBS has several options in terms of finding a path to node D via MHD2D users.
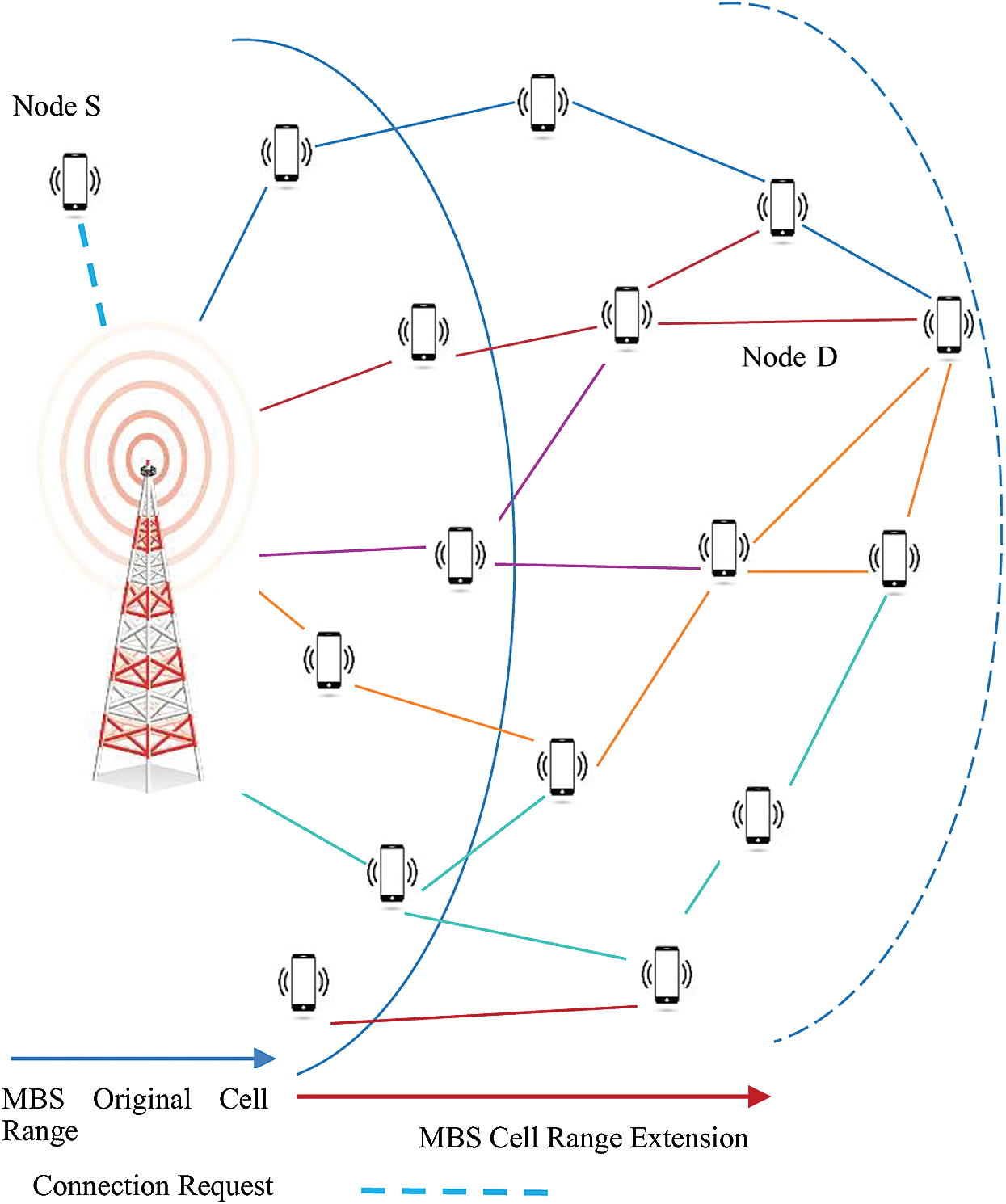
Figure 1: Proposed D2D multi-hop source-to-destination communication
For the sake of simplicity, we assume that MBS is already operating at optimized power. Hence, we have to find upper and lower bound for transmitting power of relaying devices and capacity along the path from MBS to node D to optimize an energy-efficient path as described by Eq. (1). It is also assumed that the dissipation in transceiver hardware and baseband processing is negligible. We consider a scenario (refer to Fig. 1) where a source node S wants to communicate with node D. Node S sends a connection request (Con.Req.) to MBS. Since MBS cannot directly locate node D in its cell range so it forwards a route request to the users at its cell boundary who then forwards the request to their neighbors and ultimately the request reaches the destination node. In this centralized model of route discovery, the MBS discovers the multi-hop route between node S and node D. In a decentralized case node S will directly broadcast a route request to its neighbors which will then further broadcast it to their neighbor until node D is reached. Both centralized and decentralized modes have their advantages and disadvantages, however, the comparison of the two is beyond the scope of the current research.
3 Energy Efficiency and Transmit Power Limits
We will consider two cases wherein the first case we find the transmit power and EE limits for the channel without interference while in the second case we derive the limits for the channel with interference.
3.1 Single Antenna Transmit Power Without Interference
The lower bounds of transmit power Ptlb is required to ensure that a required threshold signal to noise ratio
where Prth in Eq. (2) is the received power threshold which is the minimum acceptable received power that can ensure a signal to noise ratio (SNR) at least equal to the threshold
where N is the noise power, d is the distance between nodes, do is the reference distance which is taken equal to 1 meter for indoor communication and 100 m to 1 Km for outdoor communication, L is a constant which is the path loss computed at do and
For upper bound of Pt (transmit power) we will receive maximum power Prmax and the received SNR will be
As it is obvious that received power increases with a decrease in distance between communicating nodes, hence, we denote the minimum distance as dmin. So, the upper bound of transmit power can be derived as in Eq. (6):
So, transmit power upper bound is given as in Eq. (7):
3.2 Single Antenna Capacity and EE Without Interference
Here we are going to derive the expressions for upper and lower bounds of capacity and EE in a system without interference. Since the capacity is directly proportional to SNR so for the lower bound of capacity the transmit power will also be the lower bound and hence the SNR lower bound of
Similarly, the upper bound for capacity can be derived using
Now, the upper bound of EE can be written as in Eq. (10):
Similarly, the lower bound for EE can be written as in Eq. (11):
3.3 Single Antenna Transmit Power with Interference
In this case, we will use the Signal to Noise and Interference (SINR) ratio represented by
where P′ is the interference power received from neighboring nodes. After substituting values of received power as in the case of single antenna transmit power without interference, we can write the expression for lower bounds of transmit power for node i (
3.4 Single Antenna Capacity and EE with Interference
The expressions for lower and upper bounds of capacity for a network with interference can be derived similarly and is given by Eqs. (15) and (16) respectively:
Energy efficiency upper and lower bounds can be expressed in terms of the ratio of capacity and transmit power for a network with interference and can be expressed in Eqs. (17) and (18) respectively:
Let
Eq. (19) states the energy efficiency for a particular path p written as (EEp) is maximization problem or it’s negative (− EEp) is minimization problem. Eqs. (20) and (21) enforce the capacity constraint on the selected path for the case without interference and the case with interference respectively. Similarly, Eqs. (23)–(25) impose the constraints of transmit power without and with interference on SNR and SINR lower and upper bounds for path selection.
5 MVABC for MHD2D Path Selection
The ABC algorithm is a nature-inspired algorithm where the natural behavior of honey bee for rich nectar source exploration is used for real-world problem-solving. The idea was first proposed by Karaboga in 2005 [20] and ever since then the idea has been refined and also it has found numerous problem-solving applications [21–27]. Each food source corresponds to the solution for the optimization problem. The ABC algorithm consists of three types of bees based on their roles in the exploration process.
Scout: All potential food sources are explored by the scout bee.
Onlooker: Evaluate the nectar quality and quantity as learned from scouts traversing.
Employed Bees: Responsible for nectar collection from sources identified by the onlooker bees. If a food source is exhausted, the corresponding employed bee becomes a scout and looks for a new food source.
In MVABC, we take inspiration from the ABC algorithm and propose an algorithm for the implementation of MVABC for multi-hop path selection. Fig. 2 shows a flow chart of the pseudocode for the MVABC algorithm for path selection. The proposed algorithms are presented in the Algorithms 1–4.

When node S sends a connection request to MBS, MBS broadcasts to users/devices at the cell edge for node discovery. Through MHD2D relays, node D is discovered and a reply is generated by each intermediate node (which previously received MBS request for node discovery) and sent back to MBS. Based on the received replies, MBS generates an initial population with SN solutions representing the nodes which sent replies. Each of these D2D relay (food source positions) represent a possible solution
The following sequence takes place during the initialization step:
• Fix swarm size SN and number of cycles
• Determine the number of employed bees (EB), onlooker bees (OB), and food sources, i.e.,
For path selection problem this will equal the number of nodes.
• MBS generates random variables that will serve as the initial population within the domain of decision variables.
• MBS then calculates the fitness of the population.
• Generate initial trial vector for the population.
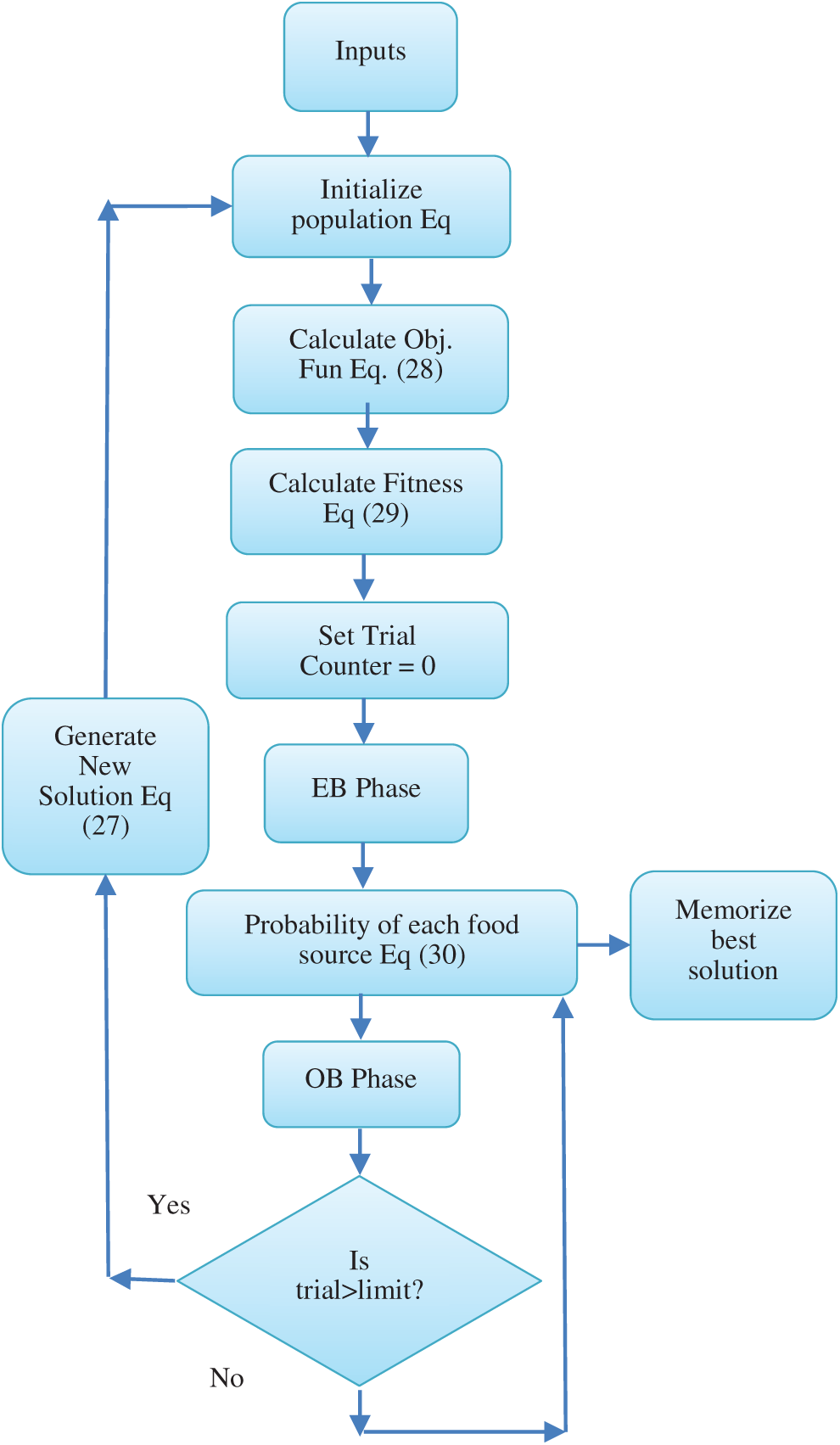
Figure 2: Flow chart of MVABC algorithm
In this phase, MBS sends a route discovery message on Np where Np represents all the possible nodes between S and D, each message sent from MBS behaves similarly to an EB. This route discovery message performs a neighborhood search similar to the EB. Since the node may already have forwarded node discovery request and received a reply, it will compare previous interaction with new interaction, similar to comparing the nectar amount of previous food source in EB memory with the nectar amount of the new food source. The old food location in memory is replaced by a new location if the new location has better nectar quality. The updated location is given by Eq. (27):
where

To generate a new solution, first, we randomly choose a variable to change for the first food source i.e., first neighbor node, then we randomly choose a partner solution Xp and generate a new solution using Eq. (27). The solution is checked for obeying upper and lower bounds and after that fitness of the new solution is calculated using the objective function of Eq. (28):
If the objective function is within the bound specified in Eqs. (10) and (11) for the case without interference or satisfies Eqs. (17) and (18) for the case with interference, then, the fitness of the population is calculated using Eq. (29):
A greedy selection is performed between old and new solutions and the fittest of the two solutions is retained. The process continues until all the nodes who sent route request-reply (food sources) have been exhausted.

Once the search process is complete and all possible paths have been visited by EB, i.e., MBS has sent route request messages on all possible paths, the D2D relays share their neighborhood information with MBS, this is similar to nectar amount being shared with OB through dance. The probability of a food source is calculated by OB (processing within MBS) using Eq. (30):
where fiti is the fitness of solution i for the EE ratio (nectar amount) it represents, where a comparison is made between old and new EE ratio values and the new one replaces the old position (node) if the new position (node) has a better fitness.
If MBS does not receive a route request reply from one of the nodes which previously sent a node discovery reply, after a wait of t time intervals, that particular node will be abandoned. In classical ABC algorithm, in the onlooker bee phase, once the probabilities are calculated for all the possible fitness values, a random number is generated. The randomly generated number is compared with the probability of ith food source (pi). If the probability is less than the random number, then a new solution is generated using Eq. (27), otherwise, the old solution is maintained. In MVABC, we replace this randomly generated number with a number (
Initially the generation of

The SB phase is entered when any solution having a trial limit greater than a maximum exceeds. When MBS cannot improve an established path any further through route discovers, then, the previous best solution is stored in the memory and a new solution is generated randomly between upper and lower bounds using Eq. (31):
where Xmin and Xmax are lower and upper bound of population respectively.
The objective function and fitness of the new solution is calculated using Eqs. (28) and (29) respectively and it replaces the old solution even if it has poor fitness compared to the old solution.
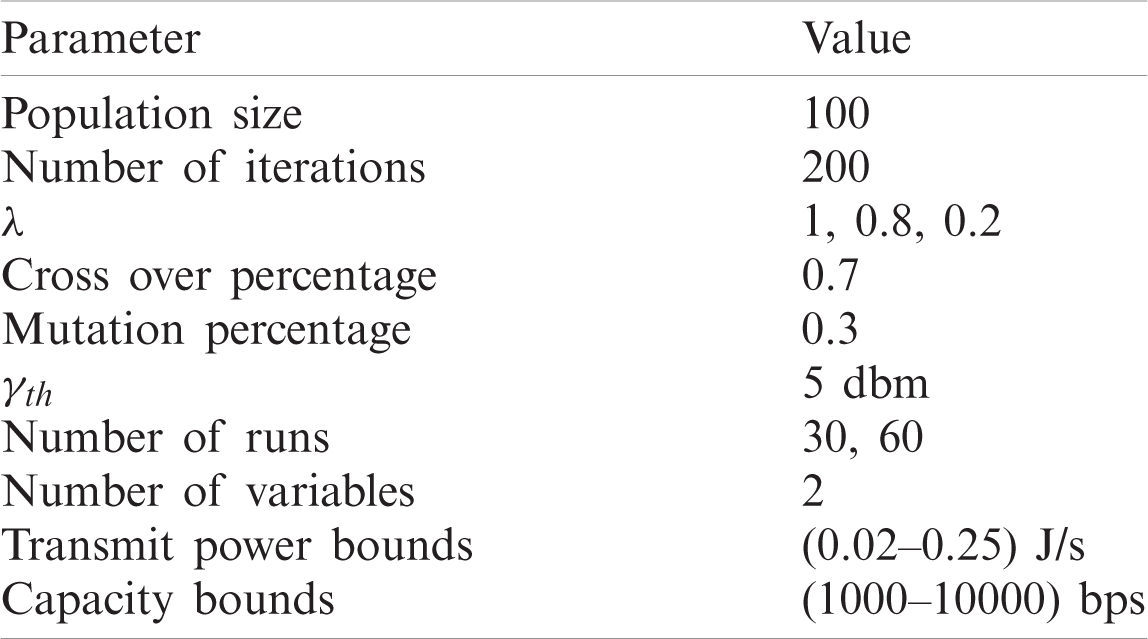
The comparison and performance analysis of the proposed algorithm was carried out in Matlab R2018b. The simulation parameters are presented in Tab. 1.
Table 1: Simulation parameters
A statistical approach similar to one utilized in [28] was used to evaluate the results. We will briefly describe the performance metrices in this sub-section and their details are given in the sub-section below along with discussion on results.
Best Cost (Mean abs(-EE)): As described in Section 1, in this research we consider maximizing the EE or minimizing the (-EE) and is presented for proposed algorithm MVABC along with classic ABC and GA.
Standard Deviation (SD): Describes the variation in mean data values.
Standard Error of Means (SEM): Measures deviation of sample’s mean from population mean.
The proposed algorithm was compared with classic ABC and GA based path selection. Both algorithms were tested using large data set with 30 and 60 runs with 200 iterations per run. The population size and cycle limit were kept the same for all the simulated cases of MVABC, GA and classic ABC.
For GA based algorithm we kept the crossover percentage at 0.7, mutation percentage at 0.3, and mutation rate at 0.1. A population size of 100 was used for all three algorithms. We calculated the mean best cost, SD and the SEM for each run.
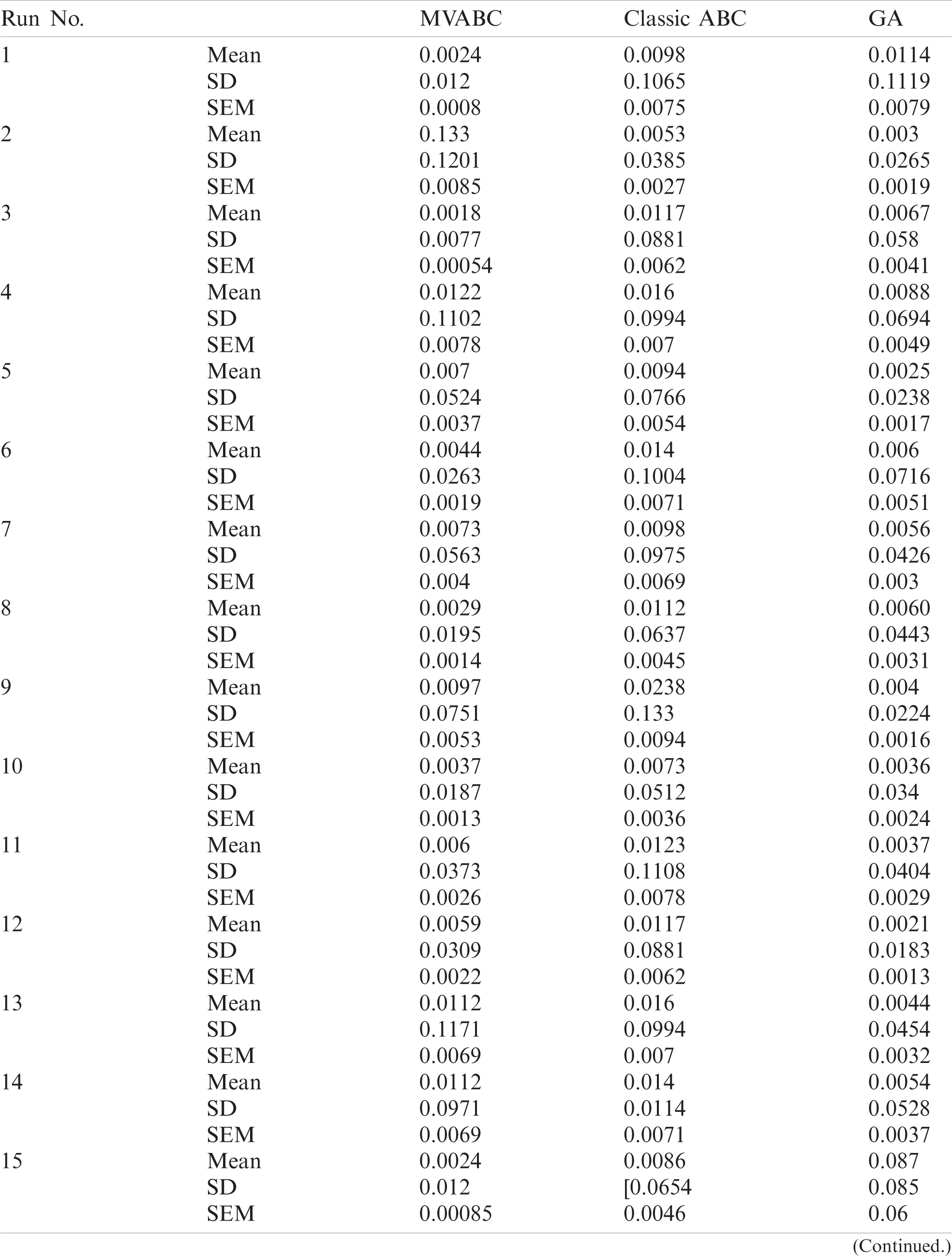
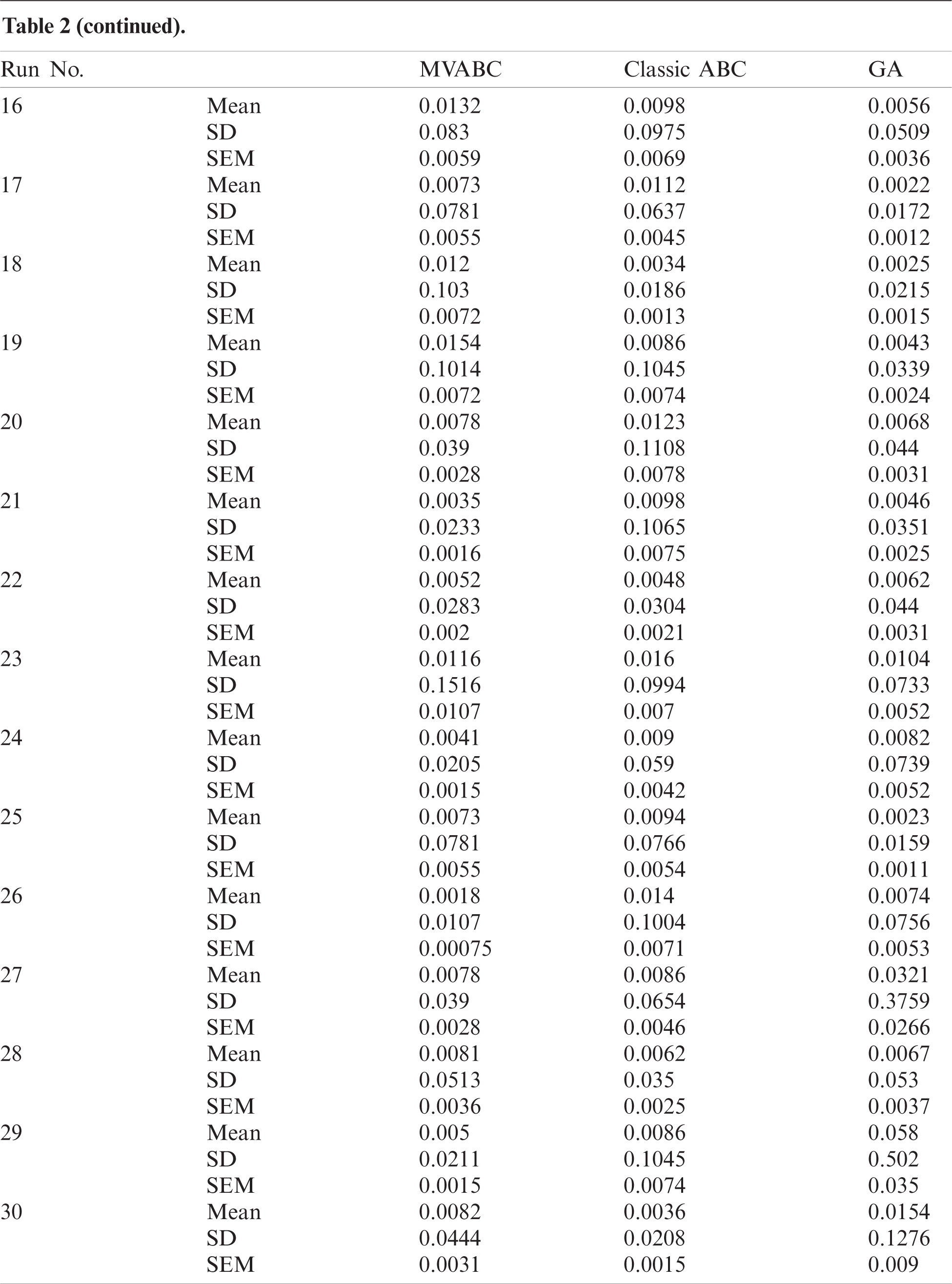
We compared GA, classic ABC and MVABC based path selection through simulation over a large data set with randomly generated seed values. The mean best, standard deviation, and SEM are given in Tab. 2 for 30 runs of each algorithm.
To show whether the experimental results obtained from MVABC, classic ABC and GA for path selection are significantly different, we perform Student’s t-test hypothesis [28]. The t-test statistically verifies if the difference in the mean values is due to the variation in sampling or does it present evidence that MVABC provides better convergence to the solution.
The t-value for the hypothesis is calculated using Eq. (32):
where grand standard deviation, SX1X2 is given by Eq. (33):
Table 2: Statistical results from 30 runs of MVABC, classic ABC and GA
where
Table 3: Summary of statistical T-test results for MVABC and classic ABC
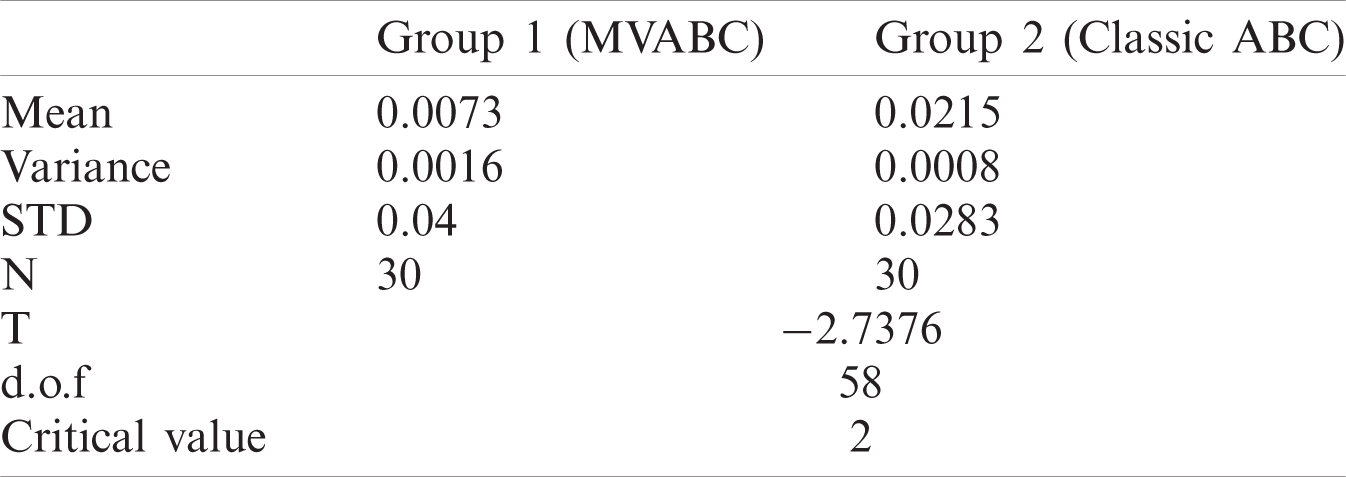
Table 4: Summary of statistical T-test results for MVABC and GA
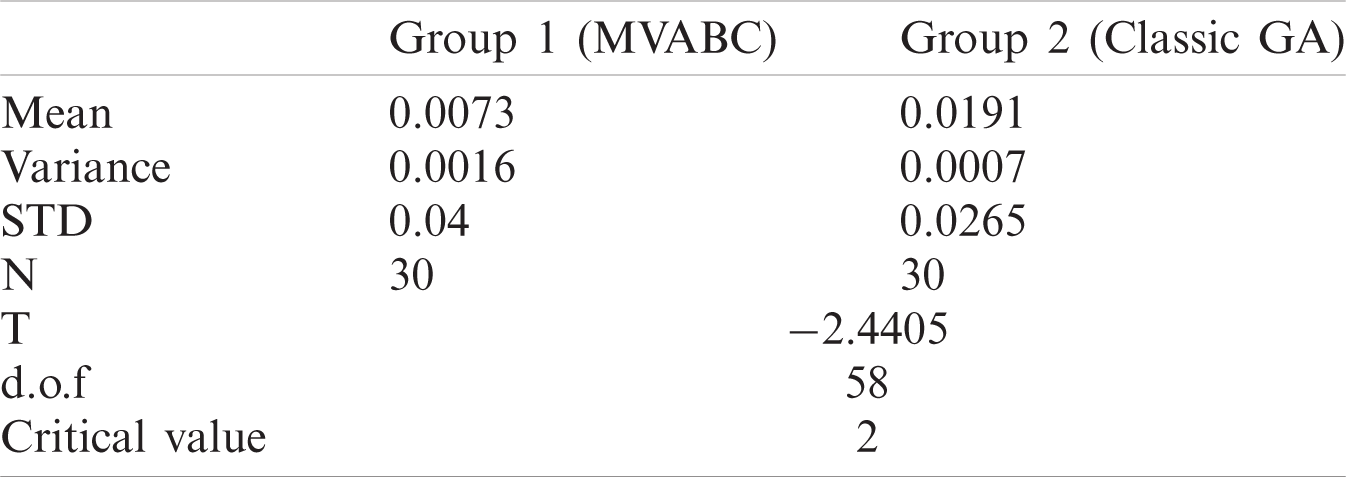
The t-test will test the null hypothesis to check whether the mean of MVABC, classic ABC and GA are equal vs. an alternate hypothesis that the mean of MVABC, classic ABC and GA are not equal and the MVABC test results hold more significance. The result of the t-test performed on the data set labeled as Group1 (MVABC) and Group 2 (classic ABC) is given in Tab. 3.
where N is the total number of runs of each algorithm, T is the t-test value (who’s absolute is compared to the critical value), d.o.f (degree of freedom) refers to maximum logically independent values that can vary with freedom in a sample of data and is given by d.o.f = 2n −2, where n is the total number of iterations. Its value is important because it helps in determining the critical value against which a hypothesis is tested. The test shows that the means of MVABC and classic ABC are significantly different at p < 0.05 significance level. Where p is the probability of having a value less than the significance level indicates that the null hypothesis is rejected and the alternate hypothesis is accepted, in other words, we can say that the mean path cost calculated by MVABC is less than that using classic ABC. This implies that the nodes selected between source to destination using MVABC represented a more energy efficient path.
Similar t-tests were performed between MVABC and GA. The statistical results are given in Tab. 4. As in the case of comparison with classic ABC, MVABC compared to GA is again capable of providing a more energy efficient path.
This can further be realized by examining the error bar graph in Fig. 3. MVABC was tested for different values of
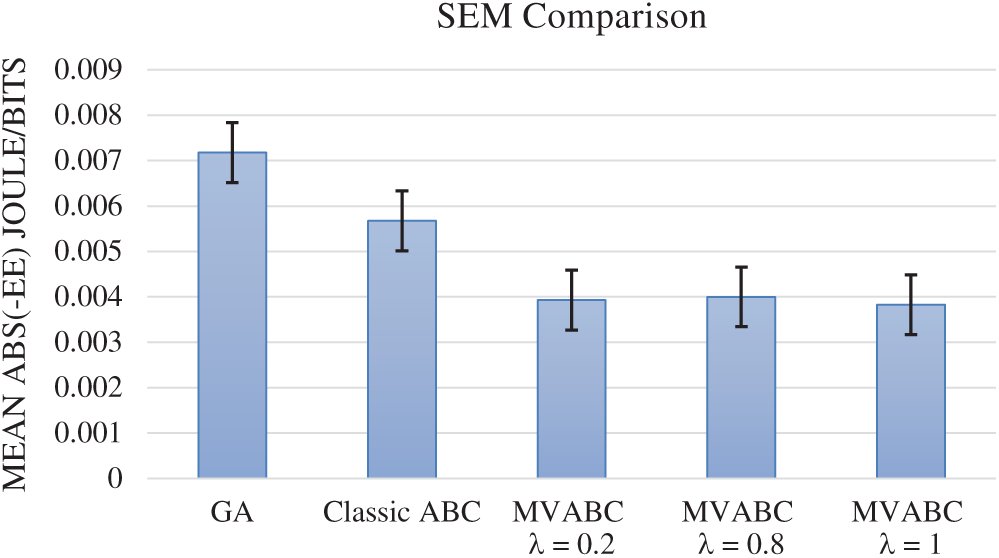
Figure 3: SEM comparison between MVABC, Classic ABC and GA
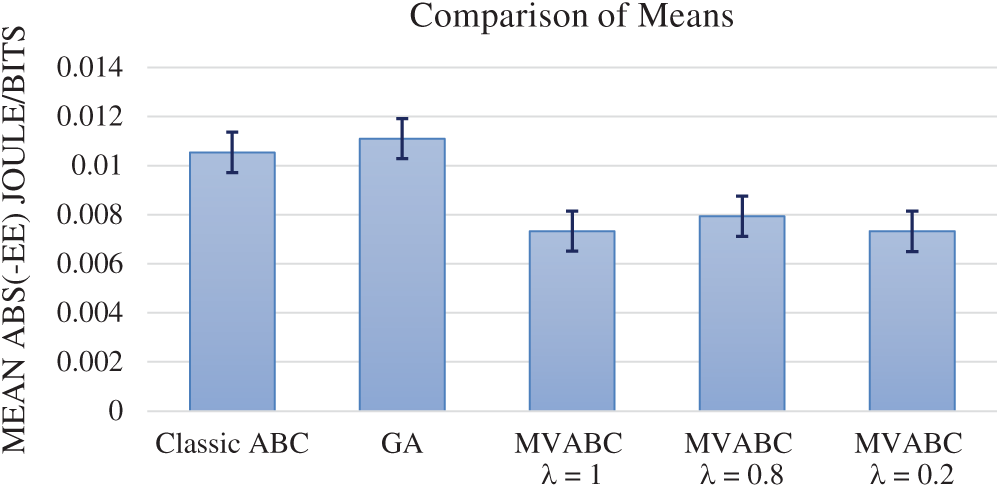
Figure 4: Comparison of means between MVABC, Classic ABC and GA
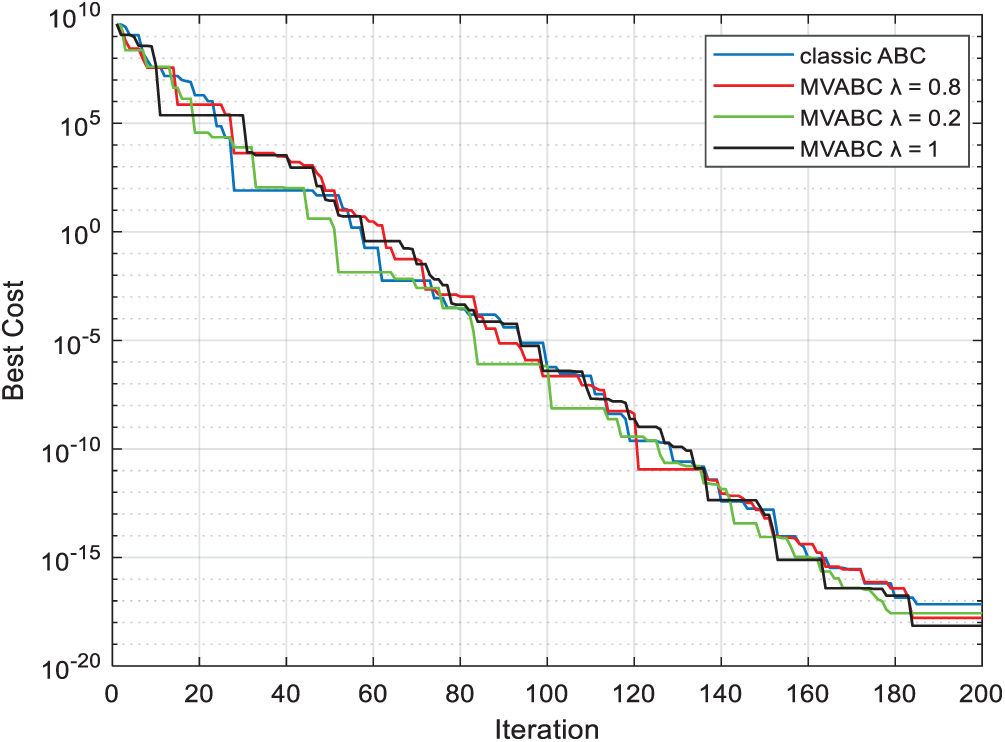
Figure 5: Comparison of different values of
This paper proposed an MHD2D link for CRE or offloading of the base station. An MVABC algorithm was proposed for path selection between source and destination for an MHD2D link. Upper and lower bounds of transmit power, capacity, and energy efficiency for the network with and without interference were derived. The proposed MVABC approach for MHD2D path selection was compared with classical ABC and GA-based MHD2D path selection for a large data set with the same population size and same upper and lower bounds for population generation. The simulated results signified the improved performance of MVABC over classic ABC and GA based approach. The simulated results were further verified using statistical techniques namely the student’s t-test, p-value, and SEM. The detailed statistical analysis confirmed that MVABC outperformed GA based MHD2D based path selection.
As future work, we will consider multi-antenna system with both centralized and decentralized approaches for path finding. We also plan on improving MVABC further in this respect and develop a generalized algorithm for single and multi-antenna systems.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Abolhasan, W. Ni, M. Abdollahi, A. Jamalipour, N. Shariati et al., “A routing framework for offloading traffic from cellular networks to SDN-based multi-hop device-to-device networks,” IEEE Transaction on Network Service Management, vol. 15, no. 4, pp. 1516–1531, 2018. [Google Scholar]
2. F. S. Shaikh and R. Wismuller, “Routing in multi-hop cellular device-to-device networks: A survey,” IEEE Communication Surveys & Tutorials, vol. 20, no. 4, pp. 2633–2657, 2018. [Google Scholar]
3. J. Lee and A. Khoryaev, “Study on further enhancements to LTE device to device (D2Duser equipment (UE) to network relays for internet of things (IoT) and wearables,” Third Generation Partnership Project, vol. 15, no. 1, pp. 1, 2018. [Google Scholar]
4. E. Joronson and E. G. Larsson, “How energy-efficient can a wireless communication system become?,” in IEEE Int. Conf. on Signals, Systems and Computers, Pacific Grove, CA, USA, pp. 1250–1256, 2019. [Google Scholar]
5. Y. Zhao, Y. Li, H. Mao and N. Ge, “Social-community-aware long range link establishment for multi-hop D2D communication networks,” IEEE Transaction on Vehicular Technology, vol. 65, no. 11, pp. 9372–9385, 2016. [Google Scholar]
6. A. Ibrahim, T. M. N. Ngatched and O. A. Dobre, “Using Bender’s decomposition for optimal power control and routing in multi-hop D2D cellular system,” IEEE Transaction on Wireless Communication, vol. 18, no. 11, pp. 5050–5064, 2019. [Google Scholar]
7. X. Zhou, S. Durrani and J. Guo, “Drone-initiated D2D aided multi-hop multicast networks for emergency information dissemination,” IEEE Access, vol. 8, pp. 3566–3578, 2019. [Google Scholar]
8. G. Chen, J. Tang and J. P. Coon, “Optimal routing for multi-hop social-based D2D communications in internet of things,” IEEE Internet of Things Journal, vol. 5, no. 3, pp. 1880–1889, 2018. [Google Scholar]
9. M. Abolhasan, M. Abdollahi, W. Ni, A. Jamalipour, N. Shariati et al., “A routing framework for offloading traffic from cellular networks to SDN based multi-hop device-to-device networks,” IEEE Transaction on Network and Service Management, vol. 15, no. 4, pp. 1516–1531, 2018. [Google Scholar]
10. F. Turjman, B. D. Deebak and L. Mostarda, “Energy aware resource allocation in multi-hop multimedia routing via the smart edge device,” IEEE Access, vol. 7, pp. 151203–151214, 2019. [Google Scholar]
11. E. M. Mohammed, B. M. Elhalawany, H. S. Khallaf, M. Zareei, A. Zeb et al., “Relay probing for millimeter wave multi-hop D2D networks,” IEEE Access, vol. 8, pp. 30560–30574, 2020. [Google Scholar]
12. H. Yuan, W. Guo, Y. Jin, S. Wang and M. Ni, “Interference-aware multi-hop path selection for device-to-device communications in a cellular interference environment,” IET Communication, vol. 11, no. 11, pp. 1741–1750, 2017. [Google Scholar]
13. H. Zhang, S. Chong, X. Zhang and N. Lin, “A deep reinforcement learning based D2D relay selection and power level allocation in mmWave vehicular networks,” IEEE Wireless Communication Letters, vol. 9, no. 3, pp. 416–419, 2020. [Google Scholar]
14. D. Ebrahimi, H. Elbiaze and W. Ajib, “Device-to-device data transfer through multi-hop relay links underlaying cellular networks,” IEEE Trans. Vehicular Tech, vol. 67, no. 10, pp. 9669–9680, 2018. [Google Scholar]
15. J. Gui and J. Deng, “Multi-hop relay-aided underlay D2D communications for improving cellular coverage quality,” IEEE Access, vol. 6, pp. 14318–14338, 2018. [Google Scholar]
16. W. Zou, Q. Pan and M. F. Tasgetiren, “An effective discrete artificial bee colony algorithm for scheduling an automatic guided vehicle in a liner manufacturing workshop,” IEEE Access, vol. 8, pp. 35063–35076, 2020. [Google Scholar]
17. S. D. Patil and L. Ragha, “Adaptive fuzzy-based message dissemination and micro artificial bee colony algorithm optimized routing scheme for vehicular ad hoc network,” IET Communication, vol. 14, no. 6, pp. 994–1004, 2020. [Google Scholar]
18. H. Fahim, S. Javaid, W. Li, I. B. Mabrouk, M. A. Hasan et al., “An efficient routing scheme for intrabody nanonetworks using artificial bee colony algorithm,” IEEE Access, vol. 8, pp. 98946–98957, 2020. [Google Scholar]
19. H. Wang, Y. Chen and S. Dong, “Research on efficient-efficient routing protocol for WSNs based on improved artificial bee colony algorithm,” IET Wireless Sensor System, vol. 7, no. 1, pp. 15–20, 2017. [Google Scholar]
20. D. Karaboga, “An idea based on honey bee swarm for numerical optimization,” Technical Report-tr-06, Erciyes Uni, vol. 200, pp. 1–10, 2005. [Google Scholar]
21. A. Toktas, D. Ustun and M. Tekbas, “Global optimization scheme based on triple-objective ABC algorithm for designing fully optimized multi-layer radar absorbing material,” IET Microwaves, Antennas & Propagation, vol. 14, no. 8, pp. 800–811, 2020. [Google Scholar]
22. Z. Chen, L. Zhang, G. Tian and E. A. Nasr, “Economic maintenance of complex systems based on discrete artificial bee colony algorithm,” IEEE Access, vol. 8, pp. 108062–108071, 2020. [Google Scholar]
23. H. Fahim, S. Javaid, W. Li, I. B. Mabrouk, M. A. Hasan et al., “An efficient routing scheme for intrabody nanonetworks using artificial bee colony algorithm,” IEEE Access, vol. 8, pp. 98946–98957, 2020. [Google Scholar]
24. G. Chen, P. Sun and J. Zhang, “Repair strategy of military communication network based on discrete artificial bee colony algorithm,” IEEE Access, vol. 8, pp. 73051–73060, 2020. [Google Scholar]
25. C. Zhao, H. Zhao, G. Wang and H. Chen, “Improvement SVM classification performance of hyperspectral image using chaotic sequences in artificial bee colony,” IEEE Access, vol. 8, pp. 73947–73956, 2020. [Google Scholar]
26. W. Q. Zou, Q. Pan and M. F. Tasgetiren, “An effective discrete artificial bee colony algorithm for scheduling an automatic guided vehicle in a linear manufacturing workshop,” IEEE Access, vol. 8, pp. 35063–35076, 2020. [Google Scholar]
27. F. Darhan, H. Mathkour and M. Arafah, “Two-step artificial bee colony algorithm enhancement for QoS aware web service selection problem,” IEEE Access, vol. 7, pp. 21787–21794, 2019. [Google Scholar]
28. D. Karaboga and B. Akay, “A comparative study of artificial bee colony algorithm,” ELSEVIER Applied Mathematics and Computation, vol. 214, no. 1, pp. 108–132, 2009. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |