DOI:10.32604/cmc.2021.016570

| Computers, Materials & Continua DOI:10.32604/cmc.2021.016570 |  |
| Article |
A Novel Hybrid Tag Identification Protocol for Large-Scale RFID Systems
1College of Information Technology, Jilin Agricultural University, Changchun, 130118, China
2Jilin Province Agricultural Internet of Things Technology Collaborative Innovation Center, Changchun, 130118, China
3Jilin Province Intelligent Environmental Engineering Research Center, Changchun, 130118, China
4Jilin Province Colleges and Universities The 13th Five-Year Engineering Research Center, Changchun, 130118, China
5Department of Agricultural Economics and Animal Production, University of Limpopo, Sovenga, 0727, Polokwane, South Africa
*Corresponding Author: Shijun Li. Email: lishijun@jlau.edu
Received: 05 January 2021; Accepted: 05 February 2021
Abstract: Radio frequency identification technology is one of the main technologies of Internet of Things (IoT). Through the transmission and reflection of wireless radio frequency signals, non-contact identification is realized, and multiple objects identification can be realized. However, when multiple tags communicate with a singleton reader simultaneously, collision will occur between the signals, which hinders the successful transmissions. To effectively avoid the tag collision problem and improve the reading performance of RFID systems, two advanced tag identification algorithms namely Adaptive M-ary tree slotted Aloha (AMTS) based on the characteristics of Aloha-based and Query tree-based algorithms are proposed. In AMTS, the reader firstly uses the framed slotted Aloha protocol to map the tag set to different time slots, and then identify the collided tags using binary search method based on collision factor or mapping table. Both performance analysis and extensive experimental results indicate that our proposed algorithms significantly outperforms most existing anti-collision approaches in tag dense RFID systems.
Keywords: RFID; anti-collision; Aloha; multi-tree; AMTS
Radio frequency identification (RFID) technology is rapidly emerging as one of key technologies for Industrial Internet of Things (IIoT) [1]. RFID system provide the ability to automatically identify and track objects and persons in a non-contact, non-line-of-sight manner. This enables the development of very different automated item management frameworks and thus provides a compelling business case for the rapid adoption of RFID systems. Many research results prove that RFID technology can be applied to various industrial applications such as factory [2], inventory management [3,4], medical privacy protection [5] and agriculture [6,7]. The technological level is also constantly innovating. Passive technology in RFID has matured. Its equipment does not require power supply and maintenance, and is being increasingly used. The components of RFID systems are multiple tags, a reader and a back-end server. When multiple RFID tags communication with a singleton reader simultaneously, interference will occur between the signals, resulting in reader to fail to fail to obtain the tag ID and thus affects the stability and settlement efficiency of the RFID system. In order to solve the tag collision problem in a dense environment, an anti-collision mechanism is needed to coordinate the communication between the reader and tags, which is named tag identification or anti-collision algorithm.
The rapid multi-tag identification is the first type of issue that attracted the attention of researchers in the RFID community. Generally speaking, mainstream tag identification algorithms are divided into two categories according to the functional characteristics: Aloha-based algorithms [8–13], deterministic algorithms [14–17] contains query tree-based and binary search algorithms. The Aloha-based algorithms are intuitive solution but they do not appear to be scalable. The efficiency of the protocols is highly affected by the cardinality. An advantage of the Aloha-based protocol is that it is simple to implement. The disadvantage of them is the slow throughput under high-traffic loads; also they are sensitive to changes in the number of tags, that is, when the frame length setting is not appropriate, the performance will drop sharply. In contrast, the performance of query tree-based algorithms [15–17] will not be affected by the tag cardinality, i.e., its performance almost maintain a constant value as the number of tags increases. One disadvantage of these protocols is that the length of probe command of such algorithm is not fixed, it will change with the change of the query prefix length during the tag identification process. In addition, query tree-based algorithm consumes more transmitted bits. Therefore, many researchers proposed hybrid algorithms [18,19]. The literature [18] shows us three multi-tag identification algorithms based on binary tree slotted Aloha (BTSA). Among them, the Splitting BTSA algorithm with the best performance has a throughput of 0.425. The literature [19] proposed a new kind of tree slotted Aloha protocol, in which the whole tag set can be divided into many smaller groups. Then the reader identify the tags group by group via tree splitting strategy. However, because both the Aloha-based algorithm and tree splitting algorithm are random access algorithm in nature, thus the algorithm proposed in [19] cannot guarantee that all tags are completely identified.
In this paper, we designed and implemented a hybrid architecture of tag identification, and proposed two hybrid tag identification algorithms. These two algorithms inherit the advantages of Aloha-based and deterministic algorithms, and abandon mutual shortcomings. In particular, our proposed algorithms do not need to provide an accurate estimation of the number of tags in collision phase, thereby avoiding the negative impact of estimation errors on performance, and reducing the computational complexity. Moreover, their efficiency will not be affected by the number of tags and tag IDs distribution.
The remainder of this paper is organized as follows. In Section 2, we reviewed the existing the anti-collision algorithms. Section 3 presents the system model and our proposed hybrid algorithm. In Section 4, mathematical analysis and performance evaluation through simulations is conducted. Section 5 concludes the whole paper.
As mentioned above, existing anti-collision algorithm mainly consists of two types: Aloha-based and deterministic algorithm. The deterministic algorithm can be further divided into two types: Query tree [14,15,17] and tree splitting [16] algorithms. In deterministic algorithm, the reader uses coding number carried by the tag to allow the tag to perform reading priority sorting. After sorting, the reader identifies the tags start from the bottom of the fork. Law [1] firstly proposed query tree (QT) anti-collision algorithm. In QT algorithm, the reader maintains a stack to store the query prefix. If the tags’ sequence number in a certain bit are the same, the reader continues to push new query prefixes into the stack. For the prefix, the reader recognizes the tags sequentially according to the order. This is the earliest QT algorithm. At present, there are many algorithms that have improved the QT classic algorithm, mainly through the eigenvalues of collision bits and the addition of additional queries. In [14], the authors proposed an improved QT algorithm to enhance the identification performance. The literature classified a large number of tag prefixes according to similarity, just like a big tree is divided into many branches, each type of the same prefix represents a tag groups, reader probes each group separately to reduce collisions and the transmissions of empty slots. However, such algorithm adds some extra queries, which increases the additional query time communication complexity in downlink. Some authors [20] proposed a query method based on a 4-ary tree to avoid unnecessary collisions and improve the efficiency of traverse. Specifically, the reader uses the characteristics of the highest two collision bits. The number of forks in the query tree can be adjusted to reduce unnecessary collision slots. The advantage of the deterministic algorithm is that it can ensure that the tag group is completely identified. Wang [21] proposed a binary search tree algorithm (PNBA) based on physical layer network coding, which pushed the conflicting signal information of multiple labels to a stack and discarded it by the traditional anti-collision algorithm. Dong [22] proposed an improved binary search conflict prevention protocol, BRTP, which allows two groups of tags to respond to a reader in the same slot in a dual-response mechanism.
In Aloha-based algorithm, each tag randomly picks up a slot to respond to the reader after extracting the parameters including frame size and communication rate from the reader’s command. The representative is the adaptive Q-algorithm based on UHF RFID standard EPC C1 Gen2 protocol. According to [23], there are three types of probe commands: Query, QueryRep, and QueryAdj. An identification round is defined as the time duration between successive probe commands issued by the reader and therefore only one Query command exists in each identification round. Therefore, the reader issues many Queryadj or QueryRep commands in order to identify tags during each identification round. In particular, QueryAdj command carries the value of parameter Q and instructs all tags to adjust their value of Q. All tags receiving the new value of Q reselect their slot counter based on the new Q (between 0 and 2Q −1); here, Q could be incremented by 1, decremented by 1, or have no change according to the adaptive Q algorithm. There are three types of access events: collision, empty, and success. The reader can send either a QueryAdj or QueryRep in the case of a collision; it can send a Query, QueryAdj, or QueryRep in the case of empty; and it can send either a QueryAdj or QueryRep in the case of success. There are four assumptions determining when to use which probe command, as follows.
1. All tags to be identified in each identification round are successfully read in one round. Thus there is only one Query command in each identification round.
2. If the access event is a collision, the reader sends a QueryAdj command to trigger tags to reselect their slot counter. The value of the Q parameter is updated by Qfp, the floating-point representation of Q, and
3. If the access event is empty, the reader sends a QueryAdj command when Q is changed or a QueryRep command when Q has no change. The update formula is
4. If the access event is success, the reader sends a QueryAdj command to trigger the tags to reselect their slot counter. The value of Q is not changed, i.e., Qfp = Qfp + 0,
The advantage of the Aloha-based algorithms represented by the Q-algorithm is that they are easy to implement on the reader side. However, the random nature of such type of algorithm will cause the performance to fluctuate with the number of tags.
3 System Model and Algorithm Description
Our proposed Adaptive M-ary tree slotted Aloha (AMTS) algorithm starts a round of identification process by broadcasting a probe command with a key parameter named frame size [24]. Each tag that receives the probe command will randomly picks up a time slot to respond to the reader and return its own ID information. Once a collision is detected, the reader will count the current value of slot counter (SC) and push it onto the stack. When the reader reads a frame, it will count all slot statistics and obtain the values corresponding to slot counter. Unlike the conventional Aloha-based anti-collision strategies, the reader does not use the number of slot statistics to estimate the number of unread tags and attempts to identify the collided tags in the following frames. In AMTS, the reader will use the query tree algorithm to directly identify the involved tags in each collision slots, which is viewed as an independent identification process of collision slots. Only when all collisions are resolved, the entire process will end. Fig. 1 depicts an example of using AMTS algorithm to identify ten tags. As shown in the figure, there are 2 collision slots in the entire frame, which are located in the 1-st slot and 5-th slot, respectively. We can see that the reader uses a 2-ary tree method to resolve three tags in the first collision slot and uses a 4-ary tree method to resolve five tags in the second collision slot. Through this example, we can intuitively know the advantages of AMTS algorithm. Specifically, we designed two AMTS algorithms, which are based on dynamic frame size adjustment (CF-AMTS) and adaptive m-ary selection (MF-AMTS). The difference between them is that the former uses a collision factor to adjusts the m-ary search and the latter uses mapping table to estimate the number of tags involved in collision slots.
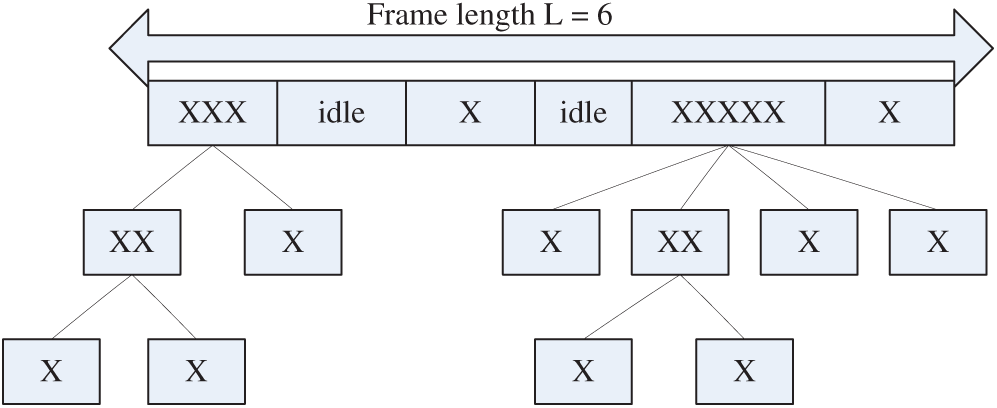
Figure 1: An illustrated example by using AMTS algorithm
In what follows, we elaborate on the principles and operating mechanisms of these two algorithms.
(1) CF-AMTS: Algorithm description
In this paper, we define a variable called collision factor, which is expressed as
In the above formula, k represents the number of collision bits in the current time slot, and n is the tag ID length. We make the following assumption that the current slot is a collision slot and there are m tags to be identified. For any bit in a string responded by the tag, the probability that it will not collide can be expressed as 1/2m −1, Eq. (1) can be rewritten as
Eq. (2) implies that the larger the value of m, the higher the collision factor. We assume that in the entire traversal tree, the highest query depth is N, which is the longest path required from the root of the traversal tree to the leaf nodes. The probability that a tag can be successfully recognized at the first level of traversal tree is expressed as
Correspondingly, we can derive the average number of slots spent by the reader to identify m tags.
According to Eq. (4), we can get the following judgment conditions.
Combining formula (2) and (5), the reader knows that it should use 2-ary tree to resolve the collided tags when m
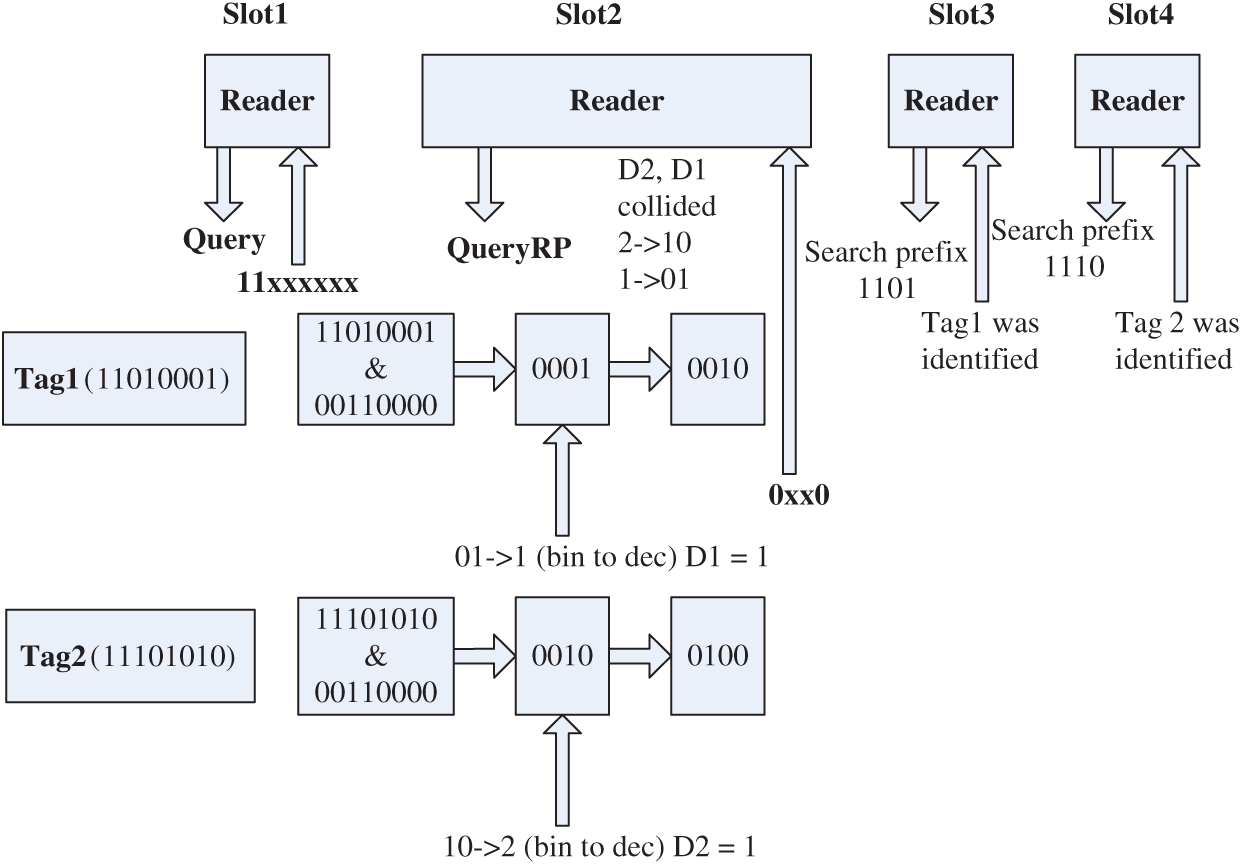
Figure 2: An example by using CF-AMTS to identify two tags in a collided slot
(2) MF-AMTS: Algorithm description
In the next, we elaborate on the second AMTS algorithm, namely MF-AMTS algorithm. The salient feature of this algorithm is to use the mapping table to estimate the tag cardinality in a collision slot.
Tab. 1 is a mapping table that maps 2-bit original data to 4-bit string. In MF-AMTS, the tag will extract its own high 2-bit ID data according to the probe command sent by the reader, and map it into a 4-bit string based on the given mapping table. It is noted that the time slot for the tag to respond to the reader is no longer randomly selected. The tag will use its own ID to match the prefix parameter in the probe command sent by the reader and determine whether it responds or not. Assume that in a 4-bit mapped data, the number of collision bits (a collided bit is denoted as “x”) is t. Then the reader will use a 4-ary tree to resolve the collided tags when t is greater than or equal to 3, otherwise it will use a 2-ary tree. We still reuses the example in Fig. 2. The index of the collision slot selected by the tags is stored in the reader’s stack. The corresponding communication procedure is described in Tab. 2. We can observe that two tags have a common prefix of 11 in slot 1, so their responding data are (01

Table 2: The communication procedure by using MF-AMTS to identify the tags in Fig. 2
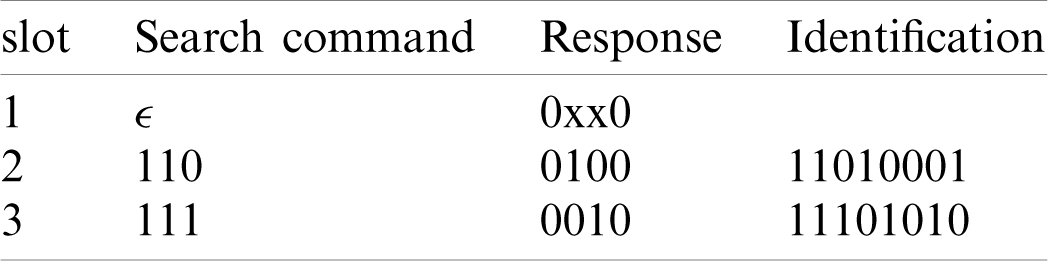
By comparing Fig. 2 and Tab. 2, we can find that the number of slots consumed by the reader to identify the same batch of tags using MF-AMTS algorithm is less than CF-AMTS algorithm. The reason is given as follows. The CF-AMTS algorithm uses QueryRP command to produce the extra slots. Fig. 3 depicts the detailed flowchart of the AMTS algorithm proposed in this paper.
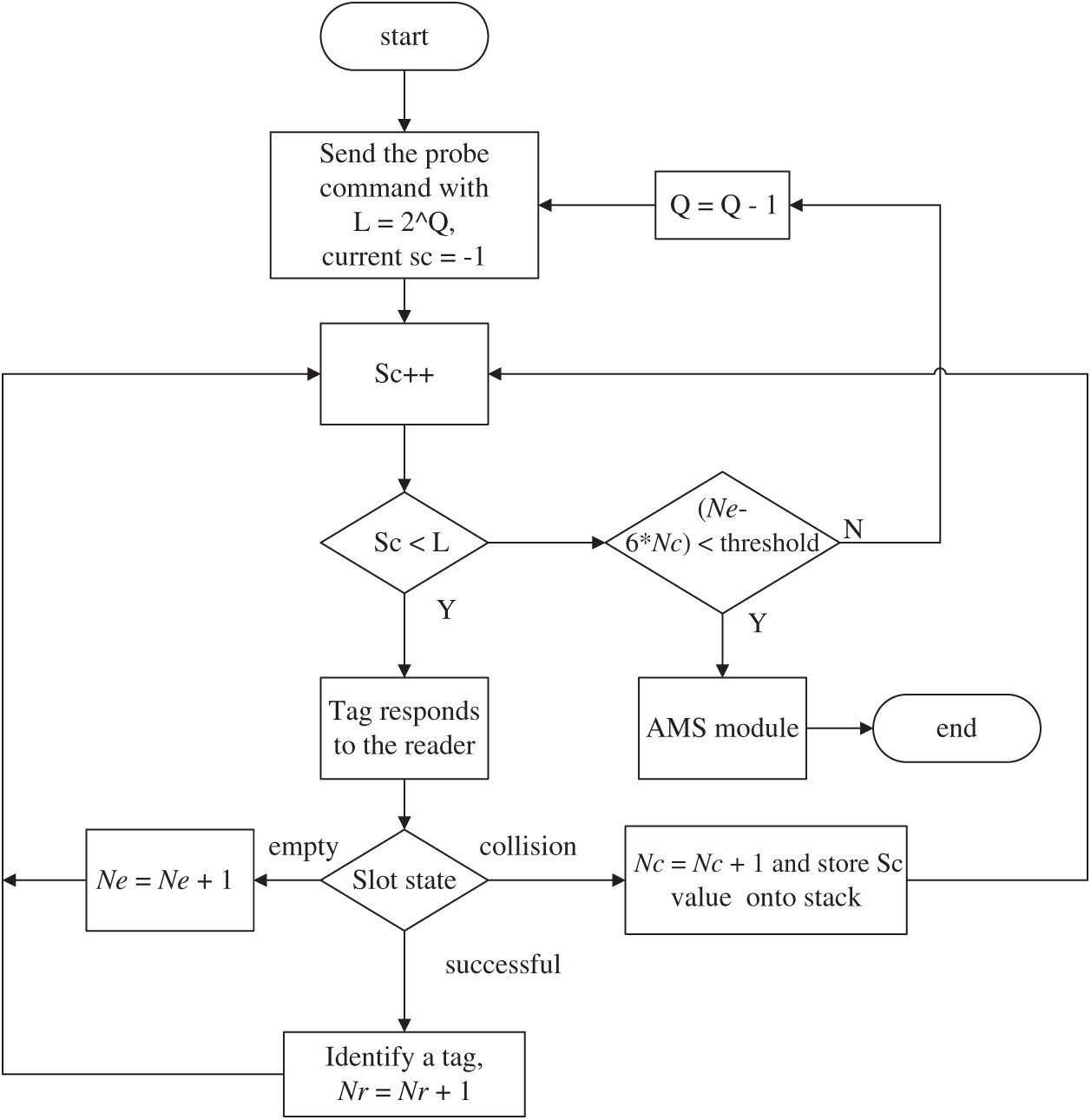
Figure 3: Flowchart of AMTS algorithm
Where Ne, Nr and Nc are the number of idle slots, successful slots and collision slots, respectively. With the expected ratios of Ne, Nr and Nc which equals to 2:1:7/24 under the condition L = 2n according to the analysis of [7]. We can derive the rule of the adjustment of Q value as
If
4 Performance Analysis and Numerical Results
We theoretically analyze the total number of slots required for our proposed two AMTS algorithms and then deduce the system efficiency. Specifically, the total number of slots can be obtained by summing the frame size L and the number of slots consumed by AMS module. We can make the following assumptions, the number of unread tags entering the AMS module is M. The average number of tags contained in each intermediate node is 3 in k-th traversal depth. In the tag identification process, if the required traversal depth is higher than k, the reader should use 2-ary tree, other it should use 4-ary tree. The total number of slots required by AMTS can be expressed as
Herein
Through Fig. 2 shown above, we can see that when the reader sends a QueryRP command once, it will consume a time slot correspondingly. Then, the number of QueryRP commands can be equivalent to the number of collision slots, i.e.,
Referring to the analysis in [15], the number of total slots (
in which m denotes the number of tags involved in current slot, j represents the traversal depth. As explained in the previous section, empty slots cam be eliminated by the introduction of QueryRP command. Therefore, the total number of slots taken by CF-AMTS to identify n tags is expressed as
Then, the total number of slots taken by MF-AMTS is calculated as Eq. (13). Where n represents the number of tags waiting to be identified, s denotes the number of success slots when the frame length is L.
Then, the system efficiency of CF-AMTS and MF-AMTS can be calculated as n/
We implement the proposed algorithm in MATLAB on a ThinkPad X1 Carbon desktop with an Intel 2.4 GHz CPU. Our simulation setting follows the specifications of the EPC C1 Gen2 standard. The number of tags is from 50 to 1000 in step of 50. The reader-to-tag transmission rate and the tag-to-reader data rate are not symmetric, which depends on specific physical implementations and practical environments. The main time parameters used in MATLAB simulations are listed in Tab. 3. All simulation results are the average of 1000 simulation runs in MATLAB.
Table 3: The main time parameters used in MATLAB simulations
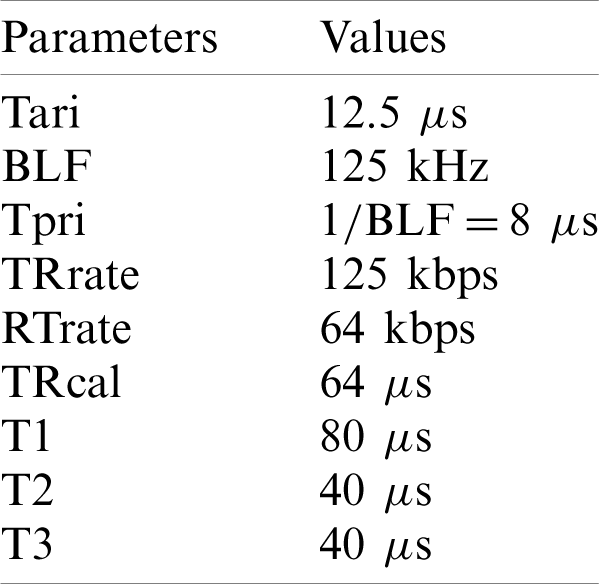
The performance of the our proposed AMTS algorithms are evaluated in terms of average required slots for one tag identification, the number of total slots, and energy efficiency. Fig. 5 shows the average required slots for one tag identification when
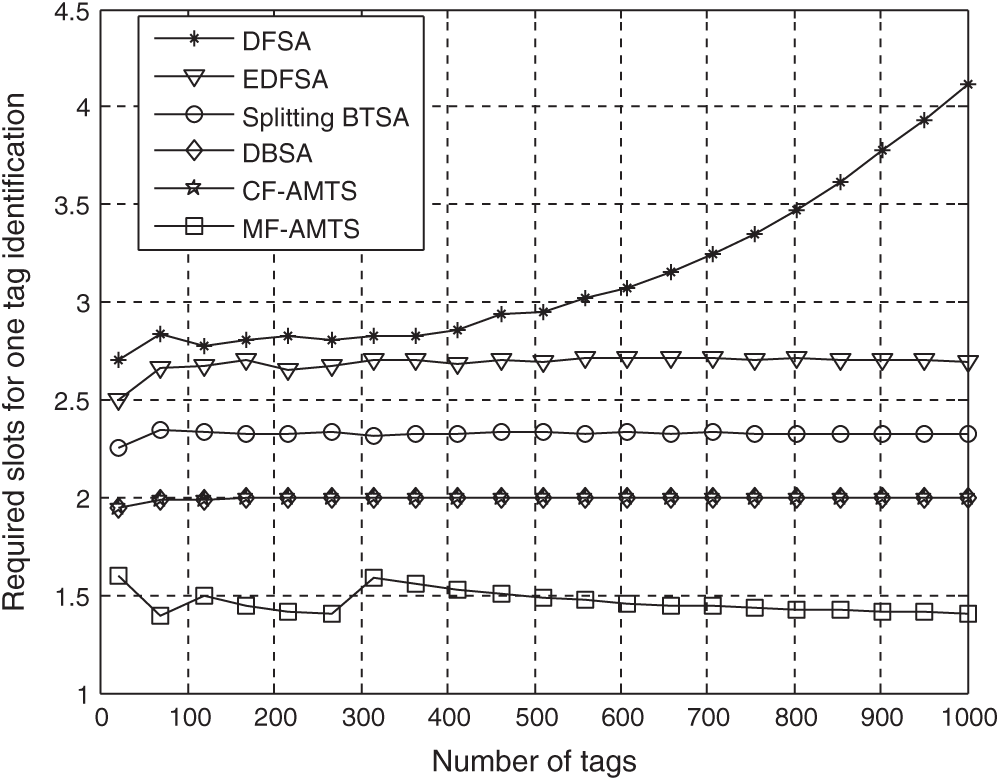
Figure 4: Average required slots of one tag identification
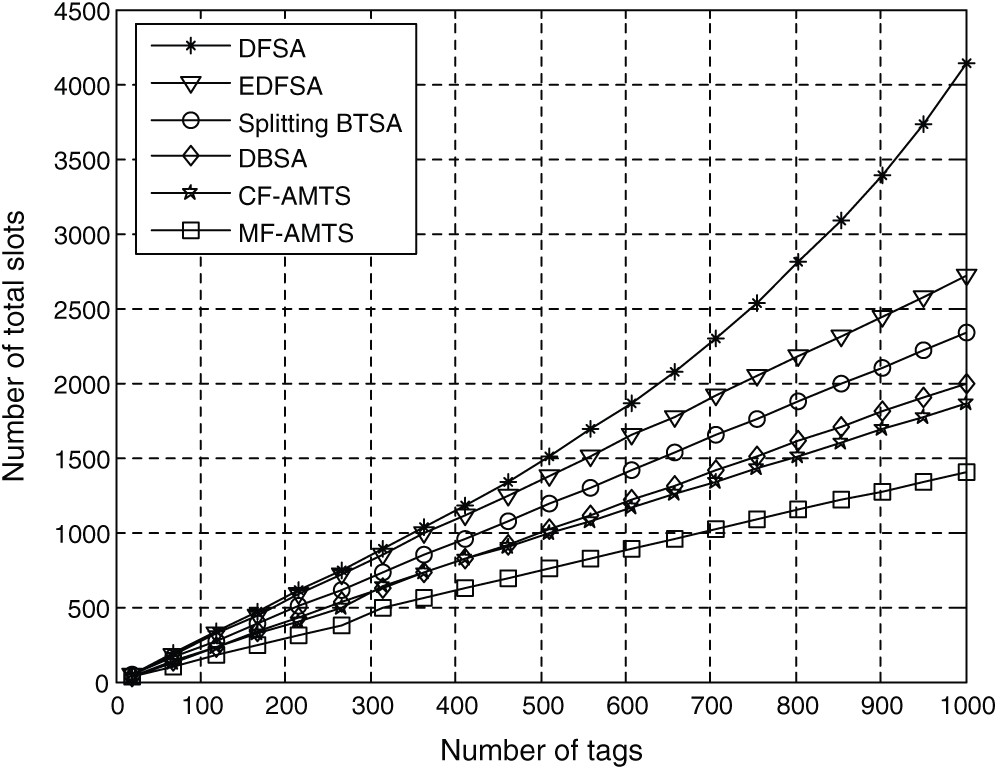
Figure 5: Total slots required to read all tags
In Fig. 5, we compare the read performance of schemes, including CF-AMTS and MF-AMTS. Similar to the results for the average required slots for one tag identification, our proposed algorithms has better performance than the other algorithms. For example, when the number of tags is 1000, the DFSA, EDFSA, Splitting BTSA and DBSA consume 4180, 2898, 2439, and 2035 of total slots to identify all the tags, respectively. As a comparison, the number of total slots required by CF-AMTS and MF-AMTS are 1875 and 1490, respectively. In other words, the CF-AMTS and MF-AMTS reduce the number of total slots by 7.86% and 26.7% over DBSA when the tag cardinality is 1000. The CF-AMTS and MF-AMTS reduce the number of total slots by 23.1% and 38.9% over Splitting BTSA when the tag cardinality is 1000.
To further evaluate the performance of our proposed algorithms. We use another important evaluation metric, i.e., energy efficiency. We define the energy efficiency metric for every energy unit eu as follows:
where Q, S and W are number of queries, slots and mode switches, respectively. eq, es and
Fig. 6 compares the energy efficiency of various algorithms. Similar to the results for the average required slots for one tag identification and the number of total slots, our proposed algorithms have better performance than the other algorithms.
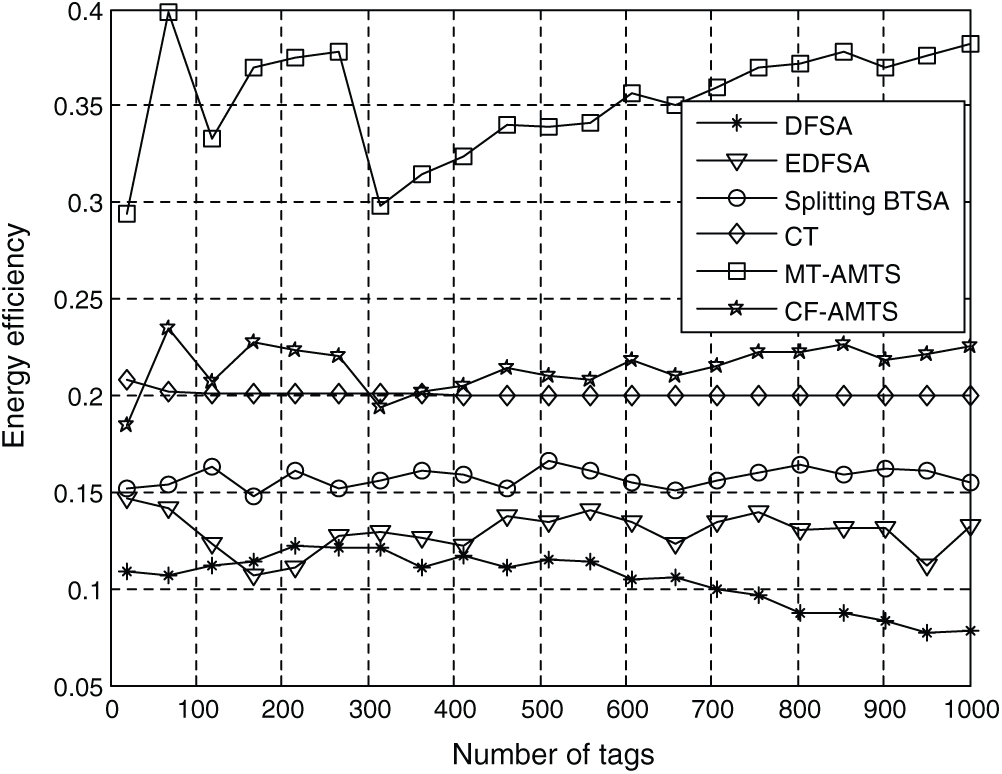
Figure 6: The comparison of various algorithms in terms of energy efficiency
In this paper, we present 2 multi-tag identification algorithms based on hybrid architecture to improve the reading efficiency in tag dense RFID scenarios. The contributions are concluded as follows. Compared with existing anti-collision algorithms, our proposed approaches in this paper not only have higher system throughput, but also do not require precise cardinality estimation of the entire tag set, and hence they can be easily implemented on low-cost RFID readers. Both theoretical analysis and various experimental results verify that our proposed algorithms are superior to prior art in terms of system throughput, the total number of slots and energy efficiency.
Funding Statement: This research was supported by The People’s Republic of China Ministry of Science and Technology [2018YFF0213606-03 (Mu Y., Hu T. L., Gong H., Li S. J. and Sun Y. H.) http://www.most.gov.cn ], the Science and Technology Department of Jilin Province [20160623016TC, 20170204017NY, 20170204038NY,20200402006NC (Mu Y., Hu T. L., Gong H. and Li S.J.) http://kjt.jl.gov.cn ], and the Science and Technology Bureau of Changchun City [18DY021 (Mu Y., Hu T. L., Gong H., and Sun Y. H.) http://kjj.changchun.gov.cn ].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Finkenzeller, RFID-Handbook Fundamentals and Applications in Contactless Smart Cards and Identification, 2nd ed. New York: John Wiley & Sons Ltd., 2003. [Google Scholar]
2. J. Feng, F. Li, C. Xu and R. Zhong, “Data-driven analysis for RFID-enabled smart factory: A case study,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 50, no. 1, pp. 81–88, 2018. [Google Scholar]
3. B. Fabian, T. Ermakova and C. Muller, “SHARDIS: A privacy-enhanced discovery service for RFID-based product information,” IEEE Transactions on Industrial Informatics, vol. 8, no. 3, pp. 707–718, 2012. [Google Scholar]
4. H. Cai, L. D. Xu, B. Xu, C. Xie, S. Qin et al., “IoT-based configurable information service platform for product lifecycle management,” IEEE Transactions on Industrial Informatics, vol. 10, no. 2, pp. 1558–1567, 2014. [Google Scholar]
5. K. Fan, W. Jiang, H. Li and Y. Yang, “Lightweight RFID protocol for medical privacy protection in IoT,” IEEE Transactions on Industrial Informatics, vol. 14, no. 4, pp. 1656–1665, 2018. [Google Scholar]
6. F. Adrion, M. Keller, G. B. Bozzolini and C. Umstatter, “Setup, test and validation of a UHF RFID system for monitoring feeding behaviour of dairy cows,” Sensors, vol. 20, no. 24, pp. 7035, 2020. [Google Scholar]
7. M. Hardie, “Review of novel and emerging proximal soil moisture sensors for use in agriculture,” Sensors, vol. 20, no. 23, pp. 6934, 2020. [Google Scholar]
8. L. Zhu and T. S. Yum, “A critical survey and analysis of RFID anti-collision mechanisms,” IEEE Communications Magazine, vol. 49, no. 5, pp. 214–221, 2011. [Google Scholar]
9. W. T. Chen, “An accurate tag estimate method for improving the performance of an RFID anticollision algorithm based on dynamic frame length ALOHA,” IEEE Transactions on Automation Science and Engineering, vol. 6, no. 1, pp. 9–15, 2009. [Google Scholar]
10. J. Su, Z. Sheng, A. X. Liu and Y. Chen, “A partitioning approach to RFID identification,” IEEE/ACM Transactions on Networking, vol. 28, no. 5, pp. 2160–2173, 2020. [Google Scholar]
11. J. Su, Z. Sheng, A. Liu, Z. Fu and Y. Chen, “A time and energy saving based frame adjustment strategy (TES-FAS) tag identification algorithm for UHF RFID systems,” IEEE Transactions on Wireless Communications, vol. 19, no. 5, pp. 2974–2986, 2020. [Google Scholar]
12. B. Li and J. Y. Wang, “Efficient anti-collision algorithm utilizing the capture effect for ISO 18000-6C RFID protocol,” IEEE Communications Letters, vol. 15, no. 3, pp. 352–354, 2011. [Google Scholar]
13. H. Chen, K. Liu, C. Ma, Y. Han and J. Su, “A novel time-aware frame adjustment strategy for RFID anti-collision,” Computers, Materials & Continua, vol. 57, no. 2, pp. 195–204, 2018. [Google Scholar]
14. L. Pan and H. Wu, “Smart trend-traversal protocol for RFID tag arbitration,” IEEE Transactions on Wireless Communications, vol. 10, no. 11, pp. 3565–3569, 2011. [Google Scholar]
15. J. Su, Z. Sheng, Z. Huang, A. X. Liu and Y. Chen, “From M-ary query to bit query: A new strategy for efficient large-scale RFID identification,” IEEE Transactions on Communications, vol. 68, no. 4, pp. 2381–2393, 2020. [Google Scholar]
16. J. Su, Z. Sheng, L. Xie and G. Wen, “Idle-slots elimination based binary splitting (ISE-BS) anti-collision algorithm for RFID,” IEEE Communications Letters, vol. 20, no. 12, pp. 2394–2397, 2016. [Google Scholar]
17. D. R. Hush and C. Wood, “Analysis of tree algorithms for RFID arbitration,” in Proc. 1998 IEEE Int. Symp. on Information Theory (Cat. No. 98CH36252IEEE, pp. 107–116, 1998. [Google Scholar]
18. H. Wu, Y. Zeng, J. Feng and Y. Gu, “Binary tree slotted ALOHA for passive RFID tag anti-collision,” IEEE Transactions on Parallel and Distributed Systems, vol. 24, no. 1, pp. 19–31, 2012. [Google Scholar]
19. J. Su, Z. Sheng, A. Liu, Y. Han and Y. Chen, “A group-based binary splitting algorithm for UHF RFID anti-collision systems,” IEEE Transactions on Communications, vol. 68, no. 2, pp. 998–1012, 2020. [Google Scholar]
20. Y. Kim, S. kim, S. Lee and K. Ahn, “Improved 4-ary query tree algorithm for anti-collision in RFID system,” in 2009 Int. Conf. on Advanced Information Networking and Applications, IEEE, pp. 699–704, 2009. [Google Scholar]
21. C. Wang, X. Shao, Y. Meng and J. Gao, “A physical layer network coding based tag anti-collision algorithm for RFID system,” Computers Materials & Continua, vol. 66, no. 1, pp. 931–945, 2021. [Google Scholar]
22. G. Dong, W. Zhang, S. Xuan, F. Qin and H. Tan, “An improved binary search anti-collision protocol for RFID tag identification,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1855–1868, 2020. [Google Scholar]
23. G. S. EPCglobal, “EPC radio-frequency identity protocols generation-2 UHF RFID specification for RFID air interface protocol for communications at 860 MHz–960 MHz,” Version 2.0.0 Ratified, 2013. [Online]. Available: https://www.gs1.org/sites/default/files/docs/epc/uhfc1g2_2_0_0_standard_20131101.pdf. [Google Scholar]
24. C. Qian, Y. Liu, R. Ngan and L. M. Ni, “ASAP: System1919,” IEEE Transactions on Parallel and Distributed Systems, vol. 24, no. 7, pp. 1277–1288, 2013. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |