Computers, Materials & Continua DOI:10.32604/cmc.2021.016553
Article

Power Allocation Strategy for Secret Key Generation Method in Wireless Communications

Bin Zhang1, Muhammad Waqas2,3, Shanshan Tu2,*, Syed Mudassir Hussain4 and Sadaqat Ur Rehman5

1School of Electronics and Information Engineering, Hunan University of Science and Engineering, Yongzhou, 425199, China
2Engineering Research Center of Intelligent Perception and Autonomous Control, Faculty of Information Technology, Beijing University of Technology, Beijing, 100124, China
3Faculty of Computer Science and Engineering, Ghulam Ishaq Khan (GIK) Institute of Engineering Sciences and Technology, Topi, 23460, Pakistan
4Department of Electronics Engineering, FICT, Balochistan University of Information Technology, Engineering and Management Sciences, Quetta, 87300, Pakistan
5Department of Computer Science, Namal Institute, Mianwali, 42200, Pakistan
*Corresponding Author: Shanshan Tu. Email: sstu@bjut.edu.cn
Received: 05 January 2021; Accepted: 28 February 2021

Abstract: Secret key generation (SKG) is an emerging technology to secure wireless communication from attackers. Therefore, the SKG at the physical layer is an alternate solution over traditional cryptographic methods due to wireless channels’ uncertainty. However, the physical layer secret key generation (PHY-SKG) depends on two fundamental parameters, i.e., coherence time and power allocation. The coherence time for PHY-SKG is not applicable to secure wireless channels. This is because coherence time is for a certain period of time. Thus, legitimate users generate the secret keys (SKs) with a shorter key length in size. Hence, an attacker can quickly get information about the SKs. Consequently, the attacker can easily get valuable information from authentic users. Therefore, we considered the scheme of power allocation to enhance the secret key generation rate (SKGR) between legitimate users. Hence, we propose an alternative method, i.e., a power allocation, to improve the SKGR. Our results show 72% higher SKGR in bits/sec by increasing power transmission. In addition, the power transmission is based on two important parameters, i.e., epsilon and power loss factor, as given in power transmission equations. We found out that a higher value of epsilon impacts power transmission and subsequently impacts the SKGR. The SKGR is approximately 40.7% greater at 250 from 50 mW at epsilon=1. The value of SKGR is reduced to 18.5% at 250 mW when epsilonis 0.5. Furthermore, the transmission power is also measured against the different power loss factor values, i.e., 3.5, 3, and 2.5, respectively, at epsilon=0.5. Hence, it is concluded that the value of epsilon and power loss factor impacts power transmission and, consequently, impacts the SKGR.

Keywords: Secret key generation rate; power allocation; physical layer; wireless communication

1  Introduction

Security is profoundly important due to the rapid increase in wireless communication. In 2018, Ericsson announced that 5G subscribers would hit 1.9 billion by the end of 2024. It is also predicted that the networks would hold 35% of data and serve 65% of the global population [1]. Researchers are exploring different ways to meet new technological requirements, such as increasing bandwidth performance, coverage areas, and latency. However, security problems have not yet matured in wireless communications. Multiple attacks, such as impersonation, eavesdropping, and information modification, may endanger wireless communications. Such attacks target the authentic users to extract secret information between authentic users. Traditional cryptographic methods are usually used to secure data based on secret keys (SKs) between authentic users [2]. However, this technique is less attractive for distributed systems since mobile devices have minimal computational resources, unlike centralized networks [3,4]. Furthermore, the SKs are dependent on every user to keep the public key certificate in traditional cryptographic [5]. Hence, mobile devices can’t carry a public key certificate in a distributed network due to limited resources [6–9].

Alternatively, Shannon’s well-known work showed that channel reciprocity among authentic users at the physical layer (PHY) had achieved special consideration [10,11]. The channel reciprocity involves generating the SKs using the channel randomness between communicating parties [12,13]. However, SKG at the physical layer is essential in identifying the information based on channel state information (CSI). It offers the opportunity to imitate or require the characteristics of channels [14]. For example, the channel randomness of authentic users is unknown to unauthorized users [15]. In addition, PHY-SKG may not require any computational complexity due to channel randomness. Also, no key management scheme is needed for PHY-SKG [16]. Furthermore, the PHY-SKG leverages the dynamic channel variations to alleviate the complication by enabling the one-time pad scheme [17]. PHY-SKG overcomes the key distribution problem, and hence, the keys are distributed dynamically based on wireless channel reciprocity.

Keeping the above discussion, the researchers in [18] proposed the received signal strength (RSS) technique for SKG. The researchers implemented the RSS technique to improve the SKG rate [19]. Nonetheless, RSS-based SKG is not feasible for a distributed network. It is because RSS requires advanced algorithms to deliver a satisfactory SKGR. The authors in [20] suggested a relay-based SKGR scheme and addressed an idle intruder’s optimal power distribution. The work indicated that SKs are generated with the help of the relay node. However, relay-based SKG is not feasible for the generation of secret keys. This is due to the reason that authentic users must also secure SKs against relay nodes. In another article, the authors have proposed the PHY-SKG scheme in [21] that takes advantage of power and error correction by exploiting RSS. Again, leveraging the RSS for SKG is not feasible because the RSS technique generates a low rate of SKs that restricts their use. To solve this problem, we consider CSI an alternative method to generate SKs in wireless communications.

Moreover, in [22], the authors considered the PHY characteristic of wireless channels, i.e., time allocation for maximizing group SKs. In [23], the authors proposed a reinforcement learning technique to generate SKs in vehicular communications. The proposed method is applicable in a dynamic environment. However, the authors did not find the channel’s variations due to vehicles’ high speed. Alternatively, we believe that the power allocation strategy enhances SKGR instead of coherence time. Essentially, the duration of coherency is for a particular time duration. Since users utilize shorter SKs in a practical scenario, the attacker can quickly collect SKs among legitimate users.

Nonetheless, the research indicates that low SKGR is the main limitation for PHY-SKG [24]. Furthermore, due to the limited period, i.e., coherence time, legitimate users produce shorter SKs. Hence, we investigate the impact of power allocations on generating and improving SKGR. Our significant achievements are summarized as follows.

•    Due to the limited time duration, the authentic users generate shorter length of SKs. Therefore, an attacker can get information about SKs among legitimate users. Conversely, we examine the power allocation strategy to generate SKs. We illustrate a power allocation scheme to investigate SKGR.

•    Our results show 72% higher SKGR (bits/sec) at higher power allocation than low power allocation. To prove our result, we also analyze other factors, such as epsilon (ϵ), and the power factor loss (α).

The rest of our paper is organized as follows. We illustrate the system model, formulation, and proposed solution in Section 2. The simulation results are discussed in Section 3. Section 4 concludes the paper.

2  System Model, Formulation, and Proposed Solution

In the system model, two authentic users, i.e., u1 and u2 are considered. First, u1 transmits the signal Su1. The receiver u2, receives the signal Ru2 = G1Su1 +nu2. Here, G1 represents the channel gain while nu2 represents the noise factor at u2. Likewise, u2 transmits the signals Su2 and u1 receives the signal, i.e., Ru1 = G2Su2 +nu1. Here, G2 represents the gain of channel while nu1 denotes the noise factor at u1. The authentic users, i.e., u1 and u2 assume the channel gain G1 and G2, respectively. Furthermore, we assume Su1 be the transmitted signal by u1. Hence, the channel gain at u2 is

Eu2=G1+Su1*∥Su1∥2nu2~MI(0,vn2+vn2∥Su1∥2),(1)

where Su1* is the conjugate of Su1. Similarly, the E at u1 is

Eu1=G2+Su2*∥Su2∥2nu1~MI(0,vn2+vn2∥Su2∥2).(2)

The fundamental description of SKGR between u1 and u2 is described as the mutual information MI(Eu1,Eu2) and coherence time, T [10,14], i.e.,

γu1,u2=1TMI(Eu1,Eu2).(3)

Since

MI(Eu1)= log2(2πe(vu12+2vn2pT)),(4)

and

MI(Eu2)= log2(2πe(vu22+2vn2pT)).(5)

The correlation coefficient between Eu1 and Eu2 is

E[(G1+Su1*∥Su1∥2nu2)(G2+Su2*∥Su2∥2nu1)]=E[G1,22]=vu1,u22.(6)

Therefore, the covariance matrix of MI[Eu1,Eu2]T is

∑ =[vu1,u22+2vn2pTvu1,u2vu1,u2vu1,u22+2vn2pT],(7)

and

MI(Eu1;Eu2)= log2((2πe)2 det(Σ)), (8)

MI(Eu1;Eu2)= log2((2πe)24(vu1,u24+vu1,u22vn2pT)p2T2). (9)

The entropy can be calculated by

MI(Eu1;Eu2)=MI(Eu1)+MI(Eu2)-MI(Eu1;Eu2).(10)

Substituting (4), (5), and (9) into (10) leads to

MI(Eu1;Eu2)=1Tlog2(1+(vu1,u24p2T2)4(vn,4+vu1,u22vn2pT)).(11)

Let p be the transmitted power, and T denotes the channel’s coherence time. Due to an optimal coherence time length T2, the signal is ∥Su1,Su2∥2=pT2. Thus,

γu1,u2=1Tlog2(1+(vu1,u24p2T2)4(vn,4+vu1,u22vn2pT)).(12)

(12) indicates that γu1,u2 is equal to the coherence time and power allocation. The SKGR is low if the coherence time increases and vice versa. On the other side, if we increase the power transmission, the SKGR increases proportionally. In this work, we suppose that the power is distributed and allocated equally to both u1 and u2. In a realistic scenario, users send data over several links concurrently by allocating power. From (12), it is also indicated that SKGR can be calculated by taking power allocation into account, i.e.,

maxpu1,pu2γu1,u2 (13)

s.t={pu1≤pu1T,pu2≤pu2T,pu1>0,pu2>0 (14)

where pu1T, and pu2T, are the total powers transmitted by u1 and u2, respectively. Nonetheless, to get the optimal solution, we need the validation of convexity and concavity of our objective functions, as mentioned in (14). From (14), the objective function’s problem for power maximization is non-concave. However, (13) indicates the objective function is concave with respect to p, and finding the optimal solution is difficult. Therefore, we optimize the γu1,u2 as a function of pu1, and pu2, respectively. Furthermore, we also considered Lagrangian form on γu1,u2 as a function of p according to [20], i.e.,

y=γu1,u2+ϵ1(pu1T-pu1)+ϵ2pu1,(15)

and assume the conditions of Karush Kuhn Tucker (KKT) as

∂y∂pu1,u2=∂γu1,u2∂pu1,-ϵ1+ϵ2=0,ϵ1(pu1T-pu1)=0,(pu1)≥0,ϵ2≥0;ϵ1≥0(16)

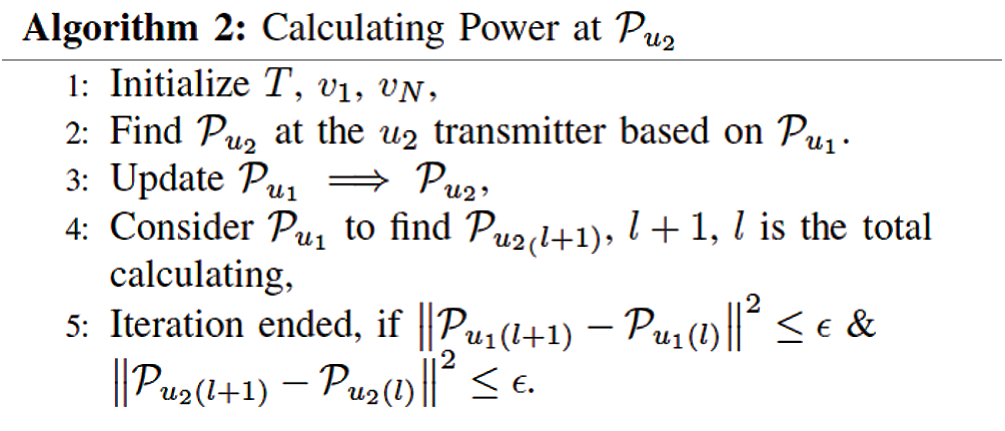
It is observed from (16) that ϵ1>ϵ2≥0. Therefore, pu1T − pu1 = 0. It is noted that the transmitter uses power higher than zero, i.e., ϵ2≥0, while comparing KKT parameters as indicated in [24–26]. It is assumed that the power distribution at the transmitter side (pu2) is initially distributed equally. Therefore, as outlined in Algorithm 1, we can resolve the proposed power allocation strategy in Algorithm 2. The symmetric method of SKG helps us to rewrite the Lagrangian for all steps of the power allocation process in a similar way. From the power allocation of u1, the following optimization problem at u2 is given by

maxpu2γu1,u2,s.t{pu2≤pu2T,pu2>0(17)

Now, we apply the same approach as discuss for the power allocation of u1, and is given by

maxpu1γu1,u2,s.t.{pu1≤pu1T,pu1>0,(18)

Algorithm 1 can be updated for the transmitter u1 based on (18). Consequently, a locally optimal solution can be achieved on both sides [22]. Thus, the power allocation of u1 is discussed in Algorithm 2.

3  Simulation Results

We figure out the SKGR by considering power allocation and to exploit different parameters in our simulation results. The coherence time is set to T = 20. The variances, i.e., v1 & vn are set to 1 [27]. The α is initialized to 4. In our simulation results, Fig. 1 shows that if we increase the power transmission, the SKGR increases accordingly. For example, at 50 mW, the SKGR is 17 bits/s when the distance between u1 and u2 is 70 m. Furthermore, the SKGR is 26 bits/s at 20 m between legitimate users by considering 50 mW power. This indicates that more power is needed to produce higher SKs. Nonetheless, when we increase the distance between u1 and u2, the SKGR decreases because of the large distances between legitimate users. This is because when the distance increases, the SNR decreases between u1 and u2, and hence, SKGR decreases. Nonetheless, the result also reveals that the SKGR rises with increasing power, regardless of the distances between u1 and u2. It proves that even though the distance can impact the SKGR because of increased power, the SKGR increases. For illustration, the SKGR is approximately equal to 25–26 bit/s at 250 mW. The results also indicate that the SKGR depends not only on the coherence time but also on the transmission power.

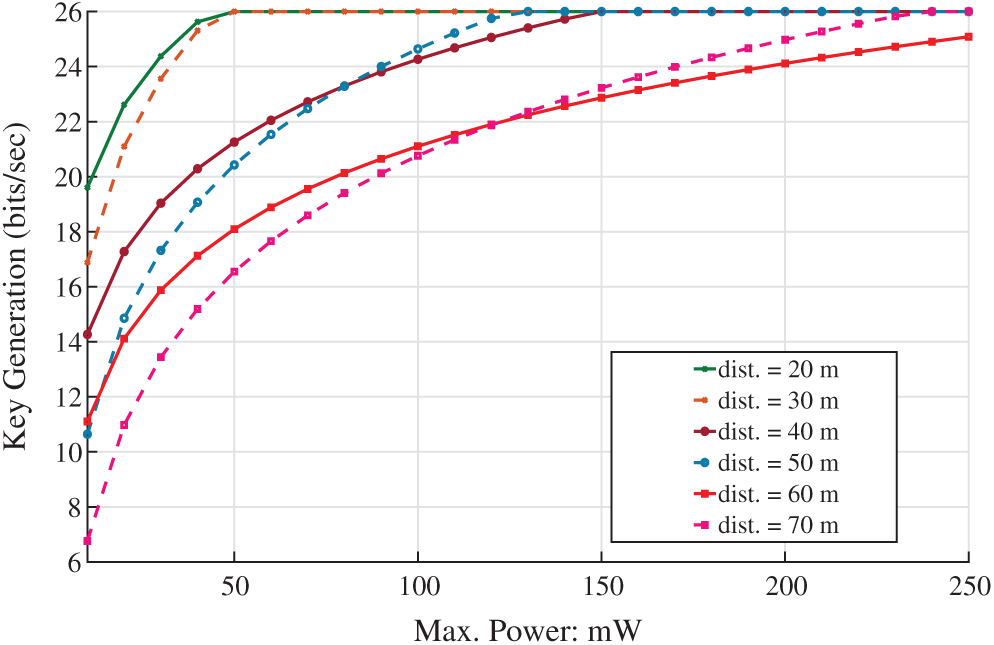
Figure 1: SKGR vs. power allocation by considering the distance

We also analyze the power transmission versus ϵ by varying the power loss factor α (ranges from 2.5 to 4). The result is significant to our work due to the power transmission’s symmetry as given in (16). The change in ϵ causes an increase in transmission power, as depicted in Fig. 2. Nevertheless, a higher power factor loss (α) would result in low transmission power than a low power factor loss (α). The transmission power at ϵ=0.5 is 100 mW at α is 4. In addition, the transmission power is approximately 148, 152, and 154mW at α=3.5, α=3 and α=2.5, respectively, at ϵ=0.5. Hence, the value of ϵ will consequently impact the power transmission at a different value of the power loss factor (α). Ultimately, it influences SKGR. This is because if power increases or decreases, the SKGR will increase or decrease accordingly.

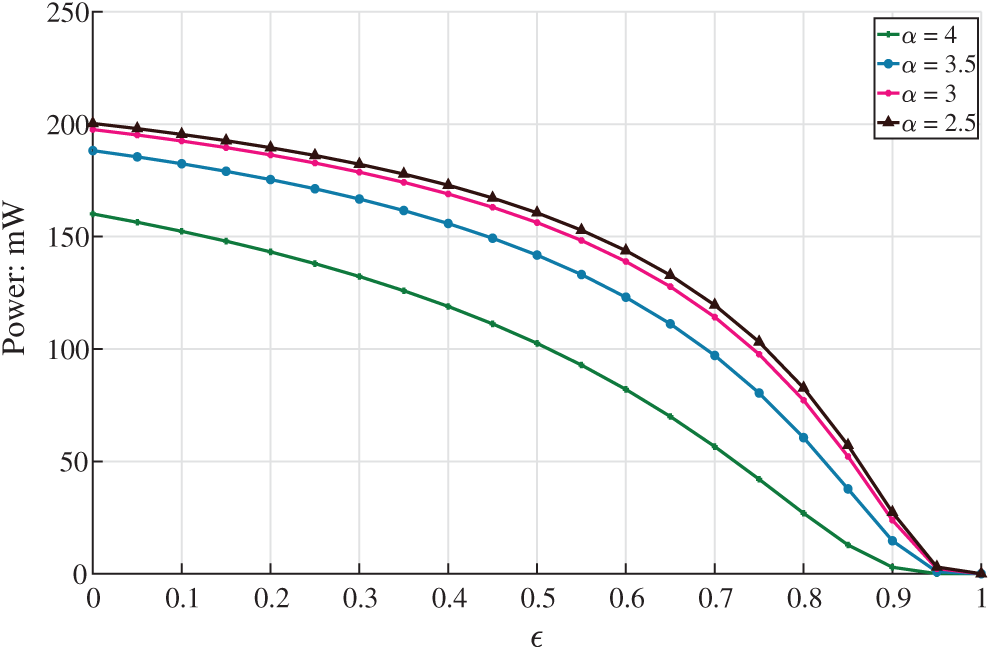
Figure 2: Power allocations vs. the value of ϵ by considering α

Finally, by varying the value of ϵ, we also investigate SKGR with respect to transmission power. It is noticed from Fig. 3 that preferably, we can get the highest SKGR when the value of ϵ=0. With the rise in transmitting power at different values of ϵ, the SKGR improves. For example, the SKGR is about 27, 23, and 20 bits/s at 100 mW, for ϵ=1, 0.5, and 0, respectively. The reason is that a higher value of ϵ impacts power transmission and subsequently impacts the SKGR. Nevertheless, by increasing the transmitting power, the SKGR is also improved. For instance, when the value of ϵ=1, the SKGR is approximately 40.7% greater at 250 from 50 mW. The SKGR is also 18.5% higher at 250 from 50 mW at ϵ=0.5.

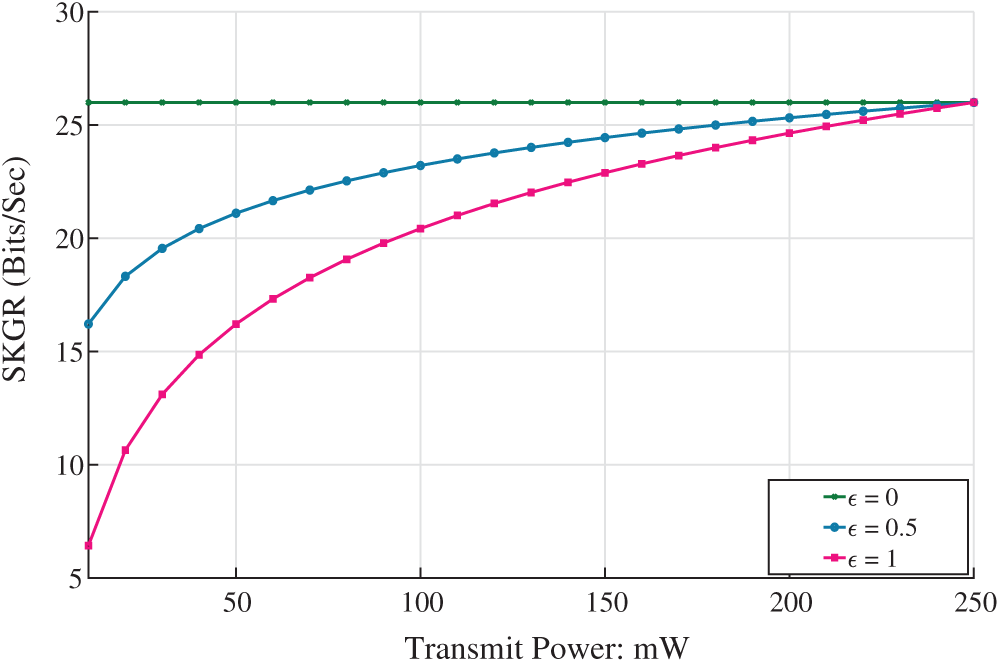
Figure 3: Verifying SKGR by increasing the power transmission based on ϵ

4  Conclusion

We introduced a mechanism to generate SKs and enhance the SKGR with power allocation. It guarantees the reliability of decentralized wireless networks. From the existing works, it is noticed that the coherence time for SKGR may not always be possible because coherence time produces a small length of SKs. Consequently, the intruders can easily obtain the SKs between authentic users. Therefore, we consider the power allocation scheme to generate SKs and enhance SKGR. Our research has shown that we can get a higher SKGR by increasing the transmitting power. The simulation results showed that SKGR is approximately 72% higher at higher transmission power. We also considered the value of ϵ, distance and power factor loss, α to verify the power allocation concept on SKGR. The SKGR is approximately 40.7% greater at 250 from 50 mW at epsilon=1. The value of SKGR is reduced to 18.5% at the same power transmission when epsilonis 0.5. Furthermore, the transmission power is also measured against the different power loss factor values, i.e., 3.5, 3, and 2.5, respectively. Hence, it is concluded that the value of epsilon and power loss factor impacts power transmission and, consequently, impacts the SKGR.

Funding Statement: This work was partially supported by the China National Key R&D Program (No. 2018YFB0803600), Natural Science Foundation of China (No. 61801008), Scientific Research Common Program of Beijing Municipal Education Commission (No. KM201910005025), the Chinese Postdoctoral Science Foundation (No. 2020M670074), Key Project of Hunan Provincial, Department of Education (No. 26420A205) and The Construct Program of Applied Characteristics Discipline in Hunan University of Science and Engineering.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Haus, M. Waqas, A. Y. Ding, Y. Li, S. Tarkoma et al., “Security and privacy in device-to-device (D2D) communication: A review,” IEEE Communication Surveys and Tutorials, vol. 19, no. 2, pp. 1054–1079, 2017. [Google Scholar]

 2.  Zhang, T. Q. Duong, A. Marshall and R. Woods, “Key generation from wireless channels: A review,” IEEE Access, vol. 4, pp. 614–626, 2016. [Google Scholar]

 3.  Y. Hu, Y. Guo, J. Liu and H. Zhang, “A hybrid method of coreference resolution in information security,” Computers, Materials & Continua, vol. 64, no. 2, pp. 1297–1315, 2020. [Google Scholar]

 4.  J. Zhang, S. Rajendran, Z. Sun, R. Woods and L. Hanzo, “Physical layer security for the internet of things: Authentication and key generation,” IEEE Wireless Communications, vol. 26, no. 5, pp. 92–98, 2019. [Google Scholar]

 5.  B. Che, L. Liu and H. Zhang, “KNEMAG: Key node estimation mechanism based on attack graph for IoT security,” Journal of Internet of Things, vol. 2, no. 4, pp. 145–162, 2020. [Google Scholar]

 6.  Y. Xu, J. Ren, Y. Zhang, C. Zhang, B. Shen et al., “Blockchain empowered arbitrable data auditing scheme for network storage as a service,” IEEE Transactions on Services Computing, vol. 13, no. 2, pp. 289–300, 2020. [Google Scholar]

 7.  X. Yan, B. Cui, Y. Xu, P. Shi and Z. Wang, “A method of information protection for collaborative deep learning under GAN model attack,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2019. [Google Scholar]

 8.  X. Yan, Y. Xu, X. Xing, B. Cui, Z. Guo et al., “Trustworthy network anomaly detection based on an adaptive learning rate and momentum in IIoT,” IEEE Transactions on Industrial Informatics, vol. 16, no. 9, pp. 6182–6192, 2020. [Google Scholar]

 9.  X. Yan, Y. Xu, B. Cui, S. Zhang, T. Guo et al., “Learning URL embedding for malicious website detection,” IEEE Transactions on Industrial Informatics, vol. 16, no. 10, pp. 6673–6681, 2020. [Google Scholar]

10. C. E. Shannon, “Communication theory of secrecy systems,” Bell System Technology Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]

11. M. Waqas, M. Ahmed, Y. Li, D. Jin and S. Chen, “Social-aware secret key generation for secure device-to-device communication via trusted and non-trusted relays,” IEEE Transactions on Wireless Communications, vol. 17, no. 6, pp. 3918–3930, 2018. [Google Scholar]

12. S. Tu, M. Waqas, S. Rehman, M. Aamir, O. Rehman et al., “Security in fog computing: A novel technique to tackle an impersonation attack,” IEEE Access, vol. 6, pp. 74993–75001, 2018. [Google Scholar]

13. C. Lv, J. Zhang, Z. Sun and G. Qian, “Information flow security models for cloud computing,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2687–2705, 2020. [Google Scholar]

14. C. D. T. Thai, J. Lee and T. Q. S. Quek, “Physical-layer secret key generation with colluding untrusted relays,” IEEE Transactions on Wireless Communication, vol. 15, no. 2, pp. 1517–1530, 2016. [Google Scholar]

15. M. Waqas, M. Ahmed, J. Zhang and Y. Li, “Confidential information ensurance through physical layer security in device-to-device communication,” in Proc. IEEE Global Communications Conf., Abu Dhabi, United Arab Emirates, pp. 1–7, 2018. [Google Scholar]

16. L. Xiao, J. L. Greenstein, N. B. Mandayan and W. Trappe, “Using the physical layer for wireless authentication in time-variant channels,” IEEE Transactions on Wireless Communication, vol. 7, no. 7, pp. 2571–2579, 2008. [Google Scholar]

17. C. Qian, X. Li, N. Sun and Y. Tian, “Data security defense and algorithm for edge computing based on mean-field game,” Journal of Cyber Security, vol. 2, no. 2, pp. 97–106, 2020. [Google Scholar]

18. M. Xia, S. Li and L. Liu, “A secure three-factor authenticated key agreement scheme for multi-server environment,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1673–1689, 2020. [Google Scholar]

19. K. Chen, B. B. Natarajan and S. Shattil, “Secret key generation rate with power allocation in relay-based LTE-A networks,” IEEE Transactions on Information Forensics and Security, vol. 10, no. 11, pp. 2424–2434, 2015. [Google Scholar]

20. H. Zhou, M. L. Huie and L. Lai, “Secret key generation in the two-way relay channel with active attackers,” IEEE Transactions on Information Forensics and Security, vol. 9, no. 3, pp. 476–488, 2014. [Google Scholar]

21. C. T. Poomagal, G. A. Sathish Kumar and D. Mehta, “Multi level key exchange and encryption protocol for internet of things (IoT),” Computer Systems Science and Engineering, vol. 35, no. 1, pp. 51–63, 2020. [Google Scholar]

22. P. Xu, K. Cumanan, Z. Ding, X. Dai and K. K. Leung, “Group secret key generation in wireless networks: Algorithms and rate optimization,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 8, pp. 1831–1846, 2016. [Google Scholar]

23. M. Waqas, S. Tu, S. Rehman, Z. Halim, S. Anwar et al., “Authentication of vehicles and road side units in intelligent transportation system,” Computers, Materials & Continua, vol. 64, no. 1, pp. 359–371, 2020. [Google Scholar]

24. X. Wang, M. Waqas, S. Tu, S. Rehman, R. Soua et al., “Power maximization technique for generating secret keys by exploiting physical layer security in wireless communication,” IET Communications, vol. 14, no. 5, pp. 872–879, 2020. [Google Scholar]

25. Y. Xu, C. Zhang, G. Wang, Z. Qin and Q. Zeng, “A blockchain-enabled deduplicatable data auditing mechanism for network storage services,” IEEE Transactions on Emerging Topics in Computing, 2020. [Google Scholar]

26. Y. Xu, C. Zhang, Q. Zeng, G. Wang, J. Ren et al., “Blockchain-enabled accountability mechanism against information leakage in vertical industry services,” IEEE Transactions on Network Science and Engineering, 2020. [Google Scholar]

27. R. Lin, H. Xu, M. Li and Z. Zhang, “Resource allocation in edge-computing based wireless networks based on differential game and feedback control,” Computers, Materials & Continua, vol. 64, no. 2, pp. 961–972, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.