Computers, Materials & Continua DOI:10.32604/cmc.2021.016467
Article

Face Recognition Based on Gabor Feature Extraction Followed by FastICA and LDA

Masoud Muhammed Hassan1,*, Haval Ismael Hussein1, Adel Sabry Eesa1 and Ramadhan J. Mstafa1,2

1Department of Computer Science, Faculty of Science, University of Zakho, Duhok, 42002, Kurdistan Region, Iraq
2Scientific Research and Development Center, Nawroz University, Duhok, 42001, Kurdistan Region, Iraq
*Corresponding Author: Masoud Muhammed Hassan. Email: masoud.hassan@uoz.edu.krd
Received: 03 January 2021; Accepted: 14 February 2021

Abstract: Over the past few decades, face recognition has become the most effective biometric technique in recognizing people’s identity, as it is widely used in many areas of our daily lives. However, it is a challenging technique since facial images vary in rotations, expressions, and illuminations. To minimize the impact of these challenges, exploiting information from various feature extraction methods is recommended since one of the most critical tasks in face recognition system is the extraction of facial features. Therefore, this paper presents a new approach to face recognition based on the fusion of Gabor-based feature extraction, Fast Independent Component Analysis (FastICA), and Linear Discriminant Analysis (LDA). In the presented method, first, face images are transformed to grayscale and resized to have a uniform size. After that, facial features are extracted from the aligned face image using Gabor, FastICA, and LDA methods. Finally, the nearest distance classifier is utilized to recognize the identity of the individuals. Here, the performance of six distance classifiers, namely Euclidean, Cosine, Bray-Curtis, Mahalanobis, Correlation, and Manhattan, are investigated. Experimental results revealed that the presented method attains a higher rank-one recognition rate compared to the recent approaches in the literature on four benchmarked face datasets: ORL, GT, FEI, and Yale. Moreover, it showed that the proposed method not only helps in better extracting the features but also in improving the overall efficiency of the facial recognition system.

Keywords: Artificial intelligence; face recognition; FastICA; Gabor filter bank; LDA

1  Introduction

Recently, biometric-adopted techniques have become the most promising option for recognizing people. Among many biometric technologies, face recognition has become the main focus of biometrics research, as it is widely employed in many fields, for instance, computer systems, artificial intelligence, access control for security facilities, automobiles, image analysis, and authentication processes. The reason why it is so widespread is that facial images can be easily accumulated without any pre-approval and can also be effortlessly obtained from a distance [1]. Although it has been an ongoing field of research since the 1960s, it is still constantly developing due to several challenges encountering the recognition systems [2,3]. These challenges are changes in illumination, facial hairs (e.g., eyebrows, beard, head hairstyle, and mustache), expressions (e.g., sadness, anger, disgust, surprise, fear, and happiness), and wearing of accessories (e.g., hats, scarf, and glasses). Because of these differences in image quality, there might be a likelihood of low variance between image samples of different individuals and high variance between image samples of the same individual. This similarity in inter-class images and dissimilarity in intra-class images can significantly deteriorate the efficacy of the recognition system [4]. Therefore, many researchers have innovated new algorithms or developed the existing ones to overcome the problems mentioned above.

In general, face recognition system consists of four consecutive phases: face detection, face alignment, feature extraction, and face recognition (see Fig. 1). Face detection refers to the process of identifying human faces in an image or video. The next step is face alignment, where some pre-processing steps are applied to the detected face images, such as transforming face images to grayscale, uniformity of facial images size. After that, the feature extraction step is performed, where facial features are extracted, such as the distance between eyes, nose width, depth of eye socket, and length of the jawline. Lastly, the face recognition system correlates the features of a person’s image with the features of all enrolled people in the database, and then the person is recognized [5].

Figure 1: Generic diagram of face recognition system [6]

Face recognition methods can be categorized into four techniques, as follows: part based technique, holistic based technique, template based technique, and feature based technique [7,8]. Part based technique identifies the vital part of facial images, and then merge artificial intelligence and machine learning tools with the part appearances for recognition. A component-based approach such as Support Vector Machine (SVM) is a part-based technique. Holistic based technique takes the entire face area as input data for the facial recognition system. Independent Component Analysis (ICA), Linear Discriminant Analysis (LDA), and Principal Component Analysis (PCA) are some methods of the holistic based technique. Template based technique compares a collection of stored templates of the faces with the input face image. Templates can be built by employing tools such as LDA, SVM, and PCA. Active Shape Model and Elastic Bunch Graph Matching are some methods of the template-based technique. Feature based technique makes use of computer vision and image processing techniques to extract features from the entire face or specific points of the face. Local Binary Pattern (LBP) and Gabor wavelet features are some methods of the feature based technique [4,8].

In this paper, a new feature extraction technique for face recognition is proposed based on the combination of Gabor-based feature extraction, FastICA, and LDA methods. The motivation behind choosing these three methods as a new fusion approach is to provide a more accurate face recognition method under different challenging conditions. As highlighted by [9], the key advantage of using Gabor filters is their invariance to pose variations, as well as their robustness against image noise and illumination variations [10]. On the other hand, FastICA and LDA are the most successful methods to find independent components and to best discriminates different classes. They provide discriminated and independent features which are robust to the facial variations as reported by [11,12]. Four face datasets: GT, Yale, FEI, and ORL are used to assess the efficiency of the proposed method under conditions where face images are varied in illumination, facial expressions, and rotations. Moreover, six well-known distance measures, namely Euclidean, Cosine, Bray-Curtis, Mahalanobis, Correlation, and Manhattan, are investigated for face classification.

The rest of the paper is structured as follows. Section 2 reviews some related recent approaches to face recognition. Section 3 provides a brief theoretical background on Gabor-based feature extraction, FastICA, and LDA methods. Besides, it presents the mathematical formulas of the six dissimilarity measures used. Section 4 elucidates the proposed face recognition method. Section 5 exhibits the experimental results. Finally, Section 6 concludes the paper and suggests some future works.

2  Literature Survey

Face recognition is still an area of active research since facial images vary in rotations, expressions, lighting, and occlusions. There are different approaches to tackle some of the above issues. One of them is to extract the most distinctive features from facial images by exploiting the merits of several feature extraction methods. In our literature survey, we focused on the recent techniques of face recognition based on a single feature extraction method or a combination of more than one method. Various approaches have been suggested in recent years to handle the challenges arisen from the face recognition system.

Aldhahab et al. [13] presented a technique based on the fusion of Discrete Cosine Transform (DCT) and Vector quantization (VQ) for face recognition. DCT method was employed to extract features from the face image. Whereas, VQ method was used to reduce the dimensionality of the extracted features. For face classification, they used Euclidean distance measure. Their experimental results exhibited an improvement in recognition rates on four face datasets: FEI, YALE, ORL, and FERET.

Aldhahab et al. [14] proposed a new method to face recognition based on Two-Dimensional Discrete Multiwavelet Transform (2D-DMWT). In their method, the face image was first partitioned into six portions, and then 2D-DMWT was applied on each portion to reduce the dimensionality of facial features. Lastly, for more data compression, L2 norm was applied. They adopted Neural Network (NN) for face classification. Their method was tested on four face datasets: FERET, FEI, YALE, and ORL.

Muqeet et al. [15] developed a new feature extraction technique for face recognition using local binary patterns (LBP) and interpolation-based directional wavelet transform (DIWT). In the implementation of DIWT, first, quadtree partitioning was employed to form the sub-bands for the directional wavelet transform. Then LBP was performed to the chosen top-level DIWT sub-bands, which ultimately extract the descriptive histogram features. Lastly, LDA was performed to get discriminant features in reduced space. In the identification process, the Nearest Neighbor (NN) classifier was employed. Three different face datasets, namely ORL, GT, and FEI, were used to test their presented technique.

Dora et al. [16] presented an Evolutionary Single Gabor Kernel (ESGK) approach based on the fusion of two bio-inspired optimization methods to overcome the computational complexity of Gabor filter banks in face recognition. These two bio-inspired methods are Particle Swarm Optimization (PSO) and Gravitational Search Algorithm (GSA), where their fusion is called PSO-GSA. The hybrid PSO-GSA was utilized to optimize the parameters of the single Gabor filter and to extract features from facial images. They also presented a new classification method based on the eigenvalue approach for face recognition. Their presented approach was assessed on five face datasets: LFW, ORL, GT, UMIST, and FERET. Experimental results confirmed the efficiency of their new proposed method compared to the conventional Gabor filter bank method.

Wei et al. [17] presented a new method to face recognition based on fuzzy set and LDA, called Complete Fuzzy LDA (CFLDA) method, where fuzzy set theory was fully integrated into LDA model. They used the nearest distance classifier for face image classification. A collection of experiments was conducted to validate the performance of their presented method on three face datasets: ORL, FERET, and Yale.

Liao et al. [18] presented two new methods for face recognition, namely logarithmic weighted sum (LWS) and extended sparse weighted representation classifier (ESWRC). LWS was used to extract facial features. Whereas, ESWRC was employed for face classification. Experimental results revealed that their presented approach performs better than the recent approaches on FERET and FEI face datasets.

Fan et al. [19] proposed an effective face recognition algorithm called joint collaborative representation, which jointly uses space-domain features and frequency-domain features. For face classification, they applied two distance-based classifiers to two sets of data (space-domain features and frequency-domain features), where they employed an adaptive weight to integrate them. Empirical results showed that their proposed method attains better results than the traditional collaborative representation method on three face datasets, namely FERET, GT, and ORL.

Ouyang et al. [20] introduced a new approach to face recognition that integrates Improved Kernel Linear Discriminant Analysis (IKLDA) algorithm with Probabilistic Neural Networks (PNNs) algorithm. IKLDA algorithm was used to reduce the dimensions of face images. For face classification, PNN algorithm was used. A collection of experiments on AR, ORL, and Yale face datasets was carried out to assess the feasibility of their presented method. Their results indicated that IKLDA+PNN method can improve both the computational efficiency and face recognition performance.

Ayyad et al. [21] presented a hybrid approach to face recognition based on the fusion of Singular Value Decomposition (SVD) and Relevance Weighted Linear Discriminant Analysis (RW-LDA) in Discrete wavelet transform domain. Their fusion method was employed to extract the significant features from facial images. They used the nearest neighbor classifier for face classification. ORL and GT face datasets were used to conduct the experiments. They concluded that the use of Z-score and Min-Max normalization techniques along with their proposed fusion method can improve the training time and recognition rate.

Song et al. [22] proposed a new approach to face recognition based on the fusion of local and global Gaussian Hermite Moments (GHMs). To extract both the local and global features of the face image, they firstly used GHMs as a facial feature, where they could construct the spatial pyramid of the face image. Then, they computed the scatter-ratio to choose the most distinctive features. Finally, for face classification, they employed Sparse Representation Classifier (SRC). A set of experiments were performed on Yale, FERET, and ORL face datasets to measure the efficiency of their proposed method. Experimental results showed that their proposed method outperforms other related fusion methods, such as (PCA+SVM), (Gabor+SRC), and (LDA+SRC).

Gou et al. [23] presented two new linear reconstruction classification techniques based upon Sparsity Augmented Collaborative Representation Classification technique (SACRC) to improve the representation classification performance. The first proposed technique is the Weighted Enhancement Linear Reconstruction Measure Classification technique (WELRMC) that incorporates data localities into SACRC. Whereas, the second proposed technique is the two-phase Weighted Enhancement Linear Reconstruction Measure Classification (TP-WELRMC) that fuses both the fine and the coarse representations into SACRC. Empirical results demonstrated that their proposed method obtains better results than the recent RBC approaches on five face datasets: LFW, IMM, ORL, GT, and Yale.

Liao et al. [24] proposed a face recognition approach based on subspace extended sparse representation and learning discriminative feature, named SESRC&LDF. In their method, each test image is deemed to have small or large pose variation. For face classification, if the test image is deemed to be the earlier, SESRC will be used. Otherwise, LDF will be employed. Empirical results demonstrated that their approach attains the highest recognition rates compared to many state-of-the-art approaches on eight face datasets: Georgia Tech, Extended Yale B, AR, Yale, FEI, LFW, UMIST, and FERET.

Based on our literature survey and to the best of our knowledge, none of the previous works has investigated the combination of Gabor feature extraction with two well-known dimensionality reduction methods, namely FastICA and LDA. Motivated by the successful use of Gabor filters in different fields, including computer vision and face recognition, it would be of great interest to examine the combination of Gabor filters with FastICA and LDA in face recognition problem. Therefore, we aim to extract features from the facial image using Gabor filter bank in the first phase, then reduce its features using FastICA method, and lastly, reduce FastICA features using LDA method. The proposed method will be evaluated on Yale, ORL, FEI, and GT face datasets. Furthermore, the performance of the proposed method will be investigated using six distance measures, e.g., Euclidean, Cosine, Bray-Curtis, Mahalanobis, Correlation, and Manhattan.

3  Background

This section reviews the techniques of face feature extraction used in the proposed method. Furthermore, it shows the mathematical background of the six dissimilarity measures used in the recognition phase.

3.1 Feature Extraction Based on Gabor Filter Bank

Gabor filters are bio-inspired convolutional kernels that have extensive use in image processing and computer vision fields [25]. These filters have two interesting characteristics: selectivity for orientation and location frequency, which are analogous to the human visual system [26]. Therefore, analyzing images using these filters are found out to be particularly useful for texture discrimination and representation [27]. In the spatial domain, a 2-D Gabor filter is a Gaussian kernel method formed by a complex sinusoidal plane wave, which is defined as in Eq. (1) [28]:

ψf,θ=f2πγηexp(−α2x′2+β2y′22σ2)exp(j2πfx′+ϕ)x′=xcosθ+ysinθy′=−xsinθ+ycosθ](1)

where f indicates the sine frequency, θ indicates the orientation of the Gabor method, ϕ represents the phase offset, α and β are the Gaussian sharpness with the major axis parallel and the minor axis perpendicular to the wave, respectively. σ indicates the standard deviation of the Gaussian envelope, and γγ indicates the spatial aspect ratio. For more information about how the Gabor filter bank is used, the reader is referred to [28].

Gabor filters with different orientations and scales can be employed to generate a Gabor filter bank. Mostly, a Gabor filter bank with eight orientations and five scales is used (see Fig. 2). These filters are used to extract features from grayscale images. The process of Gabor-based feature extraction works as follows: at first, each filter in the Gabor filter bank is convoluted with the image. Then, the resulting filtered images are down-sampled to reduce the redundant information. Next, each down-sampled image is transformed into a feature vector. After that, each feature vector is normalized to zero mean and unit variance. Finally, the normalized feature vectors are combined to produce the final feature vector of the image [9].

Figure 2: Gabor filters with eight orientations and five scales [9]

3.2 Fast Independent Component Analysis (FastICA)

FastICA is a faster and effective method for ICA, which is first suggested and invented by [29,30]. There are a few interesting points in employing FastICA rather than ICA algorithm. For instance, FastICA converges faster and requires no step size determination as compared to ICA based on a gradient-based method. FastICA obtains an independent Non-Gaussian feature by any random nonlinear function θ, whereas other methods require assessing the Probability Density Function (PDF) of the specified nonlinear functions.

FastICA method attempts to look for a local extreme of Kurtosis for the observed blending signals. The objective of the fixed point is to search for the maximum of oi=wiT′x′ which has maximum non-Gaussianity. FastICA utilizes negentropy as the objective function [12]. Reference [31] presented an easy way to approximate the negentropy function as in Eq. (2).

j′(oi)≈[E{G′(oi)}-E{G′(v)}]2(2)

where oi represents the output random variable with unit variance and zero mean, G′ represents a nonquadratic function, and v represents a Gaussian random variable with unit variance and zero mean. The approximation given in Eq. (3) leads to the use of a new objective function for estimating ICA. Thus, maximizing the function J′G′ gives one independent component. In Eq. (3), w′ represents the p-dimensional weighted vectors. The method for FastICA based on maximum negentropy objective function is elucidated in detail in [31].

jG′(w′)′=[E{G′(w′Tx′)}-E{G′(v)}]2(3)

3.3 Linear Discriminant Analysis (LDA)

LDA is a supervised linear dimensionality reduction method that looks for the subspace that best discriminates different classes. The primary purpose of LDA is to apply dimensionality reduction while keeping up as much class discriminatory information as possible [32]. It transforms a high-dimensional feature vector to a low-dimensional space so that the ratio between the inter-class scatter SB and the intra-class scatter SW is maximized. For the multi-class classification problem that contains c class labels, these scatters can be defined as in Eqs. (4) and (5) [25,33]:

SB=∑j=1c(μj-μ)(μj-μ)T (4)

SW=∑j=1c∑i=1Nj(Xij-μj)(Xij-μj)T (5)

where Xij represents the ith sample of class j, μj represents the mean of class j, c represents the number of classes, Nj represents the number of training samples in class j, and μ represents the total mean of whole classes. SB refers to the scatter of features around the total mean of whole classes, and SW refers to the scatter of features around the mean of each class [33,34].

LDA aims to minimize SW and meanwhile maximize SB. To achieve this, the ratio of |SB|/|SW| has to be maximized. This ratio is maximized when the column vectors of the projection matrix W are the eigenvectors of SW-1SW. To prevent SW from being singular, PCA is employed as a pre-processing step of LDA. Therefore, the original s-dimensional space is projected onto a medium t-dimensional space by PCA, then lastly onto an f-dimensional space by LDA (f≪t≪s) [33].

3.4 Dissimilarity Measures

Distance measures are employed to calculate the ratio of similarity or dissimilarity between two lists of numbers (for instance, vectors). There are over sixty distinct similarity measures, many of which are used to recognize faces [35]. In this paper, the proposed method investigates the performance of six well-known distance measures under conditions where face images vary in rotations, facial expressions, and illuminations. These distance measures are Euclidean [36], Cosine [37], Bray-Curtis [33], Mahalanobis [38], Correlation [38], and Manhattan [38]. The mathematical formulas of the six distance measures are presented in Eqs. (6)–(11), respectively. In the following equations, n represents the dimensionality of the face image, x represents the test face image, y represents the training face image, and xi and yi represent the ith values of x and y face images to be compared.

D(Euclidean)(x,y)=∑i=1n|xi-yi|2 (6)

D(Cosine)(x,y)=∑i=1nxiyi∑i=1n(xi)2∑i=1n(yi)2 (7)

D(Braycurtis)(x,y)=∑i=1n|xi-yi|∑i=1n|xi+yi| (8)

D(Mahalanobis)(x,y)=(xi-yi)TS-1(xi-yi) (9)

where S−1 represents the inverse of the covariance matrix between x and y.

D(Correlation)(x,y)=Cov(x,y)σxσy(10)

where Cov is the covariance and σx and σy are the standard deviations of x and y.

D(Manhattan)(x,y)=∑i=1n|xi-yi|(11)

4  The Proposed Face Recognition Method

In this section, we present our proposed approach to face recognition based on the fusion of Gabor features, FastICA, and LDA. Fig. 3 shows the block diagram of the proposed method in which consists of two main phases: training phase and recognition (testing) phase.

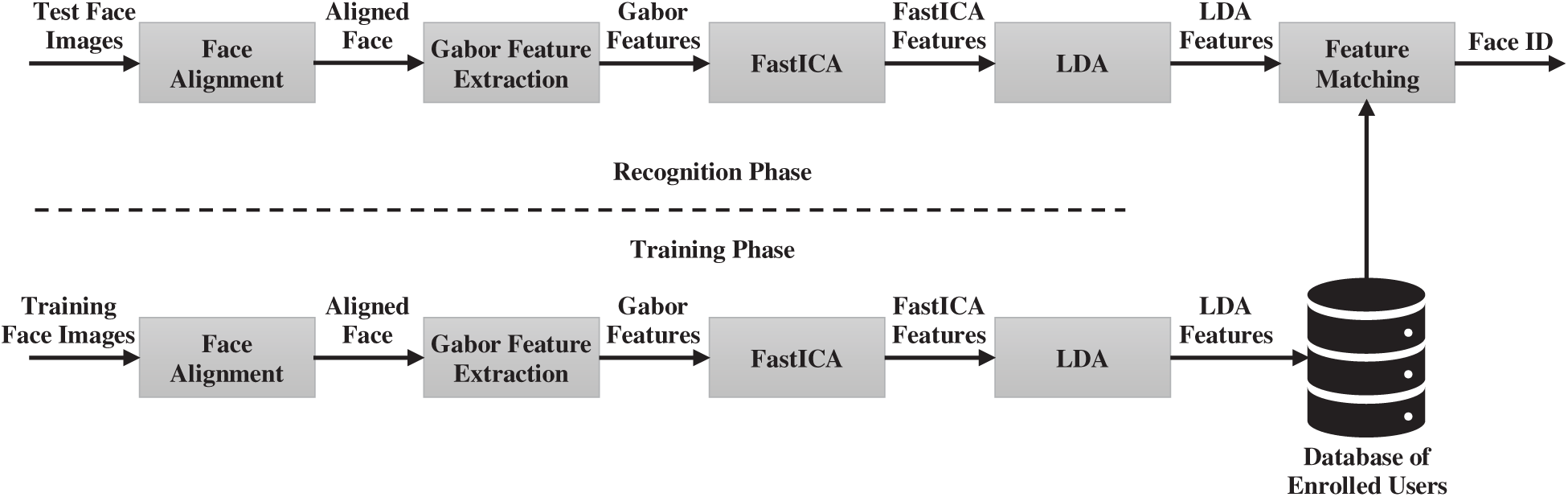
Figure 3: Block diagram of the proposed method

In the training phase, each face image was subject to the face alignment step, where face images were transformed to grayscale and resized to 64×64 pixels to have a uniform size. The reason for selecting the size of 64×64 pixels was based on independent empirical tests in which we obtained a higher rank-one recognition rate than other possible sizes. After that, Gabor-based feature extraction was used to extract features from the aligned face images.

Here is how we used Gabor-based feature extraction in the proposed method. We first generated a Gabor filter bank with eight orientations and five scales, as shown in Fig. 2 presented in Section 3.1. Then, we convoluted each filter, in the Gabor filter bank, with the aligned face image. Fig. 4 shows the results of a face image from Yale face dataset after being convoluted with forty filters depicted in Fig. 2. Since the contiguous pixels in an image are closely related in most cases, the redundant information can be reduced by down-sampling the images originating from Gabor filters [9]. Hence, each convoluted image was down-sampled by a factor of four. The reason for choosing factor four was based on empirical tests that have been conducted in our experiments. After that, each down-sampled image was transformed into a feature vector. Then, Z-score normalization was applied to each feature vector as in Eq. (12). Finally, the normalized feature vectors were merged to form the final feature vector that represents the face image.

ZScore=F-μσ(12)

where F represents the feature vector to be normalized, μ and σ represent its mean and standard deviation, respectively.

Figure 4: Results of convoluting 40 filters depicted in Fig. 2 on a face image

Since Gabor-based feature extraction results in a huge set of facial features, we employed FastICA algorithm to further reduce its dimensionality. FastICA is the most successful method to find independent components. We first found a local extreme of Kurtosis for the extracted features from the Gabor-based method in the previous step. Then, we maximized the negentropy objective function using Eq. (3) to search for the maximum of oi=wi′Tx′. After that, the approximation given in Eq. (3) was used to estimate components as independent as possible, as well as the projection matrix w′ which has the r-dimensional weighted vector. Thus, the number of desired components were found.

Subsequently, we used LDA algorithm to extract the most discriminant features extracted from FastICA to separate different classes as follows. First, the d-dimensional mean vectors for each class mc was calculated. After that, the inter-class scatter SB and the intra-class scatter SW were computed using Eqs. (4) and (5), respectively. Then, the eigenvalues (λ1,λ2,…,λd) and their corresponding eigenvectors (e1,e2,…,ed) were computed from the matrix obtained by SW-1SB. The eigenvectors were then sorted in descending order based on the eigenvalues. To form a d×k projection matrix W, we chose k eigenvectors with the largest eigenvalues. The obtained (d×k) eigenvector matrix was then used to transform the samples onto the new subspace by the matrix multiplication (Y=X×W), where X is a n×d dimensional matrix representing the n samples, and y is the transformed n×k dimensional samples in the new subspace. Finally, all the training feature vectors with their labels were stored in a database to be used for face recognition.

In the recognition phase, a feature vector was extracted for each test face image as performed in the training phase. Then, the distance between each test feature vector and all the training feature vectors, stored in the database, was computed. From the distance measure, the face ID of the training feature vectors with the minimum distance represents the identity of the test face image. Here, we investigated the performance of six distance measures, e.g., Euclidean, Cosine, Bray-Curtis, Mahalanobis, Correlation, and Manhattan, to find out which one of them works better with the proposed (Gabor+FastICA+LDA) feature extraction method. The proposed face recognition method is shown in detail in Algorithms 1 and 2.

Experimental Results

To evaluate the efficiency of the proposed method, a set of experiments were carried out on four face datasets, namely GT, ORL, Yale, and FEI. These four face datasets, briefly summarized in Tab. 1, were chosen due to their face images contain variations in illumination, expressions, postures, and occlusions in which we aim to tackle these problems. All experiments were executed using Python programming language on a personal computer with the following specifications: Intel(R) Core (TM) i7-8550u CPU @ 1.80 GHz 1.99 GHz with 12.00 GB RAM.

Table 1: Brief description of ORL, Yale, GT, and FEI face datasets

Before conducting the experiments, face images of the four used face datasets were converted to grayscale and then resized to 64×64 pixels. Only face images of the Yale face dataset were manually cropped prior to resizing. To investigate the efficiency of the proposed method under different numbers of training samples per person, we conducted six independent experiments on each face dataset. Where, we randomly selected N-facial images (N=4, 5, 6, 7, 8, 9) for each person as training samples, and then we used the remaining facial images as testing samples. To recognize the unseen test face images, the nearest distance classifier is employed with one of the six well-known distance measures found in the literature, namely Bray-Curtis, Euclidean, Manhattan, Mahalanobis, Correlation, and Cosine. Each of these distance classifiers was used independently with the proposed method to see which of them can give a higher recognition rate.

To measure the performance of the proposed method, we used cumulative match characteristic (CMC) curves [15,39]. CMC curve is employed to judge the ranking capabilities of the proposed method. Due to the random selection of training samples, the proposed method obtains different recognition rate for each run. Therefore, to avoid biases, the proposed method, for each experiment, takes the mean of ten independent runs as the average rank-one recognition rate. For FastICA and LDA methods, we used built-in functions of the Python programming language with its default parameters. We only changed the number of the components for the FastICA method to be 150, 115, 75, and 40 components across the four face datasets FEI, GT, ORL, and Yale, respectively. This is because the updated configuration has given us the best results based on trial-and-error tests. In the following subsections, first, the experiments on each of these four face datasets used are highlighted. Then, the results of the comparisons with recent face recognition approaches are presented and discussed.

5.1 Experiments on GT Face Dataset

Georgia Tech (GT) face dataset [40] includes face images of fifty persons, with fifteen different face images per person. This dataset was generated at the Georgia Institute of Technology in two or three sessions at different time intervals. The captured face images of this dataset vary in lighting, facial expression, size, and rotation. Fig. 5 shows some facial image samples of three individuals from this dataset.

Figure 5: Some samples of face images from the GT face dataset

Fig. 6 presents the average rank-one recognition rates of the six distance measures used. Choosing N=5 randomly, the average CMC for the six distance measures used are also shown in Fig. 7. It can be seen from Fig. 6 that the highest rank-one recognition rates for N-training samples (N=4,5,6,7,8,9) per person are 81.38%, 86.42%, 89.20%, 91.37%, 92.80%, and 93.50%, respectively. For instance, when selecting N=4 randomly, the highest rank-one recognition rate is obtained by the Bray-Curtis distance classifier, which is 81.38%. From the results in Figs. 6 and 7, it can be noticed that Bray-Curtis and Cosine distance classifiers perform better than Correlation, Euclidean, Manhattan, and Mahalanobis distance classifiers as they yield superior results. However, Cosine distance classifier gives better results than all other distance classifiers used when selecting N=6,7,8,9 randomly (see Fig. 6). On the contrary, Bray-Curtis distance classifier achieves the highest rank-one recognition rates when selecting N=4,5 randomly.

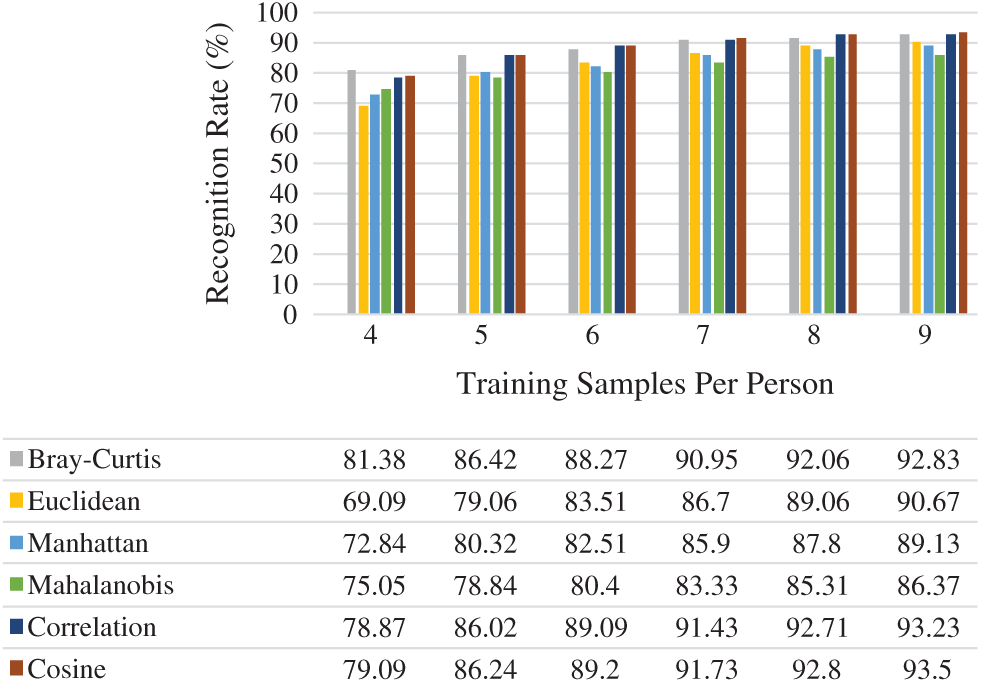
Figure 6: Rank-one recognition rate on GT face dataset

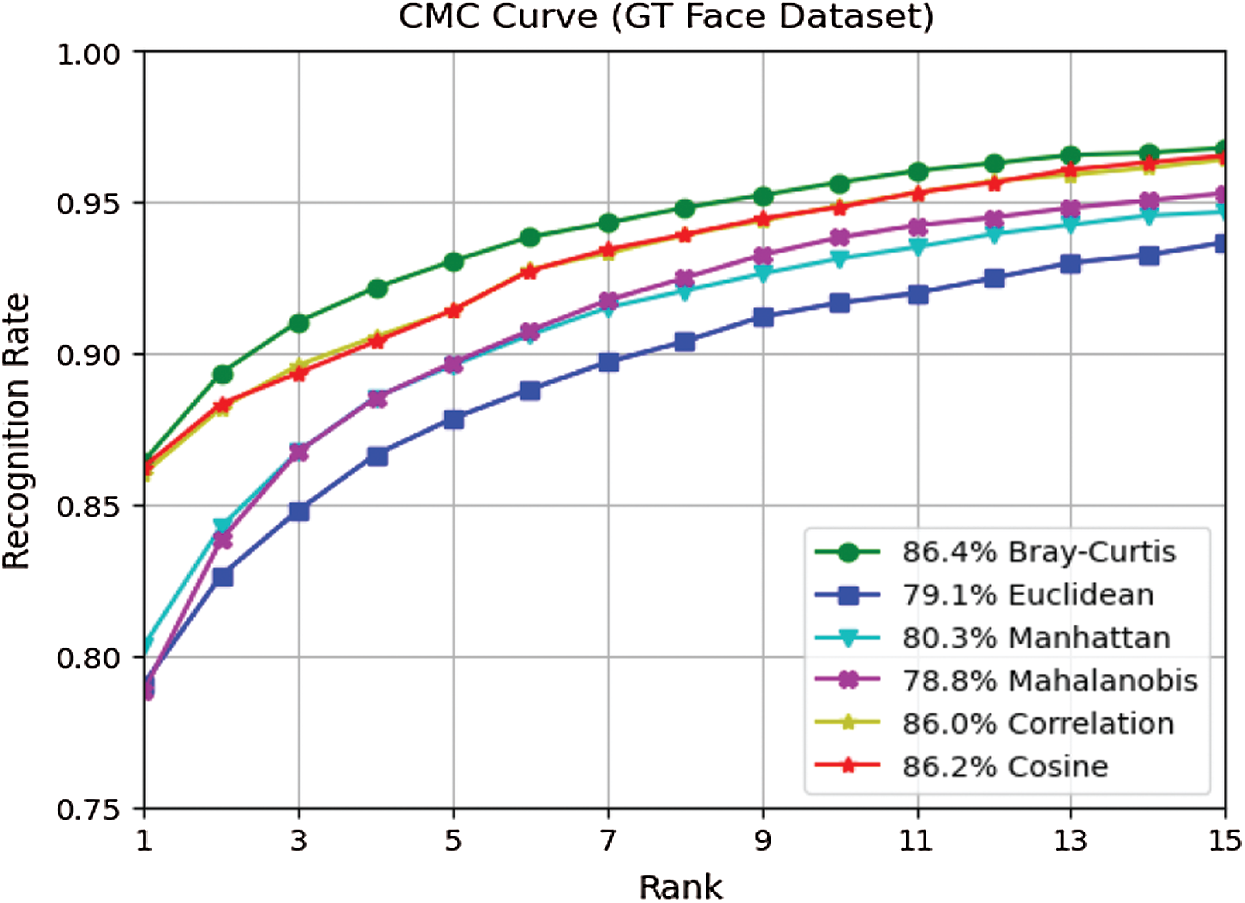
Figure 7: CMC curves of six distance measures on GT face dataset

5.2 Experiments on ORL Face Dataset

ORL face dataset [41] contains face images, in PGM format, for each of 40 distinct individuals, with ten different face images for each individual. The captured face images of this dataset vary in illumination, facial expressions (closed/open eyes, not smiling/smiling), and facial details (no glasses/glasses). Fig. 8 shows some facial image samples of three individuals from this dataset.

Fig. 9 shows the average rank-one recognition rates of the six distance measures used. Choosing N=5 randomly, the average CMC for the six distance measures used are also depicted in Fig. 10. From Figs. 9 and 10, it can be observed that the Bray-Curtis distance classifier attains better results than all other distance classifiers used when the number of training samples is either 4, 5, 6, 7, or 9 samples per person. Conversely, Correlation and Cosine distance classifiers achieve the highest rank-one recognition rates when the number of training samples is eight samples per person (see Fig. 9). This shows that Bray-Curtis, Correlation, and Cosine distance classifiers perform better than Euclidean, Manhattan, and Mahalanobis distance classifiers as they provide superior results.

Figure 8: Some samples of face images from the ORL face dataset

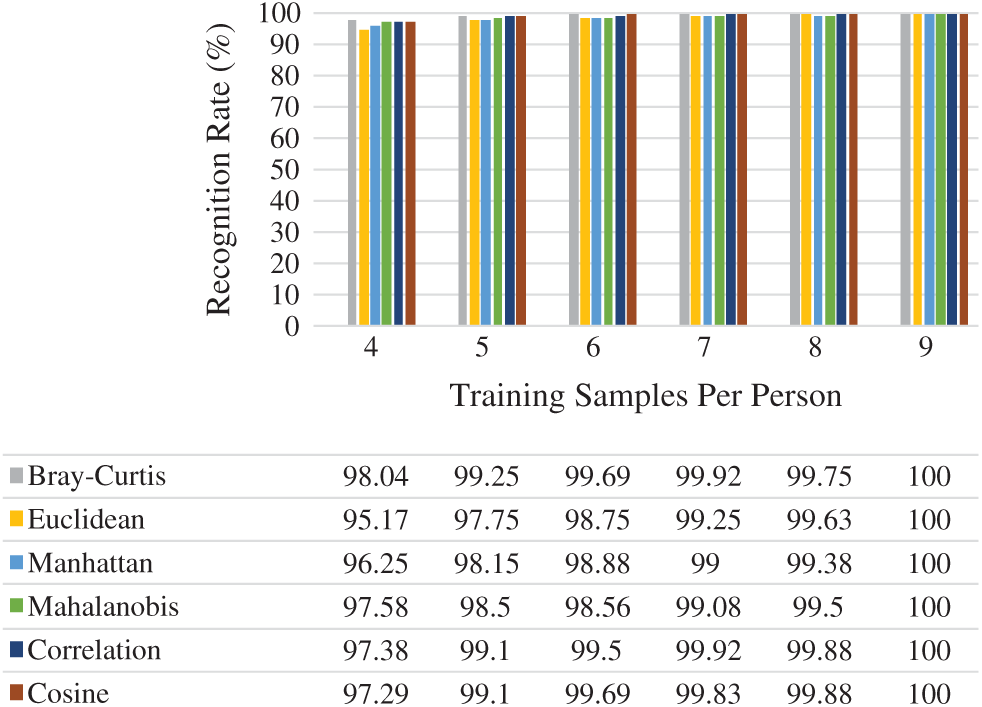
Figure 9: Rank-one recognition rate on ORL face dataset

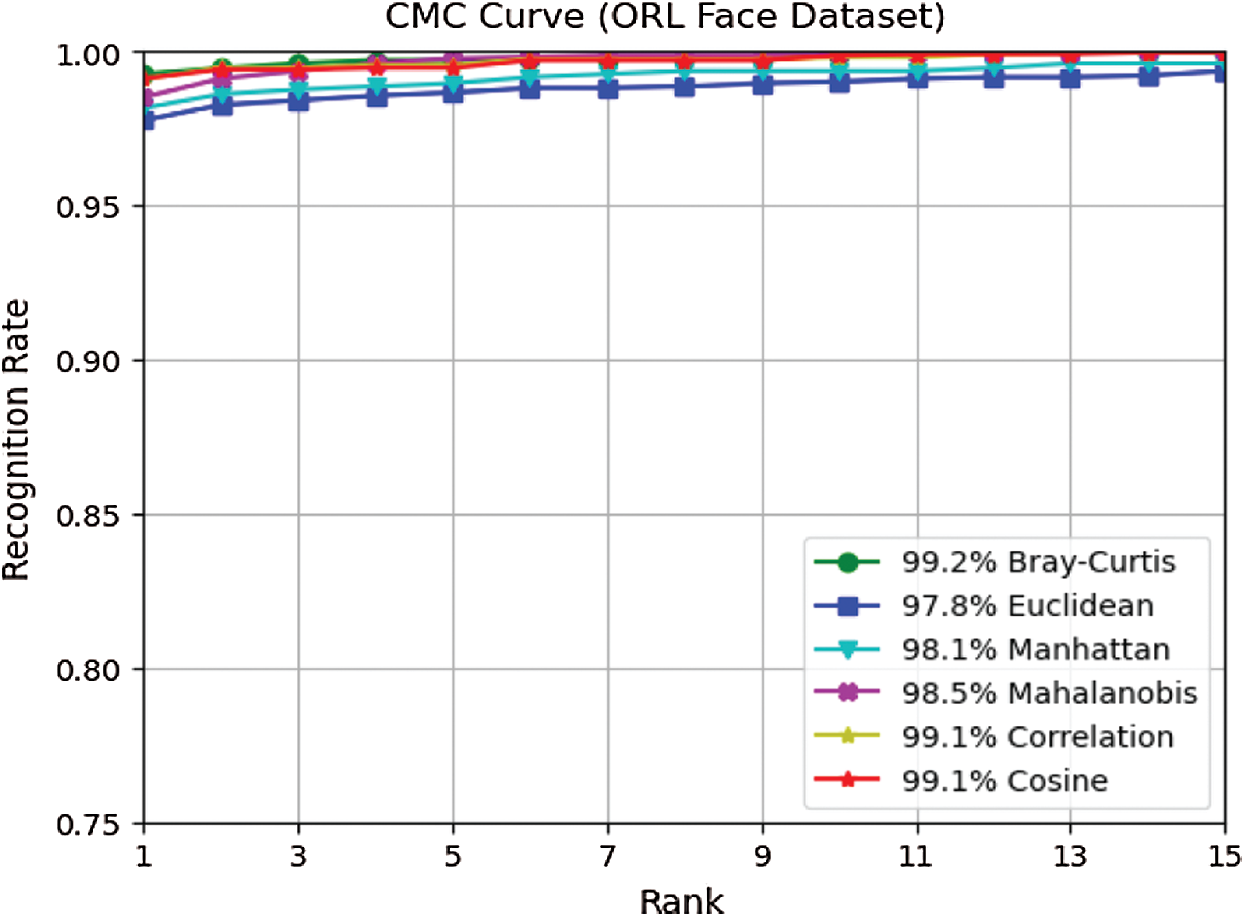
Figure 10: CMC curves of six distance measures on ORL face dataset

5.3 Experiments on Yale Face Dataset

Yale face dataset [42] comprises of different face images, in GIF format, for each of fifteen distinct subjects, with eleven different face images for each subject. The captured face images of this dataset also vary in illumination and facial expressions (normal, happy, left-light, center-light, wearing glasses, wearing no glasses, right-light, sad, surprised, wink, and sleepy). Fig. 11 shows some facial image samples of three individuals from this dataset.

Figure 11: Some samples of face images from the Yale face dataset

Fig. 12 reports the average rank-one recognition rates of the six distance measures used. Choosing N=5 randomly, the average CMC for the six distance measures used are also described in Fig. 13. It is evident from the results in Figs. 12 and 13 that the Mahalanobis distance classifier outperforms all other distance classifiers used when selecting N=4, 5 randomly. Nevertheless, Cosine distance classifier achieves the highest rank-one recognition rates when selecting N=6, 7, 9 randomly (see Fig. 12). On the other hand, Correlation distance classifier achieves the highest rank-one recognition rates when selecting N=7, 8 randomly. This indicates that the number of training samples determines the choice of the distance classifier which gives the best recognition rate.

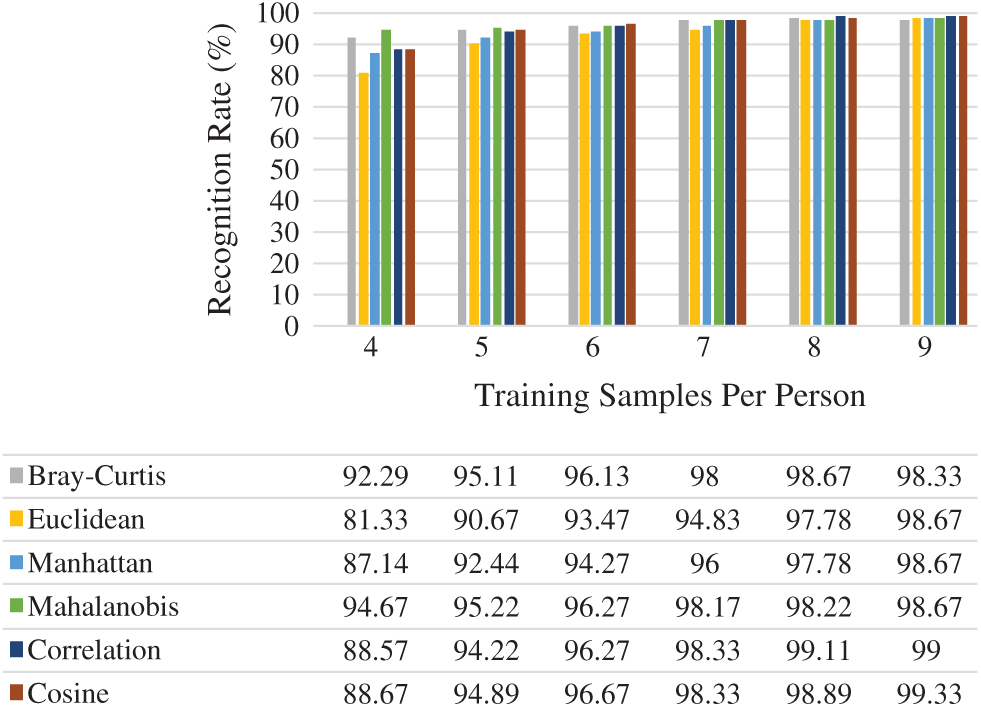
Figure 12: Rank-one recognition rate on Yale face dataset

Figure 13: CMC curves of six distance measures on Yale face dataset

5.4 Experiments on FEI Face Datasets

FEI face database [43] comprises of different face images for each of 200 distinct subjects, with 14 different face images for each subject. All face images are captured against a white homogenous background in an upright frontal position with profile rotation of up to about 180 degrees. Fig. 14 shows some facial image samples of three individuals from this dataset.

Figure 14: Some samples of face images from the FEI face dataset

Fig. 15 outlines the average rank-one recognition rates of the six distance measures used. Choosing N=5 randomly, the average CMC for the six distance measures used are also reported in Fig. 16. It is observed from Figs. 15 and 16 that the Cosine distance classifier yields superior results compared to all other distance classifiers used regardless of the number of training samples chosen for each person. On the other hand, Mahalanobis distance classifier performs worse than other distance classifiers used as it provides the lowest rank-one recognition rates.

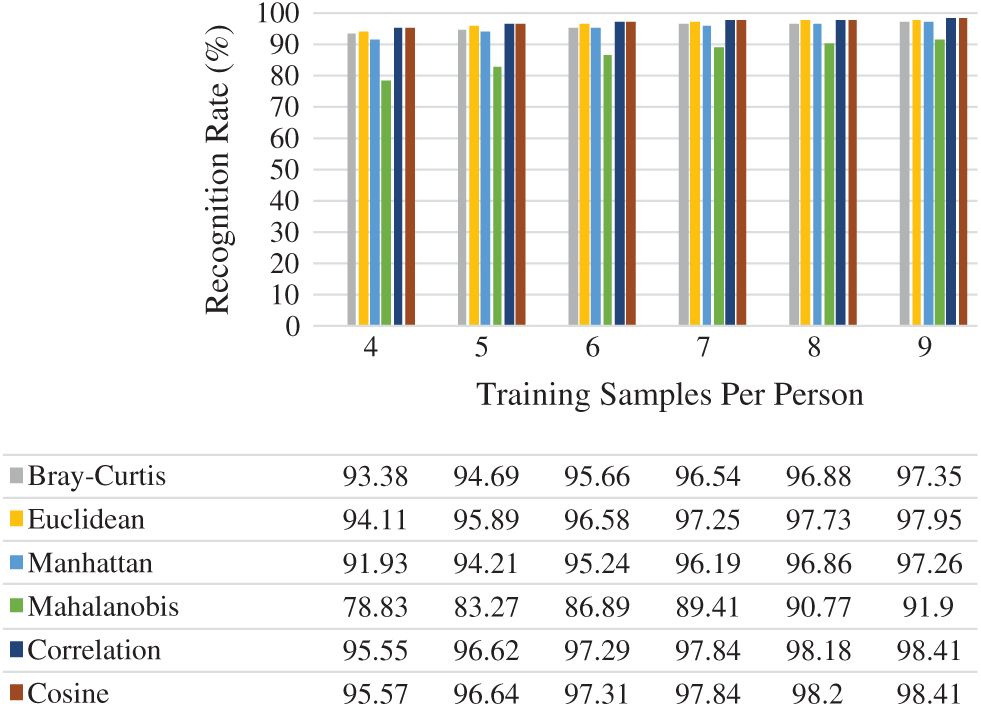
Figure 15: Rank-one recognition rate on FEI face dataset

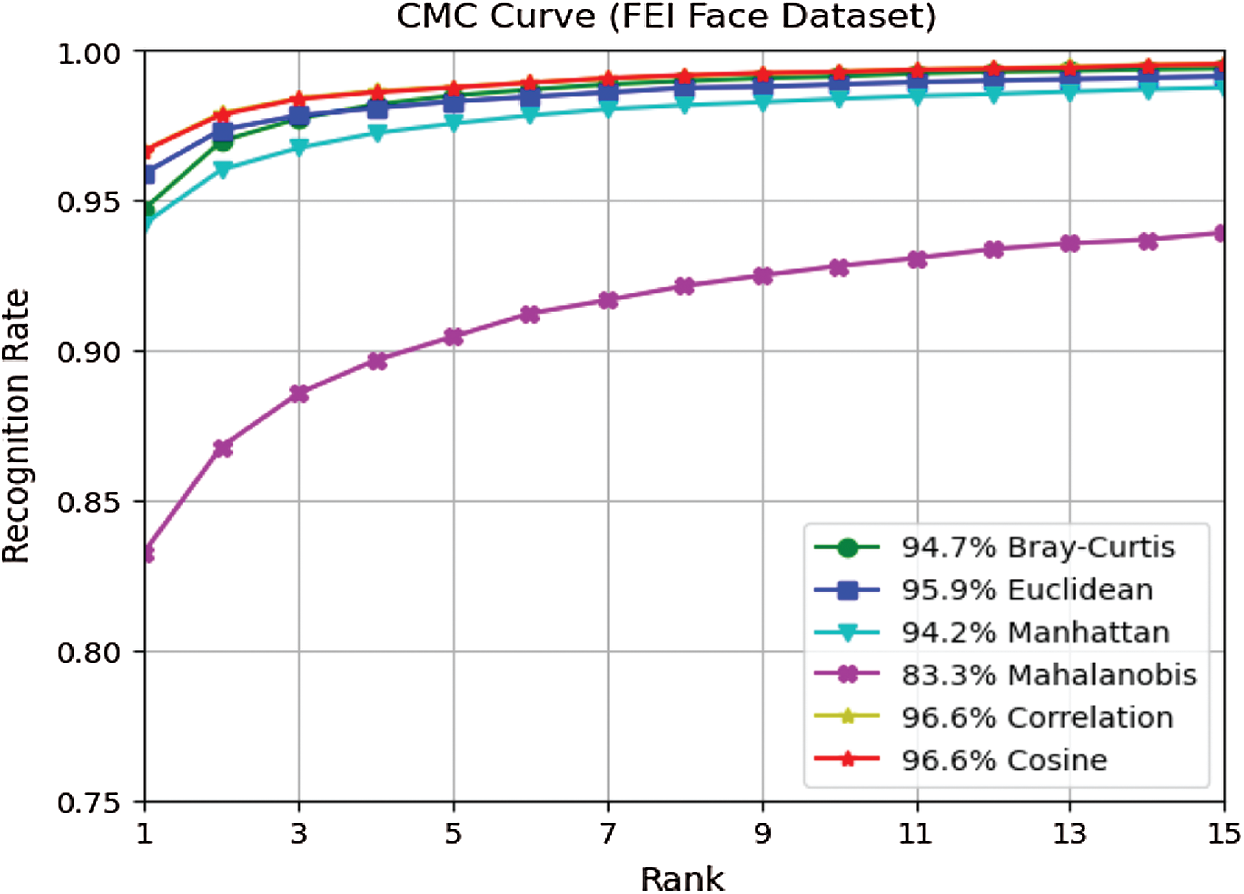
Figure 16: CMC curves of six distance measures on FEI face dataset

5.5 Discussion

From Figs. 6, 9, 12, and 15, it can be seen that in almost all cases, the recognition rate increases with the increase in the number of training samples regardless of the distance classifier used. This is reasonably acceptable because of the high probability of predicting the precise class. It can also be observed from the results in Figs. 6, 9, 12, and 15 that the recognition rate varies from one distance classifier to another. This indicates that the proposed method is consistent and sensitive to the distance measures used.

The results obtained from ORL, Yale, FEI, and GT face datasets confirmed that the proposed method is efficient under conditions in which facial images vary in illumination, expressions, postures, and occlusions, as these face datasets contain the above challenges. Moreover, choosing a distance classifier that gives the best recognition rate depends on the number of training samples used.

5.6 Comparison with Other Approaches

In this section, the results of the proposed method are compared with the recent approaches in the literature. To make the comparisons fair, we used the same number of training samples as those used in the recent methods. Besides, we chose the results of one distance classifier with the proposed method to be compared with other approaches across the four face datasets: Yale, ORL, FEI and GT. The chosen distance classifier is Cosine due to its high recognition rate among almost all the face datasets used. Tabs. 2–5 show the comparison results of the proposed method with the recent approaches on ORL, Yale, GT, and FEI face datasets, respectively.

Table 2: Comparison of the proposed method with state-of-the-art approaches on ORL face dataset

Table 3: Comparison of the proposed method with state-of-the-art approaches on Yale face dataset

Table 4: Comparison of the proposed method with state-of-the-art approaches on GT face dataset

Table 5: Comparison of the proposed method with state-of-the-art approaches on FEI face dataset

It is evident from the results in Tab. 2 that the proposed method has obtained the highest recognition rate compared to the approaches presented in [13–17,20–22] across ORL face dataset. For instance, when the number of training samples is five, our proposed method provides a recognition rate of 99.10% which is significantly higher than those provided by other methods: 97.00% by [15], 94.50% and 97.85% by [17], 97.75% by [21], and 97.50% and 95.50% by [22]. The improvement noticed in the recognition rate by our new method is about 1.25, 2.19, and 1.13 points compared to the highest recognition rate provided by other methods across the three N-training samples (N=5,6,8), respectively. This indicates that the proposed method is efficient and provides better results than the methods presented in [13–17,20–22] for the ORL face dataset.

From Tab. 3, it can be seen that the proposed method has attained the highest recognition rate compared to the methods presented in [13,14,17,20,22] across Yale face dataset. The improvement in the recognition rate by our new method is about 0.12 and 0.84 points compared to the highest recognition rate reported by other methods across the two N-training samples (N=5,8), respectively. This shows that the proposed method is also effective and yields superior results than the methods presented in [13,14,17,20,22] for the Yale face dataset.

It is noticeable from the results in Tab. 4 that the proposed method has achieved the highest recognition rate compared to the methods presented in [15,16,19,21,23]. The improvement in the recognition rate by our new method is about 9.48, 13.08, 11.17, and 5.2 points compared to the highest recognition rate given by other methods across the four N-training samples (N=7,8,9,10), respectively. This demonstrates that the proposed method is also effective and provides better results than the methods presented in [15,16,19,21,23] for the GT face dataset.

From Tab. 5, it can be noted that the proposed method has attained the highest recognition rate compared to the methods presented in [13–15,18,24] across FEI face dataset. The improvement in the recognition rate by our new method is about 4.17, 0.2, and 1.21 points compared to the highest recognition rate reported by other methods across the three N-training samples (N=7,8,11), respectively. This demonstrates that the proposed method is also effective and yields superior results than the methods presented in [13–15,18,24] for the FEI face dataset.

Based on the above experimental results, we can conclude that the proposed method outperforms state-of-the-art methods presented in the literature across the four benchmarked face datasets: ORL, Yale, FEI, and GT investigated in this paper. The main reason behind this improvement in our approach is the combination of the three well-known methods of feature extraction together to extract the most informative features. Another reason for this improvement is the use of the Cosine distance classifier to calculate the recognition rate in which it has shown to give a higher recognition rate than the other most known distance classifiers.

6  Conclusions and Future Works

This paper proposes a new approach to face recognition based on three feature extraction methods, namely Gabor-based feature extraction, FastICA, and LDA. The proposed method was assessed on four benchmarked face datasets: GT, ORL, FEI, and Yale. Six distance measures (e.g., Euclidean, Cosine, Bray-Curtis, Mahalanobis, Correlation, and Manhattan) were employed to investigate the performance of the proposed method. According to the experimental results, the proposed method achieves the highest rank-one recognition rate when compared to state-of-the-art methods in the literature. This indicates that our fusion of Gabor filters with FastICA and LDA gives a better result compared to other fusion methods suggested in the literature in terms of recognition rate. Moreover, the results of our experiments illustrated the efficacy of the new proposed method, especially under using Cosine distance measure.

The method presented in this paper appears to be robust and sensitive in identifying facial images under conditions where lightings, facial expressions, occlusions, and rotations vary, as it provides superior results for ORL, Yale, and GT, FEI face datasets. However, the main drawback of our proposed method is that it is time consuming and computationally expensive due to the use of three sophisticated feature extraction methods. To overcome this issue, research will be further extended in the future to investigate other possible fusion methods, such as combining Gabor-based feature extraction with recent bio-inspired feature selection methods like the Cuttlefish-based method presented in [44]. Moreover, further investigation can be performed on facial images captured in more noisy environments with more variations in illuminations, facial expressions, occlusions, and rotations.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Biswas and J. Sil, “An efficient face recognition method using contourlet and curvelet transform,” Journal of King Saud University—Computer and Information Sciences, vol. 32, no. 6, pp. 718–729, 2020. [Google Scholar]

 2.  H. Zhi and S. Liu, “Face recognition based on genetic algorithm,” Journal of Visual Communication and Image Representation, vol. 58, no. 8, pp. 495–502, 2019. [Google Scholar]

 3.  B. Lahasan, S. L. Lutfi and R. San-Segundo, “A survey on techniques to handle face recognition challenges: Occlusion, single sample per subject and expression,” Artificial Intelligence Review, vol. 52, no. 2, pp. 949–979, 2019. [Google Scholar]

 4.  S. Umer, B. C. Dhara and B. Chanda, “Face recognition using fusion of feature learning techniques,” Measurement, vol. 146, no. 4, pp. 43–54, 2019. [Google Scholar]

 5.  R. Neha and S. Nithin, “Comparative analysis of image processing algorithms for face recognition,” in Proc. of the Int. Conf. on Inventive Research in Computing Applications, Coimbatore, pp. 683–688, 2018. [Google Scholar]

 6.  J. Kamalakumari and D. M. Vanitha, “A survey on automatic heterogeneous face recognition,” International Journal of Advanced Research in Computer and Communication Engineering, vol. 5, no. 11, pp. 68–75, 2016. [Google Scholar]

 7.  R. Patel and S. B. Yagnik, “A literature survey on face recognition techniques,” International Journal of Computer Trends and Technology, vol. 5, no. 4, pp. 189–194, 2013. [Google Scholar]

 8.  T. Archana and T. Venugopal, “Face recognition: A template based approach,” in Proc. of the 2015 Int. Conf. on Green Computing and Internet of Things, Greater Noida, India, pp. 966–969, 2015. [Google Scholar]

 9.  M. Haghighat, S. Zonouz and M. Abdel-Mottaleb, “CloudID: Trustworthy cloud-based and cross-enterprise biometric identification,” Expert Systems with Applications, vol. 42, no. 21, pp. 7905–7916, 2015. [Google Scholar]

10. S. Meshgini, A. Aghagolzadeh and H. Seyedarabi, “Face recognition using Gabor-based direct linear discriminant analysis and support vector machine,” Computers and Electrical Engineering, vol. 39, no. 3, pp. 727–745, 2013. [Google Scholar]

11. D. S. Pankaj and M. Wilscy, “Comparison of PCA, LDA and Gabor features for face recognition using fuzzy neural network,” in Advances in Computing and Information Technology. vol. 117. Springer, pp. 413–422, 2013. [Google Scholar]

12. A. Aldhahab and W. B. Mikhael, “Face recognition employing DMWT followed by FastICA,” Circuits Systems, and Signal Processing, vol. 37, no. 5, pp. 2045–2073, 2018. [Google Scholar]

13. A. Aldhahab, T. Al-Obaidi and W. B. Mikhael, “Employing vector quantization algorithm in a transform domain for facial recognition,” in Midwest Symp. on Circuits and Systems, Abu Dhabi, pp. 1–4, 2016. [Google Scholar]

14. A. Aldhahab and W. B. Mikhael, “A facial recognition method based on DMW transformed partitioned images,” in Midwest Symp. on Circuits and Systems, MWSCAS, Boston, MA, pp. 1352–1355, 2017. [Google Scholar]

15. M. A. Muqeet and R. S. Holambe, “Local binary patterns based on directional wavelet transform for expression and pose-invariant face recognition,” Applied Computing and Informatics, vol. 15, no. 2, pp. 163–171, 2019. [Google Scholar]

16. L. Dora, S. Agrawal, R. Panda and A. Abraham, “An evolutionary single Gabor kernel based filter approach to face recognition,” Engineering Applications of Artificial Intelligence, vol. 62, no. 14, pp. 286–301, 2017. [Google Scholar]

17. Y. Wei, “Face recognition method based on improved,” in Proc.-9th Int. Conf. on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, pp. 456–459, 2017. [Google Scholar]

18. M. Liao and X. Gu, “Face recognition using improved extended sparse representation classifier and feature descriptor,” Intelligent Computing Methodologies, Conf. Proc. ICIC 2018, LNCS, vol. 10956, pp. 306–318, 2018. [Google Scholar]

19. X. Fan, K. Liu and H. Yi, “Joint collaborative representation algorithm for face recognition,” Journal of Supercomputing, vol. 75, no. 5, pp. 2304–2314, 2019. [Google Scholar]

20. A. Ouyang, Y. Liu, S. Pei, X. Peng, M. He et al., “A hybrid improved kernel LDA and PNN algorithm for efficient face recognition,” Neurocomputing, vol. 393, no. 8, pp. 214–222, 2019. [Google Scholar]

21. M. Ayyad and C. Khalid, “New fusion of SVD and relevance weighted LDA for face recognition,” Procedia Computer Science, vol. 148, no. 4, pp. 380–388, 2019. [Google Scholar]

22. G. Song, D. He, P. Chen, J. Tian, B. Zhou et al., “Fusion of global and local Gaussian-Hermite moments for face recognition,” Chinese Conf. on Image and Graphics Technologies and Applications, Communications in Computer and Information Science Book Series, vol. 1043, pp. 172–183, 2019. [Google Scholar]

23. J. Gou, J. Song, W. Ou, S. Zeng, Y. Yuan et al., “Representation-based classification methods with enhanced linear reconstruction measures for face recognition,” Computers and Electrical Engineering, vol. 79, no. 2, pp. 106451, 2019. [Google Scholar]

24. M. Liao and X. Gu, “Face recognition approach by subspace extended sparse representation and discriminative feature learning,” Neurocomputing, vol. 373, no. 1, pp. 35–49, 2020. [Google Scholar]

25. S. Khan, M. Hussain, H. Aboalsamh and G. Bebis, “A comparison of different Gabor feature extraction approaches for mass classification in mammography,” Multimedia Tools and Applications, vol. 76, no. 1, pp. 33–57, 2017. [Google Scholar]

26. B. Ameur, S. Masmoudi, A. G. Derbel and A. Ben Hamida, “Fusing Gabor and LBP feature sets for KNN and SRC-based face recognition,” in 2nd Int. Conf. on Advanced Technologies for Signal and Image Processing, Monastir, Tunisia, pp. 453–458, 2016. [Google Scholar]

27. Z. Xia, R. Lv and X. Sun, “Rotation-invariant Weber pattern and Gabor feature for fingerprint liveness detection,” Multimedia Tools and Applications, vol. 77, no. 14, pp. 18187–18200, 2018. [Google Scholar]

28. L. Li, H. Ge, Y. Tong and Y. Zhang, “Face recognition using Gabor-based feature extraction and feature space transformation fusion method for single image per person problem,” Neural Processing Letters, vol. 47, no. 3, pp. 1197–1217, 2018. [Google Scholar]

29. A. Hyvarinen and E. Oja, “A fast fixed-point algorithm for independent component analysis,” Neural Computation, vol. 9, no. 7, pp. 1483–1492, 1997. [Google Scholar]

30. A. Hyvarinen, “Fast and robust fixed-point algorithms for independent component analysis,” IEEE Transactions on Neural Networks, vol. 10, no. 3, pp. 626–634, 1999. [Google Scholar]

31. A. Hyvarinen, “New approximations of differential entropy for independent component analysis and projection pursuit,” Advances in Neural Information Processing Systems, MIT Press, vol. 10, pp. 273–279, 1998. [Google Scholar]

32. S. Sadaghiyanfam and M. Kuntalp, “Analysing the performance of LDA (Linear discriminant analysis) feature for diagnosing PAF (paroxysmal atrial fibrillation) patients,” in 2019 Scientific Meeting on Electrical-Electronics and Biomedical Engineering and Computer Science, Istanbul, Turkey, pp. 1–4, 2019. [Google Scholar]

33. H. Cho and S. Moon, “Comparison of PCA and LDA based face recognition algorithms under illumination variations,” in The Society of Instrument and Control Engineers, ICCAS-SICE, Fukuoka, Japan, pp. 4025–4030, 2009. [Google Scholar]

34. S. Niket Borade and R. P. Adgaonkar, “Comparative analysis of PCA and LDA,” in Int. Conf. on Business, Engineering and Industrial Applications, Kuala Lumpur, pp. 203–206, 2011. [Google Scholar]

35. A. Abbad, K. Abbad and H. Tairi, “Face recognition based on city-block and Mahalanobis cosine distance,” in 13th Int. Conf. on Computer Graphics, Imaging and Visualization, Beni Mellal, pp. 112–114, 2016. [Google Scholar]

36. L. Greche, M. Jazouli, N. Es-Sbai, A. Majda and A. Zarghili, “Comparison between Euclidean and Manhattan distance measure for facial expressions classification,” in Int. Conf. on Wireless Technologies, Embedded and Intelligent Systems WITS, Fes, pp. 1–4, 2017. [Google Scholar]

37. B. Lavanya and H. H. Inbarani, “A novel hybrid approach based on principal component analysis and tolerance rough similarity for face identification,” Neural Computing and Applications, vol. 29, no. 8, pp. 289–299, 2018. [Google Scholar]

38. M. A. Abuzneid and A. Mahmood, “Enhanced human face recognition using LBPH descriptor, multi-KNN, and back-propagation neural network,” IEEE Access, vol. 6, pp. 20641–20651, 2018. [Google Scholar]

39. V. Štruc and N. Pavešić, “The complete Gabor-Fisher classifier for robust face recognition,” Eurasip Journal on Advances in Signal Processing, vol. 2010, pp. 1–26, 2010. [Google Scholar]

40. “Georgia Tech Face Dataset,” [Online]. Available: http://www.anefian.com/research/face_reco.htm (Accessed 14 January 2020). [Google Scholar]

41. “ORL Face Dataset,” [Online]. Available: https://www.cl.cam.ac.uk/research/dtg/attarchive/facedata-base.html (Accessed 14 January 2020). [Google Scholar]

42. “Yale Face Dataset,” [Online]. Available: http://vision.ucsd.edu/content/yale-face-database (Accessed 14 January 2020). [Google Scholar]

43. FEI Face Dataset,” [Online]. Available: https://fei.edu.br/~cet/facedatabase.html (Accessed 14 January 2020). [Google Scholar]

44. A. S. Eesa, Z. Orman and A. M. A. Brifcani, “A novel feature-selection approach based on the cuttlefish optimization algorithm for intrusion detection systems,” Expert Systems with Applications, vol. 42, no. 5, pp. 2670–2679, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.