Computers, Materials & Continua DOI:10.32604/cmc.2021.016364
Article

Traffic Engineering in Dynamic Hybrid Segment Routing Networks

Yingya Guo1,2,3,7, Kai Huang1, Cheng Hu4,*, Jiangyuan Yao5 and Siyu Zhou6

1College of Mathematics and Computer Science, Fuzhou University, Fuzhou, 350000, China
2Fujian Key Laboratory of Network Computing and Intelligent Information Processing, Fuzhou University, Fuzhou, 350000, China
3Key Laboratory of Spatial Data Mining & Information Sharing, Ministry of Education, Fuzhou, 350003, China
4School of Information Science and Technology, Guangdong University of Foreign Studies, Guangzhou, 510006, China
5School of Computer Science and Cyberspace Security, Hainan University, HaiKou, 570228, China
6Tandon School of Engineering, New York University, New York, 10012, USA
7Department of Computing, Hong Kong Polytechnic University, Hong Hom, 999077, Hong Kong
*Corresponding Author: Cheng Hu. Email: huchengcs@gdufs.edu.cn
Received: 31 December 2020; Accepted: 02 February 2021

Abstract: The emergence of Segment Routing (SR) provides a novel routing paradigm that uses a routing technique called source packet routing. In SR architecture, the paths that the packets choose to route on are indicated at the ingress router. Compared with shortest-path-based routing in traditional distributed routing protocols, SR can realize a flexible routing by implementing an arbitrary flow splitting at the ingress router. Despite the advantages of SR, it may be difficult to update the existing IP network to a full SR deployed network, for economical and technical reasons. Updating partial of the traditional IP network to the SR network, thus forming a hybrid SR network, is a preferable choice. For the traffic is dynamically changing in a daily time, in this paper, we propose a Weight Adjustment algorithm WASAR to optimize routing in a dynamic hybrid SR network. WASAR algorithm can be divided into three steps: firstly, representative Traffic Matrices (TMs) and the expected TM are obtained from the historical TMs through ultra-scalable spectral clustering algorithm. Secondly, given the network topology, the initial network weight setting and the expected TM, we can realize the link weight optimization and SR node deployment optimization through a Deep Reinforcement Learning (DRL) algorithm. Thirdly, we optimize the flow splitting ratios of SR nodes in a centralized online manner under dynamic traffic demands, in order to improve the network performance. In the evaluation, we exploit historical TMs to test the performance of the obtained routing configuration in WASAR. The extensive experimental results validate that our proposed WASAR algorithm has superior performance in reducing Maximum Link Utilization (MLU) under the dynamic traffic.

Keywords: Traffic engineering; routing optimization; segment routing; deep reinforcement learning; ultra-scalable spectral clustering

1  Introduction

As with the rapid development of 5G and Internet of Things (IoT), various Internet applications come into being and network traffic volume has been growing explosively in Internet Service Provider (ISP) networks for the past few years. How to balance huge amount network flows to avoid network congestion and improve network performance becomes a hot topic. Traffic Engineering (TE) [1], as an efficient technique in network management, plays an important role in balancing network flows. Through TE methods, network operators can effectively avoid network congestion and improve network performance. The core of a TE framework is the routing optimization algorithms, which are closely related to the routing protocols of a network. In traditional IP networks, Open Shortest Path First (OSPF) routing protocol is the most widely used Interior Gateway Protocol (IGP). There is a weight (or cost) assigned for each link in OSPF and network flows are forwarded from the source to the destination nodes along the shortest paths. Various heuristic algorithms are proposed to optimize the OSPF link weights for better improving network performance. However, in OSPF, the shortest-paths-based routing paradigm lacks of routing flexibility and is traffic-oblivious. The flows are always routed to the next hops on the shortest paths, regardless of the current link load and network utilization. Therefore, shortest-path-based routing can easily lead to the network congestion, especially when the network traffic is dynamically changing, thus degrading the network performance.

Software Defined Networking (SDN) is an emerging centralized network architecture, where its control plane and data plane are separated. The SDN controller of the controller plane installs flow entries into the SDN switches of the data plane for better managing the route selection of flows. The flows break away from the shortest-path-routing constraint and routing gains more flexibility in the centralized SDN architecture. However, the routing flexibility of SDN comes at the expense of the abundant flow entries installing in SDN switches. The abundant flow entries pose a heavy burden for the Ternary Content Addressable Memory (TCAM) in SDN switches. The emergence of Segment Routing (SR) [2] provides a solution to implement a centralized control without introducing many flow entries in dataplane. SR, which is capable for IP network, is a novel routing paradigm. SR adds a packet header containing a sequence of Segment Identifier (SID) lists to the IP packet, and maintains all path selection policy status information at the network edge ingress node. Therefore, the intermediate node only needs to send the IP packet hop-by-hop according to the top SID in the header list. There is no need for intermediate nodes to run complex signaling protocols and maintain the status information of each flow, which greatly relieves the burden of network switches. Compared with traditional TE methods [3], implementing path selection through centralized routing configuration at the ingress nodes has good scalability and flexibility. Therefore, SR has unique advantages in achieving network load balancing in TE. However, migrating to a fully SR deployed IP network is impractical at present, due to economical and technical challenges. Therefore, a hybrid SR network, with a partial deployment of SR nodes in an IP network, will be a prevailing network architecture in the near future. How to optimize routing and achieve load balance in a hybrid SR network attracts worldwide attention from both industrial and academia.

There are three challenges for optimizing routing and improving network performance in a hybrid SR network. First, there are legacy routers running distributed routing protocol, such as OSPF and also the SR deployed switches supporting centralized control from centralized controller. The flows through legacy routers are required to be forwarded to the next hop on the shortest paths between the source and the destination. However, for the SR enabled switches, the routing gains more flexibility and the flows can be routed on all the available paths between the source and destination. The routing constraints are different for these two kinds of nodes, which poses a challenge for the routing optimization in a hybrid SR network. Second, the traffic is dynamic changing on a daily time. The optimized routing should work well under different traffic patterns in a daily time. How to represent the dynamic traffic and optimize the routing for adapting to the changing traffic poses another challenge. Therefore, designing a routing optimization algorithm that can better obtain the representative TMs and improve the network performance in a hybrid SR network with a changing traffic becomes a hot research topic.

In this paper, we firstly formulate the TE problem in a dynamic hybrid SR network as a math programming problem and prove its complexity. Then, we propose a novel algorithm WASAR, which aims to further reduce the MLU of the hybrid SR network in a traffic-changing environment. Specifically, we leverage a novel clustering method Ultra-scalable SPEctral Clustering (U-SPEC) to obtain the representative TMs and the expected TM, which can better depict the essence of traffic variation. Then, given the representative TMs and the expected TM, we optimize link weight setting offline under the distributed IP routing protocol and splitting ratio for flows through centralized SR nodes online for adapting to the changing traffic. The main contributions of this paper are shown as follows.

•      To better depict the average case of traffic and improve the network performance under the dynamic traffic, we refine the clustering method based on U-SPEC [4] for obtaining the representative TMs and the expected TM.

•      We propose a TE algorithm WASAR to optimize routing in a hybrid SR network. WASAR algorithm first exploits a U-SPEC-based clustering method to obtain the representative TMs and expected TM. Afterwards, for optimizing route selection of flows through legacy nodes and SR nodes with the aim of adapting to network traffic changes, WASAR algorithm consists of a two-stage-optimization: offline link weight setting optimization and online splitting ratio optimization.

•      In order to ensure the effectiveness of the proposed algorithm WASAR, we evaluate WASAR under three network topologies. The information of the three network topologies are: America Research and Education Network (Abilene), China Education and Research Network (CERNET) and Europe Research and Education Network (GEANT), respectively. Through extensive experiments on different network topologies and different SR nodes deployment ratios, we can observe that MLU obtained in WASAR algorithm is generally lower than that obtained from the other routing optimization algorithms in a hybrid SR network. The experimental results also show that the link weight setting and flow splitting ratio optimized in the WASAR algorithm can better adapt to the traffic demand variation than the routing configuration optimized in other routing optimization algorithms.

The rest of this paper is structured as follows. Section 2 is the related works. Section 3 is the problem formulation and its complexity analysis. In Section 4, we introduce the TE algorithm WASAR. In Section 5, we exploit real traffic datasets and topology information to evaluate the proposed algorithm under different network topologies. Finally, we conclude the paper in Section 6.

2  Related Work

In this section, we summarize the related works on routing optimization algorithms and clustering methods.

In traditional IP network, OSPF and IS-IS protocols are the most widely used intra-domain routing protocols. In OSPF and IS–IS, flows are constrained to route on the shortest paths between the source and destination. As a result, the link weight setting is important for the route selection and influences the traffic distribution in the network. Various heuristic algorithms [1,5,6] are proposed to optimize the link weight setting for improving the network performance. However, the network performance is limited by the shortest path based routing, for all the flows are routed on the shortest paths between the source and destination, which lacks of flexibility.

With the emergency of centralized network architecture, such as SDN, routing shows more flexibility. The controller can centrally control the forwarding behaviors of the centralized nodes, thus realizing a flexible routing of flows. However, due to existing challenges, a full centralized network is impractical in the short term. Thus, a hybrid network, with a partial deployment of centralized nodes in legacy distributed networks, becomes a prevailing network architecture. Agarwal et al. [7–11] propose routing algorithms to optimize the route selection for flows in hybrid SDNs or hybrid SR networks. In a hybrid SDN, Guo et al. introduce heuristic algorithms [7–9] to adjust link weights under OSPF protocol or optimize flow splitting ratio of SDN nodes to minimize the MLU of the network. The extensive experiments demonstrate that a deployment ratio of 30% SDN nodes can reap the most of benefit and the introduction of SDN nodes greatly improves the network performance. For hybrid SR networks, Cianfrani et al. [10] propose an incremental Segment Routing Domain (SRD) architecture solution. This network scenario meets two conditions: only a subset of nodes has SR capability and the goal of SR is to minimize the MLU of the network. However, the method mentioned in [10] is only applicable to SR-MPLS scenario. Due to the characteristics of SR-MPLS, there must be at least two nodes deployed SR-MPLS working normally for each SRD, and the network cannot be well utilized. Therefore, due to the limitations of SRD and the inappropriate setting of link weights, if we intend to obtain the MLU of a hybrid network equivalent to that of the full-SR network, the deployment ratio of SR nodes should be as high as 50% or higher. This obviously does not conform to the original intention of the hybrid SR network, which achieves almost the same network performance as the fully SR deployed network by deploying fewer SR nodes. Regarding the shortcomings of the algorithm proposed in [10], Tian et al. [11] propose a DRL algorithm [12,13], which is widely used in image processing [14] and text classification [15], to optimize the link weight setting and SR node deployment offline, and leverages Linear Programming (LP) solver for obtaining the optimal flow splitting ratio online. Since the traffic demand in the network is dynamically changing, WA-SRTE algorithm computes representative TMs that can better depict the traffic variations based on K-means. However, for most networks, the daily historical TM fluctuation follows the same principle, but the TMs within a day are relatively scattered. This leads to the phenomenon that the traffic demand is extremely large at certain time, but tends to be rather small at a certain time. As mentioned before, the performance of K-means algorithm is not satisfying for handling outliers. Therefore, the representative TMs and the expected TM computed by the clustering algorithm K-means cannot perfectly depict the traffic variation and the average case of traffic demands, which degrades the network performance.

K-means [16–19] method is a classical unsupervised clustering method widely used in data classification. The whole implementation process of K-means is very simple and clear, which can be divided into three steps: (a) determining the value of k, which means that the final classification result contains several types of samples; (b) selecting the initial centroid of each type from the corresponding samples; (c) obtaining the final classification set according to the sample set and its initial centroid. In this method, K-means divides the whole sample set into k clusters according to the selected distance. The selection of initialized centroids greatly influences the final clustering result and the total running time. Hence, it is necessary to determine the appropriate k centroids. The inappropriate selection of centroids may lead to the slow convergence of the algorithm. Many researchers have refined the K-means method and propose different clustering algorithms, such as K-means++ [20], Elkan K-means algorithm [21], and mini batch K-means algorithm [22], for applying it to different research fields. K-means++ algorithm is a refinement of the K-means method by randomly initializing the centroids. Elkan K-means algorithm optimizes the distance from the sample point to the centroids and mini batch K-means is suited to the clustering problems where the number of samples is large. Although the K-means methods have been widely used in different fields, they still have some shortcomings, such as sensitive to outliers and noise (the center point is easy to shift), difficult to find clusters with very different sizes, unsatisfying clustering performance with only local optimal can be guaranteed.

In our paper, we propose a new TE algorithm that refines the K-means algorithm for obtaining the representative TMs and the expected TM, so that we can better depict the traffic variations and average case of traffic demand. Then, we propose to optimize the OSPF link weight offline under the obtained expected TM through DRL algorithm, for learning the optimal link weight under OSPF and optimizing splitting ratio of centralized nodes online by solving LP.

3  Problem Formulation

In this section, we first present the network model of our TE problem in a hybrid SR network. Then, we analyze the complexity of the formulated problem.

3.1 Network Model

Our network is modeled by an undirected graph G=(V,E), where V is the router set (legacy nodes and SR nodes) and E is the unidirectional link set. c(l) and w(l)represent the capacity and OSPF weight setting of link l, respectively. Historical TM set is denoted by D={D1,D2,…,Dn}. Here, Dt∈D is the TM at time interval t. s(m),d(m) and Dt(m) denote the source node, destination node and traffic volume of demand m in Di, respectively. Each TM Di has a non-negative coefficient ri, which implies the importance of the Di. flm(w) indicates the fraction of traffic volume of demand m that routes across the link l with a weight setting w. The OSPF weight setting w and splitting ratio of centralized SR nodes both determine the routing of flows. Our objective is to obtain a routing configuration that works well under changing traffic, i.e., minimizing the MLU of the network under different TMs. To quantify this metric, we set the average sum of MLU under different TMs as our optimization goal. The definition of notations is summarized in Tab. 1.

Now, we formulate our TE problem as follows:

minimize ∑i=1nriUi (1)

∑m∈Mflm(w)⋅Dt(m)≤Umax⋅c(l)∀l∈E,t∈n (2)

∑i∈Vhi,vmt(w)-∑j∈Vhv,jmt(w)={-Dt(m)ifs(m)=vDt(m)ift(m)=v0otherwise∀m∈M,v∈V,t∈n

0≤flm(w),hi,jm(w),∀m∈M,i,j∈V,l∈E(4)

1≤w(l)≤216-1∧w(l)∈Z∀l∈E(5)

Table 1: Definition of notations

The above mathematical formulas basically depict the TE problem in a hybrid SR network. Eq. (1) introduces the goal of the algorithm, i.e., minimizing the average sum of MLU under different TMs. Eq. (2) is the capacity limit of each link in the hybrid network, i.e., the link load cannot exceed its link capacity. Eq. (3) denotes the flow conservation constraint and traffic demand satisfaction constraint. It means that for the traffic demand m, if the router that the flow passes through is an ingress node, the outgoing traffic of the router should be equal to the traffic demand volume Dt(m); if the router that flow passes through is an egress node, then the ingoing traffic of the router should be equal to the traffic demand volume Dt(m); otherwise, for an intermediate node, the ingoing traffic should be equal to the outgoing traffic for flow conservation constraint. Eqs. (4), (5) exhibits some non-negative and integer constraints.

3.2 Problem Complexity

If the OSPF link weight setting is determined and there is only one TM, the formulated optimization problem can be reduced to a multi-commodity flow problem, which can be solved in polynomial time [23]. However, in the network scenario of this paper, both link weight setting and splitting ratio of SR nodes are required to optimize for reducing Umax. Moreover, the routing should be optimized under multiple TMs, which leads to the increment of the problem complexity. Optimizing OSPF weight setting has been proved to be NP-hard [24]. Our problem is harder than the OSPF weight optimization problem. Therefore, the complexity of routing optimization under multiple TMs is proved to be NP-hard.

4  Algorithm Description

In this section, we will introduce a novel TE algorithm WASAR, which is based on U-SPEC for improving network performance in a hybrid SR network. We first present an overview of the proposed algorithm WASAR, which consists of three steps. Then, we show the three steps of the algorithm in details. Specifically, we introduce the U-SPEC clustering method exploited to cluster the historical TMs and obtain the expected TM. Then, we describe the offline OSPF weight optimization and online flow splitting ratio optimization of SR nodes under the dynamic traffic.

4.1 An Overview of WASAR

An overview of WASAR is shown in Fig. 1. As shown in Fig. 1, the algorithm first obtains the representative TMs, which can depict the dynamic traffic, through a clustering algorithm U-SPEC. The expected TM can be computed by linearly combining the representative TMs. Then, WASAR exploits the DRL algorithm to learn the optimal link weight setting and the deployment of SR nodes automatically in a hybrid network. After the link weight and SR deployment are determined, the flow splitting ratio of SR nodes is adjusted under each new TM by exploiting LP solver in an online manner. In this method, we can obtain a routing policy that performs well under dynamic traffic.

Figure 1: An overview of WASAR

4.2 Obtaining the Representative TMs

In this part, we present a density-based clustering algorithm: Ultra-scalable SPEctral Clustering (U-SPEC) [4], to cluster the historical TMs and get the representative TMs that can reflect the dynamic nature of historical TMs. Compared to K-means method, U-SPEC algorithm can perfectly handle the classification problem with large scale datasets, and greatly reduce the amount of calculation. At the same time, U-SPEC clustering algorithm has good performance in handling outliers and excellent clustering results can be achieved through U-SPEC. U-SPEC algorithm consists of three steps: Hybrid Representative TM Selection (HRTMS), Approximation of K-nearest Representatives TMs (AKRTM) and Bipartite Graph Partitioning (BGP).

Through the clustering algorithm U-SPEC, we can obtain several clusters. The corresponding cluster centroid TMs are denoted as representative TM set D={D1,D2,…,Dn}. Here, each TM Di∈D is a representative TM. We compute the ratio of number of TMs in each cluster to the total number of historical TMs and refer it as ci. Here, ci reflects the importance of the TM Di∈D in the historical TMs, which means that the larger the ci is, the more important the Di is. The expected TM Dexp that denotes the average case of TMs can be computed as follows:

(6) Dexp=c1D1+c2D2,…,+cnDn=∑i=1nciDi(3)

4.3 Routing Optimization

Given the expected TM Dexp, which denotes the average case of dynamic traffic, we begin the routing optimization in a hybrid SR network under the expected Dexp. To maintain the routing stability, OSPF link weight should be kept relatively static under different TMs. Therefore, we optimize the OSPF weight setting under the expected TM Dexp to obtain a weight setting that works well under average traffic demand. For adapting to the changing traffic in an online manner, we adjust the splitting ratio of flows through SR nodes in a centralized online method. Therefore, in the WASAR algorithm, we consider both link weight optimization and flow splitting ratio optimization process. In the following, we discuss two steps in details.

a=Umax(s1)Umax(st) (7)

rt={-e2(1α-1)ifα<10ifα=1e2(α-1)ifα>1 (8)

(1) Offline OSPF link weight optimization: With the rapid development of Artificial Intelligence (AI), machine learning is widely applied in different kinds of fields [25,26]. Compared with traditional heuristic approaches, ML algorithms are generalized, environment-adaptive and time-efficient for solving complex optimization problems. DRL, as a kind of ML algorithms, can learn the best action in a trial and error manner without prior knowledge. In DRL, an agent interacts with the environment through state, action and reward. Specifically, in each step t, the agent gets a τ st from the environment and chooses an action at. Afterwards, the state st transfers to st+1 according to action at, and environment generates a reward to the agent as a feedback for taking this action. In the offline network design stage of the WASAR algorithm, we leverage DRL [11] to optimize link weights and SR node deployment. Specifically, the definition of three factors: state, action and reward, are provided as follows.

state: In step t, state st is the link load state under TM Dt. We can compute the load on each link given the OSPF link weight and splitting ratio of SR nodes.

action: action at is the network link weight setting.

reward: reward rt is calculated according to Eqs. (7), (8), which means the more reduction of MLU, the larger reward rt is. To be specific, if the current MLU is greater than the initial MLU, then we should avoid taking this action and a negative reward is given. On the contrary, if the current MLU is smaller than the initial MLU, then we should encourage taking this action and a positive reward is given. Through the learning process, we intend to learn an optimal link weight setting that can maximize the reward function.

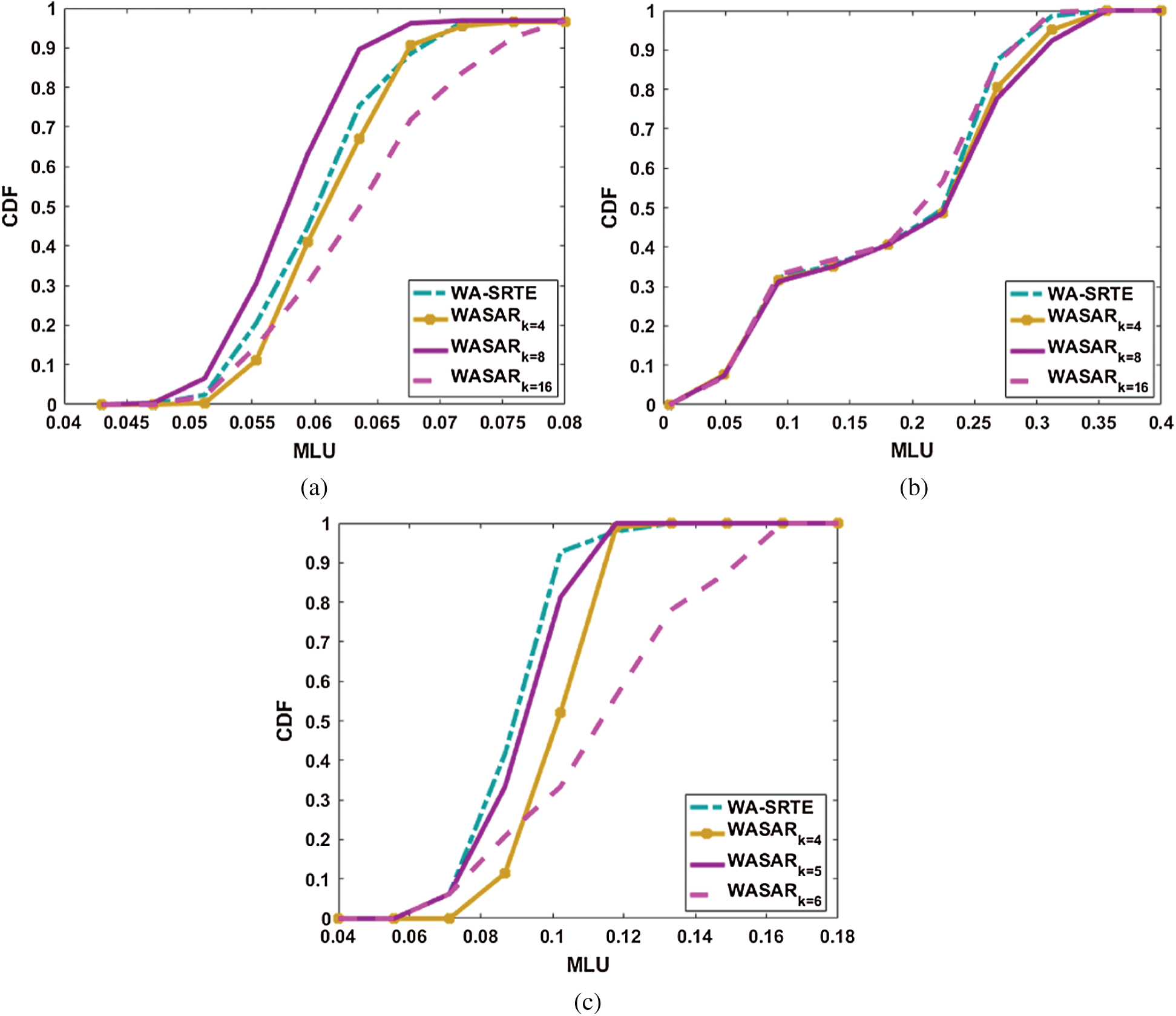
Figure 2:

In Algorithm 1, the pseudo code of WASAR algorithm in the offline network design phase is given. The input to the algorithm includes: network topology G=(V,E), initial link weight setting w0, the expected TM Dexp, and the theoretical optimal MLU MCFopt obtained by solving the multi-commodity flow problem. The output to the algorithm consists of OSPF link weight setting w, SR deployment scheme s and optimal MLU Umax.

(2) Online Flow Splitting Ratio Optimization: Given the optimized OSPF link weights, we begin the flow splitting ratio optimization for adapting to the dynamic traffic. For each new TM, when the OSPF link weight setting is determined, the available paths for each flow are determined and the original problem transforms into a multi-commodity flow problem, which is a LP problem. We solve the LP problem with a LP solver Gurobi for obtaining the optimal flow splitting ratio with the minimal Umax.

5  Evaluation

In this section, we conduct extensive experiments to demonstrate the superior performance of the algorithm WASAR. In the evaluation, we use python and keras to implement the WASAR algorithm. The experiments are conducted on a personal computer with 2.8GHz Intel CPU-core i7-7700HQ and 8GB memory. The offline weight optimization of WASAR trains the neural network with 100 episodes, 500 steps per episode. The first 80 episodes use OU process noise.

5.1 Dataset

(1) Topology information: In the experiment of this paper, the performance of WASAR algorithm is tested on three education network topologies: Abilene, CERNET and GEANT, respectively. The topology information is summarized in Tab. 2.

Table 2: Network topology information

(2) Traffic information: The TMs for the Abilene topology are given by TOTEM, the TMs for the CERNET topology are from Zhang et al. [27] and the TMs of GEANT topology are provided by Uhling [28]. The TMs for the first two topologies are measured every 5 min and the TMs for the third topology are measured every 15 min.

In the three topologies of Abilene, CERNET, and GEANT, we exploit the same initial link weight and link capacity for evaluation.

5.2 MLU Evaluation

In this part, we evaluate the TE performance of WASAR under the expected TM obtained using U-SPEC clustering algorithm. In [11], Tian et al. concluded that when the SR deployment ratio is ranging from 0.2 to 0.4 in a hybrid SR network, the network performance will be better. Therefore, we choose to record the MLU of WASAR when the SR deployment ratio is set to 0.2, 0.3, and 0.4, respectively. We compare with the algorithm WA-SRTE proposed in [11]. We plot the Cumulative Distribution Function (CDF) curves of MLU under different numbers of cluster centers with different deployment ratios of SR nodes in Figs. 1–3.

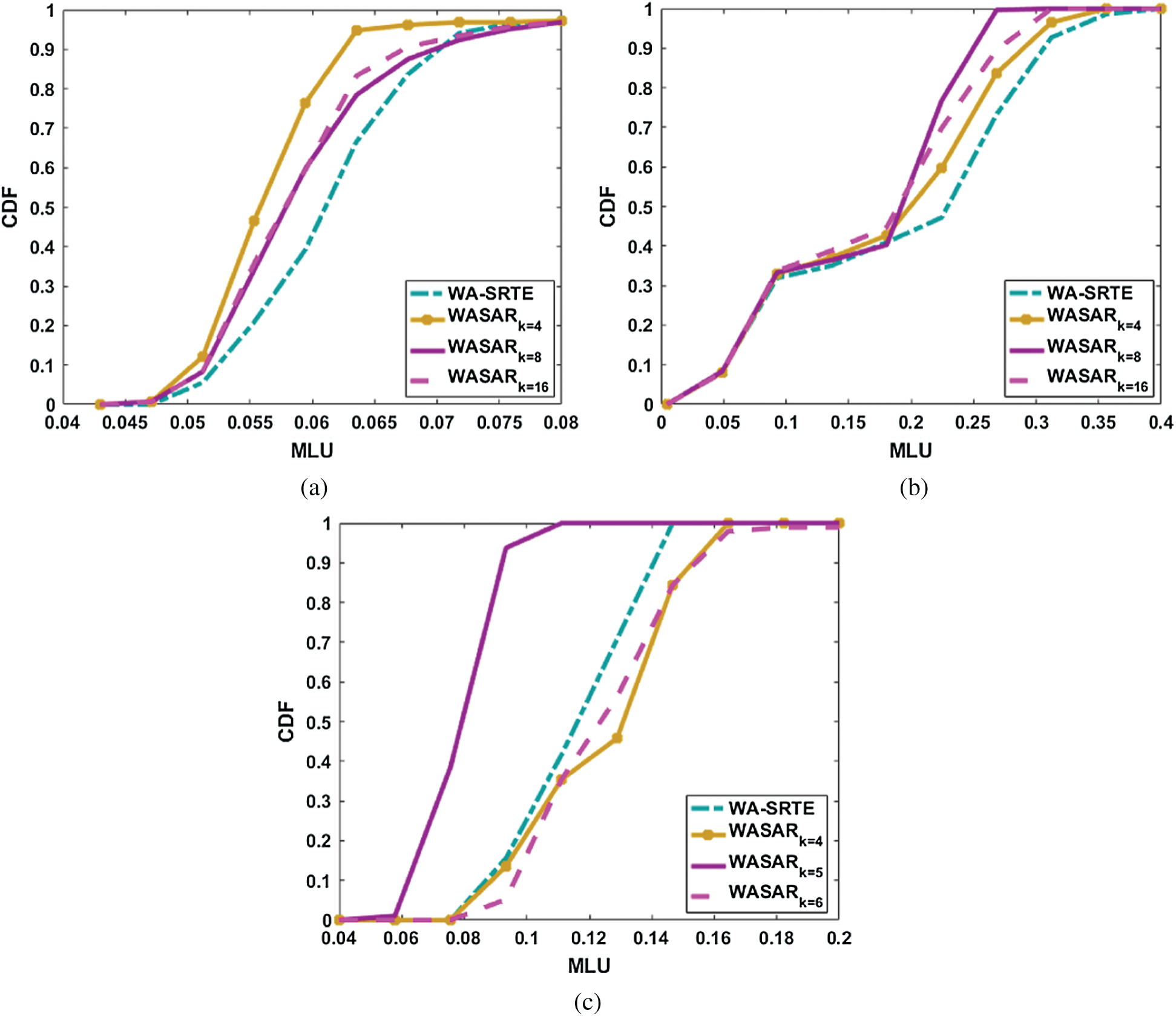
Figure 3: CDF curves of MLU under three topologies with the SR deployment ratio set to 0.2. (a) Abilene (b) CERENT (c) GEANT

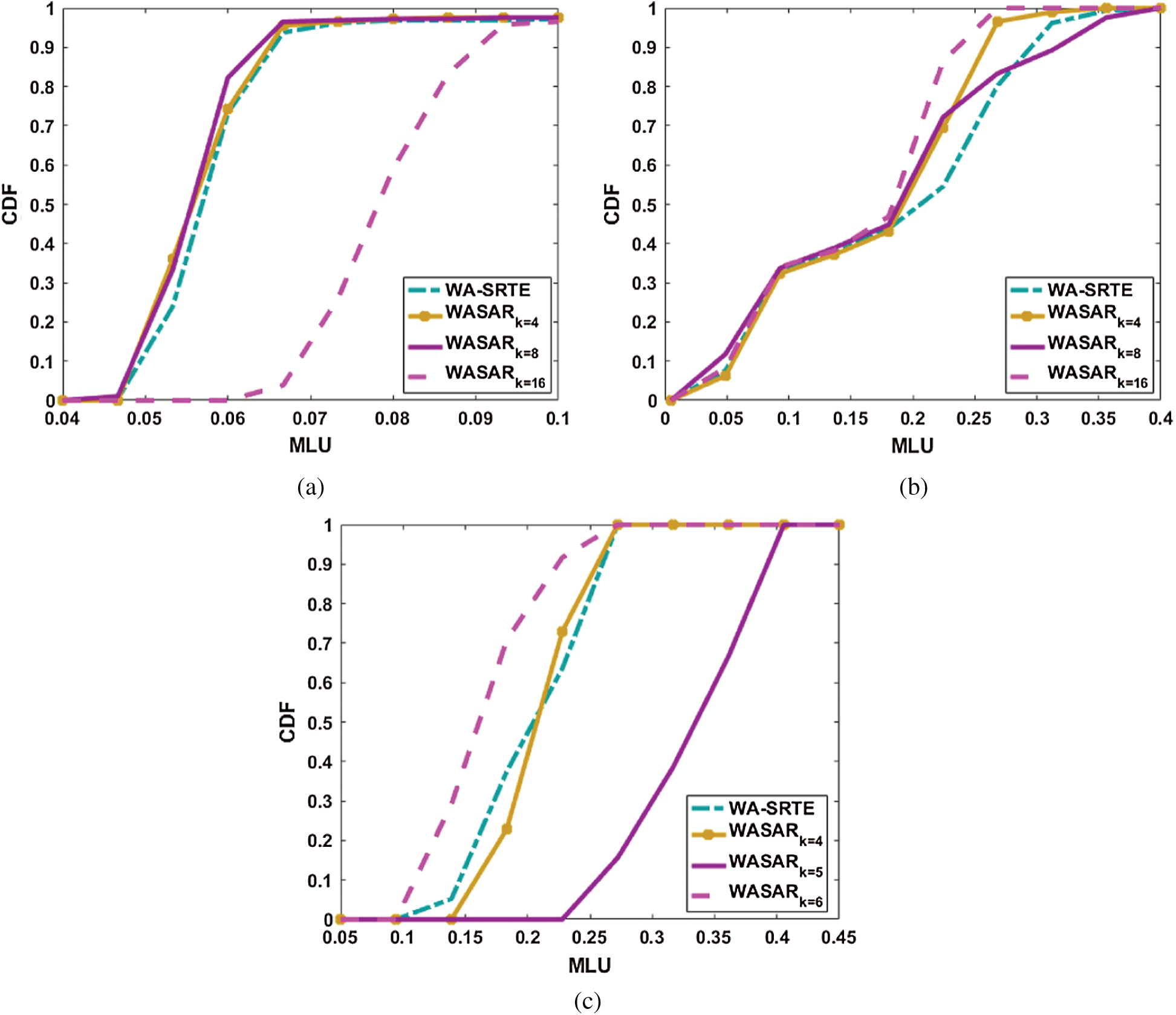
Figure 4: CDF curves of MLU under three topologies with the SR deployment ratio set to 0.3. (a) Abilene (b) CERENT (c) GEANT

As shown in Fig. 2, when the SR deployment ratio is set to 0.2, it can be seen that the MLU curves of WASAR vary under different network topologies and different number of clusters. In Abilene and CERNET topology, our proposed algorithm WASAR can obtain a lower MLU compared to WA-SRTE, when the cluster number is 8 and 16, respectively. We can observe that when the number of clusters is too small or too large, the characteristics of the representative TM will deviate from the expected value and the representative TM cannot better depict the changing traffic. In GEANT topology, the MLU under different cluster numbers of WASAR is a little higher than the MLU of WA-SRTE.

When the SR deployment rate is set to 0.3, as shown in Fig. 3, it can be observed that in Abilene, CERNET and GEANT topologies, our proposed algorithm WASAR can obtain a much lower MLU compared to WA-SRTE. At the same time, the superiority is particularly evident in Abilene and CERNET when k equals 4, 8,16 respectively. In GEANT, we can observe that the MLU of WASAR is lower than the MLU of WA-SRTE when the cluster number is 5. From the evaluation on different number of clusters, we can see that the MLU of WASAR has been greatly reduced, compared to the WA-SRTE algorithm. When the cluster number is 4 and 6, the MLU of WASAR is higher than the MLU of WA-SRTE. Similarly, it can be seen from Fig. 2c that if the number of clusters is set too large or too small, the expected TM cannot depict the variations of traffic and the TE performance will be influenced. Both the number of representative TMs and the expected TM in the weight optimization process have a great influence on the final experimental results. The experimental results demonstrate the superiority of the WASAR algorithm in minimizing the MLU of the hybrid SR network.

Similarly, when the SR deployment ratio is set to 0.4, as shown in Fig. 4, it can be observed that in Abilene, CERNET and GEANT, our proposed algorithm WASAR can obtain a much lower MLU compared to WA-SRTE. In Abilene, we can observe that the MLU of WASAR is lower than the MLU of WA-SRTE when the cluster numbers are set to 4 and 8. In CERNET, the MLU of WASAR is lower than the MLU of WA-SRTE when the cluster number are set to 4, 8 and 16, respectively. In GEANT, the MLU of WASAR is lower than the MLU of WA-SRTE when the cluster number is 6.

Figure 5: CDF curves of MLU under three topologies with the SR deployment ratio set to 0.4. (a) Abilene (b) CERENT (c) GEANT

In summary, we can observe that under different network topologies and deployment ratios, our proposed algorithm WASAR can obtain a much lower MLU compared to WA-SRTE. When the SR deployment ratio is set to 0.3, we can reap the most benefit. Moreover, it can be also observed from Fig. 2–4 that even the number of clusters changes slightly, the representative TMs and expected TM obtained through the clustering results changes. The routing optimized under different expected TMs varies significantly and the network performance is greatly influenced. Therefore, we can conclude that it is very important and necessary to obtain representative TMs and expected TM that can better depict the dynamic traffic.

5.3 Computation Time

Finally, we record the computation time of WASAR in three different topologies. We set the SR deployment ratio in the three topologies of Abilene, CERNET and GEANT to 0.3 (optimal case). All calculation time is shown in Tab. 3. The first column is the network topology, the second column is the time spent in the offline OSPF link weight optimization, and the third column is the time spent on online computation of flow splitting ratio for SR centralized nodes under various TMs.

Table 3: Computation time

As shown in Tab. 3, it can be observed that the time spent in the offline OSPF link weight optimization phase accounts for most of the running time. Since the OSPF link weight optimization is an offline process, a longer computation time is acceptable. The time spent on online routing optimization is very short and almost negligible compared to the time spent in the offline network design phase. The experiments in this paper are all carried out on a personal computer. If high-performance servers and GPU acceleration are used, the computation time will be further reduced.

6  Conclusion

This paper studies the TE problem in a hybrid SR network, which is formed by a partially deployment of SR nodes in a traditional IP network. We propose a novel TE algorithm WASAR to minimize the MLU of the hybrid SR network under the dynamic traffic, thus improving the network performance. Specially, we cluster the historical TMs to obtain representative TMs and the expected TM that reflects the average case of dynamic traffic based on U-SPEC. Then, for accommodating to the dynamic traffic, we optimize the link weight setting under OSPF using DRL and optimize flow splitting ratio through centralized nodes by solving LP problem. Experimental results show that the WASAR algorithm has superior performance in improving network performance under different network topologies and dynamic traffic. In addition, extensive experiments have demonstrated that for the routing optimization in a hybrid SR network, it is important to obtain the representative TMs and the expected TM used for link weight optimization under distributed routing protocols. In the future, we will consider implementing the algorithm in a centralized controller and running it in a practical hybrid SR network.

Funding Statement: This work is partially supported by the Educational Research Project for Young and Middle-aged Teachers of Fujian Education Department under Grant No. JAT190027, Fuzhou University Fund No. GXRC-19062, National Natural Science Foundation of China under Grant No. 62002064 and No. 61802092, the Science and Technology Planning Project of Guangzhou under Grant 202002030239.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Fortz, J. Rexford and M. Thorup. (2002). “Traffic engineering with traditional IP routing protocols,” IEEE Communications Magazine, vol. 40, no. 10, pp. 118–124. [Google Scholar]

 2.  C. Filsfils, N. K. Nainar, C. Pignataro, J. C. Cardona and P. Francois. (2015). “The segment routing architecture,” in Proc. GLOBECOM, San Diego, CA, USA, pp. 1–6. [Google Scholar]

 3.  X. P. Xiao, A. Hannan, B. Bailey and L. M. Ni. (2000). “Traffic engineering with MPLS in the Internet,” IEEE Network, vol. 14, no. 2, pp. 28–33. [Google Scholar]

 4.  D. Huang, C. Wang, J. Wu, J. Lai and C. Kwoh. (2020). “Ultra-scalable spectral clustering and ensemble clustering,” IEEE Transactions on Knowledge and Data Engineering, vol. 32, no. 6, pp. 1212–1226. [Google Scholar]

 5.  F. Bernard and M. Thorup. (2004). “Increasing internet capacity using local search,” Computational Optimization and Applications, vol. 29, no. 1, pp. 13–48. [Google Scholar]

 6.  M. Ericsson, M. G. C. Resende and P. M. Pardalos. (2002). “A genetic algorithm for the weight setting problem in OSPF routing,” Journal of Combinatorial Optimization, vol. 6, no. 3, pp. 299–333. [Google Scholar]

 7.  Y. Y. Guo, Z. L. Wang, X. Yin, X. G. Shi and J. P. Wu. (2014). “Traffic engineering in SDN/OSPF hybrid network,” in Proc. ICNP, North Carolina, NC, USA, pp. 563–568. [Google Scholar]

 8.  A. Sugam, M. Kodialam and T. V. Lakshman. (2013). “Traffic engineering in software defined networks,” in Proc. INFOCOM, Turin, Italy, pp. 2211–2219. [Google Scholar]

 9.  H. Geng, J. Yao and Y. Zhang. (2020). “Single failure routing protection algorithm in the hybrid SDN network,” Computers, Materials & Continua, vol. 64, no. 1, pp. 665–679. [Google Scholar]

10. A. Cianfrani, M. Listanti and M. Polverini. (2017). “Incremental deployment of segment routing into an ISP network: A Traffic engineering perspective,” IEEE/ACM Transactions on Networking, vol. 25, no. 5, pp. 3146–3160. [Google Scholar]

11. Y. Tian, Z. L. Wang, X. Yin, X. G. Shi, Y. Y. Guo et al. (2020). , “Traffic engineering in partially deployed segment routing over IPv6 network with deep reinforcement learning,” IEEE/ACM Transactions on Networking, vol. 28, no. 4, pp. 1573–1586. [Google Scholar]

12. K. Arulkumaran, M. P. Deisenroth, M. Brundage and A. A. Bharath. (2017). “Deep reinforcement learning: A brief survey,” IEEE Signal Processing Magazine, vol. 34, no. 6, pp. 26–38. [Google Scholar]

13. V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness et al. (2015). “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533. [Google Scholar]

14. W. Fang, L. Pang and W. N. Yi. (2020). “Survey on the application of deep reinforcement learning in image processing,” Journal on Artificial Intelligence, vol. 2, no. 1, pp. 39–58. [Google Scholar]

15. A. Zhang, B. Li, W. Wang, S. Wan and W. Chen. (2020). “Mii: A novel text classification model combining deep active learning with BERT,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1499–1514. [Google Scholar]

16. A. Likas, N. Vlassis and J. J. Verbeek. (2003). “The global k-means clustering algorithm,” Pattern Recognition, vol. 36, no. 2, pp. 451–461. [Google Scholar]

17. A. Maamar and K. Benahmed. (2019). “A hybrid model for anomalies detection in ami system combining k-means clustering and deep neural network,” Computers, Materials & Continua, vol. 60, no. 1, pp. 15–40. [Google Scholar]

18. A. A. Ahmed and B. Akay. (2019). “A survey and systematic categorization of parallel k-means and fuzzy-c-means algorithms,” Computer Systems Science and Engineering, vol. 34, no. 5, pp. 259–281. [Google Scholar]

19. A. A. M. Jamel and B. Akay. (2020). “Human activity recognition based on parallel approximation kernel k-means algorithm,” Computer Systems Science and Engineering, vol. 35, no. 6, pp. 441–456. [Google Scholar]

20. Y. J. Xu, W. Y. Qu, Z. Y. Li, G. Y. Min, K. Q. Li et al. (2014). , “Efficient k-Means++ approximation with MapReduce,” IEEE Transactions on Parallel and Distributed Systems, vol. 25, no. 12, pp. 3135–3144. [Google Scholar]

21. G. Hamerly and C. Elkan. (2004). “Learning the k in k-means,” in Proc. NIPS, San Diego, CA, USA, pp. 281–288. [Google Scholar]

22. D. Sculley. (2010). “Web-scale k-means clustering,” in Proc. WWW, New York, NY, USA, pp. 1177–1178. [Google Scholar]

23. N. Garg and J. Koenemann. (2007). “Faster and simpler algorithms for multicommodity flow and other fractional packing problems,” SIAM Journal on Computing, vol. 37, no. 2, pp. 630–652. [Google Scholar]

24. B. Fortz and M. Thorup. (2004). “Increasing internet capacity using local search,” Computational Optimization and Applications, vol. 29, no. 1, pp. 13–48. [Google Scholar]

25. H. Luo, C. Wang, Y. Q. Wen and W. Z. Guo. (2019). “3-D object classification in heterogeneous point clouds via bag-of-words and joint distribution adaption,” IEEE Geoscience and Remote Sensing Letters, vol. 16, no. 12, pp. 1909–1913. [Google Scholar]

26. H. Luo, C. Wang, C. L. Wen, Z. Y. Chen, D. W. Zai et al. (2018). , “Semantic labeling of mobile LiDAR point clouds via active learning and higher order MRF,” IEEE Transactions on Geoscience and Remote Sensing, vol. 56, no. 7, pp. 3631–3644. [Google Scholar]

27. B. Zhang, J. Bi, J. Wu and F. Baker. (2014). “CTE: Cost-effective intra-domain traffic engineering,” in Proc. SIGCOMM, Chicago, Illinois, USA, pp. 115–116. [Google Scholar]

28. S. Uhlig, B. Quoitin, J. Lepropre and S. Balon. (2006). “Providing public intradomain traffic matrices to the research community,” in Proc. SIGCOMM, Pisa, Italy, pp. 83–86. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.