DOI:10.32604/cmc.2021.015998

| Computers, Materials & Continua DOI:10.32604/cmc.2021.015998 |  |
| Article |
Deep Learning Enabled Autoencoder Architecture for Collaborative Filtering Recommendation in IoT Environment
College of Computer Engineering and Sciences, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
*Corresponding Author: Thavavel Vaiyapuri. Email: t.thangam@psau.edu.sa
Received: 17 December 2020; Accepted: 26 January 2021
Abstract: The era of the Internet of things (IoT) has marked a continued exploration of applications and services that can make people’s lives more convenient than ever before. However, the exploration of IoT services also means that people face unprecedented difficulties in spontaneously selecting the most appropriate services. Thus, there is a paramount need for a recommendation system that can help improve the experience of the users of IoT services to ensure the best quality of service. Most of the existing techniques—including collaborative filtering (CF), which is most widely adopted when building recommendation systems—suffer from rating sparsity and cold-start problems, preventing them from providing high quality recommendations. Inspired by the great success of deep learning in a wide range of fields, this work introduces a deep-learning-enabled autoencoder architecture to overcome the setbacks of CF recommendations. The proposed deep learning model is designed as a hybrid architecture with three key networks, namely autoencoder (AE), multilayered perceptron (MLP), and generalized matrix factorization (GMF). The model employs two AE networks to learn deep latent feature representations of users and items respectively and in parallel. Next, MLP and GMF networks are employed to model the linear and non-linear user-item interactions respectively with the extracted latent user and item features. Finally, the rating prediction is performed based on the idea of ensemble learning by fusing the output of the GMF and MLP networks. We conducted extensive experiments on two benchmark datasets, MoiveLens100K and MovieLens1M, using four standard evaluation metrics. Ablation experiments were conducted to confirm the validity of the proposed model and the contribution of each of its components in achieving better recommendation performance. Comparative analyses were also carried out to demonstrate the potential of the proposed model in gaining better accuracy than the existing CF methods with resistance to rating sparsity and cold-start problems.
Keywords: Neural collaborative filtering; cold-start problem; data sparsity; multilayer perception; generalized matrix factorization; autoencoder; deep learning; ensemble learning; top-K recommendations
The IoT is a new communication paradigm that digitizes the real-world environment by interconnecting vast number of smart objects and systems using Internet infrastructure. In this process, the networked smart objects can sense and generate large volume of useful data about their surroundings specifically about the product performance or customer usage patterns [1]. The data generated in the context of IoT brings excellent capability in supporting the development of value-added services and smart applications. The notion of IoT is to create a smart environment that can enable global exchange and delivery of intelligent services to improve the quality of daily life [2]. From the industry perspective, the IoT is expected to facilitate the businesses in optimizing their productivity and achieving their goals [3].
It is forecasted by Gartner that by 2021, the number of connected devices in the IoT will reach 25 billion. SAP predicts that this number will reach 50 billion by 2023. According to research by McKinsey Global, the number of connected IoT devices is set to exceed between $4 and $11 trillion in economic impact [4]. As a result, there is a general belief that the IoT will become an important source of contextual information and be ubiquitous in satisfying users’ needs through a multitude of services. Nevertheless, when users are swamped with information and offered a plethora of services, they face unprecedented difficulty in making the right decision when spontaneously selecting the desired information and appropriate services. This leads to the phenomenon called the information overload problem [5–7]. In this sense, it is of paramount importance to deploy flexible information systems that can extract effectively and efficiently valuable information from massive amounts of data. To this end, in recent years, recommender systems have been considered instrumental in alleviating the problem of information overload by effectively assisting the users in finding the potential products or services that meet their needs and match their interests from a large pool of possible options [8]. With such an indispensable role in online information systems, recommendation systems are widely recognized in many fields and have become an animated topic of research [9].
The literature has discussed two kinds of recommendation algorithm: collaborative filtering (CF) and content-based (CB) [10]. CB algorithms make recommendations based on the similarities between the item description and the user preferences. This approach ignores the relationship between items and suffers from a serendipity problem, providing recommendations with limited novelty. As a result, the effectiveness and extensibility of the system is limited [11]. Comparatively, CF algorithms are successful and are the most popular approach in many recommender systems because they make recommendations based on user interactions with items and other users with similar preferences. CF offers many advantages, such as being content-independent and efficient in providing serendipitous recommendations. Also, by considering only real quality measurements, CF is effective at providing recommendations [12].
Among various CF techniques, matrix factorization (MF) and its variants are more effective and most widely used in practice [13]. MF maps both users and items onto a shared latent space and uses the inner product of the latent vectors to model the user interaction on an item. Despite the appeal of MF, it is well known that their effective performance is hindered by three serious problems: Rating sparsity, cold-start problems, and their linear nature. Rating sparsity occurs when there is very little available rating data. A cold start occurs when making a recommendation with no prior interaction data for a user or an item. Due to its linear nature, MF fails to capture complex interactions between users and items [14].
Recently, the application of deep learning models in recommendation systems has made breakthroughs [15,16]. Several research studies in the literature have leveraged the roaring success of deep learning to change the linear structure of MF and have demonstrated the powerful ability of deep learning to gain satisfactory results [17,18]. A neural CF (NCF) was introduced [19] exploiting the benefits of MLP to capture non-linear user-item interactions. Here, the authors combine MF and MLP networks and build a new neural-based MF (NeuMF) that can capture linear and non-linear user-item interactions. Similarly, Chen et al. [20] adopted a non-sampling strategy through mathematical reasoning to learn neural recommendation models. Here, the adopted strategy proved its efficiency in learning the model parameters with reduced time complexity. However, the developed model was not validated for its effectiveness against data sparsity and cold-start problems. Recently, Thanh et al. [21] presented a DNN model called FeaNMF to improve the predictive accuracy of NCF incorporating user latent and auxiliary features. Wang et al. [22] constructed a hybrid architecture to improve predictive accuracy by combining two different kinds of neural network model, AE and MLP, to extract the latent feature vector from rating data and to describe the user-item interactions, respectively. Wan et al. [23] proposed a new continuous imputation denoising AE model and combined the new model with NCF to alleviate the data sparsity problem. Likewise, a neural-network-based CF model called a deep dual relation network (DRNet) was proposed for recommendations [24]. Unlike the previous literature, the present model captures both item–item and user-item interactions to improve the quality of the recommendation performance. Despite the success of existing models, there are still opportunities to improve the quality of recommendations.
Most of the existing NCF and NeuMF methods focus on user-item interactions and show promise in effectively learning the robust latent feature representations. However, they do not aim to extract key latent features from users and items individually. Consequently, this not only affects the feature representation of users and items but could also affect the user-item interactions. Notably, the benefits of stacked sparse autoencoder (SSAE) can be leveraged to address the setbacks of NCF. In the proposed architecture, two separate SSAE networks are employed to extract the latent features of users and items, respectively, from the implicit rating data. Then, the resulting latent features are used as an input for the two different NCF models, GMF and MLP, to capture the complex user-item interactions. The key contributions of this work are as follows:
a) Proposed model integrates SSAE within NCF framework to effectively mitigate the rating sparsity problem. Also, to overcome the possibility of overfitting and improve the accuracy of the rating prediction.
b) Proposed model effectively captures both linear and non-linear interactions between users and items employing two different NCF networks, GMF and MLP respectively.
c) Proposed model is designed to use only implicit rating data as they are comparatively easier to collect for service provider.
2.1 Neural Collaborative Filtering (NCF)
NCF is an extended version of a traditional CF model. Here, the power of neural networks is leveraged to learn and model intricate user-item interactions with multiple levels of abstraction. The general architecture of NCF consists of an input layer with a sparse user and item feature vector and a feature embedding layer to project the sparse input representations onto a dense feature vector. The obtained user and item embeddings are combined and fed through a multi-layer neural architecture for the CF process. In this process, the user and item embeddings are mapped to determine the prediction score. Here, the layers participating in CF can be customized to uncover intricate user-item interactions. Thus, the CF process through MLP is defined as follows:
In the above equation,
A simple AE comprises three layers: input, hidden, and output, as shown in Fig. 1. It aims to reconstruct the original input at its output layer. The learning process of an AE consists of two stages: Encoding and decoding [25]. On the one hand, the encoding stage uses the activation function a parameterized
On the other hand, the decoding stage uses the activation function
During the training process, the AE is trained to learn the parameter set
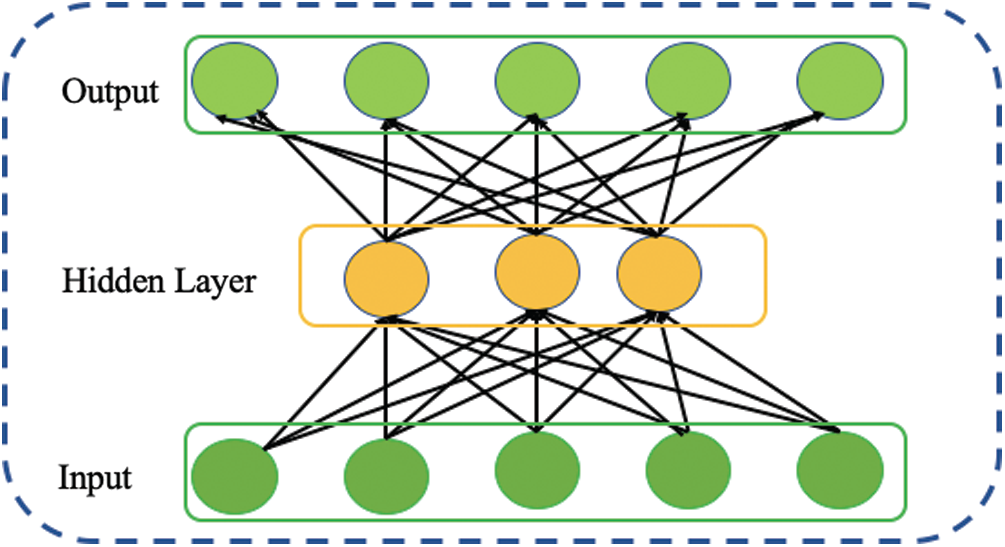
Figure 1: Structure of autoencoder network
This section presents the hybrid deep-learning-enabled AE architecture proposed for rating prediction. As shown in Fig. 2, the architecture comprises three different kinds of neural network: AE, GMF, and MLP. The proposed architecture contains two AE networks with parallel structures to learn the latent representation of users and items separately from implicit rating data. Then, the resulting latent user and item features are fed into the two instantiations of NCF, namely GMF and MLP networks, to learn user-item interactions. Finally, the output of GMF and MLP is fused through ensemble learning to generate the rating prediction. The superior quality of this architecture is that it introduces AE for the first time into the NCF framework to not only extract the primary latent features of users and items but also to alleviate the data sparsity problem. Moreover, it effectively enables the complex interactions between users and items to be captured through the ensembles of GMF and MLP to gain better prediction performance. The subsections that follow detail the working principles of the proposed architecture.

Figure 2: Proposed deep learning enabled autoencoder architecture for NCF
Given M users and N items, the user ID set is denoted by
These rating scores given by users are used to represent the feature vector for user and item. For item i, the feature vector Ii is represented as follows, using the rating scores of all users:
Similarly, the feature vector Uu is represented as follows, using the rating score of user u for all the involved items:
Here, the dimension of Uu and Ii are different because the dimensions M and N are usually unequal. As in [23,24], the present work attempts to employ minimal information, using only user ratings to achieve better rating prediction performance.
3.2 Feature Extraction Using Stacked Sparse Autoencoder (SSAE)
Motivated by recent successes of deep learning for better feature generalization, this work employs a sparse autoencoder (SAE), a variant of AE proposed in [26]. The idea behind SAE is to impose a sparsity constraint on the core idea of AE to learn the sparse features from user and item feature vectors. In essence, SAE considers a neuron in a hidden layer to be active if its activation value is close to 1; else, it considers the neuron to be inactive. Accordingly, a hidden layer becomes sparse when most neurons are inactive. Thus, the act of imposing a sparse constraint on a hidden layer, as shown in Fig. 3, restricts undesired activation and encourages SAE to learn sparse features at the level of its hidden representation.

Figure 3: Structure of sparse autoencoder (left) and stacked autoencoder (right)
Accounting for the sparsity constraint, the cost function of AE defined in Eq. (5) is then redefined with a sparsity term for SAE, as follows:
The sparsity constraint
3.3 Feature Fusion Using Generalized Neural Matrix Factorization (GMF)
GMF, which is regarded as an extension of MF under NCF, is utilized in the proposed framework to learn user-item interactions. Nonetheless, to address the data sparsity limitation of the GMF network, in the proposed framework, the latent feature vectors extracted by SSAE for the user and item undergo a CF process, as follows:
where pu and qi represent the user and item latent feature vectors generated by SSAE, respectively. Also,
In the above equation,
3.4 Feature Fusion Using Multi-Layer Perceptron (MLP)
The proposed framework employs MLP to deeply learn the critical interactions between the user and item latent feature vectors. In this first step, the latent feature vectors of users and items extracted from SSAE are concatenated and then employed in CF as follows:
The computation process of each hidden layer can be defined as follows:
Here, aL, wL and bL denote the activation function, bias vector, and weight matrix of the Lth hidden layer respectively; the [
In this work, ReLU is used as a hidden layer activation function for MLP for two reasons. First, it encourages sparse activations; second, it prevents the model from overfitting. Because the objective of the MLP model employed here is to capture the critical interaction between user and item vectors, the MLP network is designed as in [19] to follow a tower pattern with three layers. Unlike other NCF models [19,23,24], the GMF and MLP employed in this work captures the linear and non-linear interactions from latent feature vectors generated by SSAEs for users and items to achieve better performance rather being limited due to the sparsity of user preferences.
3.5 Ensemble Learning for Rating Prediction
The two models described above, GMF and MLP, which capture user-item interactions by employing linear and non-linear kernels respectively, are ensembled by concatenating their last hidden layers. Following earlier studies [19,23,24], the ensemble formulation of the final output is defined as follows:
where w and a are the weight and activation function of the output layer, respectively. Here, a sigmoid is applied as an activation function.
The effectiveness of the proposed model was investigated by choosing two benchmark datasets published by the GroupLens research group, MovieLens100K and MovieLens1M. They are real-world datasets collected through a movie recommender system with different data sparsity percentages. The MovieLens100K dataset contains 943 users and 100,000 ratings on 1,682 movies, whereas the MovieLens1M dataset contains 6,040 users and 1,000,209 rating records on 3,952 movies. In these datasets, each user has rated at least 20 movies on a scale of 1 to 5, with a rating of 5 indicating that the user liked the movie more. There are also some movies with no ratings in the datasets. These movies were removed and the discontinuous movie serial numbers were preprocessed with successive serial numbers to produce rating records for 1,682 and 3,706 movies with data sparsities of 93.70% and 95.75% in MovieLens100K and MovieLens1M, respectively.
The statistics of these datasets are illustrated in Tab. 1. Because the datasets contain explicit user feedback, a strategy like that in [23,24] was adopted to obtain the implicit feedback, which ignores the rating values and retains only the rating as 0 or 1. Also, following the same experimental setup as that in [19–24], we chose to use 90% of the observed ratings to create the training set and the remaining 10% as the testing set. Further, 10% of the training set was used to create a validation set for all these datasets.
Table 1: Statistics of movielens datasets

Generally, the presence of a non-linear activation function in a neural network induces a non-convex optimization problem and easily traps the model to local optima during the learning process. This degrades the model’s performance. Intuitively, the initialization of network parameters gains paramount importance in improving the model’s performance. For instance, when we trained our model with random initialization, it converged slowly with poor performance. This might be attributed to the co-adaption effect of training the three networks—AE, GMF, and MLP—involved in the process of feature extraction and CF simultaneously. Hence, in agreement with earlier studies [19,24], we hypothesize that the pre-training process can resolve the co-adaption effect by initializing the network parameters close to the global optimal solution. We therefore adopted pre-training to initialize the network parameters of GMF and MLP. While pre-training these networks, the robust features learnt by Auto-I and Auto-U were employed. However, for networks such as Auto-I and Auto-U, greedy layer-wise pre-training was performed with tied weights and random initialization because they are not affected by the co-adaptation effect. Further, the Adam optimizer was used in the pre-training process of GMF and MLP. After the pre-training process, the proposed recommendation model was trained with a stochastic gradient descent optimizer for two reasons: first, to achieve better generalization; second, because the Adam update rule requires previous momentum but, in our case, it was unavailable because the network parameters of GMF and MLP were initialized through the pre-training process. A batch size of 256 and learning rate of 0.001 were adopted, considering the convergence rate and lower memory requirements for computing the gradients of the trainable parameters.
The proposed recommendation model was implemented as described in Section 3 using Python and Keras deep learning libraries, with TensorFlow as the backend. The hyperparameters of the proposed model are set by using a grid search on the training dataset and performing a 5-fold cross validation. The search space and obtained optimal values for the hyperparameters of the proposed model are presented in Tab. 2.
Table 2: Hyperparameter of proposed model

To sufficiently assess the effectiveness of the proposed model for recommendation performance, we chose four of the most commonly used evaluation metrics: Mean absolute error (MAE), root mean square error (RMSE), hit ratio (HR), and normalized discounted cumulative gain (NDCG). They are formulated as follows:
The first two metrics, MAE and RMSE, were chosen with the purpose of evaluating the rating effectiveness of the proposed model because they are the ones most widely used in past literature for CF evaluation. Further, the work uses HR and NDCG metrics to evaluate the performance of the proposed model in determining top-K ranked recommendation lists. HR indicates ranking accuracy by measuring whether the preferred items are listed in the top-K recommendation list of a user. Similarly, NDCG evaluates hit positions by assigning higher scores to the hits at the top of the ranking.
5 Experimental Results and Discussion
This section explains the two sets of analysis devised to validate the performance of the proposed recommendation model. In particular, these two sets of analysis were conducted to answer the following questions:
a) Is the integration of an AE network effective in improving the performance of the proposed model?
b) Does the proposed model perform better than the existing state-of-the-art CF models?
c) Does the proposed model perform better than the existing state-of-the-art CF models with resistance to data sparsity in terms of recommendation accuracy?
First, we conducted a series of ablation analysis experiments to validate the correctness of the proposed model design and to examine the contribution of different components in the proposed model for recommendation performance. To achieve this, we developed different variants of the proposed model, as detailed below:
a) GMF: This variant was created by removing the MLP network and fusion layer from the proposed model. Further, the SSAE networks were replaced with embedding layers to learn the user and item embeddings for CF. Thus, this variant receives the user and item latent features from the embedding layers to perform the element-wise product of the user and item latent features.
b) MLP: This variant was created by removing the GMF network and fusion layer from the proposed model. Further, the SSAE networks were replaced with embedding layers to learn the user and item embeddings for CF. Thus, this variant receives the user and item latent features from the embedding layers to learn the non-linear user-item relationships.
c) GMF
a) MLP++ : This variant was created by removing the GMF network and fusion layer from the proposed model. Thus, this variant utilizes the user and item latent features extracted from the SSAE networks to learn the non-linear user-item relationships.
b) I-Autorec: This variant was created by keeping only one SSAE network and removing all other components, such as the MLP and GMF networks. This variant uses the SSAE network to reconstruct item vectors and predict the missing ratings. It is proven in the literature that I-Autorec outperforms user-based AE [27,28].
c) NeuMF: This variant was created by replacing the SSAE networks in the proposed model with embedding layers to learn the user and item embeddings for CF.
To maintain a reasonable comparison, the same network parameters and experimental setup were utilized to create the above variants and to conduct the ablation experiments. The results of the ablation experiments on the MovieLens1M dataset are presented in Tab. 3. To improve interpretability, the results in Tab. 3 are depicted in a comparison plot in Fig. 4. The ablation results shown in Tab. 3 and Fig. 4 clearly indicate the contribution and importance of each component of the proposed model for improving its performance benefits. In particular, the variant I-Autorec delivered the worst performance, with high RMSE and MAE, indicating its failure to capture the user-item interactions, which is essential for improving recommendation performance. Next, observing the performance improvement of GMF++ and MLP++ over GMF and MLP respectively, it is clear that the AE significantly contributes to learning the robust user and item latent features required to enhance the CF process. Also, the variant NeuMF performed better than the variants GMF and MLP, in accordance with the findings reported in [24]. This illustrates the significant role of the fusion strategy in learning both linear and non-linear user-item interactions in CF. When comparing the performance of NeuMF with that of the proposed model, a significant performance improvement in the proposed model can be observed. This highlights the role of the AE network in ensuring overall improvement in recommendation performance. In sum, it is evident from these observations that all components in the proposed model play an essential role and contribute greatly to its success in improving recommendation performance.
Table 3: Ablation analysis on MovieLens1M for different variants of proposed model


Figure 4: A plot comparing the performance of different ablations of proposed model
5.2 Comparative Analysis with Related Works
Two sets of experiments were conducted to compare the effectiveness of the proposed model against existing state-of-the-art models. To do this, we considered three CF models based on fusion strategy—NeuMF, I-NMF, and DRNet—and two state-of-the-art, non-fusion CF models—eALS and BPR. The main reason for this is that, to our knowledge, there are few works in the literature that leverage the benefits of fusion strategies to learn user-item interactions, as we do in our work. Further, we used the results of the papers that do address this to perform a fair comparison. If the authors did not conduct a particular type of experiment and the results were not available, this was indicated with “NA.” To demonstrate the effectiveness of the proposed model, the comparison was conducted on two benchmark datasets, MovieLens100K and MovieLens1M, from two different perspectives, as follows:
In most real-world applications, the goal of recommendation system is to generate a personalized top-K ranked list of items for the target user based on rating predictions. We therefore conducted an experiment to compare the efficiency of the proposed model with existing state-of-the-art models for top-K recommendations. The experiment analyzes all chosen models for three different values of N
Table 4: Performance comparison of proposed model against related works for Top-K recommendations on MovieLens100K

Table 5: Performance comparison of proposed model against related works for Top-K recommendations on MovieLens1M


Figure 5: Performance comparison plot of top-K recommendations for proposed model against related works on MovieLens100K

Figure 6: Performance comparison plot of top-K recommendations for proposed model against related works on MovieLens1M
The results in Tabs. 5 and 6 show that the performance of all models improves with an increase in the value of N in terms of both the HR and NDCG metrics. Also, the comparison results indicate that the fusion models namely, NeuMF, DRNet, and the proposed model, except I-NMR, outperform the non-fusion models namely, eALS and BPR, in terms of both metrics on both datasets. These results indicate that the fusion models are effective at modeling user-item interactions, leveraging the benefits of neural networks. Among the fusion models, the proposed model performs better in terms of both metrics on both datasets. This demonstrates that the integration of an AE model within a NeuMF framework helps with learning the more robust user and item features that can enable significant improvement in the CF process. In particular, with the MovieLens100K dataset, the proposed model achieved an average of 2.7% and 4.6% relative improvement compared to the NeuMF model in terms of HR and NDCG, respectively. Similarly, with the MovieLens1M dataset, the proposed model achieved an average of 2.6% and 2.3% relative improvement compared to the NeuMF model in terms of HR and NDCG, respectively. Overall, these observations prove that the proposed model performs better than the existing models in improving the performance of Top-K recommendations in terms of HR and NDCG.
5.4 Data Sparsity Cold-Start Problem
In real-world scenarios, the user-item rating matrix is exceedingly sparse and gives rise to data sparsity problems that greatly affect the performance of recommendation system. To investigate the efficacy of the proposed model in mitigating the impact of this problem, a comparative analysis was conducted by arbitrarily removing some entries from the training set and creating a sparse matrix with four different densities. For example, a sparse user-item matrix with 20% data density was created, with 20% of the user-item entries used as the training set and the remaining 80% used as the testing set. Likewise, sparse user-item matrices with densities ranging from 20% to 80% were created. Here, if the data density or the training set proportion is high, the data sparsity is low, and vice versa.
Tab. 6 records the recommendation accuracy of the proposed model by comparing other existing state-of-the-art CF models in terms of HR@10 for different data sparsity levels using two different benchmark datasets. A plot of the same data is presented in Fig. 7 for improved interpretability. The horizontal comparison of the results through different data sparsity levels on both datasets indicate that the recommendation accuracy decreases as data sparsity increases, regardless of the recommendation model used. This confirms that data sparsity impacts the accuracy of all recommendation models. The vertical comparison of the results through different models on both datasets indicates that fusion models, such as NeuMF, DRNet, and the proposed model, perform better than non-fusion models namely eALS and BPR. Another notable observation is that the proposed model shows significant improvement over DRNet and NeuMF when the data sparsity level is higher than 60%. This might be because the AE enhances the CF process of NeuMF by learning the most robust user and item features from the given training set. The comparison results at different data sparsity levels show that CF process can be improved to have higher recommendation accuracy with resistance to data sparsity if an AE is used to learn the most robust user and item latent features.
Table 6: Performance comparison against related works with different level of data sparsity


Figure 7: Performance comparison plot of proposed model against related works for different percentage of data sparsity on MovieLens100K (left) and MovieLens1M (right)
This paper proposed a hybrid deep-learning-enabled AE architecture for an NCF-based recommendation model. This paper is the first to integrate the potency of an AE into the NCF framework. The advantage gained through this integration is that SAE allows rating sparsity and cold-start problems to be overcome by extracting the primary latent features of users and items from the rating matrix separately. Later, the extracted latent features are employed to enhance the learning capability of GMF and MLP networks to effectively model the linear and non-linear user-item interactions, respectively. Finally, the proposed model combines the strengths of GMF and MLP based on ensemble learning to improve the accuracy of recommendations. In addition, the proposed model is designed to gain accuracy based solely on implicit rating data. Ablation experiments confirmed that the design decision to integrate SAE within the NCF framework is beneficial for improving the recommendation performance of the proposed model. Also, the comparative analysis results conducted on two established datasets, MovieLens100K and MoiveLens1M, proved that the proposed model is effective in improving the accuracy of top-N recommendations with resistance to rating sparsity and cold-start problems when compared to the related NCF-based recommendation models.
The proposed architecture is limited to utilizing only implicit user feedback on items. Also, it is limited to perform online recommendation. Along this line, future work can take three different directions. First, it can investigate how different types of AEs can influence the performance gain in recommendation accuracy. Second, it can investigate how effectively the inclusion of auxiliary information can be utilized to better improve recommendation accuracy. Third, it can restructure the proposed model to better support online recommendation because it is of paramount importance in modern e-commerce applications.
Funding Statement: This project was supported by the deanship of Scientific Research at Prince Sattam Bin Abdulaziz University, Alkharj, Saudi Arabia through Research Proposal No. 2020/01/17215. Also, the author thanks Deanship of college of computer engineering and sciences for technical support provided to complete the project successfully.
Conflicts of Interest: The author declare that they have no conflicts of interest to report regarding the present study.
1. Y. Yang, J. Xu, Z. Xu, P. Zhou and T. Qiu. (2020). “Quantile context-aware social IoT service big data recommendation with D2D communication,” IEEE Internet of Things Journal, vol. 7, no. 6, pp. 5533–5548. [Google Scholar]
2. R. Kashef. (2020). “Enhancing the role of large-scale recommendation systems in the IoT context,” IEEE Access, vol. 8, pp. 178248–178257. [Google Scholar]
3. D. Kozma, P. Varga and F. Larrinaga. (2020). “Dynamic multilevel workflow management concept for industrial IoT systems,” IEEE Transactions on Automation Science and Engineering, pp. 1–13, early access. [Google Scholar]
4. G. Gyarmathy. (2020). “Comprehensive guide to IoT statistics you need to know in 2020,” . [Online]. Available: https://www.vxchnge.com/blog/iot-statistics. [Google Scholar]
5. J. Matthes, K. Karsay, D. Schmuck and A. Stevic. (2020). “Too much to handle: Impact of mobile social networking sites on information overload, depressive symptoms, and well-being,” Computers in Human Behavior, vol. 105, no. 5, pp. 106217. [Google Scholar]
6. N. Idrissi and A. Zellou. (2020). “A systematic literature review of sparsity issues in recommender systems,” Social Network Analysis and Mining, vol. 10, no. 1, pp. 15. [Google Scholar]
7. H. Chen and P. Chen. (2019). “Differentiating regularization weights–A simple mechanism to alleviate cold start in recommender systems,” ACM Transactions on Knowledge Discovery from Data, vol. 13, no. 1, pp. 1–22. [Google Scholar]
8. P. Kumar and R. S. Thakur. (2018). “Recommendation system techniques and related issues: A survey,” International Journal of Information Technology, vol. 10, no. 4, pp. 495–501. [Google Scholar]
9. M. Srifi, A. Oussous, A. Lahcen and S. Mouline. (2020). “Recommender systems based on collaborative filtering using review texts—A survey,” Information-an International Interdisciplinary Journal, vol. 11, no. 6, pp. 317. [Google Scholar]
10. H. Li and D. Han. (2020). “A novel time-aware hybrid recommendation scheme combining user feedback and collaborative filtering,” IEEE Systems Journal, vol. 2020, pp. 1–12, early access. [Google Scholar]
11. M. S. Almeida and A. Britto. (2020). MOEA-RS: A content-based recommendation system supported by a multi-objective evolutionary algorithm. In: ICAISC 2020, Lecture Notes in Computer Science. vol. 12416. Cham: Springer, pp. 265–276. [Google Scholar]
12. J. Chen, B. Wang, Z. Ouyang and Z. Wang. (2020). “Dynamic clustering collaborative filtering recommendation algorithm based on double-layer network,” International Journal of Machine Learning and Cybernetics, pp. 1–17. [Google Scholar]
13. R. Mehta and K. Rana. (2017). “A review on matrix factorization techniques in recommender systems,” in Proc. IEEE CSCITA, Mumbai, India, pp. 269–274. [Google Scholar]
14. R. Du, J. Lu and H. Cai. (2019). “Double regularization matrix factorization recommendation algorithm,” IEEE Access, vol. 7, pp. 139668–139677. [Google Scholar]
15. A. Singhal, P. Sinha and R. Pant. (2017). “Use of deep learning in modern recommendation system: A summary of recent works. arXiv preprint arXiv:1712.07525, . [Online]. Available: https://arxiv.org/abs/1712.07525. [Google Scholar]
16. Z. Batmaz, A. Yurekli, A. Bilge and C. Kaleli. (2019). “A review on deep learning for recommender systems: Challenges and remedies,” Artificial Intelligence Review, vol. 52, no. 1, pp. 1–37. [Google Scholar]
17. R. Lara-Cabrera, A. González-Prieto and F. Ortega. (2020). “Deep matrix factorization approach for collaborative filtering recommender systems,” Applied Sciences, vol. 10, no. 14, pp. 4926. [Google Scholar]
18. B. Yi, X. Shen, H. Liu, Z. Zhang, W. Zhang et al. (2019). , “Deep matrix factorization with implicit feedback embedding for recommendation system,” IEEE Transactions on Industrial Informatics, vol. 15, no. 8, pp. 4591–4601. [Google Scholar]
19. X. He, L. Liao, H. Zhang, L. Nie, X. Hu et al. (2017). , “Neural collaborative filtering,” in Proc. ICWWW, Perth, Australia, pp. 173–182. [Google Scholar]
20. C. Chen, M. Zhang, Y. Zhang, Y. Liu and S. Ma. (2020). “Efficient neural matrix factorization without sampling for recommendation,” ACM Transactions on Information Systems, vol. 38, no. 2, pp. 1–28. [Google Scholar]
21. T. H. Hoang, A. P. Tuan, L. N. Van and K. Than. (2019). “Enriching user representation in neural matrix factorization,” in Proc. IEEE-RIVF, Danang, Vietnam, pp. 1–6. [Google Scholar]
22. Q. Wang, B. Peng, X. Shi, T. Shang and M. Shang. (2019). “DCCR: Deep collaborative conjunctive recommender for rating prediction,” IEEE Access, vol. 7, pp. 60186–60198. [Google Scholar]
23. X. Wan, B. Zhang, G. Zou and F. Chang. (2019). “Sparse data recommendation by fusing continuous imputation denoising autoencoder and neural matrix factorization,” Applied Sciences, vol. 9, no. 1, pp. 54. [Google Scholar]
24. D. Ji, Z. Xiang and Y. Li. (2020). “Dual relations network for collaborative filtering,” IEEE Access, vol. 8, pp. 109747–109757. [Google Scholar]
25. T. Vaiyapuri and A. Binbusayyis. (2020). “Application of deep autoencoder as an one-class classifier for unsupervised network intrusion detection: A comparative evaluation,” PeerJ Computer Science, vol. 6, no. 1, pp. e327. [Google Scholar]
26. M. A. Ranzato, C. Poultney, S. Chopra and Y. Cun. (2006). “Efficient learning of sparse representations with an energy-based model,” Advances in Neural Information Processing Systems, vol. 19, pp. 1137–1144. [Google Scholar]
27. X. He, H. Zhang, M. Y. Kan and T. S. Chua. (2016). “Fast matrix actorization for online recommendation with implicit feedback,” in Proc. ACM SIGIR, Pisa, Italy, pp. 549–558. [Google Scholar]
28. S. Rendle, C. Freudenthaler, Z. Gantner and L. Schmidt-Thieme. (2012). “BPR: Bayesian personalized ranking from implicit feedback. arXiv preprint arXiv: 1205.2618, . [Online]. Available: https://arxiv.org/abs/1205.2618. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |