Computers, Materials & Continua DOI:10.32604/cmc.2021.015590
Article

Colouring of COVID-19 Affected Region Based on Fuzzy Directed Graphs

Rupkumar Mahapatra1, Sovan Samanta2, Madhumangal Pal1, Jeong-Gon Lee3,*, Shah Khalid Khan4, Usman Naseem5 and Robin Singh Bhadoria6

1Department of Applied Mathematics with Oceanology and Computer Programming, Vidyasagar University, Midnapore, 721102, India
2Department of Mathematics, Tamralipta Mahavidyalaya, Tamluk, 721636, India
3Division of Applied Mathematics, Wonkwang University, Iksan-Si, Jeonbuk, 54538, Korea
4School of Engineering, RMIT University, Melbourne, 3001, Australia
5School of Computer Science, University of Sydney Sydney, 2006, Australia
6Department of Computer Science & Engineering, Birla Institute of Applied Sciences (BIAS), Bhimtal, Uttarakhand, 263136, India
*Corresponding Author: Jeong-Gon Lee. Email: jukolee@wku.ac.kr
Received: 29 November 2020; Accepted: 08 February 2021

Abstract: Graph colouring is the system of assigning a colour to each vertex of a graph. It is done in such a way that adjacent vertices do not have equal colour. It is fundamental in graph theory. It is often used to solve real-world problems like traffic light signalling, map colouring, scheduling, etc. Nowadays, social networks are prevalent systems in our life. Here, the users are considered as vertices, and their connections/interactions are taken as edges. Some users follow other popular users’ profiles in these networks, and some don’t, but those non-followers are connected directly to the popular profiles. That means, along with traditional relationship (information flowing), there is another relation among them. It depends on the domination of the relationship between the nodes. This type of situation can be modelled as a directed fuzzy graph. In the colouring of fuzzy graph theory, edge membership plays a vital role. Edge membership is a representation of flowing information between end nodes of the edge. Apart from the communication relationship, there may be some other factors like domination in relation. This influence of power is captured here. In this article, the colouring of directed fuzzy graphs is defined based on the influence of relationship. Along with this, the chromatic number and strong chromatic number are provided, and related properties are investigated. An application regarding COVID-19 infection is presented using the colouring of directed fuzzy graphs.

Keywords: Graph colouring; chromatic index; directed fuzzy graphs

1  Introduction

The best way to represent the relations/links among objects is graphs. Edges in crisp graphs represent the linkage between two objects, but edges in fuzzy graphs measure the degree of connectedness by using some membership values varying from [0, 1]. Kaufmann [1] introduced the fuzzy graph in 1973, and Rosenfeld [2] developed it in 1975. Samanta et al. [3,4] proposed various types of fuzzy graphs and its applications. When representing some particular types of social networks, directed graphs are more relevant than undirected graphs. For example, on Twitter, some users are following some selected popular users. Here, users are considered as nodes of graphs. Here, if two users are just connected in the network, there exists an undirected edge. Again, if one user is following another, there exists a directed edge. So, these networks can be designed by a directed graph. Thus both types of edges occur in a graph simultaneously. The measure of influences is captured/calculated only by fuzzy membership values. Today, COVID-19 [5] is the most significant problem in the world. WHO declared COVID-19 outbreak as a world health emergency on 30th January 2020 [6–8]. They first detected this virus in Wuhan, China, in December 2019. After that, this virus spread globally. Within April 2020, almost all the countries were affected by this virus. Here, all the countries are considered as nodes of networks, and there exists a directed edge between two countries if one country is affected by the virus carried from another country. So, we get a directed graph [9]. The amount of influence can also be measured by some membership value. In this study, we are going to introduce a new class of fuzzy graph.

Graph colouring is one of the oldest problems. Samanta et al. [10] introduced fuzzy colouring in fuzzy graphs. Hansen et al. [11] and Sotskov et al. [12] introduced the mixed graph colouring. Mahapatra et al. [13–23] introduced the edge colouring of a fuzzy graph and radio k colouring in fuzzy graphs. In this article, the colouring of directed fuzzy graphs is also proposed.

2  Preliminaries

Definition 1 A fuzzy graph [1] ζ=(V,σ,μ) is a non-empty set V together with a pair of functions σ:V→[0,1] andμ:V×V→[0,1] such that for all x,y∈V, μ(x,y)≤min{σ(x),σ(y)}, where σ(x) and μ(x,y) represent the membership values of the vertex x and of the edge (x, y) in ζ respectively.

The effectiveness of an edge (a, b) is defined by I(a,b)=μ(a,b)min{σ(x),σ(y)}.

Samanta et al. [10] defined fuzzy colours as the mixing of colours as follows

Definition 2 Let’s assume W={w1,w2,…,wλ},λ≥1 is the set of basic colours. Then the fuzzy set (W,h)whereh:W→(0,1] may be called the set of fuzzy colours such that 0<h(wi)≤1, the membership value of the colour wi, is the amount of wi per unit of the mixture of wi with white colour.

Definition 3 ξ=(V,σ,μ,E→) is said to be a directed fuzzy graph, where V is a non-empty set, and σ:V→[0,1] is the membership function for vertices and μ:E→→[0,1] is the membership function for edges, E→ is the set of all directed edges, such that μ(a,b)≤σ(a)∧σ(b), where σ(a) denotes the vertex membership value of vertex a and μ(a,b) denotes the edge membership value of the edge (a, b) in ξ.

2.1 Some Basic Notations

Some basic notations are shown in Tab. 1.

Table 1: Some basic notations

3  Measure of Influence of a Directed Fuzzy Graph

Sometimes two nodes of a network are connected by an edge, and their relationship may not be useful, but the amount of influence is significant. For example, the relationship between a student and a teacher may not always be good. Still, the student is influenced by the teacher. This concept is used here to measure the amount of influence. Now, we are introducing the term “the measure of influence” which can be used to measure the amount of influence between two vertices of a directed fuzzy graph. It can be formally defined In the following way:

Definition 4 Let’s assume V is a non-empty set. ξ=(V,σ,μ,E→) is a fuzzy directed graph. Then the measure of influence between two vertices a, b is denoted by ϕ→(a,b) and is defined by ϕ→(a,b)≤|σ(a)-σ(b)|.

Example 1 Fig. 1, shows a directed fuzzy graph and V={a,b,c,d,e,f} is the vertex set. Now, the vertices membership values are considered in Tab. 2, and the edge membership values are considered in Tab. 3. The amount of influence between two vertices is ϕ→(a,b)≤0.6, ϕ→(d,b)≤0.6, ϕ→(b,e)≤0.3, ϕ→(e,f)≤0.2, ϕ→(c,b)≤0.1, ϕ→(a,e)≤0.3, ϕ→(c,d)≤0.5, ϕ→(d,e)≤0.3.

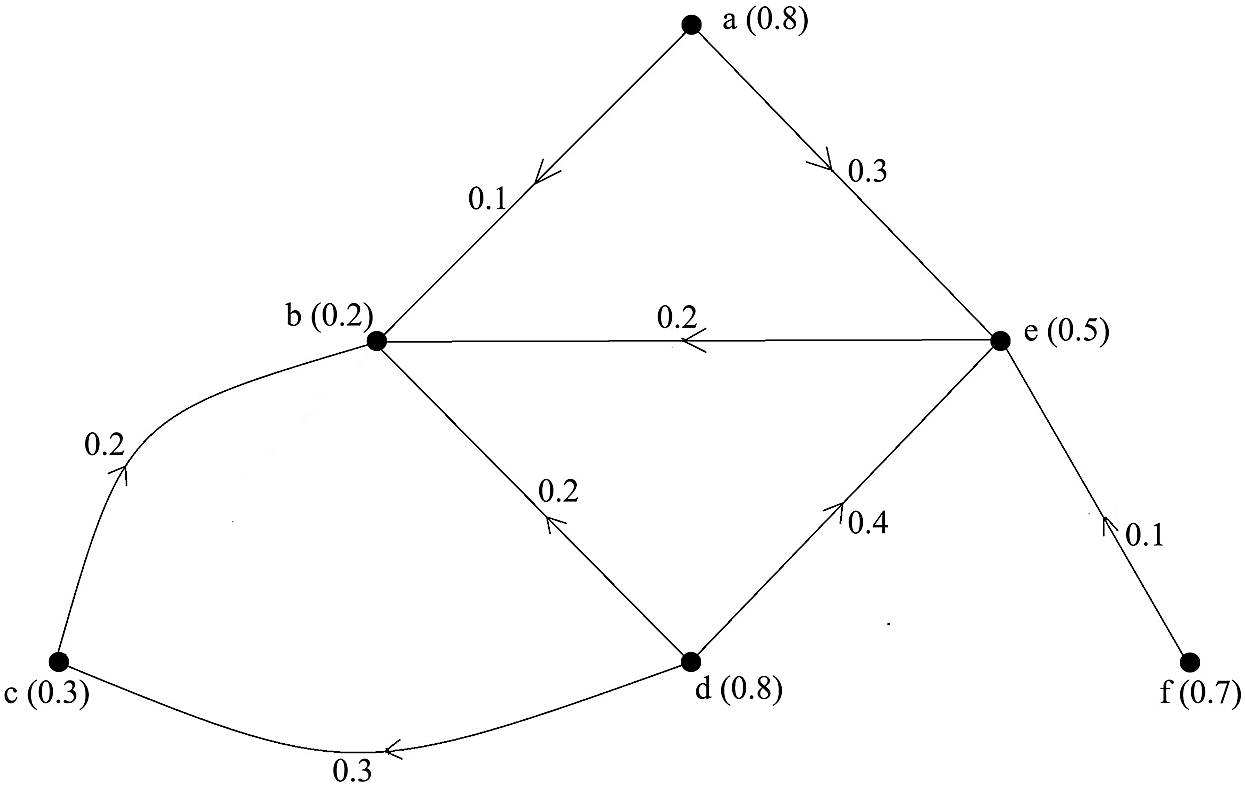
Figure 1: Fuzzy directed graph

Table 2: Vertex membership value of Fig. 1

Table 3: Edges membership value of Fig. 1

3.1 Complete Directed Fuzzy Graph

Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph. ξ can be called a complete directed fuzzy graph if the crisp underlying graph of ξ is a complete graph and μ(a,b)=σ(a)∧σ(b).

Fig. 2 shows a complete directed fuzzy graph.

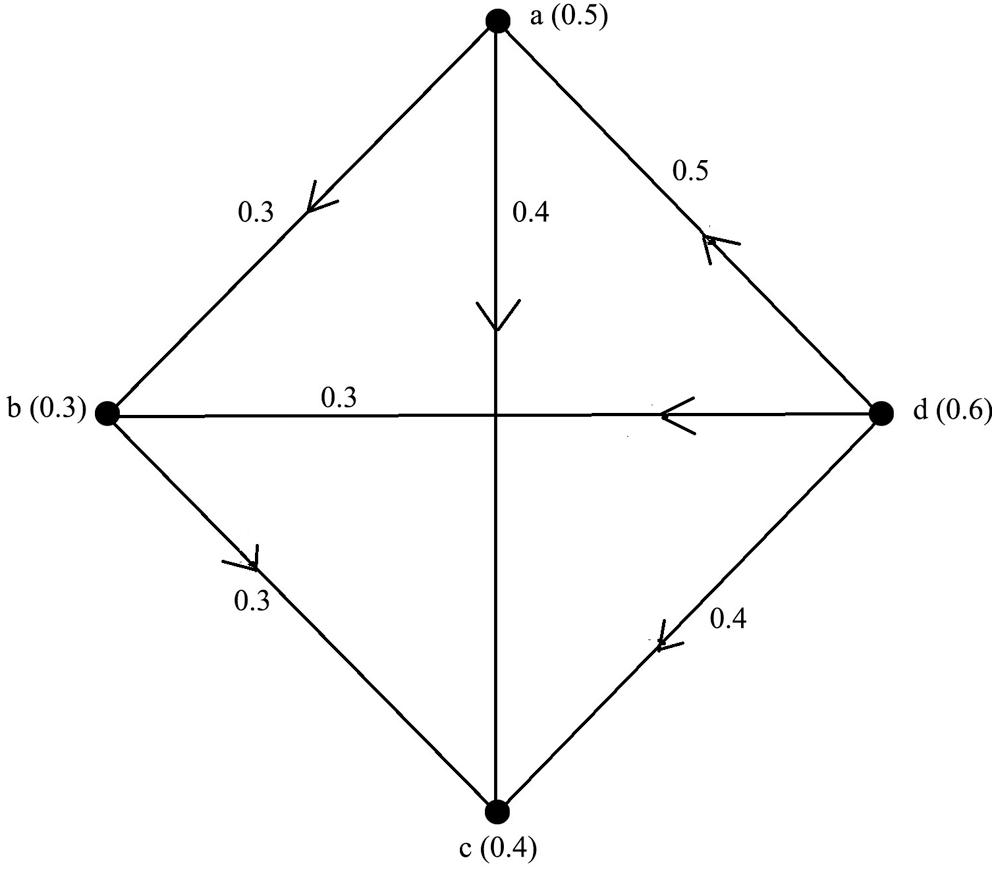
Figure 2: Complete directed fuzzy graph

Lemma 1 Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph. Then 0≤ϕ→(a,b)<1, ϕ→(a,b) is the measure of influence between the vertices a and b.

Proof. ξ is a directed fuzzy graph. So, μ(a,b)≤σ(a)∧σ(b), μ(a,b) is the edge membership value of the edge (a, b) and σ(a) is the vertex membership value of the vertex a. The membership value of a vertex is 0<σ(a)≤1. Also, ϕ→(a,b)≤|σ(a)-σ(b)| denotes the measure of influence between two nodes a and b. So, if σ(a)=σ(b) then ϕ→(a,b) gets the minimum value, and the value is 0. And the maximum value of ϕ→(a,b) is ϕ→(a,b)<1 because of 0<σ(a)≤1. So, 0≤ϕ→(a,b)<1 is true.

Theorem 1 Let’s assume ξ=(V,σ,μ,E→) is a complete directed fuzzy graph. Then ϕ→(a,b)+μ(a,b)≥σ(a)∨σ(b).

Proof. ξ is a complete directed fuzzy graph. So, μ(a,b)=σ(a)∧σ(b), μ(a,b) is the edge membership value of the edge (a, b) and σ(a) is the vertex membership value of the vertex a in ξ. Also, ϕ→(a,b)≤|σ(a)-σ(b)| denotes the measure of influence between two nodes a and b. When, σ(a)>σ(b), then the value of ϕ→(a,b)≤σ(a)-σ(b). Then, ϕ→(a,b)+μ(a,b)≥σ(a)-σ(b)+σ(b). So, ϕ→(a,b)+μ(a,b)≥σ(a). So, ϕ→(a,b)+μ(a,b)≥σ(a)∨σ(b). Similarly, we can easily show that if σ(a)<σ(b), then ϕ→(a,b)+μ(a,b)≥σ(a)∨σ(b).

3.2 Colouring of Directed Fuzzy Graph

In crisp graph colouring, two adjacent vertices have to have two different colours. Same colours in two adjacent vertices will create problems. Here, we use fuzzy colour to mark the directed fuzzy graph. Suppose, red, blue, green etc. are considered the basic colours, and (red, 0.6) is the fuzzy colour, where red is the basic colour, and 0.6 is the depth of the colour. Here, we use fuzzy colour to mark the directed fuzzy graph as follows-

Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph and R=(r1,r2,…,rk) is a set of basic colours. Now, two vertices will be taken different basic colour if they are connected by a directed edge whose effectiveness is ≥0.5 or amount of influence is ≥0.5, i.e., two vertices “a” and “b” take different basic colour if the directed edge connects them with I(a,b)≥0.5 or ϕ→(a,b)≥0.5, otherwise the basic colour may be the same. Suppose, a vertex “a” gets a colour (ri, f(ri)), where ri are the basic colour and the f(ri) is the depth of the basic colour. For simplicity, let’s consider, f(ri)=σ(a), where σ(a) is the vertex membership value of the vertex a in ξ. If a is connected to another vertex b, with an edge either effectiveness greater than 0.5 or influence greater than 0.5, b will get different basic colour (rj, f(rj)) with ri≠rjandf(rj)=σ(b).

3.3 Chromatic Index of Directed Fuzzy Graph

The minimum number of basic colours needed to colour a directed fuzzy graph is called the chromatic index of a directed fuzzy graph.

Suppose, such minimum number of basic colours is K. Now, this crisp chromatic index is not sufficient to mention the vertex’s nature or weight. Hence, the chromatic index is associated with some weight. So, the chromatic index of a directed fuzzy graph is denoted by (K, N), where K is the number of the basic colours used to colour the directed fuzzy graph, and N is the weight. The weight N is defined by

N=∑i=1K{maxjfvj(ri)}

3.4 Algorithm to Colour the Directed Fuzzy Graph

Input: A directed fuzzy graph ξ=(V,σ,μ,E→), |V| = n.

Output: Complete coloured, directed fuzzy graph.

Step 1: All the vertices are labelled as 1,2,…,n.

Step 2: Vertex “1” is assigned a colour (ri, f(ri)), where ri are the basic colour and the f(ri) is the depth of the basic colour. Then, f(ri)=σ(1), where σ(1) is the vertex membership value of the vertex “1” in ξ.

Step 3: All the directly connected vertices of “1” are labelled as 11,12,…,1m, where m number of vertices are directly connected with the vertex “1”.

Step 4: The formula does the calculation of the strength of all directly connected edges with “1” I(1,1i)=μ(1,1i)min{σ(1),σ(1i)}, where i=1,2,…,m. Also, the measure of influence ϕ→(1,1i) of all directly connected vertices with “1” is considered by the formula ϕ→(1,1i)≤|σ(1)-σ(1i)|, where i=1,2,…,m.

Step 5: Basic colours, different from what is given to “1”, are alloted to all the adjacent vertices of “1” and whose I(1,1i)≥0.5 or ϕ→(1,1i)≥0.5. The depth of the colour given is the same as their vertex membership value. The rest of the adjacent vertices of “1”, whose I(1, 1i) < 0.5 or ϕ→(1,1i)<0.5, are assigned the equal basic colour as alloted to vertex 1. The target is to use a minimum number of basic colours to mark this directed fuzzy graph.

Step 6: Steps 3–5 are repeated until all of this directed graph’s vertices have been coloured.

Step 7: Calculation is done for the chromatic index of this directed fuzzy graph (K, N) where K is the number of the basic colours used to mark the directed fuzzy graph, and N is the weight. N is calculated by the formula N=∑i=1K{maxjfvj(ri)}.

Example 2 In Fig. 1 a directed fuzzy graph has been considered, and the vertices membership values are considered in Tab. 2, and the edges membership values are considered in Tab. 3. Also, the amount of influences is considered in Tab. 4. Also, the strength of all edges of this graph is shown in Tab. 5. Now, the coloured directed fuzzy graph of Fig. 1 has been shown in Fig. 3. Here, three basic colours are used to colour this directed fuzzy graph. Also, the strength of all edges is greater than or equal to 0.5 except the edge (e, f) and the influence between the vertex eandfis0.1. So, the vertex e and f can take the same basic colour. Three basic colours red, green and blue are used for colouring this directed fuzzy graph, i.e., K = 3. The depth of colour is the vertex membership value of the corresponding vertex. Here, the red colour is given in the vertices b with membership values 0.2. The green colour is assigned to the vertices c, e, f with membership value 0.3, 0.5, 0.7 respectively. The blue colour is assigned to the vertices a, d with membership value 0.8, 0.8 respectively. So, weight N = 0.2+0.8+0.7 = 1.7. Thus, the chromatic index of this directed fuzzy graph is (3, 1.7). The coloured directed fuzzy graph of Fig. 1 has been shown in Fig. 3.

Table 4: Amount of influence between two vertices of Fig. 1

Table 5: Strength of all edges of Fig. 1

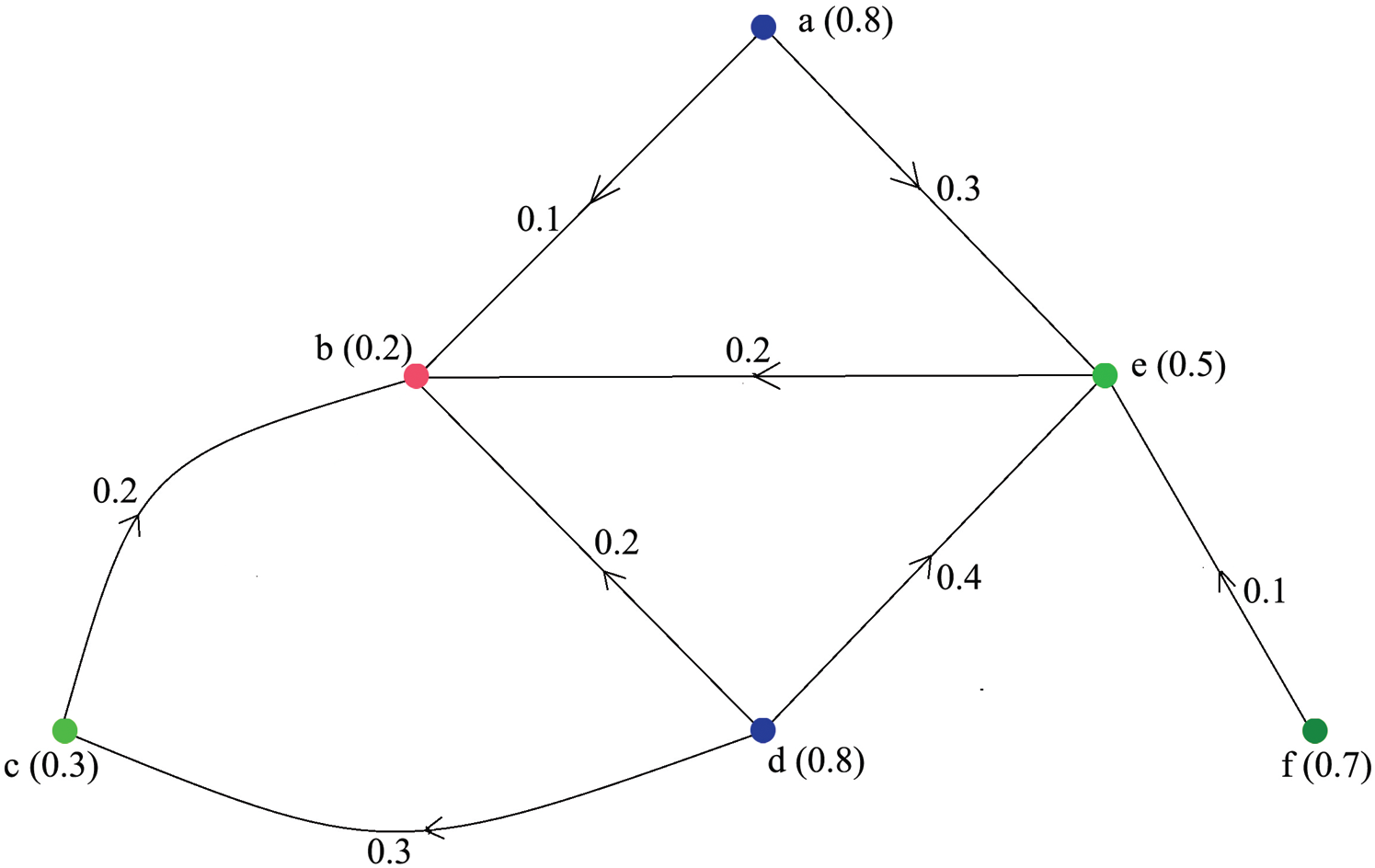
Figure 3: Colouring of directed fuzzy graph

Lemma 3 If the chromatic index of a directed fuzzy graph is (K, N), then0<N≤K.

Proof. Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph with chromatic index (K, N). It is obvious that the value of weight is always positive, i.e., the value of N is always positive, So, N > 0. Also, the membership value of each basic colour is less than or equal to 1. Now, N is the sum of the maximum membership values of each K basic colours. Hence, N≤K, i.e., 0<N≤K.

3.5 Strong Chromatic Index of Directed Fuzzy Graph

Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph, and strong chromatic index is denoted by (Ks, Ns), where Ks is the number of basic colours used for colouring ξ with each of depth greater or equal to 0.5 and Ns is the sum of maximum depth of each basic colour whose depth is greater than or equal to 0.5.

Example 3 A colouring in the directed fuzzy graph has been shown in Fig. 3. Here, the red colour is given in the vertices b with membership values 0.2. The green colour is assigned to the vertices c, e, f with membership value 0.3, 0.5, 0.7 respectively. The blue colour is given to the vertices a, d with membership value 0.8, 0.8 respectively. So, the value of Ks is 2 and the weight Ns = 0.8+0.7 = 1.5. Thus, the strong chromatic index of this directed fuzzy graph is (2, 1.5).

Theorem 3 Let’s assume ξ is a directed fuzzy graph and (K, N), (Ks, Ns) are the chromatic index and strong chromatic index of this directed fuzzy graph respectively. Then K≥KsandN≥Ns.

Proof. Let’s assume ξ=(V,σ,μ,E→) be a directed fuzzy graph. If all basic colours are strong, then chromatic index and strong chromatic index of this directed fuzzy graph are the same, i.e., K = Ks and N = Ns.

Again, if some of the basic colours are strong, then K > Ks. Then N is the sum of the maximum membership value of each basic colour and Ns is the sum of all the maximum membership values of all strong basic colours. So, in this case, N > Ns.

Lastly, none of the basic colours is strong. So, it is obvious that Ks = 0 and K > Ks. Also, Ns = 0 and N > Ns. So from these three cases, it is concluded that K≥Ks and N≥Ns.

Lemma 5 Ifξ is a directed fuzzy graph and (Ks, Ns) is a strong chromatic index of ξ, then2Ns-Ks≥0.

Proof. Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph and (Ks, Ns) is the strong chromatic index. So ξ is coloured by Ks the number of strong basic colours and each strong basic colour’s membership value is greater than or equal to 0.5. Ns is the sum of the maximum membership value of each basic colour. So, Ns≥0.5×Ks. Hence, 2Ns-Ks≥0.

Theorem 4 Let’s assume ξ is a directed fuzzy graph and (Ks, Ns) is the strong chromatic index. Then Ks2≤Ns≤Ks is true.

Proof. Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph and (Ks, Ns) is the strong chromatic index of this directed fuzzy graph ξ. So, the directed fuzzy graph ξ is colored by Ks number of strong basic colours. So, the membership value of all the strong colours is greater than and equal to 0.5. So, minimum value of each basic colour is 0.5, then Ns≥{0.5+0.5+…Kstimes}=Ks2.

So, the minimum value of strong weight is Ks2, i.e., Ks2≤Ns. Also, the maximum depth of each basic colour is 1. So, Ns≤{1+1+1+…Kstimes}=Ks. Thus, Ns≤Ks. So, Ks2≤Ns≤Ns is true.

Lemma 6 Ifξ is a directed fuzzy graph and (K, N), (Ks, Ns) are the chromatic index and strong chromatic index of this directed fuzzy graph. If K-Ks≠0 thenN-NsK-Ks≤0.5istrue.

Proof. Let’s assume ξ=(V,σ,μ,E→) is a directed fuzzy graph and K-Ks≠0. (K − Ks) is the number of basic colours whose membership value is less than 0.5. And (N − Ns) is the weight of this (K − Ks) number of colours. Thus, N − Ns = sum of maximum membership values of each basic colour. So, N-Ns≤0.5×(K-Ks).

Hence, N-NsK-Ks≤12.

4  Application of Colouring of Directed Fuzzy Graph

Graph colouring and fuzzy graphs have many real-life applications. Today, COVID-19 is a major threat to human lives. So people are conscious of tracking the places where the majority of the COVID-19 infected patients have been found. Many websites are providing live updates about COVID-19. These websites use the tool of the colouring of maps. But they are not maintaining graph colouring techniques. In this section, to capture uncertainty and direction of links of COVID19, the colouring of the directed fuzzy graphs is used to colour such infected regions.

This virus was first detected in Wuhan, China, in December 2019. Since then, it has been spreading globally. Within April 2020, almost all countries were affected by this virus. The transmission is happening due to the inter-links among countries. Here, we have considered a graph of top 10 COVID-19 affected countries. Data are taken from the website (https://www.worldometers.info/coronavirus/) dated 4th April. These countries are assumed as vertices of a directed fuzzy graph. Also, there exists an edge if any two (vertices) countries have been affected by the COVID-19.

In Tab. 6 and Fig. 4, the top ten affected countries and the number of affected patients by COVID-19 have been shown. Here, all countries are considered nodes of the concerned network. There is a directed edge between two countries (vertex) if there is any travel history between them because they are affected by another. So, we get a directed graph and Fig. 5 has shown this directed graph.

Table 6: Top ten affected counties by COVID-19 and no. of cases

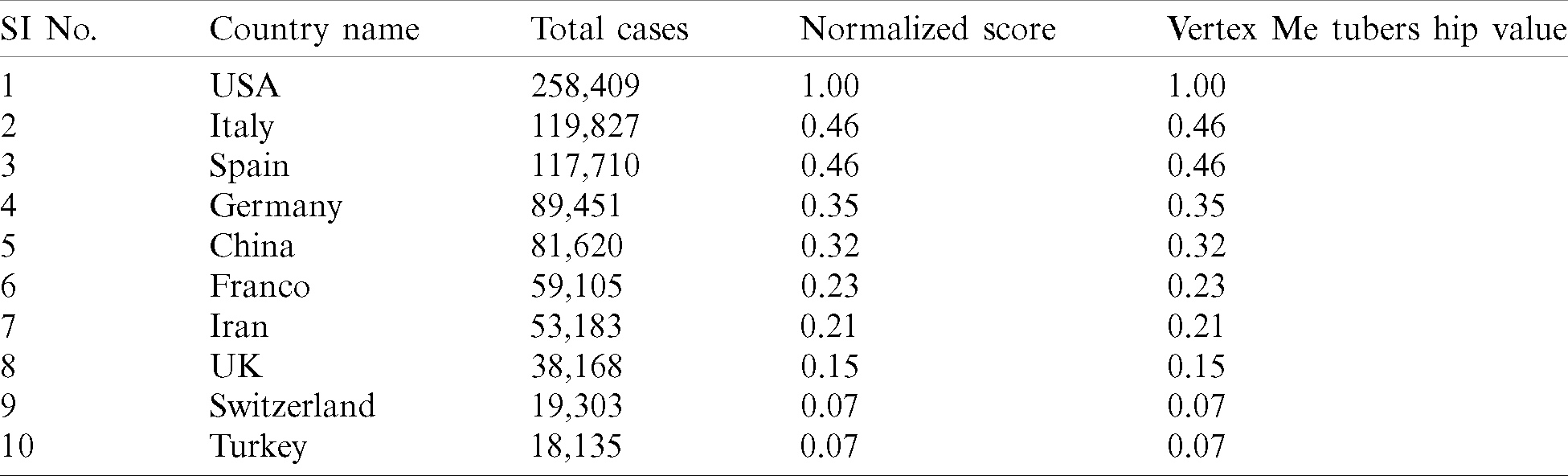
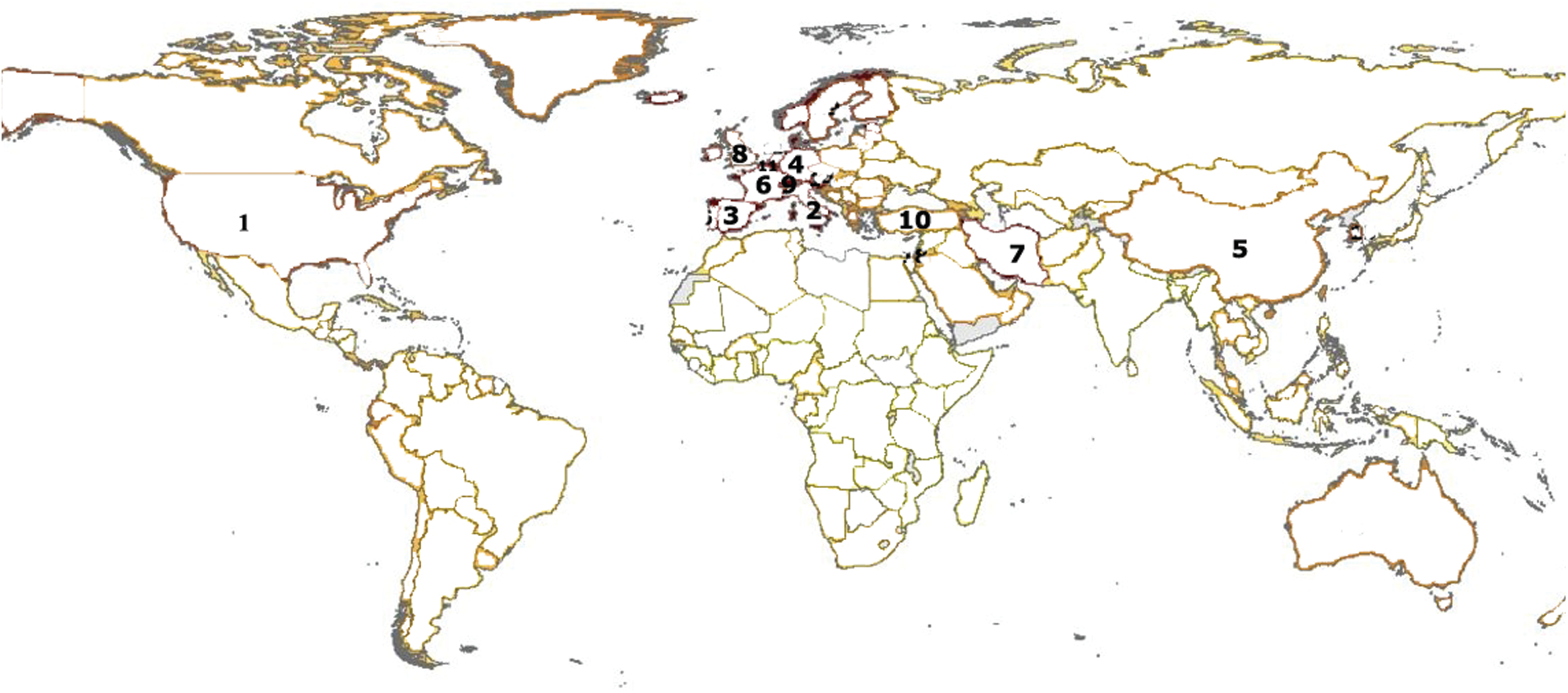
Figure 4: Top ten affected counties in a world map

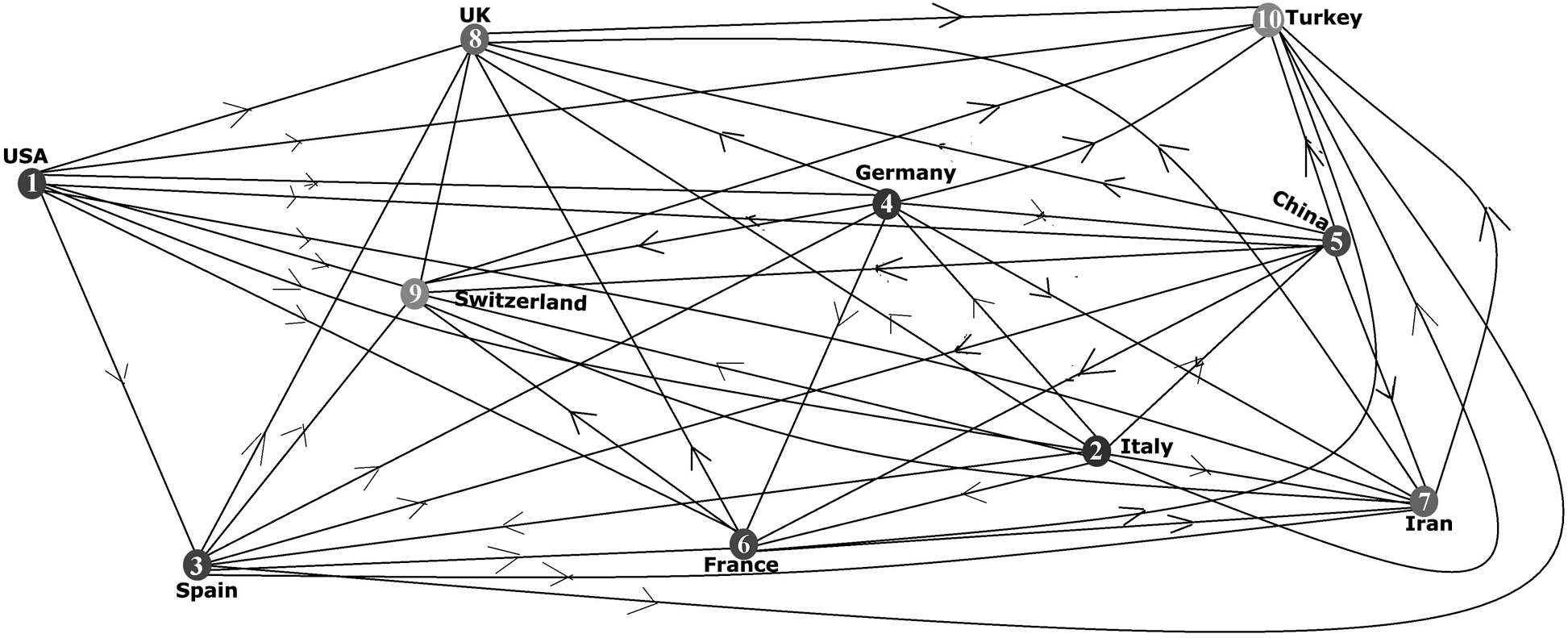
Figure 5: Directed graph of top ten affected counties by COVID-19

The normalized score is considered as a vertex membership value, and Tab. 6 has shown it. Tab. 7 has shown the travel history between the two countries last year. Here, the edge membership value of an edge = “normalized score of travel history between two counties × minimum vertex membership value of the end vertices”. Tab. 9 has shown the edge membership value of all edges. Fig. 6 has revealed this directed fuzzy graph. Now, the measure of influence between two vertices is considered a difference between two vertices membership value for this particular case. So, the influence between vertices is calculated by this formula ϕ→(a,b)=σ(a)-σ(b) and this calculation are shown in Tab. 8, and the strength of all edges is shown in Tab. 10.

Table 7: Travel history between the two countries last year

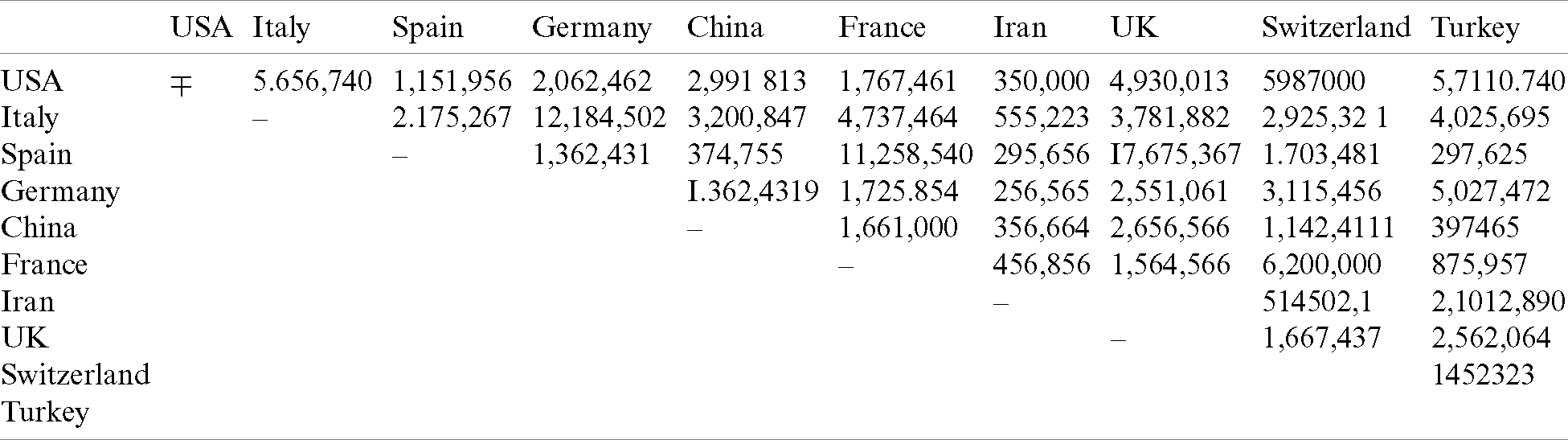
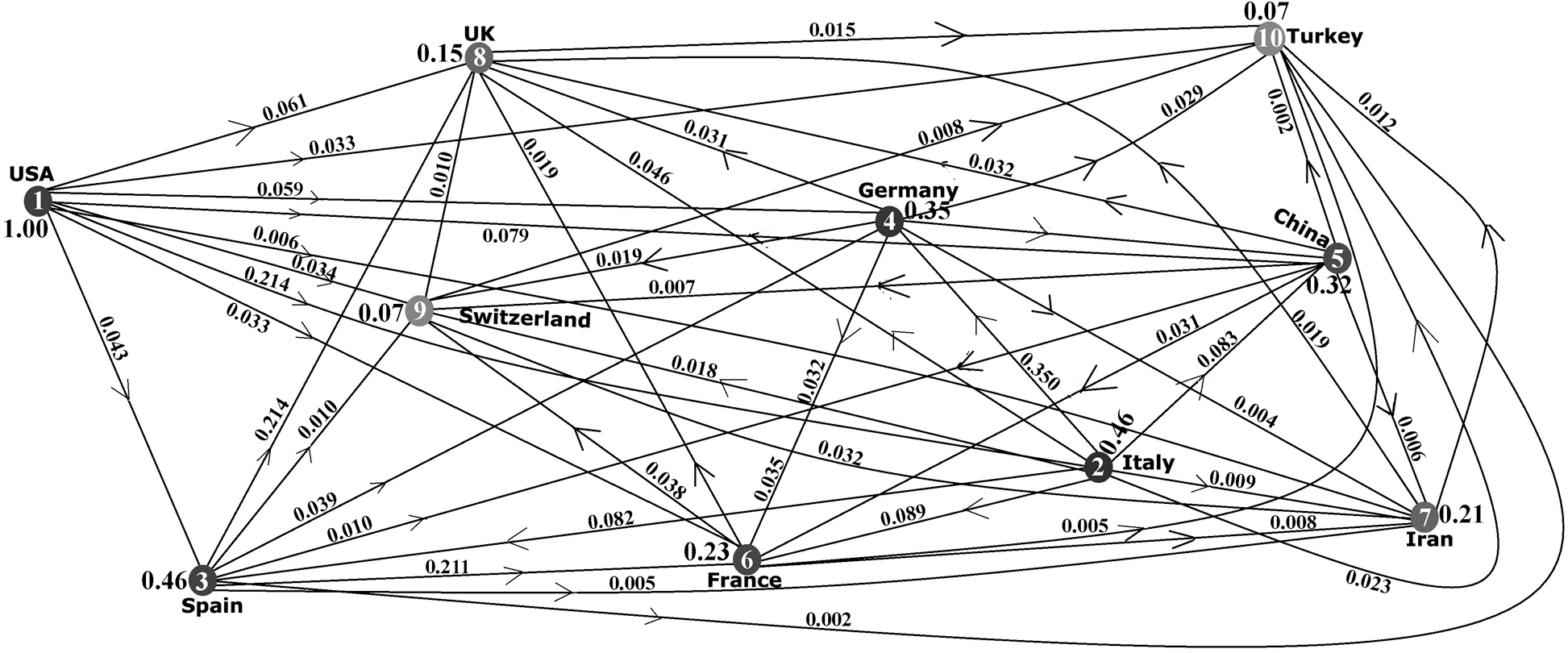
Figure 6: Directed fuzzy graph

Table 8: Measure of influence between the two vertices

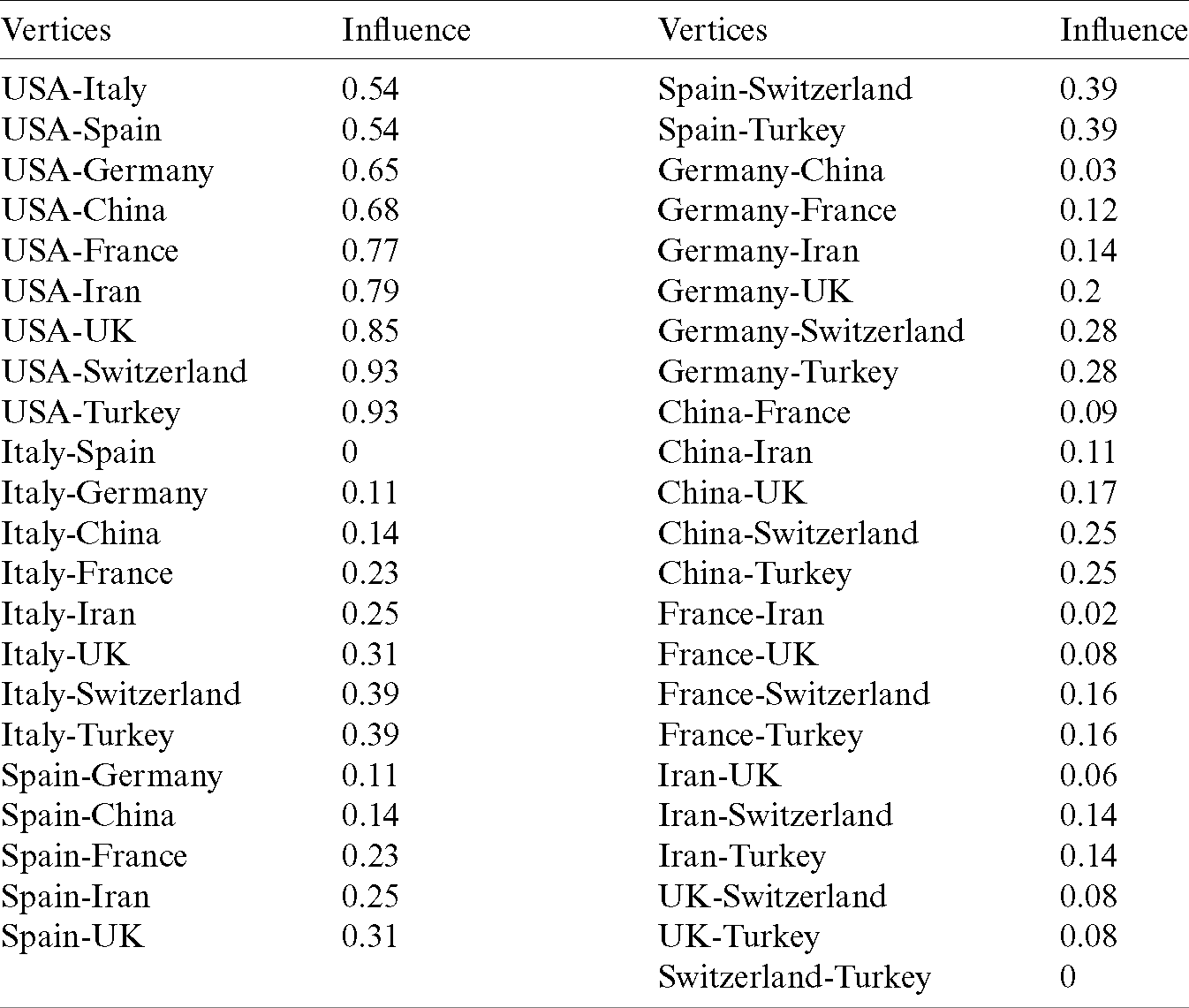
Table 9: Edge membership value of the directed fuzzy graph of Fig. 6

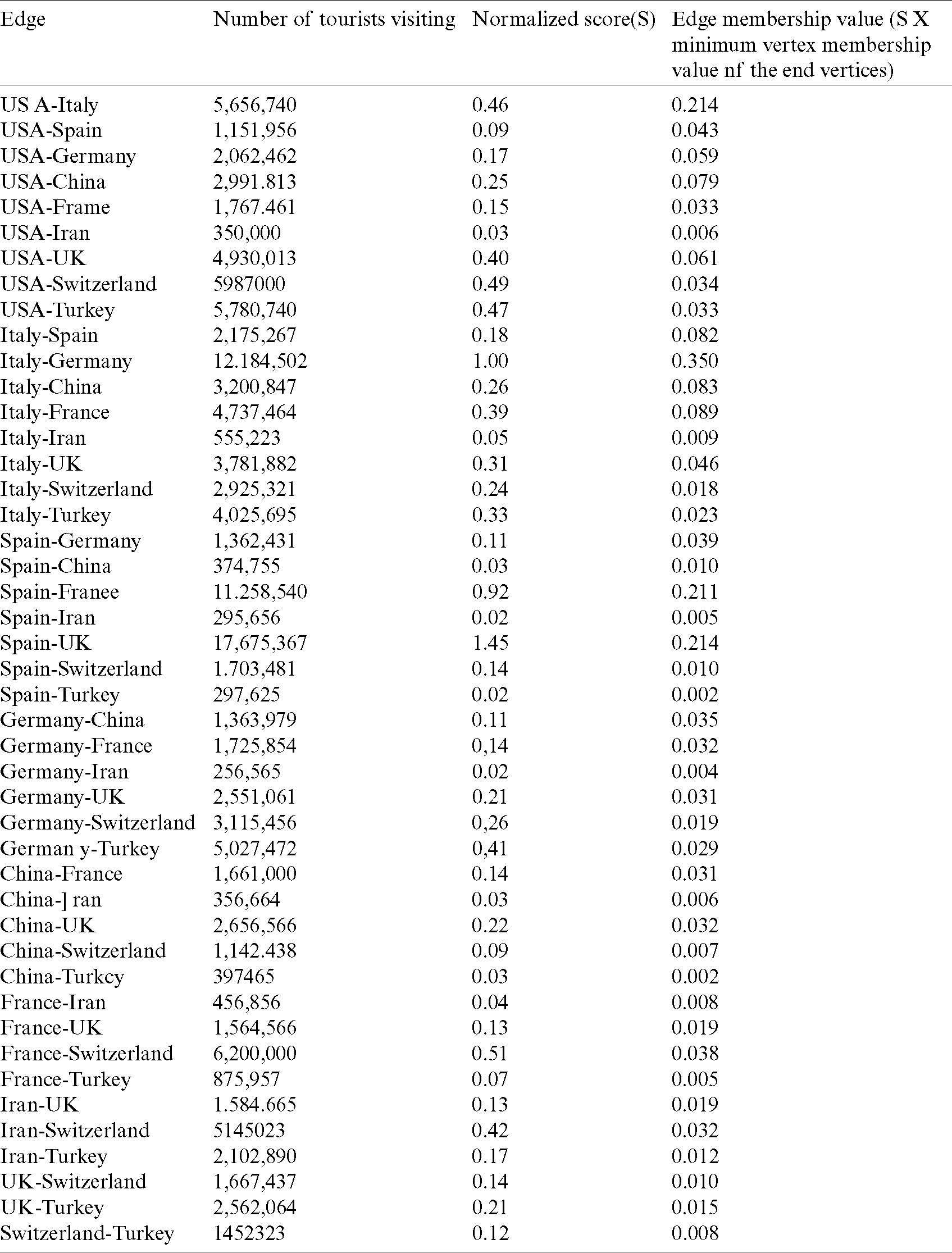
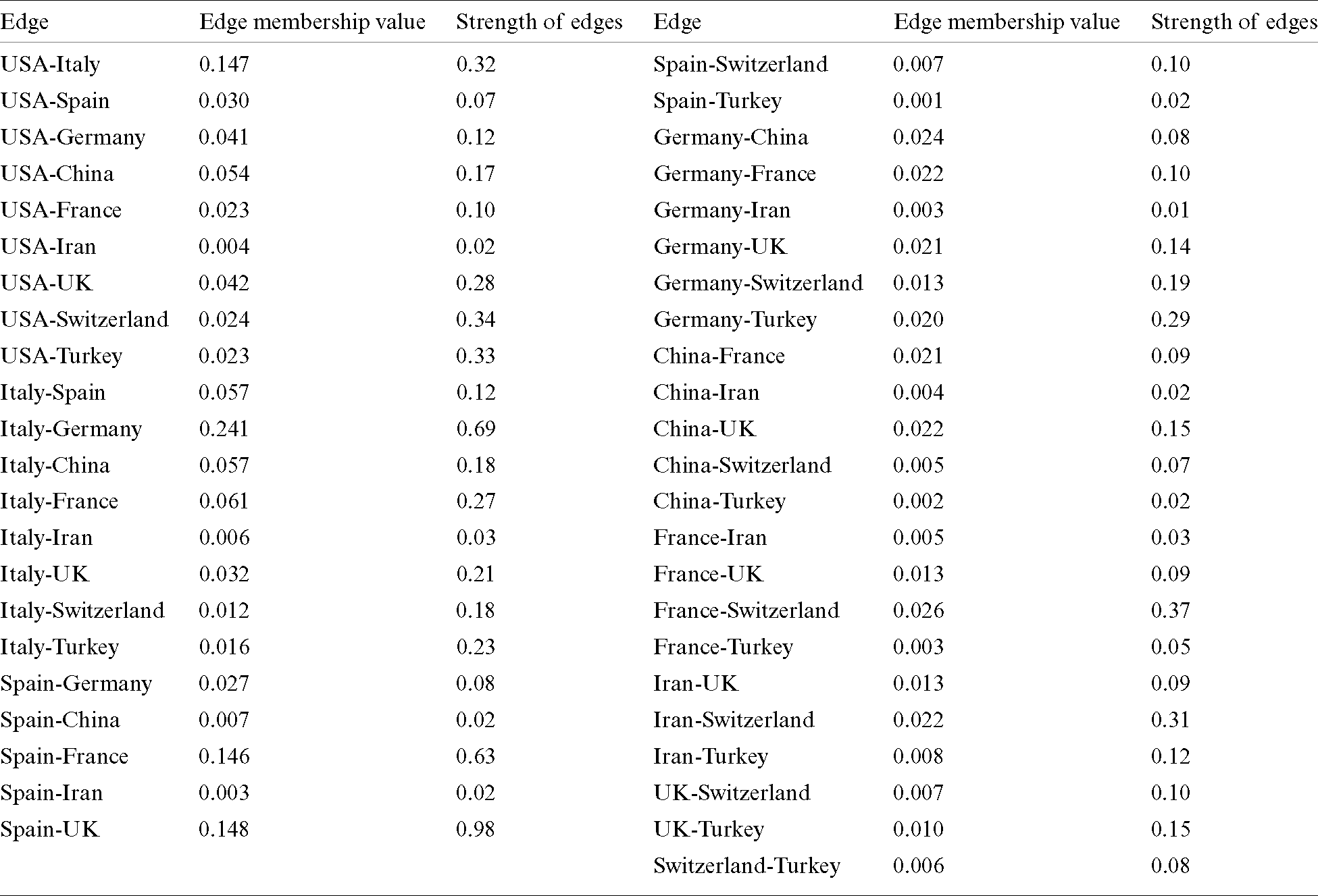
Table 10: Strength of all edges of the directed graph of Fig. 5

Now, two vertices are assigned different basic colours if they are connected by a directed edge whose effectiveness is ≥0.5, or the amount of influence is ≥0.5. So, four basic colours are used to colour this directed graph. The coloured directed fuzzy graph is shown in Fig. 7, with the same depth as of vertex membership values. The colouring of the world map of affected countries is shown in Fig. 8, with the same depth in relation to their number of affected people.

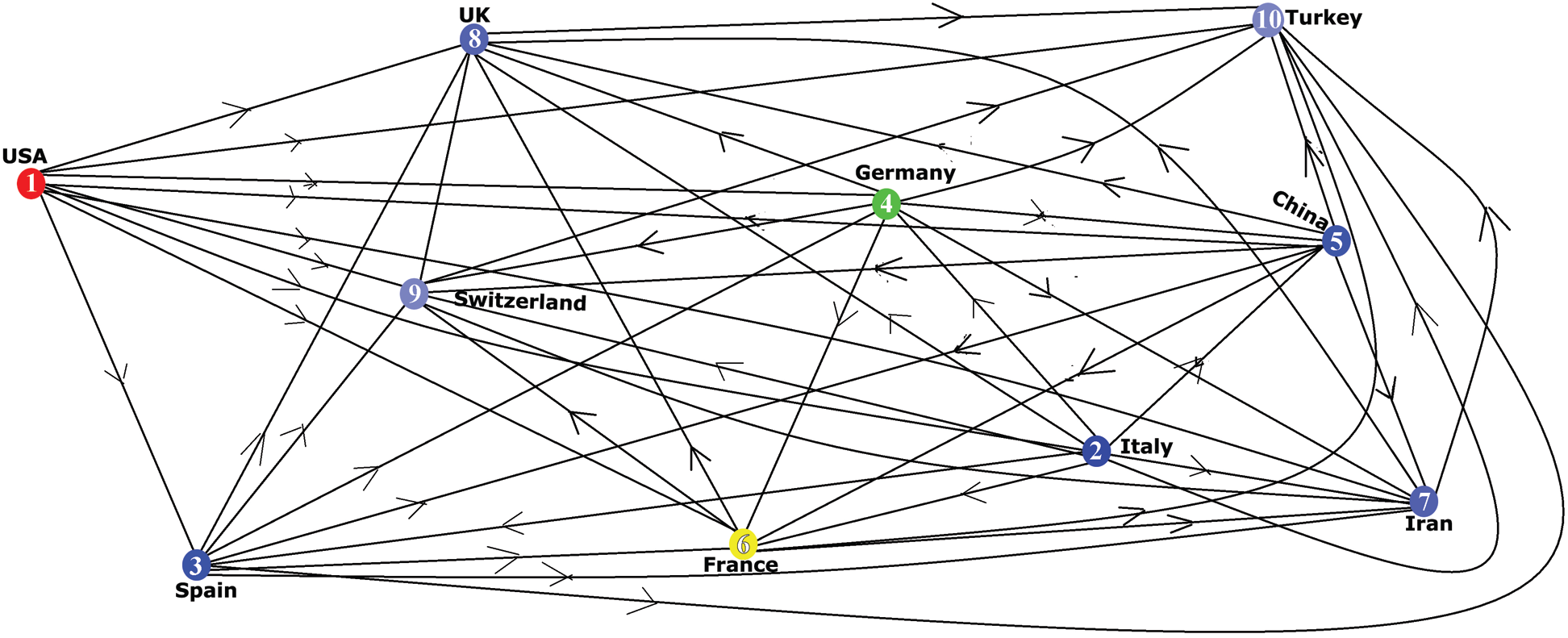
Figure 7: Colouring of the directed fuzzy graph

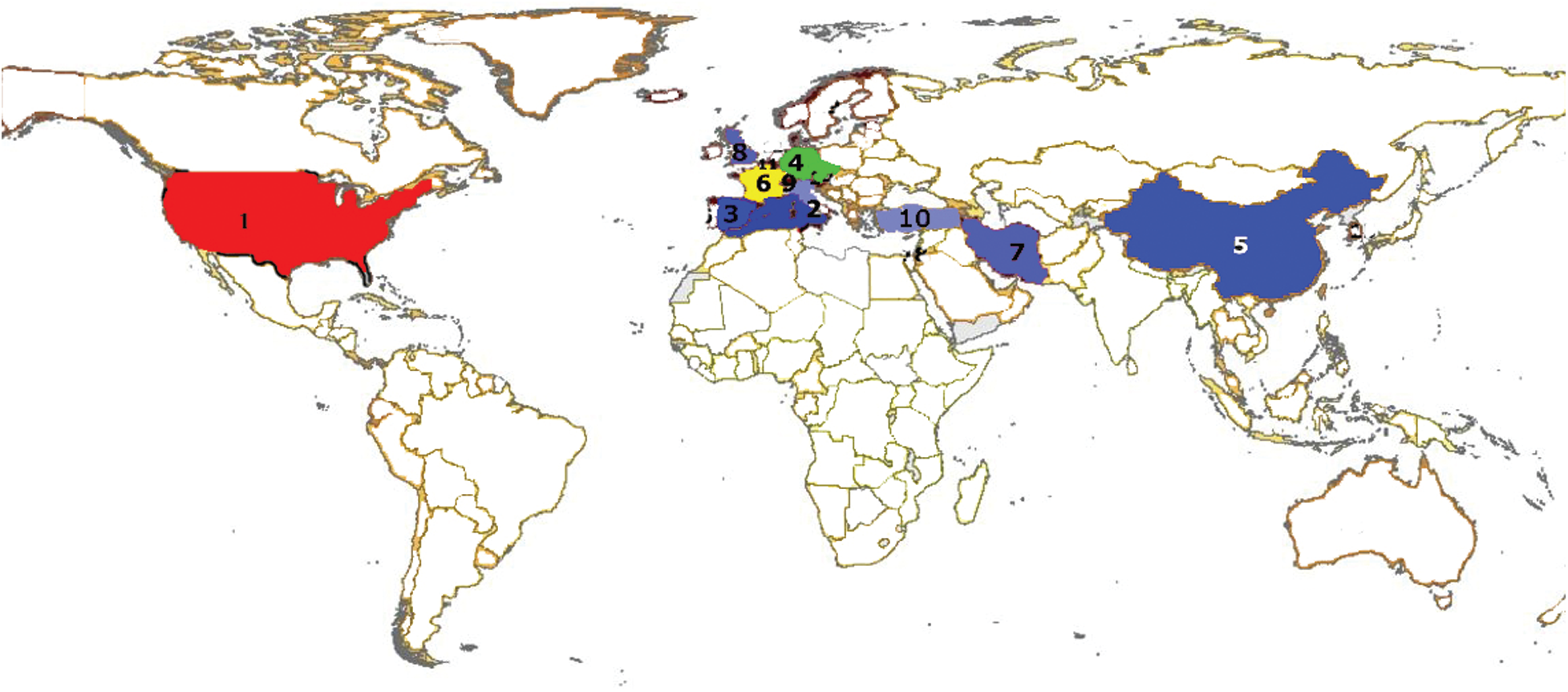
Figure 8: World map colouring using the fuzzy directed fuzzy graph colouring

4.1 Analysis of the Result

Fig. 8 shows that four basic colours have been used. In this colouring technique, two nodes are given different colours, if there exists a directed edge between them whose effectiveness is ≥0.5, or the amount of influence is ≥0.5. The depths of colours among the countries are given based on its number of affected cases.

5  Conclusion

In this paper, a new technic of a fuzzy graph colouring based on edges’ influence value has been introduced. Moreover, the term, chromatic index and strong chromatic index are defined differently. By this directed graph colouring we have represented this COVID-19 outbreak all over the world. There is one limitation of this study too. The data relating to the travellers who have been wandering across the borders has not been fully detailed.This can be made possible if the data is collected on a larger basis. Due to the limitation of the fund, the collection is not feasible for this study, but capturing the exact figure will be done in the future. Besides, the literature on directed fuzzy graphs will be explored on the basics of this article.

Funding Statement: This research was supported and funded by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2018R1D1A1B07049321).

Conflicts of Interest: The authors unanimously declare that they have no interest in reporting the present study.

References

 1.  A. Kauffman. (1973). Introduction a la Theorie des Sous-Emsembles Flous, Paris: Masson et Cie Editeurs. [Google Scholar]

 2.  A. Rosenfeld. (1975). “Fuzzy graphs,” In: L. A. Zadeh, K. S. Fu, M. Shimura (Eds.) Fuzzy Sets and Their Applications, New York: Academic Press, pp. 77–95. [Google Scholar]

 3.  S. Samanta. and M. Pal. (2015). “Fuzzy planar graphs,” IEEE Transaction on Fuzzy Systems, vol. 23, no. 6, pp. 1936–1942. [Google Scholar]

 4.  S. Samanta and M. Pal. (2013). “Fuzzy k-competition graphs and p-competition fuzzy graphs,” Fuzzy Information and Engineering, vol. 5, no. 2, pp. 191–204. [Google Scholar]

 5.  H. Lu, C. W. Stratton and Y. W. Tang. (2020). “Outbreak of pneumonia of unknown etiology in Wuhan, China: The mystery and the miracle,” Journal of Medical Virology, vol. 92, no. 4, pp. 401–402. [Google Scholar]

 6.  Q. Li, P. Wu X.Guan, X. Wang and L. Zhou. (2020). “Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia,” New England Journal of Medicine, vol. 382, no. 13, pp. 1199–1207. [Google Scholar]

 7.  A. E. Gorbalenya, S. C. Baker, R. S. Baric, R. J. Groot and C. Drosten. (2020). “The species severe acute respiratory syndrome-related coronavirus: Classifying 2019-nCoV and naming it SARS-CoV-2,” Nature Microbiology, vol. 5, no. 4, pp. 536–544. [Google Scholar]

 8.  N. Chen, X. Dong M.Zhou, J. Qu and F. Gong. (2020). “Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study,” Lancet, vol. 395, no. 10223, pp. 507–513. [Google Scholar]

 9.  C. Dalfo. (2019). “A new general family of mixed graphs,” Discrete Applied Mathematics, vol. 269, no. 4, pp. 99–106. [Google Scholar]

10. S. Samanta, T. Pramanik and M. Pal. (2016). “Colouring of fuzzy graphs,” Afrika Matematica, vol. 27, no. 1, 2, pp. 37–50. [Google Scholar]

11. P. Hansen, J. Kuplinsky and D. de Werra. (1997). “Mixed graph colorings,” Mathematical Methods of Operations Research, vol. 45, no. 1, pp. 145–160. [Google Scholar]

12. Y. N. Sotskov, A. Dolgui and F. Werner. (2001). “Mixed graph coloring for unit-time job-shop scheduling,” International Journal of Mathematical Algorithms, vol. 2, pp. 289–323. [Google Scholar]

13. R. Mahapatra, S. Samanta and M. Pal. (2020). “Applications of edge colouring of fuzzy graphs,” Informatica, vol. 31, no. 2, pp. 313–330. [Google Scholar]

14. R. Mahapatra, S. Samanta, T. Allahviranloo and M. Pal. (2019). “Radio fuzzy graphs and assignment of frequency in radio stations,” Computational and Applied Mathematics, vol. 38, no. 3, pp. 1–20. [Google Scholar]

15. R. Mahapatra, S. Samanta, M. Pal and Q. Xin. (2019). “RSM index: A new way of link prediction in social networks,” Journal of Intelligent and Fuzzy Systems, vol. 37, no. 2, pp. 2137–2151. [Google Scholar]

16. R. Mahapatra, S. Samanta, M. Pal and Q. Xin. (2020). “Link prediction in social networks by neutrosophic graph,” International Journal of Computational Intelligence Systems, vol. 13, no. 1, pp. 1699–1713. [Google Scholar]

17. U. Naseem, S. K. Khan, I. Razzak and I. A. Hameed. (2019). “Hybrid words representation for airlines sentiment analysis,” in Australasian Joint Conf. on Artificial Intelligence, Adelaide, SA, Australia, pp. 381–392. [Google Scholar]

18. U. Naseem, S. K. Khan, M. Farasat and F. Ali. (2020). “Abusive language detection: A comprehensive review,” Indian Journal of Science and Technology, vol. 12, no. 45, pp. 1–13. [Google Scholar]

19. U. Naseem, M. Khushi, S. K. Khan, N. Waheed, A. Mir, et al. (2020). , “Diabetic retinopathy detection using multi-layer neural networks and split attention with focal loss,” in Int. Conf. on Neural Information Processing, Bangkok, Thailand, pp. 26–37. [Google Scholar]

20. S. K. Khan, U. Naseem, M. Farasat and F. Ali. (2019). “Link-level performance modelling for next-generation uav relay with millimetre-wave simultaneously in access and backhaul,” Indian Journal of Science and Technology, vol. 12, no. 39, pp. 1–9. [Google Scholar]

21. S. K. Khan, U. Naseem, M. Farasat and F. Ali. (2020). “Performance evaluation of next-generation wireless (5G) UAV relay,” Wireless Personal Communications, vol. 113, no. 2, pp. 945–960. [Google Scholar]

22. S. K. Khan, U. Naseem, A. Sattar, N. Waheed, A. Mir, et al. (2020). , “UAV-aided 5G Network in Suburban, Urban, Dense Urban, and High-rise Urban Environments,” in 2020 IEEE 19th Int. Symp. on Network Computing and Applications, Cambridge, MA, USA, IEEE, pp. 1–4. [Google Scholar]

23. R. Mahapatra, S. Samanta and M. Pal. (2020). “Generalized neutrosophic planar graphs and its application,” Journal of Applied Mathematics and Computing, vol. 65, pp. 693–712. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.