DOI:10.32604/cmc.2021.015430

| Computers, Materials & Continua DOI:10.32604/cmc.2021.015430 |  |
| Article |
Language Model Using Differentiable Neural Computer Based on Forget Gate-Based Memory Deallocation
Department of Computer Science and Engineering, Sogang University, Seoul, 04107, Korea
*Corresponding Author: Ji-Hwan Kim. Email: kimjihwan@sogang.ac.kr
Received: 20 November 2020; Accepted: 02 February 2021
Abstract: A differentiable neural computer (DNC) is analogous to the Von Neumann machine with a neural network controller that interacts with an external memory through an attention mechanism. Such DNC’s offer a generalized method for task-specific deep learning models and have demonstrated reliability with reasoning problems. In this study, we apply a DNC to a language model (LM) task. The LM task is one of the reasoning problems, because it can predict the next word using the previous word sequence. However, memory deallocation is a problem in DNCs as some information unrelated to the input sequence is not allocated and remains in the external memory, which degrades performance. Therefore, we propose a forget gate-based memory deallocation (FMD) method, which searches for the minimum value of elements in a forget gate-based retention vector. The forget gate-based retention vector indicates the retention degree of information stored in each external memory address. In experiments, we applied our proposed NTM architecture to LM tasks as a task-specific example and to rescoring for speech recognition as a general-purpose example. For LM tasks, we evaluated DNC using the Penn Treebank and enwik8 LM tasks. Although it does not yield SOTA results in LM tasks, the FMD method exhibits relatively improved performance compared with DNC in terms of bits-per-character. For the speech recognition rescoring tasks, FMD again showed a relative improvement using the LibriSpeech data in terms of word error rate.
Keywords: Forget gate-based memory deallocation; differentiable neural computer; language model; forget gate-based retention vector
Various deep learning models have been used for a variety of task-specific problems [1]. For example, convolutional neural networks (CNNs) are commonly used for image and video tasks. Recurrent neural networks (RNNs) have been used for speech recognition and language model (LM) tasks. Deep learning models are usable for specific tasks if they are trained with pertinent datasets, but deep learning models adapted to specific tasks have difficulties with general-purpose tasks. General-purpose tasks are those with having different training and test sets. For example, in a question-answering task, a story composed of multiple sentences is used to train deep learning models, with these models then able to predict the next word or sentence. In the test stage (i.e., actual application), presenting a question to the trained model results in the deep learning model’s inability to predict an answer. Despite various pre-training methods, the performance of deep learning models does not achieve the best available performance on general-purpose tasks [2].
A differentiable neural computer (DNC) has been proposed for general-purpose tasks [3]. A DNC comprises a controller and an external memory. The controller is equivalent to a deep learning model. The external memory is a matrix comprising M-dimensional vectors. On general-purpose tasks, the DNC stores information about the training data into the external memory. The controller writes its output vector to the external memory and reads the information therein. When the DNC performs read and write operations, attention vectors are generated using both a content-based addressing and temporal linking methods [4]. In the testing stage, the DNC predicts the answer using information stored in the external memory. Previous work [5] showed that the DNC achieves performance close to that of the best available performance on approaches to the question-answering bAbI task [6].
However, DNCs exhibit a problem with memory deallocation during write operations. During each write operation, the external memory at time (t −1) is multiplied with an erase vector, with the attention vector generated from the current external memory. If the i-th address of the external memory must be deallocated, the i-th element of the erase vector should be 1 during the write operation. However, the erase vector is generated with a sigmoid function. Therefore, the erase vector can only be 1 when the input is infinity. For example, in a question-answering task, if a new story is used as training data to a pre-trained DNC, information unrelated to the story should be erased from external memory. However, the DNC does not do so reliably. It becomes a garbage value and that affects the attention vector. This causes performance degradation on general-purpose tasks.
In this study, we propose a DNC using forget gate-based memory deallocation (FMD). The FMD method searches for the minimum value of elements in a forget gate-based retention vector, a vector indicating the retention degree of information stored in each external memory address. Elements of the forget gate-based retention vector with a value of 0 imply that a read operation has already been performed on external memory addresses related to these elements, and these addresses are to be deallocated. The minimum value of the elements is converted to 0, and the values of the external memory at time (t −1) are multiplied by the converted forget gate-based retention vector.
We evaluate our proposed DNC on benchmark LM tasks. Previous studies have discovered that DNCs are reliable when used with reasoning problems such as LM, which predicts the next word using the previous word sequence. Although previous studies on Transformer have demonstrated performance competitive with the best available performance for LM tasks, we evaluate our proposed DNC on the Penn Treebank (PTB) and enwik8 LM tasks. In all our tests, our proposed DNC outperforms the unmodified DNC.
We organize our article as follows. Section 2 presents other works related to deep learning-based LMs. Section 3 provides a brief description of the DNC. Section 4 analyzes our proposed FMD method in detail. Finally, we present our experimental results and conclusions in Sections 5 and 6, respectively.
The LM process assigns the probability of the next word or character based on the previous word or character sequence. Modeling LM uses an n-gram LM, a conventional LM based on the Markov assumption, is used. However, n-gram LM has two drawbacks. First, it assigns a probability of 0 to an unseen n-gram. If an n-gram is not found in the training text, this n-gram becomes the unseen n-gram. Second, the value of n is limited. If n is 10 and the vocabulary size is 1000, then the number of n-grams is 100010. Thus LM is affected by the curse of dimensionality, limiting its modeling ability on large-scale datasets [7].
A deep neural network (DNN) was applied to the LM to solve the unseen n-gram problem [8]. The DNN-based LM represents each word or character in a high-dimensional vector space. The probability of the unseen n-gram can be calculated on a high-dimensional vector space generated by the DNN-based LM. Continuous bag-of-words and skip-gram are both representative DNN-based LMs [9]. However, DNN-based LMs present a few disadvantages. As n increases, the number of input layers increases as well. This causes the weight parameters to be trained in proportion to the number of input layers. The DNN can only be trained within a limited context of length n [10]. Therefore, the DNN-based LM cannot solve the curse of dimensionality.
To address the limited context size, RNNs have been used to train the LM [10]. The RNN can be modeled long range sequences because of recurrent hidden layers. In RNN-based LM, the input of a recurrent hidden layer is one word or character at time t and an output vector of the recurrent hidden layer at time (t −1). Therefore, theoretically, RNN-based LM solves the problem of a limited context size. Previous studies proposed a bidirectional RNN-based LM that demonstrated improved performance compared with unmodified RNN-based LM [11]. The bidirectional RNN-based LM is trained not only with the forward context but also with the backward context. However, it is affected by the problems of vanishing gradients and exploding gradients. The vanishing gradient problem occurs when the gradients of an activation function become 0, whereas the exploding gradient problem occurs when the gradients of the activation function become infinite [12].
To address the vanishing gradient problem, RNN-based LM uses a long short-term memory (LSTM) [13]. The LSTM comprises one or more memory cells, an input, an output, and a forget gate and controls the amplification and reduction of information. The LSTM RNN-based LM achieved a higher performance than the RNN-based LM [14]. However, training the LSTM RNN is time-consuming as each of the tree gates has to be trained. In addition, the LSTM RNN-based LM uses gradient clipping to prevent the exploding gradient problem [15]. The clipping factor for the gradient clipping technique is chosen by the developers, with the clipping factor depending on the training datasets. In particular, recent studies have shown that an LSTM RNN-based LM cannot be trained with more than 200 words or character sequences as its input [16].
To address the problem of limited context size, attention mechanisms have also been used in the LM [17]. The next word or character is related to words or characters in context, but not to all words or characters. The attention mechanism determines the words or characters that must be addressed by the attention vector generated from the input sequence [18]. Transformer is the most common model using an attention mechanism [19]. This is an encoder-decoder model that also uses a multi-head self-attention mechanism and positional encoding. The multi-head self-attention mechanism allows Transformer to address context information on different high-dimensional vector spaces in the input sequence [20]. Positional encoding applies the sine and cosine functions to the input sequence for long-context dependency [21]. Although Transformer encodes a longer context into a fixed size chunk, variable Transformer-based models have also been proposed [22].
The most widely used Transformer-based models are the bidirectional encoder representations from Transformers (BERT), generative pretrained Transformer 2 (GPT-2), and Transformer extra-long (Transformer-XL). BERT, which is a multi-layer bidirectional encoder of Transformer, is often functions as a pre-training model in natural language processing tasks [23]. The deep bidirectional encoder can be trained with the left and right context of the input sequence in all layers. BERT also demonstrates the best available performance on question-answer and named entity tasks. GPT-2 differs from BERT by using a multi-layer decoder with Transformer [24]. In LM tasks, GPT-2 achieves the best available performances in terms of bits-per-character (BPC): 0.93 with 1.5 B weight parameters. The study used 12-layer decoder blocks with 12 heads. In contrast, Transformer-XL maintains a longer context using hidden states computed at the previous time step [22]. These hidden states represent the previous context. Transformer-XL demonstrated a high perplexity of 54.52 on a word-level PTB LM task and a BPC of 0.99 on a character-level enwik8 LM task.
3 Differentiable Neural Computer
The DNC consists of a controller and an external memory, as shown in Fig. 1 [3]. A deep learning model C acts as the controller. The controller performs read and write operations on the external memory EM, which is a fixed matrix and an element of
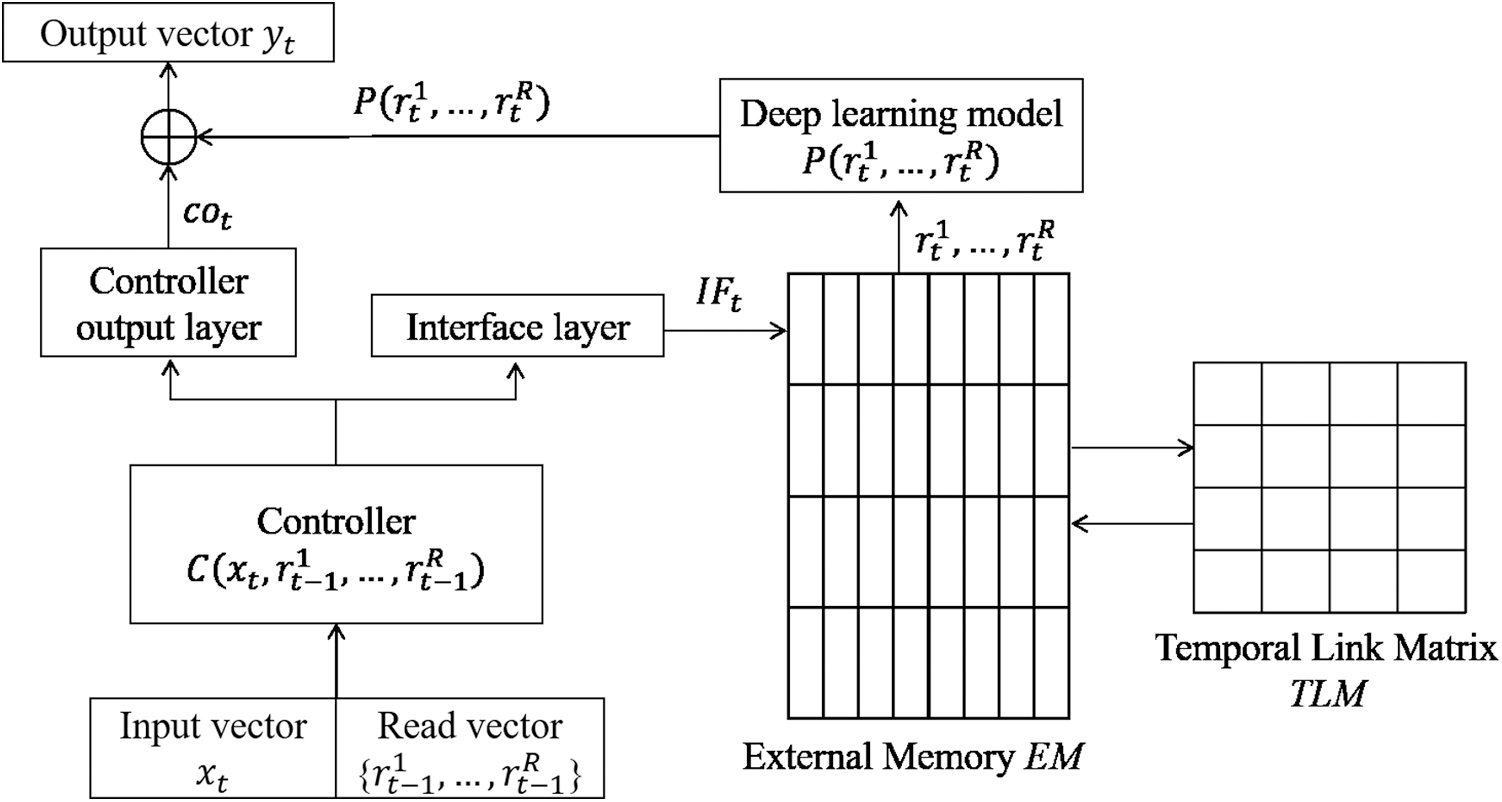
Figure 1: Simplified diagram of DNC. In this figure, the external memory has four memory vectors, and the dimension of each memory vectors is eight. The temporal link matrix is a 4
Read and write operations on the external memory require read and write weighting vectors. The DNC treats the read and write weighting vectors as attention vectors. Content-based addressing method has been used in previous studies to generate these vectors. This method calculates the cosine similarity between every memory vector and a key vector kt.
During the read operation, a specific memory area is identified by the read weighting vector, and the DNC generates read vectors. The read vector
where
During the write operation, the DNC generates the write weighting vector, which is used in the write operation as
where
4 Differentiable Neural Computer Using Forget Gate-Based Memory Deallocation
During the write operation, the DNC uses a retention vector
Read weighting vectors
In Eq. (4), if
However,
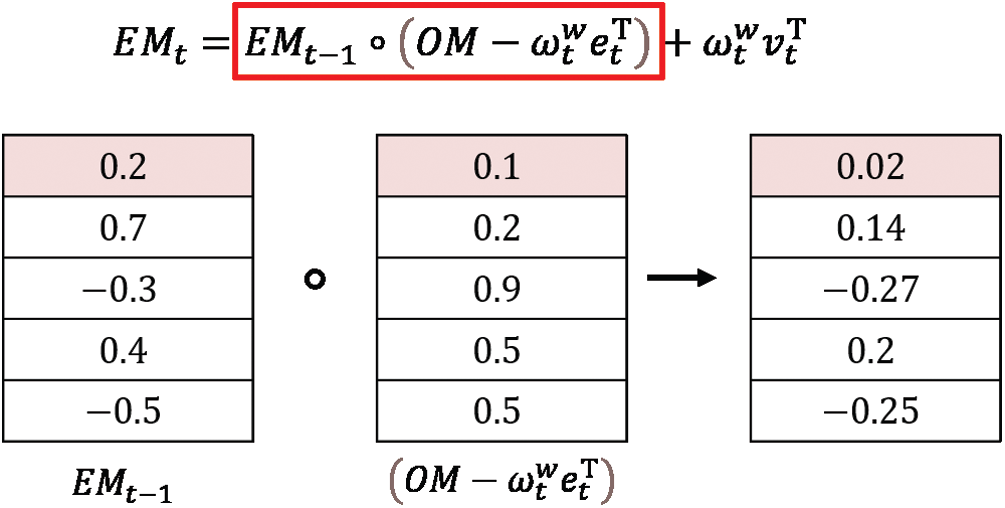
Figure 2: Example of memory deallocation in the write operation of DNC
Hence, we introduce a DNC using an FMD. A similar memory deallocation method as that shown in Eq. (5) has been proposed previously [4]. However, to deallocate the i-th external memory address with certainly,
In the proposed FMD, to obtain 0 in
where
We assume that
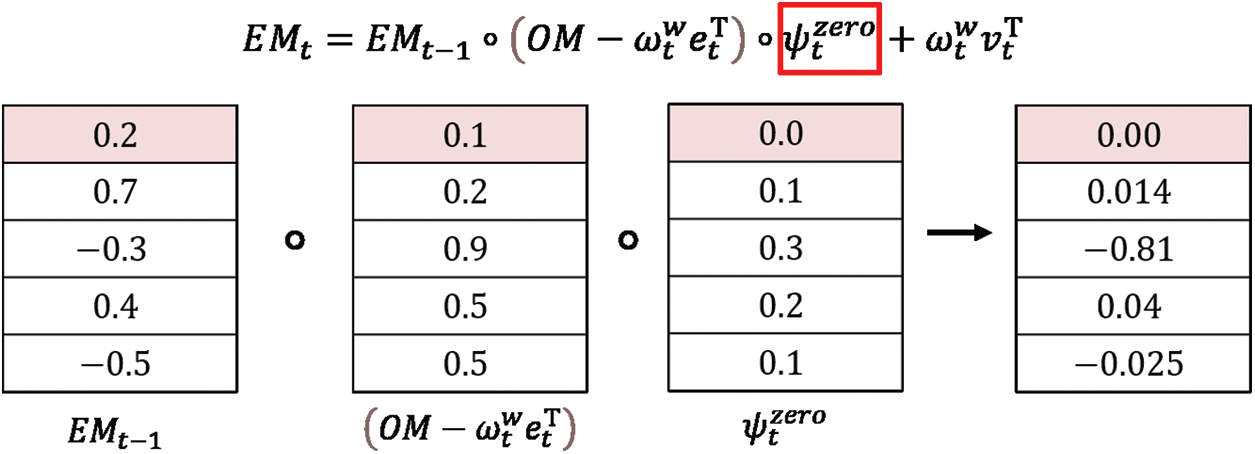
Figure 3: Example of forget gate-based memory deallocation in the write operation of DNC
The FMD searches for the minimum value of
We evaluated our proposed FMD-DNC using the character-level PTB LM and enwik8 LM for task-specific tasks. We also evaluated our proposed FMD-DNC-based LM when used as the rescoring task of speech recognition, a general-purpose task.
The character-level PTB LM task comprises characters collected from the Wall Street Journal domain [25]. The basic character-level PTB LM task does not contain the beginning of a sentence marker and the space markers between characters, making it difficult to distinguish word boundaries. Hence, in this experiment, the beginning of a sentence marker and space marker were added to the basic character-level PTB LM task. The total number of characters used for the experiments was 50. The number of characters for the training, validation, and test datasets were 4.88, 0.38, and 0.43 million, respectively. We repeated experiments for the character-level PTB LM task five times to verify the stability of LMs and test their generalization.
The enwik8 LM task contains 100 million characters of unprocessed Wikipedia text [20]. The enwik8 LM task dataset is split into 90, 5, and 5 million characters, for the training, validation, and test datasets, respectively, preserving the experimental environment of previous studies. Experiments for the enwik8 LM task were repeated three times.
For the rescoring task of speech recognition, we used the LibriSpeech corpus to train an acoustic model (AM) and LM. It consists of 920 h of speech from an audiobook domain. To train the AM, we used the Kaldi speech recognition toolkit. We used an AM based on a DNN employing a hidden Markov model. The number of hidden layers and hidden nodes were 6 and 3500, respectively. The learning rate was initialized at
where ascore is an acoustic score generated by the AM, and lmscorenn is the language score generated by neural network-based LMs. All neural network-based LMs were trained with transcriptions of a training set for the AM. It consisted of 40 million characters with 30, 5, and 5 million characters used to construct training, validation, and test sets, respectively.
We used BPC and inference time as the evaluation metrics of the LM tasks. BPC is the average number of bits for encoding one character, with a bit as the unit of entropy [20]. We defined BPC as
5.2 Character-Level PTB LM Task
The baseline LM was the LSTM RNN-based LM, which we trained using PyTorch with the following hyper-parameters: number of hidden layers, 3; number of hidden nodes for each hidden layer, 1024; number of nodes in the embedding layer, 50; learning rate initialized at
On the character-level PTB LM task, the SOTA LMs were the trellis and AWD-LSTM networks. We compared the LM based using our proposed DNC with the best available performance on LMs. The hyper-parameters of the trellis and AWD-LSTM networks were the same as those used in previous studies. In the experiments, we used a batch size of 6 and a BPTT length of 120. We applied a dropout factor of 0.5, which was not applied in the embedding, input, and output layers.
To train the basic DNC-based LM, we used the LSTM RNN for the controller. The following hyper-parameters were used: number of hidden layers, 3; number of nodes in the embedding layer, 50; numbers of hidden nodes of each hidden layer, 1024, 512, and 512. The external memory used 1024 memory vectors with 512 dimensions each. The learning rate was initialized to
To train the FMD-DNC-based LM, we used the LSTM RNN as the controller. The following hyper-parameters were used: number of hidden layers, 2; number of nodes in the embedding layer, 50; number of hidden nodes in hidden layer, 1024. The external memory used 128 memory vectors with 256 dimensions each. The learning rate was initialized to 1
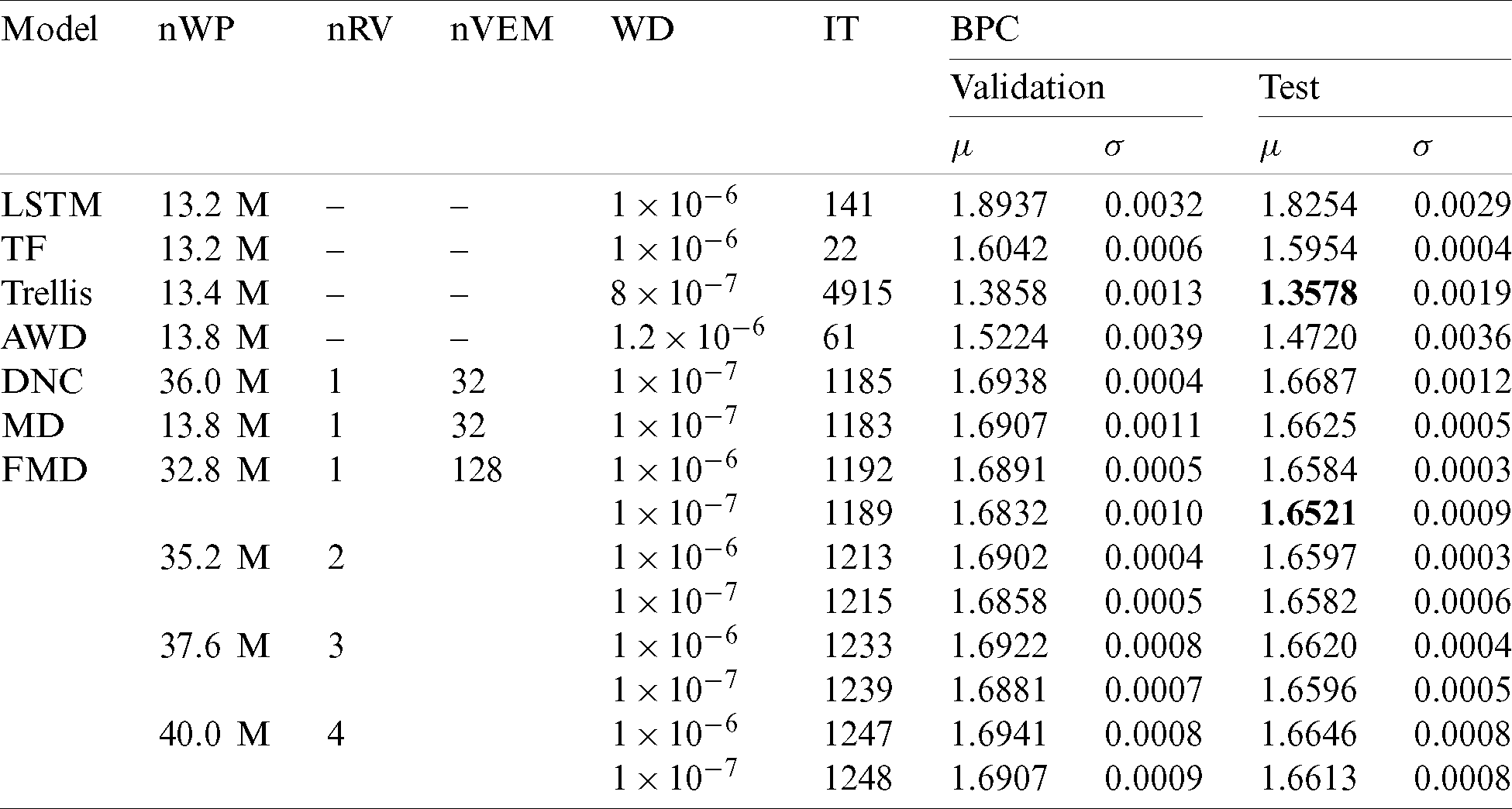
We evaluated the performance of the FMD-DNC-based LM using the number of read vectors and the value of the weight decay. The FMD-DNC-based LM with a single read vector outperformed the other FMD-DNC-based LMs with a BPC of 1.5920. While it did not achieve the best available performance of the Transformer-based LM, the FMD method showed a relative improvement of 0.41% compared with the DNC in terms of BPC. We analyzed the performance of the FMD-DNC-based LM based on the number of read vectors in three ways. First, we observed that the number of weight parameters increased according to the number of read vectors. The controller interface layer generated key vectors for the read vectors, with the number of read vectors equal to the number of key vectors. In the experiments, the key and read vectors were 256-dimensional vectors. In addition, the read vectors generated at time (t −1) affected the size of the input layer in the controller. Second, the BPC decreased based on the number of read vectors. We found that the number of read vectors was proportional to the number of weight parameters. Therefore, the character-level PTB LM task was insufficient for training the FMD-DNC-based LM. Third, the inference time was proportional to the number of read vectors and related to the first analysis, because the number of weight parameters increased based on the number of read vectors. In addition, to obtain the minimum element of
We also evaluated the performance of the FMD-DNC-based LM in terms of weight decay, which reduces overfitting by adding large penalties as the weight parameters increase [27]. To explain, we denote the set of weight parameters as P and add
Table 1: Evaluation results of FMD-DNC-based LMs on the character-level PTB LM task (TF, the Transformer; Trellis, the trellis network; AWD, the AWD-LSTM network; DNC, the vanilla DNC; MD, the MD-DNC; FMD, the FMD-DNC; nWP, number of weight parameters; nRV, number of read vectors; nVEM, number of vectors in the external memory; WD, weight decay; IT, inference time (ms/batch);
We used BPC and inference time as the evaluation metrics of the LM tasks. BPC is the average number of bits for encoding one character, with a bit as the unit of entropy [20]. We defined BPC as
For the enwik8 test, we again used LSTM RNN-based LM as the baseline, but we used the previous experimental result of that model [28]. In addition, we used the previous experimental results of the Transformer-based LM [22]. To train the plain DNC-based LM, we used the LSTM RNN as the controller. The number of hidden layers was 3, and the number of hidden nodes of the hidden layers was 1024. The number of nodes in the embedding layer was 128. The external memory consisted of 128 memory vectors with 256 dimensions each. The learning rate was initialized to
To train the FMD-DNC-based LM, we used the LSTM RNN for the controller. In experiments, we used the following hyper-parameters for the FMD-DNC-based LM: number of hidden layers, 3; number of nodes in the embedding layer, 128; number of hidden nodes for hidden layer, 1024. The external memory consisted of 128 memory vectors with 256 dimensions each. The learning rate was initialized to
Tab. 2 shows the evaluation results of the FMD-DNC-based LMs on the enwik8 LM task. We evaluated the performance of the FMD-DNC-based LM based on the number of read vectors and the weight decay value. The FMD-DNC-based LM using four read vectors outperformed the other FMD-DNC-based LMs, with a BPC of 1.3860. Although it does not match the results of the Transformer-based LM, the FMD method showed a relative improvement of 0.45% compared with the DNC in terms of BPC.
Table 2: Evaluation results of FMD-DNC-based LMs on the enwik8 LM task (TF, the Transformer; DNC, the vanilla DNC; MD, the MD-DNC; FMD, the FMD-DNC; nWP, number of weight parameters; nRV, number of read vectors; nVEM, number of vectors in the external memory; WD, weight decay; IT, inference time (ms/batch);
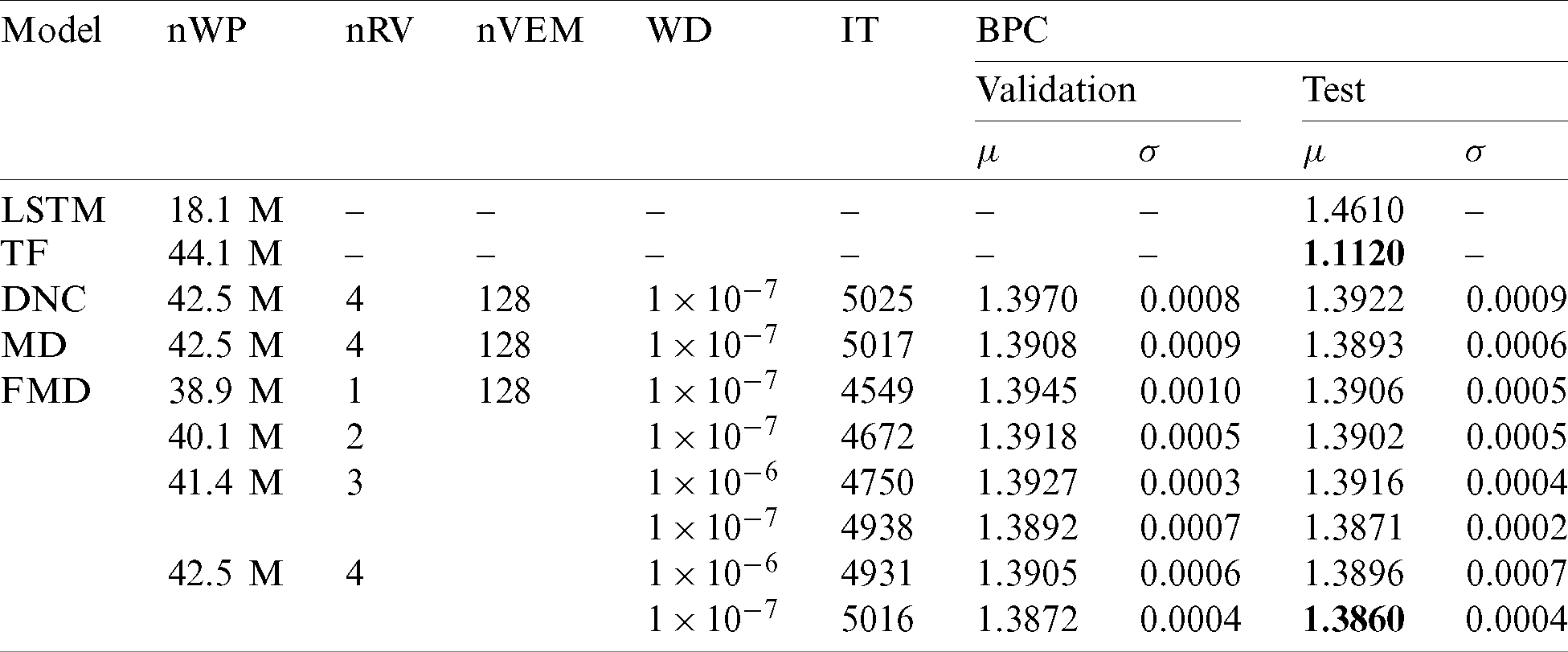
Our general notes about the performance of the FMD-DNC-based LM based on the number of read vectors are as follows. First, the number of weight parameters was twice that of Transformer. We assumed that more weight parameters were involved and better performance was demonstrated because the enwik8 LM task dataset is a large-scale dataset. However, in the experiments, the Transformer-based LM showed the best available performance. Second, we found that the BPC was higher when using more read vectors. Although it was difficult to train the FMD-DNC-based LM using 5 and more read vectors, the FMD-DNC-based LM using four read vectors outperformed the plain DNC-based LM in terms of BPC. Third, BPC decreased with the weight decay. When
5.4 Rescoring Task of Speech Recognition
We calculated the lmscorenn in Eq. (8) for the LSTM RNN, Transformer, plain DNC, MD-DNC, and FMD-DNC. The number of weight parameters for the LSTM RNN was 10.2 million, producing BPC values of 1.6428 and 1.6437 for the validation and test sets, respectively. The number of weight parameters for the Transformer-based LM was 10.4 million, producing BPC values of 1.3179 and 1.3184 for the validation and test sets, respectively. The number of weight parameters for the plain DNC, MD-DNC, and FMD-DNC were also 10.4 million. Plain DNC showed BPC values of 1.5825 and 1.5813 for the validation and test sets, respectively. MD-DNC showed BPC values of 1.5722 and 1.5729 for the validation and test sets, respectively. FMD-DNC showed BPC values of 1.5687 and 1.5690 for the validation and test sets, respectively.
Tab. 3 presents the 100-best rescoring results using the neural network-based LMs trained with transcriptions of the AM for the LibriSpeech dataset. The experimental results of the AM were the rescoring result using the acoustic score alone. The FMD-DNC-based LM showed 11.16, 33.02, and 34.58 WER according to the dev_clean, dev_other, and test_other tests, respectively. This was a relative improvement of 0.18, 0.24, and 0.03% compared with Transformer according to the dev_clean, dev_other, and test_other tests. However, with the test_clean dataset, the Transformer-based LM exhibited a relative improvement of 0.08% compared with FMD-DNC.
Table 3: 100-best rescoring results using the neural network-based LMs
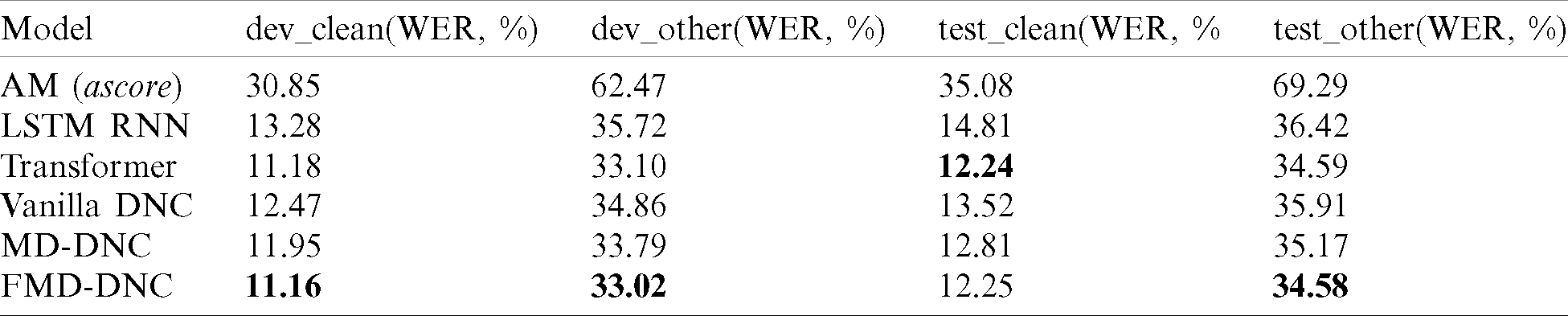
We summarize our performance findings as follows. First, although the Transformer-based LM showed a relative improvement of 19.03% compared with the FMD-DNC-based LM in terms of BPC, the FMD-DNC-based LM exhibited better performance than the Transformer-based LM on rescoring tasks. We originally anticipated that Transformer would show better performance in rescoring tasks based on it’s the best available performance on LM tasks. However, in the actual experiments, FMD-DNC showed the bset performance in rescoring tasks. Second, the FMD-DNC-based LM outperformed the MD-DNC-based LM in rescoring tasks. Therefore, our proposed FMD method outperformed the MD-DNC.
As the basic DNC has disadvantageous due to memory deallocation, we proposed an LM using FMD-DNC to address this problem. The FMD method searches for the minimum value of elements in a forget gate-based retention vector, which is a vector that indicates the retention degree of information stored in each external memory address. Our method converts the minimum value of elements to 0 and subsequently multiplies the values of the external memory at time (t −1) by the converted forget gate-based retention vector. In experiments, we applied our proposed NTM architecture to LM tasks as a task-specific domain and the rescoring of speech recognition as a general-purpose domain. On LM tasks, tests with our proposed DNC using the Penn Treebank and enwik8 LM tasks did not achieve the best available results. However, the FMD method showed a relative improvement of 0.41%–0.45% compared with DNC in terms of BPC. For testing rescoring ability in speech recognition, we evaluated our proposed DNC-based LM on the LibriSpeech task. The FMD method showed a relative improvement of 0.03%–0.24% compared with Transformer in terms of WER. For the future work, we will improve the extremely long inference time of the FMD-DNC-based LM. Furthermore, we will evaluate the FMD-DNC-based LM on WikiText-103 and One Billion Word LM tasks.
Funding Statement: This work was supported by the ICT R&D By the Institute for Information & communications Technology Promotion (IITP) grant funded by the Korea government (MSIT) [Project Number: 2020-0-00113, Project Name: Development of data augmentation technology by using heterogeneous information and data fusions].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. Mu and X. Zeng. (2019). “A review of deep learning research,” KSII Transactions on Internet and Information Systems, vol. 13, no. 4, pp. 1738–1764. [Google Scholar]
2. F. Lin, X. Ma, Y. Chen, J. Zhou and B. Liu. (2020). “PC-SAN: Pretraining-based contextual self-attention model for topic essay generation,” KSII Transactions on Internet and Information Systems, vol. 14, no. 8, pp. 3168–3186. [Google Scholar]
3. A. Graves, G. Wayne, M. Reynolds, T. Harley, I. Danihelka et al. (2016). , “Hybrid computing using a neural network with dynamic external memory,” Nature, vol. 538, no. 7626, pp. 471–476. [Google Scholar]
4. R. Csordas and J. Schmidhuber. (2019). “Improving differentiable neural computers through memory masking, de-allocation, and link distribution sharpness control,” in Proc. the 7th Int. Conf. on Learning Representations, New Orleans, LA, USA, pp. 7299–7310. [Google Scholar]
5. W. Luo and F. Yu. (2019). “Recurrent highway networks with grouped auxiliary memory,” IEEE Access, vol. 7, pp. 182037–182049. [Google Scholar]
6. A. Kumar, O. Irsoy, P. Ondruska, M. Iyyer, J. Bradbury et al. (2016). , “Ask me anything: Dynamic memory networks for natural language processing,” in Proc. the 33rd Int. Conf. on Machine Learning, New York, NY, USA, pp. 1378–1387. [Google Scholar]
7. M. Suzuki, N. Itoh, T. Nagano, G. Kurata and S. Thomas. (2019). “Improvements to n-gram language model using text generated from neural language model,” in Proc. the 44th Int. Conf. on Acoustics, Speech and Signal Processing, Brighton, UK, pp. 7245–7249. [Google Scholar]
8. Y. Bengio, R. Ducharme, P. Vincent and C. Jauvin. (2003). “A neural probabilistic language model,” Journal of Machine Learning Research, vol. 3, pp. 1137–1155. [Google Scholar]
9. G. Zhou, T. He, J. Zhao and P. Hu. (2015). “Learning continuous word embedding with metadata for question retrieval in community question answering,” in Proc. the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th Int. Joint Conf. on Natural Language Processing, Beijing, China, pp. 250–259. [Google Scholar]
10. T. Mikolov, M. Karafiat, L. Burget, J. Cernocky and S. Khudanpur. (2010). “Recurrent neural network based language model,” in Proc. the 11th Annual Conf. of the International Speech Communication Association, Makuhari, Japan, pp. 1045–1048. [Google Scholar]
11. X. Chen, A. Ragni, X. Liu and M. Gales. (2017). “Investigating bidirectional recurrent neural network language models for speech recognition,” in Proc. the 18th Annual Conf. of the Int. Speech Communication Association, Stockholm, Sweden, pp. 269–273. [Google Scholar]
12. R. Pascanu, T. Mikolov and Y. Bengio. (2013). “On the difficulty of training recurrent neural networks,” in Proc. the 30th Int. Conf. on Machine Learning, Atlanta, GA, USA, pp. 1310–1318. [Google Scholar]
13. S. Hochreiter and J. Schmidhuber. (1997). “Long short-term memory,” Neural Computation, vol. 9, no. 8, pp. 1735–1780. [Google Scholar]
14. E. Arisoy, A. Sethy, B. Ramabhadran and S. Chen. (2015). “Bidirectional recurrent neural network language models for automatic speech recognition,” in Proc. the 40th IEEE Int. Conf. on Acoustics, Speech and Signal Processing, South Brisbane, QLD, Australia, pp. 5421–5425. [Google Scholar]
15. Y. Zhang, X. Wang and H. Tang. (2019). “An improved Elman neural network with piecewise weighted gradient for time series prediction,” Neurocomputing, vol. 359, no. 2, pp. 199–208. [Google Scholar]
16. U. Khandelwal, H. He, P. Qi and D. Jurafsky. (2018). “Sharp nearby, fuzzy far away: How neural language models use context,” in Proc. the 56th Annual Meeting of the Association for Computational Linguistics, Melbourne, VIC, Australia, pp. 284–294. [Google Scholar]
17. K. Xu, J. L. Ba, R. Kiros, K. Cho, A. Courville et al. (2015). , “Show, attend and tell: Neural image caption generation with visual attention,” in Proc. the 32nd Int. Conf. on Machine Learning, Lile, France, pp. 2048–2057. [Google Scholar]
18. Y. Belinkov and J. Glass. (2019). “Analysis methods in neural language processing: A survey,” Transactions of the Association for Computational Linguistics, vol. 7, no. 4, pp. 49–72. [Google Scholar]
19. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones et al. (2017). , “Attention is all you need,” in Proc. the 31st Int. Conf. on Neural Information Processing Systems, Long Beach, CA, USA, pp. 6000–6010. [Google Scholar]
20. R. Al-Rfou, D. Choe, N. Constant, M. Guo and L. Jones. (2019). “Character-level language modeling with deeper self-attention,” in Proc. the 33rd AAAI Conf. on Artificial Intelligence, Honolulu, HI, USA, pp. 3159–3166. [Google Scholar]
21. S. Duan, H. Zhao, J. Zhou and R. Wang. (2019). “Syntax-aware transformer encoder for neural machine translation,” in Proc. the 2019 Int. Conf. on Asian Language Processing, Shanghai, China, pp. 396–401. [Google Scholar]
22. Z. Dai, Z. Yang, Y. Yang, J. Carbonell, Q. V. Le et al. (2019). , “Transformer-XL: Attentive language models beyond a fixed-length context,” in Proc. the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, pp. 2928–2988. [Google Scholar]
23. J. Devlin, M. W. Chang, K. Lee and K. Toutanova. (2019). “BERT: Pre-training of deep bidirectional transformers for language understanding,” in Proc. the Annual Conf. of the North American Chapter of the Association for Computational Linguistics, Minneapolis, MN, USA, pp. 4171–4186. [Google Scholar]
24. Y. Qu, P. Liu, W. Song, L. Liu and M. Cheng. (2020). “A text generation and prediction system: Pre-training on new corpora using BERT and GPT-2,” in Proc. the IEEE 10th Int. Conf. on Electronics Information and Emergency Communication, Beijing, China, pp. 323–326. [Google Scholar]
25. M. Marcus, M. Marcinkiewicz and B. Santorini. (1993). “Building a large annotated corpus of english: The penn treebank,” Computational Linguistics, vol. 19, no. 2, pp. 313–330. [Google Scholar]
26. D. Lee, J. S. Park, M. W. Koo and J. H. Kim. (2020). “Language model using neural turing machine based on localized content-based addressing,” Applied Sciences, vol. 10, no. 20, pp. 7181. [Google Scholar]
27. A. Gupta and S. M. Lam. (1998). “Weight decay backpropagation for noisy data,” Neural Networks, vol. 11, no. 6, pp. 1127–1137. [Google Scholar]
28. A. Mujika, F. Meier and A. Steger. (2017). “Fast-slow recurrent neural networks,” in Proc. the 31st Int.Conf. on Neural Information Processing Systems, Long Beach, CA, USA, pp. 5915–5924. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |