Computers, Materials & Continua DOI:10.32604/cmc.2021.015128
Article

Power System Resiliency and Wide Area Control Employing Deep Learning Algorithm

Pandia Rajan Jeyaraj1, Aravind Chellachi Kathiresan1, Siva Prakash Asokan1, Edward Rajan Samuel Nadar1, Hegazy Rezk2,3,*and Thanikanti Sudhakar Babu4

1Mepco Schlenk Engineering College (Autonomous), Sivakasi, Tamil Nadu, India
2College of Engineering at Wadi Addawaser, Prince Sattam Bin Abdulaziz University, Wadi Addawaser, 11991, Saudi Arabia
3Department of Electrical Engineering, Faculty of Engineering, Minia University, Minia, 61517, Egypt
4Department of Electrical and Electronics Engineering, Chaitanya Bharathi Institute of Technology, Hyderabad, 500075, India
*Corresponding Author: Hegazy Rezk. Email: hr.hussien@psau.edu.sa
Received: 07 November 2020; Accepted: 05 February 2021

Abstract: The power transfer capability of the smart transmission grid-connected networks needs to be reduced by inter-area oscillations. Due to the fact that inter-area modes of oscillations detain and make instability of power transmission networks. This fact is more noticeable in smart grid-connected systems. The smart grid infrastructure has more renewable energy resources installed for its operation. To overcome this problem, a deep learning wide-area controller is proposed for real-time parameter control and smart power grid resilience on oscillations inter-area modes. The proposed Deep Wide Area Controller (DWAC) uses the Deep Belief Network (DBN). The network weights are updated based on real-time data from Phasor measurement units. Resilience assessment based on failure probability, financial impact, and time-series data in grid failure management determine the norm H2. To demonstrate the effectiveness of the proposed framework, a time-domain simulation case study based on the IEEE-39 bus system was performed. For a one-channel attack on the test system, the resiliency index increased to 0.962, and inter-area damping ξ was reduced to 0.005. The obtained results validate the proposed deep learning algorithm’s efficiency on damping inter-area and local oscillation on the 2-channel attack as well. Results also offer robust management of power system resilience and timely control of the operating conditions.

Keywords: Neural network; deep learning algorithm; low-frequency oscillation; resiliency assessment; smart grid; wide-area control

1  Introduction

Power System Stabilizer (PSS) focuses only on damping local oscillation by generator excitation control [1]. However modern power is highly affected by both local and inter-area oscillations. This instability is further increased by demand-side energy management and distributed energy resources due to the grid-connected system [2]. A Wide Area Control (WAC) coordinates the improvement of stability and decreases inter-area oscillations in a modern power system. For efficient oscillation reduction and stability improvement, a data-driven approach in a smart grid with real-time measurement is highly necessary [3–5].

Numerous WAC methods have been proposed by many researchers, as summarized in [6]. Most conventional design architectures follow a two-level architectural framework with a lower-level local controller as PSS and WAC as an upper-level primary controller [7]. For analysis, this controller topology is robust and have an optimal control [8], adaptive control [9], model predictive control [10], Iterative learning control [11], etc. For performance evaluation, resilience indices like H2, H∞, and a mixed norm are calculated [12].

Smart grid phasor measurement unit (PMU) can provide grid-connected power system data for processing [13]. Feedback controller gain increases stability and improves inter-area damping based on real-time PMU data suggested by the western electricity coordination council (WECC). Control schemes based on the adaptive control algorithm [14], PI controller schemes [15], optimal algorithm [16], etc., have an effective role in primary level control. This causes the need for a superior advanced control scheme based on smart grid data. PMU provides exogenous inputs that aid in increasing the learning of damping inter-area oscillations for WAC.

In a smart grid system, resilience refers to the “ability if anticipating high impact, quick recovering, and prevent or mitigating similar high impact disturbance” [17]. The power grid security assessment identifies resilience strategies based on risk assessment and statistical performance index like system average interruption frequency index (SAIFI) and system average interruption duration (SAIDI) are used. FACTS devices like STATCOM [18], SVC [19], and TCSC [20] have no communication facility due to the intermittent nature of the location. For efficient inter-area oscillation, WAC represents model order reduction in a smart grid-connected system. By calculating controllability and observability, resilience computation is performed. This model has a reduced-order decentralized damping controller computed using a cross-gramian approach. Sylvester equation is used for solving cross-gramian is performed.

For IEEE 39 bus system, this WAC control approach has a higher computation time. Another traditional procedure is followed for inter-area damping PSS [21]. This control strategy needs electrical phase compensation. Also, this method makes the power system unstable. To avoid this issue in PSS, online tuning of controller parameters using fuzzy logic computation is used [22]. However, this method further increases the damping time to affect the settling time. Besides, the accuracy of parameter tuning is not affected. Another approach with synchronized phasor measurement is that the WAC controller is designed for large power systems [23]. For each terminal area, the PMU is used for data collection and processing. Based on this PMU data, a state feedback closed-loop system is formed. But by using PMU measurement in the power system results in the amplification of inter-area oscillation. Moreover, the system is observable.

To alleviate the computation complexity, an optimal WAC design problem is assigned. In [24–27], the instability caused by the power system’s structural constraints were analyzed. In [28–30], the delay in WAC measurement was considered as an objective function. However, the resilience performance assessment was not considered. In [31–33], based on steady state response, power system resilience was analyzed. Using various communication attacks and disturbance power system attack was introduced. Also, they have not considered cyber-physical attacks [34–40]. The main contributions of the proposed deep learning-based WAC method are enumerated as follows.

•    To analyze the closed-loop resilience index based on H2 norm by a data-driven approach using a deep belief network.

•    A robust inter-area oscillations damping is provided through online tuning of WAC parameter’s data-driven.

•    The resilience assessment and convergence analysis of the proposed data-driven deep learning algorithm have been experimentally validated by a case study in an IEEE 39 bus ten machine system.

The remainder of the paper is organized as follows; Section 2 develops the small-signal model formation for resilience assessment. A data-driven deep learning algorithm is described in Section 3. In Section 4, the H2 norm-based resilience index by time-domain calculation is given. In Section 5 the effectiveness of the proposed WAC scheme is validated by determining resilience assessment. Also, the convergence analysis is presented. In Section 6, inference on obtained result by comparison with a standard conventional scheme is given. Lastly, in Section 7 the conclusion of the research findings are presented.

2  Research Problem

In this research work, an N subsystem representing generator, load, bus, and other power components are reduced to two areas for study. In which area 1 is called a study area with a generator and proposed WAC controller. Area 2 is called an external area with a turbine governor, Automatic Voltage Regulator (AVR), and exciter. The complex form of the non-linear power system is given by,

ẋ(t)=f(x(t),U(t),C(t)) (1)

y(t)=g(x(t),d(t)) (2)

where x(t)∈ℝn are state variable and U(t)∈ℝm is control input, d(t)∈ℝs is a disturbance in the power system. Eqs. (1) and (2) combinedly gives a power flow relation. For reducing the inter-area oscillation flux decay model of the generator is used in the external area [18]. For obtaining minimum tuning in WAC of PMU data, this model reduction is used.

2.1 Linear Model of WAC

The main idea in WAC modeling is a real-time remote measurement. The novel data-driven approach in the design of WAC eliminates inter-area oscillation. In a real-time power system, PMUs are installed in various regions (area). Consider the local subsystem given by reduced system Eq. (3).

ẋ(t)=Axi(t)+∑i=1nBui(t)(3)

the Riccati equation control law is used for controller design. To linearize the design of WAC to dam inter-area oscillation and resilience assessment, Eq. (3) has a local study area controller namely;

u(t)=Kx(t)=WAC(4)

where K is WAC gain. u(t) is the control law for the system equation described in Eq. (3).

The linear power system model is given by;

dΔx(t)dt=Δωi (5)

MdΔx(t)dt=Δpm-DiΔx(t) (6)

TrdΔx′(t)dt=δVi-δVj

TadΔVdt=KAΔVref(t)

In the proposed linear model of the study area, PMU encounters various network attacks. Hence, an optimal design with resilience for WAC is considered by the deep learning technique. This validates the proposed deep learning-based WAC, mainly focusing on WAC’s trade-off design as an optimal and resilience-based method. The non-linearity in PMU is considered a communication failure, such that data does not transfer between bus 1→2 or 2→1. This attack is a Denial of Service (DoS) attack. The mathematical equation of attack of WAC is given by Eq. (9).

WACα=K(α)∘x(t)(7)

where α is attack matrix, ∘ represents the WAC gain and state variable Hadamard product in matrix form. Fig. 1 shows the block diagram of the proposed WAC state model with deep learning algorithm tuning.

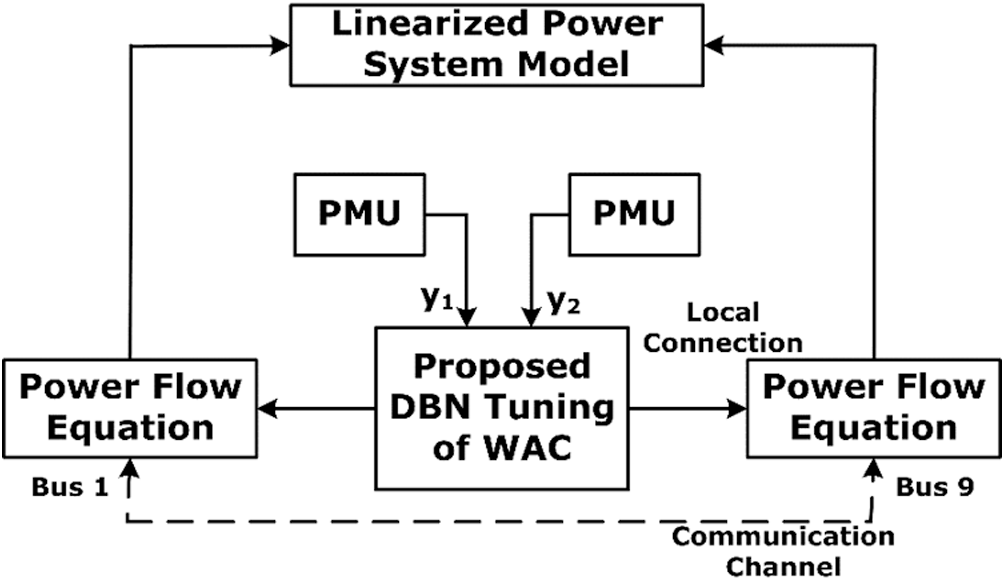
Figure 1: Block diagram of proposed WAC stability control state space model

2.2 Research Problem Formation

The proposed WAC, described in Eq. (9), is used to assess the power system’s dynamic stability with inter-area oscillation compensation. The data collected in PMU is power flow between bus 1→2 and 2→1. The reduced cross gramian model is given in Eq. (10).

[ẋnxė]=[A11A12A21A22][xnxe]+[10]ΔU(10)

The deep belief network tunes this model to reduce inter-area oscillation and resilience assessment by preserving the system’s original dynamic character. The proposed DBN produces the trade-off between system inter-area oscillation reduction and resilience assessment. Hence, the problem depends on two important analyses as follows.

•    The proposed WAC with gain K is tuned by DBN for all possible attacks.

•    To identify the most vulnerable bus that makes not resilience of the system.

To verify the effectiveness of the proposed DBN-WAC with varying operating conditions, the simulation was carried on an IEEE 39 bus system with a three-phase-to-ground fault on the external area.

Simulation scenario: In IEEE 39 bus 10 machine system three-phase-to-ground fault is introduced in the external area connecting bus 1 and 2 at time t = 0.6 s, switching the fault occurred tie line in the study area at time t = 0.7 s.

3  Proposed WAC Tuning by Deep Belief Network

This section develops a Deep Belief Network (DBN) to gain tuning in the WAC. By using the linear power system model in Eq. (4), the state variable xi is defined as;

xi:=M(2V-Vi)-Zi(11)

where Zi is the noisy measurement and Vi is the voltage at bus i. This affects the controller gain K with a different attack. The optimal tuning of the WAC by DBN is obtained by PMU data from the phasor data connection. By tuning the proposed WAC using the controlled input from PMU, the controlled output signal U1c and U2c provide modified control law given by Eq. (12).

[ẋ1(t)x2(t)̇]=[KA11B12A21+B21A22][x1(t)x2(t)]+[KB11KB12B21K+A22][U1(t)U2(t)](12)

In general, the state of tuned WAC is given by Eq. (13).

ẋc(t)=Acx(t)+BcU(t) (13)

yc(t)=Ccx(t)+DcU(t) (14)

where subscript c denote the controller state model. xc(t) is gain controlled WAC and yc(t) is controlled output vector. The proposed deep learning resilient controller is given in Fig. 2.

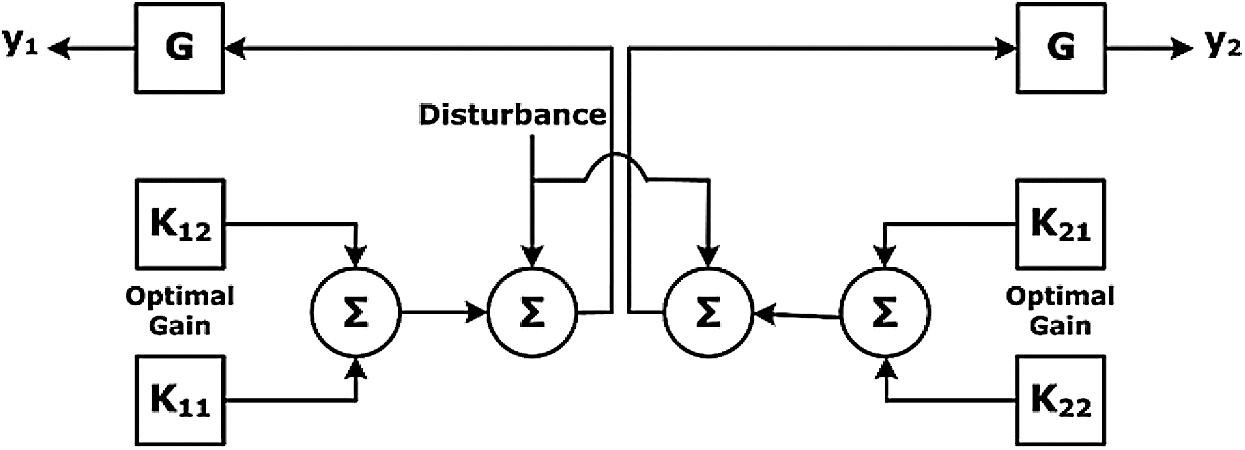
Figure 2: Set up for resilience controller with optimal gain

The component of H∞ of the resilient controller is given by Eq. (15).

K11(s)=Ci(sI-Ai)B11+D11(15)

Here, Ci represents the full order observer input layer. The tuning of controller gain gives the optimal gain K12 is made by the objective function as follows:

min∥K11fd+K12K22∥<1(16)

where, fd is the number of internal stabilizers for the designed controller. The tuned time-domain model of WAC is given by Eq. (17).

(K+1)T=Ac(KT)+Bc(KT+1) (17)

WACxc(t)=xe(KT-Td) (18)

Eq. (18) obtained input as active power flow through the line 1→2 and xe is the net reactance of the connecting buses 1 and 2. The flowchart of tuning using the DBN model is given in Fig. 3. For tuning the proposed multi-objective optimization for decreasing inter-area oscillation and increasing stability. In the study area, WAC’s gain is the maximization of Eq. (19). The second function for minimizing inter-area oscillation obtained by reducing the system’s damping ratio is given in Eq. (20).

F1= max∫t=0iK(α)dt (19)

F2= min(K(α)) (20)

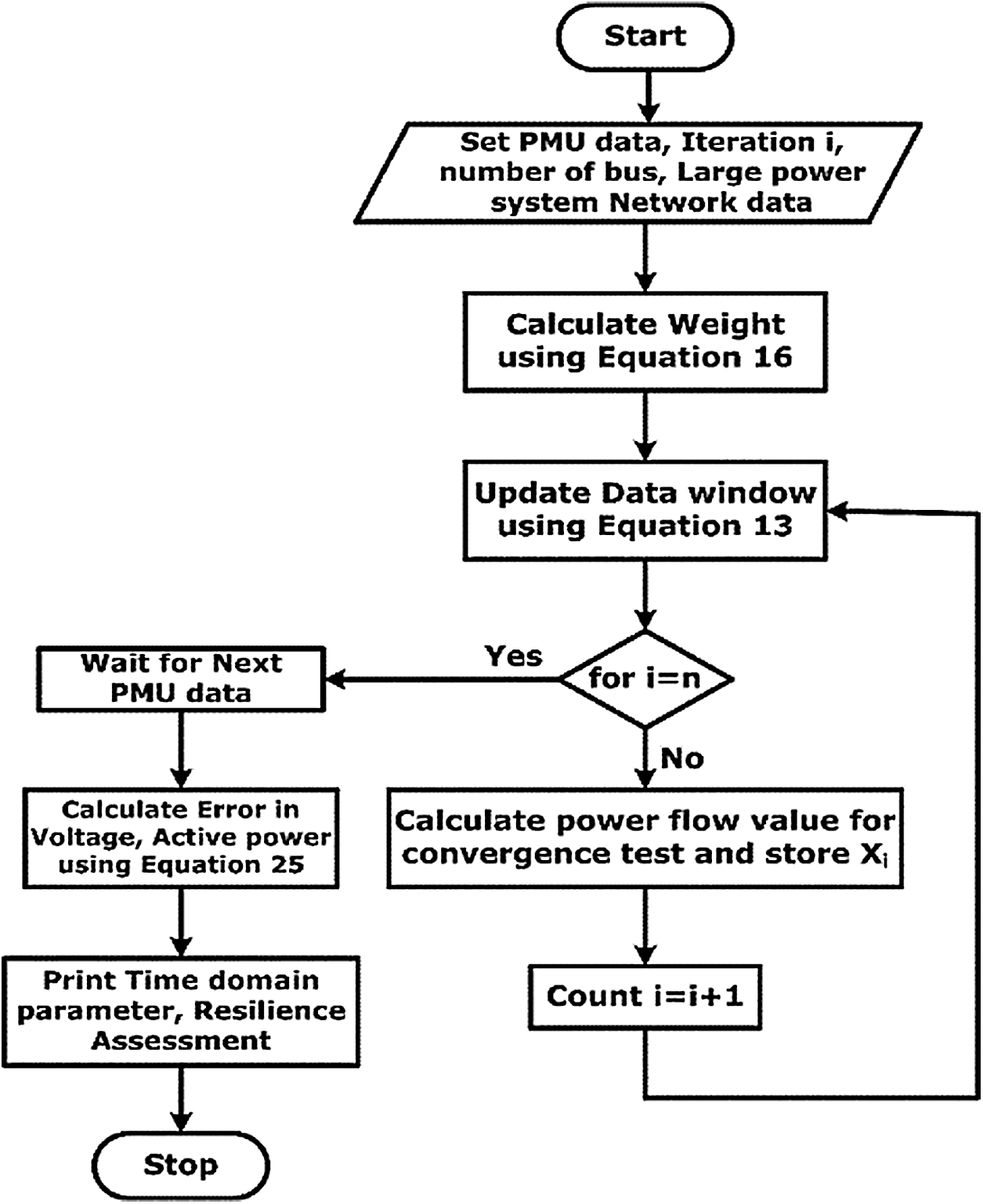
Figure 3: Flow chart of proposed DBN tuning of WAC

In the study area, the training samples are generated based on operating states. Tab. 1 presents the number of states used in the study area to train the proposed DBN model.

Table 1: Details of IEEE 39 bus system operating states for training proposed DBN

For tuning this objective function, the constraints are given by;

•    The power system model is a linearized model with the second order.

•    The generator operator in the control area.

•    The damping ratio should be greater than 0.1.

4  Proposed Resilience Assessment and Analysis

As indicated, the main objective of the proposed WAC is to help inter-area oscillations. By calculating H2 norm and mixed H2/H∞ norm the resilience assessment is performed. By introducing a DoS attack on bus 1→2, we formalize the post attached to the power system’s condition.

4.1 Mathematical Analysis of Resilience Assessment

For assessing the performance of the proposed DBN tuned WAC, a DoS attack on the bus 1→2 with gain K(α) has been considered and given by,

ẋ(t)=Ax+B(K(α))W (21)

y=cx (22)

where W denotes the updated weight for control law given in Eq. (4). For each weight updating, the Hadamard product is performed. The H2 norm of the closed-loop system is given by Eq. (23).

K(α)=K(α)∘W(23)

By solving Eq. (23) by Ricatti approach, the H2 norm is given by Eq. (24).

∥H∥2=12π∫-∞∞trace (K(jω))dω (24)

[A+BK(α)]TP(α)+CTC=0 (25)

This nominal WAC controller design was checked by DoS attack by introducing Mo with reduced dimensionality. The H2 norm in Eq. (24) is used for assessing those mentioned above.

4.2 H∞ Norm Resilience Index for Assessment

The system matrices can be defined based on DoS attack profile α∈Ao and overall DBN tuned WAC controller gain K. The objective function with DoS and tuned controller gain is given by γ(α,K). The solution for this objective function is given by Eq. (26).

γ(α,K)=M(K(α))1+M(K(α)) (26)

γ(α,K∘)=J(I,K∘)J(α,K∘) (27)

maxtrace[ETP(α)E]

A(α)P(α)+P(α)TK(α)+CTC=0

where, (I,K∘) is the identity matrix on the non-attacked external area. Hence, the resilience index for the proposed WAC is given for DoS attack α. The non-optimal controller is given by Eq. (28). This controller with nominal controller gain (K∘) is resilient under the DoS attack. Adaptive resilience involves tuning weight by changing Wi→Wi* and control input Ui→Ui*. The change in weight for each iteration with a new optimal value is ΔW=Wi-Wi*.

5  Implementation of Proposed Deep Learning Algorithm Tuned WAC

The proposed WAC is implemented in an IEEE 39 bus system for analysis and resilience assessment. In the IEEE 39 bus 10 machine system, one machine is considered as a study area, and the remaining 9 machines are considered as an external area. Tab. 1 presents the details of training states of the IEEE 39 bus 10 machines system.

To implement the linearized model of the IEEE 39 bus system, a MATLAB power system toolbox has been used. This standard model has 10 generators, in which one generator operates at the sub-transient state. Generator 1 and generator 10 connected through WAC for damping inter-area oscillation. Moreover, generator 10 is connected was a slack bus. PMU used to collect its dynamics to another controlled generator. The overall system has 90 external states.

Fig. 4 shows the implementation of the proposed DBN-WAC on the IEEE 39 bus system. We evaluate the WAC at nominal operating states. For resilience assessment bus 1→2, the DoS attack is introduced, which affects PMU data. For resilience assessment, three-phase faults are applied at bus 1→2. At simulation time t = 10 seconds, and clears the oscillations at 28 ms. This impact of fault is observed on 1st generator.

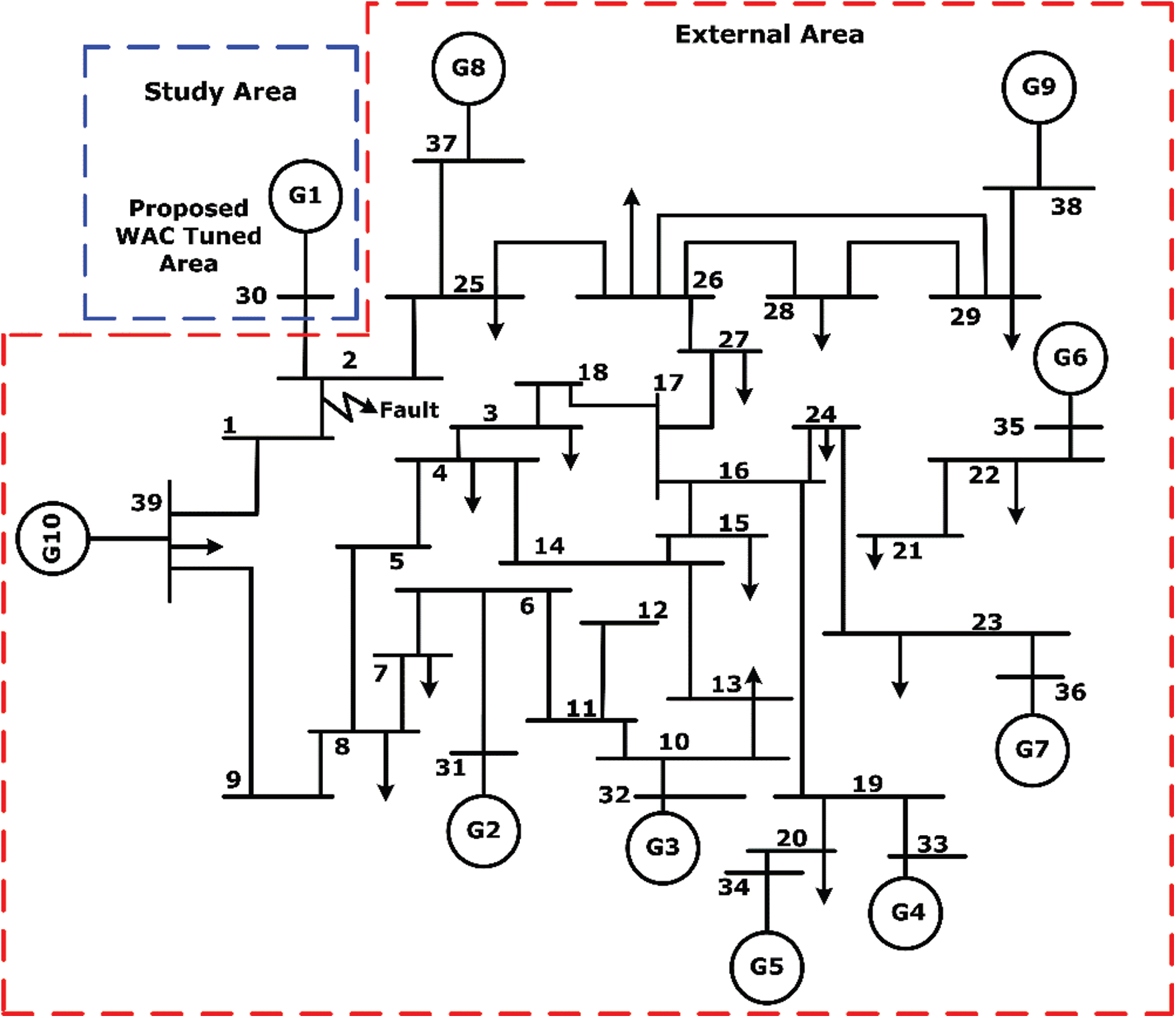
Figure 4: IEEE 39 bus 10 machine system with proposed deep learning-based WAC tuning

6  Results and Discussion

The dynamic performance was quantified under the same operating states of the test system. For quick oscillation damping verification, the proposed controller damping is verified by calculating the resilience index on channel 9→1 on the external area. The three-phase fault is perturbing generator number one with an amplitude of 0.7 p.u. for 10 s.

Fig. 5 presents the damping of low-frequency inter-area oscillation. It is observed that a significant improvement compared with the conventional PSS. Thanks to the proposed deep learning tuned WAC, the transient response is highly suppressed. In addition, the settling time is reduced. Similarly, the steady-state response is quickly obtained with less time to settle to steady-state as illustrated in Fig. 4.

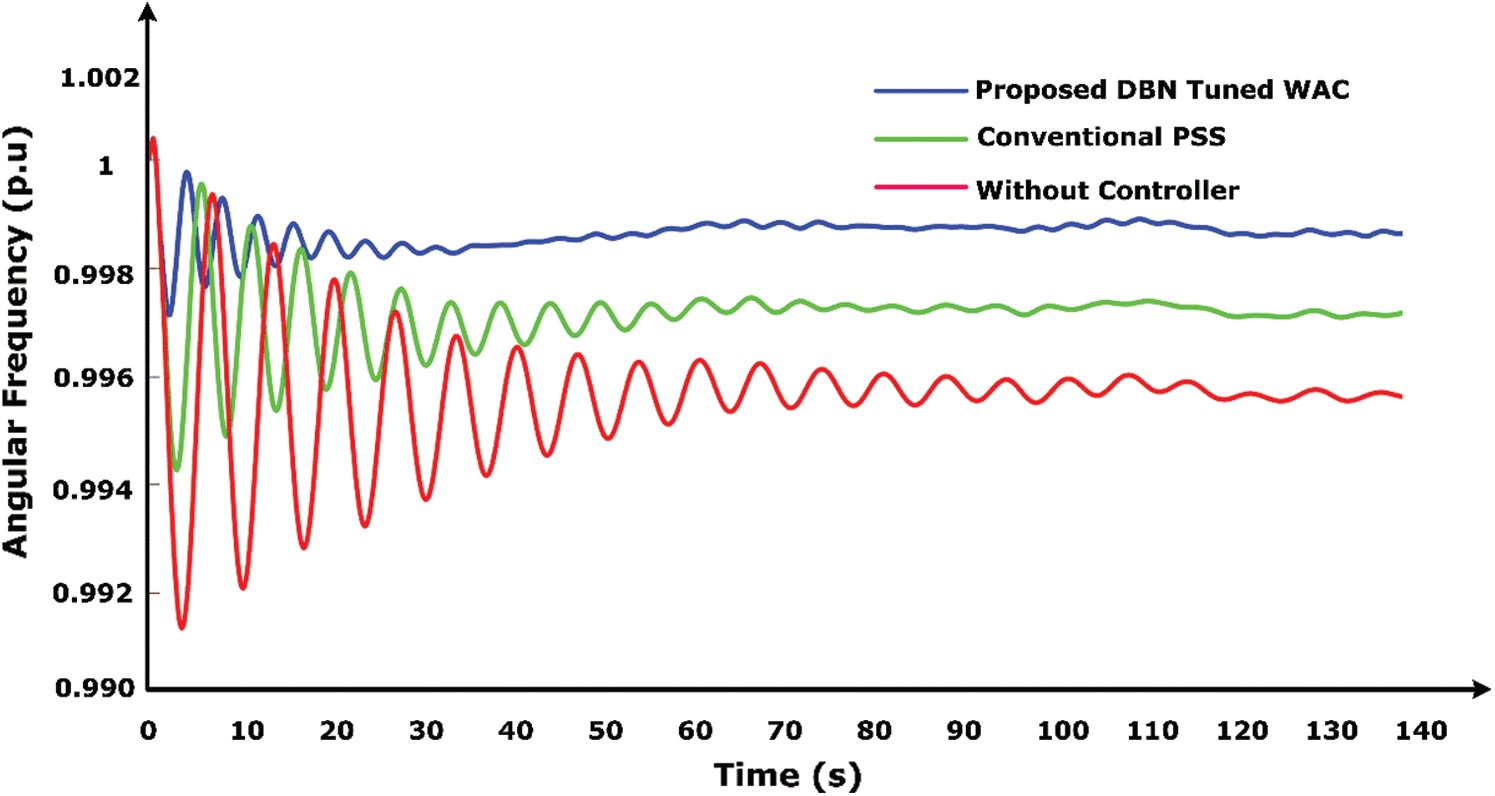
Figure 5: Contingency analysis of proposed WAC controller due to three-phase faults on IEEE 39 bus 10 machine system

6.1 Online Deep Learning Algorithm Tuning Validation

To evaluate the robustness of the proposed algorithm tuning by applying 3 phase faults. The online tuning was carried at different operating conditions. This makes the system forced to settle at different instants. For changing the operating condition, loads are added on the bus 5 to 10 in the external area; this impacts the study area. From this PMU data, online tuning is initiated. The load changed from 100 MW to 200 MW. The three-phase fault is applied after dynamic loading is initiated. The fault is applied after bus 9 at time t = 20 ms and cleared after t = 100 ms. The active power flow between bus 1 and 10 was analyzed compared to deep learning tuning WAC and offline tuning. Fig. 6 shows the active tie-line power flow in buses 1 and 2 due to a 3-phase fault.

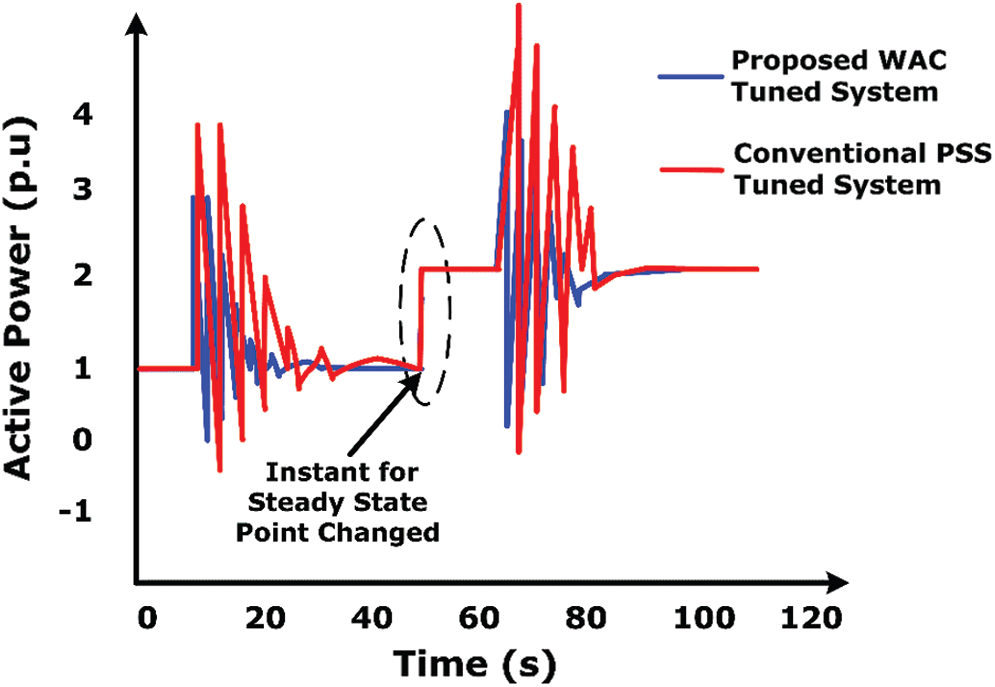
Figure 6: Comparison of tie line active power due to fault at bus 1 and bus 2 for proposed WAC and conventional PSS with steady state tracking validation

From Fig. 6, deep learning tuning quickly suppresses the oscillation and easily achieved the steady state by comparing to conventional PSS. The steady state is obtained at t = 15 ms, which confirms, after the fault is cleared after time t = 5 ms for oscillation damping.

The proposed WAC’s reliability for damping inter-area oscillation is analyzed by tracking the eigenvalue trajectories without controller, conventional PSS, and proposed controller. Fig. 7 shows the trajectory of eigenvalue with inter-area oscillation in the complex plane. From Fig. 7, we can identify the original IEEE 39 bus system has poor inter-area oscillation damping with eigenvalue ζ=0.1418 with any controller. This value is reduced to ζ=0.0785 with conventional PSS employed, but still damping is low and exhibits steady-state oscillation. The system has an eigenvalue ζ=0.0418 with proposed deep learning tuned WAC; this validates the system damped in inter-area oscillations. The damping ratio of the original system without any controller is 3.65%. The conventional PSS has slightly shifted the poles to the left of the imaginary axis with a damping ratio of 5.25%. For a change in the operating condition, the proposed deep learning tuned WAC has reduced the damping ratio to 2.15%; this increases the dynamic response by tracking the trajectory.

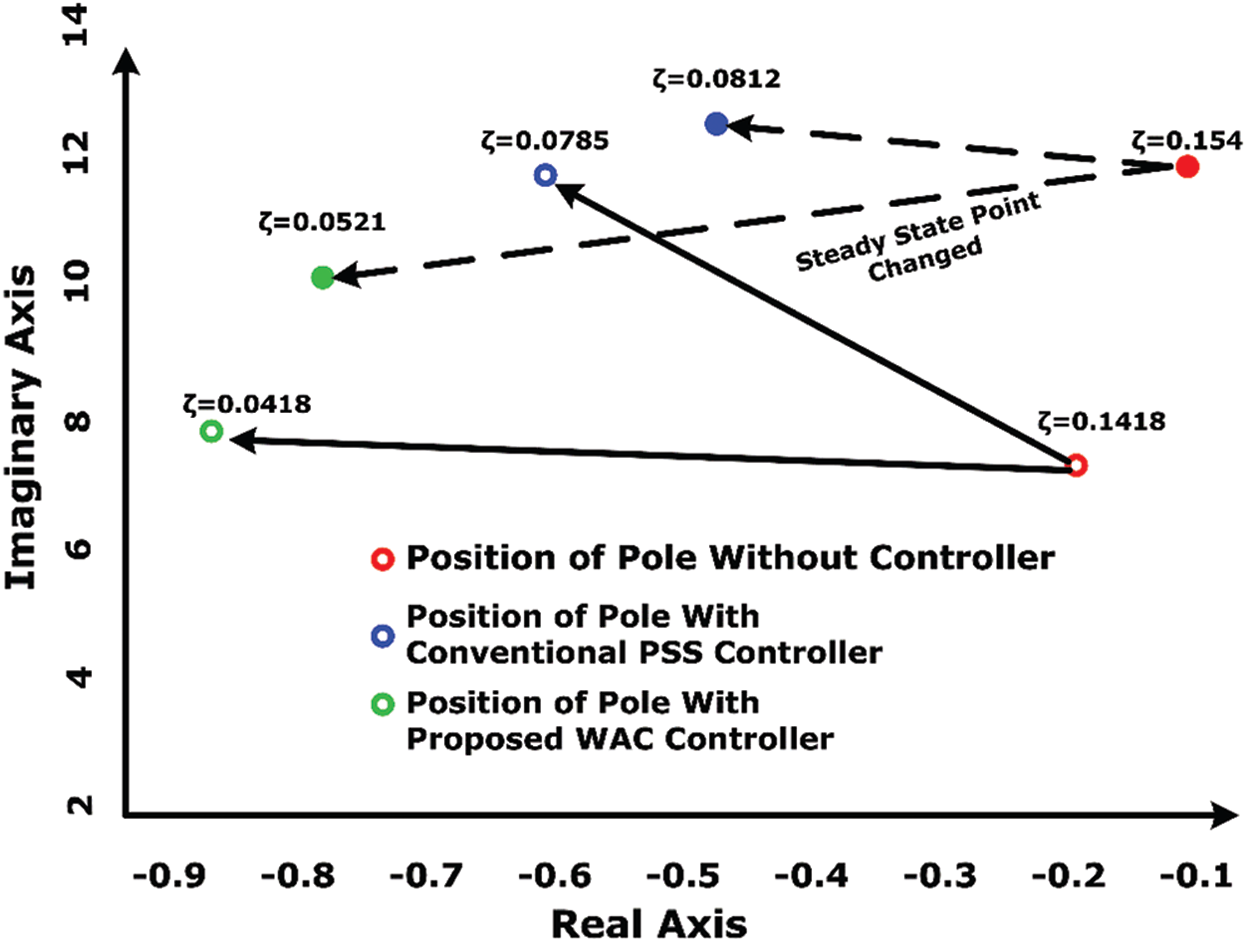
Figure 7: Comparison of eigenvalue trajectory by changing the operating state

6.2 Effectiveness by Resilience Index Assessment for Each Controller

Eq. (26) is used to estimate the resilience index by applying a DoS attack on the proposed deep WAC controller. In Tab. 2, the destabilizing attack of conventional PSS and proposed DBN-WAC is presented. Fig. 8 shows the controller resilience index for DoS attack on change bus 1→2. From Fig. 8, we can identify the resilience index is higher than the conventional PSS controller. This provides validation of the proposed WAC is more resilient than other controllers and more effective than system resilient.

Table 2: Resilience Index between bus 1→2 under DoS attach by three-phase ground faults

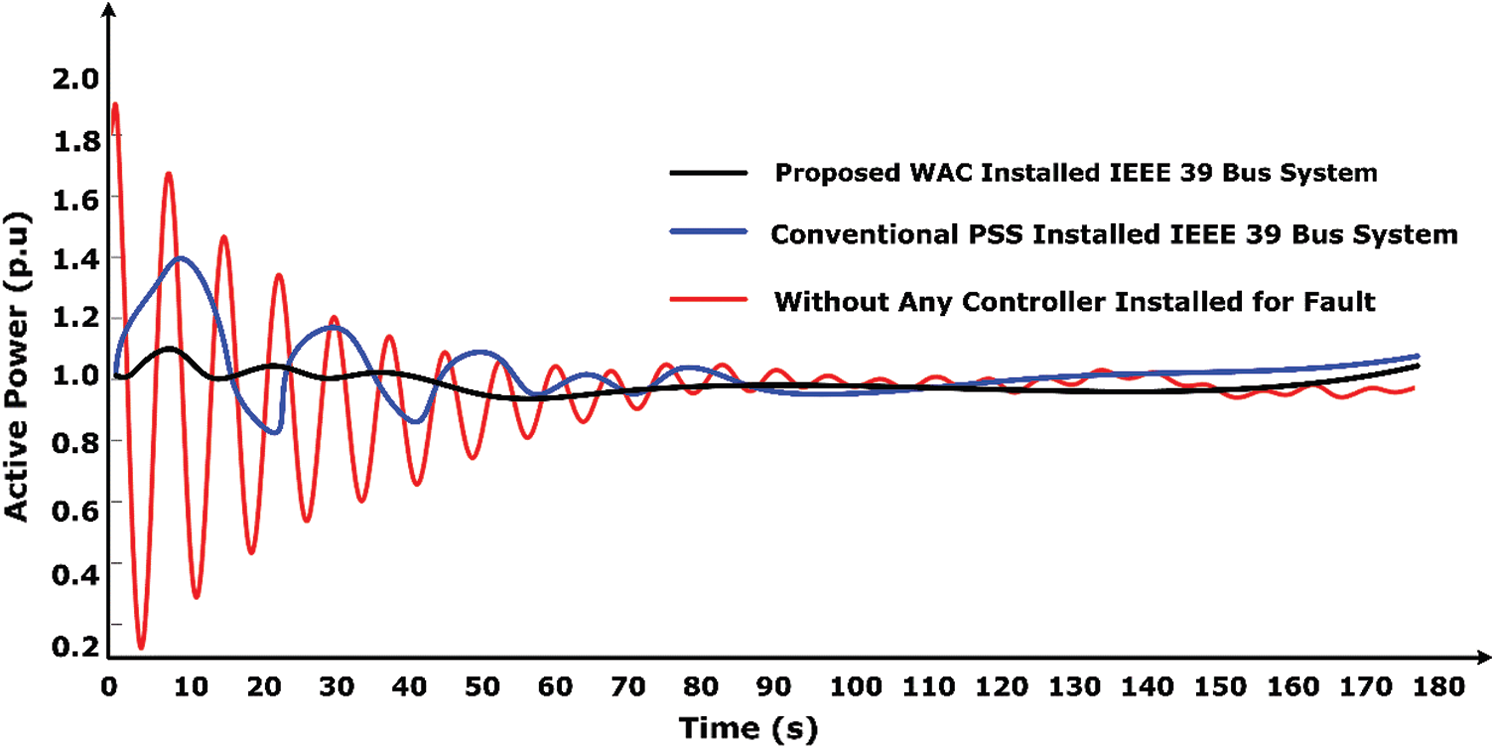
Figure 8: Resilience index of proposed WAC controller on the DoS attack

Tab. 3 presents the classification result on inter-area oscillation and local oscillation of the IEEE 39 bus test system with the proposed DBN-WAC controller and without a controller. From Tab. 3, we can identify that the system exhibits local oscillation without any controller based on a negative damping ratio. There are local, and inter-area modes for bus 4 to 7 and 21 to 29 since these modes have higher frequencies and greater damping ratios.

Table 3: Performance comparison of proposed DBN damping controllers for each inter-area mode under bus 1→2 under DoS attach by three-phase ground faults

7  Conclusion

A mathematical model of deep learning-based WAC tuning for damping inter-area oscillation and power system resilience is proposed. For communication network attacks, power system resilience is assessed and analyzed. For analysis, an IEEE 39 bus, including ten machines system, were considered, and it is divided into the study area and an external area for verification. The proposed WAC is installed in the study area. Online tuning is performed using a deep belief network by PMU data. To check the resilience and damping low-frequency oscillation, DoS attack and three-phase faults were introduced on the external area, and the effect is analyzed in the study area. H2 norm, and mixed H2/H∞ norm are calculated on the weakest communication channels. For a one-channel attack on IEEE 39 Bus test system, the resiliency index increased to 0.962, and inter-area damping ξ is reduced to 0.005. The proposed WAC framework has shown considerable improvement in reducing inter-area oscillation and fast resilience compared with conventional PSS from the obtained result. Moreover, the simulation results have highlighted the proposed deep learning algorithm’s capability to assess and quantify the resilience of power systems on various attacks. Hence, this proposed WAC scheme has an effective real-time application of a large power system smart grid.

Acknowledgement: The authors would like to thank the Management, Principal, and Renewable Energy Lab, Department of Electrical and Electronics Engineering of Mepco Schlenk Engineering College, Sivakasi, for providing the authors with the necessary facilities to carry out this research work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Li and Y. Chen. (2018). “A wide-area dynamic damping controller based on robust H∞ control for wide-area power systems with random delay and packet dropout,” IEEE Transactions on Power Systems, vol. 33, no. 4, pp. 4026–4037. [Google Scholar]

 2.  N. M. Kumar, A. A. Chand, M. Malvoni, K. A. Prasad, K. A. Mamun et al. (2020). , “Distributed energy resources and the application of AI, IoT, and blockchain in smart grids,” Energies, vol. 13, no. 21, pp. 5739. [Google Scholar]

 3.  B. P. Padhy. (2019). “Adaptive latency compensator considering packet drop and packet disorder for wide area damping control design,” International Journal of Electrical Power & Energy Systems, vol. 106, no. 57, pp. 477–487. [Google Scholar]

 4.  S. A. Kumar, M. S. P. Subathra, N. M. Kumar, M. Malvoni, N. J. Sairamya et al. (2020). , “A novel islanding detection technique for a resilient photovoltaic-based distributed power generation system using a tunable-Q wavelet transform and an artificial neural network,” Energies, vol. 13, no. 16, pp. 4238. [Google Scholar]

 5.  N. Yonghui, Z. Yidan, Z. Yan, F. Binbin and Z. Lili. (2019). “Wide-area optimal damping control for power systems based on the ITAE criterion,” International Journal of Electrical Power & Energy Systems, vol. 106, no. 4, pp. 192–200. [Google Scholar]

 6.  L. Yong, Z. Yang, L. Fang, C. Yijia and R. Christian. (2017). “Design and implementation of delay-dependent wide-area damping control for stability enhancement of power systems,” IEEE Transactions on Smart Grid, vol. 8, no. 4, pp. 1831–1842. [Google Scholar]

 7.  G. Wang, Y. Zhao, Y. Huang and Y. Wu. (2018). “An effective approach to controller placement in software defined wide area networks,” IEEE Transactions on Network and Service Management, vol. 15, no. 1, pp. 344–355. [Google Scholar]

 8.  E. C. Murilo, D. Dotta, R. Kuiava and R. A. Ramos. (2018). “A procedure to design fault-tolerant wide-area damping controllers,” IEEE Access, vol. 6, pp. 23383–23405. [Google Scholar]

 9.  Z. Kun, R. Saeed, N. Lars and Z. Boming. (2015). “Design phasor data concentrator as adaptive delay buffer for wide-area damping control,” Electric Power Systems Research, vol. 127, pp. 22–31. [Google Scholar]

10. T. Joseph, B. Tyagi and V. Kumar. (2019). “Adaptive optimal wide-area controller for multi-area power system using phasor measurement unit measurements,” IET Generation, Transmission & Distribution, vol. 13, no. 23, pp. 5284–5293. [Google Scholar]

11. N. Ali, J. S. Mehdi and E. Mahdiyeh. (2020). “Designing of wide-area damping controller for stability improvement in a large-scale power system in presence of wind farms and SMES compensator,” International Journal of Electrical Power & Energy Systems, vol. 119, pp. 1–10. [Google Scholar]

12. T. Surinkaew and I. Ngamroo. (2019). “Inter-area oscillation damping control design considering impact of variable latencies,” IEEE Transactions on Power Systems, vol. 34, no. 1, pp. 481–493. [Google Scholar]

13. A. C. Kathiresan, J. PandiaRajan, A. Sivaprakash, T. Sudhakar Babu and M. R. Islam. (2020). “An Adaptive feed-forward phase locked loop for grid synchronization of renewable energy systems under wide frequency deviations,” Sustainability, vol. 12, no. 17, pp. 1–15. [Google Scholar]

14. M. Mahshid, E. Istvan and K. Gerhard. (2020). “Fixed order non-smooth robust H∞ wide area damping controller considering load uncertainties,” International Journal of Electrical Power & Energy Systems, vol. 115, pp. 1–8. [Google Scholar]

15. M. A. Hannan, N. N. Islam, A. Mohamed, M. S. H. Lipu, P. J. Ker et al. (2018). , “Artificial intelligent based damping controller optimization for the multi-machine power system: A review,” IEEE Access, vol. 6, pp. 39574–39594. [Google Scholar]

16. S. Roy, A. Patel and I. N. Kar. (2019). “Analysis and design of a wide-area damping controller for inter-area oscillation with artificially induced time delay,” IEEE Transactions on Smart Grid, vol. 10, no. 4, pp. 3654–3663. [Google Scholar]

17. L. Zacharia, L. Hadjidemetriou and E. Kyriakides. (2018). “Integration of renewables into the wide area control scheme for damping power oscillations,” IEEE Transactions on Power Systems, vol. 33, no. 5, pp. 5778–5786. [Google Scholar]

18. A. Gholami, T. Shekari, M. H. Amirioun, F. Aminifar, H. A. Amini et al. (2018). , “Toward a consensus on the definition and taxonomy of power system resilience,” IEEE Access, vol. 6, pp. 32035–32053. [Google Scholar]

19. M. Kazem, A. Saeed and G. Sajjad. (2018). “Toward a wide-area load shedding scheme: Adaptive determination of frequency threshold and shed load values,” International Transactions on Electrical Energy Systems, vol. 28, no. 1, pp. 1–12. [Google Scholar]

20. Y. Yang, W. Tang, Y. Liu, Y. Xin and Q. Wu. (2018). “Quantitative resilience assessment for power transmission systems under typhoon weather,” IEEE Access, vol. 6, pp. 40747–40756. [Google Scholar]

21. B. J. Pierre, F. W. Bernal, D. A. Schoenwald, R. T. Elliott, D. J. Trudnowski et al. (2019). , “Design of the pacific DC intertie wide area damping controller,” IEEE Transactions on Power Systems, vol. 34, no. 5, pp. 3594–3604. [Google Scholar]

22. R. Zhang, J. Wu, M. Shao, B. Li and Y. Lu. (2018). “Transient stability prediction of power systems based on deep belief networks,” in Proc. of the 2nd IEEE Conf. on Energy Internet and Energy System Integration, Beijing, pp. 1–6. [Google Scholar]

23. P. R. Jeyaraj, E. R. S. Nadar, A. C. Kathiresan and S. P. Asokan. (2020). “Smart grid security enhancement by detection and classification of non-technical losses employing deep learning algorithm,” International Transactions on Electrical Energy Systems, vol. 30, no. 9, pp. 1–12. [Google Scholar]

24. G. Wei and W. Qiulan. (2010). “Linearized voltage stability index for wide-area voltage monitoring and control,” International Journal of Electrical Power & Energy Systems, vol. 32, no. 4, pp. 333–336. [Google Scholar]

25. S. Foad and M. I. Behnam. (2015). “Identification of inter-area oscillations using wavelet transform and phasor measurement unit data,” International Transactions on Electrical Energy Systems, vol. 25, no. 11, pp. 1–11. [Google Scholar]

26. M. Jing, W. Tong, Y. Weiyang and W. Zengping. (2014). “Design of wide-area robust damping controller based on the non-convex stable region for inter-area oscillations,” International Journal of Electrical Power & Energy Systems, vol. 55, no. 3, pp. 473–480. [Google Scholar]

27. M. Maghsoud, A. Farrokh, N. Daryoosh and G. Sajjad. (2013). “Wide-area power oscillation damping with a fuzzy controller compensating the continuous communication delays,” IEEE Transactions on Power Systems, vol. 28, no. 2, pp. 1997–2005. [Google Scholar]

28. H. Wang, P. Ju, S. Lei, Z. Wang, F. Wu et al. (2020). , “Markov decision process-based resilience enhancement for distribution systems: An approximate dynamic programming approach,” IEEE Transactions on Smart Grid, vol. 11, no. 3, pp. 2498–2510. [Google Scholar]

29. N. M. Kumar, A. Ghosh and S. S. Chopra. (2020). “Power resilience enhancement of a residential electricity user using photovoltaics and a battery energy storage system under uncertainty conditions,” Energies, vol. 13, no. 16, pp. 4193. [Google Scholar]

30. R. Spandan, P. Abhilash and N. K. Indra. (2019). “Analysis and design of a wide-area damping controller for inter-area oscillation with artificially induced time delay,” IEEE Transactions on Smart Grid, vol. 10, no. 4, pp. 3654–3663. [Google Scholar]

31. I. Ghader, K. Amin and G. Eskandar. (2017). “A new intelligent wide area-controlled islanding detection method in interconnected power systems,” International Transactions on Electrical Energy Systems, vol. 27, no. 7, pp. 1–11. [Google Scholar]

32. R. Zhipeng, D. Dong, H. Li and C. Chen. (2018). “Self-paced prioritized curriculum learning with coverage penalty in deep reinforcement learning,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 6, pp. 2216–2226. [Google Scholar]

33. P. R. Jeyaraj and E. R. S. Nadar. (2019). “Computer vision for automatic detection and classification of fabric defect employing deep learning algorithm,” International Journal of Clothing Science and Technology, vol. 31, no. 4, pp. 510–521. [Google Scholar]

34. K. Lalit and K. Nand. (2018). “Wide area monitoring of sustained oscillations using double-stage mode decomposition,” International Transactions on Electrical Energy Systems, vol. 28, no. 6, pp. 1–18. [Google Scholar]

35. S. Parimal, B. Karthikeyan, H. Ramtin and M. Elham. (2016). “Design of a wide area damping controller based on partial right eigen structure assignment,” Electric Power Systems Research, vol. 134, pp. 134–144. [Google Scholar]

36. W. Yao, L. Jiang, J. Wen, Q. Wu and S. Cheng. (2015). “Wide-area damping controller for power system interarea oscillations: A networked predictive control approach,” IEEE Transactions on Control Systems Technology, vol. 23, no. 1, pp. 27–36. [Google Scholar]

37. R. Dakota and F. O. B. John. (2018). “Multivariable loop-shaping control design for stability augmentation and oscillation rejection in wide-area damping using HVDC,” Electric Power Systems Research, vol. 157, no. 5, pp. 238–250. [Google Scholar]

38. J. A. O. Lala and C. F. Gallardo. (2020). “Adaptive tuning of power system stabilizer using a damping control strategy considering stochastic time delay,” IEEE Access, vol. 8, pp. 124254–124264. [Google Scholar]

39. I. Zenelis and X. Wang. (2018). “Wide-area damping control for interarea oscillations in power grids based on PMU measurements,” IEEE Control Systems Letter, vol. 2, no. 4, pp. 719–724. [Google Scholar]

40. M. S. Almas, L. Vanfretti, R. S. Singh and G. M. Jonsdottir. (2018). “Vulnerability of synchrophasor-based WAMPAC applications to time synchronization spoofing,” IEEE Transactions on Smart Grid, vol. 9, no. 5, pp. 4601–4612. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.