Computers, Materials & Continua DOI:10.32604/cmc.2021.014383
Article

Second Law Analysis of Magneto Radiative GO-MoS2/H2O–(CH2OH)2 Hybrid Nanofluid

Adnan1, Umar Khan2, Naveed Ahmed3, Syed Tauseef Mohyud-Din4, Dumitru Baleanu5,6,7, Kottakkaran Sooppy Nisar8 and Ilyas Khan9,*

1Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif AJ&K, 12080, Pakistan
2Department of Mathematics and Statistics, Hazara University, Mansehra, 21120, Pakistan
3Department of Mathematics Faculty of Sciences, HITEC University, Taxila Cantt, 47070, Pakistan
4University of Multan, Multan, 66000, Pakistan
5Department of Mathematics, Cankaya University, Ankara, Turkey
6Institute of Space Sciences, Magurele, 077125, Romania
7Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
8Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi, Aldawaser, 11991, Saudi Arabia
9Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, 72915, Vietnam
*Corresponding Author: Ilyas Khan. Email: ilyaskhan@tdtu.edu.vn
Received: 17 September 2020; Accepted: 12 December 2020

Abstract: Entropy Generation Optimization (EGO) attained huge interest of scientists and researchers due to its numerous applications comprised in mechanical engineering, air conditioners, heat engines, thermal machines, heat exchange, refrigerators, heat pumps and substance mixing etc. Therefore, the study of radiative hybrid nanofluid (GO-MoS2/C2H6O2–H2O) and the conventional nanofluid (MoS2/C2H6O2–H2O) is conducted in the presence of Lorentz forces. The flow configuration is modeled between the parallel rotating plates in which the lower plate is permeable. The models which govern the flow in rotating system are solved numerically over the domain of interest and furnished the results for the temperature, entropy generation and thermophysical characteristics of the hybrid as well as conventional nanofluids, respectively. It is examined that the thermal profile intensifies against stronger thermal radiations and magnetic field. The surface of the plate is heated due to the imposed thermal radiations and magnetic field which cause the increment in the temperature. It is also observed that the temperature declines against more rotating plates. Further, the entropy production increases for more dissipative effects and declines against more magnetized fluid. Thermal conductivities of the hybrid nanofluid enhances promptly in comparison with regular liquid therefore, under consideration hybrid nanofluid is reliable for the heat transfer. Moreover, dominating thermal transport is perceived for the hybrid nanofluid which showed that hybrid suspension GO-MoS2/C2H6O2–H2O is better for industrial, engineering and technological uses.

Keywords: Heat transfer; thermal radiation; Entropy Generation; GO-MoS2 hybrid nanoparticles; thermophysical characteristics

1  Introduction

The analysis of heat transfer is a topic of interest due to its variety of applications comprised in various industries and engineering. The remarkable applications of thermal transport are comprised in pharmaceutical, microelectronics, fuel cells, heat exchanger, home appliance and domestic refrigerator etc. To finish the production process of many industrial ingredients, a huge amount of heat is required. The conventional liquids like kerosene oil, engine oil, ethylene glycol EG and water are less heat transfer fluids which fail to provide the considerable heat transfer. Therefore, researchers and engineers paved their attentions to overcome these major issues of daily life, industrialist and engineers. They thought that the heat transfer in regular liquids (mentioned above) can be enhanced by adding an extra nanomaterial known as nanoparticles in the host liquid. Finally, a new class of heat transfer fluids was developed and termed as Nanofluid. Nanofluids are colloidal mixture of nanomaterial and host liquid in which both the host fluid and the nanomaterial are thermally in equilibrium. These fluids overcome the issues faced by the engineers and industrialist. Despite that nanofluids have an extra heat transfer characteristics, scientists and engineers thought that a new hybrid class of fluids could be developed and focused on a new type of fluids which has remarkable heat transfer properties as compared to that of regular liquids and nanofluids, respectively. This newly developed class is termed as Hybrid Nanofluid. These fluids are the coupling of hybrid nanoparticles in the base liquid or hybrid base liquid. The development of this newly developed heat transfer fluids almost covers the issues of the industrialist.

Hybrid nanofluids are colloidal suspension of the hybrid nanomaterials into the host liquids. Thermal conductance of the hybrid nanomaterials is high in comparison with conventional nanomaterials. Due to high thermal conductance, hybrid nanofluids are superior over the conventional nanoliquids. Therefore, the hybrid nanoliquids are extensively used in various industries where a large amount of heat transfer is required to accomplish the production processes. The applications of these fluids comprised in medical sciences, chemical engineering, biotechnology, computer chips, coatings, catalytic purposes, civil engineering, flow characteristics of the fluids in various geometries and coatings of the vehicles and in cancer therapy.

Hybrid nanofluids became very popular among the researchers, engineers and industrialist due to their better heat transfer characteristics. Therefore, researchers examined the influences of hybrid nanofluids in the flow regimes, heat transfer rate and local nusselt number in different geometries by considering different flow conditions at the boundaries and far away from the surface. In 2019, Ahmed et al. [1] examined the flow of water suspended by hybrid nanoparticles of Ag–Fe3O4 between Riga plates. In ordered to discuss more physical aspects of the flow regimes, they incorporated the influences of nonlinear thermal radiations and chemical reaction phenomenon in the energy and concentration constitutive relations, respectively. Das et al. [2] considered Cu–Al2O3/H2O hybrid nanofluid in the porous channel. Also, they encountered second law analysis and found the interesting results.

The second law analysis in the hybrid nanofluid composed by graphene and ferromagnetic nanoparticles was presented in [3]. They explored the results for thermal enhancement in the hybrid nanofluid by incorporating the magnetic field effects in the energy equation. The remarkable influences of magnetic field in the momentum and temperature of the hybrid nanofluid were examined. In 2018, Huminic et al. [4] discussed the heat transfer rate and entropy generation analysis in a flattened tube. To enhance the amount of heat transfer, they used the hybrid nanofluid and found fascinating results for entropy generation and heat transfer characteristics. In 2017, Hussain et al. [5] explored the mixed convection flow by considering the colloidal suspension of the host liquid suspended by the hybrid nanoparticles in a cavity placed horizontally. The fascinating results regarding to entropy generation and influences of magnetic field were discussed in their study. Three-dimensional squeezing flow of the hybrid liquid (water-EG) saturated by hybrid nanoparticles (Fe3O4–Ag) was presented in [6]. An effective thermal conductivity model based on various shape factors of the hybrid nanoparticles was emerged in the energy equation for better thermal enhancement. A comparative colloidal study of the nanofluid and hybrid nanofluid by considering the forced convection effects was reported in [7]. They treated the models numerically and found the results for the flow regimes and the heat transfer characteristics.

Thermal enhancement and entropy generation inspection between the parallel rotating plates situated in Cartesian frame is a topic of interest due to its multifarious applications in chemical and mechanical industries. In 2017, Ahmed et al. [8] reported the flow of chemically reacting fluid over an unsteady stretchable surface. They incorporated the influences of linear thermal radiations and cross diffusion gradients in the energy and concentration laws. They also examined the effects of convective condition in the heat transfer rate and reported the interesting results. A novel investigation of heat transfer analysis in water and EG saturated by γ-nanoparticles was examined in [9]. The effects of an effective Prandtl number are also embedded in the energy equation that showed an interesting behavior of heat transfer. Khan et al. [10] reported the numerical analysis of the nanofluids containing γ-nanoparticles and reported the fascinating results for the velocity, temperature and heat transfer. Furthermore, useful analysis of the nanofluids by considering the important flow conditions were described in [11,12].

From the literature study, it is noted that entropy generation and temperature investigation in GO-MoS2/C2H6O2–H2O hybrid nanofluid between parallel rotating plates is not reported so far. Therefore, this study is makeup to fill this significant research gap. For improved temperature and entropy generation. Moreover, thermal radiations and magnetic field effects are plugged in the energy and momentum relations. The resultant hybrid model is then tackled by numerical scheme known as RK technique. The results for the velocity, temperature and entropy generation are plotted and discussed comprehensively and finally concluding remarks of the analysis are presented.

2  Statement Geometry and Hybrid Model Formulation

2.1 Statement and Geometry

2.1.1 Nanomaterial and Host Liquid

Three-dimensional rotating flow of hybrid nanofluid between the parallel plates is considered in which:

     i)  C2H6O2–H2O is taken as hybrid base liquid

    ii)  GO-MoS2 is taken as hybrid nanomaterial.

2.2 Conditions and Assumptions

The following conditions are imposed during the analysis:

     i)  The colloidal suspension is viscous.

    ii)  The colloidal suspension is an incompressible.

   iii)  The hybrid nanoliquid and hybrid nanomaterial are thermally compatible.

    iv)  The flow of the hybrid nanofluid is electrically conducting and thermal radiations effects are considered.

     v)  The flow is unsteady.

    vi)  The lower plate is static at y=0 and upper plate is at height h and is defined as h=(ν(1-ct)a)0.5.

   vii)  The squeezed velocity of the hybrid nanofluid is Vh(t).

  viii)  The nanofluid and the plates are rotating together oriented counter clockwise with rotating velocity Ω=ωj(1-ct)-1.

    ix)  The plate at lower end is permeable and sucks the hybrid nanofluid with velocity − V0/(1 − ct).

     x)  The lower plate is stretched along x-axis with Uw=ax(1-ct)-1.

    xi)  Magnetic field is applied perpendicularly with intensity B0(1-ct)-0.5.

The flow model of the hybrid nanofluid is obtained in the view of aforementioned assumptions and the flow configuration is depicted in Fig. 1.

2.3 Governing Hybrid Model

By implementing the above-mentioned assumptions, the following magneto radiative and dissipative hybrid nanofluid model is obtained in dimensional form [13]:

∂u∂x+∂v∂y+∂w∂z=0, (1)

Ξ1(∂u∂t+u∂u∂x+v∂u∂y+2ω0(1-ct)-1w)=-∂p∂x+Ξ2(∂2u∂x2+∂2u∂y2)-Ξ3B02(1-ct)u, (2)

Ξ1(∂v∂t+u∂v∂x+v∂v∂y)=-∂p∂y+Ξ2(∂2v∂x2+∂2v∂y2),

Ξ1(∂w∂t+u∂w∂x+v∂w∂y-2w0(1-ct)-1u)=Ξ2(∂2w∂x2+∂2w∂y2)-Ξ3B02(1-ct)w,

(∂T∂t+u∂T∂x+v∂T∂y)=Ξ4Ξ5(∂2T∂x2+∂2T∂y2)+16σ*T∞33k*Ξ5∂2T∂y2+Ξ2(4(∂u∂x)2+(∂u∂y+∂v∂x)2+(∂w∂x)2(∂w∂y)2),

here, Ξi for i=1,2,…,5, represents an effective density, dynamic viscosity, electrical conductivity, thermal conductivity and heat capacity, respectively. The effective models for the conventional and hybrid nanofluids are as follows [14].

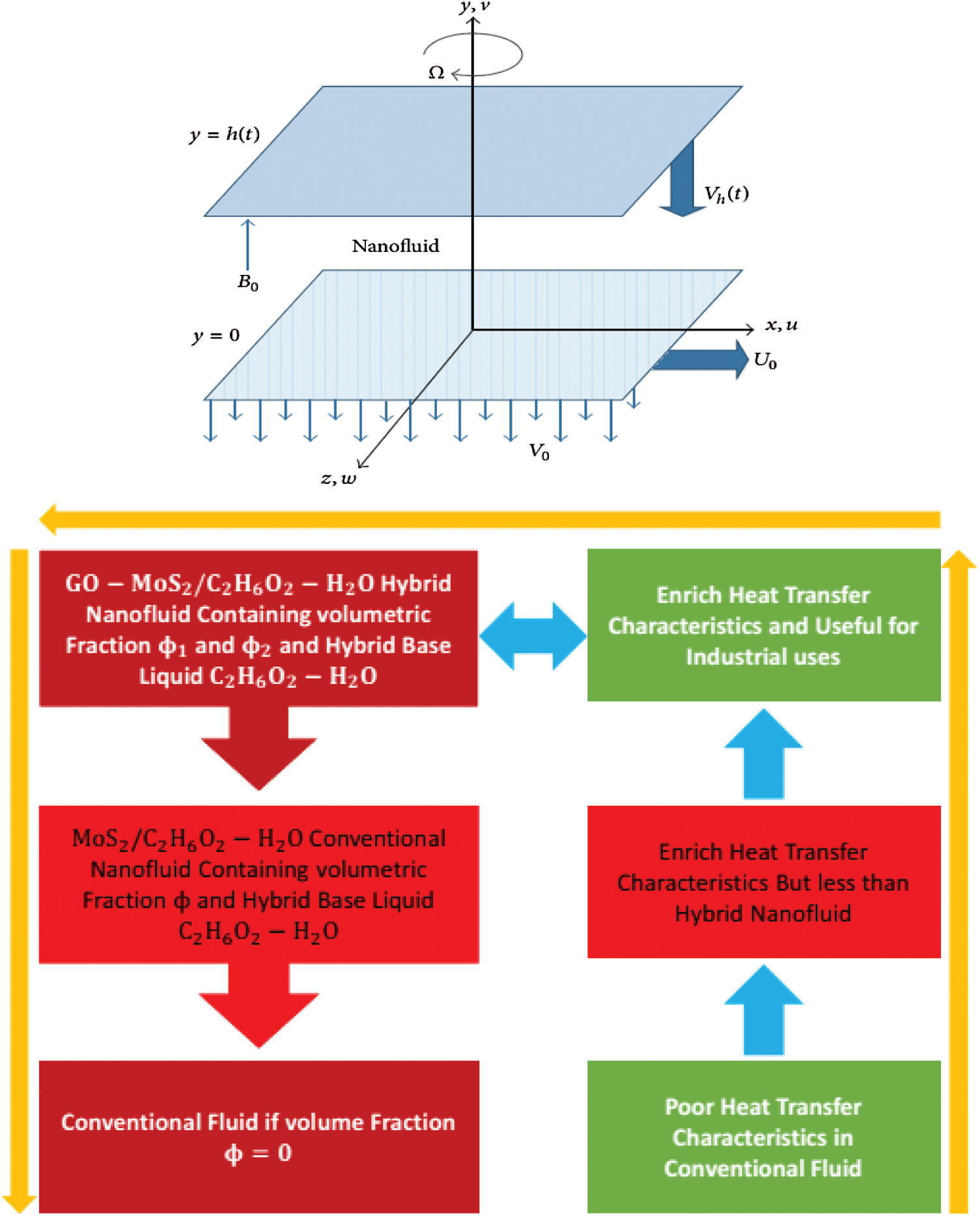
Figure 1: Configuration of the hybrid nanofluid GO-MoS2/C2H6O2–H2O flow

Table 1: Effective models for the conventional and hybrid nanofluids

In Tab. 1, m is the shapes factor and different values of m lead to three different types of nanomaterial. The shapes of these nanoparticles are given in Tab. 2.

Table 2: Shape Factor for three different sort of nanoparticles

Thermophysical properties of under consideration hybrid liquid (H2O–C2H6O2) and hybrid nanoparticles (GO-MoS2) are described in Tab. 3.

Table 3: Thermophysical attributes of the hybrid liquid and hybrid nanoparticles

The flow conditions at the plates are defined as:

(6) u=Uw=ax(1-ct)-1v=-V0(1-ct)-1w=0T=Tw}aty=0,(lower permeable plate),(3)

and

u=0v=Vh=-c2(va(1-ct))0.5w=0T=Th}aty=h(t),(at upper plate)(7)

For the particular hybrid model, the similarity variables are as follows [13]:

u=UwF′(yh(t))v=aυa(1-ct)F(yh(t))w=UwG(yh(t))β(yh(t))=T-TwTw-Thη=yh(t)}similarity transformations(8)

Incorporating the feasible invertible transformations and the partial derivatives in the governing equations, the following two models are obtained on the basis of the nanofluid models.

2.4 Dimensionless GO-MoS2/C2H6O2-H2O Model

F′′′′-((1-ϕ2)((1-ϕ1)+ϕ1ρs1ρf)+ϕ2ρs2)(1-ϕ1)2.5(1-ϕ2)2.5(3F′F′′-FF′′′+S2(3F′′+ηF′′′)+2ΩG′)-(1-ϕ1)2.5(1-ϕ2)2.5(1+3ϕ(ϕ1σ1+ϕ2σ2-σbf(ϕ1+ϕ2))(ϕ1σ1+ϕ2σ2+2ϕσbf)-σbfϕ((ϕ1σ1+ϕ2σ2)-σbf(ϕ1+ϕ2)))M2F′′=0, (10) G′′+((1-ϕ2)((1-ϕ1)+ϕ1ρs1ρf)+ϕ2ρs2)(1-ϕ1)2.5(1-ϕ2)2.5(FG′-F′G+2ΩF′-S(G+η2G′))-(1-ϕ1)2.5(1-ϕ2)2.5(1+3ϕ(ϕ1σ1+ϕ2σ2-σbf(ϕ1+ϕ2))(ϕ1σ1+ϕ2σ2+2ϕσbf)-σbfϕ((ϕ1σ1+ϕ2σ2)-σbf(ϕ1+ϕ2)))M2G=0 (11) (1+Rd(ks2+(m−1)kbf−(m−1)(kbf−ks2)ϕ2ks2+kbf(m−1)+(kbf−ks2)ϕ2))β′′−Pr((1−ϕ2)((1−ϕ1)+ϕ1(ρ c p)s1(ρ c p)f)+ϕ2(ρcp)s2)(ks2+(m−1)kbf−(m−1)(kbf−ks2)ϕ2ks2+kbf(m−1)+(kbf−ks2)ϕ2) ×(Fβ′+S2ηβ′)=0.

The dimensional flow conditions reduced in the following dimensionless form:

F(η)=AF′(η)=1G(η)=0β(η)=1}atη=0(lower plate).(9)

and

F(η)=S2F′(η)=0G(η)=0β(η)=0}atη=1(upper plate).(13)

The dimensionless flow parameters embedded in the flow models are defined by the following mathematical formulas:

A=V0ah,S=ca,Ω=ω0a,Pr=μf(Cp)fkf.(14)

2.5 Entropy Formulation

The entropy generation for the under-consideration hybrid models are given in the following way [15]:

SG*=kfT02(Ξ4+16σ*Th33kfK*)((∂T∂x)2+(∂T∂y)2)+Ξ2Th(4(∂u∂x)2+(∂u∂y+∂v∂x)2+(∂w∂x)2(∂w∂y)2)+Ξ3B02T0u2(Thermal+Radiative irreversibility)+(viscous dissipation irreversibility)(15)

here, Ξ4 and Ξ2 are described in Tab. 1 for the conventional and hybrid nanofluids, respectively.

The entropy generation due to radiative heat flux, thermal transport and friction of the hybrid nanoliquid are incorporated in Eq. (15). By plugging the appropriate invertible transformations in Eq. (15) and after performing the mathematical calculation, the following dimensionless expression is attained:

Ng=SG*SG0* (16)

Ng=(Ξ4+Rd)β′2+Pr(Ω−1)Ξ2(Ec(F′2+G2)+Ecx(F″2+G′2))+Ξ3MF′2 (17)

In Eq. (17), the characteristics entropy generation is expressed by the following formula:

SG0*=k(Tw-Th)2h2Th2(18)

The dimensionless thermal difference (Ω) appeared in Eq. (17) is expressed in the following form:

α=(Tw-Th)/Th(19)

By incorporating the expressions of Ξ4 and Ξ2, in Eq. (20), the following mathematical relations are obtained for thehybrid and conventional nanoliquids.

Ng=(kf(ks+(m−1)kf−(m−1)(kf−ks)ϕks+(m−1)kf+(kf−ks)ϕ)+Rd)β′2+Pr(α−1)(Ec(F′2+G2)+Ecx(F″2+G′2(1−ϕ)2.5 +Ξ3MF′2(MoS2/C2H6O2-H2O)(20)

and for hybrid nanoliquid (GO-MoS2/C2H6O2–H2O) is expressed as:

Ng=(kbf(ks2+(m−1)kbf−(m−1)(kbf−ks2)ϕ2ks2+kbf(m−1)+(kbf−ks2)ϕ2)+Rd)β′2 +Pr(α−1)(Ec(F′2+G2)+Ecx(F″2+G′2))(1−ϕ1)2.5(1−ϕ2)2.5+Ξ3MF″2(21)

3  Mathematical Treatment of ZnO-SAE50

Under-consideration models are highly coupled and nonlinear in nature. Therefore, exact solutions for such models are incredible. Thus, the numerical technique together with shooting method is adopted for the solutions purpose [10]. For initiation of the technique, first order IVP is obtained by using the following transformations and obtained the solutions of the models.

b1=F,b2=F′,b3=F″,b4=F‴,b5=G,b6=G′,b7=β,b8=β′.(22)

Fig. 2 represents the solution steps for the implemented mathematical technique. The following flowchart represents the implementation of the technique.

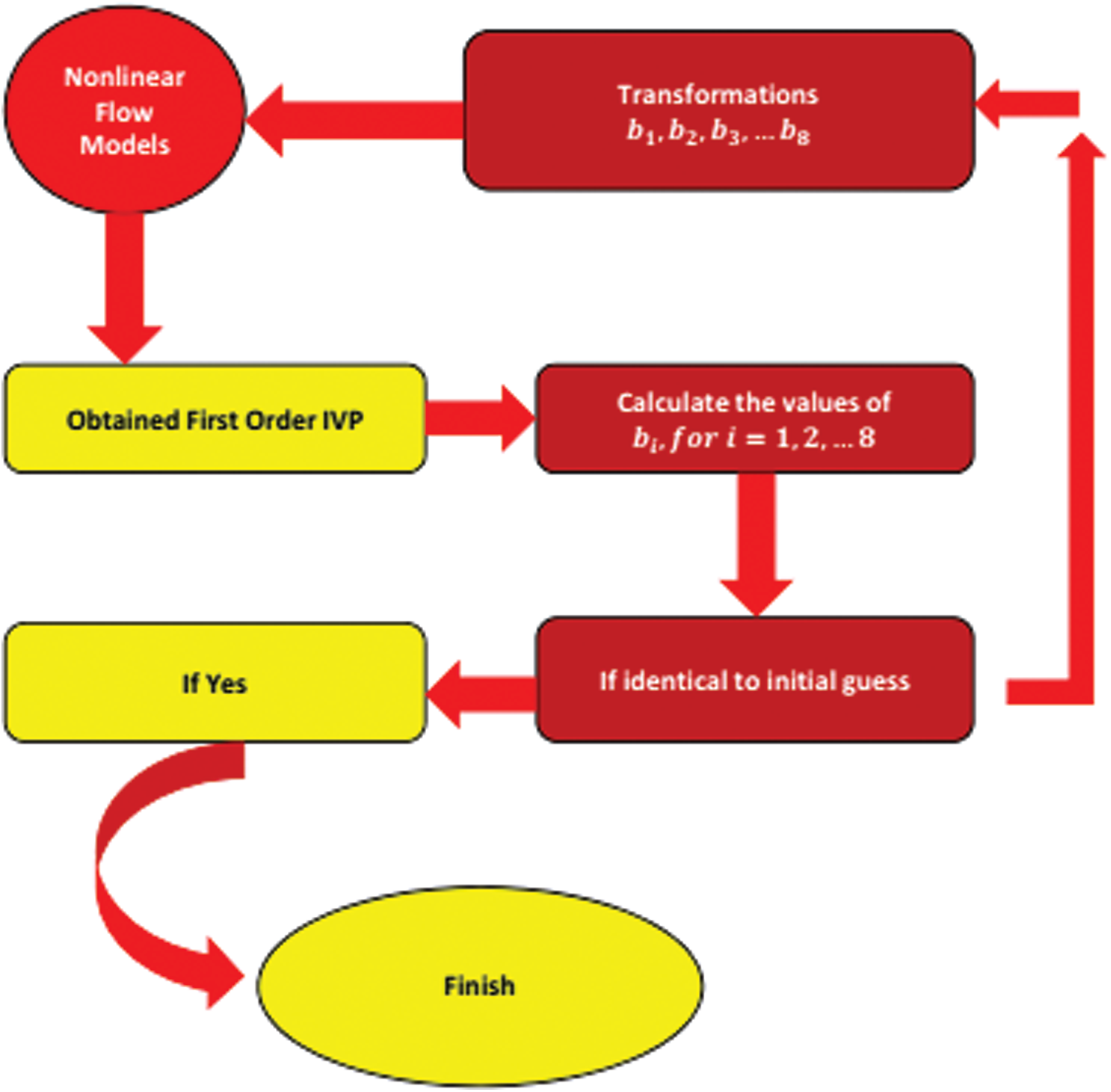
Figure 2: Flow chart for mathematical analysis of the models

4  Discussion of the Results

4.1 Thermal Field

Fig. 3 is plotted to analyzes the behavior of GO-MoS2/C2H6O2–H2O and MoS2/C2H6O2–H2O temperature against varying thermal radiations Rd. It is perceived that the temperature β(η) enhances against stronger thermal radiations for both nanofluids. Physically, the plates are heated due to thermal radiations effects due to which the internal kinetic energy of the fluid particles increases and consequently the temperature rises. For S>0, thermal field enhances abruptly because the fluid particles compressed together due to the movement of upper plate in the direction of lower once and more energy transferred between the fluid molecules which lead to increment in the fluid temperature. On the other side, slow increment in the thermal field is perceived because the energy transport between the fluid particles become slow due to away movement of the upper plate. Fig. 4 pointed the effects of Ω on the thermal field β(η). The rotational parameter Ω resists the nanofluids temperature. The decrement in the temperature is examined slow against S>0 in comparison with S<0.

Fig. 5 is decorated to analyze the thermal behavior β(η) against the induced magnetic field. It is pointed that the stronger magnetic field favors the temperature of GO-MoS2/C2H6O2–H2O and MoS2/C2H6O2–H2O nanofluids. For S>0 (upper plate moves in the direction of lower plate), abrupt increment in β(η) is examined because due to more squeezing effects the temperature rises abruptly. In GO-MoS2/C2H6O2–H2O hybrid nanofluid, the temperature enhances due to larger fraction factor. For S<0, the temperature rises slowly. Physically, for S<0, more free area produced between the plates and more particles move to fill the free space and consequently the velocity drops. Due to this decrement in the velocity, the particles friction drops and consequently the temperature rises slowly.

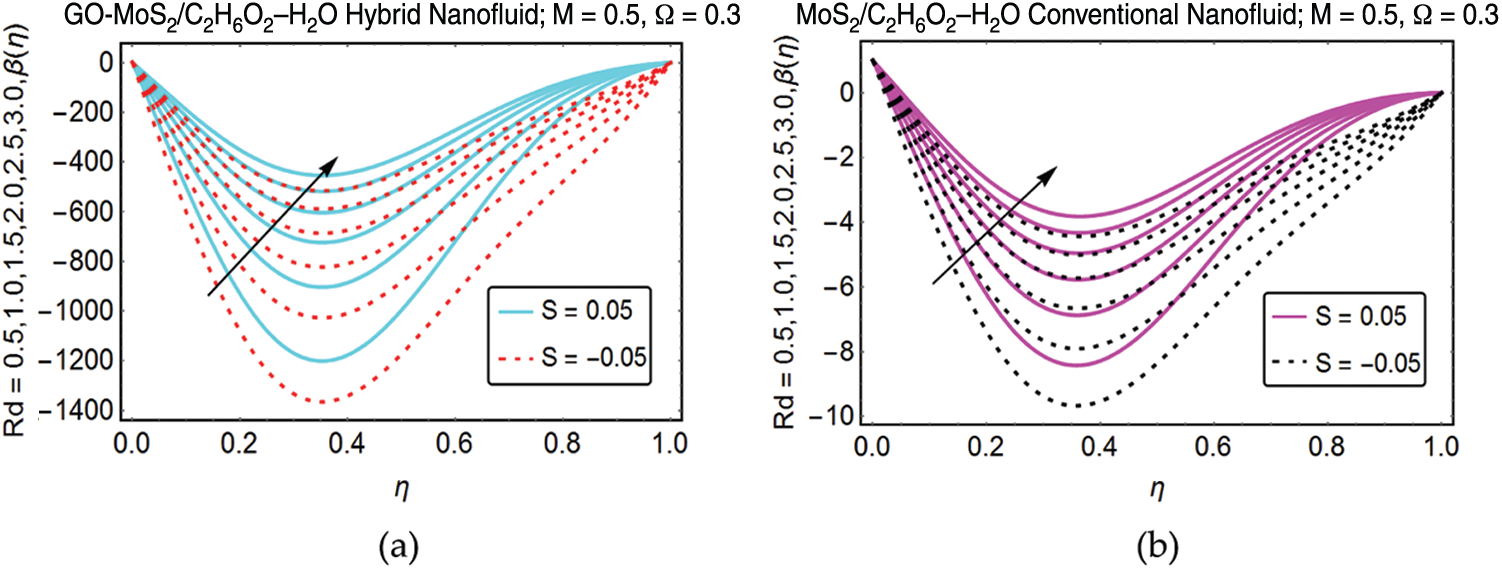
Figure 3: Influence of Rd on (a) hybrid nanofluid (b) conventional nanofluid on β(η)

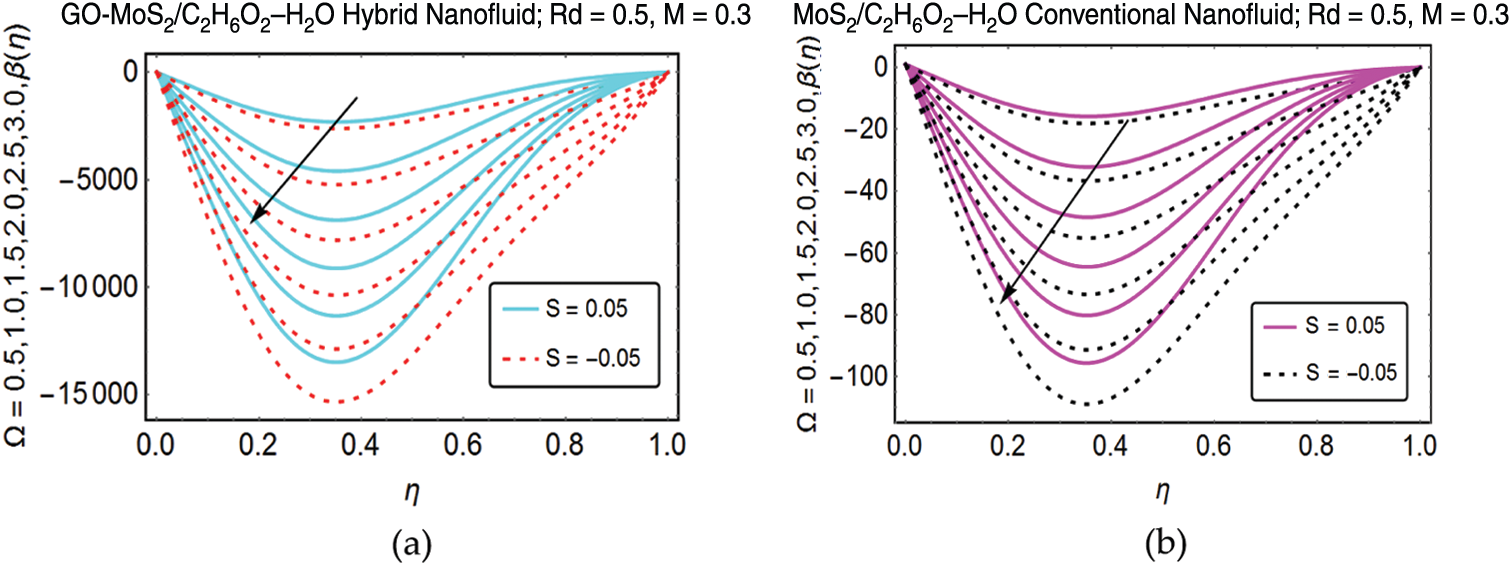
Figure 4: Influence of Ω on (a) hybrid nanofluid (b) conventional nanofluid on β(η)

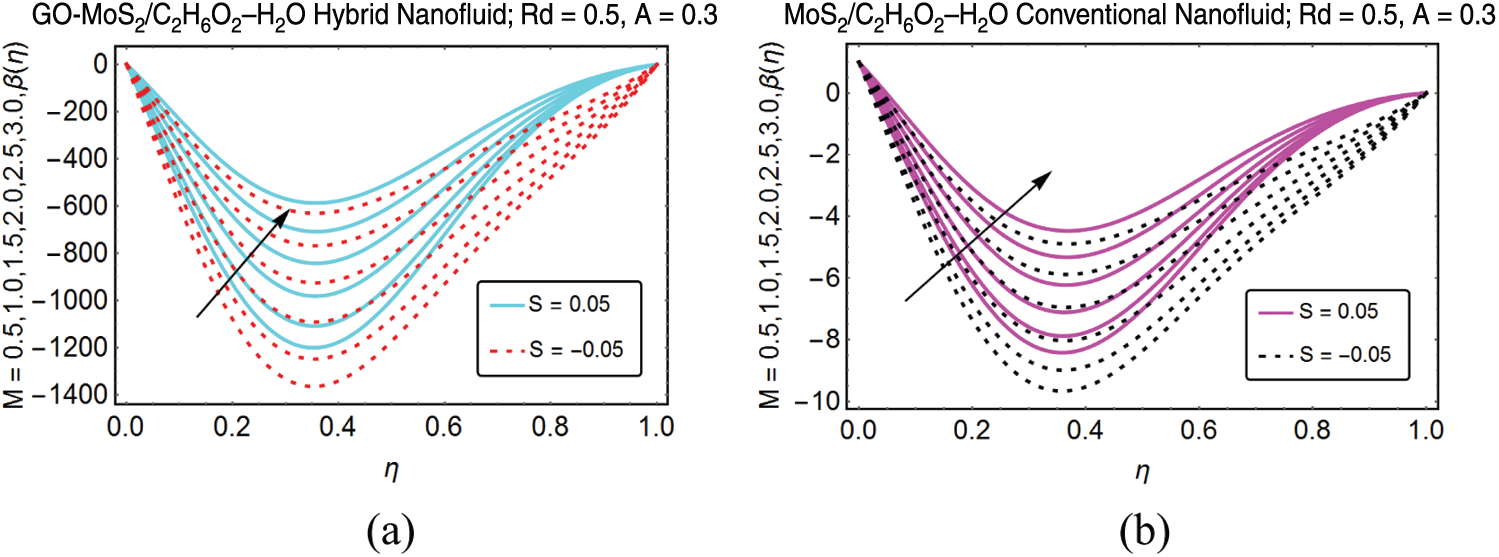
Figure 5: Influence of M on (a) hybrid nanofluid and (b) conventional nanofluid on β(η)

4.2 Entropy Analysis

The study of second law in magneto radiative nanofluids is a potential topic of interest in fluid dynamics. It is the amount of entropy produced during irreversible process. The applications of this phenomena comprised in heat pumps, air conditioners, refrigerators, heat exchanges, thermal mechanics and mixing or expanding of substances.

The effects of numerous parameters on the entropy generation in GO-MoS2/C2H6O2–H2O and MoS2/C2H6O2–H2O are pointed in Figs. 6–12. It is perceived that the entropy declines for stronger induction of magnetic field. For GO-MoS2/C2H6O2–H2O abrupt decrement is perceived near the lower plate. These effects are decorated in Fig. 6. The rotational parameter Ω resists the entropy for both sort of nanofluids.

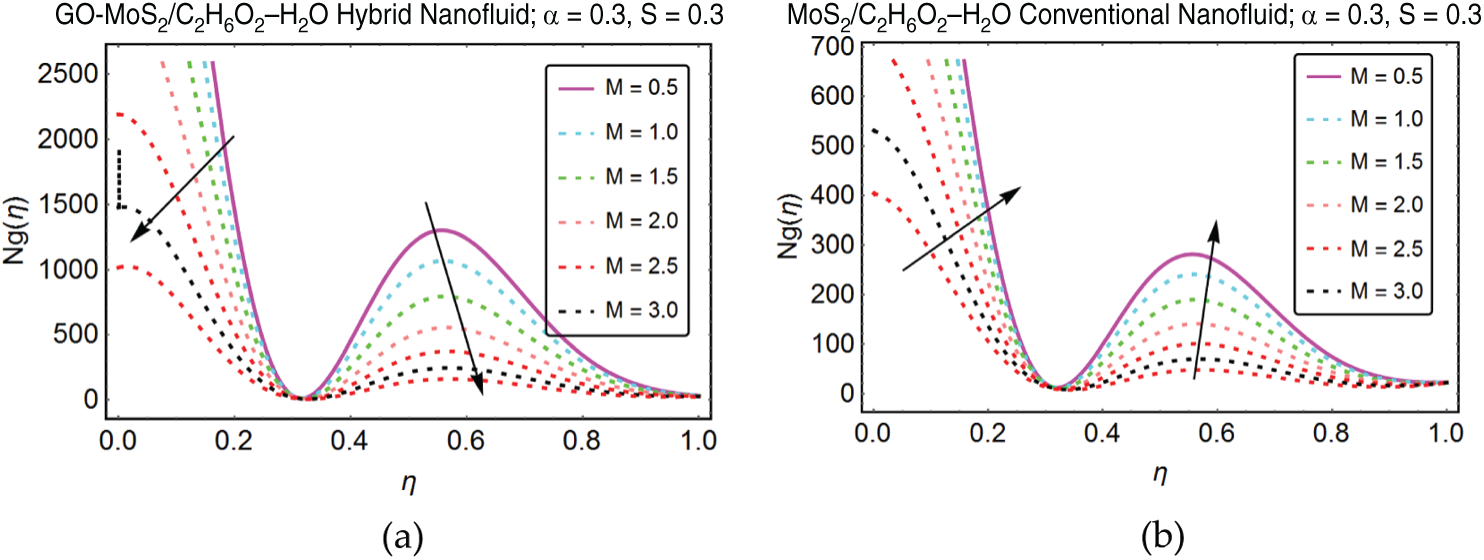
Figure 6: Influence of M on entropy generation for (a) hybrid nanofluid (b) conventional nanofluid

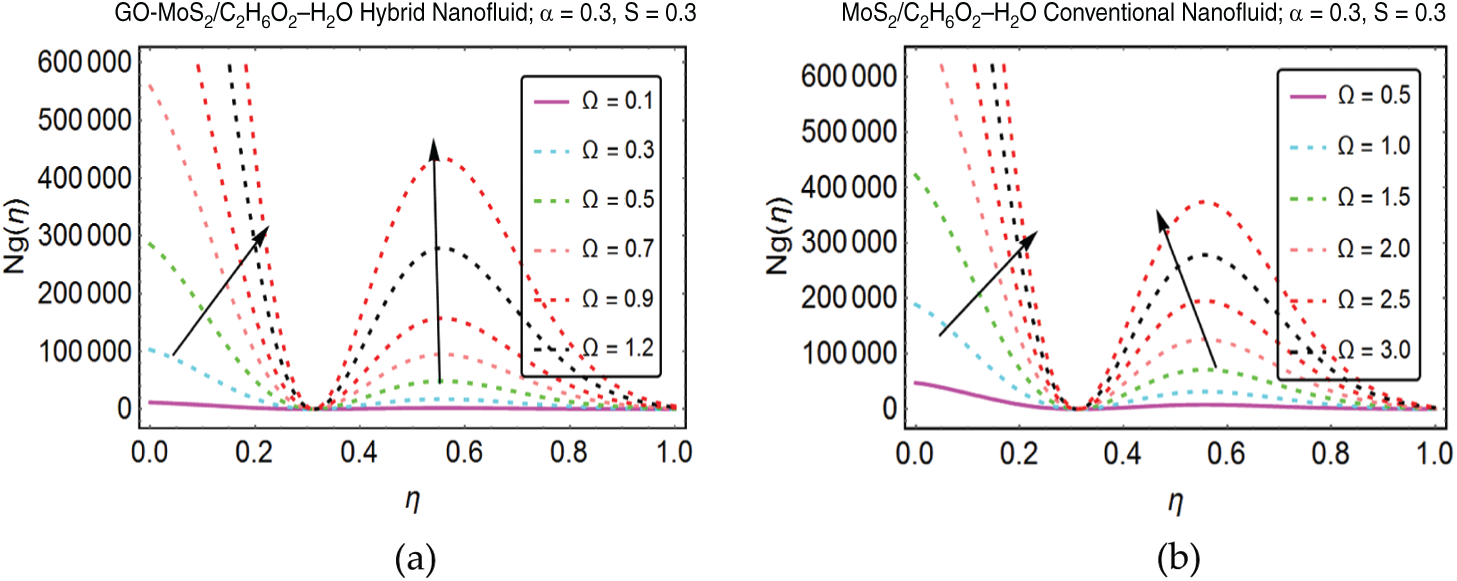
Figure 7: Influence of Ω on entropy generation for (a) hybrid nanofluid (b) conventional nanofluid

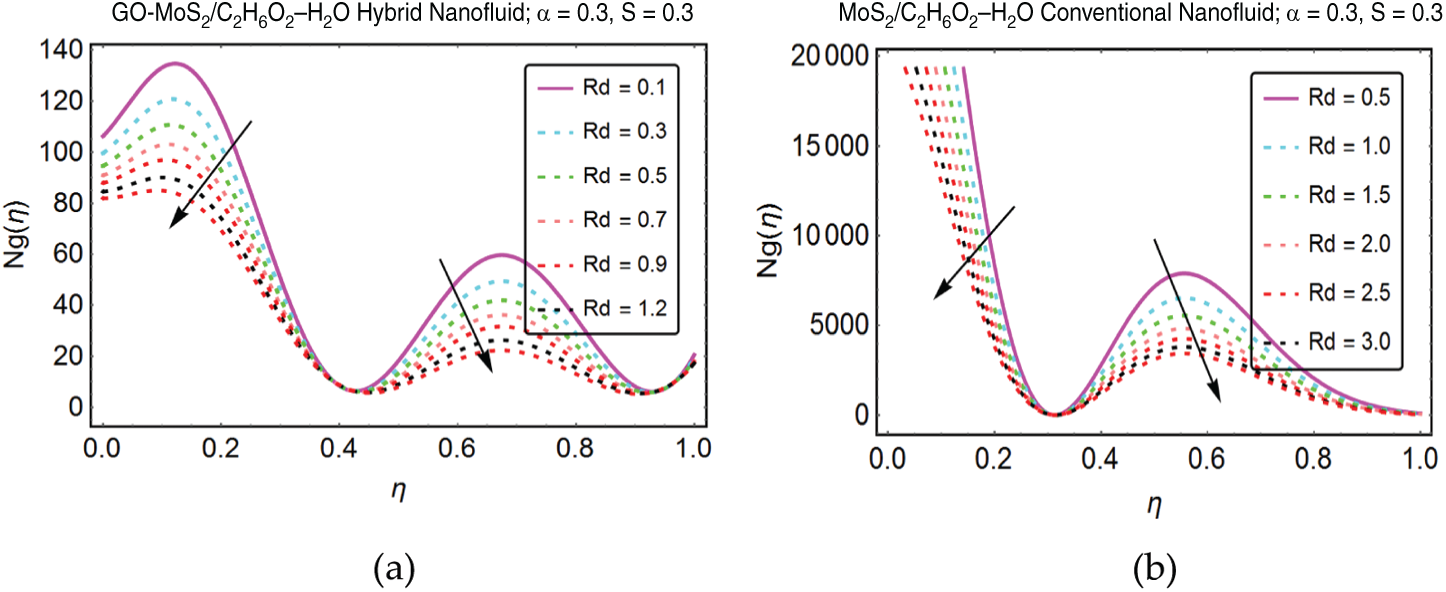
Figure 8: Influence of Rd on entropy generation for (a) hybrid nanofluid and (b) conventional nanofluid

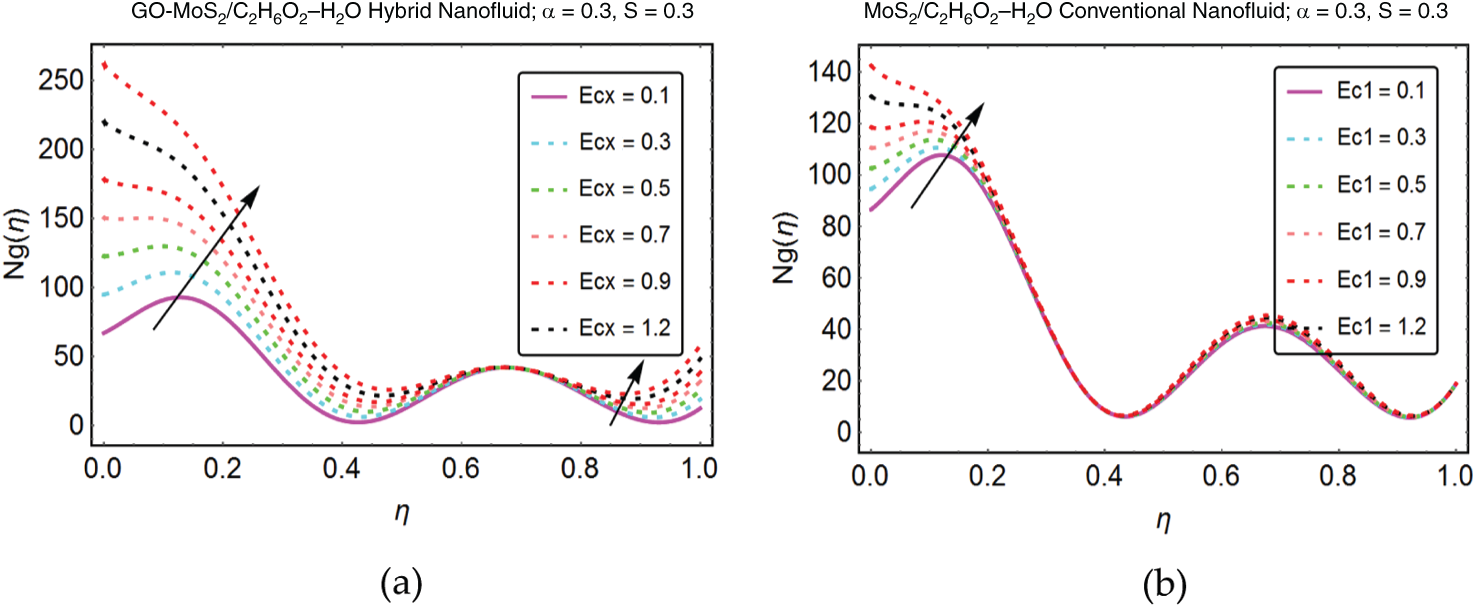
Figure 9: Influence of Ecx on entropy generation for (a) hybrid nanofluid (b) conventional nanofluid

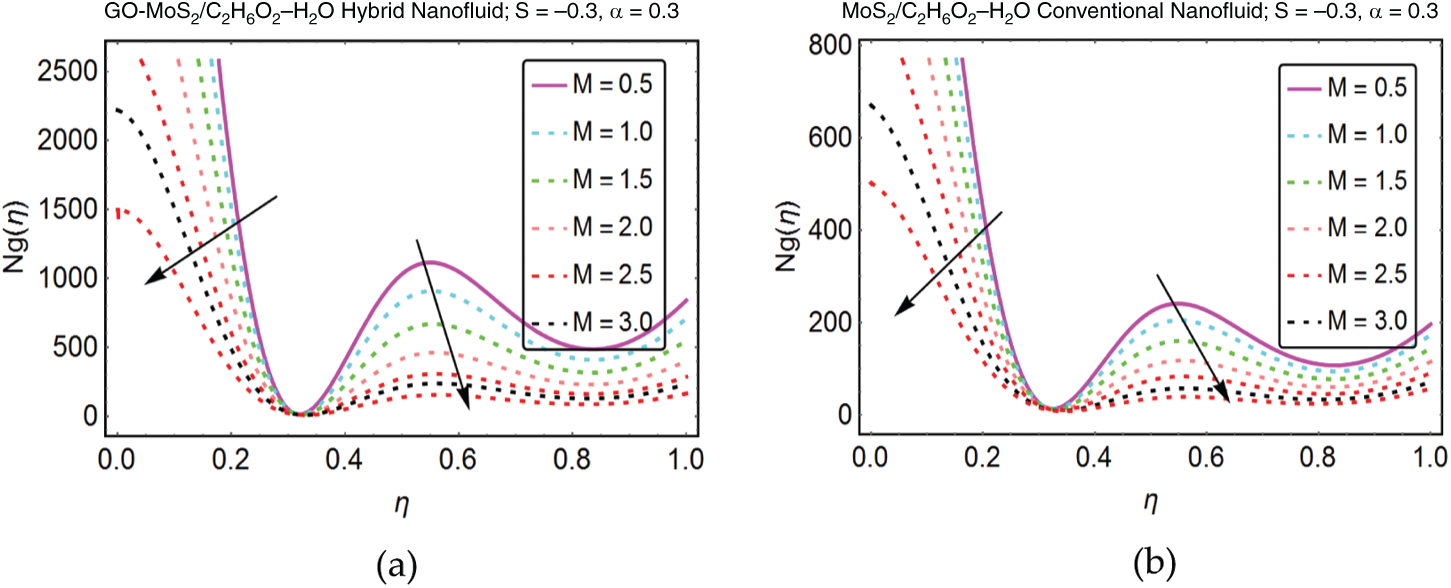
Figure 10: Influence of M, S<0 on entropy generation for (a) hybrid nanofluid (b) conventional nanofluid

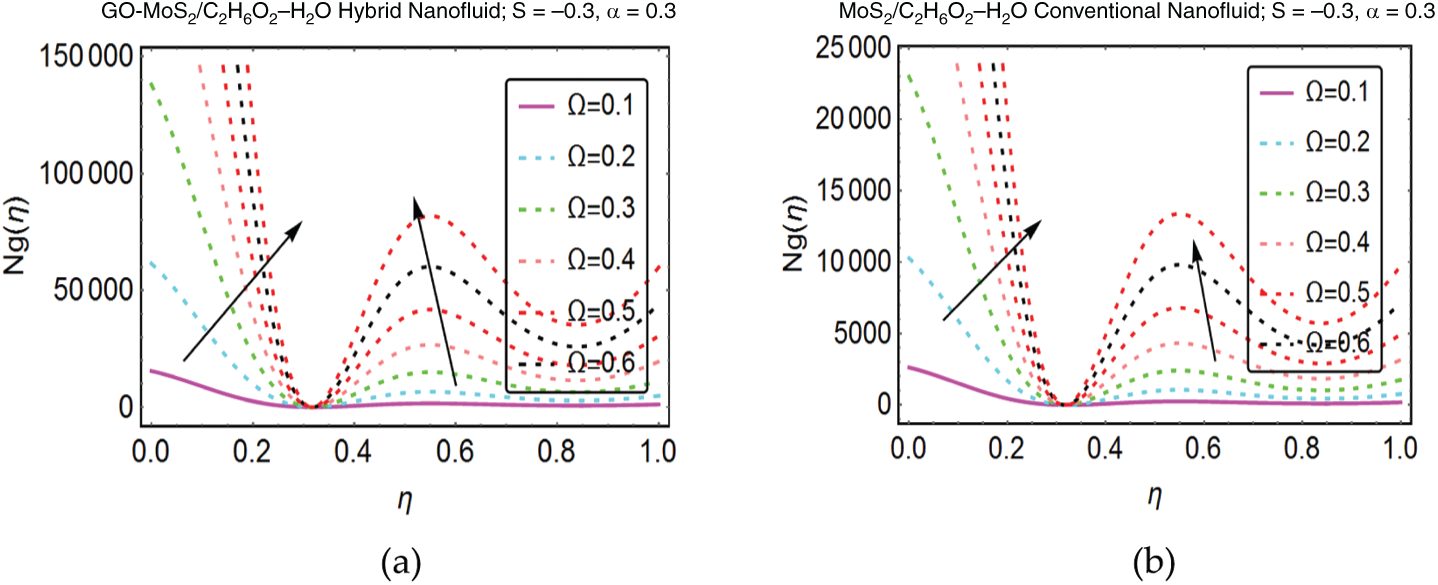
Figure 11: Influence of Ω, S<0 on entropy generation for (a) hybrid nanofluid (b) conventional nanofluid

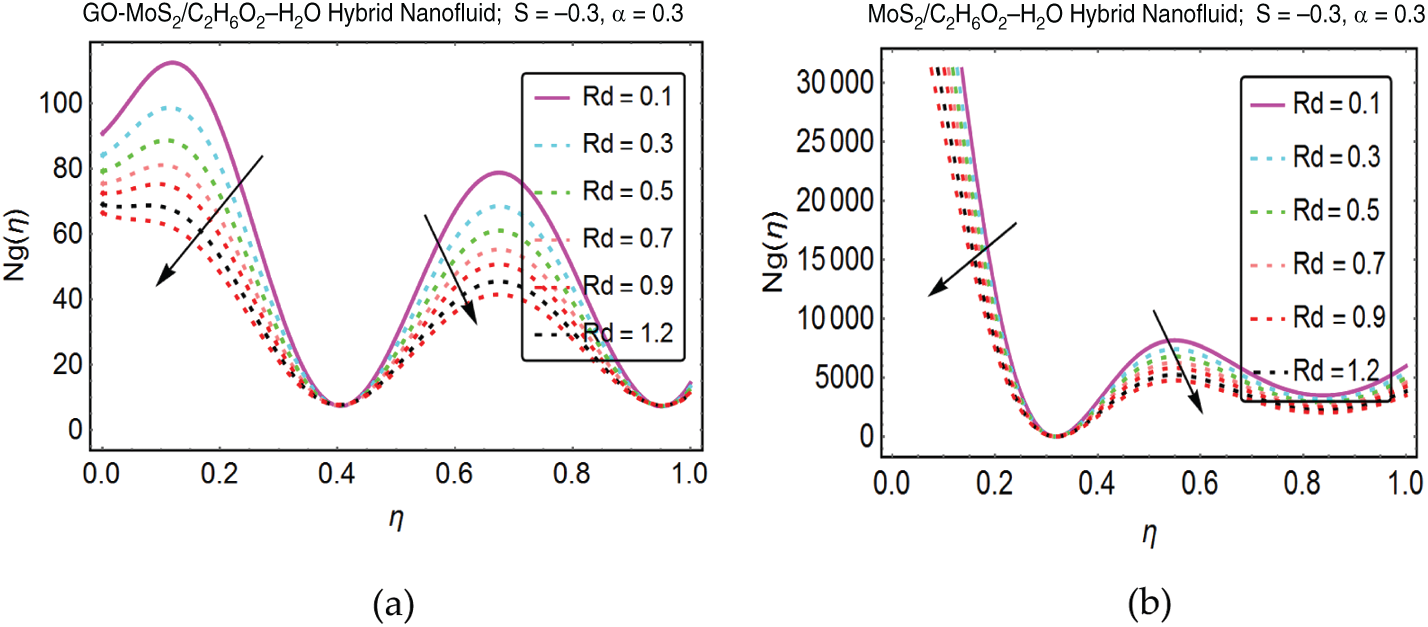
Figure 12: Influence of Rd, S<0 on entropy generation for (a) hybrid nanofluid and (b) conventional nanofluid

The behavior of entropy generation is detected for both under consideration hybrid and conventional nanofluids. It is pointed that the viscous dissipation allows the rise in entropy production because due to this, internal energy of the fluid enhances due to which the entropy increases. Moreover, it is examined that the entropy drops quickly when the upper plate moves towards the lower plate and slow decrement is perceived for away movement of the upper plate.

It is analysed that the effective thermal conductivity of the hybrid nanofluid (GO-MoS2/C2H6O2–H2O) showed dominating behaviour for varying volume fraction factor φ. Due to superior effective characteristics of the hybrid nanofluid (GO-MoS2/C2H6O2–H2O) than conventional nanofluid (MoS2/C2H6O2–H2O) therefore, the hybrid nanofluids are reliable for industrial and technological purposes.

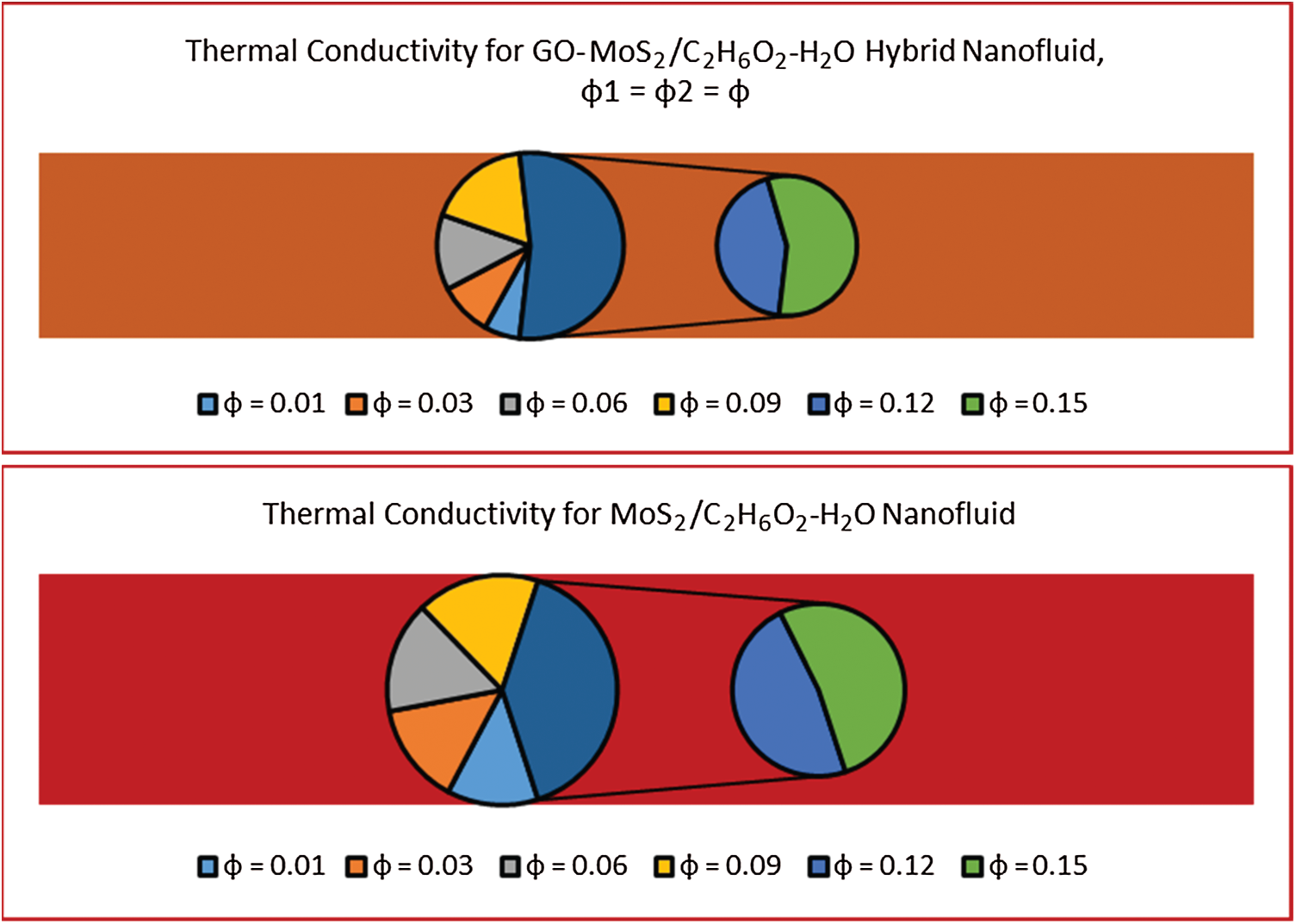
Figure 13: Influence of volume fraction on thermal conductivity for hybrid nanofluid and conventional nanofluid

5  Conclusions

The colloidal flow of GO-MoS2/C2H6O2–H2O and MoS2/C2H6O2–H2O is presented between parallel rotating magneto radiative plates. From the temperature and entropy analysis, it is investigated that the temperature of the hybrid and conventional nanofluids rises against the stronger thermal radiations. However, significant changes are perceived in the hybrid nanofluid. The temperature drops due to rotating plates in both fluids. The entropy generation increases for more dissipation effects and drops against the imposed magnetic effects. Further, prompt increment in thermal conductivities of the nanofluids is observed. It is also perceived that the hybrid nanofluid has high thermal performance, therefore, these fluids are reliable for the industrial and engineering uses.

Funding Statement: The author(s) received no specific funding for this study.

Conflict of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  N. Ahmed F. Saba, U. Khan, I. Khan, T. A. Alkanhal et al. (2019). , “Spherical shaped (Ag–Fe3O4/H2O) hybrid nanofluid flow squeezed between two Riga plates with nonlinear thermal radiation and chemical reaction effects,” Energies, vol. 12, . https://doi.org/10.3390/en12010076. [Google Scholar]

 2.  S. Das, R. N. Jana and O. D. Makinde. (2017). “MHD flow of Cu–Al2O3/water hybrid nanofluid in porous channel: Analysis of entropy generation,” Defect Diffusion Forum, vol. 377, pp. 42–61. [Google Scholar]

 3.  M. Mehrali, E. Sadeghinezhad, A. R. Akhiani, S. T. Latibari, C. H. S. Metselaar et al. (2017). , “Heat transfer and entropy generation analysis of hybrid graphene/Fe3O4 ferro-nanofluid flow under the influence of a magnetic field,” Powder Technology, vol. 308, pp. 149–157. [Google Scholar]

 4.  G. Huminic and A. Huminic. (2018). “The heat transfer performances and entropy generation analysis of hybrid nanofluids in a flattened tube,” International Journal of Heat and Mass Transfer, vol. 119, pp. 813–827. [Google Scholar]

 5.  S. Hussain, S. E. Ahmed and T. Akbar. (2017). “Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle,” International Journal of Heat and Mass Transfer, vol. 114, pp. 1054–1066. [Google Scholar]

 6.  S. Ghadikolaei, K. Hosseinzadeh and D. D. Ganji. (2018). “Investigation on three-dimensional squeezing flow of mixture base fluid (ethylene glycol-water) suspended by hybrid nanoparticle (Fe3O4–Ag) dependent on shape factor,” Journal of Molecular Liquids, vol. 262, pp. 376–388. [Google Scholar]

 7.  A. Moghadassi, E. Ghomi and F. Parvizian. (2015). “A numerical study of water based Al2O3 and Al2O3–Cu hybrid nanofluid effect on forced convective heat transfer,” International Journal of Thermal Sciences, vol. 92, pp. 50–57. [Google Scholar]

 8.  N. Ahmed, Adnan, U. Khan and S. T. Mohyud-Din. (2017). “Unsteady radiative flow of chemically reacting fluid over a convectively heated stretchable surface with cross-diffusion gradients,” International Journal of Thermal Sciences, vol. 121, pp. 182–191. [Google Scholar]

 9.  N. Ahmed, Adnan, U. Khan and S. T. Mohyud-Din. (2017). “Influence of an effective Prandtl number model on squeezed flow of γAl2O3–H2O and γAl2O3–C2H6O2 nanofluids,” Journal of Molecular Liquids, vol. 238, pp. 447–454. [Google Scholar]

10. N. Ahmed, Adnan, U. Khan, and S. T. Mohyud-Din. (2017). “3D squeezed flow of γAl2O3–H2O and γAl2O3–C2H6O2 Nanofluids: A numerical study,” International Journal of Hydrogen Energy, vol. 42, no. 39, pp. 24620–24633. [Google Scholar]

11. M. M. Rashidi, N. V. Ganesh, A. K. A. Hakeem, B. Ganga and G. Lorenzini. (2016). “Influences of an effective Prandtl number model on nano boundary layer flow of γAl2O3–H2O and γAl2O3–C2H6O2 over a vertical stretching sheet,” International Journal of Heat and Mass Transfer, vol. 98, pp. 616–623. [Google Scholar]

12. M. Sheikholeslami. (2017). “Numerical investigation of MHD nanofluid free convective heat transfer in a porous tilted enclosure,” Engineering Computations, vol. 34, pp. 1939–1955. [Google Scholar]

13. U. Khan, N. Ahmed and S. T. Mohyud-Din. (2017). “Numerical investigation for three-dimensional squeezing flow of nanofluid in a rotating channel with lower stretching wall suspended by carbon nanotubes,” Applied Thermal Engineering, vol. 113, pp. 1107–1117. [Google Scholar]

14. S. S. Ghadikolaei and M. Gholinia. (2020). “3D mixed convection MHD flow of GO-MoS2 hybrid nanoparticles in H2O–(CH2OH)2 hybrid base fluid under effect of H2 bond,” International Communications in Heat and Mass Transfer, vol. 110, pp. 104371. [Google Scholar]

15. A. S. Butt and A. Ali. (2015). “Analysis of entropy generation effects in unsteady squeezing flow in a rotating channel with lower stretching permeable wall,” Journal of the Taiwan Institute of Chemical Engineers, vol. 48, pp. 8–17. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.