DOI:10.32604/cmc.2021.013648

| Computers, Materials & Continua DOI:10.32604/cmc.2021.013648 |  |
| Article |
Rock Hyraxes Swarm Optimization: A New Nature-Inspired Metaheuristic Optimization Algorithm
1College of Computer Science and Information Technology, University of Anbar, Ramadi, Iraq
2General Directorate of Scientific Welfare, Ministry of Youth and Sport, Baghdad, Iraq
3Institute of Research and Development, Duy Tan University, Danang, 550000, Vietnam
4Faculty of Information Technology, Duy Tan University, Danang, 550000, Vietnam
*Corresponding Author: Belal Al-Khateeb. Email: belal@computer-college.org
Received: 30 August 2020; Accepted: 01 October 2020
Abstract: This paper presents a novel metaheuristic algorithm called Rock Hyraxes Swarm Optimization (RHSO) inspired by the behavior of rock hyraxes swarms in nature. The RHSO algorithm mimics the collective behavior of Rock Hyraxes to find their eating and their special way of looking at this food. Rock hyraxes live in colonies or groups where a dominant male watch over the colony carefully to ensure their safety leads the group. Forty-eight (22 unimodal and 26 multimodal) test functions commonly used in the optimization area are used as a testing benchmark for the RHSO algorithm. A comparative efficiency analysis also checks RHSO with Particle Swarm Optimization (PSO), Artificial-Bee-Colony (ABC), Gravitational Search Algorithm (GSA), and Grey Wolf Optimization (GWO). The obtained results showed the superiority of the RHSO algorithm over the selected algorithms; also, the obtained results demonstrated the ability of the RHSO in convergence towards the global optimal through optimization as it performs well in both exploitation and exploration tests. Further, RHSO is very effective in solving real issues with constraints and new search space. It is worth mentioning that the RHSO algorithm has a few variables, and it can achieve better performance than the selected algorithms in many test functions.
Keywords: Optimization; metaheuristic; constrained optimization; rock hyraxes swarm optimization; RHSO
Nature is full of social behaviors that work to accomplish many different tasks. Naturally, all these behaviors coexist in different environments, and their main goal is to survive, but there is what makes them work in the form of swarms, groups, flocks, and colonies because of hunting and mobility and defend themselves. The food search is also essential for social interactions that allow them to complete their lives and reproduction. Another reason for the swarm for some creature is navigation. Birds are the best examples of such behaviors, which migrate intercontinental in flocks appropriately [1,2].
Metaheuristic optimization techniques are used extensively to solve most of the problems; this made it very common to be used as primary methods of acquiring the optimum results of optimization problems. Especially, few of them like Genetic Algorithm (GA) [3], Grey Wolf Optimization (GWO) [4], Ant Colony Optimization (ACO) [5], Slap Swarm Optimization (SSO) [6], Artificial-Bee-Colony (ABC) [7] and Particle Swarm Optimization (PSO) [8] are very known and used in broad distinct fields. Metaheuristics have become very common for several reasons: metaheuristics are very clear. They are fundamentally inspired by physical phenomena, animal behaviors, or evolutionary concepts. Metaheuristics are easy to use, which allow researchers to mimic natural behavior, enhance or produce new metaheuristics and hybridize more than one metaheuristics. Furthermore, this simplicity helps scientists to acquire information rapidly and adapt them for problems solving. Also, flexibility indicates the applicability of metaheuristics to various problems without notable changes in the algorithm’s structure. Metaheuristics can be easily applied to various problems. Thus, all a designer need is knowing and understanding how to represent his problems. Also, most metaheuristics have derivation-free mechanisms. In inequality to gradient-based optimization approaches, metaheuristics enhance problems randomly. Metaheuristics deals with problems stochastically. The optimization process starts with random solutions, and there is no need to calculate the derivative of search spaces to find the optimal solution. Finally, metaheuristics are more capable than classical optimization strategies in managing local optima. This is due to the random nature of metaheuristics, which permit them to overcome local solutions inactivity and widely search the whole search area.
Swarm Intelligence (SI) was proposed in 1993 [9] and has been defined by Bonabeau et al. [3] as “the emergent collective intelligence of groups of simple agents”. The SI inspiration techniques are created primarily from natural habitations, herds, and flock. There are many examples of SI popular techniques, such as PSO [8], ABC [7], and ACO [5].
Regardless of the variation among metaheuristics, usually, they have a common trait, which is dividing the search process into the exploration and exploitation phases [10–12]. The exploration phase indicates the investigating process of search space as widely as possible. An algorithm must have the stochastic operators globally and randomly search within the search space to support this phase. In contrast, exploitation indicates local search capability about the concerned regions taken from the previous phase (exploration). The appropriate balance of these phases is seen as a challenging task because of the metaheuristics stochastically nature. This paper introduces a new SI technique that is inspired by the behavior of Rock Hyraxes swarms. This algorithm has few parameters that make it easy to implement; the proposed algorithm can also balance between exploration and exploitation phases, making it appropriate for solving many optimization problems. The rest of the paper is organized as follows: Section 2 shows the relevant works. Section 3 presents the Rock Hyraxes Swarm Optimization (RHSO) Algorithm inspiration and mathematical model. Section 4 presents the results and discussion of test functions. Finally, Section 5 concludes the work and suggests several future research directions.
There are three major categories of metaheuristics; those are Evolutionary Algorithm (EA), Physics-Based (PB), and Swarm Intelligence (SI) algorithms. EAs, which inspired by the genetic and evolutionary behaviors of creatures. In this branch, the most popular algorithm is the Genetic Algorithm (GA). GA was proposed by Holland in 1992 [13] to simulate Darwinian evolution concepts. Goldberg [14] extensively investigated the engineering applications of GA. Typically, the development is finished by evolving associate initial random solution in EAs. Each new population is created by the cross over and mutation of the previous generation solutions. Since the best solution can higher generate the new population, which most likely creates this new population higher than the population within the previous generation(s), this may make the initial random population converges to the best solutions over generations. An example of EAs are Differential Evolution (DE) [15], Evolutionary Programming (EP) [16], Evolution Strategy (ES) [17,18], Genetic Programming (GP) [19] and Biogeography Based Optimizer (BBO) [20]. Simon initially produced the BBO algorithm rule in 2008 [20]. The elemental set up of this algorithm program is galvanized by biology science that refers to biological organisms’ study in geographical distribution.
In physics-based techniques, the development algorithms generally simulate the physical rules. Among the physics-based metaheuristic algorithms are Gravitated Native Search (GLSA) [21], Big Bang Big Crunch (BBBC) [22], Gravitated Search Algorithm (GSA) [23], Charged System Search (CSS) [24], Artificial Reaction Improvement Rule [25], Part rule [26], Ray improvement [27] rule, Small World improvement rule [28], Galaxy based Search Algorithm (GbSA) [29] and arced area improvement [30]. Those algorithms’ method is completely unlike EAs as it uses a random set of search spaces that can communicate and move throughout search space per physical rules. This movement is enforced, for instance, exploitation gravitation, inertia force, magnetic force, weights, ray casting, and many others.
GSA is an example of a physics-based algorithm rule at that its basic physical theory is impressed by Newton’s law of universal gravitation. The GSA performs a search by employing a group of agents with lots of proportional to the value of fitness performance. Throughout iteration, the gravitated forces between them interest the masses in each another [23].
Mirjalili et al. [4] propose a new metaheuristic called Grey Wolf Optimizer (GWO) inspired by grey wolves’ behavior. The GWO algorithmic simulates the leadership hierarchy and looking mechanism of grey wolves in nature. Four grey wolves, such as alpha, delta, beta, and omega, are used to simulate the leadership hierarchy. Additionally, GWO implements three significant steps of looking; those are hunting, attacking prey, and peripheral prey.
SI methods are algorithms that simulate the social behavior of flocks, herds, swarms, or other creatures. The mechanism is near to the performance of the physics-based mostly rule; but the search agents explore looking space and simulate creatures’ collective and social intelligence. PSO proposed by Kennedy and Eberhart [8] is one of the famous SI techniques samples. PSO is inspired by the birds flocking social behavior. PSO uses multiple particles that follow the most effective particle’s position and their own to data best-obtained positions.
The last example of SI is the Bees’ swarming. Artificial Bee Colony Algorithm introduced by Dervis Karaboga et al. [31] in (2007), ABC is an associate optimization algorithm supported the intelligent behavior of bee swarm. ABC testing on tests and compare it with different algorithms like PSO and GA. The results showed that the ABC algorithm outperforms the opposite algorithms.
From all the above, it can be seen that no one metaheuristics algorithm can solve all kinds of problem domains; therefore, there is always a need for new algorithms that can address many types of problem domains.
3 Rock Hyraxes Swarm Optimization (RHSO)
The mathematical model of the proposed method, together with its inspiration, is discussed in this section.
Rock hyrax (Procavia capensis) is a small furry mammal that lives in rocky landscapes across sub-Saharan Africa and along the Arabian Peninsula coast. These mammals live in colonies usually dominated by a single male who aggressively defends his territory; the colonies sometimes up to 50 individuals. They sleep together, look for food together, and even raise their babies together (who then all play together). There are three types of hyrax, two are known as the rock (or bush) hyrax and the third as tree hyrax. In the field, it is sometimes difficult to differentiate between them [32,33].
Rock hyraxes live in areas that vary widely in ambient temperatures and provide adequate water and feed. Low metabolic rates and transparent body temperatures may have contributed to the successful extraction of the rocky protrusions isolated through their distribution [34].
The rock hyrax feeds every day in a circle formation, with their head pointing to the outside of the circle to keep an eye out for predators, such as leopards, hyenas, jackals, servals, pythons, and the Verreaux’s eagle and black eagle. When the group is feeding or basking, either the breeding male or a female (Leader) will keep a lookout from a high rock or branch and will give a sharp alarm or call if danger threatens, at which point the group will scurry for cover [35].
3.2 Mathematical Model and Algorithm
Rock hyraxes start taking solar baths for several hours and sharing places to live together; they looking for food together in a distinctive way: forming a circle with different dimensions and angles to get their food. When they find food, the Leader takes a higher place to find food and protect each other from predatory animals.
To mathematically model the Rock hyrax swarm, the population first consists of Leader and members. As mentioned above, the Leader chooses the higher and best place to observe the rest of the group.
The Leader then updates his location based on his old location using the following equation:
where
where
where
The angle (
The pseudo-code of the RHSO algorithm is shown in Algorithm 1. The RHSO starts optimization by creating random solutions in the explorative mode and calculating their fitness. Depending on their fitness, it identifies the best fitness as Leader; this represents switching from explorative mode to local exploitation mode that focuses on the promising regions when global optimal may be in a close place. Later, the Leader represents the best solution for optimization problems. The search agents start again with another set of explorative moves and subsequent turn into a new exploitation stage. The Leader updates his position based on Eq. (1), while the remaining members update their positions according to the Leader’s position, as shown in Eq. (2). Calculating the fitness of each search agent and selecting the best one as a leader. This process will continue throughout iterations; when reaching the stopping condition, the process returned the Leader as the best approximation for the optimization problem’s best solution.

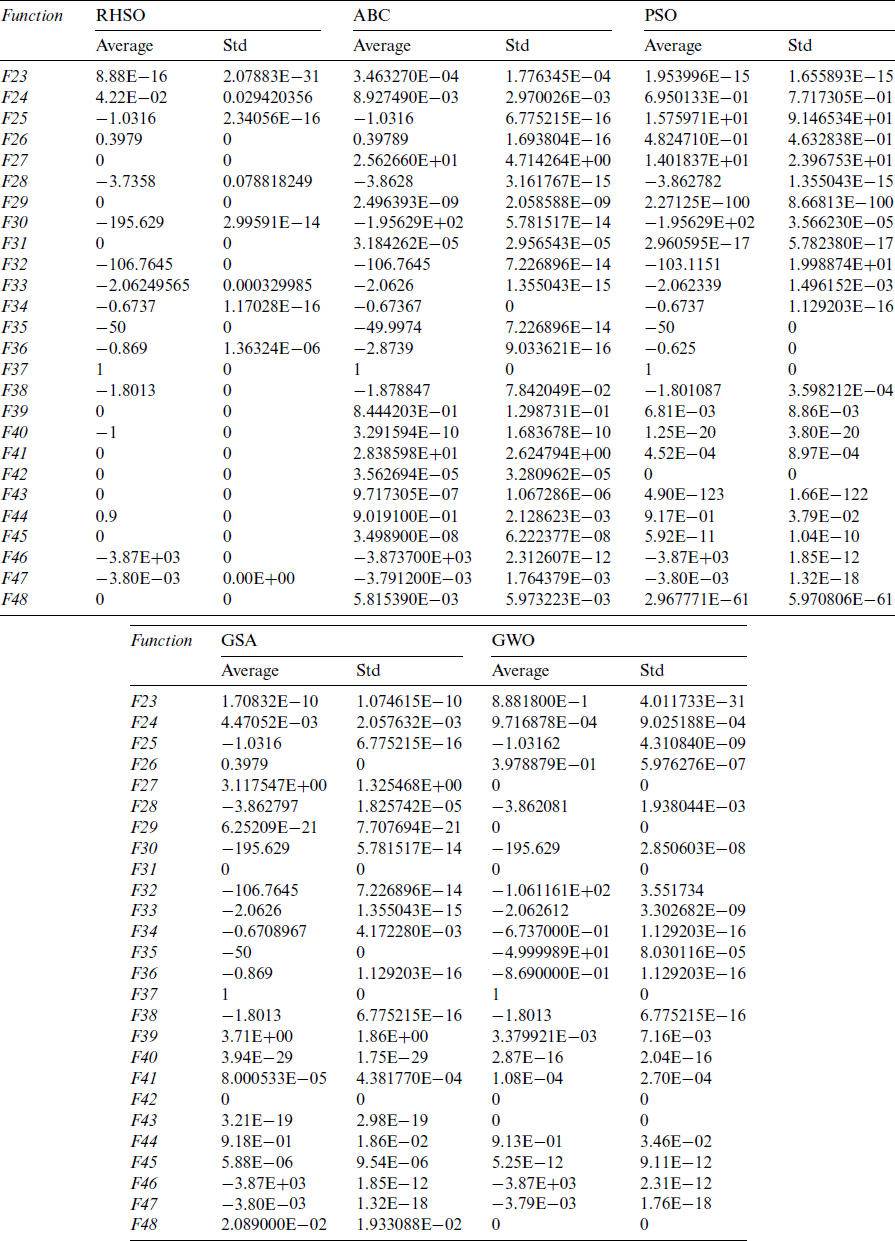
RHSO algorithm is evaluated by using 48 benchmark functions. Some of those functions are standard functions that are used in researches. These functions are chosen to be able to show the performance of RHSO and also to compare it with some known algorithms. The selected 48 test functions are shown in Tabs. 1 and 2, where D means the function’s dimension, range is the function’s search space limits, and Opt is the optimal value. The selected functions are unimodal or multimodal benchmark minimization functions. Unimodal test functions have a single optimum value; thus, they can benchmark an algorithm’s convergence and exploitation. While multimodal test functions have more than one optimum value, making them more challenging than unimodal. An algorithm should avoid all the local optima to approach and approximate the global optimum. So, exploration and local optima avoidance of algorithms can be benchmarked by multimodal test functions.
Table 1: Unimodal benchmark functions

Table 2: Multimodal benchmark functions

For each benchmark function, the RHSO algorithm and the compared algorithms are performed in the experiments under the condition of the same number of iterations (1000), independent runs for 30 times, and the population size is set to 50. The statistical results (average and standard deviation) are showed in Tabs. 3 and 4. For verifying the results, the RHSO algorithm is compared with ABC [7], PSO [8], GSA [23], and GWO [4].
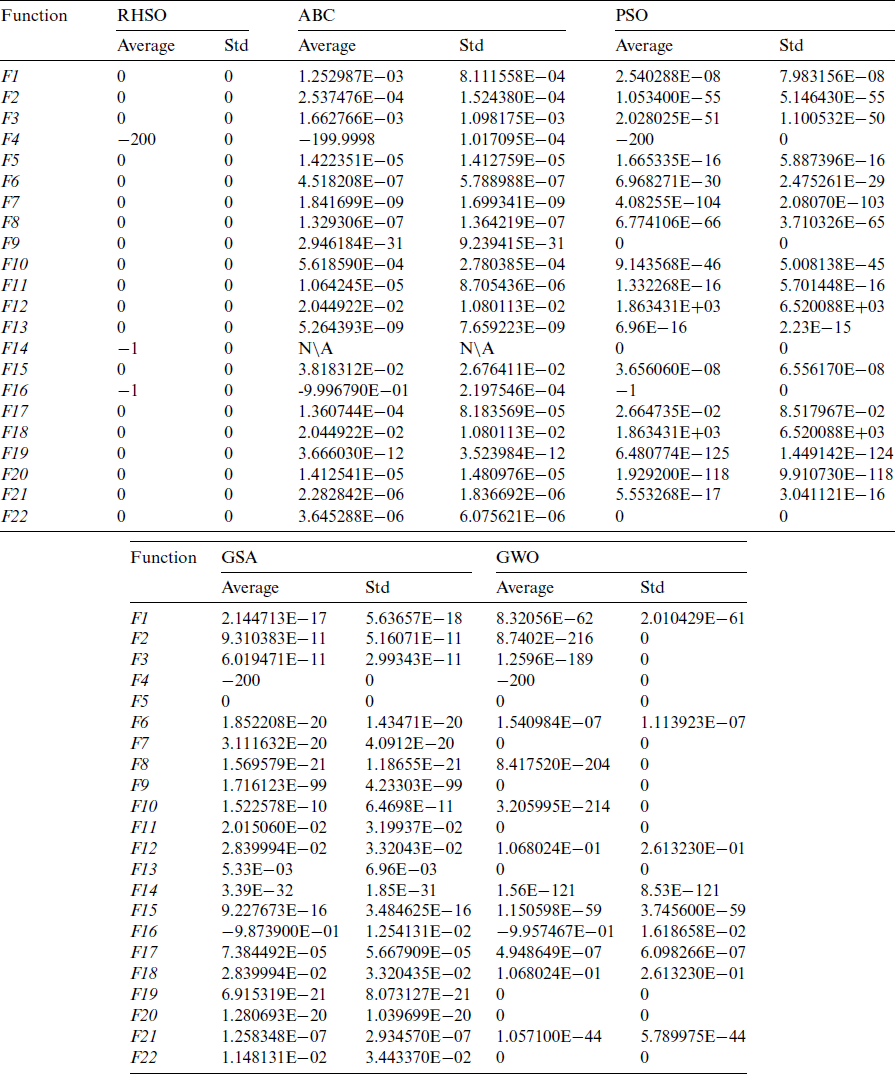
The results in Tab. 3 demonstrated that RHSO is better than the selected algorithms in all unimodal test functions. Unimodal functions test the exploitation of an algorithm. The obtained results showed RHSO superiority in exploiting the optimal value, so RHSO provides excellent exploitation ability.
For testing the exploration strength of an algorithm, the multimodal functions are used as the number growing exponentially with dimension such types of functions. The results in Tab. 4 demonstrated that RHSO is better than the selected algorithms on most multimodal functions. The obtained results show the superiority of the RHSO algorithm in terms of exploration.
The multimodal results presented in Tab. 4 demonstrated the exploitation of the proposed algorithm. Those results show the efficiency and strength of RHSO as compared to the other algorithms that are adopted for comparison. RHSO is tested on 26 multimodal test functions, at which RHSO is better and more efficient than the other algorithms. Also, RHSO can control exploitation better than other algorithms.
Based on the results in Tab. 3, the RHSO algorithm obtained the optimal value in all test functions; Therefore, RHSO has surpassed the selected algorithms, and this makes the RHSO algorithm better than they do in exploitation convergence. Those results demonstrated the accuracy, efficiency, and flexibility of the proposed algorithm.
According to the results in Tab. 4, the RHSO algorithm obtained the optimal value in 23 test functions; also, it is very close to the optimal value and better than the values of the selected algorithms for the same test functions in three test functions (F23, F24, and F28).
This paper proposed a new optimization algorithm inspired by Rock hyrax’s behavior; RHSO is proposed as an alternative technique for solving optimization problems. In the proposed RHSO algorithm, the updating of position makes the solutions move towards or outwards the goal to guarantee the search space exploitation and exploration. Forty-eight test functions are used to test the performance of RHSO in terms of exploitation and exploration. The obtained results demonstrated that RHSO was able to outperform ABC, PSO, GSA, and GWO. The obtained unimodal test functions result demonstrated RHSO algorithm exploitation superiority. After that, RHSO exploration ability is shown by the obtained multimodal test functions result. RHSO algorithm is characterized by having few variables than the other algorithms, making it easy to understand and implement. RHSO can solve various optimization problems (like scheduling, maintenance, parameters optimization, and many others). Future studies can recommend several directions, such as solving various optimization problems and developing a multi-objective version of the RHSO algorithm as RHSO is currently a single objective optimization algorithm.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. C. Muro, R. Escobedo, L. Spector and R. P. Coppinger. (2011). “Wolf-pack (Canis lupus) hunting strategies emerge from simple rules in computational simulations,” Behavioural Processes, vol. 88, no. 3, pp. 192–197. [Google Scholar]
2. J. J. L. Higdon and S. Corrsin. (1978). “Induced drag of a bird flock,” American Naturalist, vol. 112, no. 986, pp. 727–744. [Google Scholar]
3. E. Bonabeau, M. Dorigo and G. Theraulaz. (1999). Swarm Intelligence: From Natural to Artificial Systems. USA: Oxford University Press. [Google Scholar]
4. S. Mirjalili, S. M. Mirjalili and A. Lewis. (2014). “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61. [Google Scholar]
5. M. Dorigo, M. Birattari and T. Stutzle. (2006). “Ant colony optimization,” IEEE Computational Intelligence Magazine, vol. 1, no. 4, pp. 28–39. [Google Scholar]
6. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al. (2017). , “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances in Engineering Software, vol. 114, pp. 163–191. [Google Scholar]
7. B. Basturk and D. Karaboga. (2006). “An artificial bee colony (ABC) algorithm for numeric function optimization,” in Proc. of the IEEE Swarm Intelligence Symp., Indianapolis, IN, USA, pp. 4–12. [Google Scholar]
8. J. Kennedy and R. Eberhart. (1995). “Particle swarm optimization,” in Proc. of Int. Conf. on Neural Networks, Perth, WA, Australia, pp. 1942–1948. [Google Scholar]
9. G. Beni and J. Wang. (1993). “Swarm intelligence in cellular robotic systems,” in Robots and Biological Systems: Towards a New Bionics?, NATO ASI Series (Series F: Computer and Systems Sciences), vol. 102. Berlin, Heidelberg, Germany: Springer. [Google Scholar]
10. O. Olorunda and A. P. Engelbrecht. (2008). “Measuring exploration/exploitation in particle swarms using swarm diversity,” in Proc. of IEEE World Congress on Computational Intelligence, Hong Kong, pp. 1128–1134. [Google Scholar]
11. S. Mirjalili, S. Zaiton and M. Hashim. (2010). “A new hybrid PSOGSA algorithm for function optimization,” in Proc. of Int. Conf. on Computer and Information Application, Tianjin, pp. 374–377. [Google Scholar]
12. L. Lin and M. Gen. (2009). “Auto-tuning strategy for evolutionary algorithms: Balancing between exploration and exploitation,” Soft Computing, vol. 13, no. 2, pp. 157–168. [Google Scholar]
13. J. H. Holland. (1992). “Genetic algorithms,” Scientific American, vol. 267, no. 1, pp. 66–73. [Google Scholar]
14. D. Goldberg. (1989). Genetic Algorithms in Optimization, Search and Machine Learning, USA: Addison-Wesley Longman Publishing Co., Inc. [Google Scholar]
15. K. P. Rainer Storn. (1997). “Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, no. 4, pp. 341–359. [Google Scholar]
16. L. Fogel. (1999). Intelligence Through Simulated Evolution: Forty Years of Evolutionary Programming, New York: John Wiley Sons, Inc. [Google Scholar]
17. I. Rechenberg. (1989). “Evolution Strategy: Nature’s way of optimization,” in Optimization: Methods and Applications, Possibilities and Limitations, Lecture Notes in Engineering, vol. 47. Berlin, Heidelberg: Springer, pp. 106–126. [Google Scholar]
18. N. Hansen, S. D. Müller and P. Koumoutsakos. (2003). “Reducing the time complexity of the randomized evolution strategy with covariance matrix adaptation (CMA-ES),” Evolutionary Computation, vol. 11, no. 1, pp. 1–18. [Google Scholar]
19. J. R. Koza. (1994). “Genetic programming as a means for programming computers by natural selection,” Statistics and Computing, vol. 4, no. 2, pp. 87–112. [Google Scholar]
20. D. Simon. (2008). “Biogeography-based optimization,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 6, pp. 702–713. [Google Scholar]
21. B. Webster and P. J. Bernhard. (2003). “A local search optimization algorithm based on natural principles of gravitation,” in Proc. of the Int. Conf. on Information and Knowledge Engineering, Las Vegas, Nevada, USA, pp. 255–261. [Google Scholar]
22. O. K. Erol and I. Eksin. (2006). “A new optimization method: Big bang–big crunch,” Information Sciences, vol. 37, no. 2, pp. 106–111. [Google Scholar]
23. E. Rashedi, H. Nezamabadi-pour and S. Saryazdi. (2009). “GSA: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248. [Google Scholar]
24. A. Kaveh and S. Talatahari. (2010). “A novel heuristic optimization method: Charged system,” Acta Mechanica, vol. 213, no. 3–4, pp. 267–289. [Google Scholar]
25. B. Alatas. (2011). “ACROA: Artificial chemical reaction optimization algorithm for global optimization,” Expert Systems with Applications, vol. 38, no. 10, pp. 13170–13180. [Google Scholar]
26. A. Hatamlou. (2013). “Blackhole: A new heuristic optimization approach for data clustering,” Information Sciences, vol. 222, pp. 175–184. [Google Scholar]
27. M. K. A. Kaveh. (2012). “A new meta-heuristic method: Ray optimization,” Computers & Structures, vol. 112, pp. 283–294. [Google Scholar]
28. H. Z. J. Du and X. Wu. (2006). “Small-world optimization algorithm for function optimization,” in Proc. of the Second Int. Conf. on Advances in Natural Computation, Xi’an, China, pp. 264–273. [Google Scholar]
29. H. Shah-Hosseini. (2011). “Principal components analysis by the galaxy-based search algorithm: A novel metaheuristic for continuous optimization,” International Journal of Computational Science and Engineering, vol. 6, no. 1/2, pp. 132–140. [Google Scholar]
30. F. F. Moghaddam, R. F. Moghaddam and M. Cheriet. (2012). “Curved space optimization: A random search based on general relativity theory,” ArXiv, vol. abs/1208.2214, pp. 1–16. [Google Scholar]
31. D. Karaboga and B. Basturk. (2007). “A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm,” Journal of Global Optimization, vol. 39, no. 3, pp. 459–471. [Google Scholar]
32. K. J. Brown. (2003). “Seasonal variation in the thermal biology of the rock hyrax (Procavia capensis),” MS thesis, Pietermaritzburg, School of Botany and Zoology, University of KwaZulu-Natal. [Google Scholar]
33. K. J. Brown and C. T. Downs. (2007). “Basking behavior in the rock hyrax (Procavia capensis) during winter,” African Zool, vol. 42, no. 1, pp. 70–79. [Google Scholar]
34. L. Koren, O. Mokady and E. Geffen. (2008). “Social status and cortisol levels in singing rock hyraxes,” Hormones and Behavior, vol. 54, no. 1, pp. 212–216. [Google Scholar]
35. Rock hyrax. (2020). “San Diego Zoo Global Wildlife Conservancy,” . [Online]. Available: https://animals.sandiegozoo.org/animals/rock-hyrax. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |