DOI:10.32604/cmc.2021.015681
| Computers, Materials & Continua DOI:10.32604/cmc.2021.015681 | |
| Article |
Control Strategy for a Quadrotor Based on a Memetic Shuffled Frog Leaping Algorithm
1Research Laboratory in Automatic Control (LARA), National Engineering School of Tunis (ENIT), University of Tunis EL MANAR, Le Belvédère, Tunis, 1002, Tunisia
2College of Engineering at Wadi Addawaser, Prince Sattam Bin Abdulaziz University, Al-Kharj, 11911, Saudi Arabia
3Department of Electrical Engineering, Faculty of Engineering, Minia University, Minia, 61517, Egypt
4High Institute of Industrial Systems of Gabès (ISSIG), University of Gabès, Gabès, 6011, Tunisia
*Corresponding Author: Hegazy Rezk. Email: hr.hussien@psau.edu.sa
Received: 02 December 2020; Accepted: 23 January 2021
Abstract: This work presents a memetic Shuffled Frog Leaping Algorithm (SFLA) based tuning approach of an Integral Sliding Mode Controller (ISMC) for a quadrotor type of Unmanned Aerial Vehicles (UAV). Based on the Newton–Euler formalism, a nonlinear dynamic model of the studied quadrotor is firstly established for control design purposes. Since the main parameters of the ISMC design are the gains of the sliding surfaces and signum functions of the switching control law, which are usually selected by repetitive and time-consuming trials-errors based procedures, a constrained optimization problem is formulated for the systematically tuning of these unknown variables. Under time-domain operating constraints, such an optimization-based tuning problem is effectively solved using the proposed SFLA metaheuristic with an empirical comparison to other evolutionary computation- and swarm intelligence-based algorithms such as the Crow Search Algorithm (CSA), Fractional Particle Swarm Optimization Memetic Algorithm (FPSOMA), Ant Bee Colony (ABC) and Harmony Search Algorithm (HSA). Numerical experiments are carried out for various sets of algorithms’ parameters to achieve optimal gains of the sliding mode controllers for the altitude and attitude dynamics stabilization. Comparative studies revealed that the SFLA is a competitive and easily implemented algorithm with high performance in terms of robustness and non-premature convergence. Demonstrative results verified that the proposed metaheuristics-based approach is a promising alternative for the systematic tuning of the effective design parameters in the integral sliding mode control framework.
Keywords: Quadrotor; modeling; integral sliding mode control; gains tuning; advanced metaheuristics; memetic algorithms; shuffled frog leaping algorithm
The quadrotor is the most popular type of Unmanned Aerial Vehicles (UAV) thanks to its multiple applications in various areas of engineering and civilian domains [1,2]. The capacities of Vertical and Take-Off Landing (VTOL) and maneuverability prove the growing use of these vehicles. The flight dynamics stabilization of a quadrotor is a significant and hard task as it is an underactuated, nonlinear, and large-scale system [3–5]. External disturbances and model uncertainties of quadrotors further increase the complexity of these aerial vehicles. All these physical and environmental features require powerful and robust controllers’ design and tuning with systematic and low time-consuming procedures.
In the literature, various control strategies have been proposed to cover this kind of issue. In the work of Ma et al. [6], an optimal control method of an unmanned aerial helicopter with unknown disturbances has been designed based on the Hamilton-Jacobi-Bellman equation. A linear model predictive controller has been proposed for a tilt-rotor tricopter to handle the angular dynamics and vertical body velocity in [7]. In the work of Argentim et al. [8], a comparison between different linear controllers, i.e. ITAE-tuned PID, classical LQR, and LQR loop-shaping-tuned PID, has been established for the vertical attitude stabilization of a quad-copter platform. For these linear approaches, the stabilization cannot be guaranteed when the vehicle moves away from its flight domain. Since the nonlinear control approaches can rise above some of the restrictions and drawbacks of the linear case, various nonlinear control methods have been developed. In the work of Stebler et al. [9], a nonlinear output feedback controller has been designed leading to an asymptotic altitude and attitude tracking of a quadrotor UAV under model uncertainties and unknown external disturbances. In the work of Ben Ammar et al. [10], the stabilization of a quadrotor vehicle has been achieved thanks to a proposed fuzzy gains-scheduling integral sliding mode controller. The main advantage of the proposed fuzzy-tuned sliding mode controller is the complete compensation of the matched disturbances when the quadrotor is in the sliding phase. Since the sliding mode control approaches have been successfully applied for various complex systems, i.e. robot manipulators [11], electrical motors [12], underwater vehicles [13], and so on, the Integral Sliding Mode Control (ISMC) variant is adopted in this paper to stabilize the altitude and attitude dynamics of a quadrotor UAV. The ISMC is a robust variant of the canonical sliding mode control approach where an integral action is added to the general form of the sliding surface shape [14,15]. Such a control approach allows eliminating the reaching phase and guarantees the invariance from initial conditions.
Unfortunately, the ISMC approach claims the choice and tuning of several effective control parameters which make difficult the controller’s design procedure. These effective control parameters are often selected by repetitive trials-errors based methods which become hard and time-consuming for complex and large-scale systems. To overcome this drawback, several attempts have been proposed in the literature. In the work of Dydek et al. [16], an adaptive fuzzy sliding mode controller has been designed for the attitude stabilization of an unmanned vehicle under parametric uncertainties and disturbances. Such a proposed fuzzy sliding controller has allowed the reduction of the undesirable chattering phenomenon but at the expense of slow response of the system dynamics. In the work of Chang [17], fuzzy inference systems have been used to approximate the unknown attitude dynamics of the quadrotor and eliminate the reaching phase under external disturbances and uncertainties. In the work of Zhang et al. [18], an adaptive mechanism has been designed to estimate the integral sliding mode controllers’ gains to eliminate chattering behavior. All these design methods remain time-consuming, non-systematic, and difficult in terms of real-world prototyping and experimentation. So, looking for an effective and systematic tuning technique becomes a necessity instead of tedious and expensive trials-errors based methods. For this purpose, the theory of global metaheuristics and hard optimization can present a promising solution.
Several metaheuristics have been proposed in the literature and received much interest in dealing with hard and large-scale optimization problems [19]. Recently, memetic metaheuristics have shown remarkable superiority in terms of exploitation/exploration capabilities for a robust and non-premature convergence compared to the classical ones. Initially proposed by Eusuff et al. [20,21], the Shuffled Frog Leaping Algorithm (SFLA) is one of the most powerful memetic metaheuristics. In this formalism, a set of virtual frogs are partitioned into different groups called memeplexes. Within each memeplex of the swarm, the individual frogs hold ideas that can be influenced by the behavior of other frogs with better fitness and evolve through a process of memetic evolution. After a defined number of memetic evolution steps, ideas are passed among memeplexes, which are considered as different cultures of frogs. Given the high performance of this algorithm, several improvements [22–25] and applications [26–28] have been proposed in the literature.
In this paper, the selection and tuning procedure of all effective parameters of an internal sliding mode controller for a quadrotor UAV is formulated as a constrained optimization problem. The operational constraints are specified in terms of time-domain performance criteria. Such a nonlinear and large-scale optimization problem is efficiently solved based on the proposed SFLA metaheuristic compared to other global swarm intelligence algorithms. The main contribution of the proposed approach is the systematic and fast way of tuning many effective sliding mode controllers’ parameters for a nonlinear and complex system. The classical trials-errors based methods, which often lead to local solutions of the tuning problem, are no longer used and the design time is further reduced. All control performances and operational constraints are implicitly specified into the formulated optimization problem which will be solved in a single run and without recourse to a repetitive test-check procedure.
The remainder of this paper is organized as follows. In Section 2, a nonlinear model of the studied quadrotor is established thanks to the Newton–Euler formalism. Section 3 describes the formulation of the integral sliding mode controllers’ gains tuning as an optimization problem under operational constraints. Section 4 is devoted to the description of the proposed memetic shuffled frog leaping metaheuristic to solve at best the formulated tuning problem. In Section 5, demonstrative results are carried out to show the superiority and effectiveness of the proposed SFLA-tuned sliding mode control approach. Conclusions are drawn in Section 6.
A quadrotor UAV is equipped with four rotors that are independently controlled as shown in Fig. 1. The motion of such a vehicle results from changes in the rate of the rotors. The body is symmetrical, and the propellers are rigid. The thrust and drag forces are proportional to the square of the propeller’s speeds denoted as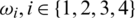 
.
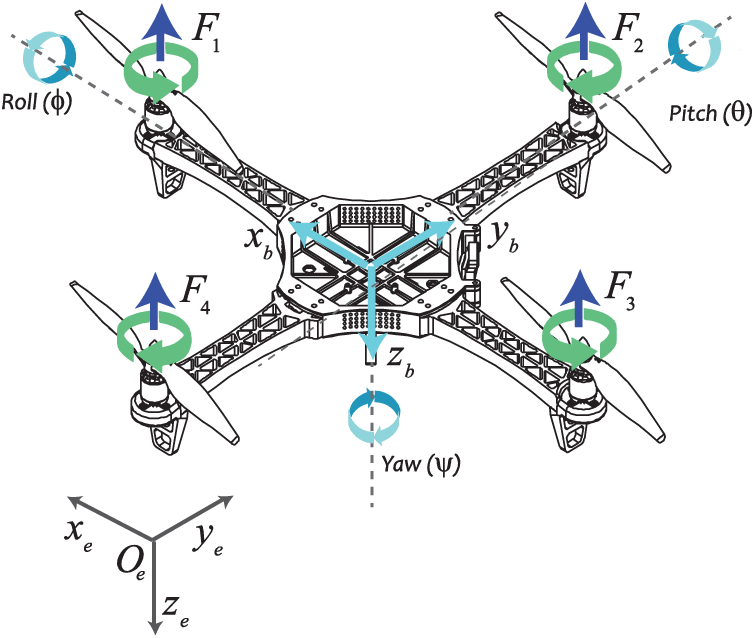
Figure 1: Mechanical structure of the quadrotor and related frames
In the flight space, the orientation of the quadrotor is accomplished by the rotation matrix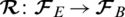 
defined as follows [29,30]:
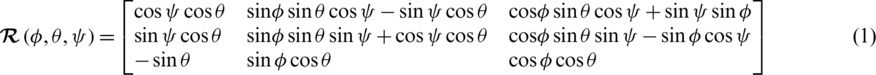
where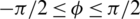 
, 
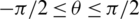, and 
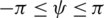are the roll, pitch, and yaw Euler angles, respectively, 
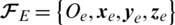and 
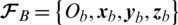are the earth- and body- frames, respectively.
The quadrotor’s position and attitude are defined as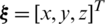 
and 
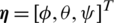, respectively. Let a vector 
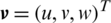denotes the linear velocity of the quadrotor in the earth-frame 
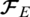, while 
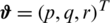represents its angular velocity in the body-frame 
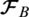. The kinematic equations of the rotational and translational motions are obtained, respectively, as follows [29,30]:
where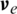 
and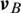 
denote the linear velocities of the drone in the earth- and body-frames, respectively.
While using the Newton–Euler formalism, a complete model of the vehicle is given as follows:
where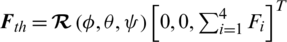 
is the thrust force of the rotors, 
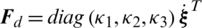is the air drag force, 
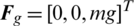is the gravity force, 
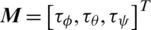denotes the total rolling, pitching, and yawing moments, 
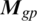and 
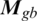are the propellers’ and quadrotor’s body gyroscopic torques, respectively, and 
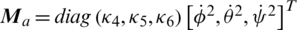is the moment resulting from the aerodynamic frictions [29,30].
Substituting the position vector and the forces expressions into Eq. (4), the following translational dynamics of the quadrotor is obtained:
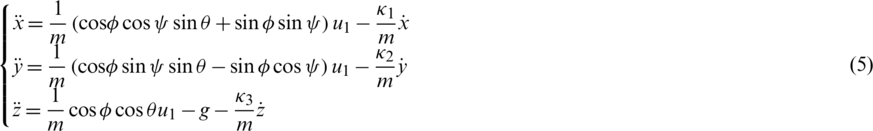
From the second part of Eq. (4), the rotational dynamics can be computed as:
where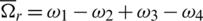 
is the overall residual rotor speed, Ix, Iy and Iz are the body inertia, Jr is the rotor inertia and 
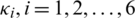are the aerodynamic friction and translational drag coefficients.
The control inputs of the quadrotor are defined as u1, u2, u3, and u4 which represent the total thrust force in the z-axis, roll, pitch, and yaw torques, respectively:
where b and d are the thrust and drag coefficients, respectively.
Finally, taking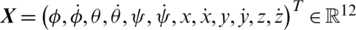 
as a state vector, a state-space representation of the studied quadrotor is obtained as follows [29,30]:
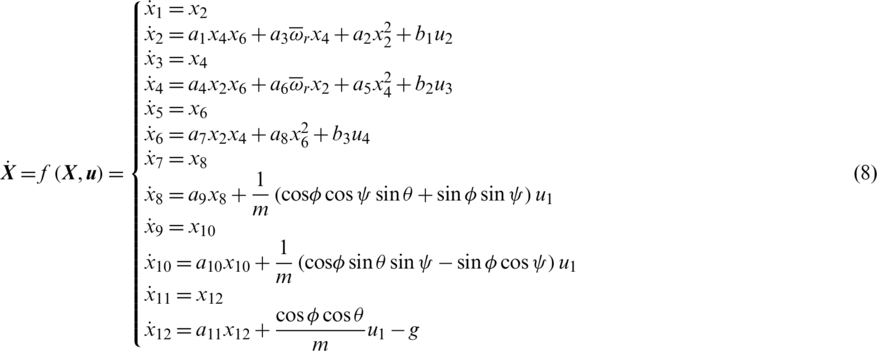
where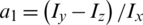 
, 
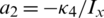, a3 = − Jr/Ix, 
, 
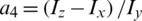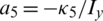, a6 = − Jr/Iy, 
, 
, 
, 
, 
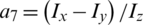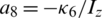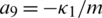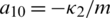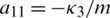, b1 = 1/Ix, b2 = 1/Iy and b3 = 1/Iz.
The control objective is to design a robust controller, with a systematic and easy tuning method of its effective design parameters, for the attitude and altitude dynamics stabilization. Desired trajectories are defined as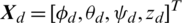 
for the outputs 
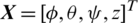, assumed to be accessible.
In the ISMC framework, the expression of the sliding surface is defined as follows [31]:
where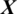 
denotes the controlled variables, 
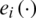is the tracking error defined as 
, 
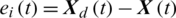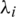are positive constants and 
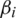are the integral gains, 
.
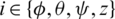The Lyapunov candidate scalar function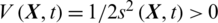
and the reaching condition
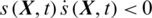lead to the following integral sliding mode control law for the altitude dynamics [10]:
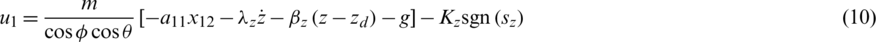
where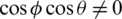 
, 
, 
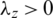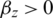, and Kz > 0 are the effective design parameters.
Following the same steps, the control laws u2, u3, and u4 responsible for generating the roll, pitch, and yaw rotations, respectively, are calculated as follows:
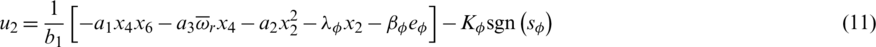
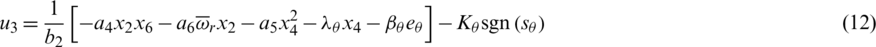
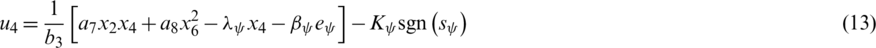
where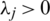 
, 
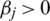, and Kj > 0, 
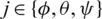, are the effective design parameters of the integral sliding mode controllers for the attitude dynamics.
3.2 Optimization-based Problem Formulation
As shown in Eqs. (10)–(13), the design of integral sliding controllers for the drone dynamics involves the tuning of several parameters, i.e., slopes of the sliding surfaces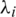 
, integral and sign functions gains 
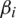and Ki, 
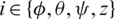. The selection of such a large number of effective control parameters is not a straightforward problem. Indeed, the classical trials-errors based procedures become ineffective, time-consuming, and do not guarantee an optimal solution to the problem. So, such a tuning procedure can be effectively solved thanks to proposed metaheuristics while considering the following formulation:
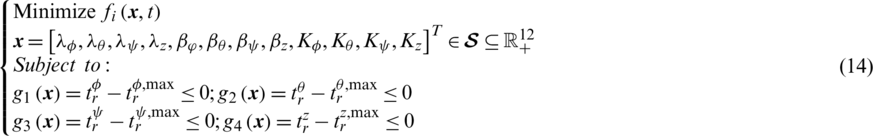
where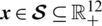 
is the vector of decision variables which contains all controllers’ gains, 
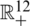denotes the 12-dimensional set of the positive real numbers, 
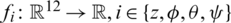are the cost functions to be minimized under operational time-domain constraints, 
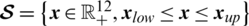denotes the bounded search space, 
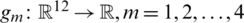are the operational constraints. The terms 
, 
, 
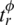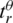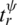, and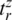 
denote the step-response rise times of the controlled dynamics. The terms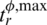 
, 
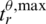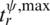, and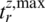 
denote their pre-specified maximum values.
The cost functions of the problem (14) are chosen, for each controlled dynamics as the Integral of Absolute Error (IAE) performance criteria, defined as follows:
where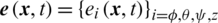 
denotes the tracking errors between the references 
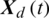and the controlled process variables 
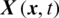, i.e., 
, 
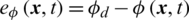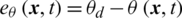, and so on.
Since the optimization problem (14) is a multi-objective type, the following aggregation function is used [19]:
where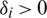 
are the weighting coefficients of the aggregation function ensuring 
.
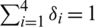To handle the constraints of the problem (14), the following static penalty function is used [19]:
where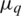 
are the scaling penalty parameters and ncon denotes the number of inequality constraints.
4 Proposed Memetic Shuffled Frog Leaping Algorithm
In the shuffled frog leaping algorithm, a population of npop frogs is randomly initialized in the feasible search space 
and portioned into nmem memeplexes. Each memeplex contains n frogs. At each iteration k, the position of the ith frog in the jth memeplex is denoted as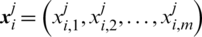 
, where 
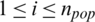and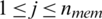 
. Then, all frogs are sorted in descending order according to their fitness following the given ranking strategy [21]. In each memeplex, the frog with the global best fitness value, evaluated in terms of the cost function, is expressed as 
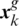. Those with the best and the worst fitness values are identified as 
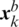and 
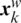, respectively. Then, a process of local search for each memeplex is performed to improve only the frogs with the worst fitness through the memetic evolution [21]. At each iteration k, the new position of the frog with the worst fitness leaps towards the position of the best one according to the following motion equations:
where rk is a random number uniformly distributed in [0,1],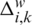 
is the change in the ith frog position, 
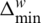and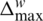 
are the minima and maximum allowed changes.
As mentioned in [22–25], if this memetic process produces a better solution, i.e.,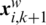 
is better than 
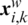, the new frog is then used to replace the old one in the memeplex. Otherwise, the motion Eqs. (18) and (19) are recalculated but concerning the global best frog 
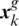instead of 
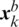. If there is no improvement, the worst frog 
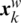will be replaced by a new randomly generated solution. The memetic evolution process is then continued for a predefined number of iterations denoted as kls. The new memeplexes are reformed according to the new order ranked by the fitness valueagain.
The main control parameters of the SFLA are: numbers of memeplexes nmem, frogs in a memeplex n, memetic generations kls, and shuffling iterations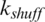
. A pseudo-code for the SFLA is given by [22–28]:
Step 1: Initialize all control parameters: npop, nmem, kls,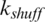 
, 
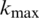, etc.
Step 2: Randomly generate the initial population and evaluate the npop solutions.
Step 3: Sort the population in descending order of fitness.
Step 4: Divide the population into nmem memeplexes.
Step 5: Call the local search mechanism for the memetic evolution process;
• Determine the best and worst solutions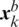 
and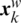 
, respectively
• Improve the worst frog position according to Eqs. (18) and (19) and repeat iterations
Step 6: Shuffle the evolved memeplexes and sort the new population
Step 7: Test the termination criterion and return the best solution.
4.3 Numerical Experimentations and Discussion
To evaluate the performance of the proposed SFLA, various standard test functions of Appendix A are used for numerical experimentation. The metaheuristics CSA, HSA, FPSOMA, and ABC are used as comparison tools. The termination criterion is set as the maximum number of iterations reaches 10000, the population size is 50 and specific control parameters are set as follows:
• SFLA [20,21]: memeplexes 5, frogs in a memeplex 10 and generations before shuffling 5.
• CSA [32]: flight length 2 and awareness probability 0.1.
• HSA [33]: harmony memory rate 0.9 and pitch adjusting rate 0.3.
• FPSOMA [34]: inertia weight 0.729, derivative 0.9, cognitive and social coefficients 0.9.
• ABC [35]: limit of abandonments 60.
The proposed metaheuristics are implemented and evaluated using a CPU Core i3, 1.70 GHz computer. The convergence histories of all reported algorithms are depicted in Fig. 2.
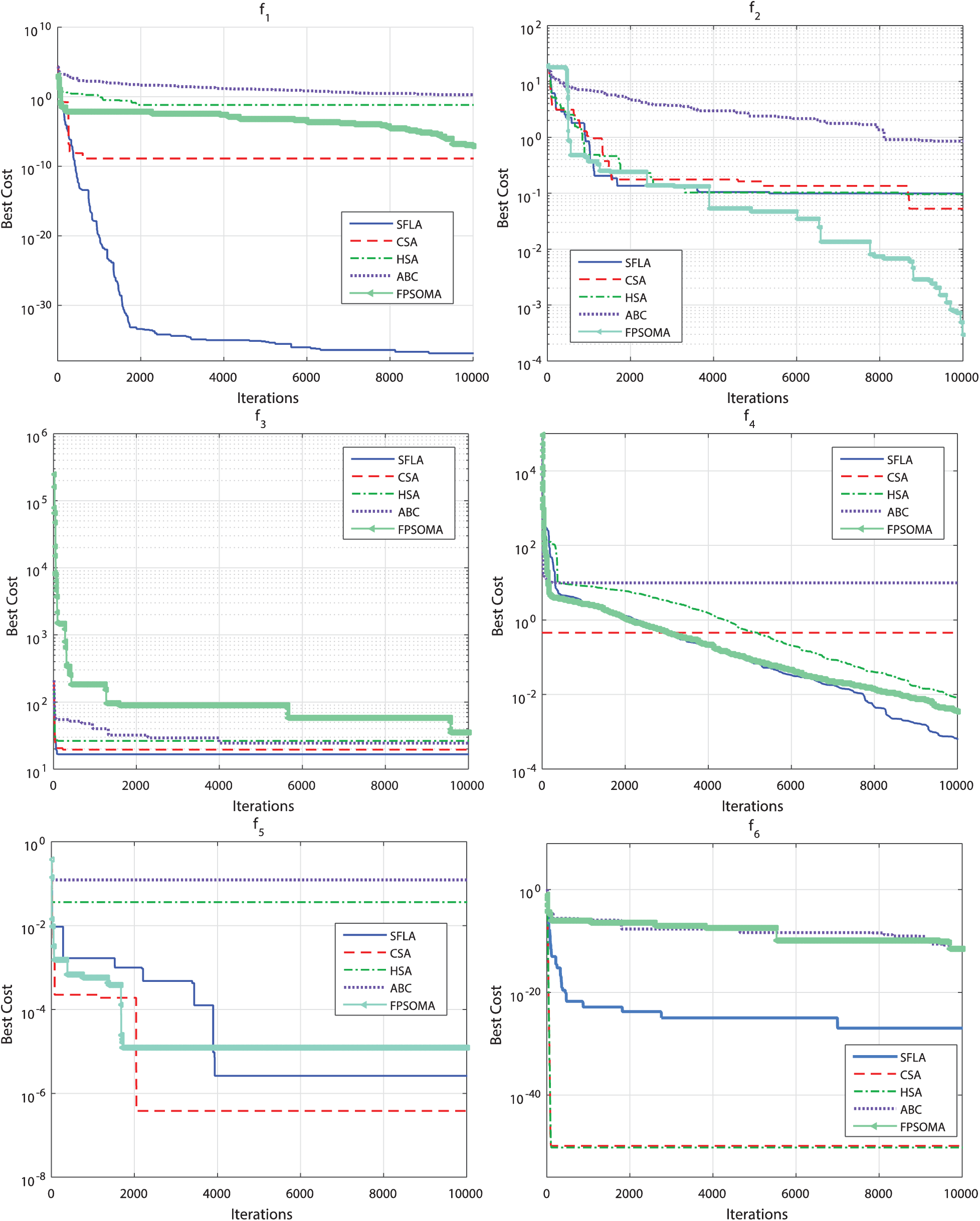
Figure 2: Convergence histories of the reported algorithms for the test functions
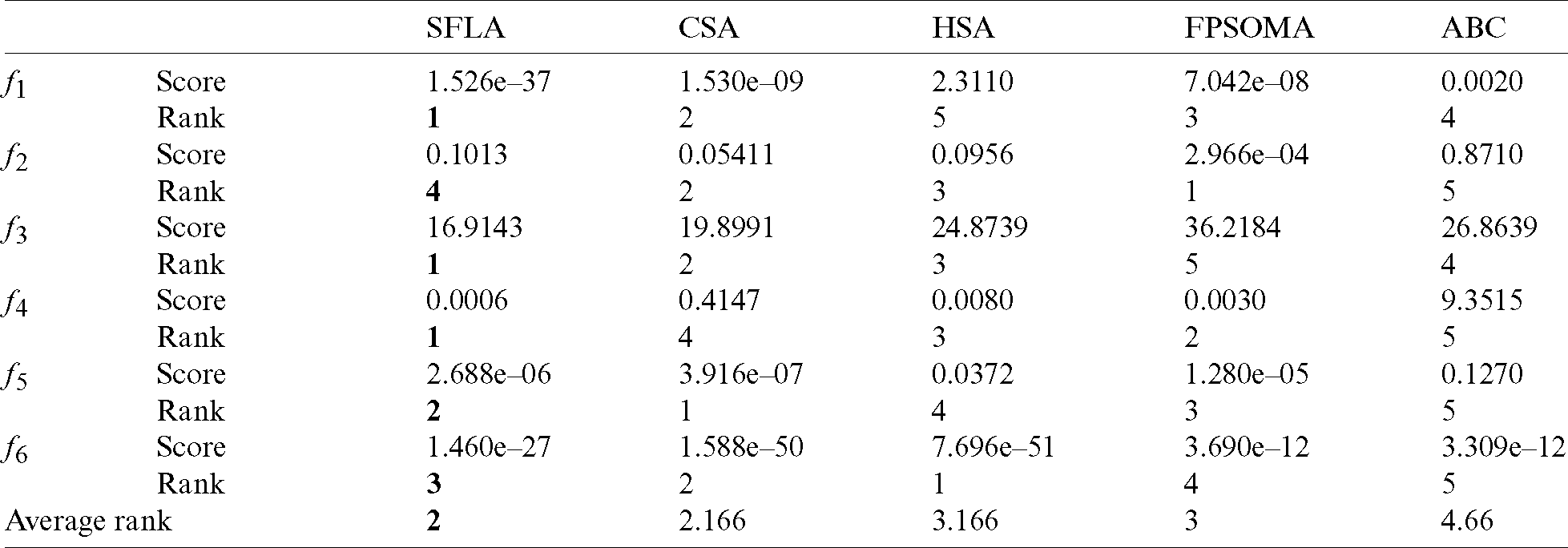
Tab. 1 summarizes the optimization results for independent 20 runs of test functions. Best, Worst, and Mean denote the best, worst and mean results for the minimization, respectively. STD is the standard deviation and ET denotes the elapsed time (in seconds). Results of rank-based Friedman’s analysis for all proposed metaheuristics are summarized in Tab. 2. From these analyses, one can note that the proposed SFLA has worthily attained the lowest average ranks compared to the remaining methods. Furthermore, it is shown that the SFLA achieved the first best computation time for test functions f1 −5 and the second one for the benchmark f6.
Table 1: Optimization results of the test functions over independent 20 runs
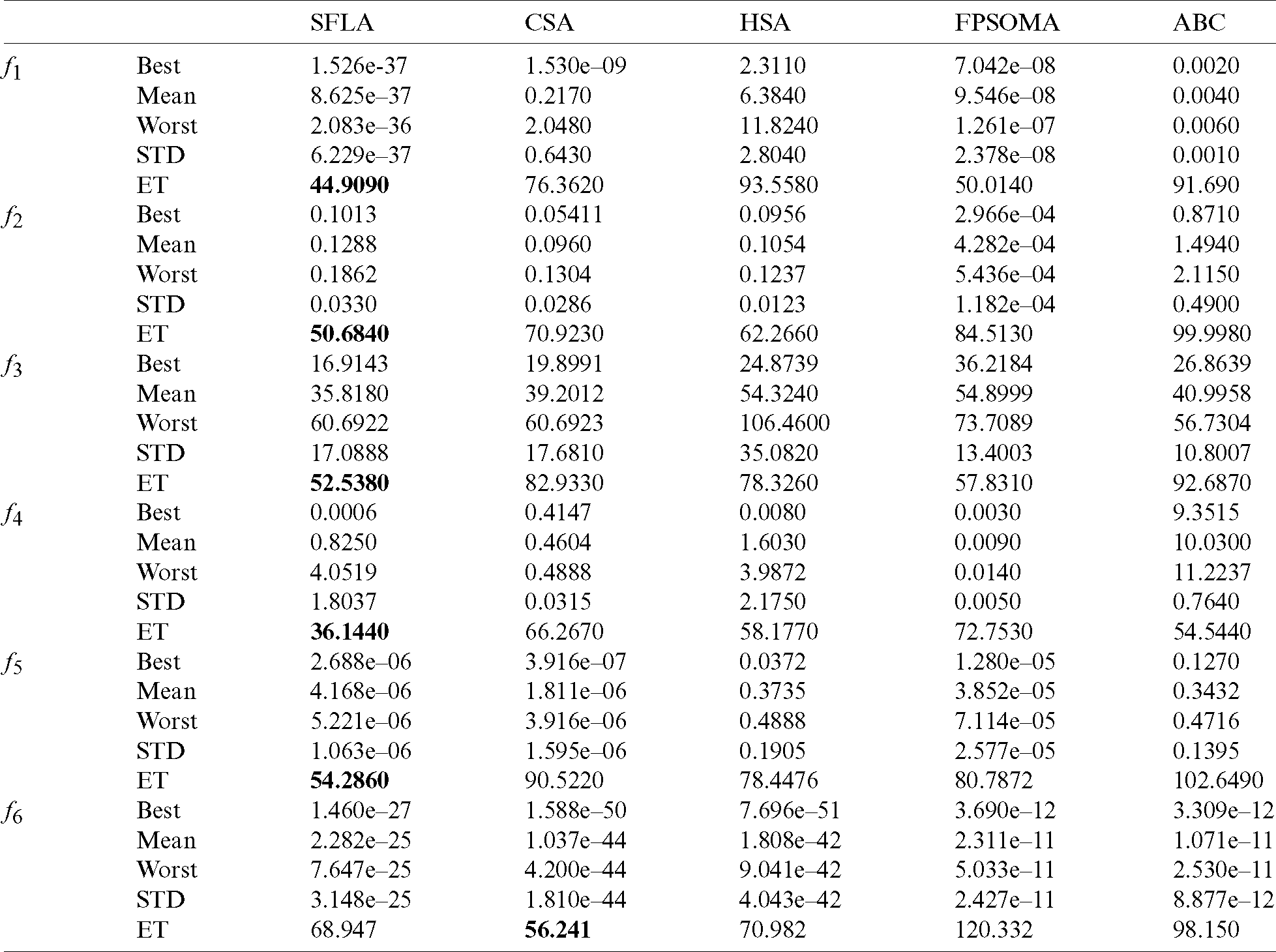
Table 2: Rank-based statistical analysis of best performances
5 Application to the ISMC Gains’ Tuning
The numeric values of the studied quadrotor’s parameters are given in Appendix B. The proposed model of such a vehicle has been validated in our previous works [10,29,30].
5.1 Simulation Results and Discussion
The reported algorithms were independently executed 20 times for the problem (14) over 100 iterations and using a population size of 50. Such a set of control parameters is deduced after various runs, where the number of iterations is raised for different values of the population size as shown in Tab. 3. Increasing the number of population and iterations allows for better results but with prohibitive computation times. Tab. 4 shows the statistical results over the independent 20 runs. The convergence histories of all proposed algorithms are given in Fig. 3.
Table 3: Optimization results of (14) for different number of iterations and generations
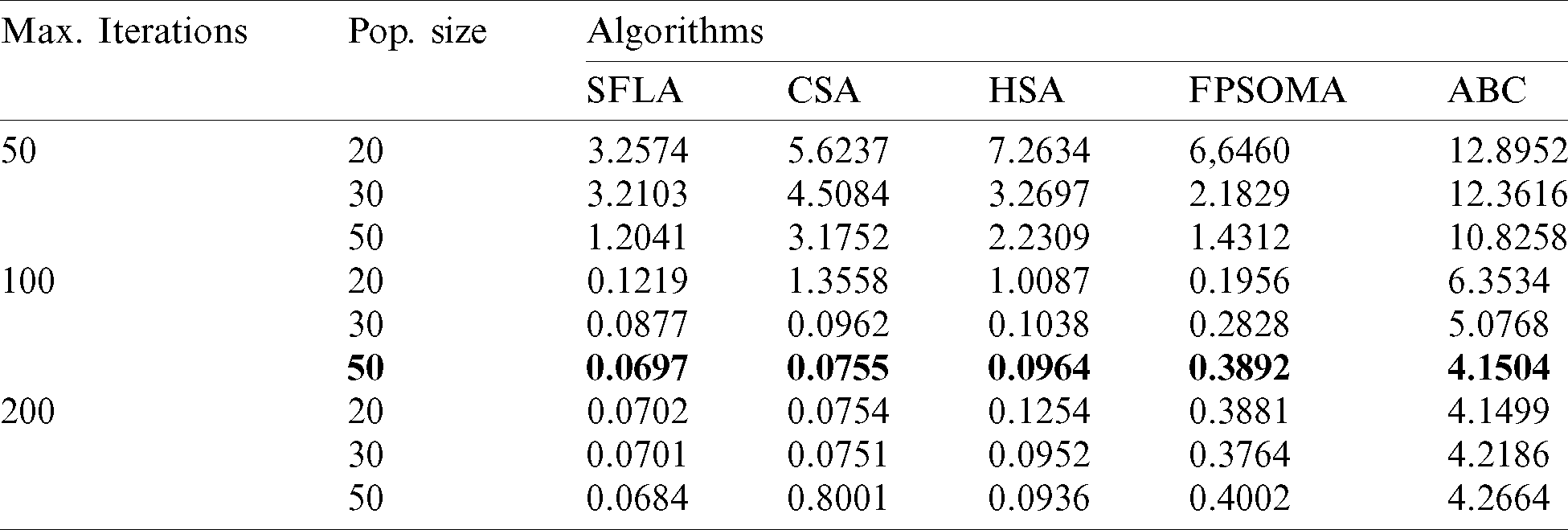
Table 4: Optimization results of the problem (14) over independent 20 runs
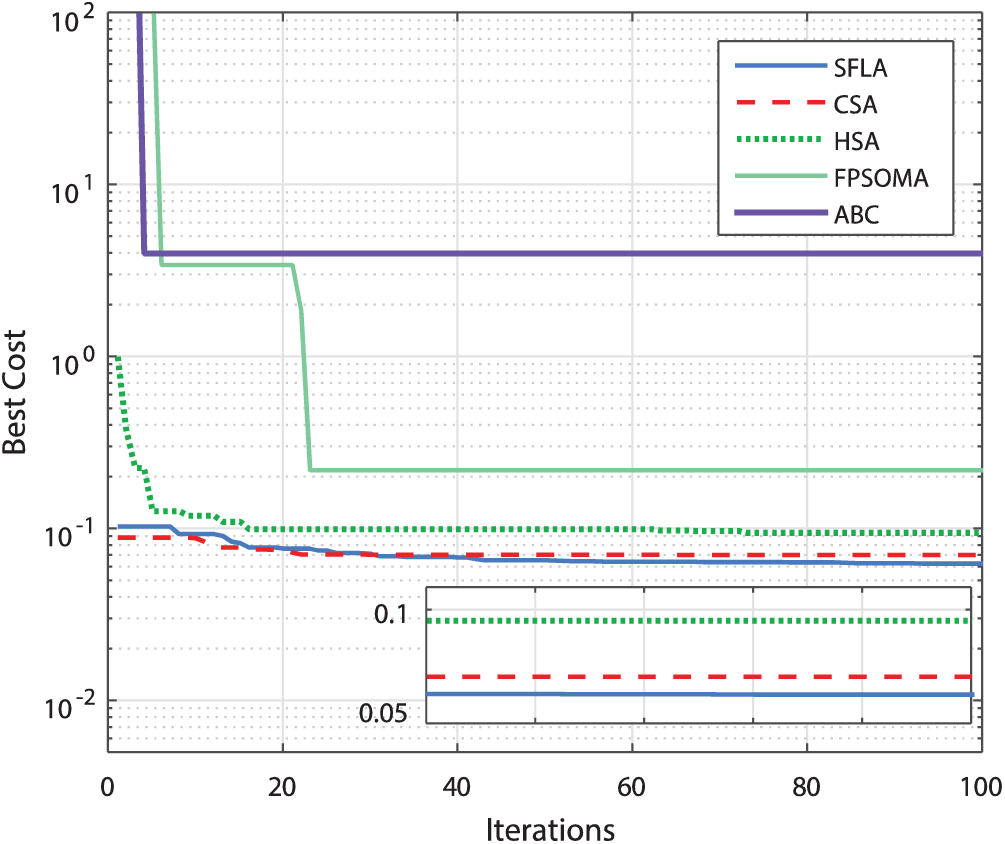
Figure 3: Convergence histories of the reported algorithms for problem (14)
From these numerical experimentations and demonstrative results, the best performance in terms of solutions quality, fastness, and exploitation/exploration capabilities is always obtained with the SFLA-based tuning approach. Such a memetic algorithm greatly outperforms all other reported metaheuristics especially against the well-known premature convergence problem as depicted by convergence curves of Fig. 3. The STD metric of the SFLA-tuned ISMC case is the best compared to those of all reported CSA, HSA, FPSOMA, and ABC algorithms. This highlights the interest of the local search operator and the memetic aspect of such a global metaheuristic. The computation time is always the least in the case of SFLA which further proves the contribution of such a control tuning method. For the closed-loop performance evaluation, the effectiveness of the SFLA-tuned ISMC approach is shown in Fig. 4 for the attitude and altitude dynamics stabilization. For the given initial conditions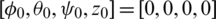 
, the quadrotor dynamics are successfully stabilized around the desired references 
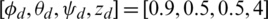with comparative performance. The system responses are further damped in the SFLA-tuned controllers. The rise and settling times are improved and the disturbance rejection at simulation time 10 sec is guaranteed with a fast and smooth behavior against all other algorithms. A large overshoot with remarkable oscillations is shown for the CSA- and FPSOMA-tuned controllers.
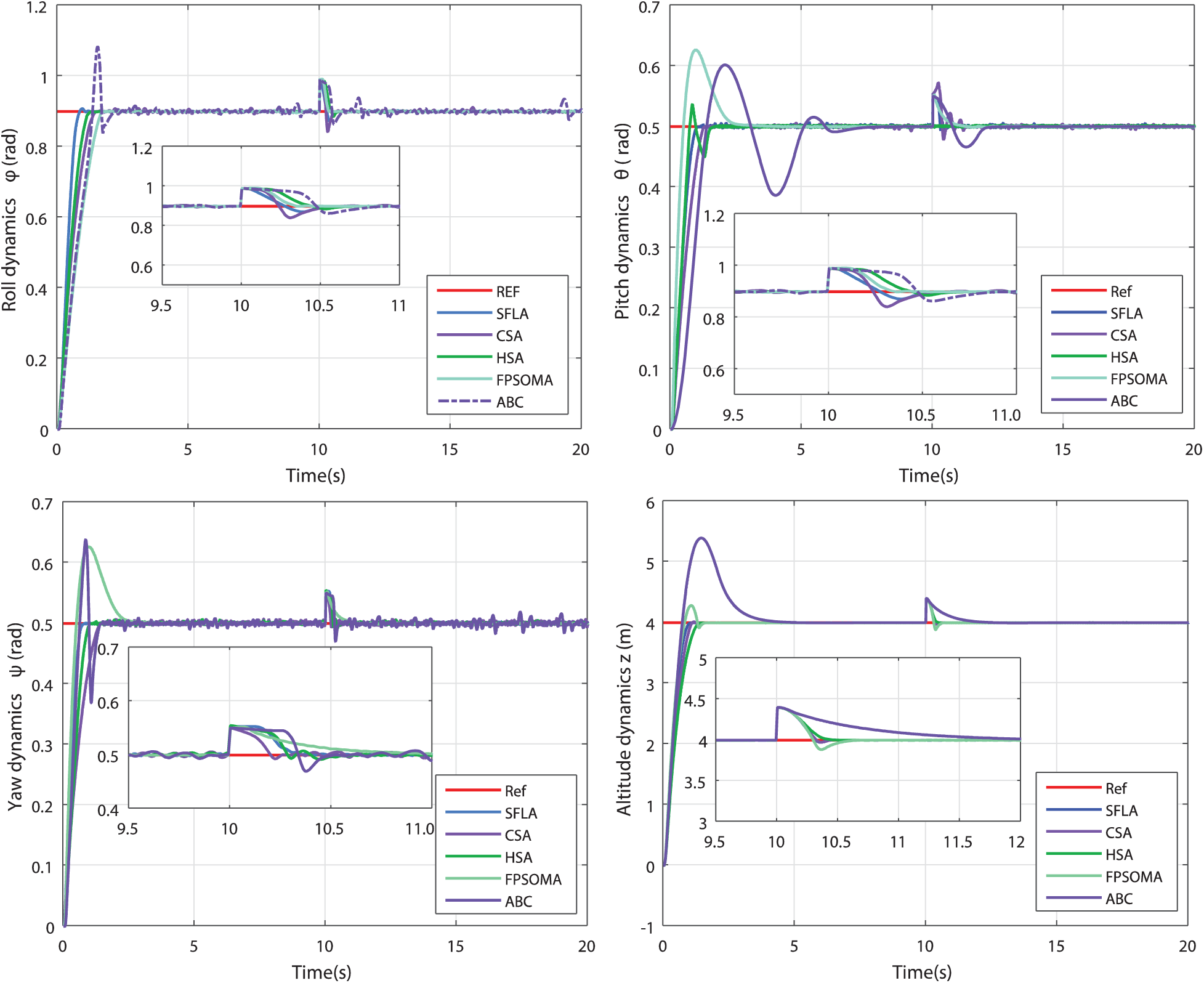
Figure 4: Time-domain performances of the controlled dynamics
5.2 Comparison with Classical ISMC Approaches
A comparative study based on the closed-loop time-domain performance is performed for the SFLA-tuned ISMC and classical ones without optimization. The cases of classical sliding mode control (SMC) [29,30], integral sliding mode control with the sign and saturation types of functions (ISMC-sign and ISMC-sat) [10] are considered.
The simulation results of Fig. 5 indicate the superiority of the SFLA-tuned controller compared to other algorithms. Indeed, all proposed methods stabilize the attitude and attitude dynamics, but the step responses are further damped and improved in the case of SFLA-based tuning algorithms. All other performance metrics are summarized for each controlled dynamics in Tabs. 5 to 8. In terms of control signal dynamics and chattering behaviors, the SFLA-tuned controllers present the best reductions of the undesirable chattering phenomenon as depicted in Fig. 6. The control signals are smoother and the oscillations as in the case of cases sign-SMC, sign-ISMC, and sat-ISMC are eliminated.
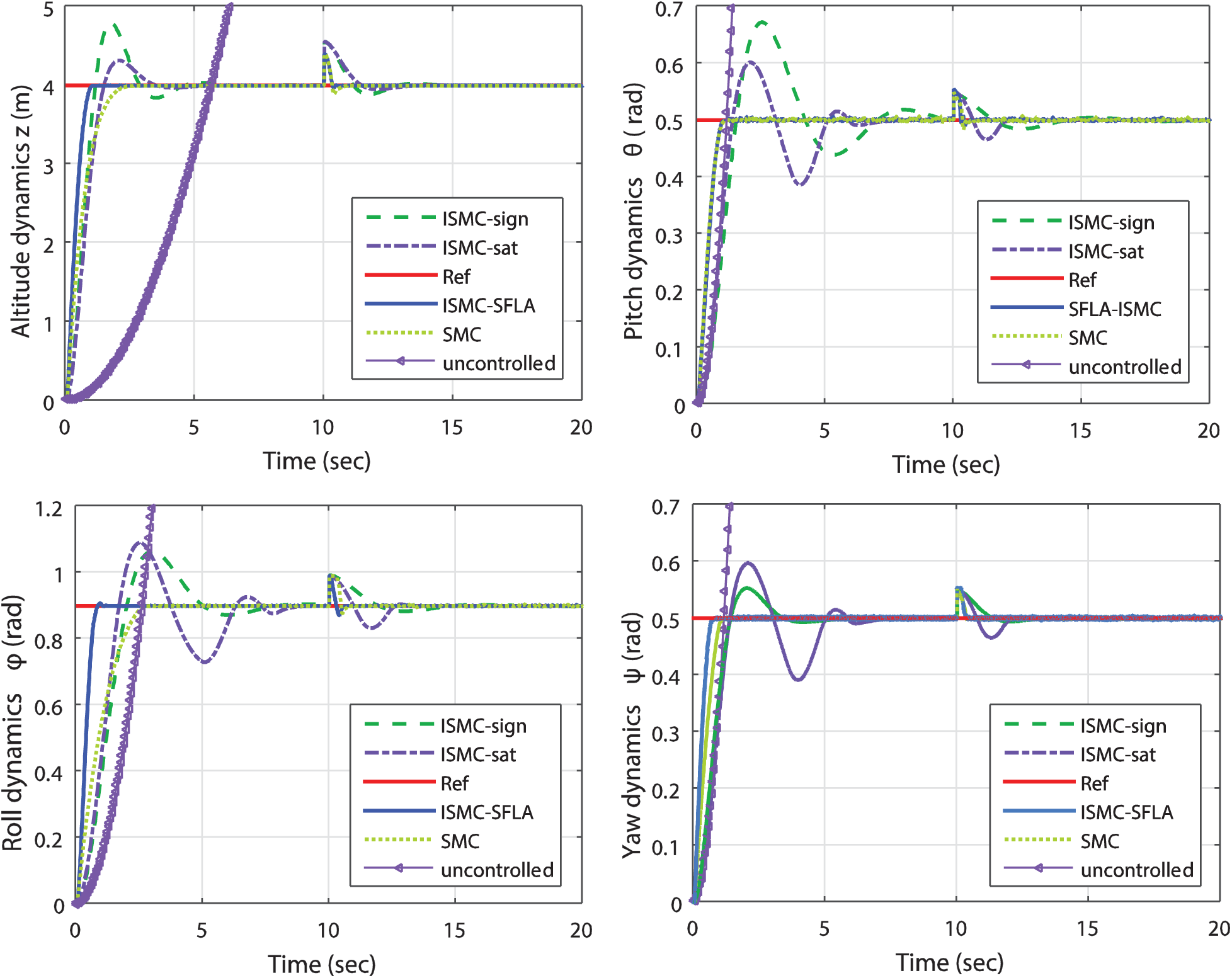
Figure 5: Performances comparison of the proposed SFLA-tuned controllers
Table 5: Time-domain performances comparison: altitude dynamics
Table 6: Time-domain performances comparison: pitch dynamics
Table 7: Time-domain performances comparison: roll dynamics
Table 8: Time-domain performances comparison: yaw dynamics
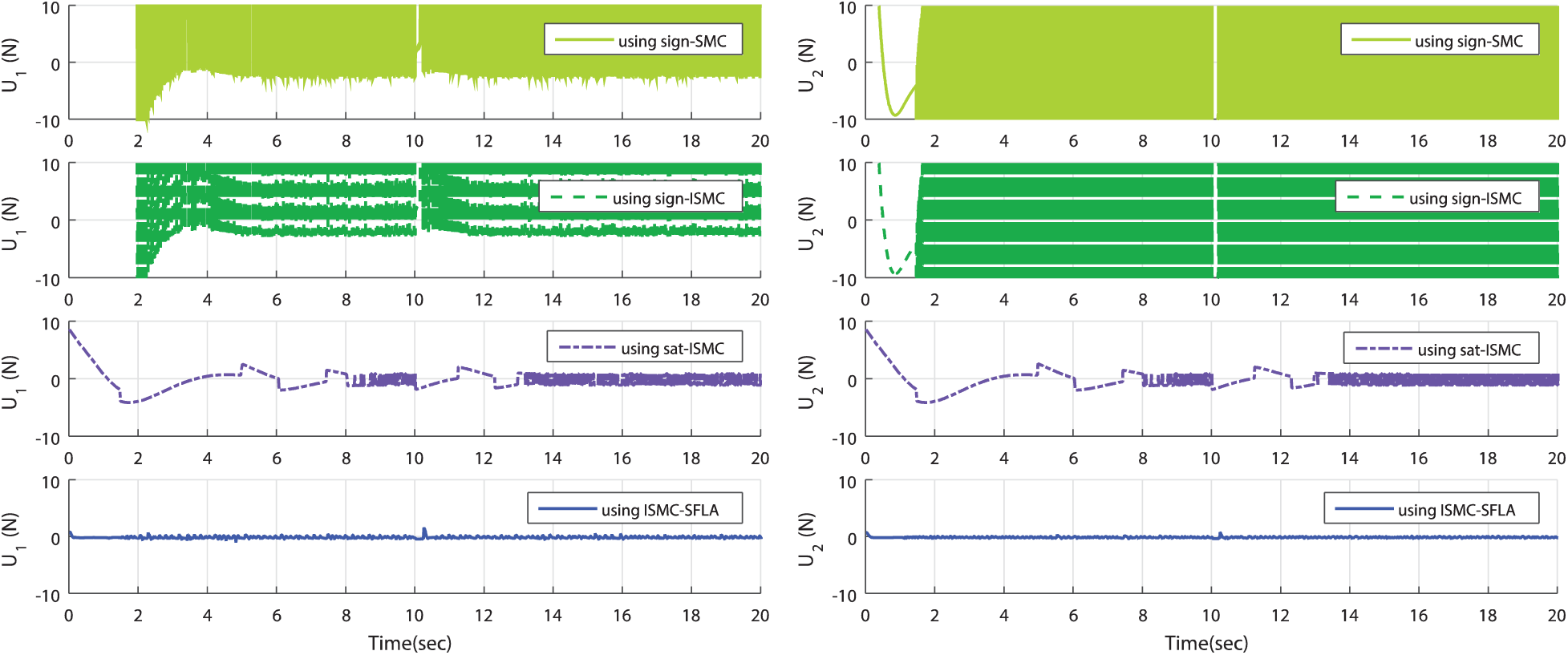
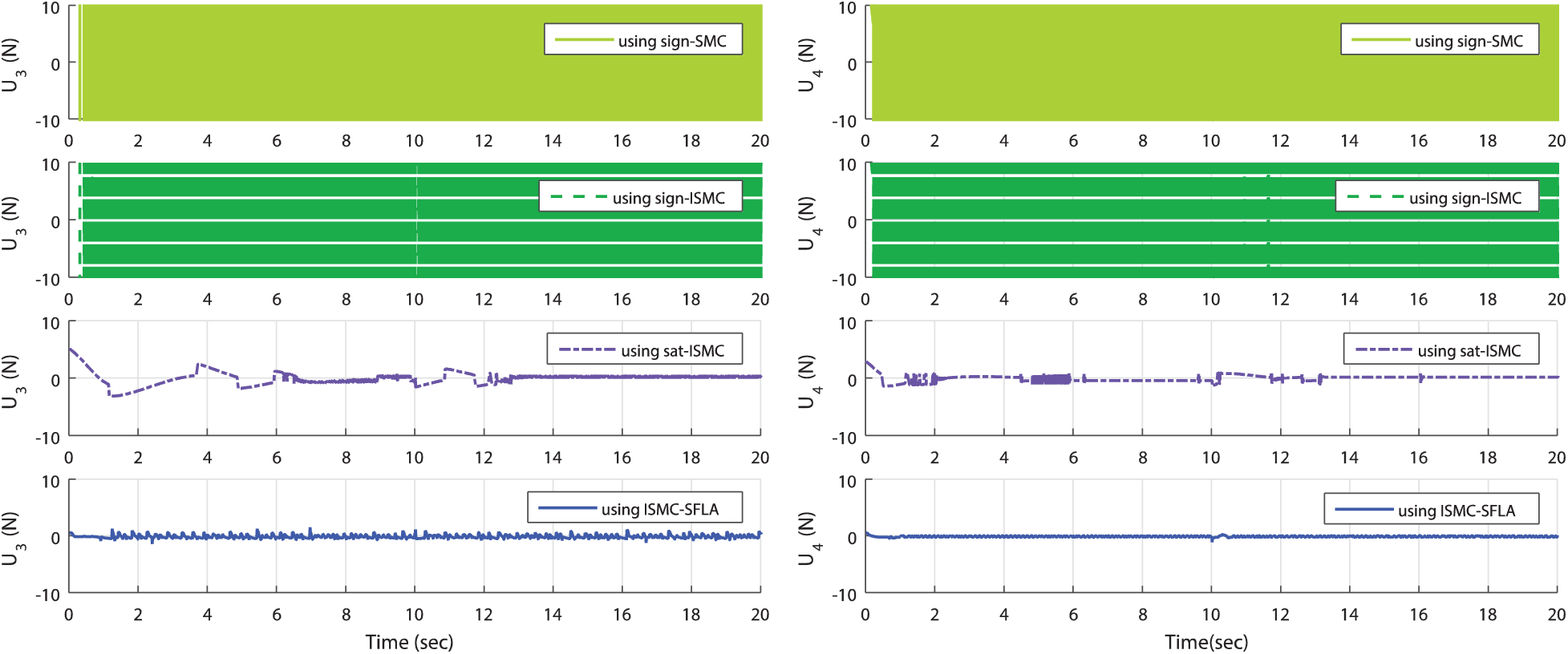
Figure 6: SFLA-based designed control laws for dynamics stabilization
As with all metaheuristics, the control parameters selection is critical for SFLA performance improvement. The sensitivity of such a memetic algorithm concerning the variation of its main parameters is studied for the problem (14). Fig. 7 gives the different convergence dynamics of SFLA under arbitrary variation of n and kls parameters, respectively. In all these scenarios, the convergence of the algorithm is always guaranteed but with degraded performance in terms of the exploitation/exploration capacities and the computing time. The proposed SFLA metaheuristic finds better results for problem (14) with the control parameters’ values of n = 10 and kls = 5. Indeed, and as shown in [21], the number of memeplexes nmem is also an important control parameter. As the population size increases, the function evaluations increase. Besides, when selecting nmem, it is important to make sure that n is not too small. If there are too few frogs selected in a sub-memeplex, the information exchange is slow, resulting in longer solution times. The other main parameter is kls which can take any value greater than 1. If kls is small, the memeplexes will be shuffled frequently, reducing idea exchange on the local scale. However, if kls is large, each memeplex will be shrunk into a local optimum.
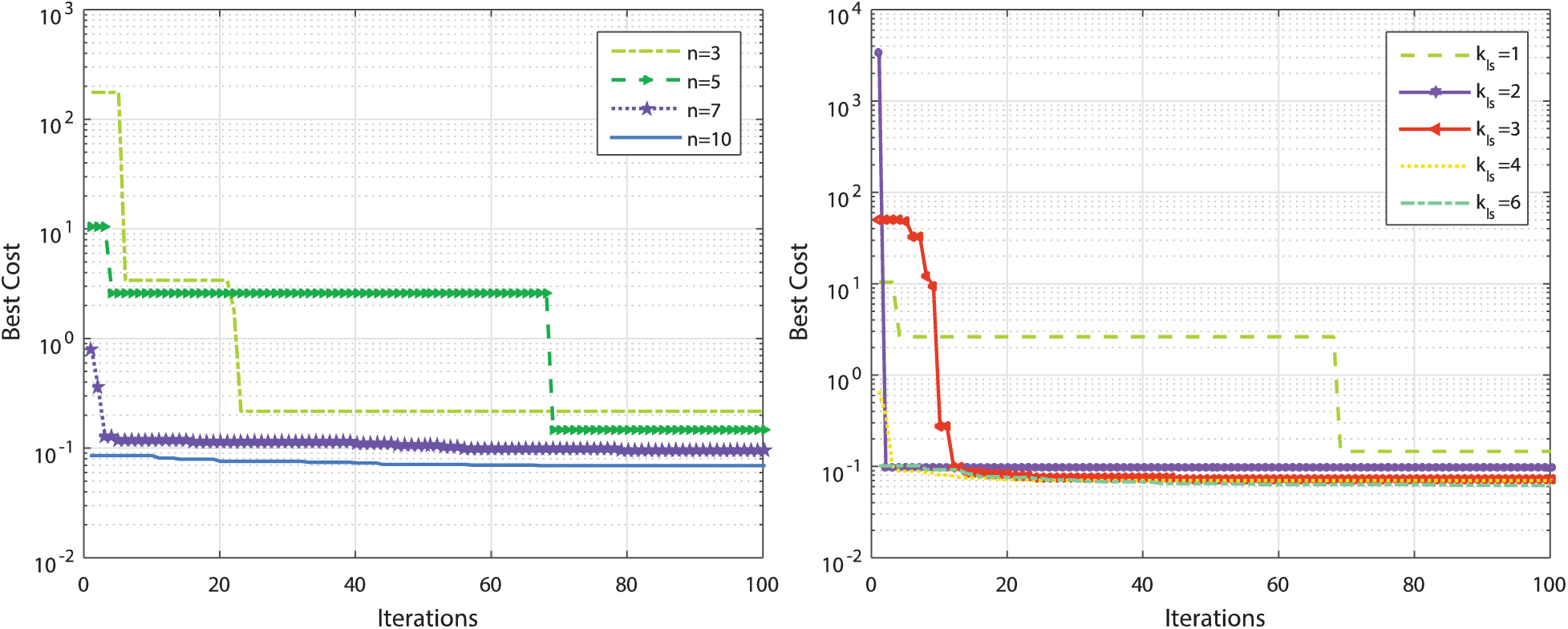
Figure 7: Convergence robustness of the SFLA under control parameters variations
In this paper, a systematic tuning strategy of all effective design parameters of the integral sliding mode control is proposed and successfully applied for the stabilization of a quadrotor UAV. The tuning parameters’ procedure has been formulated as a constrained optimization problem and efficiently solved thanks to the proposed memetic SFLA metaheuristic. The classical trials-errors methods are no longer used, and the design time is further reduced. Numerical experiments were first performed to evaluate the proposed metaheuristics on standard test function benchmarks. Rank-based statistical analyses have been then presented to conclude on the performance of the different metaheuristics. While using the Newton–Euler formalism, a nonlinear model of the studied quadrotor UAV has been established and used in the altitude and attitude controllers’ design and tuning. Demonstrative results, in terms of solutions optimality and time-domain performance, show the superiority and effectiveness of the proposed SFLA-tuned ISMC approach in comparison with other CSA, FPSOMA, HSA, and ABC competitive algorithms. With a local search mechanism, the robustness and insensitivity of the proposed SFLA metaheuristic are further improved. The use of such a memetic algorithm as an alternative to design more advanced control approaches is promising in the UAV framework.
Future works deal with the real-world experimentation of the SFLA-tuned ISMC approach using an embedded hardware/software board. The formulation of the proposed metaheuristics algorithms in an online tuning framework is also investigated.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Y. B. Sebbane. (2016). Smart Autonomous Aircraft: Flight Control and Planning for UAV, 1 ed., New York, USA: CRC Press, Taylor & Francis Group. [Google Scholar]
2. K. Valavanis and G. J. Vachtsevanos. (2015). Handbook of Unmanned Aerial Vehicles, 1 ed., Dordrecht, Netherlands, Netherlands: Springer. [Google Scholar]
3. R. Lozano. (2010). Unmanned Aerial Vehicles: Embedded Control, 1 ed., London, UK: Wiley-ISTE. [Google Scholar]
4. P. Castillo, R. Lozano and A. E. Dzul. (2005). Modelling and Control of Mini-Flying Machines, 1 ed., London, UK: Springer. [Google Scholar]
5. I. Fantoni and R. Lozano. (2002). Non-linear Control for Underactuated Mechanical Systems, 1 ed., London, UK: Springer-Verlag. [Google Scholar]
6. H. Ma, M. Chen and Q. Wu. (2019). “Inverse optimal control for unmanned aerial helicopters with disturbances,” Optimal Control Applications and Methods, vol. 40, no. 1, pp. 152–171. [Google Scholar]
7. A. Prach and E. Kayacan. (2018). “An MPC-based position controller for a tilt-rotor tricopter VTOL UAV,” Optimal Control Applications and Methods, vol. 39, no. 1, pp. 343–356. [Google Scholar]
8. L. M. Argentim, W. C. Rezende, P. E. Santos and R. A. Aguiar. (2013). “PID, LQR and LQR-PID on a quadcopter platform,” in Proc. of the 2nd ICIEV, Dhaka, Bengladech. [Google Scholar]
9. S. Stebler, W. Mackunis and M. Reyhanoglu. (2016). “Nonlinear output feedback tracking control of a quadrotor UAV in the presence of uncertainty,” in Proc. of the 14th ICARCV, Phuket, Thailand. [Google Scholar]
10. N. B. Ammar, S. Bouallègue and J. Haggège. (2018). “Fuzzy gains-scheduling of an integral sliding mode controller for a quadrotor unmanned aerial vehicle,” International Journal of Advanced Computer Science and Applications, vol. 9, no. 3, pp. 132–141. [Google Scholar]
11. V. I. Utkin and H. C. Chang. (2002). “Sliding mode control on electro-mechanical systems,” Mathematical Problems in Engineering, vol. 8, no. 4–5, pp. 451–473. [Google Scholar]
12. I. C. Baik, K. H. Kim and M. J. Youn. (2000). “Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique,” IEEE Transaction on Control Systems Technology, vol. 8, no. 1, pp. 47–54. [Google Scholar]
13. Y. S. Song and M. R. Arshad. (2015). “Sliding mode depth control of a hovering autonomous underwater vehicle,” in Proc. of 5th ICCSCE, George Town, Malaysia, pp. 435–440. [Google Scholar]
14. K. Young. (1978). “Controller design for a manipulator using theory of variable structure systems,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 8, no. 2, pp. 101–109. [Google Scholar]
15. Y. Pan, Y. H. Joo and H. Yu. (2018). “Discussions on smooth modifications of integral sliding mode control,” International Journal of Control, Automation, and Systems, vol. 16, no. 2, pp. 586–593. [Google Scholar]
16. Z. T. Dydek, A. M. Annaswamy and E. Lavretsky. (2010). “Adaptive control of quadrotor UAVs in the presence of actuator uncertainties,” in Proc. of AIAA Infotech@Aerospace 2010, Atlanta, Georgia, pp. 1–9. [Google Scholar]
17. S. Chang and W. Shi. (2017). “Adaptive fuzzy time-varying sliding mode control for quadrotor UAV attitude system with prescribed performance,” in Proc. of 29th CCDC, Chongqing, China, pp. 4389–4394. [Google Scholar]
18. Y. Zhang and P. Yan. (2018). “An adaptive integral sliding mode control approach for piezoelectric nano-manipulation with optimal transient performance,” Mechatronics, vol. 52, no. 1, pp. 119–126. [Google Scholar]
19. M. Gendreau and J. Y. Potvin. (2019). Handbook of Metaheuristics, 3 ed., Gewerbestrasse, Switzerland: Springer International Publishing AG. [Google Scholar]
20. M. M. Eusuff and K. Lansey. (2003). “Optimization of water distribution network design using the shuffled frog leaping algorithm,” Journal of Water Resources Planning & Management, vol. 129, no. 3, pp. 210–225. [Google Scholar]
21. M. M. Eusuff, K. Lansey and F. Pasha. (2006). “Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization,” Engineering Optimization, vol. 38, no. 2, pp. 129–154. [Google Scholar]
22. W. Bi, F. Yu, N. Cao, W. Huo, G. Cao et al. (2020). , “Research on data extraction and analysis of software defect in IoT communication software,” Computers Materials & Continua, vol. 65, no. 2, pp. 1837–1854. [Google Scholar]
23. X. Duan, T. Niu and Q. Huang. (2018). “An improved shuffled frog leaping algorithm and its application in dynamic emergency vehicle dispatching,” Mathematical Problems in Engineering, vol. 2018, no. 7896926, pp. 1–34. [Google Scholar]
24. M. Jadidoleslam and A. Ebrahimi. (2015). “Reliability constrained generation expansion planning by a modified shuffled frog leaping algorithm,” International Journal of Electrical Power & Energy Systems, vol. 64, no. 4, pp. 743–751. [Google Scholar]
25. G. Y. Zhu and W. B. Zhang. (2014). “An improved shuffled frog-leaping algorithm to optimize component pick-and-place sequencing optimization problem,” Expert Systems with Applications, vol. 41, no. 15, pp. 6818–6829. [Google Scholar]
26. D. Prakash, A. Tripathi and T. K. Sharma, “Application of shuffled frog-leaping algorithm in regional air pollution control, ” in Soft Computing: Theories and Applications, M. Pant, K. Ray, T. K. Sharma, S. Rawat, A. Bandyopadhyay, 1 ed., Singapore: Springer-Singapore, pp. 397–403, 2018 [Google Scholar]
27. J. Vijaya Kumar and D. M. Vinod Kumar. (2014). “Generation bidding strategy in a pool based electricity market using shuffled frog leaping algorithm,” Applied Soft Computing, vol. 21, no. 5, pp. 407–414. [Google Scholar]
28. K. K. Bhattacharjee and S. P. Sarmah. (2014). “Shuffled frog leaping algorithm and its application to 0/1 knapsack problem,” Applied Soft Computing, vol. 19, no. 1, pp. 252–263. [Google Scholar]
29. N. Ben Ammar, S. Bouallègue and J. Haggège. (2016). “Modeling and sliding mode control of a quadrotor unmanned aerial vehicle,” in Proc. of the 3th ACECS, Hammamet, Tunisia, pp. 834–840. [Google Scholar]
30. N. Ben Ammar, S. Bouallègue, J. Haggège and S. Vaidyanathan. (2017). “Chattering free sliding mode controller design for a quadrotor unmanned aerial vehicle,” in Applications of Sliding Mode Control in Science and Engineering, S. Vaidyanathan, C. H. Lien, 1 ed., Germany: Springer-Verlag, pp. 61–79. [Google Scholar]
31. J. E. Slotine and W. Li. (1991). Applied Nonlinear Control, 1 ed., New Jersey, USA: Prentice Hall. [Google Scholar]
32. A. Askarzadeh. (2016). “A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm,” Computers & Structures, vol. 169, no. 2, pp. 1–12. [Google Scholar]
33. K. S. Lee and Z. W. Geem. (2005). “A new meta-heuristic algorithm for continuous engineering optimization: Harmony search theory and practice,” Computer Methods in Applied Mechanics and Engineering, vol. 194, no. 36–38, pp. 3902–3933. [Google Scholar]
34. Y. Mousavi and A. Alfi. (2015). “A memetic algorithm applied to trajectory control by tuning of fractional order proportional-integral-derivative controllers,” Applied Soft Computing, vol. 36, no. 3, pp. 599–617. [Google Scholar]
35. S. Bouallègue, F. Toumi, J. Haggège and P. Siarry, “Advanced metaheuristics-based approach for fuzzy control systems tuning,” in Complex System Modeling and Control Through Intelligent Soft Computations, Q. Zhu and A. T. Azar, 1 ed., Germany: Springer-Verlag, pp. 627–653, 2015 [Google Scholar]
Appendix A: Benchmark test functions
Appendix B: Quadrotor’s model parameters
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |
