DOI:10.32604/cmc.2021.014981
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014981 | |
| Article |
Adaptive Signal Enhancement Unit for EEG Analysis in Remote Patient Care Monitoring Systems
1Department of Electronics and Communication Engineering, J. N. T. University, Kakinada, 533003, India
2Department of Electronics and Communication Engineering, JNTUK-UCEV, Vizianagaram, 535003, India
*Corresponding Author: Ch. Srinivas. Email: chsrinivaseeg@gmail.com
Received: 31 October 2020; Accepted: 29 November 2020
Abstract: In this paper we propose an efficient process of physiological artifact elimination methodology from brain waves (BW), which are also commonly known as electroencephalogram (EEG) signal. In a clinical environment during the acquisition of BW several artifacts contaminates the actual BW component. This leads to inaccurate and ambiguous diagnosis. As the statistical nature of the EEG signal is more non-stationery, adaptive filtering is the more promising method for the process of artifact elimination. In clinical conditions, the conventional adaptive techniques require many numbers of computational operations and leads to data samples overlapping and instability of the algorithm used. This causes delay in diagnosis and decision making. To overcome this problem in our work we propose to set a threshold value to diminish the problem of round off error. The resultant adaptive algorithm based on this strategy is Non-linear Least mean square (NL2MS) algorithm. Again, to improve this algorithm in terms of filtering capability we perform data normalization, using this algorithm several hybrid versions are developed to improve filtering and reduce computational operations. Using the method, a new signal enhancement unit (SEU) is realized and performance of various hybrid versions of algorithms examined using real EEG signals recorded from the subject. The ability of the proposed schemes is measured in terms of convergence, enhancement and multiplications required. Among various SEUs, the MCN2L2MS algorithm achieves 14.6734, 12.8732, 10.9257, 15.7790 dB during the artifact removal of RA, EMG, CSA and EBA components with only two multiplications. Hence, this algorithm seems to be better candidate for artifact elimination.
Keywords: Adaptive algorithms; artifacts; brain waves; clipped algorithms; signal enhancement unit; wireless EEG monitoring
Electroencephalogram (EEG) is the key tool to illustrates the functionality of various segments of the brain. Any physiological abnormality in the brain results abnormalities in the biopotentials generated in the neurons and causes medical ill conditions in the patient. As per the surveys of world health organization reported in [1–4] brain wave disorders responsible majority of mortality during nowadays. Hence, high resolution EEG signals are needed in the diagnosis of several deceases. During the acquisition of brain waves, various physiological components like respiration artifact, muscle potential, cardiac activity and potential due to eye blink will contaminates the brain wave component. In clinical scenario these un-wanted components are considered as respiration artifacts (RA), Electro Muscle Artifact (EMA), Cardiac signal artifact (CSA) and Eyeblink artifact (EBA). These artifacts contaminate the signal quality, which is required for abnormality identification. Therefore, in remote EEG monitoring as well as in automatic EEG monitoring systems an important task is artifact removal. Since the artifacts masks the tiny features of brain wave, it is highly desirable to eliminate these artifacts and to facilitate high resolution brain wave for analysis and diagnosis. Among the various techniques of artifact removal, the adaptive artifact elimination is a promising method. This is because adaptive techniques are able to vary the weights based on input noisy signal. Also, among various physiological signals, the brain wave has a very non-stationary pattern. Thus, conventional filtering techniques are not suitable for artifact elimination in brain waves. Hence, adaptive FIR filters are the best solution in this process. Several adaptive filtering techniques are developed to eliminate artifacts from physiological signals. These are presented in several contributions like [5–10]. In the presence of artifacts, the brain waves are ambiguous and needed to be eliminated. Due to technological developments in the brain wave analysis several techniques like brain computer interface (BCI), source localization, remote health care monitoring, machine learning, etc., also needs pre-processing of brain waves to facilitate high resolution EEG components for diagnosis. Several such contributions are found in the literature [11–14]. Therefore, a typical remote health monitoring network consists of signal recording machine, telemetry link, brain computer interface and control station. Another important aspect of a remote brain care system is computational complexity.
In wireless EEG monitoring systems, the computational complexity is a major concern to be concentrated. If the received filter length is large, much time is required to perform the filtering operations, which are in terms of additions and multiplications. This cause overlapping of data values at the input of the SEU. To achieve less computational complexity, we develop the hybrid versions of MN2L2MS and clipped algorithms based on [15]. In [16] a methodology of less computational operations is presented based on sign-based algorithms. During some serious situation of the patient, some samples of EEG component becomes zero and undergo fluctuations, cause weight variations and leads to ambiguities in abnormality identification. To overcome such ambiguities, we set a threshold to error value based on the frame work presented in [17–19]. By introducing this threshold in conventional LMS, it is modified as Non-Linear LMS (NL2MS). To improve convergence speed and to improve filtering capability we apply data normalization. The normalization with respect to data vector of Non-Linear LMS is termed as Normalized Non-Linear LMS (N2L2MS). This increase the number of computations of the denominator part of the algorithm equal to tap length. To avoid this, we modified the N2L2MS algorithm such that, the normalization is performed with respect to maximum of the input vector instead of all the values of the vector. As a result, the number of multiplication operations required in the denominator is only one. This algorithm is termed as Modified N2L2MS (M N2L2MS) algorithm. The resultant algorithms are Modified Clipped N2L2MS (MCN2L2MS) algorithm, Modified Sign (MSN2L2MS) algorithm and Modified Sign Sign N2L2MS (MS2N2L2MS) algorithm. Using this adaptive FIR frame work we develop a signal enhancement unit (SEU) to eliminate various physiological components from brain wave in clinical scenario. The performance of various algorithms in SEU are tested experimentally using real EEG signals.
2 Hybrid Adaptive Filter for Brain Wave Enhancement
In the artifact elimination process the key element is the adaptive algorithm, which trains the FIR filter to change its coefficients. Let us consider ‘L’ to be the length of FIR filter. To facilitate ability to alter coefficients of filter in accordance to the artifact component this FIR filter is associated with an adaptive algorithm initially. Based on this strategy and using the framework of artifact elimination we develop an efficient adaptive artifact eliminator (AAE) which has better convergence, filtering ability, stability and less computational complexity. Fig. 1 shows a typical schematic diagram of an AAE. Let 
, here, E is the recorded signal of EEG, which combines the definite brain activity component (
) and artifact component (
).
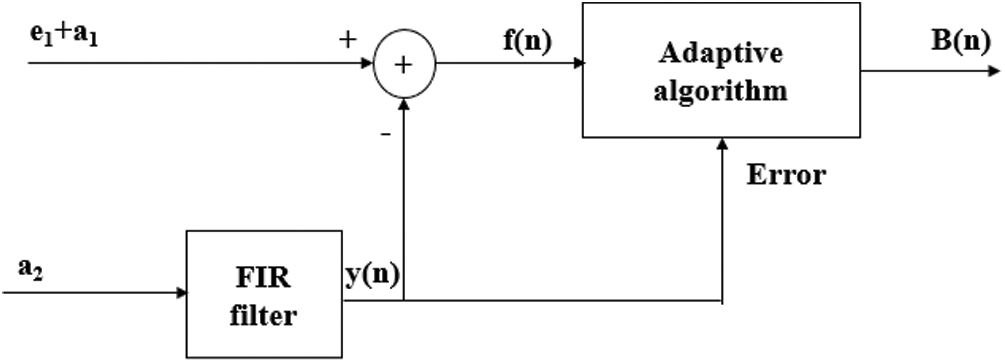
Figure 1: Typical block diagram of signal enhancement unit for brain wave analysis
A random component 
is taken as reference component. The weight coefficient vector is w(n) of the filter in SEU, y(n) is the convolution between w(n) and a2. The adaptive algorithm trains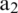 
, become close to 
, so that the summer performs the operation of 
. As the number of iterations are going on, 
come close to each other and maximum of their components get cancel with each other and actual brain wave component B(n) will come out of SEU. The component f(n) is the feedback signal, it drives the adaptive algorithm as error signal, based on this the weight updating process will be repeated. The mathematical expression for the LMS driven SEU is given by, 
. In this expression, w(
) is the next weight coefficient of the filter, w(n) is the present weight vector, ‘s’ is the step size of the adaptation, E(n) is the input brain wave which is contaminated with physiological and non-physiological artifacts, f(n) is the feedback signal. The major limitation of the conventional LMS is gradient noise amplification [20,21]. Normalized version of LMS (NLMS) achieves better convergence and enhancement [22,23]. The mathematical recursion for this technique is written as,
Here, the step size parameter is written as,
In the next version of NLMS we normalize the step size with the maximum value of data vector E(n). This minimizes the number of computations in the denominator of the weight update recursion.
In physiological signal monitoring applications during critical conditions minute errors leads ambiguity in diagnosis. During critical conditions the decision has to be make instantaneously. To avoid this, a non-linear operation is combined with LMS algorithm, which results non-linear LMS (NL2MS) and is able to eliminate the ambiguities of round-off errors [24,25]. We use this property of NL2MS in the process of artifact elimination in EEG signals. This nonlinearity is defined as,
where d is threshold.
When applied to the error signal, it converts the LMS update recursion equation to
This is the mathematical recursion for NL2MS algorithm. To achieve better convergence and enhancement we combine this NL2MS algorithm with NLMS and results normalized non-linear LMS (N2L2MS). The mathematical expression for this algorithm is given as,
where 
A generalized flow diagram for the proposed SEU for brain wave enhancement is shown in Fig. 2. As in remote patient care monitoring applications the computational complexity of the processing techniques is a key element. If the number of multiplication operations for updating the weight coefficients increases the samples at the input port increases and overlap on each other and causes information loss. To overcome this problem, the impulse response of the receiver must be increased, but minimizing the number of computational operations of signal conditioning technique is an optimum solution. So, we developed hybrid versions of adaptive algorithms by combining the N2L2MS algorithm with sign-based algorithms. The three-familiar sign-based algorithms are clipped algorithm, sign algorithm and sign sign algorithm. The hybrid versions of N2L2MS and signed algorithms are named as, clipped N2L2MS algorithm (CN2L2MS), sign N2L2MS (S N2L2MS), sign sign N2L2MS (S2N2L2MS) algorithms respectively. Again, these normalized versions of the algorithms suffer with a problem of computational complexity due to normalization. This is due to the normalization with respect to the input data vector of length ‘L’. In this operation ‘L’ number of multiplications are needed. To avoid this problem further N2L2MS is modified such that in the data normalization operation, the normalization is performed with respect to the maximum data value of the input vector. These versions of the proposed algorithms are called modified N2L2MS algorithm (MN2L2MS), modified clipped N2L2MS algorithm (MCN2L2MS), modified sign N2L2MS algorithm (MS N2L2MS), modified sign N2L2MS algorithm (MS2 N2L2MS) respectively.
Figure 2: Flow chart of adaptive artifact cancellation algorithm for EEG analysis
The weight update recursions for modified N2L2MS algorithm is given as,
where 
Here, ms(n) is the modified step size, which is the normalized version with respect to maximum value of data vector instead of normalization with respect to entire input data vector. This minimized computational complexity in the denominator by an amount 
, only one multiplication is needed for this maximum data normalization. Now we propose to combining clipped algorithm with MN2L2MS algorithm we can minimize the number of computations for performing the filtering process. The theory and analysis of clipped algorithm is presented in [15]. The resultant algorithm is modified clipped N2L2MS algorithm (MCN2L2MS). Its weight update phenomenon mathematically can be written as,
where 
is a clipping function and is represented as follows,
Similarly, by combining Sign LMS (SLMS) and Sign Sign LMS (SSLMS) with MN2L2MS results MSN2L2MS and MS2 N2L2MS algorithms respectively. The weight update mechanism for these techniques can be written as,
Therefore, using these algorithms, namely, N2L2MS, MN2L2MS, MCN2L2MS, MSN2L2MS and MS2N2L2MS we develop various signal enhancement units. The convergence curves for LMS algorithm and its signed algorithms versions are shown Fig. 3. These illustrations are plotted between MSE and iteration number. MSE is calculated using the relation, i.e., 
[21]. These curves are obtained during the Gaussian noise removal process to test the feasibility of adaptive algorithms in the adaptation process. From Fig. 3 among the algorithms LMS outperforms, but the convergence characteristics of CLMS is just inferior than LMS. Fig. 4 confirms that maximum normalization strategy improves the convergence performance of the algorithms. In this case, also the clipped version of MN2L2MS is just inferior than MN2L2MS.
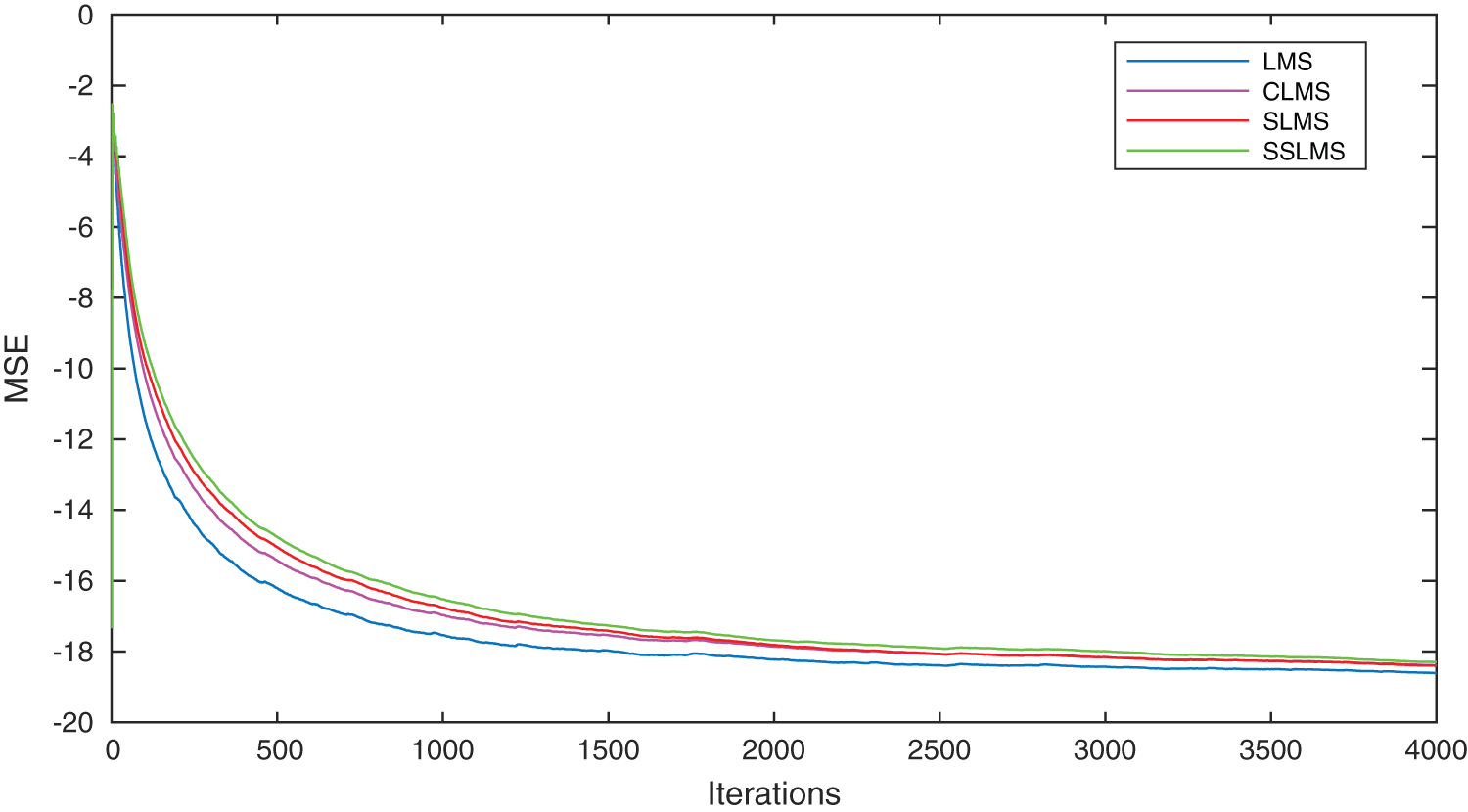
Figure 3: Convergence analysis curves for LMS and its signum variants
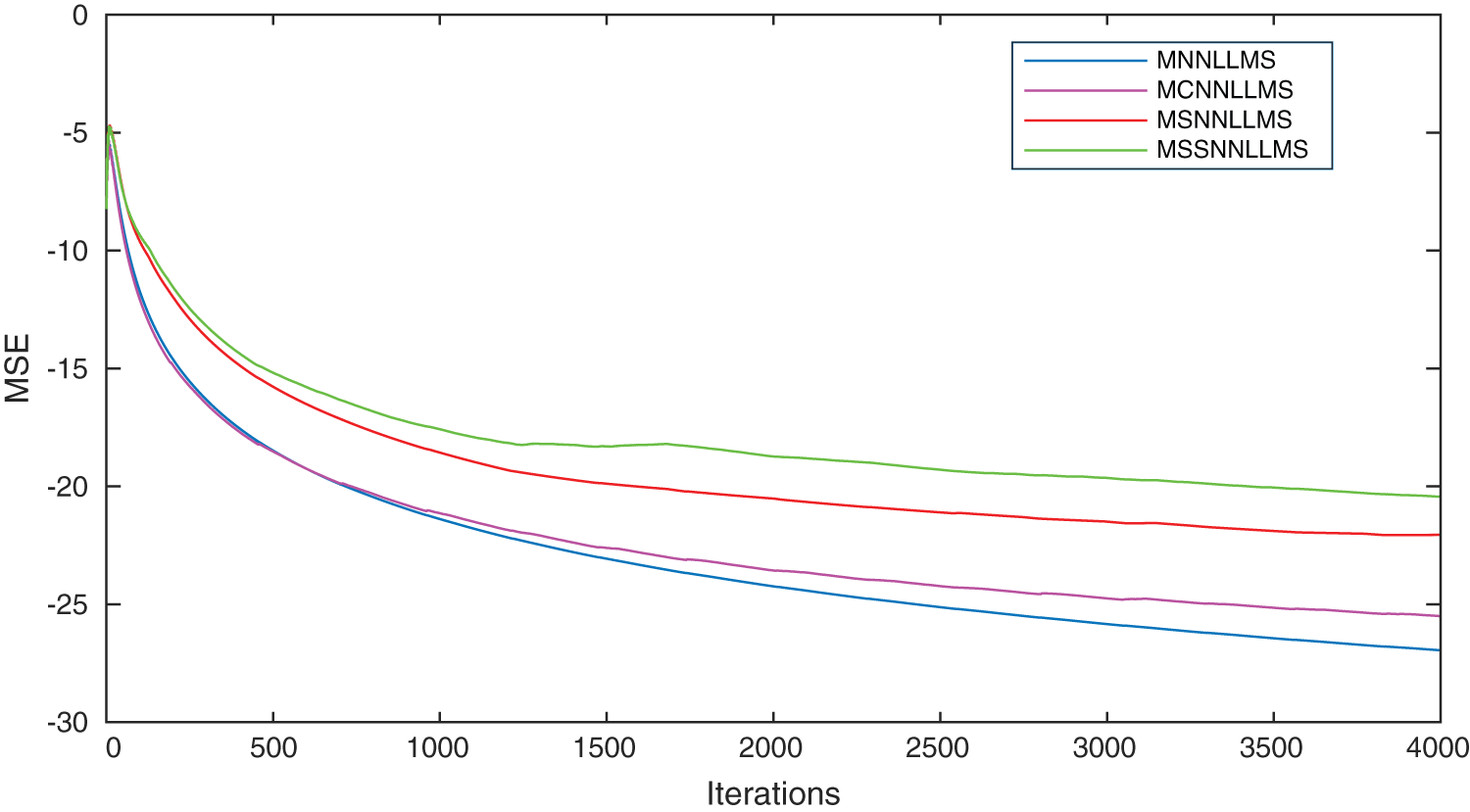
Figure 4: Convergence characteristics of N2L2MS and its hybrid versions
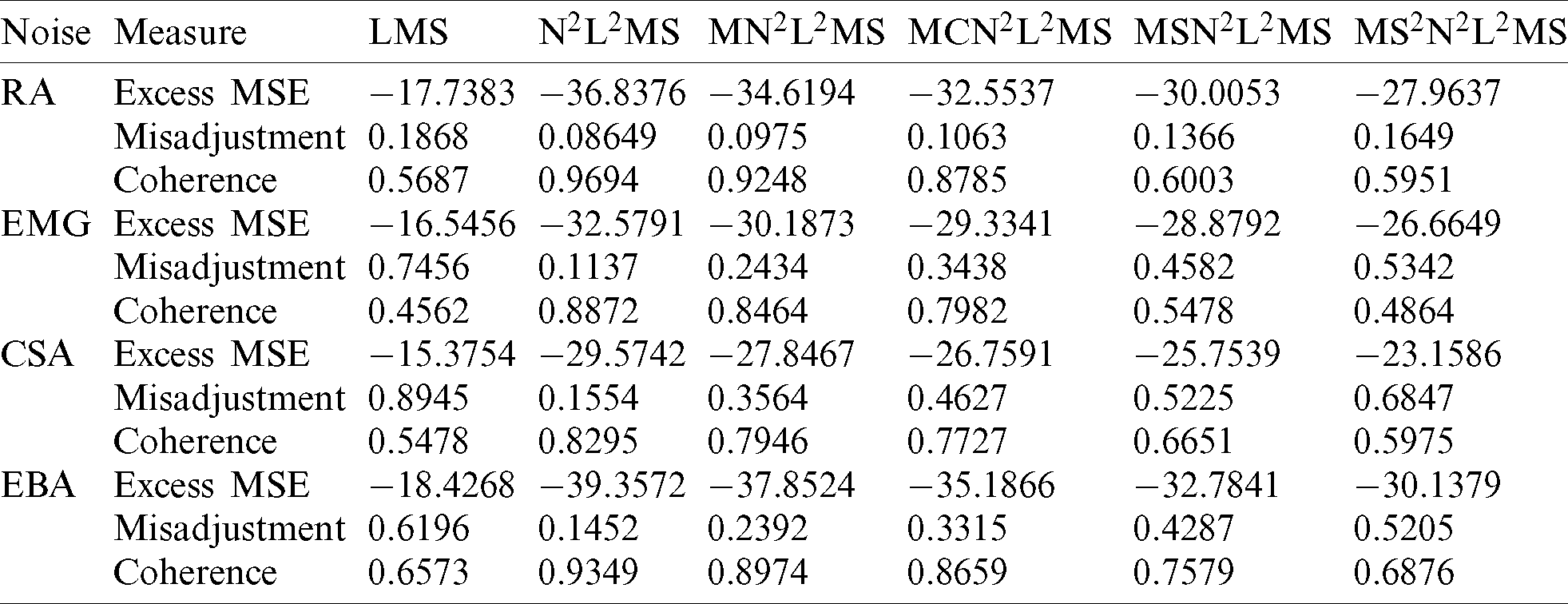
The computational complexity of the above-mentioned enhancement techniques is shown in Tab. 1. In signal processing circuits, the signum based techniques require a smaller number of multiplications than their counterparts because of clipping operations. So, we have used these signum based hybrid versions in our realizations to minimize the computational burden of the proposed SEU. Among the three sign-based algorithms MCN2L2MS, MSN2L2MS and MS2N2L2MS, MS2N2L2MS has less computational complexity. But as the data vector and error component are undergoing clipping results in the much quantity of information will be missed in the signal enhancement operation. Hence, the filtering ability of the technique is poor. This is also evident form the filtering ability presented in the next section. The MN2L2MS has the complexity in terms of multiplications equal to MSN2L2MS, but due to error clipping its resolution is inferior than MN2L2MS. So, MSN2L2MS is also not a good candidate for artifact elimination process. Whereas, in MCN2L2MS the data vector is clipped and its computational complexity is nearly equal to conventional LMS in terms of multiplications with increased convergence characteristics. Also, the number of multiplications required in the second part of the weight update recursion is independent of filter length. Therefore, based on the analysis of various algorithms in terms of convergence characteristics and number of multiplications, the MCN2L2MS is seems to be a better candidate for brain wave analysis in wireless EEG monitoring devices as well as in remote health care monitoring systems.
Table 1: Complexity of various adaptive algorithms for artifact elimination in brain waves
3 Experimental Results and Analysis
To demonstrate the ability of the signal enhancement scheme in health care monitoring contest we have recorded several brain waves in various physiological scenarios using the Emotive EPOC brain wave acquisition headset [24]. These electrodes are arranged according to a grid as per the international 10–20 system, these are designated as per the method presented in [25]. By utilizing brain computer interface method, we collected brain waves from 5 different subjects with both physiological and non-physiological artifacts. The EPOC acquisition system samples the channels at a rate of 128 PPS, all these pulses are in the 4-byte floating-point format corresponding to the bio-potential for individual electrode. In these experiments, we have collected 10,000 samples of EEG signal from the subject. To facilitate a high-resolution signal, we have shown 1000 samples of the brain data. The performance of various SEUs in the process of signal conditioning is measured in terms of signal to noise ratio improvement (SNRI), excess mean square error (EMSE), misadjustment (MSD) and correlation. The SNRI is defined as the difference in the signal to noise ratio before the operation of artifact removal and after the operation of artifact removal. It is the excess amount of the error than the minimum mean square error of the adaptive process. Whereas minimum mean square error is the minimum amount of error obtained by an optimum filter. It is a dominant parameter to compare different adaptive algorithms. Correlation is the similarity between the filtering signal and a clean signal without any artifacts. These performance measures are measured in ten experiments on individual data and averaged. These results are shown in Tabs. 2 and 3. Also, these performance measures are illustrated in Figs. 9–12. A Gaussian noise with 0.01 variances from the mean of the brain wave data is added to resemble channel noise in a wireless EEG system, the step size parameter is taken as 0.01. In our work, we used five diversified samples of brain data, the data set consists of five samples namely, EEG1, EEG2, EEG3, EEG4 and EEG5 to obtain consistent results from SEUs. To perform experiments using the recorded data, we developed various SEUs using LMS, N2L2MS, MN2L2MS, MCN2L2MS, MSN2L2MS, MS2N2L2MS algorithms. A typical noise generator is used in the experiments to facilitate reference signal to the signal enhancement unit. The filter length is chosen as 5. As the filter length increases the filtering process will be accelerated but excess mean square error also increases. This in turn decreases the signal to noise ratio. So, we have chosen filter length as 5. The experimental findings of artifact elimination are described case by case in the following sub-sections.
Table 2: Performance measures in terms of SNRI for signal enhancement process (in dBs)
Table 3: Performance measures in terms of EMSE [dBs], MSD [dimension less] and CHO [dimension less] for signal enhancement process
3.1 Adaptive Artifact Elimination of Respiration Artifacts (RA) From EEG Signals
This experiment proves the RA elimination process from EEG component. The raw brain wave component is taken as input to the SEU as shown in Fig. 1, this input component is a combination of actual brain action potential and non-physiological noise contamination, it is designated as 
. The reference signal given to the adaptive FIR filter is 
. The adaptive algorithm trains the FIR filter coefficients, such that 
becomes closer to 
. The experimental results after artifact elimination is shown in Fig. 5. From this figure, it is depicted that Figs. 5e and 5f are showing high-resolution brain wave components than other subplots. These are results are obtained due to SEUs based on N2L2MS and its signum based variants. Again, by examine the performance measures in terms of convergence rate, SNR, excess mean square error, misadjustment, among the various algorithms N2L2MS based SEU achieves highest performance measures. But, among all the algorithms MCN2L2MS based SEU requires less amount of computational complexity in terms of multiplications by an amount of filter length, in this case it is ‘L’, shown in Tab. 1. However, in terms of other performance measures MCN2L2MS is little bit inferior than N2L2MS algorithm based SEU. This fact is depicted by examine Fig. 5, Tabs. 2 and 3. Therefore, as a tradeoff the little bit inferior performance of MCN2L2MS based SEU could be tolerated than SEU based on N2L2MS, as MCN2L2MS needs lesser number of multiplications by an amount ‘L’, which is filter length in this case. Hence, MCN2L2MS based SEU is suitable for elimination of artifacts from brain waves for EEG analysis in remote health care monitoring applications.
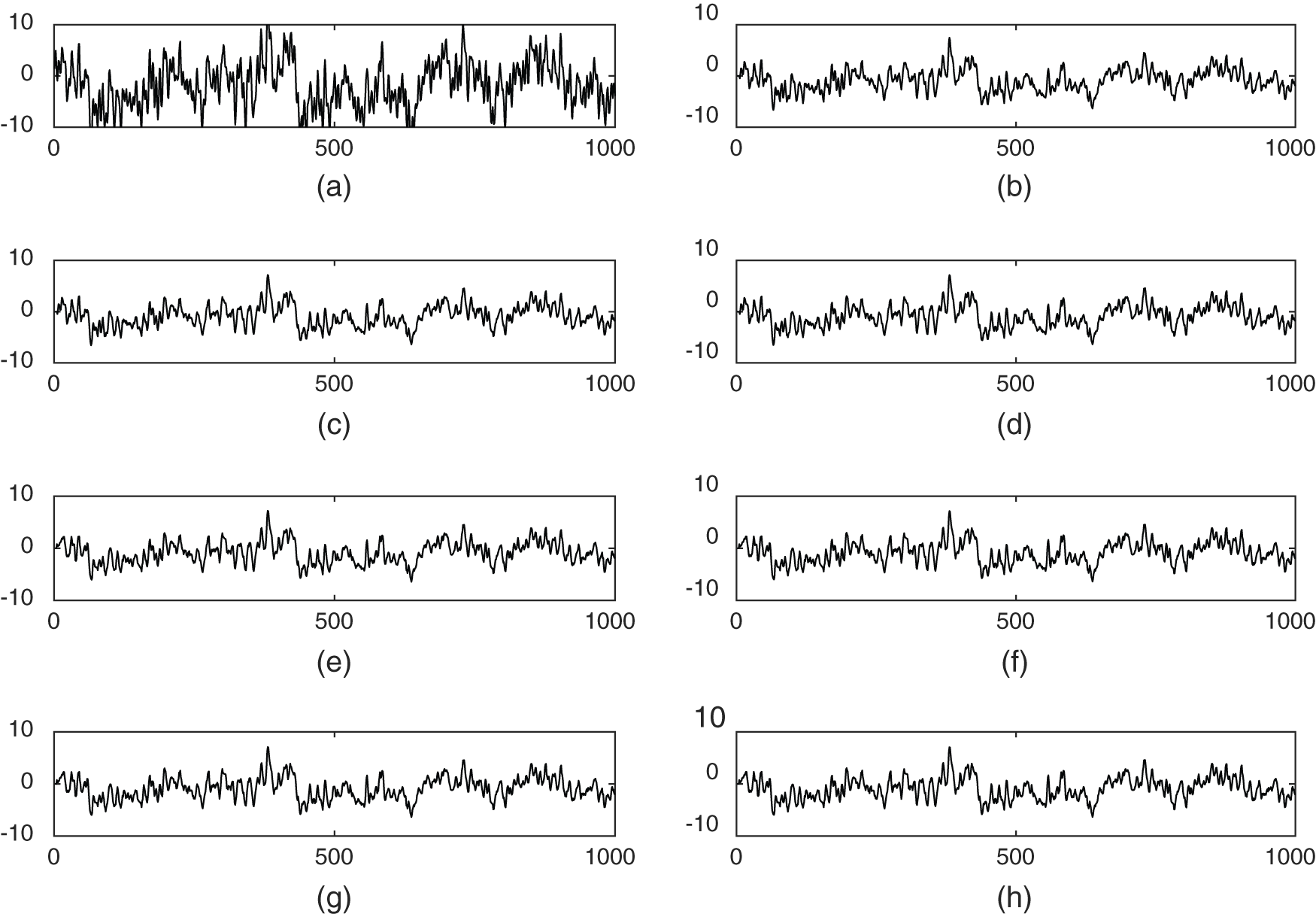
Figure 5: Adaptive artifact cancellation of RA from EEG signals: (a) noisy raw EEG component, (b) sample of RA component, (c) output from LMS based SEU, (d) output from N2L2MS based SEU, (e) output from MN2L2MS based SEU, (f) output from MCN2L2MS based SEU, (g) output from MSN2L2MS based SEU, (h) output from MS2N2L2MS based SEU (data values are shown on x-axis; signal amplitudes are shown on y-axis signal)
3.2 Adaptive Artifact Elimination of Electro-Myo-Gram (EMG) and EEG Signals
This experiment proves the respiration artifact elimination process from EEG signal. The raw brain wave component is taken as input to the SEU as shown in Fig. 1, this input component is a combination of actual brain action potential and non-physiological noise contamination, it is designated as 
. The reference signal given to the adaptive FIR filter is 
. The adaptive algorithm trains the FIR filter coefficients, such that 
becomes closer to 
. The experimental results after artifact elimination is shown in Fig. 6. From this figure, it is depicted that Figs. 6e and 6f are showing high-resolution brain wave components than other subplots. These are results are obtained due to SEUs based on N2L2MS and its variants. Again, by examine the performance measures in terms of convergence rate, SNR, excess mean square error, misadjustment, among the various algorithms N2L2MS based SEU achieves highest performance measures. But, among all the algorithms MCN2L2MS based SEU requires less amount of computational complexity in terms of multiplications by an amount of filter length, in this case it is ‘L’, shown in Tab. 1. However, in terms of other performance measures MCN2L2MS is little bit inferior than N2L2MS algorithm based SEU. This fact is depicted by examine Fig. 6, Tabs. 2 and 3. Therefore, as a tradeoff the little bit inferior performance of MCN2L2MS based SEU could be tolerated than SEU based on N2L2MS, as MCN2L2MS needs lesser number of multiplications by an amount ‘L’, which is filter length in this case. Hence, MCN2L2MS based SEU is suitable for elimination of artifacts from brain waves for EEG analysis in remote health care monitoring applications.
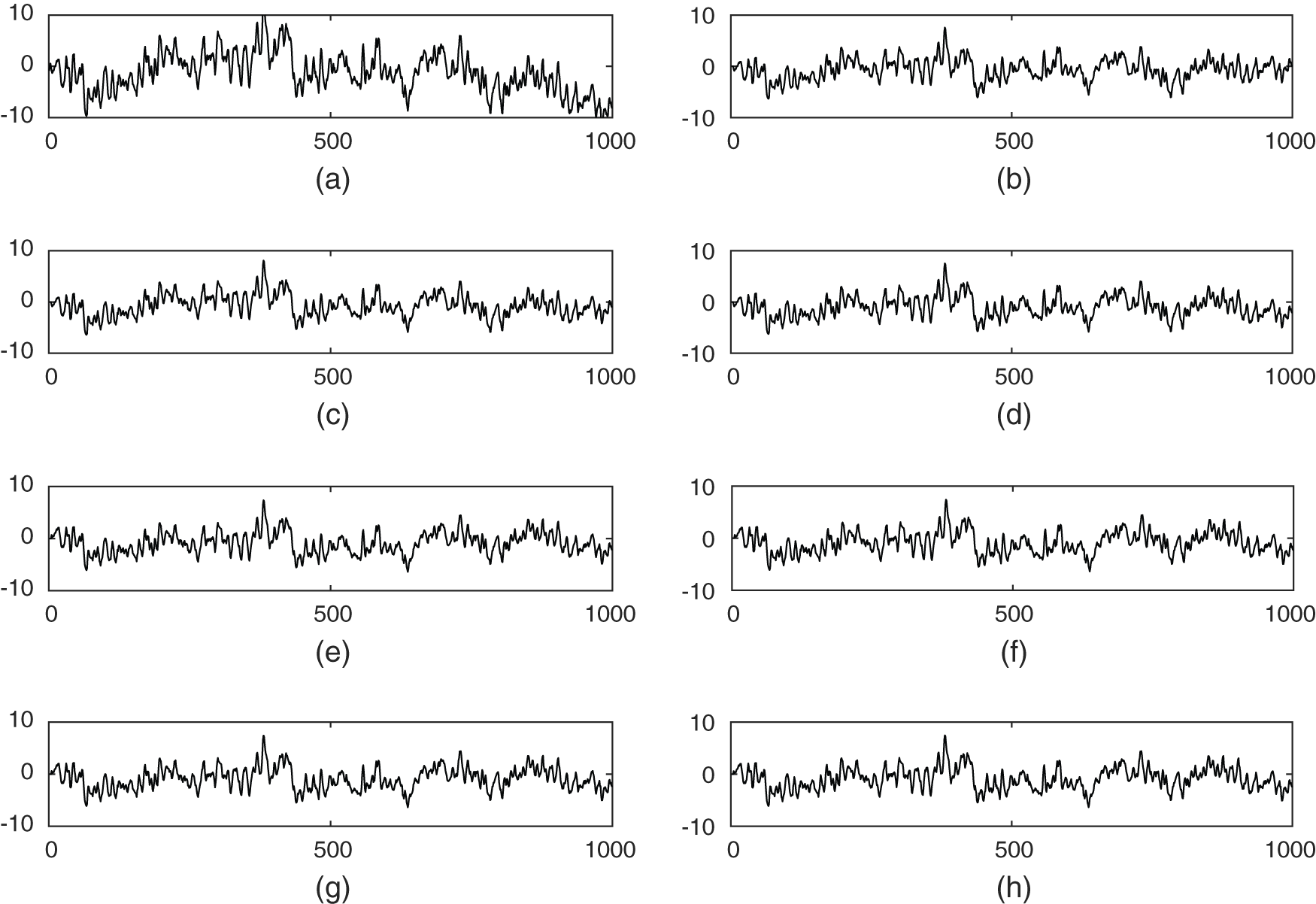
Figure 6: Adaptive artifact cancellation of EMG from EEG signals: (a) noisy raw EEG component, (b) sample of EMG component, (c) output from LMS based SEU, (d) output from N2L2MS based SEU, (e) output from MN2L2MS based SEU, (f) output from MCN2L2MS based SEU, (g) output from MSN2L2MS based SEU, (h) output from MS2N2L2MS based SEU (data values are shown on x-axis; signal amplitudes are shown on y-axis signal)
3.3 Adaptive Artifact Elimination of Cardiac Signal Artifact (CSA) and EEG Signals
This experiment proves the cardiac signa artifact elimination process from EEG component. The raw brain wave component is taken as input to the SEU as shown in Fig. 1, this input component is a combination of actual brain action potential and non-physiological noise contamination, it is designated as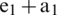 
. The reference signal given to the adaptive FIR filter is 
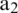. The adaptive algorithm trains the FIR filter coefficients, such that 
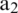becomes closer to 
. The experimental results after artifact elimination is shown in Fig. 7. From this figure, it is depicted that Figs. 7e and 7f are showing high-resolution brain wave components than other sub plots. These are results are obtained due to SEUs based on N2L2MS and MCN2L2MS algorithms. Again, by examine the performance measures in terms of convergence rate, SNR, excess mean square error, misadjustment, among the various algorithms N2L2MS based SEU achieves highest performance measures. But, among all the algorithms MC N2L2MS based SEU requires less amount of computational complexity in terms of multiplications by an amount of filter length, in this case it is ‘L’, shown in Tab. 1. However, in terms of other performance measures MCN2L2MS is little bit inferior than N2L2MS algorithm based SEU. This fact is depicted by examine Fig. 7, Tabs. 2 and 3. Therefore, as a tradeoff the little bit inferior performance of MCN2L2MS based SEU could be tolerated than SEU based on N2L2MS, as MCN2L2MS needs lesser number of multiplications by an amount ‘L’, which is filter length in this case. Hence, MC N2L2MS based SEU is suitable for elimination of artifacts from brain waves for EEG analysis in remote health care monitoring applications.
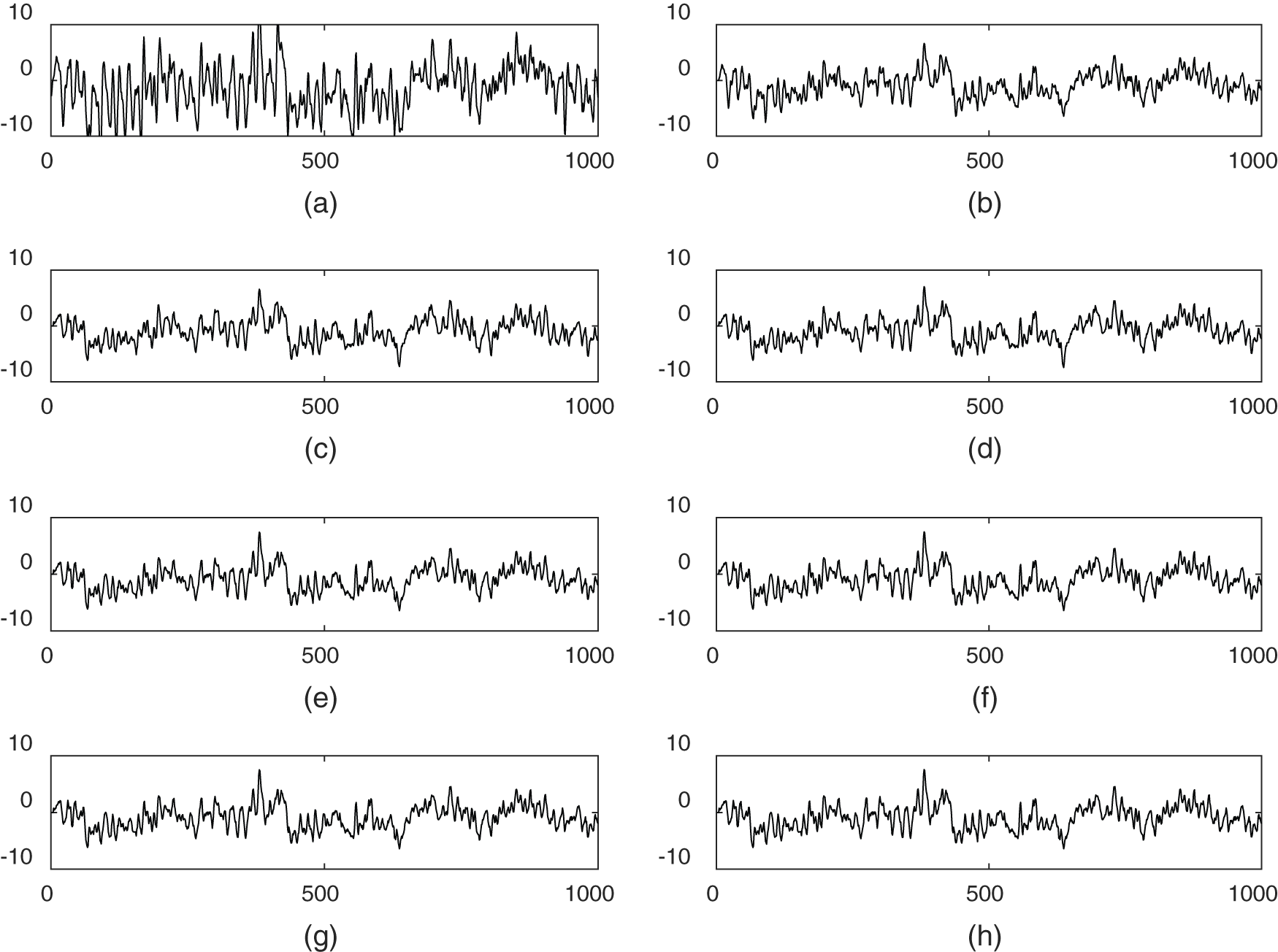
Figure 7: Adaptive artifact cancellation of CSA from EEG signals: (a) noisy raw EEG component, (b) sample of CSA component, (c) output from LMS based SEU, (d) output from N2L2MS based SEU, (e) output from MN2L2MS based SEU, (f) output from MCN2L2MS based SEU, (g) output from MSN2L2MS based SEU, (h) output from MS2N2L2MS based SEU (data values are shown on x-axis; signal amplitudes are shown on y-axis signal)
3.4 Adaptive Artifact Elimination of Eye Blink Artifact (EBA) from Brain Waves
This experiment proves the EBA elimination process from brain wave component. The raw brain wave component is taken as input to the SEU as shown in Fig. 1, this input component is a combination of actual brain action potential and non-physiological noise contamination, it is designated as 
. The reference signal given to the adaptive FIR filter is 
. The adaptive algorithm trains the FIR filter coefficients, such that 
becomes closer to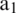 
. The experimental results after artifact elimination is shown in Fig. 8. From this figure, it is depicted that Fig. 8e and 8f are showing high-resolution brain wave components than other subplots. These are results are obtained due to SEUs based on N2L2MS and its variant algorithms. Again, by examine the performance measures in terms of convergence rate, SNR, excess mean square error, misadjustment, among the various algorithms N2L2MS based SEU achieves highest performance measures. But, among all the algorithms MCN2L2MS based SEU requires less amount of computational complexity in terms of multiplications by an amount of filter length, in this case it is ‘L’, shown in Tab. 1. However, in terms of other performance measures MCN2L2MS is little bit inferior than N2L2MS algorithm based SEU. This fact is depicted by examine Fig. 8, Tabs. 2 and 3. Therefore, as a tradeoff the little bit inferior performance of MCN2L2MS based SEU could be tolerated than SEU based on N2L2MS, as MCN2L2MS needs lesser number of multiplications by an amount ‘L’, which is filter length in this case. Hence, MCN2L2MS based SEU is suitable for elimination of artifacts from brain waves for EEG analysis in remote health care monitoring applications.
Figure 8: Adaptive artifact cancellation of EBA from EEG signals: (a) noisy raw EEG component, (b) sample of EBA component, (c) output from LMS based SEU, (d) output from N2L2MS based SEU, (e) output from MN2L2MS based SEU, (f) output from MCN2L2MS based SEU, (g) output from MSN2L2MS based SEU, (h) output from MS2N2L2MS based SEU (data values are shown on x-axis; signal amplitudes are shown on y-axis signal)
This research demonstrates a new method for developing adaptive artifact eliminator to facilitate high-resolution brain waves for wireless EEG monitoring, remote health care monitoring applications in the contest of BCI. The proposed N2L2MS based SEUs achieved good filtering ability, convergence rate, less computational complexity of the adaptive algorithms. To examine these characteristics various SEUs based on N2L2MS, MN2L2MS, MCN2L2MS, MSN2L2MS, MS2N2L2MS algorithms are developed and demonstrated the brain wave enhancement. These implementations are compared with the performance of SEUs based on conventional LMS algorithm. Among these implementations N2L2MS based SEU achieved highest values of performance measures like SNR, EMSE, misadjustment, convergence, except computational complexity. This is evident from Figs. 9–12, Tabs. 1–3. From the experimental results among LMS, N2L2MS and M N2L2MS based SEUs the N2L2MS out performs. Again, when comparing N2L2MS and its hybrid versions of sign algorithms the performance of MS2N2L2MS, diverges more than MN2L2MS due to error clipping, data error clipping. When we compare the performance measures of N2L2MS and MCN2L2MS based SEUs in terms of SNR, EMSE, misadjustemnt convergence rate, the performance of MCN2L2MS is little inferior than N2L2MS. But, the computational complexity of MCN2L2MS is ‘L’ times less than N2L2MS. Hence, it becomes more attractive for wireless and remote health care monitoring applications.
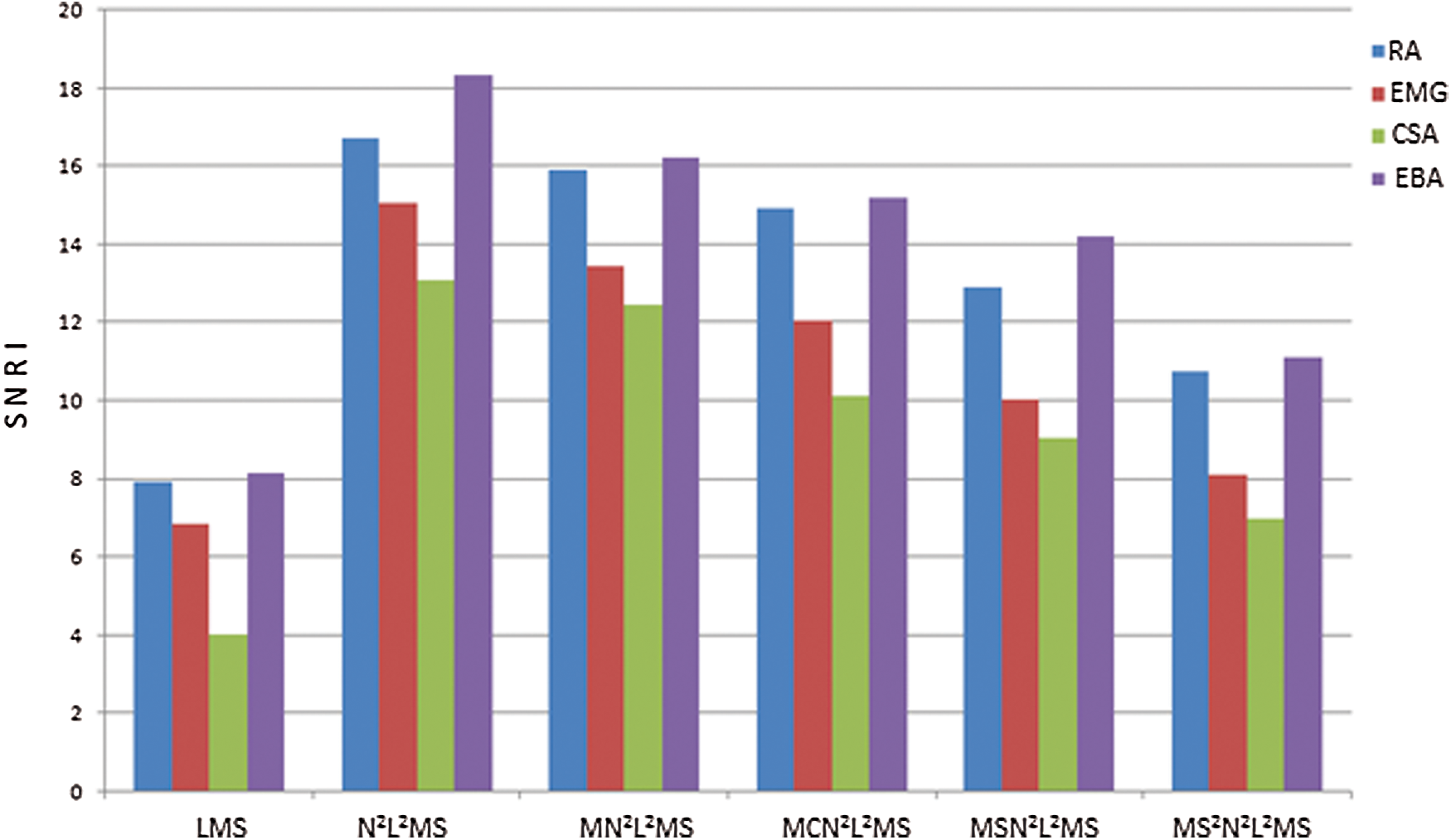
Figure 9: Bar diagram illustrating the SNRI calculated using various SEUs
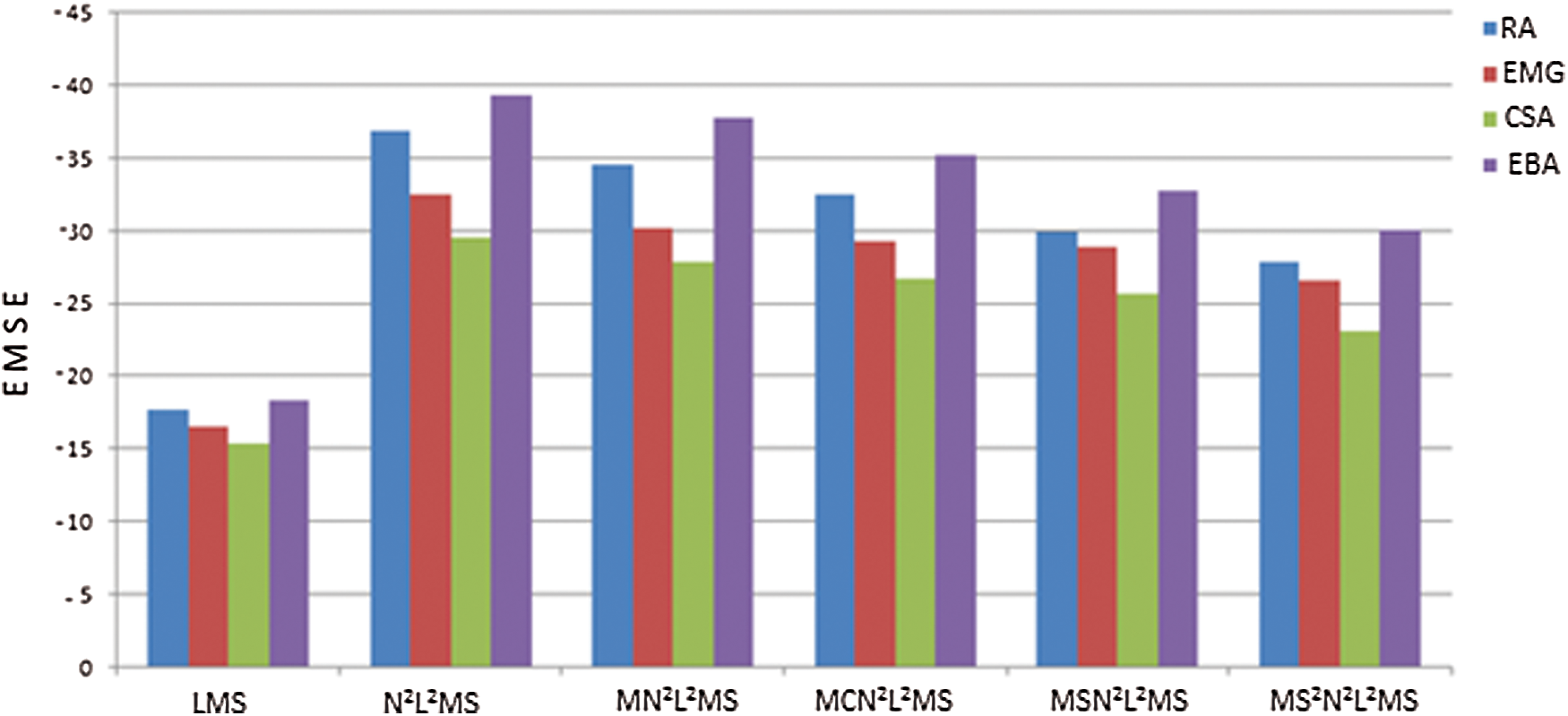
Figure 10: Bar diagram illustrating the EMAE calculated using various SEUs
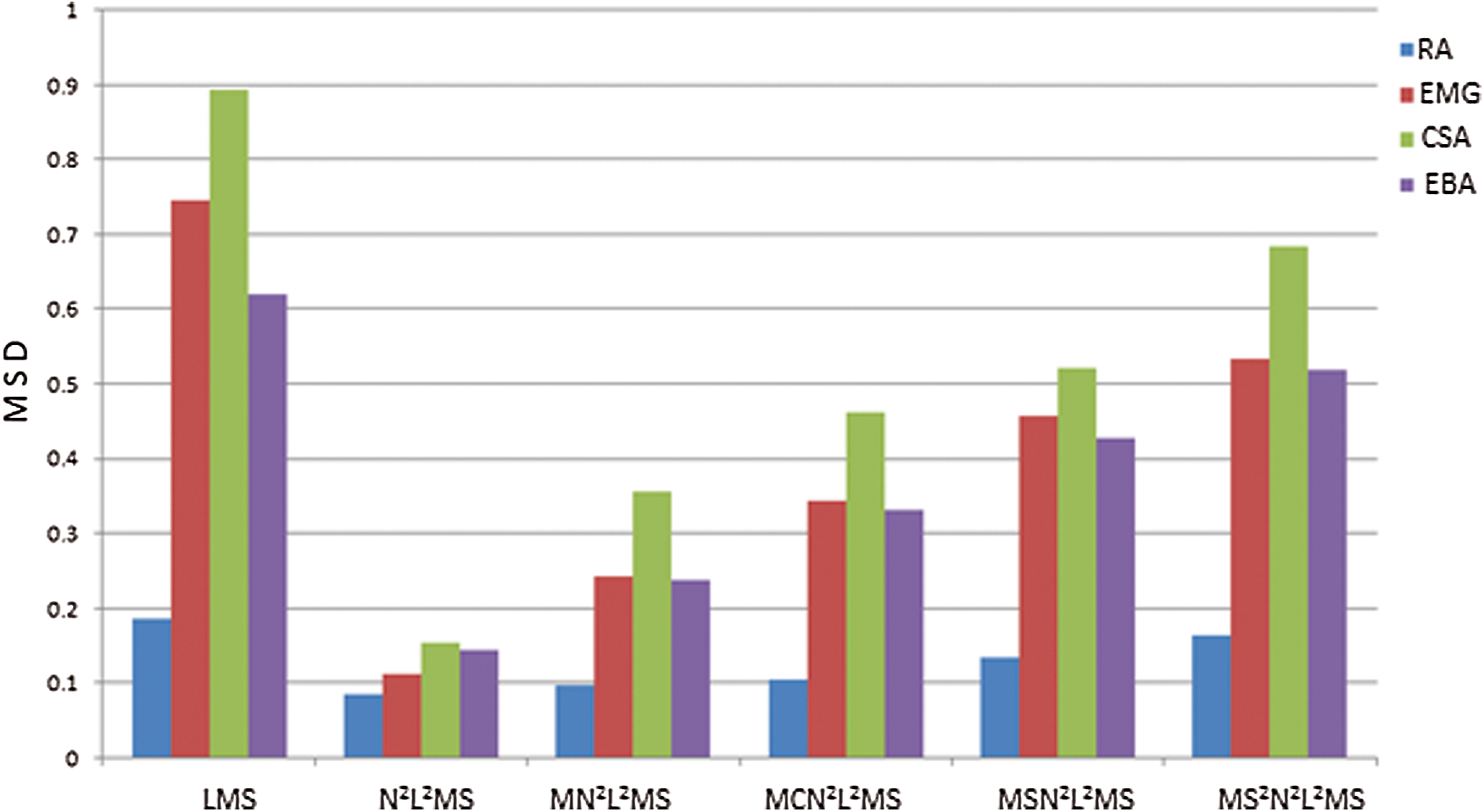
Figure 11: Bar diagram illustrating the MSD calculated using various SEUs
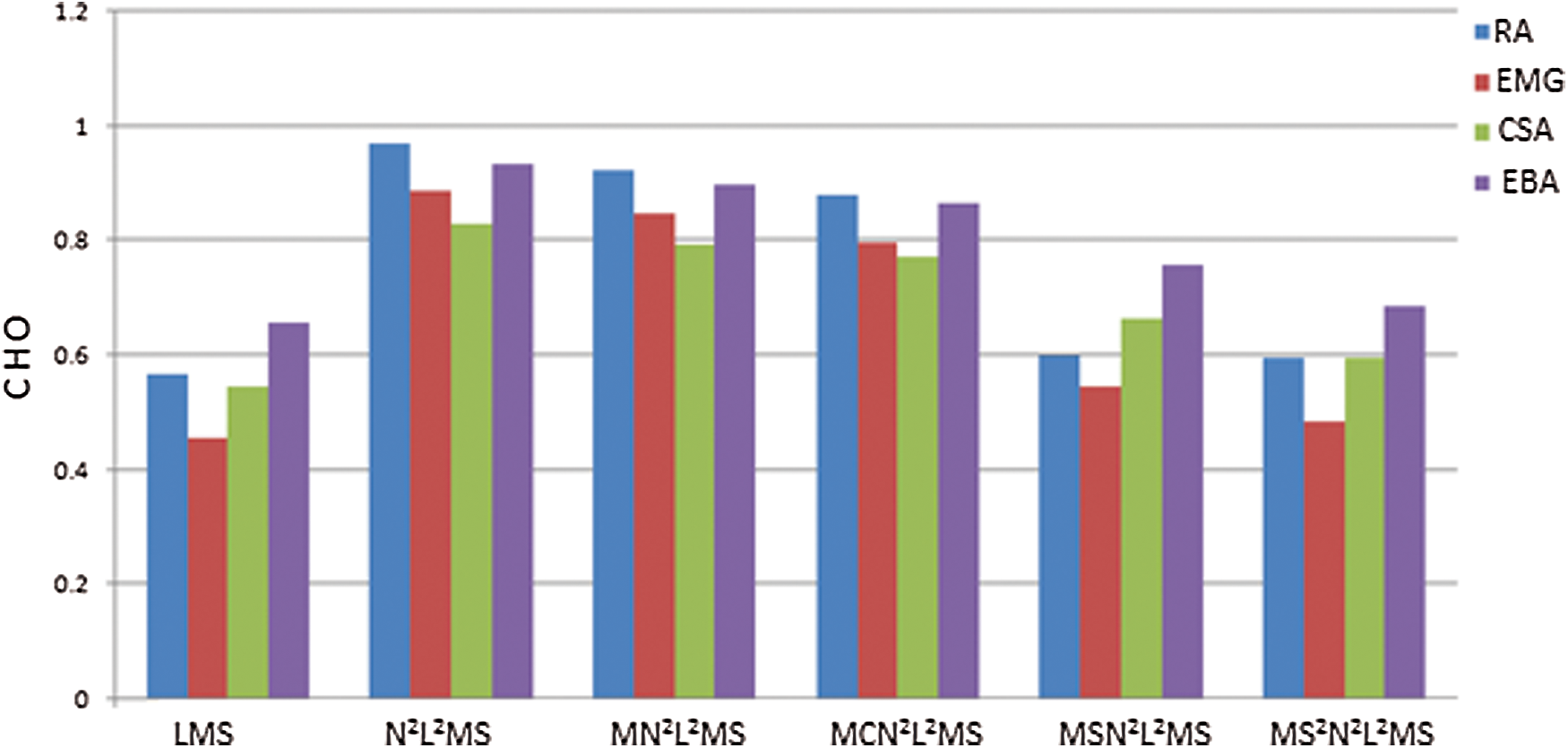
Figure 12: Bar diagram illustrating coherence calculated using various SEUs
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Chan. (2017). Ten years in public health, 2007–2017. In: World Health Organization, Geneva: World Health Organization, , 978-92-4-151244-2. [Google Scholar]
2. World Health Organization. (2017). The world health report: Research for universal health coverage, Geneva: World Health Organization, , 978-92-4-156459-5. [Google Scholar]
3. World Health Organization. (2017). World health statistics 2017: Monitoring, health for the SDGs. In: Sustainable Development Goals, Geneva: World Health Organization, , 978-92-4-156548-6. [Google Scholar]
4. World Health Organization. (2017). Communicating risk in public health emergencies: A WHO guideline for emergency risk communication (ERC) policy and practice, Geneva: World Health Organization, , 978-92-4-155020-8. [Google Scholar]
5. M. Z. Ur Rahman, R. A. Shaik and D. V. R. K. Reddy. (2010). “Cancellation of artifacts in the ECG signals using block adaptive filtering techniques, Research book entitled Software Tools and Algorithms for Biological Systems, Software tools and algorithms for biological systems, Advances in Experimental Medicine and Biology, vol. 696, USA: Springer Nature, pp. 505–513. [Google Scholar]
6. S. S. Mirza and M. Z. Ur Rahman. (2017). “Efficient adaptive filtering techniques for thoracic electrical bio-impedance analysis in health care systems,” Journal of Medical Imaging and Heath Informatics, vol. 7, no. 9, pp. 1126–1138. [Google Scholar]
7. M. Z. Ur Rahman and S. S. Mirza. (2016). “Process techniques for human thoracic electrical bio-impedance signal in remote healthcare systems,” IET Healthcare Technology Letters, vol. 3, no. 2, pp. 1–5. [Google Scholar]
8. I. Soumya, M. Z. Ur Rahman, D. V. R. K. Reddy and A. L. Ekuakille. (2015). “Efficient block processing of long duration biotelemetric brain data for health care monitoring,” Review of Scientific Instruments, vol. 86, no. 3, pp. 35003. [Google Scholar]
9. G.V.S. Karthik, S. Y. Fathima, M. Z. Ur Rahman, S. R. Ahamed and A. L. Ekuakille. (2013). “Efficient signal conditioning techniques for brain activity in remote health monitoring network,” IEEE Sensors Journal, vol. 13, no. 9, pp. 3276–3283. [Google Scholar]
10. M. Z. Ur Rahman, S. R. Ahamed and D. V. R. K. Reddy. (2012). “Efficient and simplified adaptive noise cancellers for ECG sensor based remote health monitoring,” IEEE Sensors Journal, vol. 12, no. 3, pp. 566–573. [Google Scholar]
11. A. Nijholt and D. Tan. (2008). “Brain-computer interfacing for intelligent systems,” IEEE Intelligent Systems, vol. 23, no. 3, pp. 72–79. [Google Scholar]
12. B. J. Lance, S. E. Kerick, A. J. Ries, K. S. Oie and K. McDowell. (2012). “Brain computer interface technologies in the coming decades,” Proceeding of the IEEE, vol. 100, no. 13, pp. 1585–1599. [Google Scholar]
13. J. van Erp, F. Lotte and M. Tangermann. (2012). “Brain computer interfaces: Beyond medical applications,” Computer, vol. 45, no. 4, pp. 26–34. [Google Scholar]
14. G. Schalk and E. C. Leuthardt. (2011). “Brain-computer interfaces using electrocorticographic signals,” IEEE Reviews in Biomedical Engineering, vol. 4, pp. 140–154. [Google Scholar]
15. B. F. Boroujeny. (1998). Adaptive filters-theory and applications. Chichester, U.K: Wiley. [Google Scholar]
16. M. Z. Ur Rahman, S. R. Ahamed and D. V. R. K. Reddy. (2011). “Efficient sign based normalized adaptive filtering techniques for cancelation of artefacts in ECG signals: Application to wireless biotelemetry,” Signal Processing, vol. 91, no. 2, pp. 225–239. [Google Scholar]
17. M. Heiss. (1996). “Optimal dead-zone characteristic for minimizing the a-posteriori error in basis function networks,” in IEEE Proceedings of the 35th Conf. on Decision and Control, Kobe, Japan, pp. 476–477. [Google Scholar]
18. M. Heiss. (1996). “Error-minimizing dead zone for basis function networks,” IEEE Transactions on Neural Networks, vol. I, no. 6, pp. 1503–1506. [Google Scholar]
19. M. Z. Ur Rahman, S. R. Ahamed and D. V. R. K. Reddy. (2012). “A non-linearities based noise canceller for cardiac signal enhancement in wireless health care monitoring,” in IEEE Global Humanitarian Technology Conference, Seattle, WA, USA. [Google Scholar]
20. P. S. R. Diniz. (2008). Adaptive filtering, algorithms and practical implementation. 3 ed., Switzerland: Springer Publishers. [Google Scholar]
21. S. Haykin. (2013). Adaptive filter theory. Eaglewood Clirs, NJ: Prentice-Hall. [Google Scholar]
22. J. E. Greenberg. (1998). “Modified LMS algorithms for speech processing with an adaptive noise canceller,” IEEE Transactions on Speech and Audio Processing, vol. 6, no. 4, pp. 338–351. [Google Scholar]
23. S. C. Douglas. (1994). “A family of normalized LMS algorithms,” IEEE Signal Processing Letters, vol. 1, pp. 1352–1365. [Google Scholar]
24. S. Emotiv, Brain computer interface technology, EMOTIV Inc.: San Francisco, CA, USA, http://emotiv.com. [Google Scholar]
25. J. Malmivuo and R. Plonsey. (1995). Bioelectromagnetism: Principles and applications of bioelectric and biomagnetic fields. Oxford, U.K: Oxford University Press. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |