DOI:10.32604/cmc.2021.014172
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014172 | |
| Article |
Intrusion Detection System Using FKNN and Improved PSO
College of Computing and Informatics, Saudi Electronic University, Saudi Arabia, Riyadh
*Corresponding Author: Raniyah Wazirali. Email: r.wazirali@seu.edu.sa
Received: 03 September 2020; Accepted: 30 November 2020
Abstract: Intrusion detection system (IDS) techniques are used in cybersecurity to protect and safeguard sensitive assets. The increasing network security risks can be mitigated by implementing effective IDS methods as a defense mechanism. The proposed research presents an IDS model based on the methodology of the adaptive fuzzy k-nearest neighbor (FKNN) algorithm. Using this method, two parameters, i.e., the neighborhood size (k) and fuzzy strength parameter (m) were characterized by implementing the particle swarm optimization (PSO). In addition to being used for FKNN parametric optimization, PSO is also used for selecting the conditional feature subsets for detection. To proficiently regulate the indigenous and comprehensive search skill of the PSO approach, two control parameters containing the time-varying inertia weight (TVIW) and time-varying acceleration coefficients (TVAC) were applied to the system. In addition, continuous and binary PSO algorithms were both executed on a multi-core platform. The proposed IDS model was compared with other state-of-the-art classifiers. The results of the proposed methodology are superior to the rest of the techniques in terms of the classification accuracy, precision, recall, and f-score. The results showed that the proposed methods gave the highest performance scores compared to the other conventional algorithms in detecting all the attack types in two datasets. Moreover, the proposed method was able to obtain a large number of true positives and negatives, with minimal number of false positives and negatives.
Keywords: FKNN; PSO approach; machine learning-based cybersecurity; intrusion detection
The world has entered the era of cyber networking and the Internet of Things (IoT). Many people use the internet for communication and business purposes. Confidential data of every individual are available on the internet, where many the sites can be hacked for siphoning-off private information, thus causing a negative impact on digital interactions. Therefore, an intrusion detection system (IDS) was developed to prevent stealing users’ private data; it detects suspicious behaviors of intruders and avert malicious activities. For this, several classification models have been created, evolving from traditional statistical methods to machine learning approaches. Previously, different kinds of statistical approaches, such as logistic regression, multivariate discriminant technique, and factor analysis, were used for intrusion detection purposes. Recent research in machine learning (ML) and artificial intelligence (AI) techniques, including support vector machine (SVM) [1], Bayesian network models [2,3], artificial neural network (ANN) [4], and k-nearest neighbor (KNN) [5,6] approaches, have been implemented for the detection of malicious activities in cybersecurity. The ANN classification model is considered to be the most efficient approach for IDS, though it is challenging to precisely program it for IDS due to its black-box nature.
The KNN approach is user-friendly, easily understandable, and interpretable with a high accuracy and precision rate. The KNN approach equally weighs the selected neighbors irrespective of their space from a particular point. A more advanced form of the KNN approach is typically used, the fuzzy KNN, which applies fuzzy logic, by allocating a degree of membership to the groups due to the space from each k-nearest neighbor. Every point is assigned a specific value for detection purposes. The nearest point to a particular one is allocated a higher degree of membership than the one at a larger distance from the query (particular point). Therefore, the group with the highest value is considered the winner. The FKNN approach has already been applied to biological and image data [7–9]. However, no major research has been done using the FKNN for IDS. In the literature [6], While the FKNN approach was used to determine the unknown intruder, no comprehensive information about fuzzy strength (m) and neighborhood size (k) has been elucidated. In this article, a comprehensive overview of the FKNN approach related to k and m is presented in regards to the IDS system for cybersecurity purposes.
Other than opting for the best algorithm, feature selection also plays a vital role in IDS for selecting the subgroups of attributes from the group of original attributes. Feature selection is used to create the best possible learning model. Feature selection has three main advantages. First, it can enhance the probability performance of interpreters; second, it can offer speedy and economical interpreters; and third, it can deliver a better understanding of the ongoing processes that create the data [10]. In IDS, genetic algorithms (GAs) [11] are often used for choosing the input features [12,13] or to elucidate proper hyper-parameter values of the interpreter [14,15] using the SVM approach [16]. As compared to the GA, the PSO approach [17] contains no mutation or crossover processes. This approach is user friendly, needs less time for processing, and has a low cost. In addition, it fine-tunes the position and velocity of every point in such a way that it can differentiate accurately between the best local and global variables. All the elements have a strong capability to search around, helping the swarm to find the ideal solution.
In terms of practical tasks, the PSO and GA take a lot of computational time for processing. Therefore, computing techniques need to be improved. To increase the search and optimization process, implementation of binary and continuous PSO approaches should be done by making use of open multiprocessing that is a transferrable; an accessible model can assist in developing a parallel use of platforms [18].
In this paper, we discussed an adaptive FKNN approach that uses PSO algorithm by defining the neighborhood size (k) and fuzzy parameter (m). In addition, the binary PSO was used for detecting and defining the most significant features. The contribution and efficacy of the proposed IDS model were authenticated by relating them to other state-of-the-art classification models based on real-life scenarios. The experimental visualization outcome showed that the proposed topology can attain the proper parameters as well as display a high discerning power because of the feature selection tool. A comparison among the series and parallel models was performed. We also analyzed the parallel model of TVPSO-FKNNm and we found that it can greatly decrease the computational processing/run-time.
The fKNN and time-variant particle swarm optimization (TVPSO) are explained in Section 2. In Section 3, relevant studies of intrusion detection based on the k-nearest neighbors and PSO are discussed. Section 4 explains the proposed method and the algorithm of the FKNN-TVPSO. We provide the experimental outcomes in Section 5 and compare them with other techniques. In Section 6, we present the conclusion.
2.1 Fuzzy K-Nearest Neighbor Algorithm
The KNN algorithm is the first of its kind being a simple and nonparametric classification algorithm where a group allocates rendering to the most-known group amidst the k-nearest neighbors. The fuzzy form of the KNN was first proposed by Keller in 1985 by integrating fuzzy logic into the KNN technique and he named it the “fuzzy-KNN-classifier algorithm (FKNN).” Instead of separate groups, like in the KNN, the fuzzy affiliations of points are allocated to several groups with the following formulation:
where 
and 
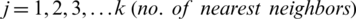. The fuzzy parameter (m) defines the weight given to the distance of each point while computing the neighbor’s contribution to the membership value. The value is selected as 
. 
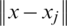is the space between the x and its jth nearest neighbor xi. Several distance metrics, such as Euclidean distance, Mahalanobis distance, and Hamming distance, can be selected to measure 
. In this research, the Euclidean distance was given preference. uij is the membership unit of pattern xj from the training group to class I between the k-nearest neighbor of x. The two ways to define uij are the crisp membership and nonmembership in class and the fuzzy membership, where KNN of each set is allocated to the membership in each group using the following equation:
where nj is the number of neighbors belonging to the jth class. It must be noted that memberships allocated by (2) must fulfill the following equations:
In this research, we found that the fuzzy method has excellent classification precision. After calculating the membership of a particular point, it is then allocated to the group having the highest membership number, as shown as follows:
2.2 Time-Variant Particle Swarm Optimization (TVPSO)
This approach was inspired by organisms’ social behavior, for instance, fish swimming in a school and birds flocking together. This approach was first developed by Kennedy and Eberhart [19]. In this technique, each point is taken as a unit in d-dimensional space, with some velocity and position. The position vector of the ith unit is symbolized as 
. The velocity is characterized as 
. Both of these parameters are updated using the following equations:
where 
, i.e., the previous position, 
, i.e., the best unit among all, r1 and r2 are random numbers, and vi, j is the velocity.
The inertia weight (w) is considered for the global survey and local utilization. A large weight assists in a global search, while a small weight eases the local search. W is updated for algorithm utilization using (9), which is also known as the “time-varying inertia weight”:
, and t is the running iteration.
The magnitudes of the unit’s velocity in the local and global directions are defined by the acceleration coefficients, i.e., c1 and c2. The concept of the time-varying acceleration coefficient (TVAC) for balancing the search space among the global survey and local usage was implemented in another study [20] which was also deployed in this research to ensure a better solution search. TVAC can be represented mathematically by the following equations:
where c1f, c1i, c2f, c2i are constants, and tmax is the maximum number of iterations.
The binary PSO is defined as the search in an isolated space where a unit changes its position in a space limited to zero and one at every dimension. Upon perceiving a high velocity, 1 is assigned, and for lower values, 0 is assigned to the unit. For changing the velocity from the continuous to the probability space, the sigmoid function is used (Eq. (12)).
The new unit position is updated using the following equation:
where rnd is a uniform random number ranging between 0 and 1.
The KNN has been discussed in detail in the literature [21]. KNN model does not comprise any kind of learning phase, so it is also known as a “lazy learner.” It does not memorize the data for training. The KNN categorizes new data from already-available datasets based on parallel measures by using three of the distance metrics, i.e., the Euclidean distance, Mahalanobis Distance, and Hamming Distance, which help in forecasting and predicting about the hidden data point.
There are obstacles arising from using a simple KNN algorithm, and a new extended algorithm of KNN, the fuzzy KNN technique, was developed to prevent unbalanced normal and intrusion data by building up the feature vectors in the FKNN based on the clustering query point fuzzy conditions [17]. We experimentally found that the fuzzy KNN model performance is far better and greater than the conventional TANN (triangle area based nearest neighbors) and CANN (combined cluster centers and nearest neighbors) classifiers. According to the outcomes of the conducted research in this paper, the precision rate of FKNN is said to be 98.73%, while that of TANN is 98.47% and CANN has an accuracy rate equal to 96.07%. The intrusion detection rate of the FKNN is 96.23%, the TANN’s rate is equal to 94.5%, and that of the CANN algorithm is up to 86.05%. The third calculated parameter was the false alarm rate for the FKNN, TANN, and CANN, which was 0.28%, 0.4%, and 0.75% respectively.
A semisupervised methodology was implemented to lessen the false alarm rate and improve the detection rate in IDS using the KNN hyper-parameter approach with cross-validation [22]. In this approach, for every unlabeled dataset, the KNN of the training set is categorized and after gaining statistical data from the KNN hyper-parameter tuning, namely, a neighboring dataset of each group, distance weight, metric, and new data points are taken as the attacking group or normal group. The NSL-KDD dataset was employed for analyzing the robustness of the model.
The fusion approach was implemented for intrusion detection, and it uses cross classifiers’ techniques, including the SVM, PSO, and K-NN on the KDD99 dataset [23]. The accuracy of the SVM was 97%, the accuracy of the KNN was 98%, and the accuracy of the PSO was 99.8% (the highest accuracy) during an R2L attack. Compared to the above three classifiers, the fusion model had an accuracy rate of 98.55%.
The IDS was performed over the KDD99 dataset using KNN-ACO and the SVM approach and the accuracy rate of the classifiers was observed [5]. This approach generated fewer false alarms than the rest of the classifiers. The accuracy rate was also mentioned in the paper for the KNN-ACO and was equal to 94.17%. The accuracy rate of the backpropagation neural network (BPNN) was 93% and SVM had an 83% accuracy rate. The false alarm rate for KNN-ACO, BPNN, and SVM was 5.82%, 6.90%, and 16.90% respectively.
The CANN and KNN approaches and classifiers were explained using k-means clustering over the NSL-KDD dataset [24]. The FKNN approach was used for categorizing the data. The FKNN approach had a good accuracy rate and detection rate and a low false alarm rate.
The fuzzy c-means approach, distance-weighted KNN approach, and Dempster Shafer Theory were executed to identify the unknown attack in IDS by evaluating the functions and probabilities on the KDD99 dataset [6]. The accuracy, false alarm, and detection rate were measured using these approaches of the KNN algorithm, and the authors found that implementing fuzzy KNN logic was far better than other approaches.
The PSO-based KNN approach was implemented for the secured transfer of information from the server station to the mobile devices and laptops [25]. The results obtained from this research showed the increased accuracy in the PSO-KNN approach (up to 2%).
The PSO based approach using the SVM-KNN methodology was implemented for assembling classifiers into one category on the KDD99 dataset [26]. The distance weight method was executed using the weighted majority algorithm (WMA) for creating ensemble classifiers. The results were high-performance ensemble classifiers compared to other traditional algorithms.
The two-layered hybrid classification and detection process was proposed using the KDD99 dataset [27]. The first layer consists of the GBGT approach, which detects the DoS attack, while the second layer is comprised of the KNN feature selection classifier that is improved and enhanced by the FOA to identify and split the non-DoS data from the normal, U2L, and R2L probes. All of these classifiers were examined based on their accuracy, recall rate, and detection rate. The grouping of the DoS data using the KNN approach on two attacks (such as the back, teardrop, smurf, and Neptune pod) had a high recall rate. The precision rate of the smurf and Neptune attacks was greater than 99%, while that of the back and pod was greater than 60%. The authors concluded that the KNN methods have a high performance compared to the SVM-ANN methods.
In the KNN-based TSA, the feature selection approach for intrusion detection was implemented for reducing feature severance while the KNN was deployed for classification purposes on the KDD99 dataset for improving the efficiency and accuracy of the IDS system [28]. It was experimentally observed that the accuracy of the KNN-PSO was 87.34%, while that of the TSA-KNN was 87.34%.
The hybrid KNN approach was implemented for intrusion detection on the NSL-KDD dataset and evaluated experimentally [29,30]. The KNN approach was far better than the rest of the algorithms applied.
Based on the literature review above, the PSO approach using the fuzzy KNN method was selected for optimization because it could obtain a better accuracy in the IDS system in addressing various kinds of cyber attacks.
The methodology implemented to conduct this research is the TVPSO-FKNN [31]. Using this model, the FKNN classifier can automatically be optimized by analyzing the k and m parameters and detecting and categorizing the class of best distinct features. So, for this, the binary and continuous PSO approaches were linked together for feature selection and classification. The attained feature was taken as the input to the categorized FKNN approach. In this section, the parameter encoding and the fitness function are discussed first. Then, the first serial PSO methodology in terms of the TVPSO-FKNN is elaborated upon.
The decision variables (fuzzy logic parameters) were encoded using the binary representation, and integer representation within the search bound. While it is easy to represent the search bound for the fuzzy strength with integer representation, the k-neighborhood set and the feature set are lists of values that can be represented with binary values. Eqs. (14) and (15) are examples of binary representation of the k-neighborhood set
The fitness function was designed to obtain the optimal fuzzy logic parameters, which was done with cross-validation using 20% of the data as the validation set. Machine learning performance metrics (accuracy, precision, recall, and f1 score) were introduced to evaluate the fuzzy KNN model obtained from each combination of parameters. The accuracy, precision, recall, and f1 score were calculated at every training stage on the validation set using the formula defined in (16)–(19). Since we were concerned with reducing the false positive rate, the accuracy and the F-score were used to design the fitness function, as given by (20)
4.3 Serial Implementation of the Proposed Approach
The following steps were followed using the TVPSO-FKNN approach for constructing a series PSO algorithm.
Step 1: Encode the particles using 
dimensions, considering k and m as the first two continuous values. The remaining n dimensions are the Boolean feature mask; tag 1 if selected and 0 if discarded.
Step 2: Initialize each individual by random numbers while characterizing PSO units with the upper and lower velocity bounds.
Step 3: Train the FKNN approach with the selected features.
Step 4: Higher fitness values are achieved when units have a high fitness value and a smaller number of the selected features. By taking into consideration the accuracy, precision, recall, and f-score parameters, objective functions are designed and calculated, as shown in (19).
Step 5: Increase the iteration time.
Step 6: Increase the population numbers by updating the position and velocity of m and k and their feature using (7), (8), (12), and (13) for every unit.
Step 7: Train the FKNN using the obtained feature vector from Step 6 and calculate each unit fitness value using (20).
Step 8: Update the personal ideal fitness value (pfit) and position (pbest) in comparison to the best value present in the memory slot.
Step 9: On reaching the maximum population size, move to Step 10, otherwise, repeat the process starting from Step 6.
Step 10: Update (gfit) and (gbest) after comparing gfit with pfit in the overall population. The dominating parameter is stored in the memory.
Step 11: The process moves ahead if the stopping criteria are satisfied; otherwise it is repeated from Step 5.
Step 12: Finally, the ideal (k and m) parameters and feature subset from the best unit (gbest) are obtained.
4.4 Parallel Implementation of the Proposed Approach
To improve the optimization performance and reduce the computational time of the model, TVPSO-FKNN was implemented in parallel on a multicore processor using OpenMP. The following steps were used with the TVPSO-FKNN approach for constructing a series PSO.
Pseudocode of the parallel TVPSO-FKNN approach is as follows:
“Initializing parameters”
“Training of FKNN model”
“Calculating fitness”
“While (
)/*current no. of iteration, maximum no. of iteration*/.”
“For each unit”
“Updating velocity”
“Updating position”
“Training FKNN model”
“Calculating pfit”
“Calculating pbest”
“End For”
“Calculating gfit”
“Calculating gbest”
“
”
“End while”
The intrusion prevention dataset discussed in KDD-NSL [32] and CICIDS2017 [33] was used to improve the intrusion detection system. These datasets were comprised of 43 and 78 features, respectively, as regarded to network traffic when optimized in a separate group. The CICID2017-based dataset contained network traffic taken for a period of five days, i.e., Monday, 3 July 2017 to Friday, 7 July 2017, with six types of attacks with normal network traffic. The NSL-KDD dataset used four types of attacks with normal network traffic. Group labels were tagged in such a way that each data set had an equal number of samples. We collected 500 samples from the CICID2017 dataset, and 1000 samples from the NSL-KDD for each type of attack. The proposed methodology was implemented for the effective classification of every type of networking traffic.
The OpenMP platform and MATLAB software were used for the implementation of the proposed methodology by making use of statistics, machine learning (ML), and the neural network toolbox. Four algorithms were implemented (PSO, FKNN, KNN, and GA) from the start. Two of the algorithms (BPNN and PNN) were established using the NN-toolbox of MATLAB 7.0. The technical specifications of the computer used for simulation purposes were as follows:
Intel Quad–Core Xeon 2.0 GHz CPU
The search range of two parameters, k and m, for both the datasets were as follows:
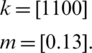
The values set for c1i, c1f, c2i, and c2f were 2.5, 0.5, 0.5, and 2.5, respectively [20]. The values for wmax and wmin were 0.9 and 0.4, respectively. Parameter setting for proposed TVPSO-FKNN in (NSL-KNN & CICID2017) was as follows:
For the GA-FKNN, the following values of parameters were set to
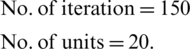
5.3 Experimental Results and Discussion
The proficiency of two models (fuzzy KNN-GA and fuzzy KNN-TVPSO) were evaluated on two datasets by making use of performance metrics mentioned in (16)–(19). The outcomes were compared with those of traditional ML techniques (PNN, Decision Tree, SVM, and KNN) [34]. The experimental results of the NSL-KDD and CICIDS2017 datasets are shown in Tabs. 1 and 2, respectively.
Table 1: Experimental result that compares the performance metric of other classifiers with the proposed solution using the NSL-KDD dataset
Table 2: Experimental result that compares the performance metric of other classifiers with the proposed solution using the CICIDS 2017 dataset
From our results, we found that the performance score of the proposed model was the highest compared to the rest of the algorithms for detecting and identifying every type of attack for two datasets. The average performance of the proposed model and other models was calculated for a single value and presented in Tabs. 1 and 2. The F1-score of PNN is 49.35, for the KNN, it is 89.9, for the SVM, it is 71.39, and that of the decision tree is 92.33. The F-scores for the proposed model using the fuzzy logic KNN with TVPSO and GA were 94.25 and 92.46, respectively. The proposed approaches have a better performance than conventional methods. The evaluated precision accuracy of the proposed techniques and the rest of the IDS models is listed in Tab. 3. The proposed algorithms (FKNN-GA AND FKNN-PSO) have a high accuracy and detection rate and a lower false alarm rate.
Table 3: Accuracy evaluation for NSL-KDD and CICIDS
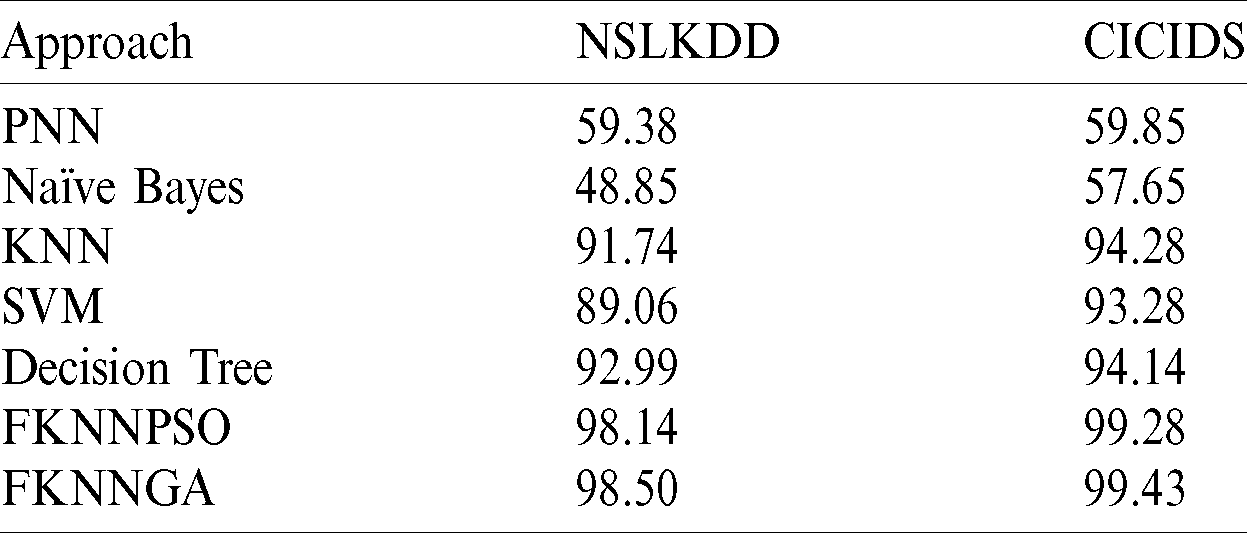
Tabs. 4 and 5 represent the summary of all the results deduced from the above-mentioned algorithms (PNN, SVM, decision tree, KNN, FKNNPSO, and FKNN-GA) for two datasets (NSL-KDD and CICIDS2017). The proposed algorithms offer high precision rate, recall, and F-scores. In Tab. 6, the testing and training time of two datasets for the suggested methods and other classifiers are shown. We observed that FKNNPSO and FKNNGA do not have fast detecting time as compared to the other models, which is why the parallel implementation of the proposed approaches was performed to eliminate the processing time problem. Nevertheless, the proposed approaches have a higher performance rate than the rest of the classification methods.
Table 4: Result summary for NSL-KDD dataset
Table 5: Result summary for CICIDS dataset
Table 6: Test and train time analysis
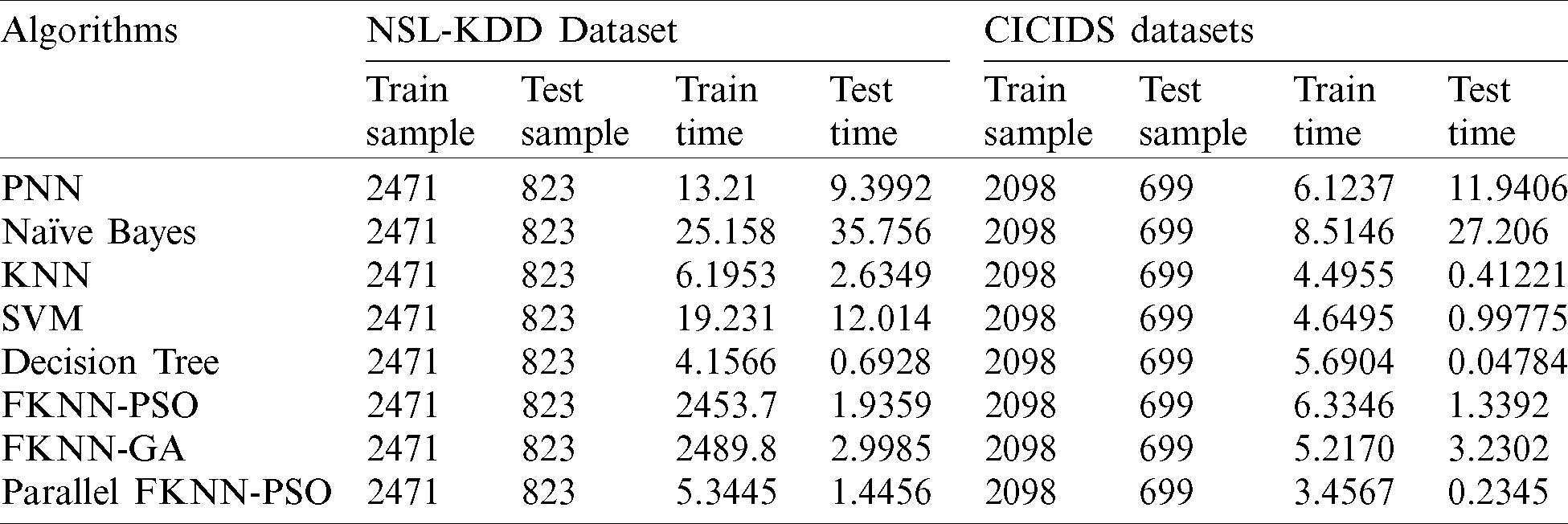
To analyze the number of times the algorithm detected an attack, a confusion matrix was determined [35]. Tabs. 7 and 8 show this matrix for the NSL-KDD set intended for optimization of PSO and GA approach. Tabs. 9 and 10 explain the matrix for the CICIDS2017 set. On observing the diagonal of each matrix, we found that the proposed models showed a high number of true positives and negatives and small number of false positives and negatives.
Table 7: Confusion matrix for NSL-KDD dataset using FKNPSO algorithm
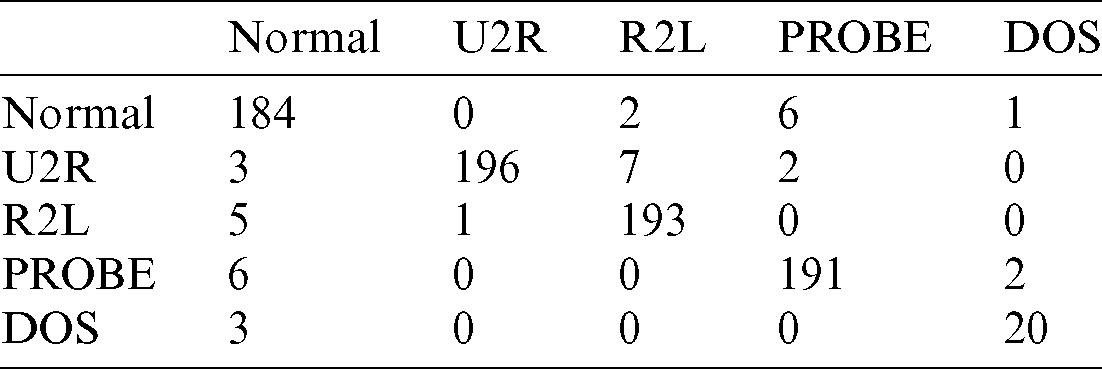
Table 8: Confusion matrix for NSL-KDD dataset using FKNNGA algorithm
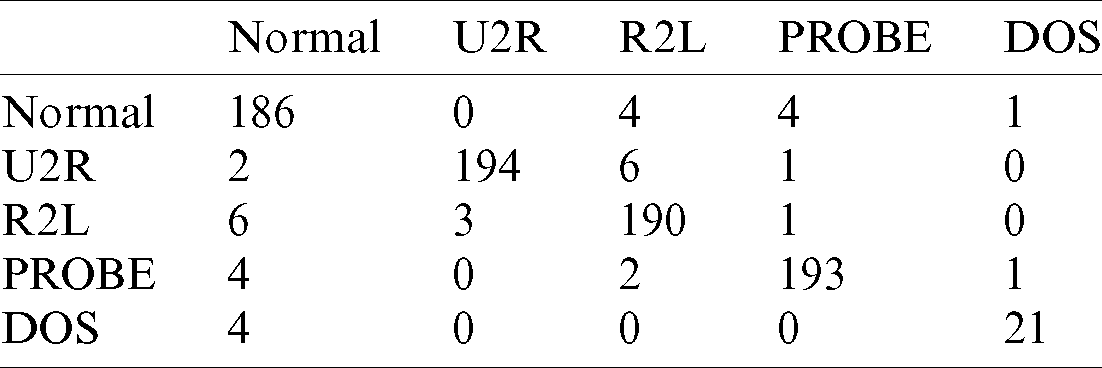
Table 9: Confusion matrix for CICIDS dataset using PSO algorithm
Table 10: Confusion matrix for CICIDS dataset using the GA algorithm
Figs. 1 and 2 depict the evolutionary process, showing that fold #1 is the best among the ten-fold cross-validation in the FKNN-TVPSO using the NSL-KDD and CICIDS2017 datasets. These results were measured based on the best global position. The fitness of the local best positions on the training sets was measured to gain the best fitness of the population in every generation. These evolutionary processes were intriguing because the fitness curves progress from iteration 1 to 100 and reveal no major progression after 40 in the KDD-NSL approach and 3 in CICIDS2017. The stopping criteria is 100 iterations. In the beginning, there is a rapid increase in fitness of the evolution, but after a specific number of iterations, this rapid increase slows. Even then, the stability feature of the fitness remains the same until the stopping criteria are reached. This illustrates that FKNN-TVPSO topology can quickly congregate towards the global target and efficiently find the solution. The phenomenon proves the value of FKNN-TVPSO in developing parameters (k and m) and features via the TVPSO algorithm.
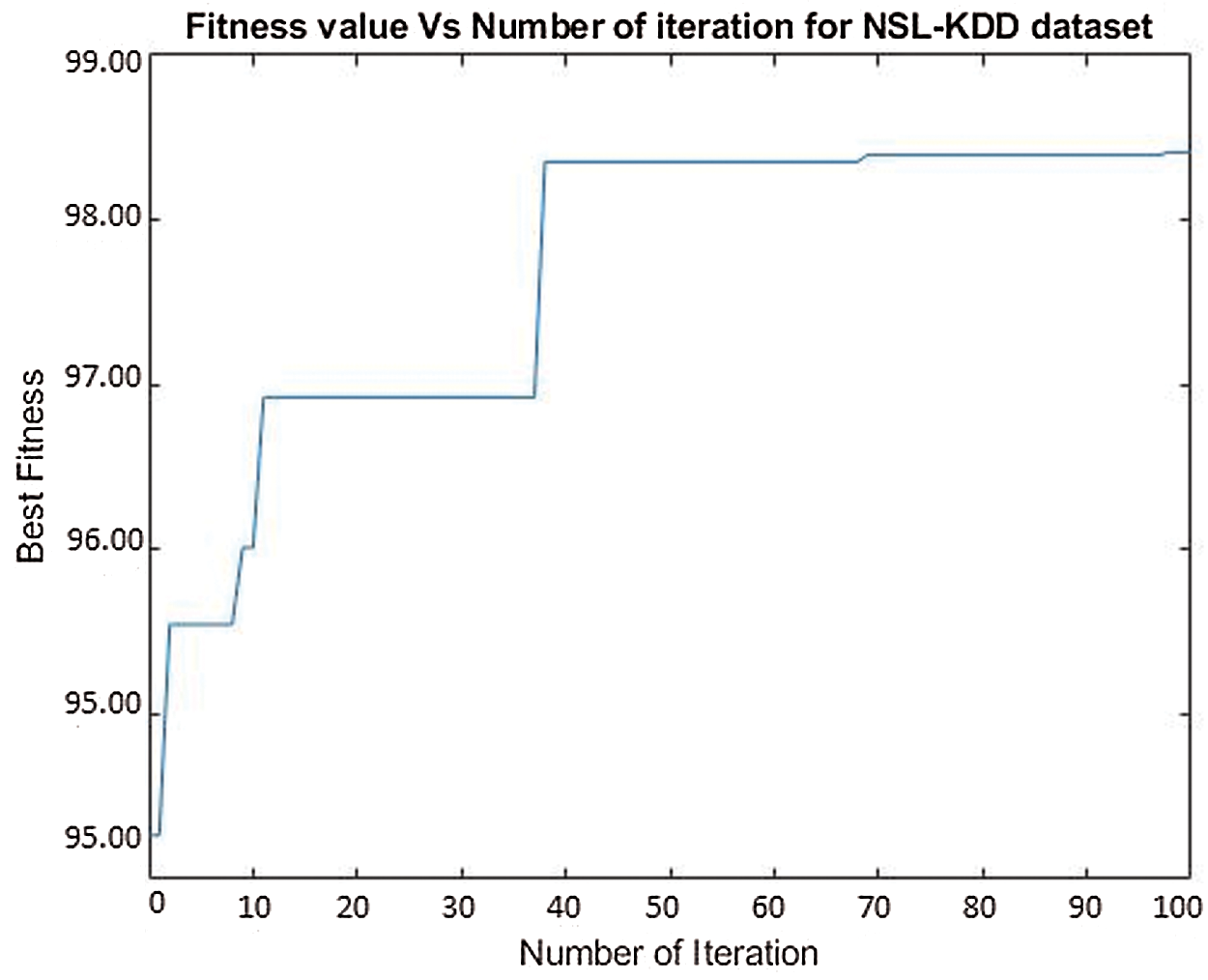
Figure 1: Fitness value vs. number of iterations for NSL-KDD
Figure 2: Fitness value vs. number of iterations for CICIDS
This research offers a novel approach for IDS. The main approach of this research is the implementation of the TVPSO algorithm assisting the FKNN classifier to gain the highest classification performance. The continuous TVPSO is employed to identify parameters k and m of the FKNN, while binary TVPSO is taken into consideration for recognizing the most discrete feature. Both of these TVPSO approaches are executed in a parallel environment for decreasing the processing time. Experimental outcomes illustrate the performance of proposed models to be significantly better than the rest of the state-of-the-art classifiers in place of the IDS system. Experiments show that the parallel implementation of the FKNN-TVPSO is a strong feature selection tool in detecting the best distinct function for intrusion detection (IDS). Nevertheless, the proposed model has a high computation efficiency.
Hence, it is concluded that the proposed FKNN-TVPSO technique is the best in IDS for a cybersecurity system. It should be noted that this technique efficiently performs on the data. Parallel implementation will take to major development when smearing with larger datasets of the detection system before future use. Future analysis should focus on assessing the proposed algorithm for larger datasets.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors state that they have no conflicts of interest to report regarding the present study.
1. S. Ding, Z. Shi, D. Tao and B. An. (2016). “Recent advances in support vector machines,” Neurocomputing, vol. 211, pp. 1–3. [Google Scholar]
2. S. Benferhat, T. Kenaza and A. Mokhtari. (2008). “A Naive bayes approach for detecting coordinated attacks,” in 32nd Annual IEEE Int. Computer Software and Applications Conf., Turku, Finland, pp. 704–709. [Google Scholar]
3. M. Panda and M. R. Patra. (2007). “Network intrusion detection using naïve bayes,” International Journal of Computer Science and Network Security, vol. 7, no. 12, pp. 258–263. [Google Scholar]
4. T. C. Truong, Q. B. Diep and I. Zelinka. (2020). “Artificial intelligence in the cyber domain: Offense and defense,” Symmetry, vol. 12, no. 3, pp. 410. [Google Scholar]
5. S. Vishwakarma, V. Sharma and A. Tiwari. (2017). “An intrusion detection system using KNN-ACO algorithm,” International Journal of Computer Applications, vol. 171, no. 10, pp. 18–23. [Google Scholar]
6. X. Jing, Y. Bi and H. Deng. (2016). “An innovative two-stage fuzzy KNN-DST classifier for unknown intrusion detection,” International Arab Journal of Information Technology, vol. 13, no. 4, pp. 8. [Google Scholar]
7. Y. Huang and Y. Li. (2004). “Prediction of protein subcellular locations using fuzzy KNN method,” Bioinformatics, vol. 20, no. 1, pp. 21–28. [Google Scholar]
8. J. Sim, S. Y. Kim and J. Lee. (2005). “Prediction of protein solvent accessibility using fuzzy k-nearest neighbor method,” Bioinformatics, vol. 21, no. 12, pp. 2844–2849. [Google Scholar]
9. S. Yu, S. D. Backer and P. Scheunders. (2002). “Genetic feature selection combined with composite fuzzy nearest neighbor classifiers for hyperspectral satellite imagery,” Pattern Recognition Letter, vol. 23, no. 3, pp. 183–190. [Google Scholar]
10. I. Guyon and A. Elisseeff. (2003). “An introduction to variable and feature selection,” Journal of Machine Learning Research, vol. 3, no. 1, pp. 1157–1182. [Google Scholar]
11. P. G. Majeed and S. Kumar. (2014). “Genetic algorithms in intrusion detection systems: A survey,” International Journal of Innovation and Applied Studies, vol. 5, no. 3, pp. 9. [Google Scholar]
12. D. I. Mahmood and S. M. Hameed. (2016). “A feature selection model based on genetic algorithm for intrusion detection,” Iraqi Journal of Science, vol. 1, pp. 168–175. [Google Scholar]
13. K. S. Desale and R. Ade. (2015). “Genetic algorithm based feature selection approach for effective intrusion detection system,” in Int. Conf. on Computer Communication and Informatics, Coimbatore, India, pp. 1–6. [Google Scholar]
14. M. R. Gauthama Raman, N. Somu, K. Kirthivasan, R. Liscano and V. S. Shankar Sriram. (2017). “An efficient intrusion detection system based on hypergraph—Genetic algorithm for parameter optimization and feature selection in support vector machine,” Knowledge-Based Systems, vol. 134, pp. 1–12. [Google Scholar]
15. M. Farhan and M. G. (2019). “Efficient botnet detection using feature ranking and hyperparameter tuning,” International Journal of Computer Applications, vol. 182, no. 48, pp. 55–60. [Google Scholar]
16. W. Hu, Y. Liao and V. R. Vemuri. (2003). “Robust support vector machines for anomaly detection in computer security,” in Proc. Int. Conf. on Machine Learning and Applications, pp. 168–174. [Google Scholar]
17. S. Budilaksono, A. Riyadi, A. Lukman, D. Dedi, M. Saputra et al. (2020). , “Comparison of data mining algorithm: PSO-KNN, PSO-RF, and PSO-DT to measure attack detection accuracy levels on intrusion detection system,” Journal of Physics Conference Series, vol. 1471, no. 1, pp. 10–12. [Google Scholar]
18. O. Almomani. (2020). “ A feature selection model for network intrusion detection system based on PSO, GWO, FFA and GA algorithms,” Symmetry, vol. 12, no. 6, pp. 10–46. [Google Scholar]
19. R. Eberhart and J. Kennedy. (1995). “A new optimizer using particle swarm theory,” in Proc. of the Sixth Int. Sym. on Micro Machine and Human Science, Nagoya, Japan, pp. 39–43. [Google Scholar]
20. A. Ratnaweera, S. K. Halgamuge and H. C. Watson. (2004). “Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients,” IEEE Transactions on Evolutionary Computation, vol. 8, no. 3, pp. 240–255. [Google Scholar]
21. T. Cover and P. Hart. (1967). “Nearest neighbor pattern classification,” IEEE Transactions on Information Theory, vol. 13, no. 1, pp. 21–27. [Google Scholar]
22. R. Wazirali. (2020). “An improved intrusion detection system based on KNN hyperparameter tuning and cross-validation,” Arabian Journal of Science and Engineering, vol. 45, no. 4, pp. 10859–10873. [Google Scholar]
23. E. G. Dada. (2017). “A Hybridized svm-knn-pdapso approach to intrusion detection system,” Faculty Seminar Series: University of Maiduguri, vol. 8, pp. 14–21. [Google Scholar]
24. H. Shapoorifard and P. Shamsinejad. (2017). “Intrusion detection using a novel hybrid method incorporating an improved KNN,” International Journal of Computer Applications, vol. 173, no. 1, pp. 5–9. [Google Scholar]
25. A. R. Syarif and W. Gata. (2017). “Intrusion detection system using hybrid binary PSO and K-nearest neighborhood algorithm,” in 2017 11th Int. Conf. on Information & Communication Technology and System, Surabaya, Indonesia, pp. 181–186. [Google Scholar]
26. A. A. Aburomman and M. B. Ibne Reaz. (2016). “A novel SVM-KNN-PSO ensemble method for intrusion detection system,” Applied Soft Computing, vol. 38, pp. 360–372. [Google Scholar]
27. A. A. Diro and N. Chilamkurti. (2018). “Distributed attack detection scheme using deep learning approach for internet of things,” Future Generation Computer System, vol. 82, pp. 761–768. [Google Scholar]
28. C. Reggiani, Y. A. L. Borgne and G. Bontempi. (2017). “Feature selection in high-dimensional dataset using MapReduce,” in Artificial Intelligence. BNAIC 2017. Communications in Computer and Information Science, Springer, Cham, vol. 823, pp. 101–115. [Google Scholar]
29. A. M. Sharifi, S. A. Kasmani and A. Pourebrahimi. (2015). “Intrusion detection based on joint of k-means and KNN,” Journal of Convergence Information Technology, vol. 10, no. 5, pp. 42–51. [Google Scholar]
30. T. Khorram and N. Baykan. (2018). “Feature selection in network intrusion detection using metaheuristic algorithms,” International Journal of Advanced Research, Ideas and Innovations in Technology, vol. 4, no. 4, pp. 704–710. [Google Scholar]
31. H. L. Chen, B. Yang, G. Wang, J. Liu, X. Xu et al. (2011). , “A novel bankruptcy prediction model based on an adaptive fuzzy k-nearest neighbor method,” Knowladge-Based System, vol. 24, no. 8, pp. 1348–1359. [Google Scholar]
32. M. Tavallaee, E. Bagheri, W. Lu and A. A. Ghorbani. (2009). “A detailed analysis of the KDD CUP 99 data set,” in 2009 IEEE Sym. on Computational Intelligence for Security and Defense Applications, Ottawa, ON, Canada, pp. 1–6. [Google Scholar]
33. I. Sharafaldin, A. Habibi Lashkari and A. A. Ghorbani. (2008). “Toward generating a new intrusion detection dataset and intrusion traffic characterization,” in Proc. of the 4th Int. Conf. on Information Systems Security and Privacy, Funchal, Madeira, Portugal, pp. 108–116. [Google Scholar]
34. M. Zhang, J. Guo, B. Xu and J. Gong. (2015). “Detecting network intrusion using probabilistic neural network,” in 2015 11th Int. Conf. on Natural Computation, Zhangjiajie, China, pp. 1151–1158. [Google Scholar]
35. K. Peng, V. Leung, L. Zheng, S. Wang, C. Huang et al. (2018). , “Intrusion detection system based on decision tree over big data in fog environment,” Wireless Communications and Mobile Computing, vol. 2018, pp. 1–10. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |