DOI:10.32604/cmc.2021.014699
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014699 | |
| Article |
Optimal Reordering Trace Files for Improving Software Testing Suitcase
1School of Measurement and Communication, Harbin University of Science & Technology, Harbin, China
2Computer Science Department, College of Computer and Information Sciences,AlImam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
3Department of Computer Science, Faculty of Applied Science, Taiz University, Taiz, Yemen
4School of Mathematics, Thapar Institute of Engineering and Technology, Deemed University, Patiala, 147004, India
5Institute of Research and Development, Duy Tan University, Da Nang, 550000, Vietnam
6Faculty of Information Technology, Duy Tan University, Da Nang, 550000, Vietnam
7Department of Computer Science, Nourabad Mamasani Branch, Islamic Azad University, Mamasani, Iran
8Fractional Calculus, Optimization and Algebra Research Group, Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
9Fakulti Teknologi dan Sains Maklumat, Universiti Kebangsan Malaysia, UKM Bangi, Selangor, 43600, Malaysia
*Corresponding Author: Hamid Parvin. Email: parvin@iust.ac.ir
Received: 10 October 2020; Accepted: 16 November 2020
Abstract: An invariant can be described as an essential relationship between program variables. The invariants are very useful in software checking and verification. The tools that are used to detect invariants are invariant detectors. There are two types of invariant detectors: dynamic invariant detectors and static invariant detectors. Daikon software is an available computer program that implements a special case of a dynamic invariant detection algorithm. Daikon proposes a dynamic invariant detection algorithm based on several runs of the tested program; then, it gathers the values of its variables, and finally, it detects relationships between the variables based on a simple statistical analysis. This method has some drawbacks. One of its biggest drawbacks is its overwhelming time order. It is observed that the runtime for the Daikon invariant detection tool is dependent on the ordering of traces in the trace file. A mechanism is proposed in order to reduce differences in adjacent trace files. It is done by applying some special techniques of mutation/crossover in genetic algorithm (GA). An experiment is run to assess the benefits of this approach. Experimental findings reveal that the runtime of the proposed dynamic invariant detection algorithm is superior to the main approach with respect to these improvements.
Keywords: Dynamic invariant detection; software testing; genetic algorithm
Program invariants are rules or equations among program variables staying constant and unaffected for the successive program runs with various input parameters. Invariants could have been used to develop real and reliable programs. For example, in a search program to find an element in an array of integer values, the array elements must be unchanged, and counter of the array that is to move through array elements must be at most equal to the length of the array after the function returns. Invariants have a significant impact on software engineering, especially automatic software engineering [1]. They help programmers to develop better programs, to document the program operations, to generate the test-cases automatically, to validate their programs, and etc. They are also effective in software testing which allows a programmer to assess if their program behavior is valid or not [2–4]. For example, if a programmer knows that the variable values are not always constant with regards to invariants, he/she can infer that his/her code could have some bugs.
Invariants are often useful relative to two different programs (even with different algorithms) and can even allow programmers to test and verify their programs. For example, when an individual writes a program to organize a set of data, he/she will decide whether his/her program is accurate or it has bugs by comparison of his/her program invariants with those of an actual and consistent form of the program; for example, consider a merge ordering code. The assumption, here, is that “the invariants of the evaluated program will be exactly the same with those of the absolute reliable sort program (e.g., merge sort program).” In addition, the mentioned invariants are particularly effective in documenting and introducing a program attribute when a program does not contain documentation and explanation. In this context, if a new code-writer needs to understand the attributes of the program for modification or extension, the invariants may be very effective in achieving this objective, especially when the program is large and has big and unstructured codes.
Ruthruff et al. [5] offer expressive and practical descriptions for the experimental program analysis with an explanation of the use of invariants. This further discusses how experimental program analysis contributes to three problems in software engineering: the transformation of programs, their testing, and their programs.
As invariants can be used to help programmers improve maintainability, readability, verification, documentation, and many other aspects of their programs, therefore, the software engineering researchers recently have interested in this field. Also, programmers are encouraged to extract programs’ invariants and then test their programs regarding the detected invariants.
There are two general methods to detect invariants: (1) Static invariant detection approach and (2) Dynamic invariant detection approach. Each approach has its weaknesses and strengths. The output of dynamic methods often is not reliable; therefore, we say that methods of dynamic invariant detection approach are unreliable. Static methods are also too difficult to be developed. Both of them are also considered to be time-consuming approaches.
Artificial intelligence is important and useful in many applications [6–15]. It can be applied in many actual issues [16–25]. While some of its applications are theoretic [26–35], but in many of its applications, the traditional artificial intelligence techniques can be used. The optimization techniques as a sub-field in artificial intelligence have many applications in real world problems [36,37]. The paper tackles the problem of invariant generation from traces using artificial intelligence. The contribution aims at improving the runtime of Daikon, a well-known method/tool to generate the program invariants. The key insight in this paper is to reorder the trace files so that the amount of computation required to check whether candidate invariants are satisfied is reduced. This is done by considering a form of lazy computation based on the fact that if none of the variables in a constraint changed its value compared to the preceding row, there is no need to re-compute the constraint. Machine learning techniques are used for reordering.
The present article first discusses related work in Section 2. Then, the problem and its motivation are briefly defined. We then describe the dynamic invariant detection approach in Section 3. Later on Section 3, we also address the drawbacks of dynamic approaches. Section 4 will elaborate on two ideas on optimizing Daikon runtime and improving its speed. Section 5 provides a comparison between the results of the latest innovations with the previous version of Daikon, according to a couple of C language programs. Section 6 experimentally shows that the proposed ideas are useful in real code, and the proposed ideas can decrease the runtime of the dynamic invariant detection approach. Ultimately, the conclusion and future work will be discussed in Section 7.
It seems to be two general methods for detecting invariants, as mentioned: static and dynamic. In the static methods, the analysis of program source codes through the use of compiler techniques is taken into account (e.g., extraction of data flow graphs in the program source code). In contrast, dynamic methods gather information from program implementation; profiling and testing are instances. This implies that dynamic methods utilize real values determined during the implementation of programs and define statistical relationships between variables dependent on their values [38]. In Section 3, dynamic approaches are described in depth.
Several methods, including ESC and Key for java and LClint for C, are available to extract invariant in a static way [38,39]. The greatest obstacle in static invariant detection is challenges a programmer can encounter. Codes monitoring and rules detection between variables according to values may be a difficult task, particularly in the case that the programmer needs to include some complicated cases such as pointers, polymorphisms, etc.
Some of the greatest disadvantages in dynamic methods are as follows: (1) They are unreliable and (2) They are costly, and above all, (3) They do not provide extremely accurate responses. Daikon which implements an algorithm considered to be one of the dynamic invariant detection approaches is the most suitable software until now [40] comparing to other dynamic invariant detection tools like [41–44].
As another advantage of Daikon, we can mention that it is open-source software, and everybody can modify and improve it. Nevertheless, this tool has several disadvantages. Several investigations to improve Daikon efficiency have been performed. Many modifications of Daikon have been presented up until now. The newest Daikon version, for example, contained a number of different approaches for equivalent variables, constant dynamic variables, elimination of weaker invariants, and variable hierarchy [40,45].
In order to create an approximate temporal model of actions, Silvaa et al. [46] discuss the issue of combining several traces of a similar program. In addition, Java proof-of-concept implementations of the trace merging algorithms are given through the NuSMV Tool.
Mili et al. [47] apply a relational refinement calculus to reach this complicated issue systematically. It provides a means, under some circumstances, to automatically extract the function of loops or their approximation. Similar to Daikon, they achieve acceptable outcomes.
Costa et al. [48] propose a runtime verification approach on the basis of design-by-contract to enhance Java Card applications’ safety. For this purpose, they suggested JCML, a specification extracted from Java modeling language.
In this paper, the author proposes two techniques to improve the runtime efficiency of the extraction of program invariants (preconditions, postconditions, and loop invariants) during dynamic invariant detection (i.e., recording values of variables during program executions at the selected observation points and the discovery of statistical relations between the variables). The first technique is the reduction of the quantity of program variables that should be evaluated. The second technique is the sorting of the recorded data traces based on the number of variables in which values in the various runs have not been modified.
2.1 Brief Problem Definition and Motivations
Program invariants are equations or rules between program variables that stay unchanged and constant with regard to successive program runs with various input parameters. Invariants could be applied to create real and accurate programs. Invariants are detected in two general ways: static and dynamic. The main challenge in static detection is the challenges a programmer will encounter. Dynamic approaches, on the other hand, obtain information from program executions. In dynamic approaches, two of its biggest drawbacks are that they are unreliable and time-consuming. Daikon, which implements a dynamic invariant detection algorithm, is the most suitable software until now.
In this paper, our contribution is to offer two ideas to improve the runtime of the extraction of invariants based on a dynamic invariant approach. To reduce its runtime, initially, the effective factors must be calculated on the runtime in dynamic methods. Then, it will be tried to decrease the runtime of the algorithm based on these factors. Based on previous researches, the main factor involved in its runtime order is the number of the variables that are in the scope of the tested program. Therefore, one idea is to reduce the number of variables that must be checked.
3 Dynamic Invariants Detection Algorithm
As seen in Fig. 1, Daikon implements the program with multiple input parameters and derives the values of variables at particular program points, such as procedural inputs and outputs. It is worthy to note that these specific program points are abbreviated by program points. Then, it saves the values of variables in a data-trace file that its extension is dtrace. Daikon has a database of possible invariants and tests each combination of one, two, and three variables. An invariant is reported if and only if it has a confidence value bigger than a user-defined value.
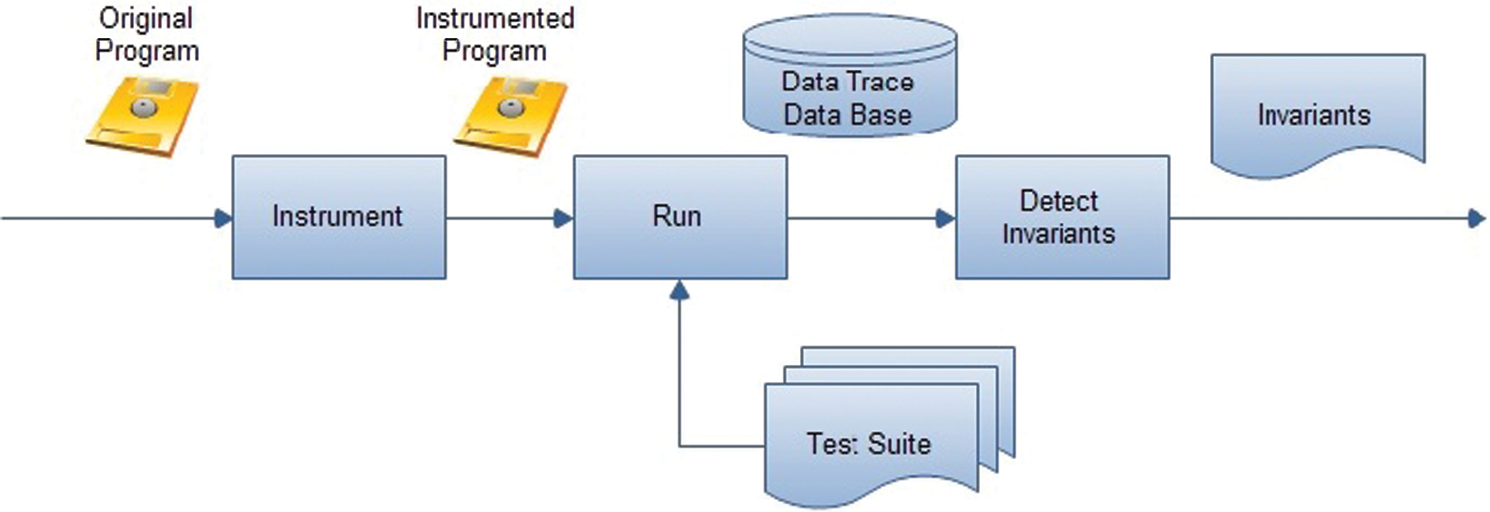
Figure 1: Dynamic invariant detection algorithm implemented by Daikon
Unary invariants are invariants that are identified in a single variable. For example, X > a provides a variable named X that is considerably higher compared to a constant value referred to as a. For another instance,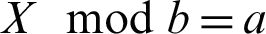 
indicates the variable X residual divided by constant b is a constant value referred to as a. The invariants X > Y and X = Y + c represent a couple of binary invariant instances, and the invariant Y = aX + bZ is a ternary invariant taken into account by Daikon that the notations a and b indicates a couple of constant values and the notations X, Y and Z implies three variables [49].
Daikon also extracts the latent or derived variables and treats them just like other variables. Daikon finds three types of invariants in every program point. The program points include precondition, postcondition, and loop invariants. The precondition invariants are rules between variables before entering to program point. The postcondition invariants are rules between variables after exiting of program point, and loop invariants refer to rules between variables through every iteration loop in the program point.
As previously demonstrated, Daikon implements the dynamic invariant approach. First of all, the Daikon instruments program; it means a series of codes must be inserted into the original code at the all of the program points to save the values of variables. Daikon has an option to use one of two special tools to obtain this objective: Chicory or Kvasir.
They are two different sub-tools in Daikon. Both are open-source and have been developed with Java. Kvasir could be implemented only in Linux and generates an “Enter Procedure” and an “Exit Procedure” for every procedure in the source code. It writes the values of variables on “Enter Procedure” when program the program control enters into the procedure (precondition). It also writes the values of variables on “Exit Procedure” when the program control exits the procedure (postcondition) according to [49]. Daikon utilizes the resultant outputs of the instrumental tools to detect invariants by recording results in a file. Fig. 2 shows a sample source code. The corresponding output of Kvasir to Fig. 2 was presented in Fig. 3.
Figure 2: A sample source code in C language
Figure 3: Kvasir’s corresponding output to the code depicted by Fig. 1
As the user can see from Figs. 2 and 3, the Enter and Exit sections were specified for 
and main functions in the source code product. As stated earlier, the values of the variables are obtained.
The algorithms that are to detect the dynamic invariants have several drawbacks. One of their major challenges is their long run duration. Daikon runtime is on the basis of the number of variables inside the assessed domain, the size of programs, the number of running programs, and the number of templates for which the variables are evaluated is stated by Eq. (1). This is the time required to demonstrate whether invariants are falsified or verified.
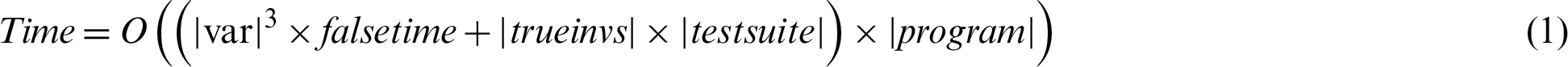
Invariants involve a maximum of three variables; thus, a cubic number of possible invariants is available. Only the invariants including one, two and three variables were found by Daikon. In the next section, two ideas will be proposed that, if applied, would substantially reduce the runtime needed for dynamic invariant detection [49].
4 New Ideas for Improving Invariant Detection
As you can find out in previous sections, the runtime of the algorithm is linear in terms of the number of the variables that are to be checked for invariant detection. The present article attempts to offer two new ideas to reduce the runtime of the algorithm by decreasing the number of the variables that are to be checked for invariant detection. We expect that the following improvements to the Daikon source code would boost its performance considerably. Note that although the Daikon source code has been changed, the output invariants were also precisely the same as they were. Then, every idea will be evaluated to show its effect. Section 4.1 shows the properties of the variables which do not need to be tested. In addition, the second concept follows the first. The second idea is to sort data-trace files so that the algorithm time order could be decreased. This is evaluated in Section 4.2.
In this section, it is tried to introduce a property that if a variable has it, it does not need to be checked. While runtime will effectively be reduced by eliminating these variables, these variables have not any effect on final invariants. Consider that the Daikon algorithm runs multiple input-parameter programs and then derives and tracks the variable values. There are many extracted variables and function parameters and other variables that, in subsequent runs, do not alter values, but Daikon tests them in subsequent runs. Furthermore, it is not crucial to measure unmodified variables values during subsequent runs.
For example, assume that there are three variables called X, Y and Z with respectively 3, 4 and 5 values. Also, presume that several of the invariants that are actually to be tested are X < Y, Y < Z, X = 3, Y = 4, etc. Assume that the values of such variables alter into respectively 3, 4 and 2 in the following program run. It should be noted that no invariants identified in variables X and Y have to be checked since the values for these variables have not changed from the latest run. This implies that the reliabilities of the invariants already described by these unaffected variables remain unchanged. Invariants such as Y = 4, X < Y and X = 3 are remained true (as the previous run), but invariants including the variable Z have to be re-checked, as their values might be changed. The invariant Y < Z is not accurate in this instance; therefore, this vector needs to be filtered.
Section 5 will discuss the results of this idea. Findings demonstrate that these modifications significantly reduced the runtime. With regards to findings, as predicted, the runtime is in the best possible state in the case that there are a few number of variations in the values of variables in sequential runs; and in the worst case where there is no similarity in the values of variables in consequential program runs. This is why data-trace files have to be classified first of all depending on minor variations in the values of variables, in the second idea addressed in depth in Section 4.2.
Within this subsection, a method of sorting data-trace files is attempted to be found according to minimal variations in the quantity of the variables, the values of which are altered consecutively. (a) It is costly and very time-consuming to sort data-trace files using the deterministic techniques because of factorial order. (b) Finding the best ordering of the data-trace files to minimize modifications in values of variables of consecutive runs is an NP problem. (c) On the other hand, it is not necessary to achieve the best combination of data-trace files; it means a combination that is close enough to the best is admissible. Therefore, it is concluded from (a), (b) and (c) that the use of a non-deterministic heuristic approach, such as a genetic algorithm, is an excellent choice [50]. Details of the used genetic algorithm are offered in the next section.
4.2.1 Chromosome Representation
The chromosome representation model is the first section to be discussed in designing a genetic algorithm. Chromosomes are employed in this problem, and their length is equal to the quantity of data-trace files and their gens occupied by a unique integer number from one and the quantity of data-trace files; therefore, the value of each gen differs from others implying that each chromosome is a permutation from one to the quantity of data-trace files. As an example, in six test cases in Tab. 1, check the variables’ values extracted through Kvasir during the first program. If we want Daikon to take into consideration these data-trace files in order [1 2 3 4 5 6], the corresponding chromosome is presented by Fig. 4a as it is in Tab. 1, whereas if we want Daikon to take into consideration these data-trace files in order [5 6 1 2 3 4], the corresponding chromosome is presented by Fig. 4b as it is in Tab. 2.
Table 1: The variables’ values resulted from Kvasir over the initial program
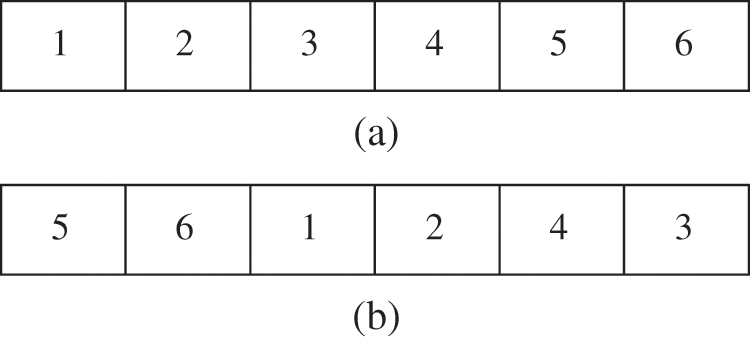
Figure 4: (a) Chromosome corresponding with Tab. 1 data-trace file; (b) Chromosome corresponding with Tab. 2 data-trace file
Table 2: The variables’ values in Tab. 1 in a non-effective reordering
Cross over operator is the next part that will be debated in designing a genetic algorithm. The cycle cross over approach is selected in this paper. Cycle crossover creates a child in which each gene has a correspondent from one parent cycle. See Fig. 5, for instance, that depicts two parents and the resulting children following the cyclic crossover [51].
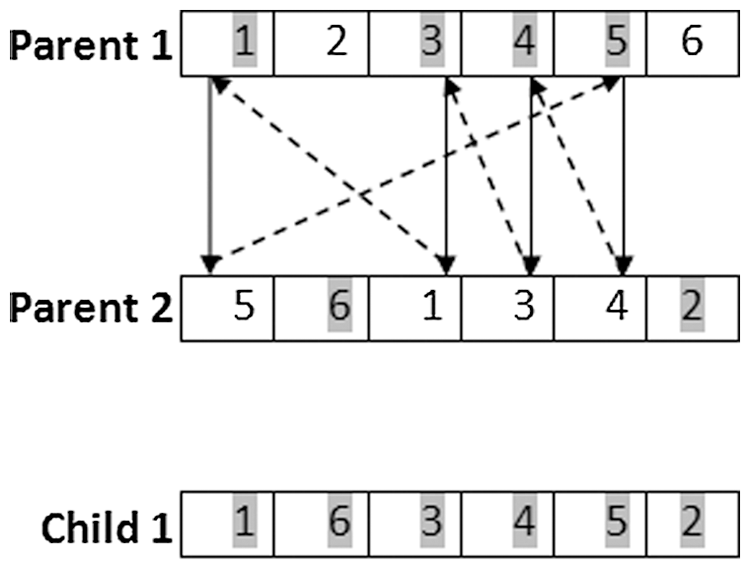
Figure 5: Cyclic crossover of two parents and their children
The possibility of mutation is adjusted to be an actual positive value of approximately 0; 0.001 is chosen here. It is also used for every chromosome. This operator exchanges the values of two random gens.
Truncation selection is considered to be our genetic algorithm selection operator. Chromosomes such as children and their parents are, first of all, classified based on their fitness function values in this selection. Then, the greatest of all are chosen as a new genetic algorithm population.
The data track files are sorted on the basis of lowest discrepancies in the quantity of variables, the values of which change in successive runs. The fitness function is described as discrepancies in the quantity of variables, the values of which are altered. As it can be seen in Tab. 1, the variables are altered only at eight points. There are four differences in 3.dtrace and four variations on the running of 4.dtrace; however, Tab. 2 indicates a total of twelve discrepancies in 1.dtrace, 3.dtrace, and 4.dtrace runs. Therefore, the initial combination of trace data files is stronger compared to the next combination. Tabs. 1 and 2 have fitness values of eight and twelve, respectively.
Two C-language programs are applied to conduct the experimentations. In the first program, Kvasir is run, the source of which is shown for six times in Fig. 2, and the values of variables are indicated in Tab. 1.
The Daikon’s source code is then changed to avoid checking unmodified variables in the resulting data-trace files. The term “Trace” is often changed such that the data is written, while each variable is tested. On the basis of evidence, the term “Trace” appears sixteen times in the case that the unrevised version of Daikon is implemented on the data in Tab. 1. Each occurrence of “Trace” on the output indicates that Daikon has tested all templates for invariants. Nevertheless, when the revised Daikon variant is implemented with the above-noted improvement (to prevent checking unmodified variables), the term “Trace” only appears eight times. It means that the occurrences of the word “Trace” is reduced to half; thus, it demonstrates that runtime decreases appropriately. Even so, the term “Trace” appears 12 times while the program is running in the following setup. The explanation is that this arrangement possesses more differences in the values of variables.
As shown in Tab. 1, the variables are changed only at eight points. In Tab. 2, the variables are changed at twelve points. As reported earlier, when the greatest or the almost superior combination of data-trace files is chosen according to the minimal differences in the values of variables, the performance will be improved significantly as long as the first change over Daikon is regarded.
For a further illustration, the source code seen in Fig. 6 is checked and is identical to the source code in Fig. 2; however, it employed pointers.
Figure 6: The sample source code of Fig. 2 using the pointers
The subsequent calculations are based on six Kvasir runs for variables in Tab. 3.
Table 3: The variables’ values resulted from Kvasir over the second program
After the original Daikon has been implemented for the variables’ values addressed in Tab. 3, the term “Trace” has been written 35 times, and when the revised version of the Daikon (prevented to check unmodified variables) is run over them, it is appeared 35 times, because in the previous run all the variables are given different values than the corresponding ones. If the revised Daikon is implemented on the corresponding combination of data-trace files resulted from genetic algorithms, for example, Tab. 4, after which the term “Trace” occurs 23 times, although, in the main Daikon, the term “Trace” occurs 35 times as in previous case.
Table 4: The variables’ values in Tab. 3 reordered by GA in an effective manner
For experimental justification, the algorithm is run on three versions of a function with 5, 10, and 20 variables. The used function for experimentations is merge sort.
Run-time of original Daikon in terms of millisecond is depicted in Fig. 7. The results are averaged over 30 distinct runnings of the algorithms. The horizontal axis shows the length of the test suit or data-trace files. Run-time of the proposed algorithm (including 
) is depicted in Fig. 8.
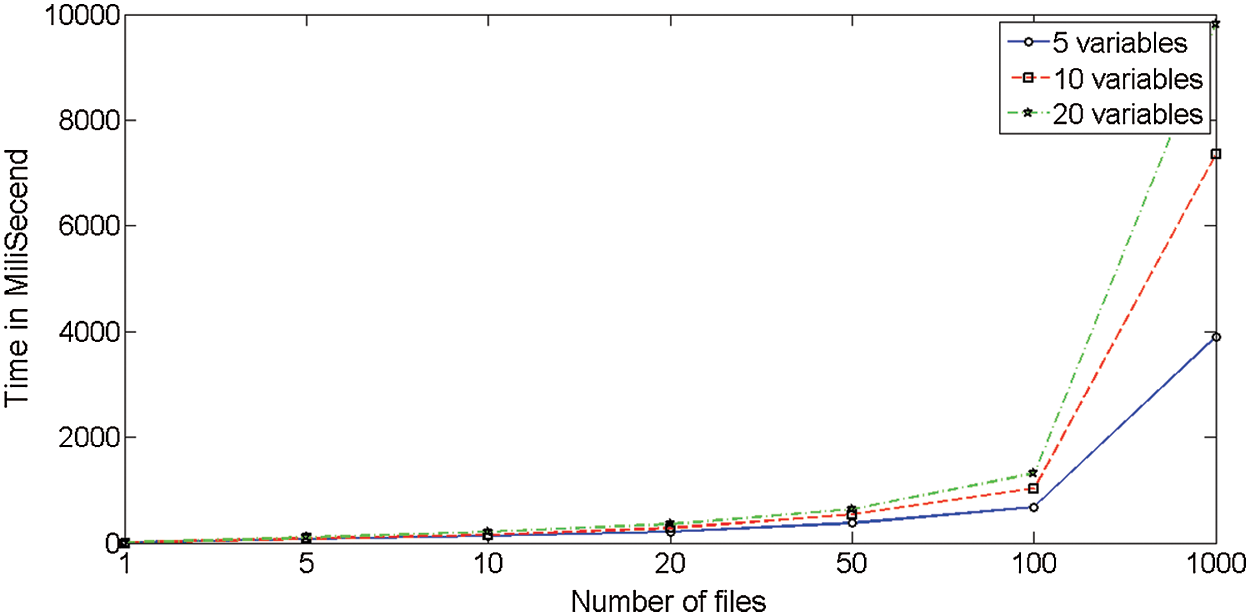
Figure 7: Run-time of original Daikon in terms of millisecond
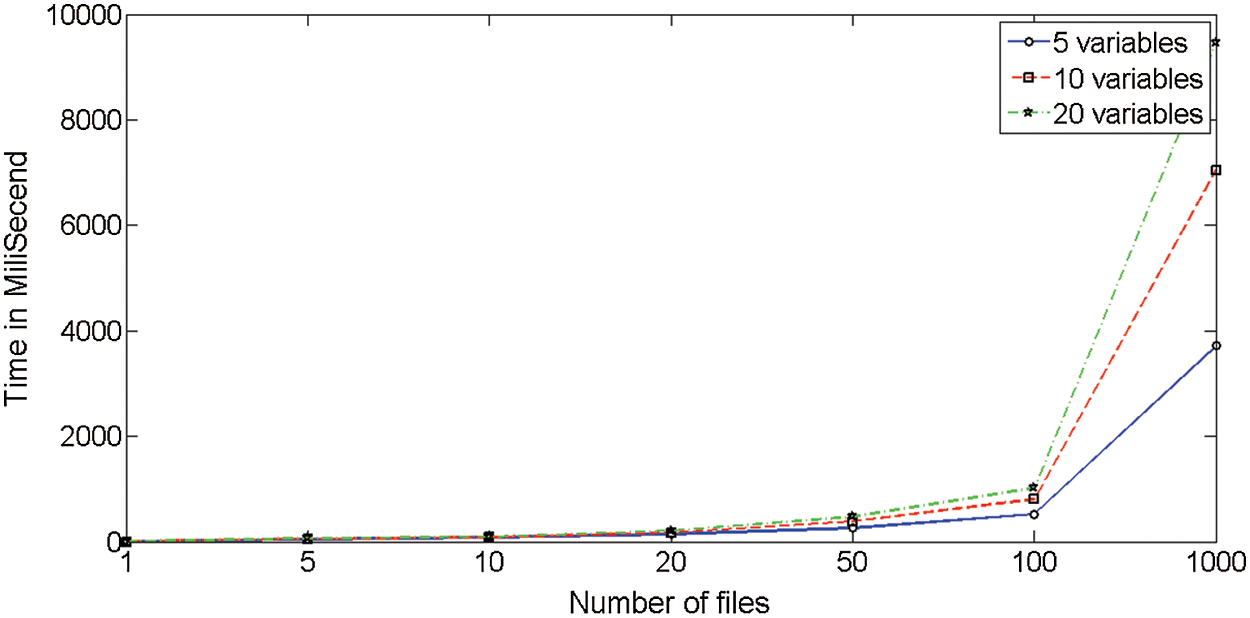
Figure 8: Run-time of proposed algorithm (including 
) in terms of millisecond
Runtime improvements of the proposed algorithm (including 
) in comparison with the simple Daikon is shown in Fig. 9. The improvements are averaged over 30 distinct runnings of the algorithms. As you can infer from Fig. 8, you can conclude that “the bigger data-trace files or the number of input variables, the more reason to use the proposed algorithm.”
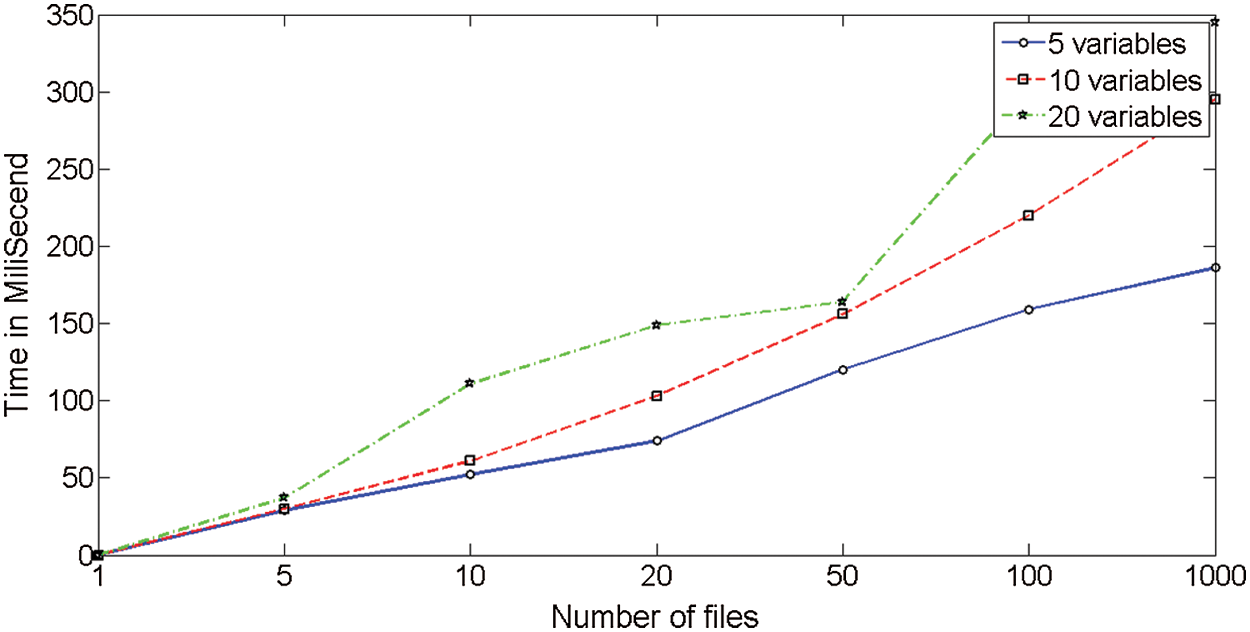
Figure 9: Improvement of the proposed algorithm in terms of running time
It is also worthy of mentioning that Fig. 8 depicts the runtime improvements of the modified Daikon over the original Daikon: It means the runtime of the original Daikon has subtracted the runtime of the modified Daikon in each case. It is also worthy of mentioning that the runtime improvements of the modified Daikon over the original Daikon are not regular. This can be due to system scheduling.
7 Conclusion and Further Works
The greatest challenge in detection of a program invariants is the huge cost needed to prepare a detector software. Therefore, dynamic invariant detection methods have emerged instead of dynamic invariant detection ones. But, the runtime of dynamic invariant detection methods is also the most important and considerable issue. Since invariants play a significant role in software testing, the reduction of its runtime would certainly contribute to the field of software engineering. An open-source computer software, i.e., Daikon, is used as our dynamic invariant detection algorithm. Daikon proposes a dynamic invariant detection algorithm based on several runs of the tested program; then, it gathers the values of its variables, and finally, it detects relationships between the variables based on a simple statistical analysis. It is observed that the runtime for the Daikon invariant detection tool is dependent on the ordering of traces in the trace file. A genetic algorithm is proposed to reorder traces in the trace file in order to reduce differences in adjacent trace files. It is concluded when the data-trace files or the number of input variables are bigger, it is more efficient to use the proposed algorithm. As in real-world software codes, the variables may be potentially very frequent, the improvement achieved by this paper will be more important.
Acknowledgement: This paper has been initially submitted on “August 5” by Hamid Parvin. As the paper has new author in revision, the EiC proposed authors to decline the paper at “October 6” and resubmit it. On “October 10,” they resubmitted it and it was finally accepted at “16 November.”
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. M. Kalpana, K. Tamizarasu and A. E. Jeyakumar. (2014). “A fuzzy logic based framework for assessing the maturity level of Indian small scale software organizations,” Computer Systems Science & Engineering, vol. 29, no. 2, pp. 153–167.
2. I. Beschastnikh, Y. Brun, M. D. Ernst, A. Krishnamurthy and T. E. Anderson. (2012). “Mining temporal invariants from partially ordered logs,” Operating Systems Review, vol. 45, no. 3, pp. 39–46.
3. J. W. Nimmer and M. D. Ernst. (2002). “Automatic generation of program specifications,” in Proc. of Int. Sym. on Software Testing and Analysis, Rome, Italy, pp. 232–242.
4. Y. Kataoka, M. D. Ernst, W. G. Griswold and D. Notkin. (2001). “Automated support for program refactoring using invariants,” in Proc. of Int. Conf. on Software Maintenance, pp. 736–743.
5. J. R. Ruthruff, S. Elbaum and G. Rothermel. (2010). “Experimental program analysis,” Information and Software Technology, vol. 52, no. 4, pp. 359–379.
6. H. Niu, N. Khozouie, H. Parvin, H. Alinejad-Rokny, A. Beheshti et al. (2020). , “An ensemble of locally reliable cluster solutions,” Applied Sciences, vol. 10, no. 5, pp. 1891.
7. M. R. Mahmoudi, M. Mahmoudi and A. Pak. (2019). “On comparing, classifying and clustering several dependent regression models,” Journal of Statistical Computation and Simulation, vol. 89, no. 12, pp. 2280–2292.
8. A. R. Abbasi, M. R. Mahmoudi and Z. Avazzadeh. (2018). “Diagnosis and clustering of power transformer winding fault types by cross-correlation and clustering analysis of FRA results,” IET Generation, Transmission & Distribution, vol. 12, no. 19, pp. 4301–4309.
9. S. B. Rodzman, S. Hasbullah, N. K. Ismail, N. A. Rahman, Z. M. Nor et al. (2020). , “Fabricated and Shia Malay translated hadith as negative fuzzy logic ranking indicator on Malay information retrieval,” ASM Science Journal, vol. 13, no. 3, pp. 100–108.
10. M. M. Abdulnabi, R. Hassan, R. Hassan, N. E. Othman and A. Yaacob. (2018). “A fuzzy-based buffer split algorithm for buffer attack detection in internet of things,” Journal of Theoretical and Applied Information Technology, vol. 96, no. 17, pp. 5625–5634.
11. M. A. A. M. Zainuri, E. A. Azari, A. A. Ibrahim, A. Ayob, Y. Yusof et al. (2019). , “Analysis of adaptive perturb and observe-fuzzy logic control maximum power point tracking for photovoltaic boost DC–DC converter,” International Journal of Advanced Trends in Computer Science and Engineering, vol. 8, no. 1.6, pp. 201–210.
12. Z. M. Rodzi and A. G. Ahmad. (2020). “Fuzzy parameterized dual hesitant fuzzy soft sets and its application in TOPSIS,” Mathematics and Statistics, vol. 8, no. 1, pp. 32–41.
13. A. M. S. Bahrin and J. M. Ali. (2020). “Hybrid fuzzy-disturbance observer for estimating disturbance in styrene polymerization process,” IOP Conference Series Materials Science and Engineering, vol. 778, no. 1, pp. 12089.
14. E. Dodangeh, B. Choubin, A. N. Eigdir, N. Nabipour, M. Panahi et al. (2020). , “Integrated machine learning methods with resampling algorithms for flood susceptibility prediction,” Science of the Total Environment, vol. 705, 135983.
15. B. Choubin, M. Abdolshahnejad, E. Moradi, X. Querol, A. Mosavi et al. (2020). , “Spatial hazard assessment of the PM10 using machine learning models in Barcelona, Spain,” Science of the Total Environment, vol. 701, 134474. [Google Scholar]
16. B. Choubin, A. Mosavi, E. H. Alamdarloo, F. S. Hosseini, S. Shamshirband et al. (2019). , “Earth fissure hazard prediction using machine learning models,” Environmental Research, vol. 179, 108770. [Google Scholar]
17. S. Qummar, F. G. Khan, S. Shah, A. Khan, S. Shamshirband et al. (2019). , “A deep learning ensemble approach for diabetic retinopathy detection,” IEEE Access, vol. 7, pp. 150530–150539. [Google Scholar]
18. B. Choubin, M. Borji, A. Mosavi, F. Sajedi-Hosseini, V. P. Singh et al. (2019). , “Snow avalanche hazard prediction using machine learning methods,” Journal of Hydrology, vol. 577, 123929. [Google Scholar]
19. S. Shamshirband, E. J. Nodoushan, J. E. Adolf, A. A. Manaf, A. Mosavi et al. (2019). , “Ensemble models with uncertainty analysis for multi-day ahead forecasting of chlorophyll a concentration in coastal waters,” Engineering Applications of Computational Fluid Mechanics, vol. 13, no. 1, pp. 91–101. [Google Scholar]
20. S. M. J. Jalali, S. Ahmadian, A. Khosravi, S. Mirjalili, M. R. Mahmoudi et al. (2020). , “Neuroevolution-based autonomous robot navigation: A comparative study,” Cognitive Systems Research, vol. 62, pp. 35–43. [Google Scholar]
21. M. Maleki, D. Wraith, M. R. Mahmoudi and J. E. Contreras-Reyes. (2020). “Asymmetric heavy-tailed vector auto-regressive processes with application to financial data,” Journal of Statistical Computation and Simulation, vol. 90, no. 2, pp. 324–340. [Google Scholar]
22. A. R. Soltani, A. R. Nematollahi and M. R. Mahmoudi. (2019). “On the asymptotic distribution of the periodograms for the discrete time harmonizable simple processes,” Statistical Inference for Stochastic Processes, vol. 22, no. 2, pp. 307–322. [Google Scholar]
23. M. H. Heydari, Z. Avazzadeh and M. R. Mahmoudi. (2019). “Chebyshev cardinal wavelets for nonlinear stochastic differential equations driven with variable-order fractional Brownian motion,” Chaos Solitons & Fractals, vol. 124, pp. 105–124. [Google Scholar]
24. M. Maleki, J. E. Contreras-Reyes and M. R. Mahmoudi. (2019). “Robust mixture modeling based on two-piece scale mixtures of normal family,” Axioms, vol. 8, no. 2, pp. 38. [Google Scholar]
25. A. R. Zarei, A. Shabani and M. R. Mahmoudi. (2019). “Comparison of the climate indices based on the relationship between yield loss of rain-fed winter wheat and changes of climate indices using GEE model,” Science of the Total Environment, vol. 661, pp. 711–722. [Google Scholar]
26. M. R. Mahmoudi, M. H. Heydari and Z. Avazzadeh. (2018). “On the asymptotic distribution for the periodograms of almost periodically correlated (cyclostationary) processes,” Digital Signal Processing, vol. 81, pp. 186–197. [Google Scholar]
27. M. Maleki and M. R. Mahmoudi. (2017). “Two-piece location-scale distributions based on scale mixtures of normal family,” Communications in Statistics-Theory and Methods, vol. 46, no. 24, pp. 12356–12369. [Google Scholar]
28. A. R. Nematollahi, A. R. Soltani and M. R. Mahmoudi. (2017). “Periodically correlated modeling by means of the periodograms asymptotic distributions,” Statistical Papers, vol. 58, no. 4, pp. 1267–1278. [Google Scholar]
29. M. Maleki, R. B. Arellano-Valle, D. K. Dey, M. R. Mahmoudi and S. M. J. Jalali. (2017). “A Bayesian approach to robust skewed autoregressive processes,” Calcutta Statistical Association Bulletin, vol. 69, no. 2, pp. 165–182. [Google Scholar]
30. M. R. Mahmoudi, M. Mahmoudi and E. Nahavandi. (2016). “Testing the difference between two independent regression models,” Communications in Statistics-Theory and Methods, vol. 45, no. 21, pp. 6284–6289. [Google Scholar]
31. J. J. Pan, M. R. Mahmoudi, D. Baleanu and M. Maleki. (2019). “On comparing and classifying several independent linear and non-linear regression models with symmetric errors,” Symmetry, vol. 11, no. 6, pp. 820. [Google Scholar]
32. M. R. Mahmoudi, M. H. Heydari and R. Roohi. (2019). “A new method to compare the spectral densities of two independent periodically correlated time series,” Mathematics and Computers in Simulation, vol. 160, pp. 103–110. [Google Scholar]
33. M. R. Mahmoudi, M. H. Heydari and Z. Avazzadeh. (2019). “Testing the difference between spectral densities of two independent periodically correlated (cyclostationary) time series models,” Communications in Statistics-Theory and Methods, vol. 48, no. 9, pp. 2320–2328. [Google Scholar]
34. M. R. Mahmoudi. (2018). “On comparing two dependent linear and nonlinear regression models,” Journal of Testing and Evaluation, vol. 47, no. 1, pp. 449–458. [Google Scholar]
35. M. R. Mahmoudi, M. Maleki and A. Pak. (2018). “Testing the equality of two independent regression models,” Communications in Statistics-Theory and Methods, vol. 47, no. 12, pp. 2919–2926. [Google Scholar]
36. S. Golzari, M. N. Zardehsavar, A. Mousavi, M. R. Saybani, A. Khalili et al. (2019). , “KGSA: A gravitational search algorithm for multimodal optimization based on k-means niching technique and a novel elitism strategy,” Open Mathematics, vol. 16, no. 1, pp. 1582–1606. [Google Scholar]
37. M. H. Heydari, A. Atangana, Z. Avazzadeh and M. R. Mahmoudi. (2020). “An operational matrix method for nonlinear variable-order time fractional reaction-diffusion equation involving Mittag-Leffler kernel,” European Physical Journal Plus, vol. 135, no. 2, pp. 1–19. [Google Scholar]
38. D. Evans, J. Guttag, J. Horing, Y. M. Tan and L. CLint. (1994). “A tool for using specification to check code,” in Proc. of ACM SIGSOFT Sym., New York, NY, USA, pp. 87–96. [Google Scholar]
39. H. Schmitt and B. Weiß. (2007). “Inferring invariants by static analysis in KeY,” University of Karlsruhe. [Google Scholar]
40. M. D. Ernst, J. H. Perkins, P. J. Guo, S. McCamant, C. Pacheco et al. (2007). , “The daikon system for dynamic detection of likely invariants,” Science of Computer Programming, vol. 69, no. 1–3, pp. 35–45. [Google Scholar]
41. M. B. Dwyer and L. A. Clarke. (1994). “Data flow analysis for verifying properties of concurrent programs,” ACM Transactions on Software Engineering and Methodology, vol. 13, no. 4, pp. 359–430. [Google Scholar]
42. J. E. Cook and A. L. Wolf. (1998). “Discovering models of software processes from event-based data,” ACM Transactions on Software Engineering and Methodology, vol. 7, no. 3, pp. 215–249. [Google Scholar]
43. J. E. Cook and A. L. Wolf. (1998). “Event-based detection of concurrency,” ACM SIGSOFT Software Engineering Notes, vol. 23, no. 6, pp. 35–45. [Google Scholar]
44. R. Lencevicius, U. Hoèlzle and A. K. Singh. (1997). “Query-based debugging of object-oriented programs,” in Proc. of Object-Oriented Programming, Systems, Languages, and Applications, pp. 1–10. [Google Scholar]
45. J. H. Perkins and M. D. Ernst. (2004). “Efficient incremental algorithms for dynamic detection of likely invariants,” in Proc. of Int. Conf. on Adaptive and Natural Computing Algorithms, Ljubljana, Slovenia, pp. 381–390. [Google Scholar]
46. P. S. Silvaa and A. C. V. Meloa. (2009). “Model checking merged program traces,” Electronic Notes in Theoretical Computer Science, vol. 240, pp. 97–112. [Google Scholar]
47. A. Mili, R. B. Ayed, S. Aharon and C. Nadkarni. (2009). “Harnessing a refinement theory to compute loop functions,” Electronic Notes in Theoretical Computer Science, vol. 243, pp. 139–155. [Google Scholar]
48. U. S. Costa, A. M. Moreira and M. A. Musicante. (2009). “Specification and runtime verification of java card programs,” Electronic Notes in Theoretical Computer Science, vol. 240, pp. 61–78. [Google Scholar]
49. M. D. Ernst, W. G. Griswold, Y. Kataoka and D. Notkin. (2000). “Dynamically discovering program invariants involving collections.” Technical Report UW-CSE-99-11-02, University of Washington. [Google Scholar]
50. M. Mitchell. (1998). An Introduction to Genetic Algorithms. Cambridge: MIT Press. [Google Scholar]
51. A. Moraglio, Y. H. Kim, Y. Yoon, B. R. Moon and R. Poli. (2006). “Generalized cycle crossover for graph partitioning,” Evolutionary Computation, vol. 23, no. 6, pp. 445–474. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |