DOI:10.32604/cmc.2021.014682
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014682 | |
| Article |
Cardiac Arrhythmia Disease Classification Using LSTM Deep Learning Approach
Department of Information and Communication Engineering, Dongguk University, Seoul, 100-715, Korea
*Corresponding Author: Yangwoo Kim. Email: ywkim@dongguk.edu
Received: 08 October 2020; Accepted: 01 November 2020
Abstract: Many approaches have been tried for the classification of arrhythmia. Due to the dynamic nature of electrocardiogram (ECG) signals, it is challenging to use traditional handcrafted techniques, making a machine learning (ML) implementation attractive. Competent monitoring of cardiac arrhythmia patients can save lives. Cardiac arrhythmia prediction and classification has improved significantly during the last few years. Arrhythmias are a group of conditions in which the electrical activity of the heart is abnormal, either faster or slower than normal. It is the most frequent cause of death for both men and women every year in the world. This paper presents a deep learning (DL) technique for the classification of arrhythmias. The proposed technique makes use of the University of California, Irvine (UCI) repository, which consists of a high-dimensional cardiac arrhythmia dataset of 279 attributes. In this research, our goal was to classify cardiac arrhythmia patients into 16 classes depending on the characteristics of the electrocardiography dataset. The DL approach in the form of long short-term memory (LSTM) is an efficient technique to deal with reduced accuracy due to vanishing and exploding gradients in traditional DL frameworks for big data analysis. The goal of this research was to categorize cardiac arrhythmia patients by developing an efficient intelligent system using the LSTM DL algorithm. This approach to arrhythmia classification includes classification algorithms along with noise removal techniques. Therefore, we utilized principal components analysis (PCA) for noise removal, and LSTM for classification. This hybrid comprehensive arrhythmia classification approach performs better than previous approaches to arrhythmia classification. We attained a highest classification accuracy of 93.5% with the DL based disease classification system, and outperformed the earlier approaches used for cardiac arrhythmia classification.
Keywords: Deep learning; machine learning; LSTM; disease classification; arrhythmia
Heart disease is one of the most prevalent diseases worldwide, causing significant morbidity and mortality. Heart problems have been one of the main causes of death in the last twelve months, with more than 385,000 people dying every year due to heart disease. In the United States alone, a heart attack occurs every 34 s [1,2]. The most prominent symptom of heart disease is an irregular heartbeat, a condition known as cardiac arrythmia. The most commonly used tool for analyzing the activity of the heart is the electrocardiogram (ECG), in which electrical signals produced by the heart are recorded from electrodes placed on the body, to graphically visualize the patterns of activity [3]. The main variables generated by ECG signals are P, Q, and QRS complex waves. There are various fundamental parameters essential for the study of the interval, shape, and relationships of P, Q, and QRS complex wave variables in heart disease patients. Any sudden variation in these constraints indicates a disease of the heart which causes the heartbeat to be inconsistent, either faster or slower than normal. Arrythmia may have any of an extensive range of causes [4]. Arrythmia should therefore be recognized and treated as soon as possible. Usually, arrhythmia presents with the sudden onset of a cardiac problem such as inadequate blood flow from the heart, insufficiency of breath, chest pain, exhaustion, or unconsciousness. ECG reveals abnormal signals [5,6]. Arrhythmias fall into two broad groups, known as bradycardia and tachycardia. The type of arrhythmia in which the heartbeat is lower than 60 beats per minute (bpm) is known as bradycardia, while the type of arrhythmia in which the heartbeat can reach up to 100 bpm is known as tachycardia [7]. With the development of remotely controlled healthcare systems for cardiac disease patients, the importance of efficient and accurate arrhythmia classification and detection is becoming evident. Diagnostic systems using different machine learning (ML) methods have been developed in the past few years, to improve the accuracy of arrhythmia classification from ECG recorded signals, a non-trivial task [8]. The choice of suitable techniques for heart disease detection and classification is not easy. It involves the consideration of context, analysis of data, and the needs of specific patients [9]. ML approaches use algorithms that permit the computer to learn from experience, without explicit programming. The aim is to produce an algorithm that can take a set of patterns and automatically generalize from early information with or without human involvement. Unsupervised ML algorithms include cluster analysis, or clustering. Clustering is a method for assigning observations to various groups, based on the similarity of items in each group. Clustering algorithms have been used in several intelligent disease diagnosis systems [10–15].
Computer-aided diagnosis (CAD) has become a major area of research. CAD uses ML approaches to evaluate patient data, whether images or non-image data, and assess the patient’s condition. The output can be used to assist clinicians in their decision making and can lead to improved diagnosis [16]. Al-Antari et al. [17] developed a DL detection and classification system based on an integrated CAD system to enhance the diagnosis of breast lesions. Initially, the DL you only look once (YOLO) real time object detector was implemented and evaluated for breast lesion detection from full mammograms. Then, DL classifiers, such as convolutional neural networks (CNN), ResNet-50, and InceptionResNet-V2, were evaluated for breast lesion classification. The DL system was evaluated using five-fold cross-validation on two different databases of digital X-ray mammograms. Yassin et al. [18] produced a systematic review that aimed to evaluate the state of the art in CAD detection systems for breast cancer. Chan et al. [19] provided a comprehensive overview of CAD systems for classifying ECG signals. CAD systems have benefits over the manual evaluation of ECG signals. Diagnosis is fast and reliable, and the incorporation of DL techniques into CAD systems has been shown to increase the classification performance. The diagnostic accuracy of CAD systems can be improved by the use of a large number of ECG data sample with which to train the system. Many algorithms and techniques have been developed for data mining, particularly those using supervised ML methods. The choice of appropriate methods has been a focus of research among researchers developing systems for the diagnosis and classification of arrhythmias.
To enhance the prediction accuracy of arrhythmia classification, we propose a novel DL approach, used with a noise removal technique. We established a novel approach to a deep learning system for classifying a patient into one of 16 categories of arrhythmia. This DL approach for arrhythmia classification has great potential in the medical industry. The classification helps to discriminate between the presence and absence of arrhythmia. The dataset used for the simulation was acquired from the UCI ML arsenal, and evaluation demonstrated an enhancement in classification accuracy. The significant contributions of this research are:
1. A PCA feature selection technique built around a long short-term memory (LSTM) DL classifier for choosing the most relevant features, to obtain maximum multiclass classification accuracy.
2. Obtaining meaningful information from data features to produce maximum accuracy.
3. Identification of a class imbalance problem that often arises in high dimensional datasets.
4. A comparison of our hybrid DL and PCA approach with state-of-the-art arrhythmia classification techniques based on conventional ML approaches. The simulation results indicate that our hybrid DL had a better classification accuracy and outperformed other advanced ML approaches.
The rest of the paper is structured as follows. In Section 2, we discuss related work and the background of arrhythmia classification. In Section 3, the research methodology and our proposed novel approach are described. In Section 4, we present the results of simulation of our novel DL approach. Finally, Section 5 summarizes the research and provides possible future work, before concluding the paper.
In the last two decades, numerous techniques have been proposed for efficient and accurate detection and classification of cardiac arrhythmia. These approaches range from simple statistical learning to standard machine learning, to recent deep learning techniques
Existing arrhythmia classifications are primarily based on supervised learning algorithms. Samad et al. [20] used a supervised ML classifier for arrhythmia detection in his classic paper. Decision trees (DTs), a well-known supervised algorithm, have been used for effective arrhythmia classification. Another supervised ensemble approach, known as a random forest (RF) and created by resampling, has been shown to enhance the detection of arrhythmia [21]. Batra et al. [22] used various ML techniques, including neural networks (NNs), DT, random forests, and support vector machines (SVMs) for arrhythmia detection and classification, after applying attribute selection methods to ECG data. Fazel et al. [23] implemented several ML approaches, including RF, SVM, LR, DT, and naïve Bayes (NB) to classify arrhythmias into 16 classes. Feature, or attribute, selection algorithms are important in fields such as ML, data mining, and pattern recognition, particularly when using large datasets. We developed a new feature selection technique based on vital mutual information, which was evaluated on unsupervised information [24]. To confirm the effectiveness of the technique, experiments were carried out on the UCI repository dataset, using different representative classification techniques. For the choice of appropriate attributes from the arrhythmia dataset, the new ensemble-based model is anticipated in [25], in which a subset of the attributes from ECG data is selected, and then classifiers are trained on each subset.
Conventional SVMs have their drawbacks, so a twin SVM technique was used by Khemchandani et al. [26] for binary classification. The multi-classification problem has been solved using modified twin support vector machines (TSVMs) and applied to real-world problems. Guvenir et al. [27] developed a novel technique, known as VF15, to classify arrhythmias. The VF15 algorithm provides an easy and efficient way to estimate feature values and performs well compared to a previous basic algorithm for arrhythmia classification. In other classification techniques, such as NNs, a feature value must be substituted by a new value. The VF15 algorithm provides a probability distribution of class membership, instead of assigning cases to single categories. Elsayed [28] applied vector quantization NNs to arrhythmia datasets for the detection and classification of arrhythmia patients. They also used a dimensionality reduction algorithm on six learning vector quantization (LVQ) NNs to identify the presence or absence of arrhythmia. Jadhav et al. [29] classified arrhythmia patients using an artificial neural network on a typical 12-lead ECG dataset. Missing values in the ECG data were managed by substituting feature values with the neighboring value from the same class. MLPs trained using backpropagation were implemented for the classification of arrhythmia. Similar work was carried out by Jadhav et al. [30], who classified arrhythmias using a generalized feed-forward neural network (GFNN). The GFNN was trained using backpropagation and used to classify cases into normal and abnormal arrhythmia classes. Kholi et al. [31,32] implemented an SVM classifier for cardiac arrhythmia classification, along with four well-known approaches: One-against-one, fuzzy and Decision, one-against-all, and decision directed acyclic graph (DDAG) algorithms. The one-against-all approach outperformed the other approaches. Soman et al. [33] performed arrhythmia classification using various ML approaches, such as J48, NB, and OneR. The results of their simulation study show that J48 and NB had better accuracy than the One R ML approach. Bortolan et al. [34] provided an extremely interactive and easy-to-use environment for analysis of ECG datasets. They used self-organizing maps (SOM) for the study of ECG signals. SOMs are valuable for identifying structure within ECG patterns. Niazi et al. [35] developed an efficient hybrid approach to arrhythmia classification using SVMs and KNNs, and enhanced accuracy was attained by combining a sequential forward search (SFS) algorithm for the selection of informative features with the F1-score.
The problem of class imbalance has attracted substantial attention from the research community [36,37]. The class imbalance problem is caused by inadequate data distribution, where one class comprises the majority of samples, while others have fewer samples. The classification problem becomes more complex as the dimensionality of the data increases, owing to unbalanced classes and unbounded data values. Kotsiantis et al. [38] used various ML methods to deal with the class imbalance problem. Sonak et al. [39] also evaluated various approaches to class imbalance issues. Most algorithms target the majority data samples, while ignoring the minority data samples. Minority samples arise irregularly in the data, but they are persistent. Data preprocessing algorithms and techniques for feature selection are the main methods for addressing the unbalanced data problem, and every technique has some gains and some losses [40]. The arrhythmia dataset has a high-dimensional imbalance problem involving missing feature values, missing features of interest, or the presence of only cumulative data. The data tend to be noisy, containing outliers and errors, and inconsistent, containing discrepancies in names or codes.
To address the issue of imbalance, we employed over-sampling, in which we increased the number of instances in the minority class by randomly duplicating them to produce more examples of the minority class in the sample. Although this approach has some risk of overfitting the data, no information was lost, and this approach outperformed the under-sampling technique.
Although the approaches discussed above have shown reasonable accuracy in classifying arrhythmias, it is important to make some enhancements, such as refining the accuracy. Therefore, DL techniques are increasingly being used, with ANNs becoming the focus of research into performance enhancement when solving high-dimensional data problems. DL has been used in a variety of computationally complex problems, such as computer vision, for detection, preprocessing, classification, and segmentation of images. Generally, there are two essential requirements for successful DL-based approaches: (i) Hierarchical feature illustrations and learning ability, and (ii) The capability to handle very high-dimensional data to extract patterns. Previous methods have used shallow as well as DL approaches [41,42].
Existing arrhythmia classification approaches are largely based on conventional ML methods, which offer less focus on precise feature selection and classification. With the rapid advancement of methods for dealing with high dimensional data, and increases in computing power, DL techniques have been used in numerous fields. To address these issues, we developed a novel hybrid DL approach involving choosing maximally distinguishing features using an enhanced feature collection technique, which is useful for boosting the performance of classification of arrhythmia data. We applied an LSTM deep learning approach for classification, together with PCA, to determine the presence or absence of arrhythmia. In these approaches, the accuracy of classification of arrhythmia can still be enhanced, and the choice of the most informative attributes remains challenging. The life-threatening nature of arrhythmia means that prediction and analysis must be extremely precise to be used in the medical field. The proposed approach highlights these issues by selecting several distinctive features using an improved feature selection mechanism, which helps to improve the classification performance. In this research, we propose an arrhythmia decision system and efficient models relying on this approach. An overview of the state-of-the-art approaches is given in Tab. 1.
Table 1: Overview of the state-of-the-art approaches to arrhythmia classification
LSTMs are extensively used in disease classification, because of their efficacy and strength. LSTM is a DL classification technique that has been applied in numerous research projects addressing disease classification [45,46]. PCA is a well-known dimensionality reduction method, which can handle high dimensional data. It has been used in the development of various disease diagnosis systems, to eliminate unnecessary information present in the initial data [47,48].
A flow diagram of the proposed approach to the detection and classification of arrythmias is shown in Fig. 1.
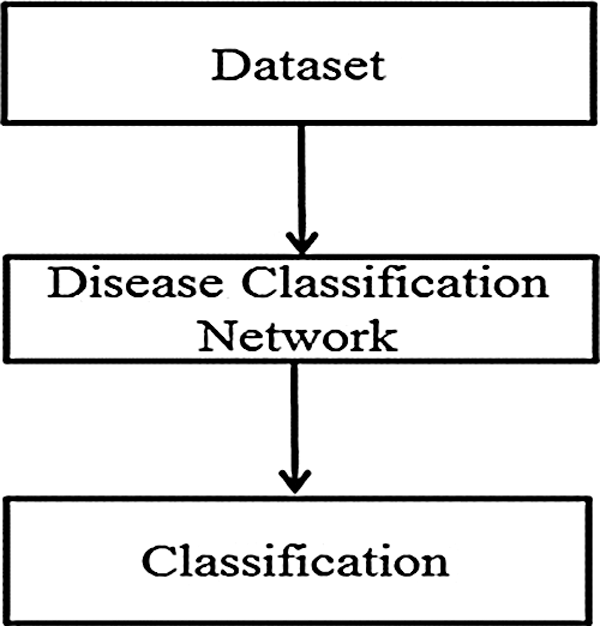
Figure 1: Flow diagram of the proposed approach to arrhythmia disease classification
3.1 Disease Classification Network
The arrhythmia disease classification network consists of three main steps, as shown in Fig. 2.
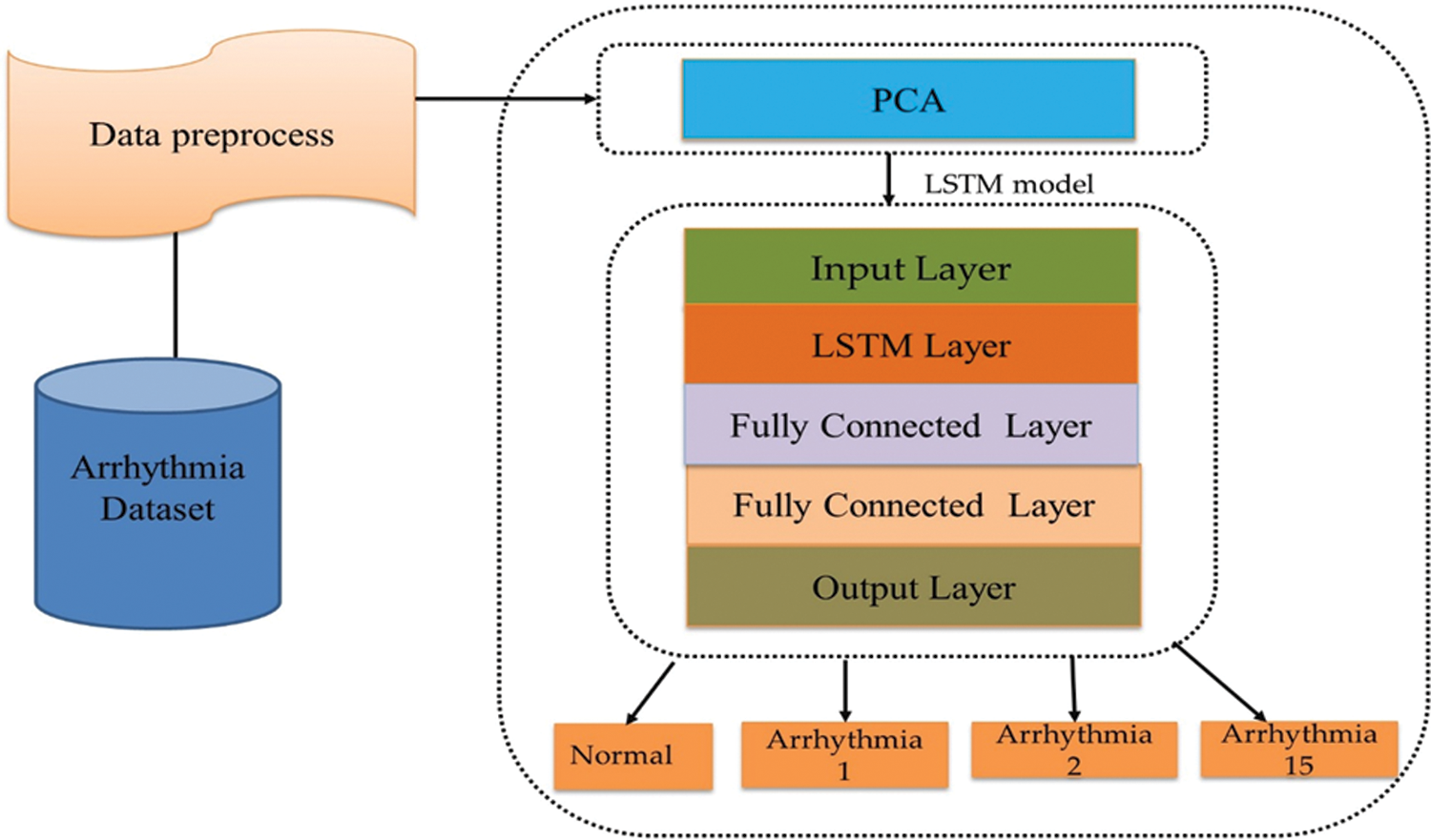
Figure 2: Disease classification network
The features in the arrythmia dataset have large numeric values, which have considerable influence on classification accuracy, in contrast to those features which have small numeric values. The dataset used in this research has an inclusive numeric variation for various attributes. To reduce the influence of the response variables for these types of features, data normalization was used. The objective of data normalization is to enhance the performance of the classification model, by restricting the influence of the features with higher values. For data normalization, a scaling and centering approach which increases the numeric stability of the proposed system was used.
Feature selection is a method for choosing a subset of the features in the training set and using these features in classification. There are two main objectives of feature selection. The primary objective is to generate a training set which allows the classifier to perform more effectively by reducing the size of the feature set. The secondary objective is to improves the classification accuracy by removing noisy features from the dataset. A commonly used feature selection method is principal components analysis (PCA), which we used in our proposed arrhythmia classification approach.
PCA is a statistical method applicable to multiclass datasets and is useful for dimensionality reduction while retaining significant information in the dataset [49–51]. PCA has four fundamental aims. The first aim is to extract maximum meaningful information from data. The second is to reduce the amount of data by keeping the most valuable information. The third aim of PCA is to shorten the details of data to extract the maximum meaningful information from the data. The third one is to compress the amount of data by keeping unique maximum valuable characterizing information. The fourth aim of PCA is to reduce the amount of detail in the data. Feature selection is useful for observing and evaluating the structure of the data; the fourth goal of the PCA algorithm. The analysis of data is attained by transforming the data into the original class of variables, known as principal components (PCs).
The PCs are uncorrelated and arranged in such a way that a few PCs capture the maximum amount of variation in the dataset. The first PC represents the dimension with the largest variation, while the second component defines a dimension with the next highest variation. PCA was selected for this research because it is appropriate to the analysis technique used. If the data are linear and correlated, then PCA will achieve useful compression and retain the maximum amount of the information present in the initial dataset.
There are 279 attributes in the arrhythmia dataset, and it was not possible to extract information from all of the features. A large number of features provide limited information that is not available to doctors evaluating the ECG report of arrhythmia patients. The arrhythmia dataset was therefore reduced using PCA.
LSTM [52,53] is an improved version of RNN in which the current output depends on the previous state. The algorithm overcomes the drawbacks of traditional RNN, in ways such as using gradient descent when dealing with the problem of long-term dependencies [54]. LSTM has been effective in applications such as handwriting recognition [55], natural language processing machine translation [56], and speech recognition [57]. Conventional RNN calculates its 
recurrent hidden state, and the 
output depends on the preceding hidden state ht −1 as well as current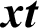 
input as follows:
where W, U, V represent the weight metrics between the present hidden state 
and the preceding hidden state 
, current input, and output, respectively, while g(.) and f(.) represent the element-wise activation function. Traditional RNNs can utilize information about the previous situation, but the present output depends not just upon the previous information, but also on the incoming context information. To overcome this issue, bidirectional RNNs were developed. However, during training, bidirectional RNNs suffer from the vanishing and exploding problem while processing the long-term dependencies. The vanishing and exploding problem means that BRNN are not suitable for use in situations with longer dependencies. This is a key issue in recurrent networks [58].
To overcome this problem a superior RNN structure was proposed, generally known as long short-term memory (LSTM). LSTMs can manage the gradient explode and vanish issues in an efficient way. All of the hidden layers of a conventional RNN are substituted by memory blocks, which form a memory cell intended to store information, accompanied by three important gates used to update the information. The three gates input, output, and forget are shown in Fig. 3.
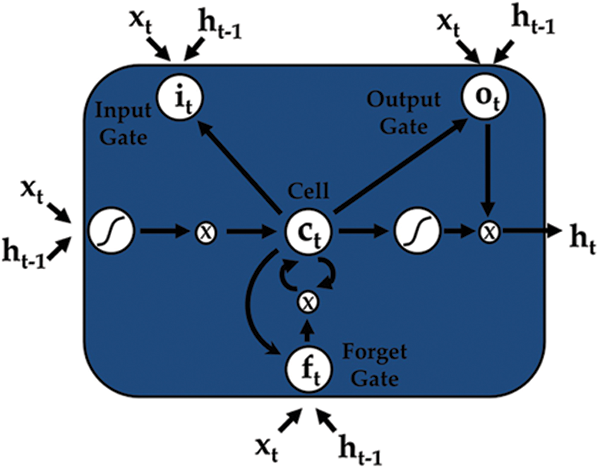
Figure 3: An LSTM cell
Given an input sequence of data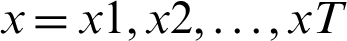 
, the prediction period T, and the hidden state of memory chunks are 
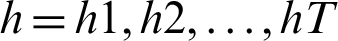, and the output sequence is 
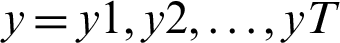. LSTM can be helpful for computing the improved hidden state as:
where 
is the memory cell, the input gate is denoted by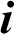 
and represents the new information added to the memory cell, the forget gate is denoted by f and handles the clearing of cell memory, and the output gate is represented by O, and manages the amount of exposure of memory content. The entries of gating vectors always remain within the limits (0, 1). There is a full flow of information when the gate value is 1, and a complete block, with no flow of information, when the gate value is 0. W (i; f; o) and U (i; f ;o) are the LSTM constraints. The sigmoid activation function and hyperbolic tangent activation function are denoted by 
(.) and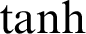 
(.), respectively, and element-wise multiplication is denoted by the symbol 
. In this way, LSTM addresses issues of longer dependencies.
3.2 Classification of the Cardiac Arrhythmia
We classified cardiac arrhythmia using the LSTM DL approach incrementally (Fig. 2). The training information consisted of arrhythmias belonging to p categories, so for every set xi, we have Y (xi), a group of real arrhythmias, and G (xi), a group of estimated arrhythmia types produced by the various classifiers. A set of labels or classes of the arrhythmia type is specified as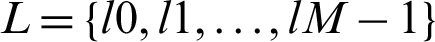 
, and the accurate output vector y has N elements such that 
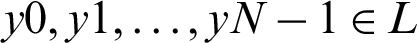. The performance parameters of the confusion matrix–-recall, precision, F1-value score, and the root mean squared error were evaluated. We can quantize the elements of the confusion matrix for our multiclass cardiac arrhythmia classification problem as follows:
where the delta functions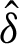 
(x) can be described as follows:
Cij can be applied to calculate the performance constraints, including the PPVw weighted precision, TPRw weighted recall, and F1 value, (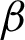
) of the cardiac arrhythmia multiclass classification of the predicted population labels against the true population labels using the following formulas:
where PPV (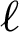
), TPR (
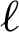), and (
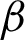) are the precision, recall, and F1 by labels, respectively. We computed the root means square error (RMSE) using Eq. (15).
After completion of training, the LSTM model was used to score the test set, to compute the estimated population set against genetic variations, and calculate the confusion matrix parameters for the multiclass classification setting, using Eq. (10). For prediction using an LSTM, we randomly divided the sequence data into training, testing, and validation sets including 70%, 20%, and 10% of the data, respectively. Fig. 4 shows our LSTM DL network for categorizing arrhythmia into 16 groups. Our LSTM DL consisted of five LSTM, four dense layers, and an output layer. The input signal consisted of a sequence of electrocardiography signals. The LSTM takes an input sequence xt, at time t and measures the value of the hidden state ht.
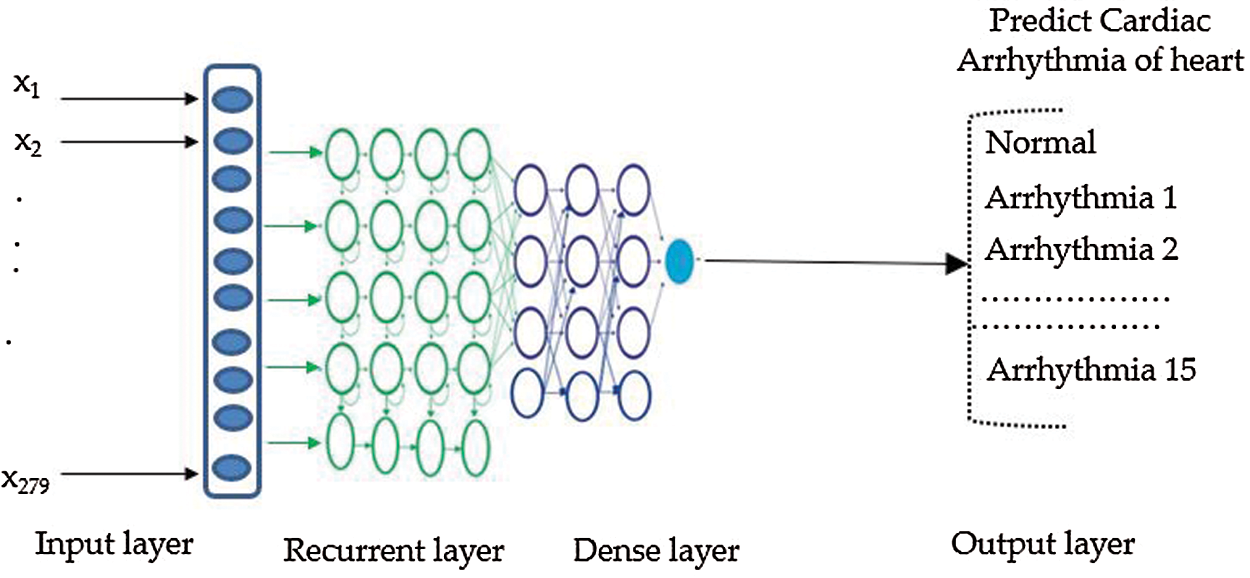
Figure 4: Recurrent LSTM model
We then trained the LSTM, which takes one sequence at every time point and produces a prediction vector by decreasing the value of cross-entropy of the correct predictions in contrast with the predicted distribution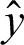 
of N elements such that 
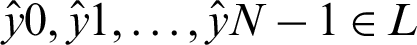. When training the model using the LSTM DL approach with PCA, keeping the test set distinct from the validation set allows us to train the model and learn the hyperparameters for the trained model. We made good use of the ADADELTA learning rate technique, which automatically links the gain of learning rate annealing as well as the training momentum, to avoid slow convergence of the LSTM DL model.
The three most widely used activation functions are the sigmoid, the tanh, and the ReLU functions [59]. The sigmoid activation function takes a real number and squashes it so that it is always between 0 and 1, as shown in Eq. (16), which shows that for negative input the output approaches 0, whereas it becomes 1 for large positive-valued inputs.
The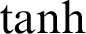 
function is slightly different from the sigmoid nonlinear activation function, as it squashes the real input value numbers into the range between −1 and 1, as in Eq. (17).
The rectified linear unit (ReLU) activation function performs faster than the sigmoid and tanh activation functions, which are nonlinear, and is valuable for eliminating the gradient problem which occurs during training using backpropagation [60,61]. In [62] the authors showed that the speed of training achieved by ReLU is six times that of the tanh activation function. Therefore, we used ReLU to achieve faster training times, and to prevent the gradient effect. The ReLU was initially employed in Boltzmann machines, and is formulated as depicted in Eq. (18).
ReLU was used in the DL LSTM model for improved regularization, and the drop out possibility was fixed at a high value, 1.2 in our case, to avoid possible overfitting problems. In the output layer, the softmax activation function was used to produce a probability distribution over the classes.
The metrics of the confusion matrix precision, recall, F1 Score, and root mean squared error were computed, and the LSTM DL-based approach score and accuracy were calculated.
In this section, we discuss the way in which we implemented the LSTM DL with the PCA approach described in Section 3. First, we describe the dataset used in this study, then we demonstrate the execution. The overall goal of the research was to achieve qualitative and quantitative learning using an implementation of the high dimensional data analysis structure proposed in this article. The experimental outcome based on this implementation will be described in detail in the following section.
4.2 Description of the Dataset
The dataset used was obtained from the UCI ML Repository [27]. There are 452 instances. Every row depicts the medical data of a different patient. The electrocardiography-associated dataset contains 279 features, such as weight, height, and age. The main goal of our experiment was to categorize the arrhythmia records as presence and absence in 16 distinct classes. Class 01 of arrhythmia represented the normal ECG, while classes 02 to 15 represented different abnormal classes of arrhythmia, and class 16 represented an unlabeled category of patients. A shown in Fig. 5 a large number of classes belong to no arrhythmia, with 245 instances belonging to class 01, and 185 instances divided among 14 various types of arrhythmia classes, with the last 22 records being uncategorized.
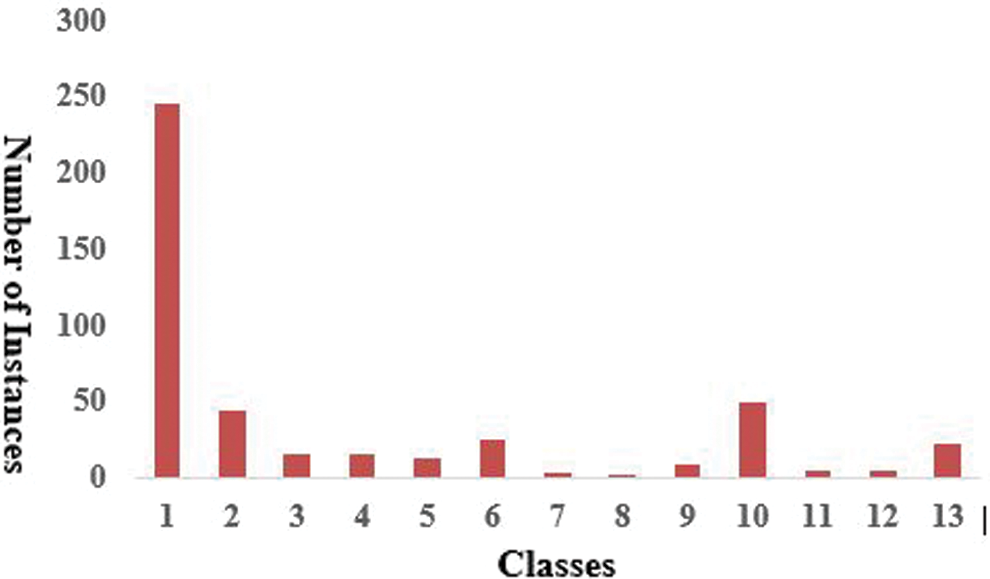
Figure 5: Distribution of arrhythmia instances in several classes
The major problem related to arrhythmia classification was the insufficient amount of training instances given the number of features. The majority of records are classified as no arrhythmia, missing feature values are around 0.33%, and feature values can be either discrete or continuous. Overall, it is a multiclass arrhythmia classification problem.
This section presents the experimental work on arrhythmia disease classification using the LSTM DL approach.
For comparison, experiments using other techniques published in the literature were carried out using the same high dimensional arrhythmia dataset. The LSTM was implemented in Java using the deep learning framework Deeplearning4j. The arrhythmia classifications were carried out on a system with a 32bit core i7, 64-bit Ubuntu 12.04 OS v2.3.0, Java (JDK) 1.8, and Deeplearning4j 1.0.1-alpha. The DL LSTM model was trained on a NVidia 1080 TitanX GPU with CUDA and cuDNN to make the general pipeline faster. Initially, the arrhythmia dataset contained 452 instances and 279 attributes. Due to the presence of a large proportion of missing values (around 0.33%), as well as zero-value columns, it became essential to preprocess and rescale the arrhythmia dataset while retaining its consistency and relevance. Consequently, those columns and rows which contained zeros or missing values were eliminated from the initial dataset. We also eliminated those classes which contained an irrelevant number of instances. The dataset was reduced using PCA, to produce a dataset which contained 377 instances and 166 attributes, separated among six classes in such a way that class 1 represented the normal ECG, classes 2 to 5 denoted various types of arrhythmia, and class 6 denoted unclassified records. We used the LSTM to classify the experimental dataset. For LSTM classification, 70% of the arrhythmia data was used for training, 20% for validation, and 10% for testing the model. To demonstrate the classification accuracy of the arrhythmia prediction, we used the confusion matrix metrics of precision, recall, and F1 score values. These performance metrics exceeded 90% on the training data, and about 88% accuracy on the test data. We trained the LSTM with a unique sample every time, The LSTM therefore managed to model the long-short-term dependencies perfectly. Based on this robustness, the LSTM outperformed the previous machine learning approaches. Thus, using a robust LSTM network, we tried to overcome the vanishing gradients and exploding gradients problem with truncated backpropagation through time (BPTT) during training. However, using BPTT, it was hard to overcome the vanishing gradients and exploding gradients problem.
We therefore trained the LSTM using truncated propagation through time (TBPTT). We took a full sequence and only used backpropagation gradients for some time steps from the selected time block in a continuous way for many epochs. Using this approach, the LSTM managed to model the non-linearity very well and handled very long sequences representing longer-term dependencies. To further improve the performance, we experimented with gradient clipping, which helps to combat the vanishing gradients. We also used dropout, and l2 regularization, feature scaling, and batch normalizations while training our LSTM, which helped us to avoid the regularization issue. Tab. 2 illustrates the success of our LSTM DL based model with dimensionality reduction using PCA.
Table 2: Performance metrics of deep learning models
Our approach produced better classification accuracy than previous techniques. The average training accuracy of our approach was more than 90%, better than the other techniques, and was comparable with state-of-the-art approaches. Fazel et al. [23] applied various ML approaches and attained a maximum accuracy of 72.7%. Guvenir et al. [27] established a new supervised ML process known as VF15, and applied it to the cardiac arrhythmia dataset, achieving 62% accuracy. Samad et al. [20] applied various ML classifiers for the diagnosis of cardiac arrhythmias and achieved a maximum accuracy of 66.9%. Kholi et al. [31,32] implemented a support vector machine (SVM) classifier for arrhythmia classification and achieved a maximum accuracy of 73.4%, as shown in Tab. 3.
Table 3: Comparison of LSTM DL model with previous models using cardiac arrhythmia dataset
In this research, we developed a new deep learning approach for the study of high dimensional data. We implemented an LSTM DL approach for the classification of arrhythmia. PCA was used for dimensionality reduction. Our approach to high-dimensional data analysis using DL performed better in terms of accuracy than previous ML and deep learning structures. The arrhythmia dataset was taken from the UCI ML repository.
LSTM is useful for high dimensional data analysis, and can handle very large datasets in small periods, with low computational complexity and high accuracy. However, there is still a need for further research into clustering, noise removal, and different classification techniques for arrhythmia.
In the future, we will apply LSTM with clustering and noise removal algorithms to different domains. In the dataset used in this work, most of the instances belong to class 1 and the other classes contain only two to three instances, so this kind of misclassification probability is maximized when using various algorithms. Class 1 has the greatest influence on the output of the prediction model, so to improve predictions in future it is necessary to obtain as many instances in the other classes as possible. The output of the algorithm would be more valuable if the arrhythmia dataset features were grouped according to their physical similarity. For example, the cases with abnormal P waves could be in one group, and all variables with abnormal Q waves in another group. The performances of these approaches could then be compared.
Funding Statement: This research was supported by the Ministry of Science, ICT, Korea, under the Information Technology Research Center support program (IITP-2020-2016-0-00465), (www.msit.go.kr) supervised by the IITP (Institute for Information & Communications Technology Promotion).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. Go, D. Mozaffarian and V. L. Roger. (2014). “Executive summary: Heart disease and stroke statistics,” Updated Report from the American Heart Association, vol. 129, no. 3, pp. 399–410.
2. Available: http://en.wikipedia.org/wiki/Cardiac arrhythmia (accessed on 15 September 2020).
3. W. M. Zuo, W. G. Lu, K. Q. Wang and H. Zhang. (2008). “Diagnosis of cardiac arrhythmia using kernel difference weighted KNN classifier,” in Proc. of the Computers in Cardiology, Bologna, Italy, pp. 253–256.
4. E. Alickovic and A. Subasi. (2016). “Medical decision support system for diagnosis of heart arrhythmia using DWT and random forests classifier,” Journal of Medical Systems, vol. 40, no. 108, pp. 1–12.
5. S. U. Kumar and H. H. Inbarani. (2017). “Neighborhood rough set-based ECG signal classification for diagnosis of cardiac diseases,” Soft Computing, vol. 21, no. 16, pp. 4721–4733.
6. Y. Ozbay and B. Karlik. (2001). “A recognition of ECG arrhythmias using artificial neural networks,” in Proc. IEEE Engineering in Medicine and Biology Society, Istanbul, Turkey, pp. 1680–1683.
7. A. Mustaqeem, S. M. Anwar and M. Majid. (2018). “Multiclass classification of cardiac arrhythmia using improved feature selection and SVM invariants,” Computational and Mathematical Methods in Medicine, vol. 2018, pp. 1–11.
8. M. M. Al Rahhal, Y. Bazi and H. A. Hichri. (2016). “Deep learning approach for active classification of electrocardiogram signals,” Information Sciences, vol. 345, pp. 340–354.
9. C. G. Nayak, G. Seshikala and U. Desai. (2016). “Identification of arrhythmia classes using machine-learning techniques,” International Journal of Biology and Biomedicine, vol. 1, pp. 48–53.
10. C. H. Hsing. (2014). “A hybrid intelligent model of analyzing clinical breast cancer data using clustering techniques with feature selection,” Applied Soft Computing, vol. 20, pp. 4–14. [Google Scholar]
11. E. R. Hruschka and N. F. Ebecken. (2006). “Extracting rules from multilayer perceptron’s in classification problems: A clustering-based approach,” Neurocomputing, vol. 70, no. 3, pp. 384–397. [Google Scholar]
12. M. Nilashi. (2016). “A soft computing approach for diabetes disease classification,” Health Informatics Journal, vol. 24, no. 4, pp. 379–393. [Google Scholar]
13. M. Nilashi, O. Ibrahim and A. Ahani. (2016). “Accuracy improvement for predicting Parkinson’s disease progression,” Scientific Reports, vol. 6, no. 1, pp. 34–181. [Google Scholar]
14. M. Nilashi, O. Ibrahim, H. Ahmadi and L. Shahmoradi. (2017). “A knowledge-based system for breast cancer classification using the fuzzy logic method,” Telematics and Informatics, vol. 4, no. 34, pp. 133–144. [Google Scholar]
15. K. Polat. (2012). “Classification of parkinson’s disease using a feature weighting method on the basis of fuzzy C-means clustering,” International Journal of Systems Science, vol. 4, no. 4, pp. 597–609. [Google Scholar]
16. Y. Hagiwara, H. Fujita, S. L. Oh, J. H. Tan, R. S. Tan. (2018). et al., “Computer-aided diagnosis of atrial fibrillation based on ECG signals: A review,” Information Sciences, vol. 467, pp. 99–114. [Google Scholar]
17. M. A. Al-Antari, S. M. Han and T. S. Kim. (2020). “Evaluation of deep learning detection and classification towards computer-aided diagnosis of breast lesions in digital x-ray mammograms,” Computer Methods and Programs in Biomedicine, vol. 196, pp. 1–38. [Google Scholar]
18. N. I. Yassin, S. Omran, E. E. M. Houby and H. Allam. (2018). “Machine learning techniques for breast cancer computer aided diagnosis using different image modalities a systematic review,” Computer Methods and Programs in Biomedicine, vol. 156, pp. 25–45. [Google Scholar]
19. H. P. Chan, L. M. Hadjiiski and R. K. Samala. (2020). “Computer-aided diagnosis in the era of deep learning,” Medical Physics, vol. 47, no. 5, pp. 218–227. [Google Scholar]
20. S. Samad, S. A. Khan and A. Haq. (2014). “Classification of arrhythmia,” International Journal of Electrical Energy, vol. 2, no. 1, pp. 57–61. [Google Scholar]
21. A. Ozcift. (2011). “Random forests ensemble classifier trained with data resampling strategy to improve cardiac arrhythmia diagnosis,” Computers in Biology and Medicine, vol. 41, no. 5, pp. 265–271. [Google Scholar]
22. A. Batra and V. Jawa. (2016). “Classification of arrhythmia using conjunction of machine learning algorithms and ECG diagnostic criteria,” International Journal of Biology and Biomedicine, vol. 1, pp. 1–17. [Google Scholar]
23. A. Fazel, F. Algharbi and B. Haider. (2014). “Classification of cardiac arrhythmias patients,” CS229 Final Project Report. [Google Scholar]
24. H. Liu, J. Sun, L. Liu and H. Zhang. (2009). “Feature selection with dynamic mutual information,” Pattern Recognition, vol. 42, no. 7, pp. 1330–1339. [Google Scholar]
25. E. Namsrai, T. Munkhdalai, M. Li, J. Shin, O. Namsrai et al. (2013). , “A feature selection-based ensemble method for arrhythmia classification,” Journal of Information Processing Systems, vol. 9, no. 1, pp. 31–40. [Google Scholar]
26. R. Khemchandani and S. Chandra. (2007). “Twin support vector machines for pattern classification,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 5, pp. 905–910. [Google Scholar]
27. H. A. Guvenir, B. Acar, G. Demiroz and A. Cekin. (1997). “A supervised machine learning algorithm for arrhythmia analysis,” IEEE Computers in Cardiology, vol. 24, pp. 433–436. [Google Scholar]
28. A. M. Elsayed. (2009). “Classification of ecg arrhythmia using learning vector quantization neural networks,” in Proc. ICCES, Cairo, Egypt, pp. 139–144. [Google Scholar]
29. S. M. Jadhav, S. L. Nalbalwar and A. A. Ghatol. (2010). “Arrhythmia disease classification using artificial neural network model,” in Proc. ICCIC, Coimbatore, India, pp. 653–656. [Google Scholar]
30. S. M. Jadhav, S. L. Nalbalwar and A. A. Ghatol. (2010). “Generalized feedforward neural network based cardiac arrhythmia classification from ECG signal data,” in Proc. IMS, Seoul, South Korea, pp. 351–356. [Google Scholar]
31. N. Kohli, N. K. Verma and A. Roy. (2010). “SVM based methods for arrhythmia classification in ECG,” in Proc. ICCCT, Allahabad, Uttar Pradesh, India, pp. 486–490. [Google Scholar]
32. N. Kohli and N. Verma. (2012). “Arrhythmia classification using svm with selected features,” International Journal of Engineering, Science and Technology, vol. 3, no. 8, pp. 22–31. [Google Scholar]
33. T. Soman and P. O. Bobbie. (2005). “Classification of arrhythmia using machine learning techniques,” WSEAS Transactions on Computers, vol. 4, pp. 548–552. [Google Scholar]
34. G. Bortolan and W. Pedrycz. (2002). “An interactive framework for an analysis of ECG signals,” Artificial Intelligence in Medicine, vol. 24, pp. 109–132. [Google Scholar]
35. K. A. K. Niazi, S. A. Khan, A. Shaukat and M. Akhtar. (2015). “Identifying best feature subset for cardiac arrhythmia classification,” in Proc. of the Science and Information Conf., London, UK, pp. 494–499. [Google Scholar]
36. R. C. Prati, G. E. Batista and D. F. Silva. (2015). “Class imbalance revisited: A new experimental setup to assess the performance of treatment methods,” Knowledge and Information Systems, vol. 45, pp. 247–270. [Google Scholar]
37. R. Longadge and S. Dongre. (2013). “Class imbalance problem in data mining review,” ArXiv, vol. V1, pp. 1305–1707. [Google Scholar]
38. S. Kotsiantis, D. Kanellopoulos and P. Pintelas. (2006). “Handling imbalanced datasets: A review,” GESTS International Transactions on Computer Science and Engineering, vol. 30, pp. 25–36. [Google Scholar]
39. A. Sonak, R. Patankar and N. Pise. (2016). “A new approach for handling imbalanced dataset using ANN and genetic algorithm,” in Proc. ICCSP, Chennai, India, pp. 6–8. [Google Scholar]
40. B. Krawczyk. (2016). “Learning from imbalanced data: Open challenges and future directions,” Progress in Artificial Intelligence, vol. 5, pp. 221–232. [Google Scholar]
41. Z. C. Lipton, J. Berkowitz and C. Elkan. (2015). “A critical review of recurrent neural networks for sequence learning,” ArXiv, vol. V4, pp. 1506–1519. [Google Scholar]
42. R. V. Kumar, K. P. Soman and P. Poornachandran. (2017). “Applying convolutional neural network for network intrusion detection,” in Proc. ICACCI, Udupi, India, pp. 1222–1228. [Google Scholar]
43. A. G. Persada, N. A. Setiawan and H. A. Nugroho. (2013). “Comparative study of attribute reduction on arrhythmia classification dataset,” in Proc. ICITEE, Yogyakarta, Indonesia, pp. 68–72. [Google Scholar]
44. M. Embrechts, B. Szymanski and K. Sternickel. (2003). “Use of machine learning for classification of magneto cardiograms,” in Proc. of Systems, Man and Cybernetics, Washington, DC, USA, pp. 1400–1405. [Google Scholar]
45. T. Pham, T. Tran, D. Phung and S. Venkatesh. (2017). “Predicting healthcare trajectories from medical records: A deep learning approach,” Journal of Biomedical Informatics, vol. 69, pp. 218–229. [Google Scholar]
46. T. Wang, R. G. Qi and M. Yu. (2018). “Predictive modeling of the progression of alzheimer’s disease with recurrent neural networks,” Scientific Reports (Nature Publisher Group), vol. 8, pp. 1–12. [Google Scholar]
47. D. Çalişir and E. Dogantekin. (2011). “A new intelligent hepatitis diagnosis system: PCA-LSSVM,” Expert Systems with Applications, vol. 38, no. 8, pp. 10705–10708. [Google Scholar]
48. H. L. Chen, C. C. Huang and X. G. Yu. (2013). “An efficient diagnosis system for detection of Parkinson’s disease using fuzzy K-nearest neighbor approach,” Expert Systems with Applications, vol. 40, no. 1, pp. 263–271. [Google Scholar]
49. B. Moore. (1981). “Principal component analysis in linear systems: Controllability, observability, and model reduction,” IEEE Transactions on Automatic Control, vol. 26, no. 1, pp. 17–32. [Google Scholar]
50. M. Nilashi, O. Bin Ibrahim, N. Ithnin and N. H. Sarmin. (2015). “A multi-criteria collaborative filtering recommender system for the tourism domain using expectation maximization and PCA,” Electronic Commerce Research and Applications, vol. 14, no. 6, pp. 542–562. [Google Scholar]
51. M. Nilashi, O. B. Ibrahim, N. Ithnin and R. Zakaria. (2015). “A multi-criteria recommendation system using dimensionality reduction and neuro-fuzzy techniques,” Soft Computing, vol. 19, no. 11, pp. 3173–3207. [Google Scholar]
52. F. Tong, Z. Luo and D. Zhao. (2017). “A deep network based integrated model for disease named entity recognition,” in In proc. BIBM, Kansas City, MO, USA, pp. 618–621. [Google Scholar]
53. S. Hochreiter and J. Schmid Huber. (1997). “Long short-term memory,” Neural Computation, vol. 9, no. 8, pp. 1735–1780. [Google Scholar]
54. Y. Bagnio, P. Simard and P. Frasconi. (1994). “Learning long-term dependencies with gradient descent is difficult,” IEEE Transactions on Neural Networks, vol. 5, no. 2, pp. 157–166. [Google Scholar]
55. A. Graves, M. Liwicki, H. Bunke, J. Schmid Huber and S. Fernández. (2007). “Unconstrained on-line handwriting recognition with recurrent neural networks,” in Proc. Advances in Neural Information Processing Systems, Vancouver, British Columbia, Canada, pp. 1–8. [Google Scholar]
56. I. Sutskever, O. Vinyals and Q. V. Le. (2014). “Sequence to sequence learning with neural networks,” arXiv, vol. v3, pp. 1–9. [Google Scholar]
57. A. Graves, A. R. Mohamed and G. Hinton. (2013). “Speech recognition with deep recurrent neural networks,” in Proc. on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada. IEEE, pp. 6645–6649. [Google Scholar]
58. D. Kang, Y. Lv and Y. Y. Chen. (2017). “Short-term traffic flow prediction with lstm recurrent neural network,” in Proc. ITSC, Yokohama, Japan, pp. 1–6. [Google Scholar]
59. Available: http://cs231n.github.io/neural-networks-1/. (Accessed on 15 August 2020). [Google Scholar]
60. X. Glorot, A. Bordes and Y. Bengio. (2011). “Deep sparse rectifier neural networks,” in Proc. on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, pp. 315–323. [Google Scholar]
61. V. Nair and G. E. Hinton. (2010). “Rectified linear units improve restricted boltzmann machines,” in Proc. of the Int. Conf. on Machine Learning, Haifa, Israel, pp. 807–814. [Google Scholar]
62. A. Krizhevsky, I. Sutskever and G. E. Hinton. (2012). “ImageNet classification with deep convolutional neural networks,” in Proc. Neural Information Processing Systems, Curran Associates, New York, NY, USA, pp. 1097–1105. [Google Scholar]
63. A. E. Hegazy, M. A. Makhlouf and G. S. El-Tawel. (2020). “Improved slap swarm algorithm for feature selection,” Journal of King Saud University-Computer and Information Sciences, vol. 32, no. 3, pp. 335–344. [Google Scholar]
64. K. Polat, S. Şahan and S. Güneş. (2006). “A new method to medical diagnosis: Artificial immune recognition system (AIRS) with fuzzy weighted pre-processing and application to ecg arrhythmia,” Expert Systems with Applications, vol. 31, no. 2, pp. 264–269. [Google Scholar]
65. R. N. Abirami and P. D. Raj. (2020). “Cardiac arrhythmia detection using ensemble of machine learning algorithms,” Soft Computing for Problem Solving, vol. 1057, pp. 475–487. [Google Scholar]
66. S. K. Pandey. (2020). “ECG arrhythmia detection with machine learning algorithms,” Data Engineering and Communication Technology, vol. 1079, pp. 409–417. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |