[BACK]
Computers, Materials & Continua
DOI:10.32604/cmc.2021.014674		 images
Article

Flower Pollination Heuristics for Nonlinear Active Noise Control Systems

Wasim Ullah Khan1,*, Yigang He1, Muhammad Asif Zahoor Raja2, Naveed Ishtiaq Chaudhary3, Zeshan Aslam Khan3 and Syed Muslim Shah4

1School of Electrical Engineering and Automation, Wuhan University, Wuhan, 430072, China
2Future Technology Research Center, National Yunlin University of Science and Technology, Yunlin, 64002, Taiwan
3Department of Electrical Engineering, International Islamic University, Islamabad, Pakistan
4Department of Electrical Engineering, Capital University of Science and Technology, Islamabad, Pakistan
*Corresponding Author: Wasim Ullah khan. Email: kwasim814@whu.edu.cn
Received: 07 October 2020; Accepted: 11 November 2020

Abstract: Abstract In this paper, a novel design of the flower pollination algorithm is presented for model identification problems in nonlinear active noise control systems. The recently introduced flower pollination based heuristics is implemented to minimize the mean squared error based merit/cost function representing the scenarios of active noise control system with linear/nonlinear and primary/secondary paths based on the sinusoidal signal, random and complex random signals as noise interferences. The flower pollination heuristics based active noise controllers are formulated through exploitation of nonlinear filtering with Volterra series. The comparative study on statistical observations in terms of accuracy, convergence and complexity measures demonstrates that the proposed meta-heuristic of flower pollination algorithm is reliable, accurate, stable as well as robust for active noise control system. The accuracy of the proposed nature inspired computing of flower pollination is in good agreement with the state of the art counterpart solvers based on variants of genetic algorithms, particle swarm optimization, backtracking search optimization algorithm, fireworks optimization algorithm along with their memetic combination with local search methodologies. Moreover, the central tendency and variation based statistical indices further validate the consistency and reliability of the proposed scheme mimic the mathematical model for the process of flower pollination systems.

Keywords: Active noise control; computational heuristics; volterra filtering; flower pollination algorithm

1  Introduction

The trend of exploiting the potential of bio/nature-inspired soft computing techniques is growing in the research community due to their extensive use in optimization problems arising in engineering, science and technology [1–5]. For instance, heat transfer model [6], magnetohydrodynamics [7], nonlinear system identification [8], atomic physics [9], nonlinear optics [10], plasma physics [11], and scheduling problem [12,13]. Recently, a new meta-heuristic name as flower pollination algorithm (FPA) is introduced by Yang [14] for efficiently solving nonlinear, constrained, single/multi-objective optimization problems [15–18]. The mathematical model for the process of flow pollination of the flowering plants is used to due develop the FPA meta-heuristic. Few potential applications of FPA include photovoltaic system optimization [19], dimension improvement [20], truss structures [21], wireless sensor network [22,23], feature selection [24], control of power systems [25], biometric systems [26], wind speed forecasting [27], image segmentation [28,29], antenna synthesis [30], power flow problem [31,32], neural network optimization [33], chaotic systems identification [34] and bio-impedance models [35]. These illustrative applications are motivations for the authors to exploit the potential of FPA based meta-heuristic for solving the optimization problems of nonlinear active noise control (ANC) systems.

The ANC is a fundamental problem in control engineering and has been studied extensively with both traditional and different local/global optimization techniques [36]. The well-known local search methods used in ANC systems are based on the least mean squares approach [37–44]. The local search algorithms are easy to implement but suffer from premature convergence, i.e., local minima issues. To overcome these issues, different global search based soft computing techniques are proposed such as, genetic algorithms (GAs) [45,46], particle swarm optimization (PSO) [47–49], backtracking search heuristics [50], fireworks algorithm [51], and artificial neural networks [52]. The optimization strength of FPA looks promising to be exploited for ANC problems as an alternate, accurate, reliable, and robust computing paradigm. The innovative contributions of the current study are given as:

•    The design of FPA based intelligent computing paradigm is presented for an effective solution of nonlinear ANC systems.

•    Mean squared error based merit function with nonlinear Volterra series filtering is formulated.

•    The accurate and robust performance of the FPA based ANC for various noise interferences in the case of different primary and secondary path scenarios prove the efficacy of the approach.

•    Central tendency and variation based statistical indices validate the consistency and reliability of the proposed scheme.

The rest of the manuscript is prepared as: ANC model is given in Section 2. The design approach is described in Section 3. Section 4 presents the results and the comparative studies with state of the art counterparts, and conclusions are given in Section 5.

2  System Model: ANC

The conventional block diagram of ANC based controller is given in Fig. 1, and the proposed model of nonlinear ANC with FPA is shown in Fig. 2. The algorithm used for filter’s coefficients update belongs to a class of nature-inspired heuristics named FPA. In the proposed mechanism, the reference microphone detects the source noise and error microphone measures the output response of a system. When anti-noise and source noise signals combine silence zone is created. The proposed mechanism works on the principle of superposition theorem [53]. Related information for ANC system model can be seen in [54–56] and citations mentioned therein.

images

Figure 1: Graphical representation of general analogy of ANC system

images

Figure 2: Process block structures of proposed flower pollination algorithm based ANC system

3  System Methodology

The methodology for ANC modeling with FPA consists of two phases; (1) formulating fitness function (2) presenting optimization mechanism based on FPA. The detailed flowchart in terms of process block structure is shown in Fig. 3.

images

Figure 3: Process blocks for flower pollination based heuristics for ANC system

3.1 Modeling for ANC

Block diagram of proposed ANC controller is given in Fig. 2 while the adjustable parameter L-tap weights, i.e., decision variables of optimization algorithm, for ANC system based on nonlinear filtering with Volterra series is given mathematically as:

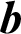images

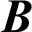here images(k) represents coefficients Volterra filter at instance k. Let images be a set of contestant solutions of ANC systems, i.e., elements of FPA, a set of k numbers of images as in (1) construct images as follows

images

The input noise interference or source signal s(k) and output of nonlinear adaptive Volterra filtering b(k) with length 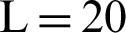images, i.e., VF-T1, for the population B, then ANC system using (1) and (2) is written as:

images

Accordingly, Volterra filtering of type 2 (VF-T2) with L = 35 for the ANC system using Eqs. (1) and (2) is written as:

images

Similarity, for Volterra filtering of type 3 (VF-T3) in case of the length of the Volterra filter L = 65 in ANC system is given by:

images

In case of images are the response of secondary path transfer function C(z) with L-tap weights/coefficients is written as:

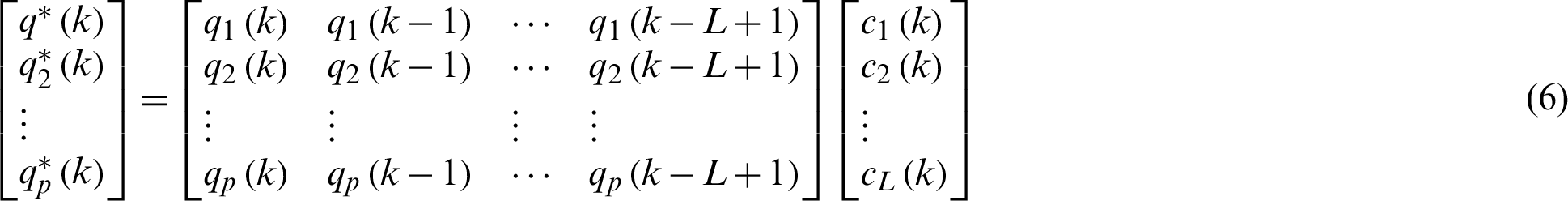
images

The fitness or merit function for ANC model is given as:

images

for

images

Here v(k) and images are the desired and estimated responses of the primary and secondary paths, respectively. and is the response of the secondary path. Eq. (7) equivalently represented as:

images

In the case of perfect model, one has fitness function u = 0, so optimization mechanism is exploited for tuning of fitness (7), such that the magnitude of residual error of the ANC system is reduced substantially. In the next section, optimization of ANC system with FPA is presented.

3.2 Optimization: Flower Pollination Algorithm

The FPA is a mathematical model inspired by the process of pollination dynamics in flowers during the reproduction mechanism [14]. Yang et al. [15] introduced FPA in early 2012 as an alternate optimization solver for both global and local search. Most of the flower plants reproduction strategy is based on the pollination process in which pollen is transferred from one plant to another plant of flowers by butterflies, insects, birds, and bees. The pollination process is segmented into biotic and abiotic types. Biotic type flower pollination is also called cross-pollination, i.e., the main form of flowering pollination, in which pollens are transferred by insects and birds. The majority of flowering plants use biotic pollination procedures for pollen spread over a long distance via Lèvy flights. While in abiotic pollination, the flowering plants does not required pollinators and 10% of total flowering plants follow such pollination. In abiotic, the distance covered by the pollinators is short and such types of actions are considered as local search. Biotic and abiotic characteristics of pollinators are used to design an optimization algorithm called FPA. The four basics rules of FPA based heuristic are introduced by Yang in 2012 as follows:

Rule 1.    Global pollination carried out via biotic/cross pollination procedures with the help of insects, birds and bees to transport the pollens.

Rule 2.    Abiotic or self-pollination process is adapted for efficient local search.

Rule 3.    Flower fidelity process based reproduction probability.

Rule 4.    Switching probability between 0 and 1 is exploited for feasible local and global pollination process [21].

The impressive swarm based optimization characteristics of FPA is exploited by the scholars from different fields [57–60]. The mathematical mechanism of FPA bases of these four rules are given as follows [25]:

images

where, images stands for pollen vector for ith candidate solution at iteration t, images represents best solution at current iteration and L stands for Lèvy flight represented as:

images

here images represents the gamma function while distribution is effective for images and images. The local search with FPA is represented as:

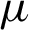images

here, images be the uniform distribution between 0 and 1, images and images are jth and kth pollens vectors from different flowers of the same plant, respectively. In this study, the meta-heuristics of FPA based ANC is implemented as shown in Fig. 3, while the pseudocode is presented in Algorithm 1.

4  Results and Discussion

The results of detailed ANC experimentations are presented here for multiple independent executions of the FPA. Three ANC problems are implemented based on different lengths (L) of Volterra filter (VF), i.e., L = 20, 35, and 65 in the case of VF-T1, VF-T2, and VF-T3, respectively. The FPA based ANC system are evaluated for sinusoidal/random/complex random noise interferences having linear primary path (LPP), nonlinear primary path (NPP), linear secondary path (LSP) and nonlinear secondary path (NSP). The transfer function for LPP is:

images

While, in case of LSP, the transfer function is defined as

images

The NPP transfer function is given as:

images

images

Let qimages(k), i.e., an anti-noise signal is generated by the NSP as:

images

images

The simulations are conducted in Matlab R2017b running under Windows 10 environment on DESKTOP-73HVB7M, with Intel(R) Core(TM) i7-4790 CPU@3.60 GHz, 16-GB RAM.

4.1 Problem 1: ANC Model for Sinusoidal, Random and Complex Random Signals of VF-T1

In this problem, FPA based ANC system is exploited for Case 1: ANC for LPP and NSP (ANC-LPP-NSP), Case 2: ANC for NPP and LSP (ANC-NPP-LSP) and, Case 3: ANC for NPP and NSP (ANC-NPP-NSP). The ANC primary/secondary paths are defined in Eqs. (13)–(18).

Reliable inferences on the outcome of ANC are presented for hundred independent trials of the FPA and result in the form of graphical representation of the statistics are given in Fig. 4 for different cases of sinusoidal noise interference. While the results in case of random and complex random noise scenarios are presented in Fig. 5. The results illustrated in Figs. 4 and 5 show that the proposed FPA based outcomes are effective for reliable treatment of ANC systems having LPP, LSP, NPP and NSPs.

images

Figure 4: Results of fitness achieved for 100 runs of flower pollination algorithm for ANC with VF-T1 filtering each sinusoidal noise scenario of problem 1. (a) Un-sorted results of sinusoidal noise based ANC-LPP-NSP. (b) Sorted results for sinusoidal noise based ANC-LPP-NSP. (c) Un-sorted results of sinusoidal noise based ANC-NPP-LSP. (d) Sorted results for sinusoidal noise based ANC-NPP-LSP. (e) Un-sorted results of sinusoidal noise based ANC-NPP-NSP. (f) Sorted results for sinusoidal noise based ANC-NPP-NSP

images

Figure 5: Results of fitness achieved for 100 runs of flower pollination algorithm for ANC with VF-T1 filtering in case of random and complex random. (a) Un-sorted results of all three scenarios of random noise. (b) Sorted results of all three scenarios of random noise. (c) Unsorted results of complex random noise based ANC-LPP-NSP. (d) Sorted results of complex random noise based ANC-LPP-NSP. (e) Unsorted results of complex random noise based ANC-NPP-LSP. (f) Sorted results of complex random noise based ANC-NPP-LSP. (g) Unsorted results of complex random noise based ANC-NPP-NSP. (h) Sorted results of complex random noise based ANC-NPP-NSP

The performance of the FPA is further examined through histogram plots and statistical measures of minimum (MIN), mean, and standard deviation (STD). The histogram plots are provided in Fig. 6 for all cases of Problem 1. While the statistical operators are given in Tab. 1 and one may observe that the results of random VF-T1 are relatively better than that of sinusoidal, but a bit degraded to complex random. Moreover, the small STD values further validate the precision of the proposed FPS based ANC controllers.

images

Figure 6: Comparison with histogram analysis for 100 runs of flower pollination algorithm for ANC system for each noise scenario of problem 1. (a) Results of sinusoidal noise based ANC-LPP-NSP with VF-T1. (b) Results of sinusoidal noise based ANC-NPP-LSP with VF-T1. (c) Results of sinusoidal noise based ANC-NPP-NSP with VF-T1. (d) Results of random noise based ANC-LPP-NSP with VF-T1. (e) Results of random noise based ANC-NPP-LSP with VF-T1. (f) Results of random noise based ANC-NPP-NSP with VF-T1. (g) Results of complex random noise based ANC-LPP-NSP with VF-T1. (h) Results of complex random noise based ANC-NPP-LSP with VF-T1. (i) Results of complex random noise based ANC-NPP-NSP with VF-T1

Table 1: Comparison through statistical operators for flower pollination algorithm based ANC system for each scenarios of problem 1

images

The computational complexity of the FPA based ANC controllers is evaluated via mean time of execution required for the optimization and results for mean along with STD are tabulated in Tab. 2. It is observed that the average time lies around images, images and images for sinusoidal VF-T1, random VF-T1, and complex random VF-T1 cases.

Table 2: Complexity of flower pollination algorithm for ANC cases of problem 1 under different noise interferences

images

4.2 Problem 2: ANC Model for Sinusoidal, Random and Complex Random Signals of VF-T2

In problem 2, FPA based ANC system is implemented for Case 1: ANC for LPP and NSP (ANC-LPP-NSP), Case 2: ANC for NPP and LSP (ANC-NPP-LSP) and, Case 3: ANC for NPP and NSP (ANC-NPP-NSP).

Graphical representation of the statistical outcomes for hundred independent trials of the FPA based ANC for each case of different noise interferences are given in Fig. 7. The statistical operators are given in Tab. 3. The fitness values of FPA based ANC system for ANC-LPP-NSP, ANC-NPP-LSP and ANC-NPP-NSP are around 10-05 to 10-06 for sinusoidal, 10-04 to 10-05 for random and 10-04 to 10-06, for complex random noise interferences of VF-T2. The results for different scenarios presented in Fig. 8 show that the proposed FPA controllers are effective for the reliable treatment of ANC systems.

images

Figure 7: Results of fitness achieved for 100 runs of flower pollination algorithm for ANC with VF-T2 filtering each noise scenario of problem 2. (a) Sinusoidal noise all three cases. (b) Sinusoidal sorted all three cases. (c) Random noise all three cases. (d) Random sorted all three cases. (e) Complex random all three cases. (f) Complex random sorted cases

Table 3: Comparison through statistical operators for flower pollination algorithm based ANC system for each scenarios of problem 2

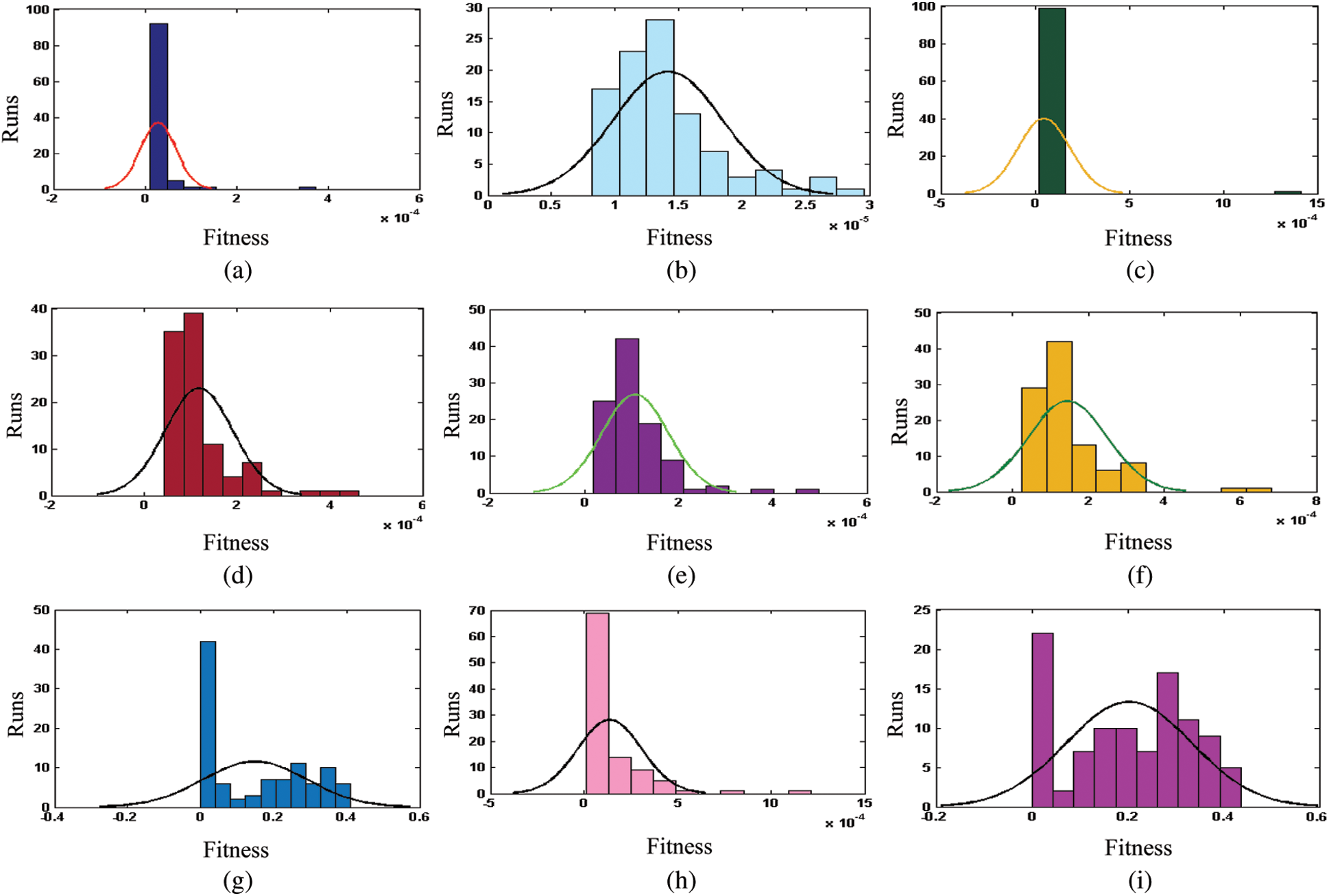
images

images

Figure 8: Comparison with histogram analysis for 100 runs of flower pollination algorithm for ANC system for each noise scenario of problem 2. (a) Results of sinusoidal noise based ANC-LPP-NSP with VF-T2. (b) Results of sinusoidal noise based ANC-NPP-LSP with VF-T2. (c) Results of sinusoidal noise based ANC-NPP-NSP with VF-T2. (d) Results of random noise based ANC-LPP-NSP with VF-T2. (e) Results of random noise based ANC-NPP-LSP with VF-T2. (f) Results of random noise based ANC-NPP-NSP with VF-T2. (g) Results of complex random noise based ANC-LPP-NSP with VF-T2. (h) Results of complex random noise based ANC-NPP-LSP with VF-T2. (i) Results of complex random noise based ANC-NPP-NSP with VF-T2

The performance of the FPA based ANC systems is further investigated through histogram plots and STATISTICAL operators and it is observed that the results of random VF-T2 are better than that of complex random but inferior to sinusoidal VF-T2. One may decipher that relatively better accuracy is attained for ANC system based sinusoidal and random noise signals. While the results of ANC with sinusoidal noise are consistently found better than random noise scenarios.

The computational complexity analyses for the optimization of FPA based ANC is evaluated based on mean time and STD. The results of complexity are given in Tab. 4 and analysis show that the average time lies around images for sinusoidal, images for random and images for complex random noise interferences for ANC system with VF-T2 filtering cases.

Table 4: Complexity of flower pollination algorithm for ANC cases of problem 2 under different noise interferences

images

4.3 Problem 3: ANC Model for Sinusoidal, Random and Complex Random Signals of VF-T3

In this problem, FPA based ANC system is exploited for different primary/secondary path scenarios. The proposed FPA based ANC are conducted for hundred independent trials and graphical representation of the statistics in sort and unsorted plots are given in Fig. 9. The histograms are provided in Fig. 10 for each case of problem 3, while the statistics are provided in Tab. 5. It is observed that the results of random VF-T3 are better than that of complex random but inferior to sinusoidal VF-T3. Relatively better outcomes in term of accuracy are observed for FPA based ANC system in case of sinusoidal and random noise interferences. The comparison shows that sinusoidal noise interference based ANC with VF-T3 are consistently superior than each random noise scenario.

images

Figure 9: Results of fitness achieved for 100 runs of flower pollination algorithm for ANC with VF-T3 filtering each noise scenario of problem 3. (a) Sinusoidal noise all three cases V3. (b) Sinusoidal noise sorted all cases V3. (c) Random noise all three cases V3. (d) Random noise sorted all cases V3. (e) Complex random noise NP-LSP V3. (f) Complex random sorted NP-LSP V3

images

Figure 10: Comparison with histogram analysis for 100 runs of flower pollination algorithm for ANC system for each noise scenario of problem 3. (a) Results of sinusoidal noise based ANC-LPP-NSP with VF-T3. (b) Results of sinusoidal noise based ANC-NPP-LSP with VF-T3. (c) Results of sinusoidal noise based ANC-NPP-NSP with VF-T3. (d) Results of random noise based ANC-LPP-NSP with VF-T3. (e) Results of random noise based ANC-NPP-LSP with VF-T3. (f) Results of random noise based ANC-NPP-NSP with VF-T3. (g) Results of complex random noise based ANC-LPP-NSP with VF-T3. (h) Results of complex random noise based ANC-NPP-LSP with VF-T3. (i) Results of complex random noise based ANC-NPP-NSP with VF-T3

Table 5: Comparison through statistical operators for flower pollination algorithm based ANC system for each scenarios of problem 3

images

The computational complexity analyses for the optimization of FPA based ANC is also evaluated based on mean execution time and STD, and results are provided in Tab. 6. The analysis show that the average time lies around images for sinusoidal, images for random and images for complex random noise interferences of ANC with VF-T3 cases, respectively.

Table 6: Complexity of flower pollination algorithm for ANC cases of problem 3 under different noise interferences

images

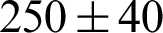The computational complexity of FPA based ANC is examined with counterpart optimization solvers. The computational complexity on mean execution time index of BSA and BSA-SQP results for sinusoidal noise signal are lie around images, images and images for FIR, VF-1 and VF-2, respectively, while images and images for random and complex random noise signals, respectively [50]. The complexity of variants of GAs and its moments combination of IPA, i.e., GA-IPM-1 to 12, for ANC with FIR filter with sinusoidal, random and complex random noise interference is images, images, and images, respectively. Computational complexity of nature inspired heuristics of PSO and its hybridized methodologies with PSO-IP, PSO-AS, PSO-SQP, and PSO-NM for ANC system based on FIR filtering for all three noise variations is around images [49]. The computational complexity on mean values of respective FWA, enhanced FWA and adaptive FWA are around images, images, and images for sinusoidal noise signal, images, images, and images for random noise signal and images, images, and images for complex random signal [51]. One can quite evidently observe that the complexity requirements of FPA based ANC system is relatively superior from GAs, BSA and FWA along with their memetic combination with local search methodologies. While the results of PSO based variants are efficient from rest but these results are for ANC systems based on FIR filtering having relatively inferior in accuracy from FPA based ANC.

4.4 Comparative Study with Reported Results

Comparative studies of FPA results for ANC systems are made with reported studies based on adaptive genetic algorithm AGA [58], variants of memetic combination of GAs with interior-point (IP) algorithm, i.e., GA-IPA-1, to GA-IPA-12 [59], nature-inspired heuristic via particle swarm optimization (PSO) and its hybrid with IP (PSO-IP), active-set (PSO-AS), sequential quadratic programming (PSO-SQP) and Nelder-Mead (PSO-NM) methods [49], backtracking search optimization algorithm (BSA) and its hybrid with SQP (BSA-SQP) [50], and variants of fireworks algorithm (FWA) [51]. One may decipher from all these reported results and statistical observation that the accuracy and convergence of FPA are in good agreement with state of the art methodologies for all three ANC problems. An additional advantage of FPA based ANC is that optimization of decision variables is based on a standalone algorithm with the ability of both local and global search whereas most of the reported results are based on hybrid methodologies.

images

Figure 11: Pseudocode for flower pollination algorithm for nonlinear ANC

5  Conclusions

A novel design of nature-inspired heuristic of FPA is presented for the identification problem in nonlinear ANC with interferences. Different ANC scenarios by considering linear/nonlinear and primary/secondary paths are evaluated by determining coefficients of three different Volterra filters, i.e., VF-T1, VF-T2 and VF-T3. The performance of the FPA based ANC is verified through consistently achieving reasonable gauges of statistical operators in terms of accuracy, convergence and complexity measures. The performance is further validated via histogram analysis to prove that the FPA based ANC systems are reliable, accurate, stable and robust but the performance of the VF-T3 is comparatively better. The accuracy of FPA based ANC is in good agreement with state of the art counterpart solvers based on GA, PSO, BSA and FWA along with their hybrid with local search. In the future, one may explore to enhance the performance of ANC system by implementation of recently introduced fractional derivative definition [60–64]. Moreover, the proposed methodology can be exploited to efficiently solve various complex engineering optimization problems [65–68].

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant Nos. 51977153, 51977161, 51577046, State Key Program of National Natural Science Foundation of China under Grant Nos. 51637004, National Key Research and Development Plan “important scientific instruments and equipment development” Grant No. 2016YFF010220, Equipment research project in advance Grant No. 41402040301.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1.  X. S. Yang, S. Deb, S. Fong, X. He and Y. X. Zhao. (2016). “From swarm intelligence to metaheuristics: Nature-inspired optimization algorithms,” Computer, vol. 49, no. 9, pp. 52–59.

2.  A. Panda and S. Pani. (2016). “A symbiotic organisms search algorithm with adaptive penalty function to solve multi-objective constrained optimization problems,” Applied Soft Computing, vol. 46, pp. 344–360.

3.  R. M. Rizk-Allah, A. E. Hassanien and S. Bhattacharyya. (2018). “Chaotic crow search algorithm for fractional optimization problems,” Applied Soft Computing, vol. 71, pp. 1161–1175.

4.  A. Bouchachia, R. Mittermeir, P. Sielecky, S. Stafiej and M. Zieminski. (2010). “Nature-inspired techniques for conformance testing of object-oriented software,” Applied Soft Computing, vol. 10, no. 3, pp. 730–745.

5.  S. Mirjalili. (2015). “Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm,” Knowledge-Based Systems, vol. 89, pp. 228–249.

6.  M. A. Z. Raja, A. Mehmood, A. Rehman Aur, A. Khan and A. Zameer. (2018). “Bio-inspired computational heuristics for Sisko fluid flow and heat transfer models,” Applied Soft Computing, vol. 71, pp. 622–648.

7.  A. Mehmood, A. Zameer and M. A. Z. Raja. (2018). “Intelligent computing to analyze the dynamics of Magnetohydrodynamic flow over stretchable rotating disk model,” Applied Soft Computing, vol. 67, pp. 8–28.

8.  M. A. Z. Raja, A. A. Shah, A. Mehmood, N. I. Chaudhary and M. S. Aslam. (2016). “Bio-inspired computational heuristics for parameter estimation of nonlinear Hammerstein controlled autoregressive system,” Neural Computing and Applications, vol. 29, pp. 1–20.

9.  Z. Sabir, M. A. Manzar, M. A. Z. Raja, M. Sheraz and A. M. Wazwaz. (2018). “Neuro-heuristics for nonlinear singular Thomas-Fermi systems,” Applied Soft Computing, vol. 65, pp. 152–169.

  1. I. Ahmad, S. Ahmad, M. Awais, S. U. I. Ahmad and M. A. Z. Raja. (2018). “Neuro-evolutionary computing paradigm for Painlevé equation-II in nonlinear optics,” European Physical Journal Plus, vol. 133, pp. 184.
  2. M. A. Z. Raja, F. H. Shah and M. I. Syam. (2017). “Intelligent computing approach to solve the nonlinear Van der Pol system for heartbeat model,” Neural Computing and Applications, vol. 30, pp. 1–25.
  3. X. Li and G. Liang. (2016). “An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem,” International Journal of Production Economics, vol. 174, pp. 93–110.
  4. J. Mou, G. Liang, Q. Guo and J. Mu. (2017). “A hybrid heuristic algorithm for flowshop inverse scheduling problem under a dynamic environment,” Cluster Computing, vol. 20, no. 1, pp. 1–15.
  5. X. S. Yang. (2012). “Flower pollination algorithm for global optimization,” in Unconventional Computation and Natural Computation, Lecture Notes in Computer Science, vol. 7445, Berlin, Heidelberg: Springer.
  6. X. S. Yang, M. Karamanoglu and X. He. (2013). “Multi-objective flower algorithm for optimization,” Procedia Computer Science, vol. 18, pp. 861–868.
  7. X. S. Yang, M. Karamanoglu and X. He. (2014). “Flower pollination algorithm: A novel approach for multiobjective optimization,” Engineering Optimization, vol. 46, no. 9, pp. 1222–1237.
  8. X. He, X. S. Yang, M. Karamanoglu and Y. Zhao. (2017). “Global convergence analysis of the flower pollination algorithm: A discrete-time Markov Chain approach,” Procedia Computer Science, vol. 108, pp. 1354–1363.
  9. S. Dötterl, L. M. Wolfe and A. Jürgens. (2005). “Qualitative and quantitative analyses of flower scent in Silene latifolia,” Phytochemistry, vol. 66, no. 2, pp. 203–213.
  10. D. Yousri, T. S. Babu, D. Allam, V. K. Ramachandaramurthy and M. B. Etiba. (2019). “A novel chaotic flower pollination algorithm for global maximum power point tracking for photovoltaic system under partial shading conditions,” IEEE Access, vol. 7, pp. 121432–121445.
  11. Y. Zhou and W. Rui. (2016). “An improved flower pollination algorithm for optimal unmanned undersea vehicle path planning problem,” International Journal of Pattern Recognition & Artificial Intelligence, vol. 30, no. 4, 1659010.
  12. G. Bekdaş, S. M. Nigdeli and X. S. Yang. (2015). “Sizing optimization of truss structures using flower pollination algorithm,” Applied Soft Computing, vol. 37, pp. 322–331.
  13. T. T. Nguyen, J. S. Pan and T. K. Dao. (2019). “An improved flower pollination algorithm for optimizing layouts of nodes in wireless sensor network,” IEEE Access, vol. 7, pp. 75985–75998.
  14. Z. Wang, H. Xie, D. He and S. Chan. (2019). “Wireless sensor network deployment optimization based on two flower pollination algorithms,” IEEE Access, vol. 7, pp. 180590–180608.
  15. F. Wang, S. Ma, H. Wang, Y. Li, Z. Qin et al. (2018). , “A hybrid model integrating improved flower pollination algorithm-based feature selection and improved random forest for NOX emission estimation of coal-fired power plants,” Measurement, vol. 125, pp. 303–312.
  16. S. D. Madasu, M. L. S. S. Kumar and A. K. Singh. (2018). “A flower pollination algorithm based automatic generation control of interconnected power system,” Ain Shams Engineering Journal, vol. 9, no. 4, pp. 1215–1224.
  17. D. Rodrigues, G. F. A. Silva, J. P. Papa, A. N. Marana and X. S. Yang. (2016). “EEG-based person identification through binary flower pollination algorithm,” Expert Systems with Applications, vol. 62, pp.
  18. W. Zhang, Z. Qu, K. Zhang, W. Mao, Y. Ma et al. (2017). , “A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting,” Energy Conversion & Management, vol. 136, pp. 439–451.
  19. L. Shen, C. Fan and X. Huang. (2018). “Multi-level image thresholding using modified flower pollination algorithm,” IEEE Access, vol. 6, pp. 30508–30519.
  20. K. Li and Z. Tan. (2019). “An improved flower pollination optimizer algorithm for multilevel image thresholding,” IEEE Access, vol. 7, pp. 165571–165582.
  21. U. Singh and R. Salgotra. (2018). “Synthesis of linear antenna array using flower pollination algorithm,” Neural Computing and Applications, vol. 29, no. 2, pp. 435–445.
  22. B. Mahdad and K. Srairi. (2016). “Security constrained optimal power flow solution using new adaptive partitioning flower pollination algorithm,” Applied Soft Computing, vol. 46, pp. 501–522.
  23. J. P. Ram and N. Rajasekar. (2016). “A novel flower pollination based global maximum power point method for solar maximum power point tracking,” IEEE Transactions on Power Electronics, vol. 32, no. 11, pp. 8486–8499.
  24. H. Chiroma, A. Khan, A. I. Abubakar, Y. Saadi, M. F. Hamza et al. (2016). , “A new approach for forecasting OPEC petroleum consumption based on neural network train by using flower pollination algorithm,” Applied Soft Computing, vol. 48, pp. 50–58.
  25. S. Xu, W. Yong and L. Xue. (2017). “Parameter estimation for chaotic systems via a hybrid flower pollination algorithm,” Neural Computing and Applications, vol. 30, pp. 1–17.
  26. D. A. Yousri, A. M. Abdelaty, L. A. Said, A. S. Elwakil, B. Maundy et al. (2019). , “Parameter identification of fractional-order chaotic systems using different Meta-heuristic optimization algorithms,” Nonlinear Dynamics, vol. 95, no. 3, pp. 2491–2542.
  27. N. V. George and G. Panda. (2013). “Advances in active noise control: A survey, with emphasis on recent nonlinear techniques,” Signal Processing, vol. 93, no. 2, pp. 363–377.
  28. L. Hui, Z. Ming and W. Ser. (2002). “A weight-constrained FxLMS algorithm for feedforward active noise control systems,” IEEE Signal Processing Letters, vol. 9, no. 1, pp. 1–4.
  29. D. P. Das and G. Panda. (2004). “Active mitigation of nonlinear noise processes using a novel filtered-s LMS algorithm,” IEEE Transactions on Speech and Audio Processing, vol. 12, no. 3, pp. 313–322.
  30. B. Huang, Y. Xiao, J. Sun and G. Wei. (2013). “A variable step-size FXLMS algorithm for narrowband active noise control,” IEEE Transactions on Audio Speech & Language Processing, vol. 21, no. 2, pp. 301–312.
  31. M. S. Aslam and M. A. Z. Raja. (2015). “A new adaptive strategy to improve online secondary path modeling in active noise control systems using fractional signal processing approach,” Signal Processing, vol. 107, pp. 433–443.
  32. Z. Qiu, C. M. Lee, Z. H. Xu and L. N. Sui. (2016). “A multi-resolution filtered-x LMS algorithm based on discrete wavelet transform for active noise control,” Mechanical Systems & Signal Processing, vol. 66, pp. 458–469.
  33. Z. Tong, J. Liang, Z. Liang and Z. Li. (2017). “A new FXLMS algorithm with offline and online secondary-path modeling scheme for active noise control of power transformers,” IEEE Transactions on Industrial Electronics, vol. 64, no. 8, pp. 6432–64
  34. W. J. Kozacky and T. Ogunfunmi. (2013). “An active noise control algorithm with gain and power constraints on the adaptive filter,” EURASIP Journal on Advances in Signal Processing, vol. 2013, no. 1, pp. 17.
  35. S. M. Shah, R. Samar, N. M. Khan and M. A. Z. Raja. (2016). “Fractional-order adaptive signal processing strategies for active noise control systems,” Nonlinear Dynamics, vol. 85, no. 3, pp. 1363–1376.
  36. K. S. Tang, K. F. Man, S. Kwong, C. Y. Chan and C. Y. Chu. (1996). “Application of the genetic algorithm to real-time active noise control,” Real-Time Systems, vol. 11, no. 3, pp. 289–302.
  37. M. A. Z. Raja, U. Ahmed, A. Zameer, A. K. Kiani and N. I. Chaudhary. (2019). “Bio-inspired heuristics hybrid with sequential quadratic programming and interior-point methods for reliable treatment of economic load dispatch problem,” Neural Computing and Applications, vol. 31, no. 1, pp. 447–475.
  38. N. V. George and G. Panda. (2012). “A particle-swarm-optimization-based decentralized nonlinear active noise control system,” IEEE Transactions on Instrumentation & Measurement, vol. 61, no. 12, pp. 3378–3386.
  39. N. K. Rout, D. P. Das and G. Panda. (2016). “Particle swarm optimization based nonlinear active noise control under saturation nonlinearity,” Applied Soft Computing, vol. 41, pp. 275–289.
  40. M. A. Z. Raja, M. S. Aslam, N. I. Chaudhary, M. Nawaz and S. M. Shah. (2019). “Design of hybrid nature-inspired heuristics with application to active noise control systems,” Neural Computing and Applications, vol. 31, no. 7, pp. 2563–2591.
  41. W. U. Khan, Z. Ye, N. I. Chaudhary and M. A. Z. Raja. (2018). “Backtracking search integrated with sequential quadratic programming for nonlinear active noise control systems,” Applied Soft Computing, vol. 73, pp. 666–683.
  42. W. U. Khan, Z. Ye, N. I. Chaudhary and M. A. Z. Raja. (2019). “A novel application of fireworks heuristic paradigms for reliable treatment of nonlinear active noise control,” Applied Acoustics, vol. 146, pp. 246–260.
  43. H. Zhao, X. Zeng, Z. He, S. Yu and B. Chen. (2016). “Improved functional link artificial neural network via convex combination for nonlinear active noise control,” Applied Soft Computing, vol. 42, pp. 351–359.
  44. S. M. Kuo and D. R. Morgan. (2002). “Active noise control: A tutorial review,” Proceedings of the IEEE, vol. 87, no. 6, pp. 943–973.
  45. C. Y. Chang and K. K. Shyu. (2003). “Active noise cancellation with a fuzzy adaptive filtered-X algorithm,” IEE Proceedings: Circuits, Devices and Systems, vol. 150, no. 5, pp. 416–422.
  46. S. K. Behera, D. P. Das and B. Subudhi. (2014). “Functional link artificial neural network applied to active noise control of a mixture of tonal and chaotic noise,” Applied Soft Computing, vol. 23, pp. 51–60.
  47. S. Gholami-Boroujeny and M. Eshghi. (2012). “Nonlinear active noise cancellation using a bacterial foraging optimisation algorithm,” IET Signal Processing, vol. 6, no. 4, pp. 364–373.
  48. X. S. Yang, M. Karamanoglu and X. He. (2014). “Flower pollination algorithm: A novel approach for multiobjective optimization,” Engineering Optimization, vol. 46, no. 9, pp. 1222–1237.
  49. C. Y. Chang and D. R. Chen. (2010). “Active noise cancellation without secondary path identification by using an adaptive genetic algorithm,” IEEE Transactions on Instrumentation and Measurement, vol. 59, no. 9, pp. 2315–2327.
  50. M. A. Z. Raja, M. S. Aslam, N. I. Chaudhary and W. U. Khan. (2018). “Bio-inspired heuristics hybrid with interior-point method for active noise control systems without identification of secondary path,” Frontiers of Information Technology & Electronic Engineering, vol. 19, no. 2, pp. 246–2
  51. O. A. Arqub and M. Al-Smadi. (2018). “Atangana–Baleanu fractional approach to the solutions of Bagley–Torvik and Painlevé equations in Hilbert space,” Chaos, Solitons & Fractals, vol. 117, pp. 161–167.
  52. 61. O. A. Arqub and B. Maayah. (2018). “Numerical solutions of integrodifferential equations of Fredholm operator type in the sense of the Atangana–Baleanu fractional operator,” Chaos, Solitons & Fractals, vol. 117, pp. 117–124.
  53. 62. O. A. Arqub and B. Maayah. (2019). “Fitted fractional reproducing kernel algorithm for the numerical solutions of ABC: Fractional Volterra integro-differential equations,” Chaos, Solitons & Fractals, vol. 126, pp. 394–402.
  54. 63. O. A. Arqub and B. Maayah. (2019). “Modulation of reproducing kernel Hilbert space method for numerical solutions of Riccati and Bernoulli equations in the Atangana-Baleanu fractional sense,” Chaos, Solitons & Fractals, vol. 125, pp. 163–170.
  55. O. A. Arqub and N. Shawagfeh. (2019). “Application of reproducing kernel algorithm for solving Dirichlet time-fractional diffusion-Gordon types equations in porous media,” Journal of Porous Media, vol. 22, no. 4, pp. 411–434.
  56. C. Anitescu, E. Atroshchenko, N. Alajlan and T. Rabczuk. (2019). “Artificial neural network methods for the solution of second order boundary value problems,” Computers, Materials & Continua, vol. 59, no. 1, pp. 345–359.
  57. F. Li, C. Ou, Y. Gui and L. Xiang. (2019). “Instant edit propagation on images based on bilateral grid,” Computers, Materials & Continua, vol. 61, no. 2, pp. 643–656.
  58. K. Zhu, S. Ying, N. Zhang, R. Wang, Y. Wu et al. (2020). , “A performance fault diagnosis method for SaaS software based on GBDT algorithm,” Computers, Materials & Continua, vol. 62, no. 3, pp. 1161–1185.
  59. Y. Ruan, S. Marsh, X. Xue, Z. Liu and J. Wang. (2020). “The quantum approximate algorithm for solving traveling salesman problem,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1237–1247.
images This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.