DOI:10.32604/cmc.2021.013488
| Computers, Materials & Continua DOI:10.32604/cmc.2021.013488 | |
| Article |
A Fast and Effective Multiple Kernel Clustering Method on Incomplete Data
1Changsha Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation, School of Computer and Communication Engineering, Changsha University of Science and Technology, Changsha, 410114, China
2Hunan Key Laboratory of Smart Roadway and Cooperative Vehicle-Infrastructure Systems, Changsha University of Science and Technology, Changsha, 410114, China
3Faculty of Engineering and Information Technology, Global Big Data Technologies Centre, University of Technology Sydney, Ultimo, NSW, 2007, Australia
4Department of Computer Engineering, Chonnam National University, Gwangju, 61186, Korea
5Computer Science Department, Community College, King Saud University, Riyadh, 11437, Saudi Arabia
6Department of Mathematics and Computer Science, Faculty of Science, Menoufia University, Shebin-El-kom, 32511, Egypt
*Corresponding Author: Gwang-Jun Kim. Email: kgj@chonnam.ac.kr
Received: 08 August 2020; Accepted: 12 September 2020
Abstract: Multiple kernel clustering is an unsupervised data analysis method that has been used in various scenarios where data is easy to be collected but hard to be labeled. However, multiple kernel clustering for incomplete data is a critical yet challenging task. Although the existing absent multiple kernel clustering methods have achieved remarkable performance on this task, they may fail when data has a high value-missing rate, and they may easily fall into a local optimum. To address these problems, in this paper, we propose an absent multiple kernel clustering (AMKC) method on incomplete data. The AMKC method first clusters the initialized incomplete data. Then, it constructs a new multiple-kernel-based data space, referred to as K-space, from multiple sources to learn kernel combination coefficients. Finally, it seamlessly integrates an incomplete-kernel-imputation objective, a multiple-kernel-learning objective, and a kernel-clustering objective in order to achieve absent multiple kernel clustering. The three stages in this process are carried out simultaneously until the convergence condition is met. Experiments on six datasets with various characteristics demonstrate that the kernel imputation and clustering performance of the proposed method is significantly better than state-of-the-art competitors. Meanwhile, the proposed method gains fast convergence speed.
Keywords: Multiple kernel clustering; absent-kernel imputation; incomplete data; kernel k-means clustering
In many real-world scenarios, it is always easy to collect a large amount of data from the normal condition [1–3]. But it is often time-consuming and expensive to label them for supervised learning methods. On the other hand, it is very difficult to obtain data from the abnormal condition [4,5]. The above difficulties require the analytics methods should be in an unsupervised fashion. Moreover, the data are always collected from multiple sources [6]. Thus, it is necessary to employ the multiple-view clustering method [7], which is a critical technique for analyzing heterogeneous data from multiple sources [8]. Unlike single-view clustering [9,10], multiple-view clustering further integrates information from different sources that may have various data types and distributions. This integration poses significant challenges [11] to the multiple-view clustering approach. Most works dealing with multiple-view clustering focus on learning a unified clustering result that reflects consistent or complementary information contained in different sources [12–15]. However, they are unable to appropriately capture complex distributions (e.g., inseparable distribution) in each data source [16], which is difficult because these complex distributions reflect the essential information in the data.
In order to capture complex distributions, recent multiple-view clustering methods have introduced multiple kernels into their learning procedure; these methods are known as multiple kernel clustering methods [17–22]. The multiple kernel clustering method adopts multiple kernels to learn complex distributions and reformulates the integration of multiple-source information as a convex optimization problem. Ordinarily, the multiple kernel clustering method first captures the complex distributions in each data source using various kernels, namely base kernels; these base kernels project heterogeneous data into a homogeneous representation space [23,24]. The method then integrates multiple-source information by means of a unified kernel learning procedure, i.e., leverages the linear combination of several base kernels to generate a unified one. Subsequently, the method clusters objects according to the unified kernel which reflects the complex object relationships among multiple sources. As a result, multiple kernel clustering can achieve remarkable clustering performance on multiple-source data with complex distributions.
Although multiple kernel clustering methods can effectively cluster on multiple-source data with complex distributions, they may be heavily affected by a data incompleteness problem: namely, some data values in one or multiple sources may be missing due to lacking observations, data corruption, or environmental noise. The data incompleteness problem exists in a variety of scenarios, including neuro-imaging [25], computational biology [26], text security analysis [27], and medical analysis [28]. Most current multiple kernel clustering methods are unable to be implemented directly on data affected by the incompleteness problem. The main reason for this failure lies in the fact that a kernel matrix generated from a data source with missing values will be incomplete, as well as that a multiple kernel clustering method cannot learn a unified kernel based on incomplete base kernel matrices.
To tackle the data incompleteness problem, various absent-kernel imputation methods have been proposed. These methods impute an absent-kernel matrix according to different assumptions and strategies [29–31]. The representative imputation methods include zero-value imputation [29], mean value imputation [29], k-nearest-neighbor value imputation [29], and expectation-maximization value imputation [29]. More recently, several methods have further incorporated an imputation process with a clustering process and thereby significantly improved clustering performance [32–36].
Although the above absent-kernel imputation methods can enable multiple kernel clustering in the presence of the data incompleteness problem, they are still affected by several issues. Firstly, most of the above absent-kernel imputation methods ignore the relations between kernels when imputing missing values. It is very important that these relations are considered during absent-kernel imputation, they may reflect the redundant information contained in kernels [1]; this information can then be used as essential evidence for missing value imputation. Secondly, clustering methods that integrated with the above advanced absent-kernel imputation methods are less effective and less efficient than other state-of-the-art clustering methods. For example, the clustering accuracy and time-efficiency of both the multiple kernel k -means clustering in [32] and the localized multiple k -means clustering method used in [33] are worse than that of the unsupervised multiple kernel extreme learning machine [21]. Consequently, the accuracy of these absent-kernel imputation methods may be unsatisfactory, and their time cost may also be very large.
To address the above problems, this paper proposed an absent multiple kernel clustering (AMKC) method, which learns on unlabeled incomplete data from multiple sources and achieves high effectiveness and a fast learning speed. The AMKC method first adopts multiple kernels that map data from multiple sources into multiple kernel spaces, where the missing values are randomly imputed. It then conducts a three-stage procedure to iteratively cluster data, integrate multiple-source information, and impute missing values. In the first stage, AMKC clusters data based on a unified kernel learned. This clustering process can converge in limited iterations with a fast speed and excellent clustering performance. In the second stage, AMKC constructs a new multiple-kernel-based data space from multiple sources that contain incomplete data; this is done in order to learn the kernel combination coefficients so as to construct the unified kernel, which will be further used in the first stage of the next iteration. This construction enables improved information integration on multiple-source data with complex distributions. In the third stage, AMKC imputes the missing values in each base-kernel matrix, jointly considering the clustering objective and the relations between the kernels. AMKC performs this three-stage procedure iteratively until the convergence of its clustering performance. In summary, the main contributions of this paper can be outlined as follows:
1. It provides an effective multiple kernel clustering method for incomplete multi-source data. As AMKC avoids a local optimal solution, it significantly improves clustering performance.
2. It provides an efficient multiple kernel clustering method. AMKC can converge within a limited number of steps, which improves training speed and reduces the time cost of clustering.
3. It provides a high-precision absent-multiple-kernel imputation method. AMKC considers not only the relations between different kernels, but also the ties between kernel relations and the clustering objective. Consequently, the proposed method generates reliable and precise complete kernels.
We carry out extensive experiments on six datasets in order to evaluate the clustering performance of AMKC. Moreover, we adopt averaged relative error to measure the degree of recovery of the absent-kernel matrices imputed by AMKC. The experimental results demonstrate that: (1) AMKC performs better than comparison methods on datasets with a high missing ratio; (2) AMKC’s joint optimization and clustering process enable better clustering performance on the experimental datasets. This strong evidence supports the superior kernel imputation and clustering performance of AMKC.
The workflow of the AMKC method is illustrated in Fig. 1. In this architecture, AMKC adopts an iterative three-stage procedure to cluster data, learn kernel combination coefficients, and impute absent-kernel matrices. In the first stage, AMKC clusters data based on a unified learned kernel. This clustering process can converge in limited iterations, rapidly and with high clustering performance. In the second stage, AMKC constructs a new multiple-kernel-based data space to learn the kernel combination coefficients; this construction enables better information integration on multiple-source data with complex distributions. In the third stage, AMKC imputes the missing values in each base-kernel matrix. AMKC then performs this three-stage procedure iteratively until convergence of its clustering performance occurs.
Figure 1: Workflow of the proposed AMKC method
2.2 First Stage: Kernel K-Means Clustering
The first step in the first stage is to conduct kernel k-means clustering on a unified imputed and learned kernel. This unified kernel, which is a weighted combination of the observed values in the absent-kernel matrices, is calculated as follows:
where m is the number of the employed base kernel matrices; 
is an optimal base kernel matrix, which is learned and imputed in the third stage in the next iteration. Initially, 
inherits the observed values in the p -th absent-kernel matrix with other values as 0 . 
is a set of combination coefficients that satisfies 
and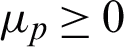 
. In the AMKC learning process, all coefficients in 
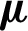are initialized as 1/m . Following initialization, these coefficients will be learned in the second stage of the AMKC’s iterative three-stage procedure. With the unified learned kernel 
, we can formalize the kernel k -means clustering’s objective function as below:
where the cluster assignment matrix 
, cij indicates whether the i-th object belongs to the j -th cluster, n is the number of the objects in a dataset, nc is the number of clusters,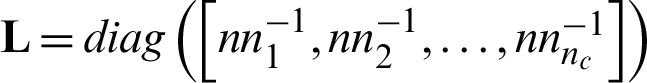 
, 
refers to the number of objects in the j-th cluster, and 
is a k -dimensional vector in which all values are 1. It should be a remarkable fact here that it is very difficult to solve Eq. (2) directly, as the values in 
are discrete (i.e., either 0 or 1); one solution would be to relax Eq. (2) by allowing 
to take real values. Accordingly, Eq. (2) can be reduced to:
where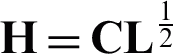 
including the clustering performance. The clustering label of an object is determined by the elements in its corresponding row of 
. Here, AMKC sets the clustering pseudo-label yi of the i-th object xi in the dataset as the 
, where 
is the ij-th element of 
. In order to obtain the optimal 
for improving the clustering results, we follow the way in [37] to solve Eq. (3). As a result, the nc eigenvectors relating to the nc largest eigenvalues from 
are selected as the optimal 
.
2.3 Second Stage: Kernel Combination Coefficients Learning
In the second stage, the set of combination coefficients 
in Eq. (1) are learned in a transformed space. Following [38], AMKC formulates the combination coefficients learning process as a binary classification problem. More specifically, AMKC first constructs a kernel feature space, referred to as K-space, based on imputed kernel matrices and the clustering pseudo-labels learned in the first stage.
Initially, the p -th imputed kernel matrix is set as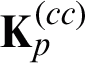 
; this will be learned and imputed in the third stage following initialization. If the data in the K -space is denoted as 
, the given multiple-sources dataset is 
, then the transformation from multiple kernel matrices of 
to 
can be expressed as follows:
where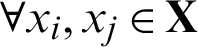 
, 
is the result corresponding to object xi and xj from the p -th kernel matrix, while 
is an object in 
transformed from object xi and xj in 
by m base kernel matrices. Thus, all data in the K -space can be denoted as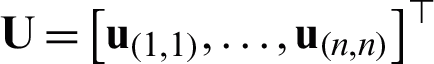 
, while the label S(xi, xj) of 
in the K -space can be defined from the pseudo-labels yi and yj of objects xi and xj as follows:
Following the above K-space construction, AMKC learns the optimal combination coefficients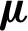 
for the unified kernel 
through a closed-form solution [39]:
or:
where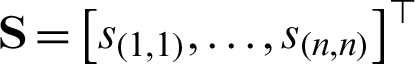 
, C is a trade-off parameter. Eqs. (6) and (7) are suitable for datasets with different characteristics. AMKC uses Eq. (6) to quickly learn the optimal 
for a large-scale dataset. For data obtained from a large number of different sources, AMKC adopts Eq. (7) to calculate the optimal solution with more efficiency. The learned optimal 
will be employed to construct the unified and imputed kernel 
in the first stage in the next iteration.
2.4 Third Stage: Absent-Kernel Matrices Imputation
The AMKC method learns and imputes absent-kernel matrices in the third stage based on the clustering pseudo-label and kernel combination coefficients learned in the first and second stages, respectively. The learning objective can be formalized as follows:
In the third stage, AMKC regards 
and 
as constants. AMKC utilizes the optimal 
, which is generated on m base kernels in the first stage, and the optimal m combination coefficients 
, which are optimized in the second stage. Thus, the optimization in Eq. (8) is equivalent to the optimization problem in Eq. (9) in respect of 
:
When approached directly, the optimization problem in Eq. (9) appears to be intractable due to 
being of m number of different kernel matrices. Thus, we solve this optimization problem to impute the missing value of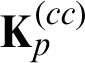 
from the perspective of matrix decomposition. Let 
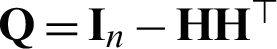, Eq. (9) can be decomposed as m independent sub-problems equivalently. The p -th sub-problem is formalized as follows:
Because 
is PSD (Positive Semi-Definite) in the above sub-problem [32], the optimal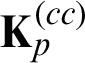 
in Eq. (10) can be obtained by using a closed-form expression. Let 
be decomposed as 
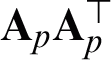, and 
with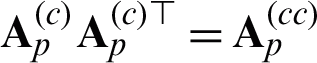 
. Here, 
meaning the p -th kernel sub-matrix calculated from the objects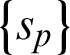 
s whose p -th view are present. With the similar form, the matrix 
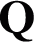in Eq. (10) can be expressed in block form as
As a result, by rewriting the optimization problem in Eq. (10), a closed-form expression in Eq. (11) can be obtained for the optimal 
, which will be used to impute and update the unified kernel 
in the next iteration.
The iterative three-stage procedure of AMKC is outlined in Algorithm 1.
As noted above, it is not easy to simultaneously optimize the three variables 
, 
and 
at different stages, as 
is both incomplete and independent. Accordingly, in the iterative three-stage procedure, AMKC optimizes these three variables independently. At each stage, AMKC optimizes one of these variables and treats the others as constants. In this way, AMKC can obtain the local optimal values of these three variables after the iteration converges. AMKC determines the iteration convergence based on the changes in the loss value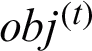 
of the clustering objective function Eq. (3), where t refers to the t -th iteration. More specifically, AMKC defines a convergence index as 
. If the value of cov is smaller than a pre-defined 
, AMKC will stop the iterative procedure.
In order to demonstrate the fast learning speed of the proposed method AMKC, we theoretically analyze and discuss its time complexity in this section. The time complexity of AMKC is primarily determined by three components: kernel k -means clustering, kernel combination coefficient learning, and absent-kernel matrices imputation.
Suppose the number of objects is n, the number of base kernels is m. For kernel k-means clustering in the first stage, its time complexity can be reduced from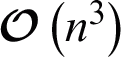 
to 
via cluster shifting [40]. For the second stage: kernel combination coefficient learning, if the optimal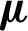 
is learned by solving Eq. (6), then the time complexity is 
, while that is 
by solving Eq. (7). For absent-kernel matrices imputation in the third stage, the time cost depends on three matrix operations in Eq. (11), the time complexity of which is 
, where c and l refer to the number of objects with incomplete and complete values, respectively, c + l = n . Because both c and l are less than or equal to n,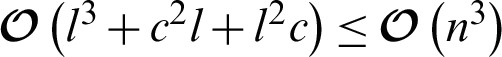 
. Above all, time complexity of AMKC in each iteration is mainly determined by 
or 
in the second stage. Obviously, if m < n , then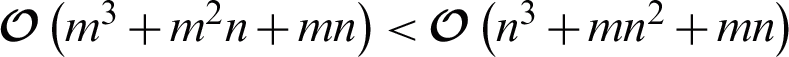 
. Thus, in order to reduce the time complexity in each iteration for achieving a fast learning speed, AMKC is best to use Eq. (6) when n is very large, while using Eq. (7) for m is very large. Namely, the time complexity of AMKC in an iteration is 
or 
. Accordingly, the time complexity of AMKC in nt iterations is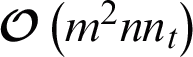 
or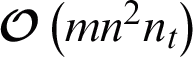 
. In practical terms, nt also effects the efficiency of AMKC. Fortunately, AMKC is able to theoretically converge within finite iterations, as demonstrated in Theorem 1, and nt can be empirically proved to be a very small number when the convergence condition is met, as shown in Fig. 7.
In this section, we theoretically testify that AMKC algorithm can converge within finite steps to support its fast learning speed.
Theorem 1. The AMKC algorithm (see Algorithm 1) can converge to a local optimum within finite iterations.
Proof. Given a dataset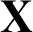 
, AMKC first conducts kernel k -means clustering with the clustering loss 
. Suppose the number of all possible partitions is y , and each partition is represented by a cluster assignment matrix 
. Their assignment matrices are different when the two partitions are different; otherwise, they are identical.
Assuming that the number of clusters nc is finite, for nt iterations, AMKC generates a series of imputed kernels 
(i.e., 
) and a series of cluster assignment matrices 
(i.e., 
). Given a cluster assignment matrix 
and an imputed unified kernel 
, the clustering loss in AMKC is denoted as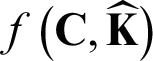 
.
In the first stage, the kernel k -means clustering converges to a minimal solution. The AMKC achieves 
in the nt-th iteration; moreover, since the unified kernel has been imputed and the clustering also converges to a minimal solution,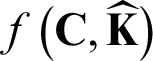 
is strictly decreasing (i.e., 
). Assuming that 
, there are at least two identical assignment matrices in the series of cluster assignment matrices 
(i.e., 
, 
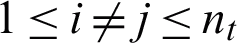). Because 
, we can infer that 
; therefore, the value of the clustering loss does not change (i.e., 
). In this case, the convergence criterion of AMKC is satisfied and the AMKC algorithm stops. Since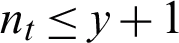 
, AMKC (Algorithm 1) converges to a local optimum in finite iterations.
In order to evaluate the AMKC’s performance, we conduct experiments on six datasets; namely, Iris [41], Lib [41], Seed [41], Isolet [41], Cifar [42], and Caltech256 [43]. Of these data sets, Iris, Lib, Seed and Isolet are collected from UCI data repository [41], and are commonly used to evaluate multi-view learning methods [18,44] and multiple kernel learning methods [21,38]. Furthermore, these four datasets were all collected from different real-life scenarios with different characteristics, enabling a comprehensive evaluation of the proposed method from different perspectives. The remaining datasets, i.e., Cifar and Caltech256 have also been commonly used to evaluate machine learning method in recent research. For Cifar and Caltech256, we chose 300 and 10 objects belonging to each cluster respectively. The important statistics including the number of objects, base kernels, and classes of these datasets are listed in Tab. 1; The base kernels used in the experiments include three kinds of kernel, namely, linear kernel, polynomial kernels with degree 
, and Gaussian kernels with kernel width falling within the range of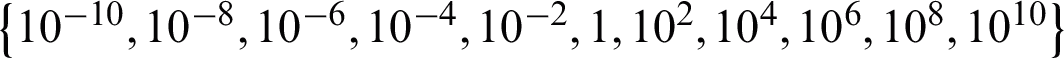 
.
The clustering performance of AMKC is compared with other two-stage clustering methods for incomplete kernels. The comparison methods firstly complete the absent base kernels with special values learned by different imputation methods, and then conduct multiple kernel k -means clustering (MKKM) [45] on the imputed kernels. In our experiments, four representative imputation methods are employed; namely, zero imputation (ZI), mean imputation (MI), k -nearest-neighbor imputation (KNN), and alignment maximization imputation (AF). For convenience, the methods combined MKKM with different imputation methods are denoted as 
, 
, 
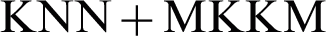and 
, respectively. Furthermore, the state-of-the-art method 
[32], which iteratively performs clustering and kernel imputation, is also employed for comparison. We do not include the MVKC method [35] in our clustering performance comparison because of its high computational cost, even for small amounts of data. Instead, we simply compared MVKC with AMKC in terms of imputation precision.
4.1.3 Absent Kernel Generation
We follow the approach in [32] to generate absent kernels. More specifically, 
objects are randomly selected, where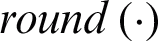 
means that rounds each input element to the nearest integer, 
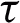is the missing ratio. The 
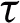is set to 
. Subsequently, we predefine a random threshold 
, and generate a random vector 
obeying uniform distribution. For 
, if 
holds, the selected 
objects will be deleted for the p -th base kernel.
To reduce the impact caused by the tested datasets and randomness of the kernel k -means clustering, for the same parameters 
, 
, and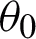 
, the absent-base-kernel matrices are randomly generated 10 times by randomly selecting different objects to be absent. Furthermore, for each series of generated absent-base-kernel matrices, we repeatedly carry out random initialization 20 times for extensive experiments.
To accurately evaluate the clustering performance and effectiveness of the methods of interest, we measure the clustering results through three performance measures: clustering accuracy (ACC), normal mutual information (NMI) and Purity. Differently-parameterized results of ACC, NMI and Purity are aggregated by averaging them, respectively. Since the proposed method combines kernel imputation and clustering, we can get new imputed kernel matrices and clustering results at the same time. In order to verify the degree of recovery of AMKC for absent kernel matrices, we measure the average relative error (ARE) [35,46] between the complete missing values and the original value among all views.
4.2 Recovery of the Absent Kernels
To validate the degree of recovery achieved by the proposed AMKC, when the base kernels are diverse, our results are compared with several state-of-the-art kernel matrix completion methods, namely, Multi-view Kernel Completion (MVKC) [35] and MKKM with incomplete Kernels (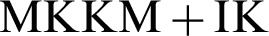
) on the Iris dataset with various kernels. We generated three sets of kernel matrices with various kernels and different parameters. In more detail, as shown in Fig. 2, KH1, KH2 and KH3 are denoted those combined with three Gaussian kernels, one linear kernel and two Gaussian kernels, and three linear kernels, respectively. We then randomly generated the missing matrices based on KH1, KH2, and KH3 and applied the comparison methods to them. Finally, the average relative error (ARE) (Eq. (11)) [35,46] is taken to measure the error between the predicted kernel matrix and the original matrices KH1, KH2 and KH3. The average relative error is computed over all missing data points for all views, as follows:
where np is the number of missing samples in the p -th view, 
is the set of indices of all missing data in the p -th view, 
and 
refer to the learned imputed kernel matrix and the original complete one.
Figure 2: ARE comparison on various kernels. (a) KH1, (b) KH2, (c)KH3
The ARE values for the comparison methods are presented in Fig. 2. We can see from the figure that the proposed method generally predicts missing values more accurately than MVKC and 
on the Gaussian kernel. When the base kernel contains a non-linear kernel (Gaussian kernel), the MVKC performs no better than 
and MVKC (see Figs. 2a and 2b) due to the prior assumption on the linear assumption. Since the proposed method considers connection among kernels and clustering guidance, regardless of the type of the composed kernel, the proposed method is able to recover the absent kernels more efficiently, as in Fig. 2.
4.3 Clustering Performance Analysis
The clustering results of different clustering methods for incomplete data are shown in Figs. 3–5. Respectively, they present a comparison of the ACC, NMI, and Purity of six clustering methods on each dataset. It can be seen that the proposed method outperforms other comparison methods on six datasets. And the clustering performance of the proposed AMKC remains robust as the missing ratio grows larger, while the clustering performance of the other comparison methods, especially 
, 
, 
, exhibits a quick downward. As the term ACC can measure the distance between the learned clustering pseudo-labels and actual ones to some extent, the higher ACC for large missing ratios can prove that the proposed method is able to effectively restore datasets through its iterative process.
Figure 3: ACC comparison of different methods on six datasets. (a) Iris, (b) Lib, (c) Seed, (d) Isolet, (e) Cifar, (f) Caltech256
Figure 4: NMI comparison of different methods on six datasets. (a) Iris, (b) Lib, (c) Seed, (d) Isolet, (e) Cifar, (f) Caltech256
Figure 5: Purity comparison of different methods on six datasets. (a)Iris, (b) Lib, (c) Seed, (d) Isolet, (e) Cifar, (f) Caltech256
In order to investigate comprehensively the effectiveness of the proposed method, the aggregated ACC, NMI and Purity along with their standard deviations (
) are listed in Tabs. 2–4, respectively. It is clear that the proposed method obtained the best performance shown in bold. Namely, the proposed method performs better than other comparison methods in all datasets, which is consistent with the conclusion from Figs. 3–5. The superiority of the proposed method can be attributed to joint optimization on clustering, combination coefficients and kernel imputation. In the three-stage procedure of the proposed method, the clustering information are employed to guide the kernel imputation into an optimum, while the good imputed unified kernel prompts the clustering result. Thus, the clustering performances of the proposed method can be greatly improved.
Table 2: Comparison of aggregated ACC (
std) on six datasets
Table 3: Comparison of aggregated NMI (
std) on six datasets
Table 4: Comparison of aggregated purity (
std) on six datasets
4.4 Comparison with Baseline Algorithm
Since the proposed method can simultaneously achieve clustering and kernel imputation as the extend of the unsupervised multiple kernel extreme learning machine (UMK-ELM) [21], we provide TUMK-ELM (the two-stage UMK-ELM) [37] as a baseline and compare the clustering performance of the proposed method with four aforementioned imputation methods: ZI, MI, KNN, and AF imputation (They referred to as 
, 
, 
, and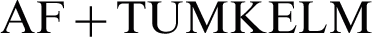 
).
Here, we carry out the experiments only on the Iris, Lib, and Seed datasets. Moreover, taking the ACC for example, the corresponding ACC values of each method in each appointed dataset with a variety of missing ratio are calculated. Our experimental results (see Fig. 6) demonstrate that the performance of the proposed method (line in black) is the closest to that of TUMK-ELM (line in red), where the datasets used in TUMK-ELM are complete. This indicate that the proposed method can not only obtain good clustering results, but is also able to achieve outstanding imputation performance.
Figure 6: ACC comparison of the baseline with different imputationalgorithms. (a) Iris, (b) Lib, (c) Seed
4.5 Convergence Speed Analysis
In order to investigate the convergence speed of the proposed AMKC method, additional experiments are carried out on three main datasets (Iris, Lib and Seed). The results of the objective value (obj in Algorithm 1) in each iteration for the fixed missing ratio 0.9 are shown in Fig. 7. From Fig. 7, we can observe that the objective value tends to converge quickly. As the convergence speed of the objective value determine AMKC’s convergence speed, the experimental results demonstrate AMKC can converge within only a few iterations on these three datasets. Thus, the proposed method has a fast convergence speed.
Figure 7: The objective value of the proposed method per iterationwith missing ratio of 0.9. (a) Iris, (b) Lib, (c) Seed
As the multiple-kernel clustering method has promising and competitive performance, it can be widely employed in various applications. In order to cope with incomplete data or base kernels, we proposed a new multiple-kernel clustering method with absent kernels, which jointly cluster and impute the incomplete kernels to achieve clustering performance. Our method iteratively performs three stages utilizing an optimization strategy to obtain optimal clustering information, combination coefficients and imputed kernels, so better clustering for the absent kernels are gained. Extensive experiments on six datasets have verified the improved performance of the proposed method.
Acknowledgement: This work was funded by the Researchers Supporting Project No. (RSP-2020/102) King Saud University, Riyadh, Saudi Arabia.
Funding Statement: This research was funded by National Natural Science Foundation of China under Grant Nos. 61972057 and U1836208, Hunan Provincial Natural Science Foundation of China under Grant No. 2019JJ50655, Scientific Research Foundation of Hunan Provincial Education Department of China under Grant No. 18B160, Open Fund of Hunan Key Laboratory of Smart Roadway and Cooperative Vehicle Infrastructure Systems (Changsha University of Science and Technology) under Grant No. kfj180402, the “Double First-class” International Cooperation and Development Scientific Research Project of Changsha University of Science and Technology under Grant No. 2018IC25, the Researchers Supporting Project No. (RSP-2020/102) King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest: The authors declare no conflict of interest.
References
1. J. Wang, Y. Yang, T. Wang, R. S. Sherratt and J. Zhang. (2020). “Big data service architecture: A survey,” Journal of Internet Technology, vol. 21, no. 2, pp. 393–405.
2. F. Yu, L. Liu, H. Shen, Z. Zhang, Y. Huang et al. (2020). , “Dynamic analysis, circuit design and synchronization of a novel 6D memristive four-wing hyperchaotic system with multiple coexisting attractors,” Complexity, vol. 2020, no. 12, pp. 1–17.
3. J. Wang, Y. Zou, L. Peng, L. Wang, O. Alfarraj et al. (2020). , “Research on crack opening prediction of concrete dam based on recurrent neural network,” Journal of Internet Technology, vol. 21, no. 4, pp. 1161–1170.
4. J. Wang, Y. Tang, S. He, C. Zhao, P. K. Sharma et al. (2020). , “LogEvent2vec: Logevent-to-vector based anomaly detection for large-scale logs in internet of things,” Sensors, vol. 20, no. 9, pp. 2451.
5. Y. Chen, J. Tao, Q. Zhang, K. Yang, X. Chen et al. (2020). , “Saliency detection via improved hierarchical principle component analysis method,” Wireless Communications and Mobile Computing, vol. 2020, pp. 8822777.
6. X. Shen, W. Liu, I. W. Tsang, Q. S. Sun and Y. S. Ong. (2018). “Multilabel prediction via cross-view search,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 9, pp. 4324–4338.
7. S. Bickel and T. Scheffer. (2004). “Multi-view clustering,” in Fourth IEEE Int. Conf. on Data Mining (ICDM’04Brighton, UK, pp. 19–26.
8. L. Xiang, X. Shen, J. Qin and W. Hao. (2019). “Discrete multi-graph hashing for large-scale visual search,” Neural Processing Letters, vol. 49, no. 3, pp. 1055–1069.
9. J. Wang, Y. Gao, W. Liu, W. Wu and S. J. Lim. (2019). “An asynchronous clustering and mobile data gathering schema based on timer mechanism in wireless sensor networks,” Computers, Materials & Continua, vol. 58, no. 3, pp. 711–725.
10. Z. Zhou, J. Qin, X. Xiang, Y. Tan, Q. Liu et al. (2020). , “News text topic clustering optimized method based on TF-IDF algorithm on spark,” Computers, Materials & Continua, vol. 62, no. 1, pp. 217–231. [Google Scholar]
11. C. Zhu, L. Cao, Q. Liu, J. Yin and V. Kumar. (2018). “Heterogeneous metric learning of categorical data with hierarchical couplings,” IEEE Transactions on Knowledge and Data Engineering, vol. 30, no. 7, pp. 1254–1267. [Google Scholar]
12. K. Chaudhuri, S. M. Kakade, K. Livescu and K. Sridharan. (2009). “Multi-view clustering via canonical correlation analysis,” in Proc. of the 26th Annual Int. Conf. on Machine Learning, Montreal, Quebec, Canada, pp. 129–136. [Google Scholar]
13. J. Liu, C. Wang, J. Gao and J. Han. (2013). “Multi-view clustering via joint nonnegative matrix factorization,” in Proc. of the 2013 SIAM Int. Conf. on Data Mining, Austin, Texas, USA, pp. 252–260. [Google Scholar]
14. W. Lu, X. Zhang, H. Lu and F. Li. (2020). “Deep hierarchical encoding model for sentence semantic matching,” Journal of Visual Communication and Image Representation, vol. 71, 102794. [Google Scholar]
15. Z. Liu, Z. Lai, W. Ou, K. Zhang and R. Zheng. (2020). “Structured optimal graph based sparse feature extraction for semi-supervised learning,” Signal Processing, vol. 170, 107456. [Google Scholar]
16. Y. Yang and H. Wang. (2018). “Multi-view clustering: A survey,” Big Data Mining and Analytics, vol. 1, no. 2, pp. 83–107. [Google Scholar]
17. G. Tzortzis and A. Likas. (2012). “Kernel-based weighted multi-view clustering,” in IEEE 12th Int. Conf. on Data Mining, Brussels, Belgium, pp. 675–684. [Google Scholar]
18. D. Guo, J. Zhang, X. Liu, Y. Cui and C. Zhao. (2014). “Multiple kernel learning based multi-view spectral clustering,” in Int. Conf. on Pattern Recognition, Milan, Italy, pp. 3774–3779. [Google Scholar]
19. X. Liu, S. Zhou, Y. Wang, M. Li, Y. Dou et al. (2017). , “Optimal neighborhood kernel clustering with multiple kernels,” in 31st AAAI Conf. on Artificial Intelligence, San Francisco, USA, pp. 2266–2272. [Google Scholar]
20. J. Wang, J. Qin, X. Xiang, Y. Tan and N. Pan. (2019). “CAPTCHA recognition based on deep convolutional neural network,” Mathematical Biosciences and Engineering, vol. 16, no. 5, pp. 5851–5861. [Google Scholar]
21. L. Xiang, G. Zhao, Q. Li, W. Hao and F. Li. (2018). “TUMK-ELM: A fast unsupervised heterogeneous data learning approach,” IEEE Access, vol. 6, pp. 35305–35315. [Google Scholar]
22. Q. Wang, Y. Dou, X. Liu, F. Xia, Q. Lv et al. (2018). , “Local kernel alignment based multi-view clustering using extreme learning machine,” Neurocomputing, vol. 275, pp. 1099–1111. [Google Scholar]
23. W. Li, H. Liu, J. Wang, L. Xiang and Y. Yang. (2019). “An improved linear kernel for complementary maximal strip recovery: Simpler and smaller,” Theoretical Computer Science, vol. 786, pp. 55–66. [Google Scholar]
24. Y. T. Chen, J. J. Tao, L. W. Liu, J. Xiong, R. L. Xia et al. (2020). , “Research of improving semantic image segmentation based on a feature fusion model,” Journal of Ambient Intelligence and Humanized Computing, vol. 29, no. 2, pp. 753. [Google Scholar]
25. L. Yuan, Y. Wang, P. M. Thompson, V. A. Narayan and J. Ye. (2012). “Multi-source learning for joint analysis of incomplete multi-modality neuroimaging data,” in Proc. of the 18th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Beijing, China, pp. 1149–1157. [Google Scholar]
26. G. Chechik, G. Heitz, G. Elidan, P. Abbeel and D. Koller. (2008). “Max-margin classification of data with absent features,” Journal of Machine Learning Research, vol. 9, pp. 1–21. [Google Scholar]
27. L. Xiang, S. Yang, Y. Liu, Q. Li and C. Zhu. (2020). “Novel linguistic steganography based on character-level text generation,” Mathematics, vol. 8, pp. 1558. [Google Scholar]
28. J. M. Jerez, I. Molina, P. J. García-Laencina, E. Alba, N. Ribelles et al. (2010). , “Missing data imputation using statistical and machine learning methods in a real breast cancer problem,” Artificial Intelligence in Medicine, vol. 50, no. 2, pp. 105–115. [Google Scholar]
29. Z. Ghahramani and M. I. Jordan. (1994). “Supervised learning from incomplete data via an EM approach,” in Advances in Neural Information Processing Systems, Denver, Colorado, USA, ACM, pp. 120–127. [Google Scholar]
30. A. Trivedi, P. Rai, H. Daumé III and S. L. Duvall. (2010). “Multiview clustering with incomplete views,” The Twenty-Fourth Annual Conf. on Neural Information Processing Systems, Vancouver, Canada, vol. 224, pp. 1–7. [Google Scholar]
31. W. Shao, X. Shi and S. Y. Philip. (2013). “Clustering on multiple incomplete datasets via collective kernel learning,” in IEEE 13th Int. Conf. on Data Mining, Dallas, Texas, USA, pp. 1181–1186. [Google Scholar]
32. X. Liu, M. Li, L. Wang, Y. Dou, J. Yin et al. (2017). , “Multiple kernel k-means with incomplete kernels,” in Thirty-First AAAI Conf. on Artificial Intelligence, California, USA, pp. 2259–2265. [Google Scholar]
33. X. Zhu, X. Liu, M. Li, E. Zhu, L. Liu et al. (2018). , “Localized incomplete multiple kernel k-means,” in Proc. of the 27th Int. Joint Conf. on Artificial Intelligence, Stockholm, Sweden, pp. 3271–3277. [Google Scholar]
34. Y. Ye, X. Liu, Q. Liu and J. Yin. (2017). “Consensus kernel k-means clustering for incomplete multi-view data,” Computational Intelligence and Neuroscience, vol. 2017, 3961718. [Google Scholar]
35. S. Bhadra, S. Kaski and J. Rousu. (2017). “Multi-view kernel completion,” Machine Learning, vol. 106, no. 5, pp. 713–739. [Google Scholar]
36. L. Zhao, Z. Chen, Y. Yang, Z. J. Wang and V. C. M. Leung. (2018). “Incomplete multi-view clustering via deep semantic mapping,” Neurocomputing, vol. 275, pp. 1053–1062. [Google Scholar]
37. S. Jegelka, A. Gretton, B. Schölkopf, B. K. Sriperumbudur and U. VonLuxburg. (2009). “Generalized clustering via kernel embeddings,” in Annual conf. on Artificial Intelligence, Québec City, Québec, Canada: Springer, pp. 144–152. [Google Scholar]
38. C. Zhu, X. Liu, Q. Liu, Y. Ming and J. Yin. (2015). “Distance based multiple kernel ELM: A fast multiple kernel learning approach,” Mathematical Problems in Engineering, vol. 2015, no. 6, pp. 1–9. [Google Scholar]
39. G. B. Huang, Q. Y. Zhu and C. K. Siew. (2006). “Extreme learning machine: Theory and applications,” Neurocomputing, vol. 70, no. 1–3, pp. 489–501. [Google Scholar]
40. A. Kumar, P. Rai and H. Daume. (2011). “Co-regularized multi-view spectral clustering,” in Proc. of the 24th Int. Conf. on Neural Information Processing Systems, New York, USA, pp. 1413–1421. [Google Scholar]
41. D. Dua and C. Graff. (2017). “UCI machine learning repository,” . [Online]. Available: http://archive.ics.uci.edu/ml. [Google Scholar]
42. A. Krizhevsky and G. Hinton. (2009). Learning Multiple Layers of Features from Tiny Images. Technical Report, Citeseer, Statecolich, PA, USA. [Google Scholar]
43. G. Griffin, A. Holub and P. Perona. (2006). “Cal-tech256 image dataset,” . [Online]. Available: http://www.vision.caltech.edu/Image_Datasets/Caltech256/. [Google Scholar]
44. X. Cai, F. Nie and H. Huang. (2013). “Multi-view k-means clustering on big data,” in Twenty-Third Int. Joint Conf. on Artificial Intelligence, Menlo Park, California, USA, pp. 2598–2604. [Google Scholar]
45. S. Yu, L. Tranchevent, X. Liu, W. Glanzel, J. A. K. Suykens et al. (2011). , “Optimized data fusion for kernel k-means clustering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 34, pp. 1031–1039. [Google Scholar]
46. M. Xu, R. Jin and Z. H. Zhou. (2013). “Speedup matrix completion with side information: Application to multi-label learning,” in Advances in Neural Information Processing Systems, Nevada, USA, pp. 2301–2309. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |