DOI:10.32604/cmc.2021.012739
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012739 | |
| Article |
Novel Analytical Thermal Performance Rate Analysis in ZnO-SAE50 Nanolubricant: Nonlinear Mathematical Model
1Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif, AJ&K, 12080, Pakistan
2Department of Mathematics and Statistics, Hazara University, Mansehra, 21120, Pakistan
3Department of Mathematics, HITEC University, Taxila, Cantt, 47070, Pakistan
4University of Multan, Multan, 66000, Pakistan
5Department of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, 72915, Vietnam
6Department of Mechanical Engineering, College of Engineering, King Saud University, Al-Riyadh, 11421, Saudi Arabia
7Department of Physical Chemistry, Electrochemistry and Corrosion Laboratory, National Research Centre, Cairo, 12622, Egypt
*Corresponding Author: Ilyas Khan. Email: ilyaskhan@tdtu.edu.vn
Received: 11 July 2020; Accepted: 30 August 2020
Abstract: The investigation of local thermal transport rate in the nanolubricants is significant. These lubricants are broadly used in environmental pollution, mechanical engineering and in the paint industry due to high thermal performance rate. Therefore, thermal transport in ZnO-SAE50 nanolubricant under the impacts of heat generation/absorption is conducted. The colloidal suspension is flowing between parallel stretching disks in which the lower disk is positioned at z = 0 and upper disk apart from distance d. The problem is transformed in dimensionless version via described similarity transforms. In the next stage, an analytical technique (VPM) is implemented for the solution purpose. The graphical results against multiple flow parameters were furnished over the region of interest and explained comprehensively. It is imperative to mention that the results are plotted for ZnO-SAE50 and conventional liquid as well. Further, rapid motion of the fluid is perceived against high Reynolds and 
parameters. The wall shear stresses at the upper end rises for multiple Reynolds and 
while; decrement is detected at the lower end. The significant contribution of an internal heat source is noted for thermal performance rate at the upper end. Foremost, the local heat transport rate declines at the lower disk. By altering Reynolds number, prompt heat transfer rate is gained at the upper disk and increasing behavior of the local heat transport rate is slow at the lower disk. From the study, it is concluded that the nanolubricants have high thermal characteristics. Therefore, such fluids are reliable to use in above stated areas.
Keywords: Zno-SAE50 nanolubricant; thermal performance; local heat transport; numerical algorithm; skin friction
The heat transport properties in the regular liquids are very poor in view of industrialist, engineers and scientists. However, remarkable heat transport is essential to finished many industrial products. Therefore, regular liquids are not suitable for such processes. To overcome the problems faced by the industrialist, a new category of fluids is developed called “Nanofluids” [1]. In these fluids, tiny sized solid particles stably dispersed in the regular liquids and no slip occur between them. The inspection of heat transport in these fluids under certain restrictions is significant from engineering view point.
The heat transfer with squeezing effects bounded by two disks in parallel position was reported in [2]. They found the flow behavior against multiple quantities via Variational Iteration technique and explained comprehensively. They revealed that the thermal behavior of the fluid is in direct proportion while inverse behavior of the fluid velocity is detected against different quantities. The influence of graphene oxide based colloidal mixture on the heat transfer is examined in [3]. They plugged the brownian effects in the energy law for novelty of the study. It was detected that the higher magnetic effects resist the fluid motion and significant increment in the fluid thermal behavior was reported. The fluid velocity and temperature against velocity and thermal slips was introduced in [4]. They found the tabulated results for the shear stresses and local thermal performance of the fluid by assigning the vales to multiple ingrained quantities. Further, for reliability of the presented work, they made comparative analysis by adopting two separate techniques and detected that both the results are in line with each other.
In 2017, Vajravelu et al. [5] presented the analysis regarding to the heat transport in the colloidal composition. They merged thermal conductance with variable characteristics in the energy equation to improve the thermal performance of the fluid. Moreover, they examined that the fluid temperature and concentration are directly proportional to thermal conductance. A novel inspection of nanofluid thermal transport by plugging the influence of Cattaneo–christov model in radiative energy equation were pointed in [6]. They analyzed the behavior of thermal and velocity trends against varying parameters in finite region. The inspection of local heat transport between parallel disks was done in [7]. Recently, Sobamowo et al. [8] inspected the magneto-radiative flow regimes of third grade fluid between two disks placed in parallel position. They found that the thermal transport in the fluid enhanced for higher radiative effects and it drops against higher Prandtl values. The flow and improved thermal transport in GO-MoS2/H2O-C2H6O2 hybrid nanoliquid was presented in [9]. They pointed the effects of thermal relaxation and radiative parameters on the thermal transport and motion of the fluid. Further, decorated results revealed that the thermal transport significantly enhances in hybrid nanoliquids.
Recently, Khan et al. [10] studied second law analysis by considering bioconvection colloidal model. They conducted the study between stretchable disks. They decorated the results for biothermal fields against multiple parameters and explained comprehensively. The increment in radial velocity for higher stretching and magnetic effects. Further, rise in motile gyrotactic profile against Peclet and Lewis parameters are reported in the study. The heat transport inspection in magnetized rotating hybrid nanoliquid between two surfaces inspired by radiative heat flux and Ohmic heating is presented in [11]. They examined the behavior of hybrid nanoliquid flow for preeminent parameters and also reported that the local thermal performance of the liquid enhances against merging parameters. Aziz et al. [12] conducted boundary analysis inspired by power law fluid over stretchable surface. They revealed that augmentation in power index parameter declines the shear stresses and Sherwood number. Novel inspection of entropy generation in Sisko liquid over stretchable surface was done in [13]. They inspected the model numerically and pointed the effects of ingrained quantities in the flow regimes. The effects of embedded parameters on the entropy generation and Bejan number are painted and explained comprehensively.
Analytical inspection of thermal analysis in nanoliquid by considering inconstant Lorentz forces was revealed in [14]. The direct relation between local thermal performance rate and thermophoretic parameter is reported in the study. Mohamed et al. [15] reported the heat transport investigation in magneto-nanofluid and tackled the model analytically. They found the notable effects of the solid tiny particles on the thermal performance. To validate the analysis, a comparative table was provided which proved the authenticity of the adopted technique and painted results against different flow quantities. Some significant thermal analysis in the colloidal suspensions under multiple physical situations and geometries were perceived in [16–18].
The exact flow analysis in the flow between two disks was pointed in [19]. They considered the disks which accelerated in Cylindrical coordinates and found the closed solution for the momentum equation. The effects of physical parameters on the fluid velocity was portrayed in the analysis. The study of mass and heat transport under the impacts of activation energy and chemical reaction parameters in magnetized mixed convective fluid was pointed in [20]. The flow and heat transport behavior and mixed convective flow characteristics with addition of internal heat sink/source was stated in [21,22], respectively. Lately, Nayak et al. [23] stated detailed heat transport in ZnO-SAE50 nanolubricant with the impacts of thermal radiations, mixed convection and Lorentz forces.
The study of nanolubricant is significant in paint, automobile industries, and aerodynamics. Form the survey, it is pointed out that no one revealed the thermal transport and shear stresses analysis in the colloidal flow of ZnO-SAE50 nanolubricant under the action of activation energy parameter. Therefore, the analysis is conducted to point out the behavior of flow and thermal analysis in the colloidal mixture between two disks placed in parallel position. This study will fill the significant gap in the scientific literature regarding to the thermal analysis in the nanolubricant. The colloidal model transformed in dimensionless type via successful implementation of defined similarity transforms and then Runge–Kutta algorithm is implemented for the solution purpose. The results are decorated against multiple physical parameters and comprehensive discussion is provided against the plotted results.
2 Formulation of Nanolubricant Model
Consider the flow of ZnO-SAE50 nanolubricant between two disks placed parallel to each other. The disks are apart by distance d. Further, the lower disk is at the culmination of the Cylindrical frame and upper is at z = d. The temperature at the upper end maintained fixed and the lower end is subjected to an exothermic nature of surface reaction. An incompressibility, laminar, steady, no slip between the tiny material and host liquid and the tiny particles and host liquid is in thermal equilibrium are the assumptions that retained in the analysis. The flow of ZnO-SAE50 is described in Fig. 1.
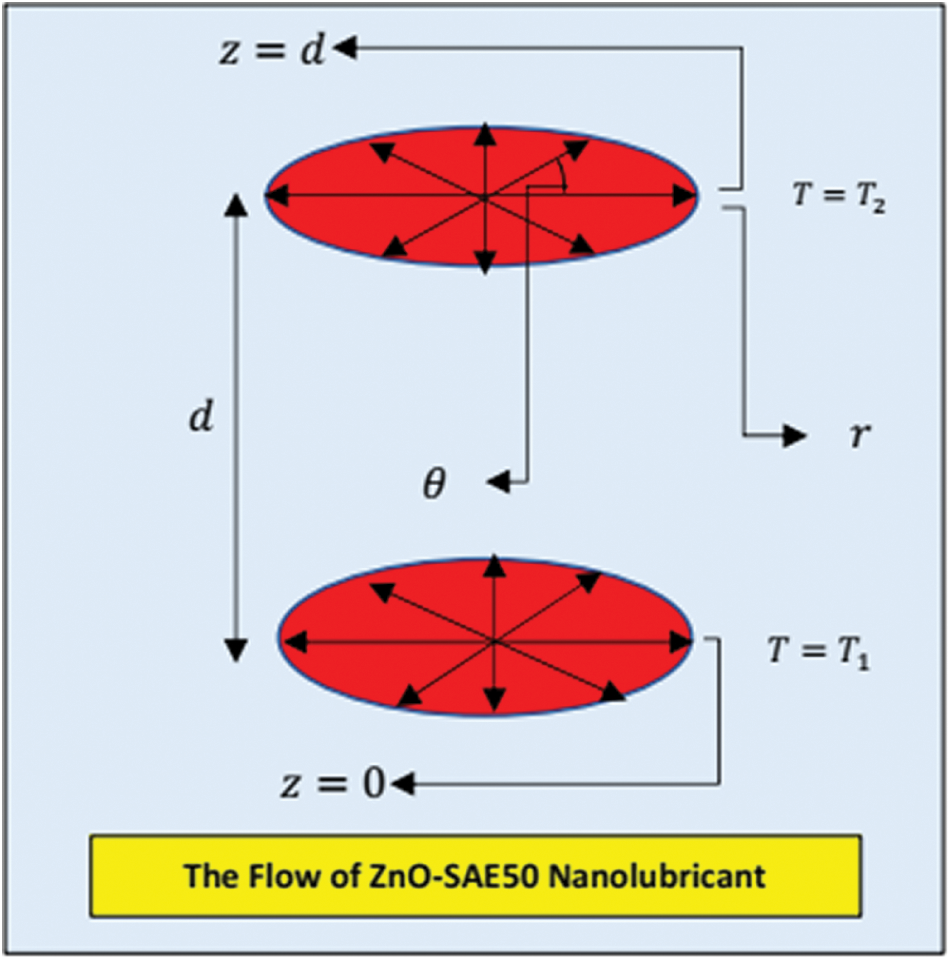
Figure 1: Schematic of the model
The supporting governing model for ZnO-SAE50 described by the following relations [19–21]:
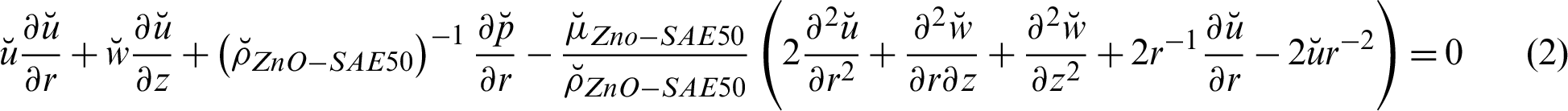
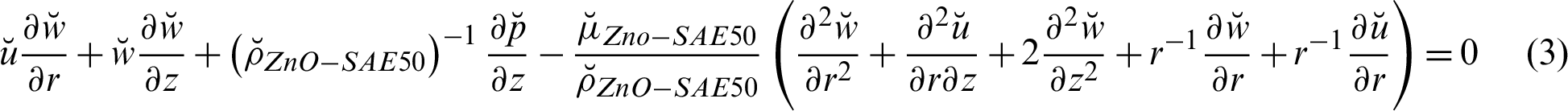
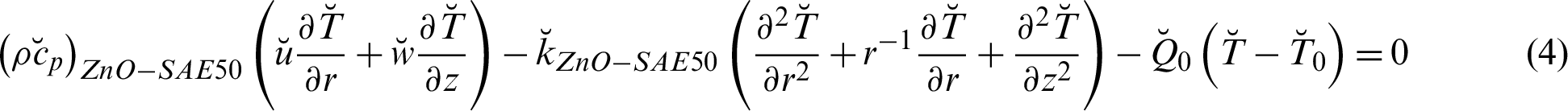
The relevant flow conditions are:
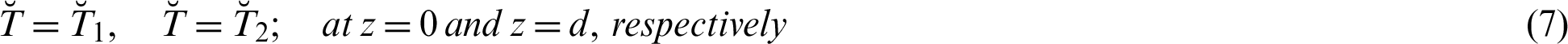
The relevant similarity transforms labeled in Eq. (7):
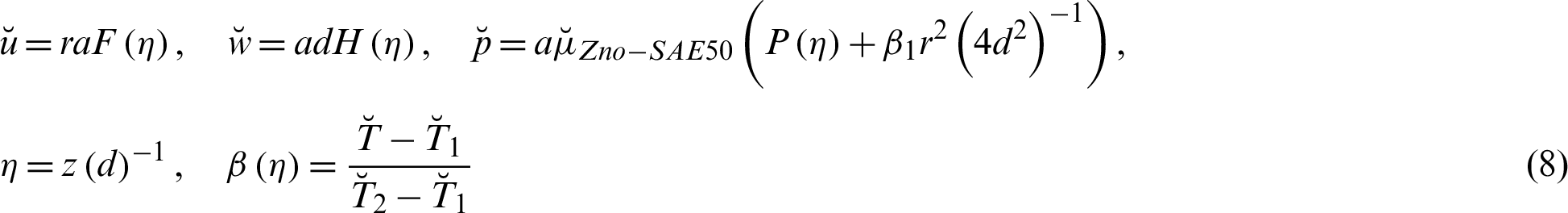
2.2 Effective Models for ZnO-SAE50
The following correlations are adopted for thermal performance of ZnO-SAE50nanolubricant [23]:
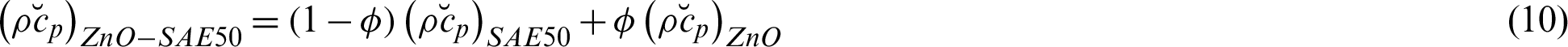
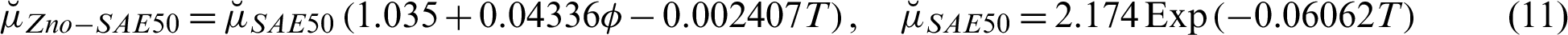
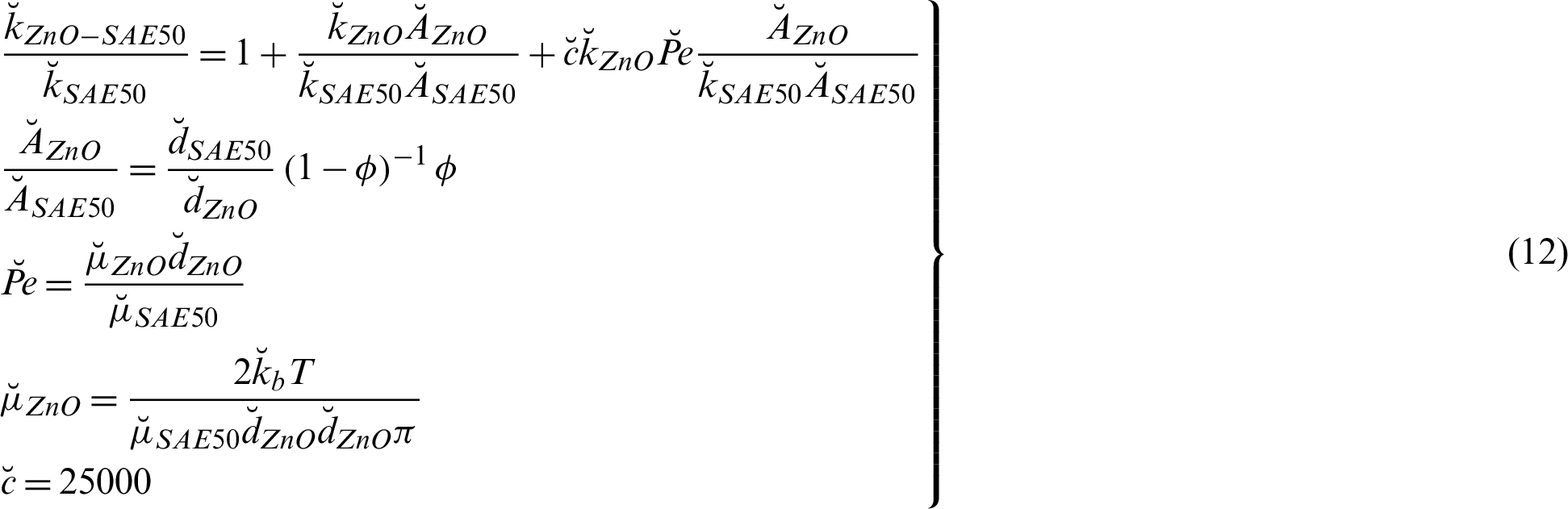
The thermophysical values against ZnO and SAE50 are described in Tab. 1.
Table 1: Thermophysical values of ZnO and SAE50 [23]
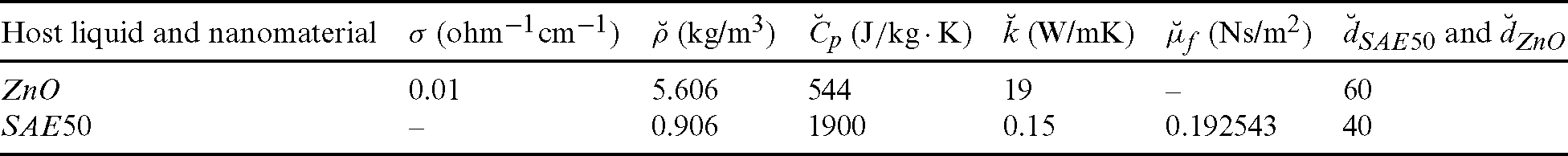
2.3 Dimensionless ZnO-SAE50 Model
After plugging the self-similar transforms and the effectsive models for ZnO-SAE50 in the model labeled in Eqs. (1)–(7), the following version is attained:
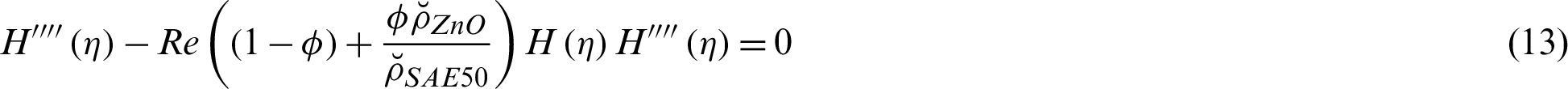
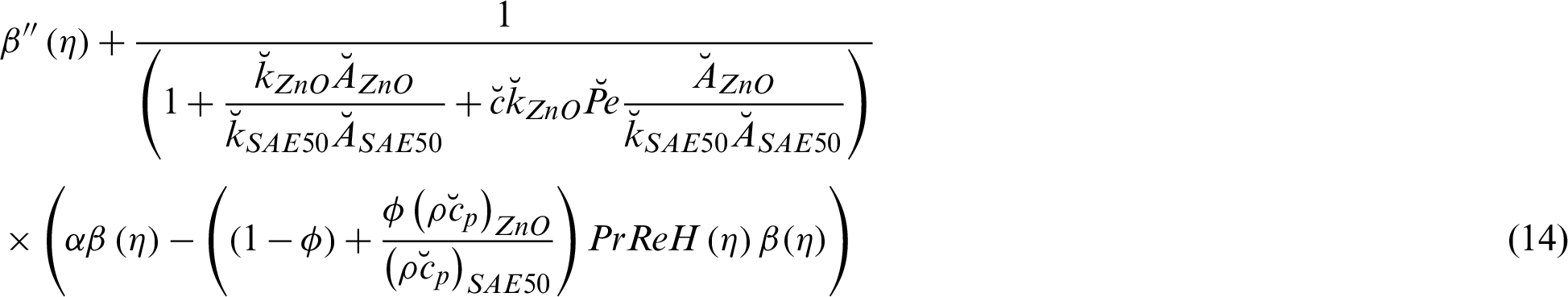
The flow conditions are:
In Eqs. (13) and (14), dimensionless parameters are Reynolds number 
, heat source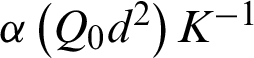 
, Prandtl number Pr 
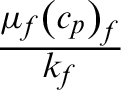and stretching parameter 
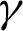(ca−1).
2.4 Shear Stresses and Local Thermal Performance Rate
The mathematical formulas for dimensionless shear stresses and local thermal performance rate are described as:
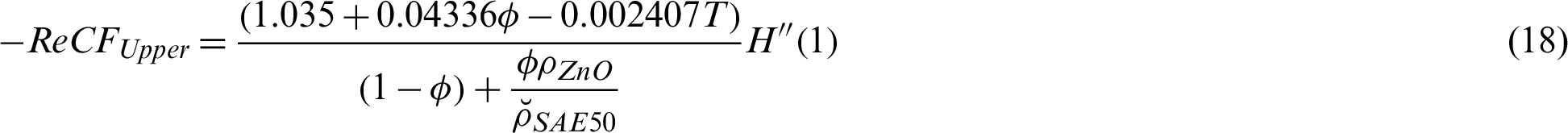
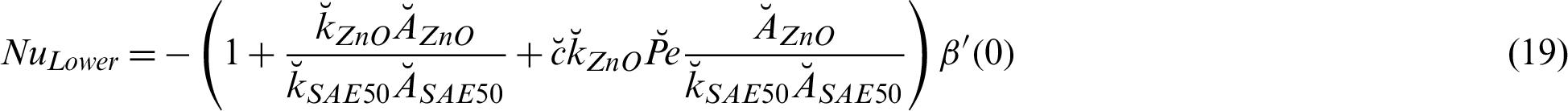
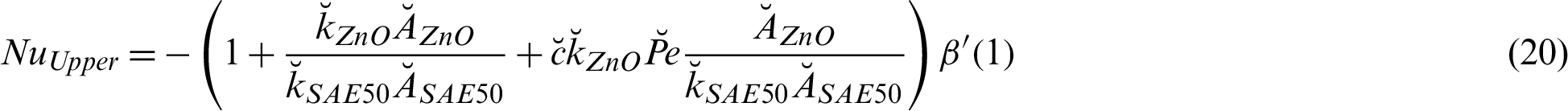
3 Mathematical Analysis of ZnO-SAE50 Model
The model ZnO-SAE50 is solved by adopting Variation of Parameters technique. The technique is implemented by using the following steps:
Firstly, write ZnO-SAE50 colloidal model in the following form:
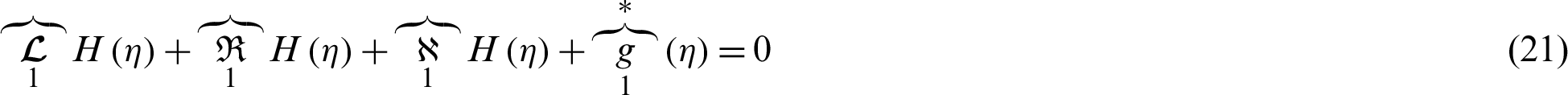
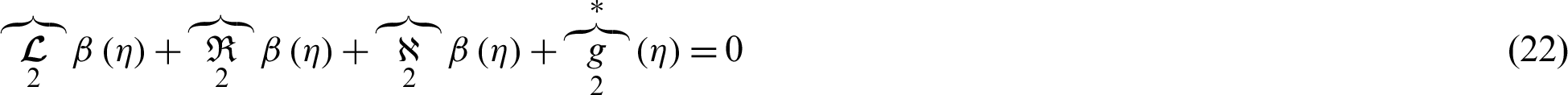
In Eqs. (21) and (22), 
are highest linear operators, 
are linear operators of one less order, 
are nonlinear terms for the velocity and temperature equations, respectively.
The Lagrange multipliers for the model are computed by adopting the following formulas:
In Step 3, initial guesses are computed by using the following formulas:
Finally, the following iterative scheme is used to compute the solution of the model:
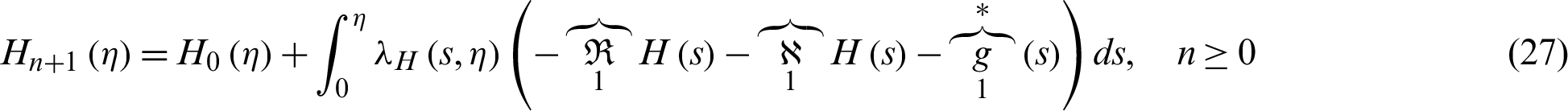
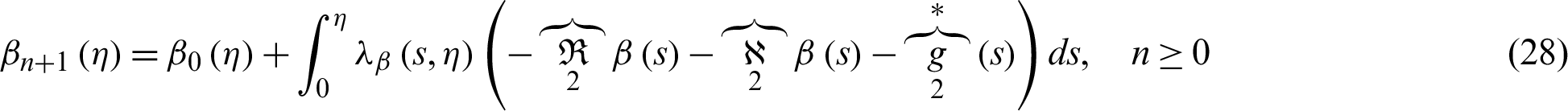
Higher order approximations of the solutions are computed from the recursive relations plugged in Eqs. (27) and (28), respectively.
4 Results and Discussion for ZnO-SAE50 Model
4.1 ZnO-SAE50 Velocity Behavior
The velocities 
and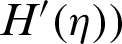 
against the stretching disk parameter 
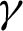are painted in Fig. 2 for multiple values. It is significant to highlight that 
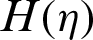is the fluid velocity against z and 
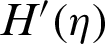is against r directions, respectively. Further, the comparative results are painted for ZnO-SAE50 and conventional fluid. From the inspection of painted results, it is surveyed that the velocity in rises vertically and dual behavior is inspected against r direction. Physically, for increasing stretching parameter, the flowing area over the disks increases due to which the particles of ZnO-SAE50 and conventional liquid flow freely. Therefore, the velocity upturns quickly. From the comparative inspection, it is surveyed that the rising behavior of the velocity is abrupt against conventional liquid. Physically, ZnO-SAE50 becomes denser due to effective correlations. Therefore, due to high density of ZnO-SAE50, intermolecular forces between the particles become prevail that resist the motion. For conventional liquid, abrupt increase in the velocities is pointed. The reason is that the regular liquid is less dens comparative to ZnO-SAE50 in which intermolecular forces are weak and the particles moves freely. Therefore, the velocity rises promptly. The dual velocity curves against z direction is painted in Fig. 2b. The velocity declines promptly at the upper disk while, slow increment is detected near the lower disk surface. The maximum upturns in 
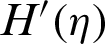are surveyed in the middle area.
Figure 2: The velocities against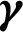 
(a) 
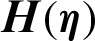(b)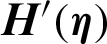 
The velocities against preeminent flow parameter called Reynolds number are painted in Fig. 3. It is analyzed that against stronger Reynolds number, 
significantly rises in the flowing area. For ZnO-SAE50, rise in 
is prompt comparative to regular liquid. This behavior of the velocity depends on the Reynolds number. As, this is the ratio of inertial to viscous forces. Therefore, viscous force prevails for ZnO-SAE50 mixture due to which abrupt variations are detected. Physically, due to low viscosity of the regular liquid, the velocity intensifies slowly for regular liquid phase comparative to nanolubricant. Fig. 3a is painted to accessed these trends. The trends in the velocity along r coordinate by increasing the Re values are decorated in Fig. 3b. The velocity of the nanolubricant and regular liquid rises very slowly and turning point of the velocity is perceived at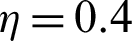 
. At the surface of upper and lower disks, these alterations are detected very slow.
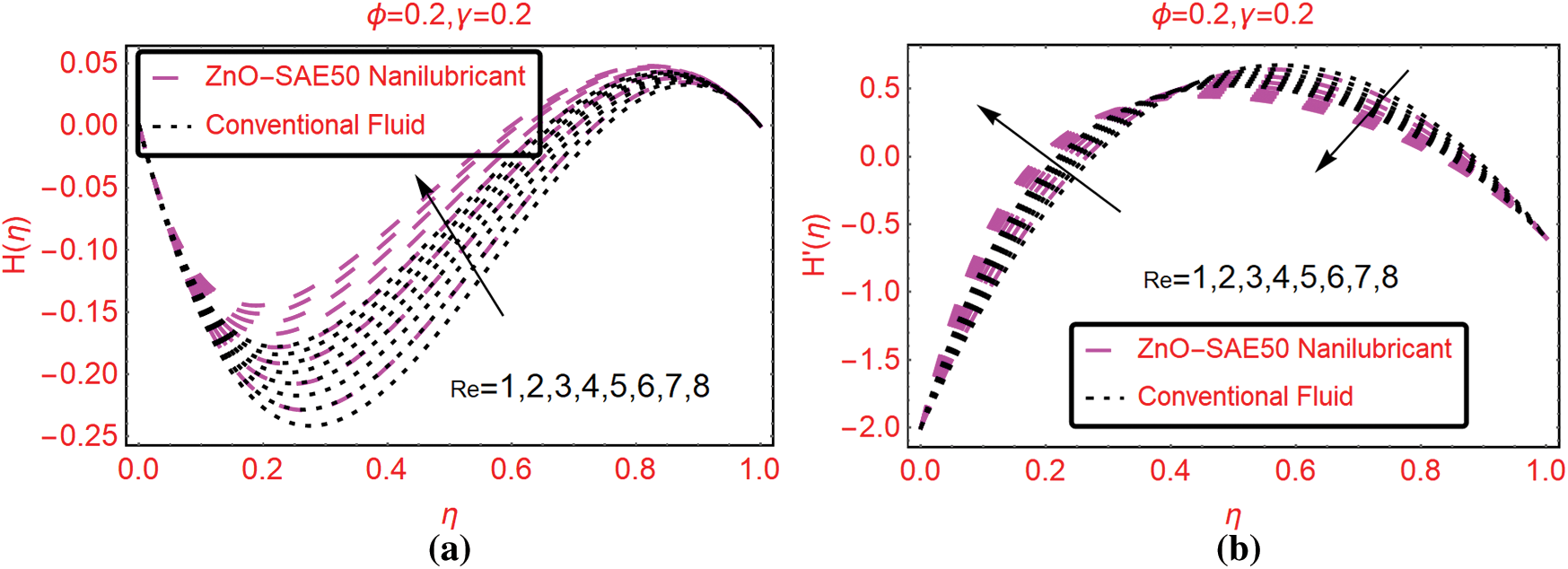
Figure 3: The velocities against 
(a) 
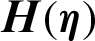(b)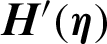 
4.2 ZnO-SAE50 Shear Stresses Trends
The analysis of shear stresses is significant from industrial view point. The tendencies in the shear stresses against rising Reynolds values are decorated in Fig. 4. It is noticeable that the shear stresses and Reynolds values are in direct relation with each other. Physically, against high Reynolds values, the motion of ZnO-SAE50; consequently, the shear stresses rise. The shear stresses at the upper disk against high Reynolds values are captured in Fig. 5. The inverse proportion between Reynolds and shear stresses is pointed form the analysis. The shear stresses decline promptly at the upper end for smaller Reynolds values. By increasing the Reynolds values, decrement in the shear stresses becomes slow. In other words, the shear stresses absolutely enhanced against stronger Reynolds number.
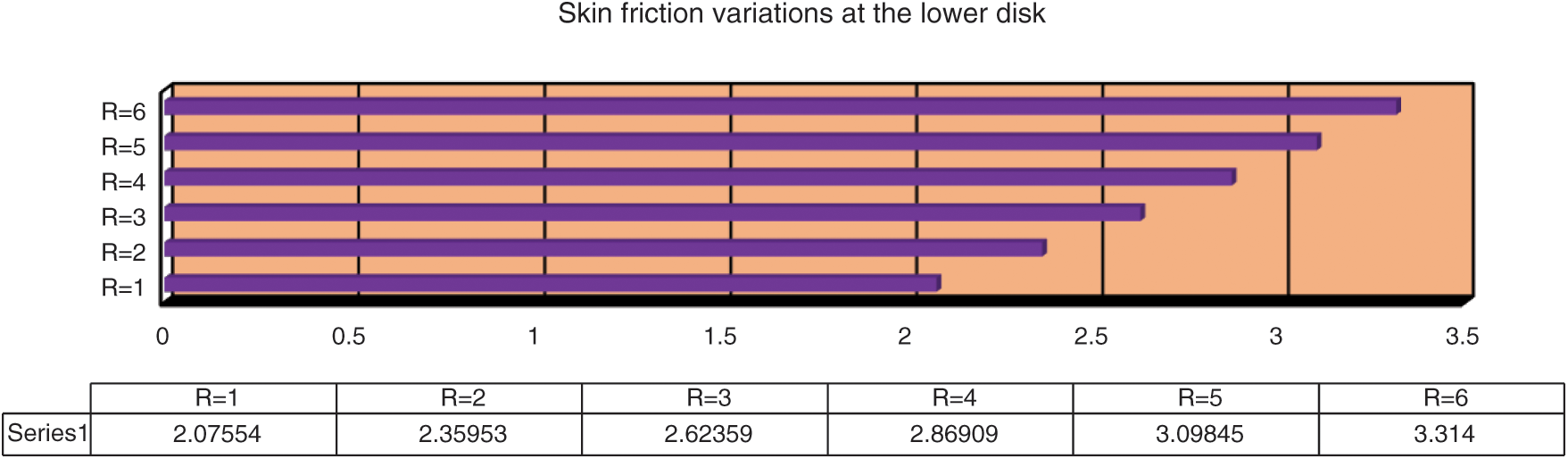
Figure 4: The shear stresses against Re at the lower disk
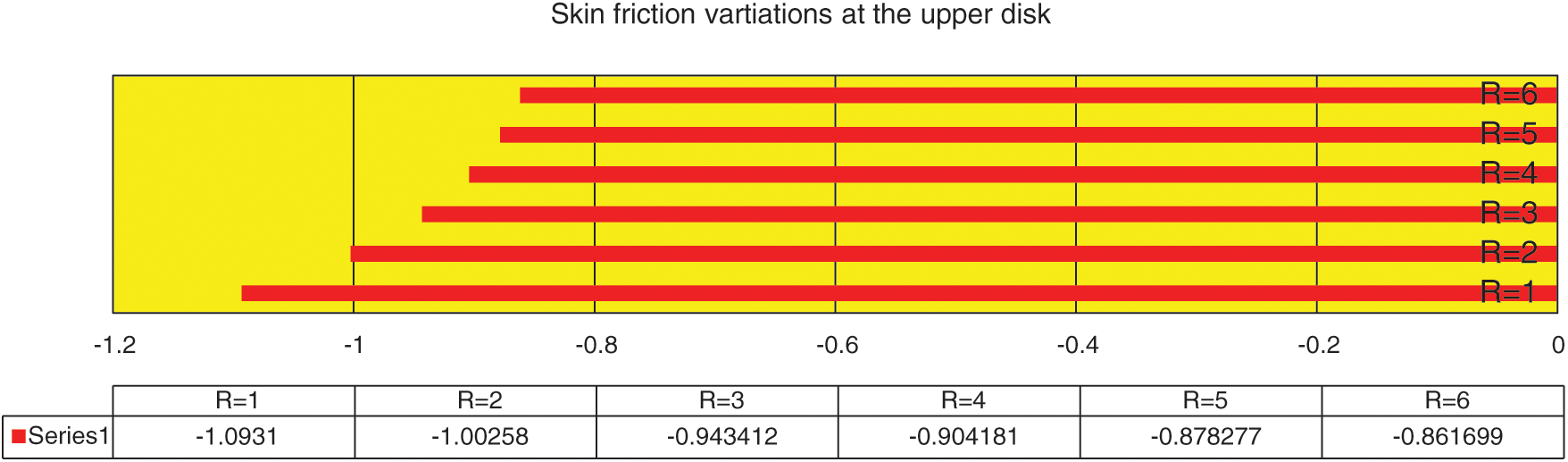
Figure 5: The shear stresses against Re at the upper disk
The stretching parameter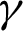 
significantly affect the shear stresses on the disk surface. These effects are elucidated in Fig. 6 against multiple 
values. It is pointed maximum shear stresses at the disk surface. Physically, due to stretching of the surface, the flowing region over the surface expands due to which more fluid particles flow over the surface. Therefore, maximum trends of shear stresses transport are pointed from Fig. 6. Against smaller 
, slow increasing effects of the shear stresses are determined at the lower surface. On the other end, absolute maximum trends are determined against smaller stretching of the disk. These are captured in Fig. 7.
Figure 6: The shear stresses against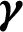 
at the lower disk
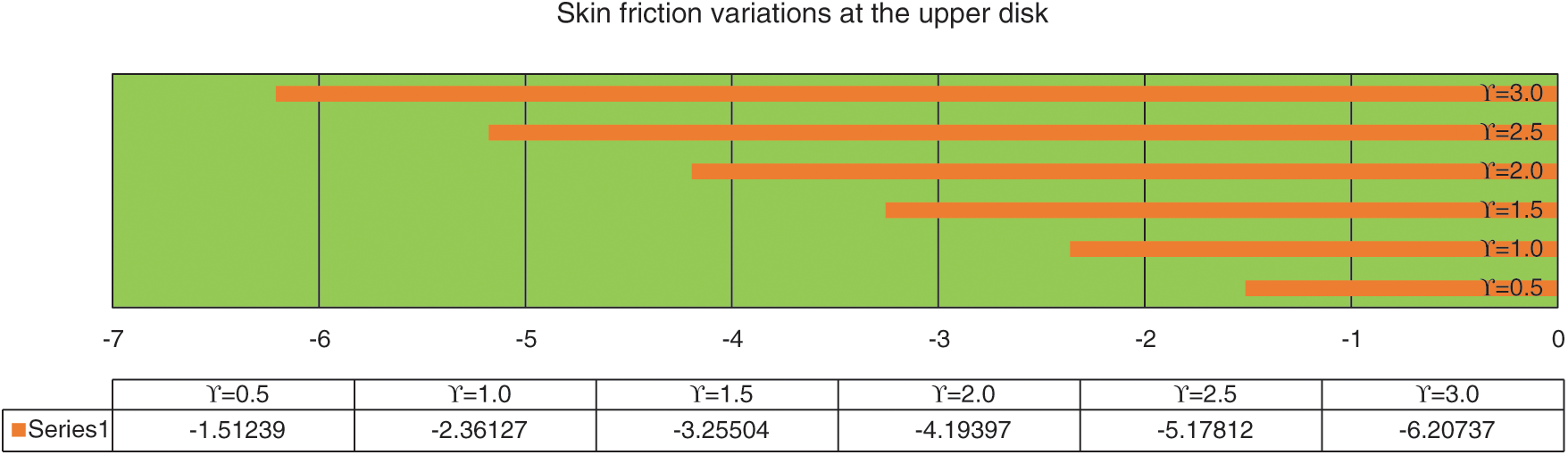
Figure 7: The shear stresses against 
at the upper disk
4.3 ZnO-SAE50 Local Thermal Performance Rate
The local thermal performance in ZnO-SAE50 is significant for aerodynamic and paint industry. Therefore, to survey the trends of local thermal behavior in ZnO-SAE50 against 
and Re, Figs. 8a and 8b are painted, respectively. The local thermal performance is detected at both lower and upper surfaces. From Fig. 8a, it is inspected that at the upper end, the local thermal performance improved for more stretchable surface. Physically, due to more stretching rate, the disk surface increases and the particles freely flow which allow the prompt collisions between the particles. Consequently, the thermal performance rate rises. At the lower surface, these influences are reverse. Significant declines in the local thermal performance rate is perceived 
values. The effects of Re are captured in Fig. 8b by altering Re. It is seen that the Reynolds values are in direct relation with local thermal performance rate at both lower and upper surfaces. However, at the lower surface very slow increasing trends are detected. The streamline behavior against multiple Re values are decorated in Fig. 9.
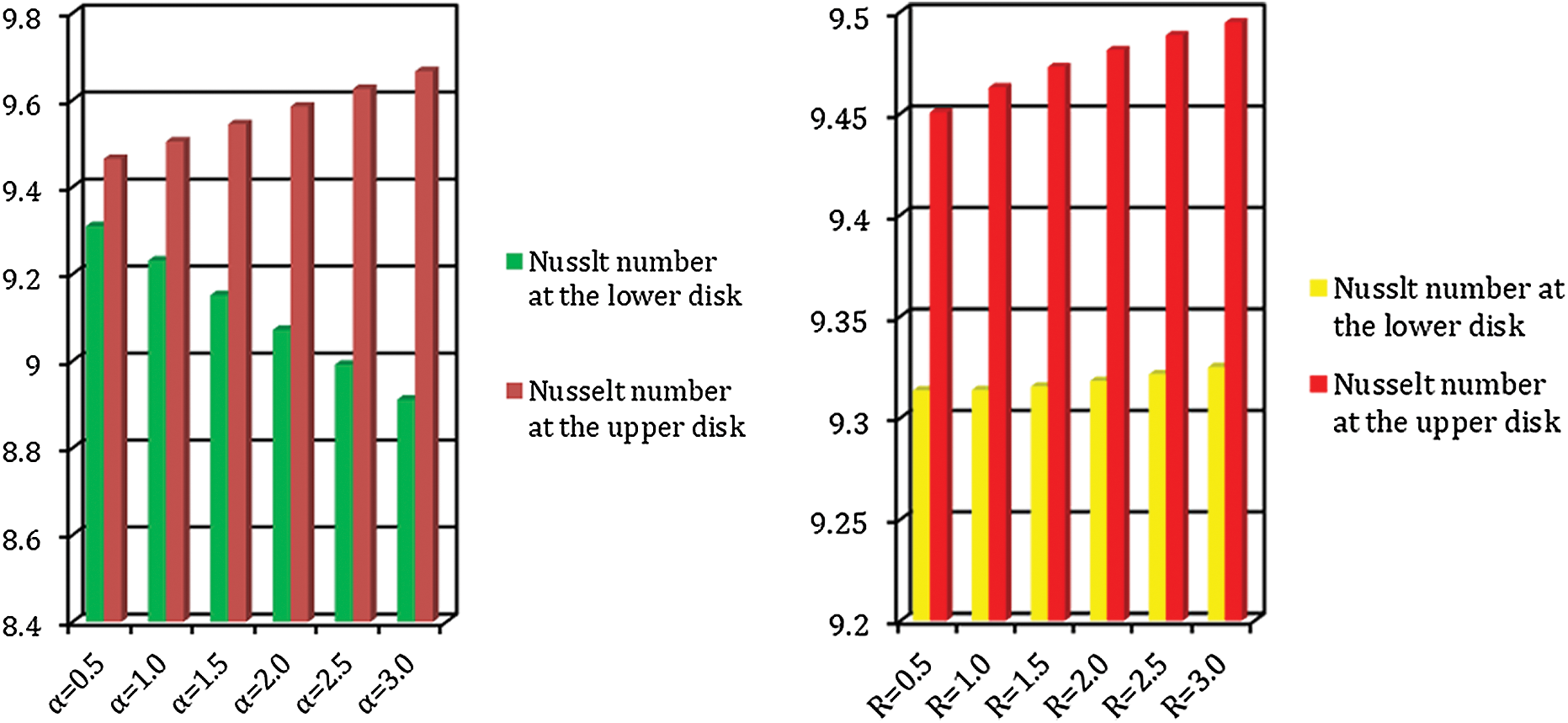
Figure 8: The local thermal performance against (a) 
(b) Re
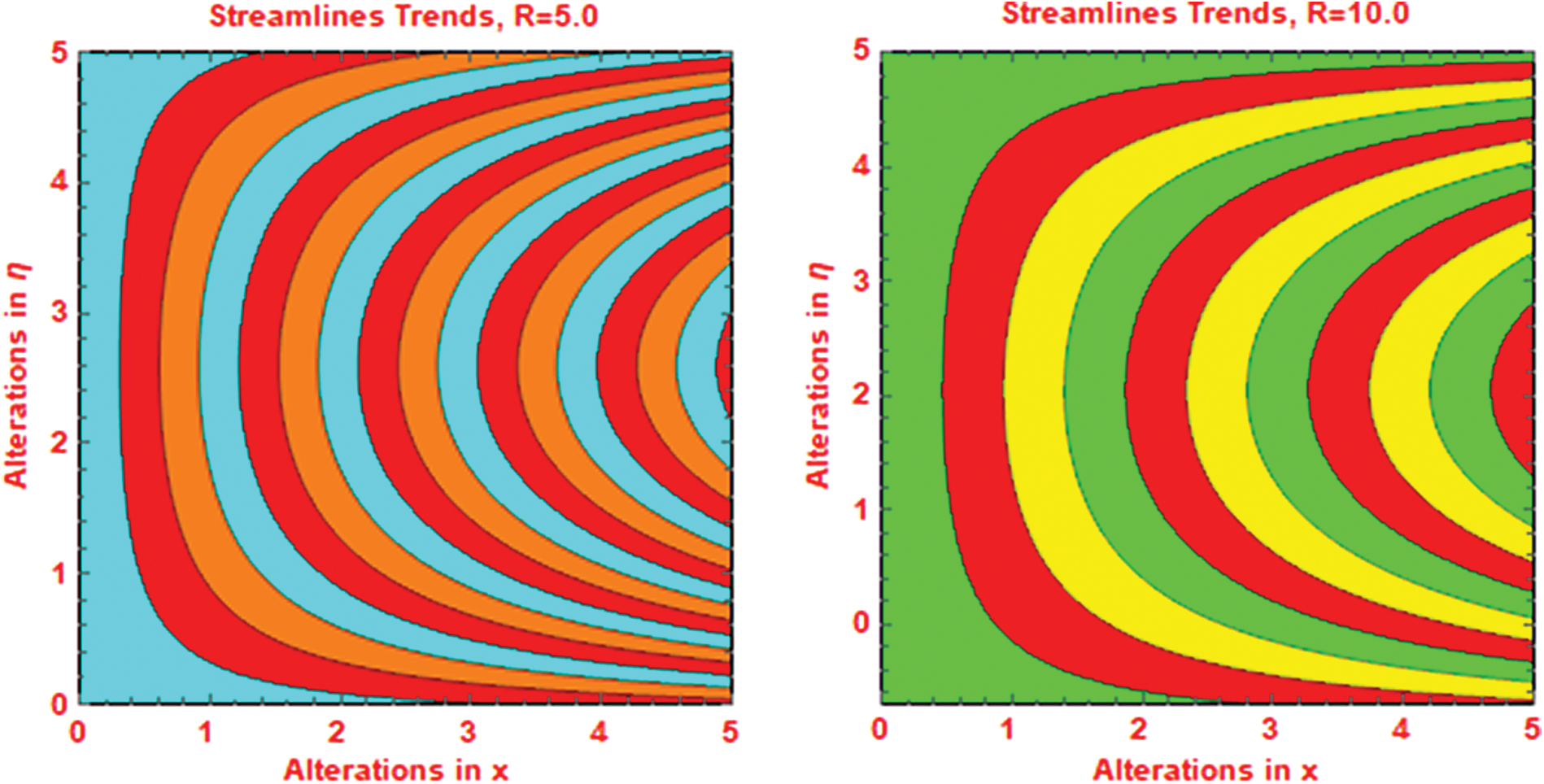
Figure 9: Streamlines behavior against (a)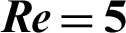 
(b)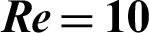 
The analysis of the velocity, shear stresses and local thermal performance rate in ZnO-SAE50 nanolubricant between stretchable disks is conducted. The solutions for the model are attained via VPM and the results are painted against multiple parameters. It is pointed that the velocity of regular liquid is prompt comparative to ZnO-SAE50 against higher stretching of the disks and dual behavior is inspected for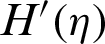 
. The shear stresses at the lower surface promptly rises against Re and 
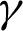, respectively; while absolute increasing trends are perceived at the upper surface. The local thermal performance in ZnO-SAE50 is improved for Re and 
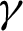. From the study, it is pointed that ZnO-SAE50 nanolubricant is better conductor. Therefore, it is better for uses in various industries where large amount of thermal transport amount is required.
Funding Statement: Researchers supporting Project number (RSP-2020/33), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. N. Ahmed, A. S. Adnan, U. Khan, S. T. Mohyud-Din, I. Khan et al. (2020). , “Radiative colloidal investigation for thermal transport by incorporating the impacts of nanomaterial and molecular diameters (dnanoparticles, dfluidApplications in multiple engineering systems,” Molecules, vol. 25, no. 8,pp. 1896.
2. S. I. Khan, N. Ahmed, U. Khan, S. U. Jan and S. T. Mohyud-Din. (2015). “Heat transfer analysis for squeezing flow between parallel disks,” Journal of the Egyptian Mathematical Society, vol. 223, no. 2, pp. 445–450.
3. M. Azimi and R. Riazi. (2015). “Heat transfer analysis of GO-water nanofluid flow between two parallel disks,” Propulsion and Power Research, vol. 4, no. 1, pp. 23–30.
4. A. Hussain, S. T. Mohyud-Din and T. A. Cheema. (2012). “Analytical and numerical approaches to squeezing flow and heat transfer between two parallel disks with velocity slip and temperature jump,” Chinese Physics Letters, vol. 29, no. 11, pp. 114705.
5. K. Vajravelu, K. V. Prasad, C. O. Ng and H. Vaidya. (2017). “MHD squeeze flow and heat transfer of a nanofluid between parallel disks with variable fluid properties and transpiration,” International Journal of Mechanical and Materials Engineering, vol. 12, no. 1, pp. 336.
6. A. S. Dogonchi, A. J. Chamkha, S. M. Seyyedi and D. D. Ganji. (2018). “Radiative nanofluid flow and heat transfer between parallel disks with penetrable and stretchable walls considering cattaneo-christov heat flux model,” Heat Transfer, vol. 47, no. 5, e21339.
7. A. T. Prata, C. D. M. Pilichi and R. T. S. Ferreira. (1995). “Local heat transfer in axially feeding radial flow between parallel disks,” Journal of Heat Transfer, vol. 117, no. 1, pp. 47–53.
8. M. G. Sobamowo, A. A. Yinusa and S. T. Aladenusi. (2020). “Impacts of magnetic field and thermal radiation on squeezing flow and heat transfer of third grade nanofluid between two disks embedded in a porous medium,” Heliyon, vol. 6, no. 5, e03621.
9. S. T. Mohyud-Din, Adnan, U. Khan, N. Ahmed, I. Khan et al. (2020). , “Thermal transport investigation in magneto-radiative GO-MoS2/H2O-C2H6O2 hybrid nanofluid subject to cattaneo-christov model,” Molecules, vol. 25, no. 11, pp. 2592.
10. N. S. Khan, Q. Shah, A. Bhaumik, P. Kuman, P. Thounthing et al. (2020). , “Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks,” Scientific Reports, vol. 10, no. 1,pp. 173. [Google Scholar]
11. A. J. Chamkha, A. S. Dogonchi and D. D. Ganji. (2019). “Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating,” AIP Advances, vol. 9, e5086247. [Google Scholar]
12. M. A. E. Aziz and A. M. Aly. (2020). “MHD boundary layer flow of a power-law nanofluid containing gyrotactic microorganisms over an exponentially stretching surface,” Computers, Materials & Continua, vol. 62, no. 2, pp. 525–549. [Google Scholar]
13. M. A. E. Aziz and A. M. Aly. (2020). “Entropy generation for flow and heat transfer of sisko-fluid over an exponentially stretching surface,” Computers, Materials & Continua, vol. 62, no. 1,pp. 37–59. [Google Scholar]
14. M. Hatami, J. Dengwei, S. Dongxing, M. Sheikholeslami and D. D. Ganji. (2015). “Heat transfer and flow analysis of nanofluid flow between parallel plates in presence of variable magnetic field using HPM,” Journal of Magnetism and Magnetic Materials, vol. 396, pp. 275–282. [Google Scholar]
15. K. Mohamed, S. M. Rafik, B. Rabah, M. M. Rashidi and H. Ammar. (2018). “Heat transfer in hydro-magnetic nano-fluid flow between non-parallel plates using DTM,” Journal of Applied and Computational Mechanics, vol. 4, no. 4, pp. 352–364. [Google Scholar]
16. N. Acharya, K. Das and P. M. Kundu. (2019). “On the heat transport mechanism and entropy generation in a nozzle of liquid rocket engine using ferrofluid: A computational framework,” Journal of Computational Design and Engineering, vol. 6, no. 4, pp. 739–750. [Google Scholar]
17. M. Jawad, Z. Shah, S. Islam, E. Bonyah and A. Z. Khan. (2018). “Darcy-forchheimer flow of MHD nanofluid thin film flow with joule dissipation and Navier’s partial slip,” Journal of Physics Communications, vol. 2, no. 11, pp. 115014. [Google Scholar]
18. S. Mousavisani, J. Khalesi, H. Golbaharan, M. Sepehr and D. D. Ganji. (2019). “Influence of inclined Lorentz forces through a porous media on squeezing Cu-H2O nanofluid in the presence of heat source/sink,” International Journal of Numerical Methods for Heat & Fluid, vol. 30, no. 5, pp. 2563–2581. [Google Scholar]
19. T. Fang and J. Zhang. (2008). “Flow between two stretchable disks: An exact solution of the Navier Stokes equations,” International Communications in Heat and Mass Transfer, vol. 35, no. 8, pp. 892–895. [Google Scholar]
20. N. Khan, T. Mahmood, M. Sajid and M. S. Hashmi. (2016). “Heat and mass transfer on MHD mixed convection axisymmetric chemically reactive flow of Maxwell fluid driven by exothermal and isothermal stretching disks,” International Journal of Heat and Mass Transfer, vol. 92, pp. 1090–1105. [Google Scholar]
21. R. A. V. Gorder, E. Sweet and K. Vajravelu. (2010). “Analytical solutions of a coupled nonlinear system arising in a flow between stretching disks,” Applied Mathematics and Computation, vol. 216, no. 5, pp. 1513–1523. [Google Scholar]
22. N. Khan, H. A. Nabwey, M. S. Hashmi, S. U. Khan and I. Tlili. (2020). “A theoretical analysis for mixed convection flow of maxwell fluid between two infinite isothermal stretching disks with heat source/sink,” Symmetry, vol. 12, no. 62, pp. 62. [Google Scholar]
23. M. K. Nayak, J. Prakash, D. Tripathi and V. S. Pandey. (2019). “3D radiative convective flow of ZnO-SAE50 nano-lubricant in presence of varying magnetic field and heterogeneous reactions,” Propulsion and Power Research, vol. 8, no. 4, pp. 339–350. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |