DOI:10.32604/cmc.2021.012649
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012649 | |
| Article |
A Phase Estimation Algorithm for Quantum Speed-Up Multi-Party Computing
1Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET), Jiangsu Engineering Center of Network Monitoring, School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Department of Computer Science and Engineering, Michigan State University, East Lansing, 48824, MI, USA
3State Key Laboratory of Internet of Things for Smart City and Department of Electromechanical Engineering, University of Macau, 999078, Macau
*Corresponding Author: Zhi-Xin Yang. Email: zxyang@um.edu.mo
Received: 07 July 2020; Accepted: 08 August 2020
Abstract: Security and privacy issues have attracted the attention of researchers in the field of IoT as the information processing scale grows in sensor networks. Quantum computing, theoretically known as an absolutely secure way to store and transmit information as well as a speed-up way to accelerate local or distributed classical algorithms that are hard to solve with polynomial complexity in computation or communication. In this paper, we focus on the phase estimation method that is crucial to the realization of a general multi-party computing model, which is able to be accelerated by quantum algorithms. A novel multi-party phase estimation algorithm and the related quantum circuit are proposed by using a distributed Oracle operator with iterations. The proved theoretical communication complexity of this algorithm shows it can give the phase estimation before applying multi-party computing efficiently without increasing any additional complexity. Moreover, a practical problem of multi-party dating investigated shows it can make a successful estimation of the number of solution in advance with zero communication complexity by utilizing its special statistic feature. Sufficient simulations present the correctness, validity and efficiency of the proposed estimation method.
Keywords: Edge computing security; multi-party computing; quantum algorithm; phase estimation; communication complexity
In recent years, security and privacy in edge computing have become a major challenge to the increased scale of information processing in sensor networks. Some people say that the data created by Internet of Things (IoT) sensors must be better protected. With more and more data protection regulations, new public awareness of tracking and the explosion of devices, simple device password solutions are no longer enough.
A new architecture using Security Agents should be constructed actively in local routers and networks to deal with Internet of Things security and computing, rather than offloading digital processing to data centers or clouds, or actually trying to execute it on IoT devices with limited resources. From the perspective of [1], Internet of Things security should be handled at the network level, not at the device level, in order to achieve the best results.
Different from the security framework based on edge computing proposed in [1], we focus on another way to solve this problem, which is known as quantum computing that can accomplish both security and speed-up. Information stored and transmitted in a quantum state cannot be identified by eavesdroppers thanks to the measurement principle in quantum mechanics [2]. It means that the quantum method is able to be naturally secure as the message can be coded physically at the quantum level. What’s more, quantum speed-ups are fascinating discoveries in recent years. The key technique to gain such an advantage is so-called quantum computing which is applicable to solve a series problems in such a wide range of quantum information processing. It can reduce the algorithm complexity in multimedia processing [3–5] and benefit the information security as well through protecting communication from eavesdropping [6–8]. Some papers focus on the states preparation for quantum communication [9,10]. And other field like quantum machine learning has gain much attention of computer scientists [11].
This special quantum parallelism totally different from conventional information techniques also can be applied in communication complexity which is a standard that can determine how much communication cost spent in a distributed computing task [12–14]. The first big progress proposed by Shor make the decoding RSA secret keys easy, which is definitely hard to implement in the classical case [15]. This class of quantum algorithms such as Shor’s can downgrade the computation complexity from NP to P, but not applicable to the most of the classical algorithms. More generally, the database search algorithm called the Grover’s quantum search algorithm has a larger range application to its classical counterpart than Shor’s; however, the speed-up efficiency is mostly quadric level only [16–22]. The implementation of this type of quantum distributed (QD) algorithms for multi-party computing (MPC) definitely requires Grover’s iteration [23–26].
One of the prerequisites for applying Grover’s iteration is to know the number of solutions in order to determine the optimal number of iterations [16–18]. However, for many practical problems, it is difficult to know how many solutions the problem itself exactly has before it is answered. To solve this problem, a key algorithm called quantum phase estimation is used to estimate a possible number of solutions of one specific problem that uses Grover’s iteration in the solving process [16].
We propose a distributed algorithm of phase estimation, which is used to estimate the number of solutions of MPC problem, and study how much quantum communication complexity is added to QD algorithm by using this method.
Additionally, considering the constraints of the statistical characteristics of the MPD (multi-party dating) problem, which can schedule appointments among different users and is seen as one of the practical applications of MPC, we develop the distributed estimation algorithm for estimating the number of solutions. This algorithm can be implemented without any multi-party communication through some simple local calculations. Finally, given many simulation results about this estimation algorithm prove the efficiency and correctness of the proposed method.
2 Estimation of the Number of Solutions of MPC Problem Based on Universal Discriminant Function
The quantum speed-up model of two-party computing is first discussed in paper [23]. It shows the communication complexity of a two-party quantum distributed computing based on Boolean-valued model is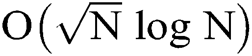 
.
For a reasonable extension of two-user model proposed in [23], we introduce the MPC model based on the same composite Boolean-valued function. Supposing that there are K users, marked as user 1 to user K, provided with the function in turn.
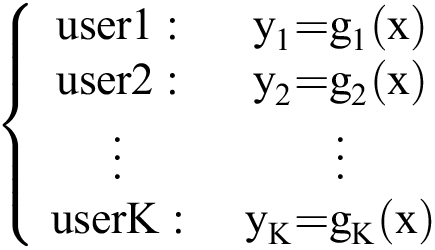
The kth user wants to compute the function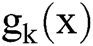 
,
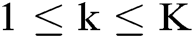. The function 
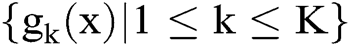could be arbitrary function in the application, but only satisfying that they share the same function domain and codomain. Besides, denote the function 
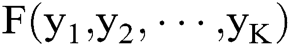as an arbitrary K-ary Boolean-valued function, only to satisfy that 
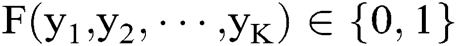and 
, 
.
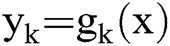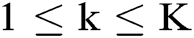Without loss of generality, denote the domain of function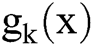 
as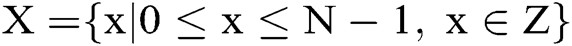 
, the length of X is N. For the convenience let N be an integer that satisfies 
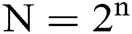(As for the case of 
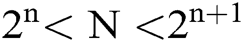, simply have 
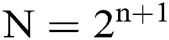, the expanded part of X does not influence on the solving of the problem), therefore it’s feasible to use the length of 
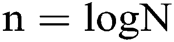bits information to describe the function domain. And similarly, supposing that the codomain of 
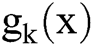is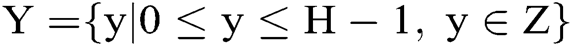 
, and the length to store the codomain information is 
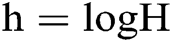bits. So we have
,
,
.
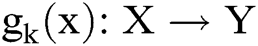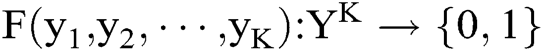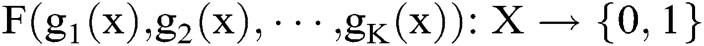In summary, the goal of our research on the multi-party computing task is to find a solution x to equation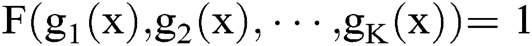 
by comparing the results of K arbitrary functions 
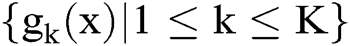calculation held by the multi-users. And the total communication complexity of quantum distributed algorithms that are designed to solve this MPC problem is determined as 
.
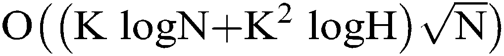Any quantum distributed algorithm for MPC needs to know the number of solutions of a specific problem. When the number of solutions is unknown, the number of solutions must be estimated.
Grover’s database search problem is iterated by phase estimation algorithm, and the rotation angle of Grover problem is estimated by success rate and m bit accuracy [2].
For the MPC problem studied, we need to design a multi-party phase estimation algorithm to estimate the number of solutions of the MPC problem. The communication cost of the new phase estimation algorithm is deduced and evaluated.
According to the result of phase estimation algorithm of Grover’s search problem in paper [2], the input of our phase estimation algorithm for MPC problem is two quantum registers, the first is t-qubit, the initial value is n + 1 qubit, and the second is n + 1 qubit. And we can conclude the whole steps of phase estimation algorithm in Tab. 1.
Table 1: Phase estimation algorithm
Assuming that the estimation error probability of the algorithm is 0, the probability of obtaining the rotation angle of M bit accuracy is obtained after measurement. The estimation error of rotation angle at this time. And the error of the number of solutions at this time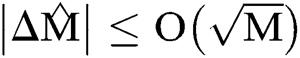 
.
Since the accuracy and success rate of the estimates depend on the magnitude of M and e, the setting of both will ultimately affect the upper limit. Here, we note that if the accuracy is assumed, the substitution Eq. (1) is obtained.
The estimation algorithm needs to call Grover’s iteration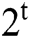 
times altogether. Therefore, the algorithm totally requires 
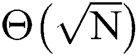times of Grover’s iterations.
For MPC problems, Oracle operations are distributed, which means that estimation algorithms are also distributed. Each Grover’s iteration in Fig. 1 consists of distributed quantum computing. The DOO quantum circuit of the phase estimation algorithm is shown in Fig. 1.
Figure 1: Quantum circuit for DOO
Theorem 1: Communication complexity required by phase estimation algorithms for MPC problem is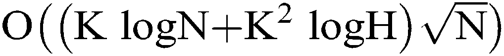
.
Proof: The communication complexity of the estimation algorithm can be deduced from the above results.
Firstly, in the DOO part, in the forward communication process from user 1 to user K, the communication cost is as follows:
.
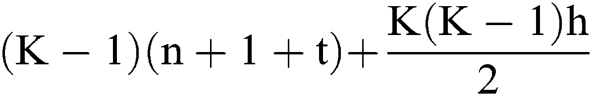The upper bound of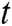 
in Eq. (1) is substituted, and the upper bound is expanded as
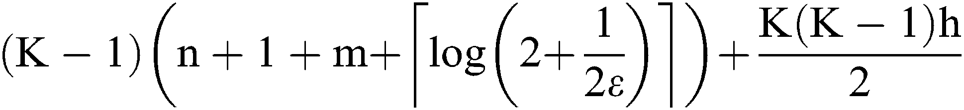
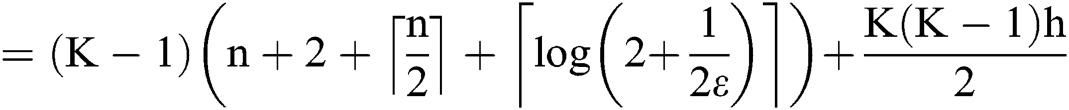
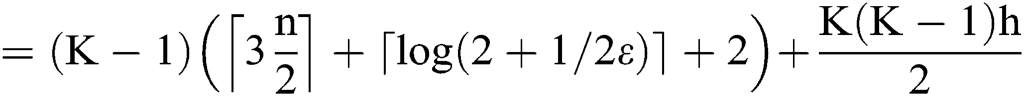
Similarly, the reverse communication process has the same communication overhead as the forward process. Therefore, the communication overhead of a complete DOO is:
.
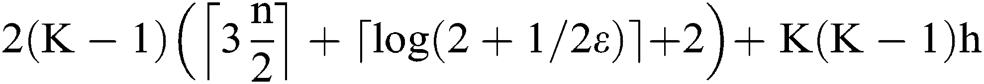According to the conclusion that the MPC phase estimation algorithm needs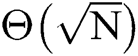 
times of Grover’s iterations, the communication complexity of the phase estimation algorithm can be expressed as
.
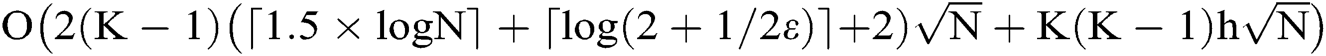By given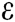
, 
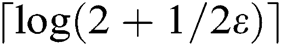is a constant value. So after simplifying the above equation, we can get
.
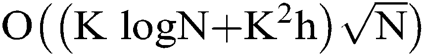By replacing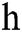 
which is the information length of function range of MPC with 
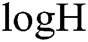, the expression of communication complexity to be proved is obtained as 
.
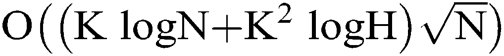It can be seen that the phase estimation algorithm has the same communication complexity as the MPC quantum distributed algorithm. This means that using phase estimation algorithm to estimate the number of solutions in advance will not increase the communication complexity of MPC quantum distributed algorithm.
3 Estimation of the Solutions Amount of MPD Problem
An MPD problem is related to the appointment scheduling issue [24–26]. Paper [23] shows us a quantum computing result for two-party appointment. For the MPD case it belongs to MPC problems and actually is a Boolean-valued model as well.
Suppose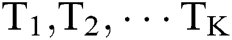 
are the calendars of K users respectively. Where
And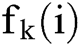 
denotes whether the kth user is idle or not on day i. The discriminant function of the corresponding MPD problem is
Obviously, for any i, if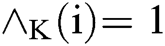 
then the K users succeeded in dating; Otherwise, it means the K users do not have any same free day in their calendar, the appointment task will fail.
Assuming that K users want to make a successful appointment with a certain probability P, the length of the schedules prepared by users will be constrained. Obviously, the more users participate in the joint appointment, the longer the schedule of the appointment will be on the premise of guaranteeing a certain success rate. Therefore, given the expected probability P of successful appointment, under the premise of K users’ appointment, to meet P the probability of successful appointment, the relationship between the length of the schedule N and P is
For MPD problems, the probability distribution of M which denotes the number of solutions satisfies the following equation
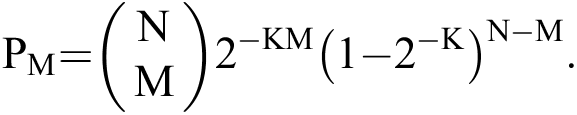
Let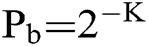 
. It is known that M obeys Bernoulli distribution, that is 
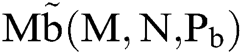. Therefore, it is easy to obtain the statistical average (mathematical expectation) of M.
And the standard deviation of M is:
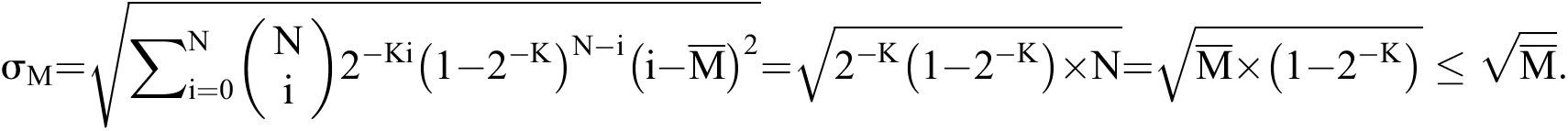
The above formula shows that if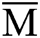 
the mathematical expectation of M is chosen as the estimated value of M; the average error of the estimated value is 
.
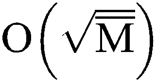Comparing with the phase estimation algorithm discussed in the previous section, we find that:
On the one hand, the estimation error obtained by using the phase estimation algorithm is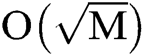 
after calculating the statistical average, the error is 
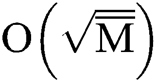. This has the same complexity as the case of using 
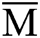as the estimation.
On the other hand, it can be inferred that the communication complexity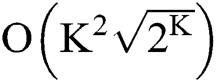
and the cost of other local quantum computation are needed if the phase estimation algorithm is used to estimate the number of solutions of MPD problem. However, it is much easier to get the numerical value of 
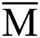without any multi-party communication. At most, it is necessary to use classical computers locally to get a mathematical expectation of Bernoulli distribution. The cost is negligible compared with MPD problem.
For the MPD problem, we choose the estimation method of using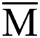 
to improve the performance of the algorithm. Next, we will analyze the impact of the difference between the estimated value and the real value on the performance of the quantum distributed algorithm in a given MPD problem.
According to paper [2], for a search problem whose number of solutions is M and the total search length is N, the Grover’s search algorithm is equivalent to the process of gradually rotating the quantum state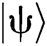 
to the vicinity at each angle. Here,
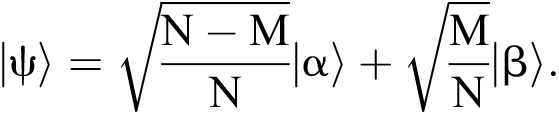
Suppose we perform a specific MPD task, and its actual number of solutions is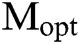 
. It is known that the angle between the initial state 
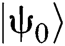and the orthogonal ground state 
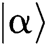is
The corresponding optimal number of iterations is
where CI (x) means that if the fractional part of X is greater than 0.5, it is rounded up; if the fractional part of X is less than or equal to 0.5, it is rounded down. In addition, the error probability of QD algorithm measurement results is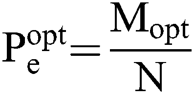
.
Therefore, when estimating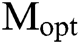 
by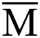 
, it can be obtained
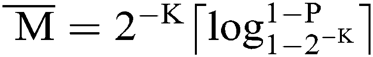. When the number of users K is large enough, it can be calculated through 
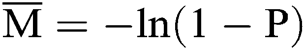. Referring to the solving process of Eqs. (5) and (6), it is easy to know that the number of iterations using estimates is as follows.
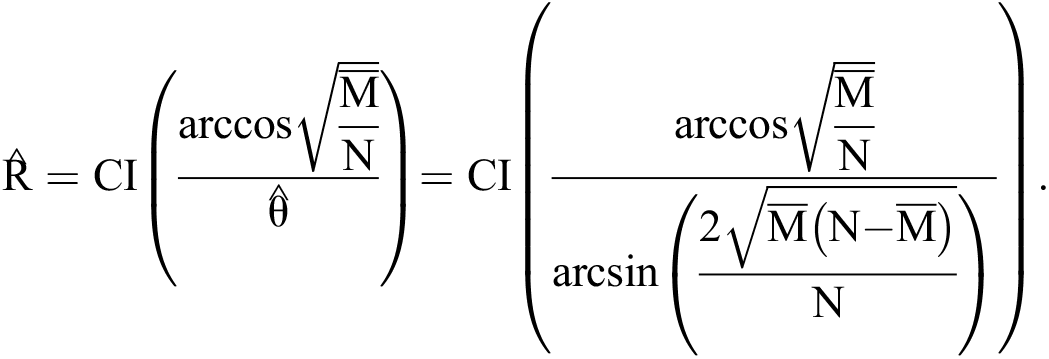
As depicted in Fig. 2, this is equivalent to regard the initial state 
as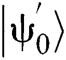 
, and rotating it to the area near to
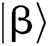by iterations. Therefore, according to Eq. (5), it is easy to figure that in the process of solving the MPD problem the actual rotation angle is 
.
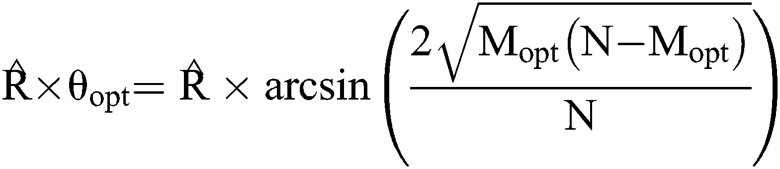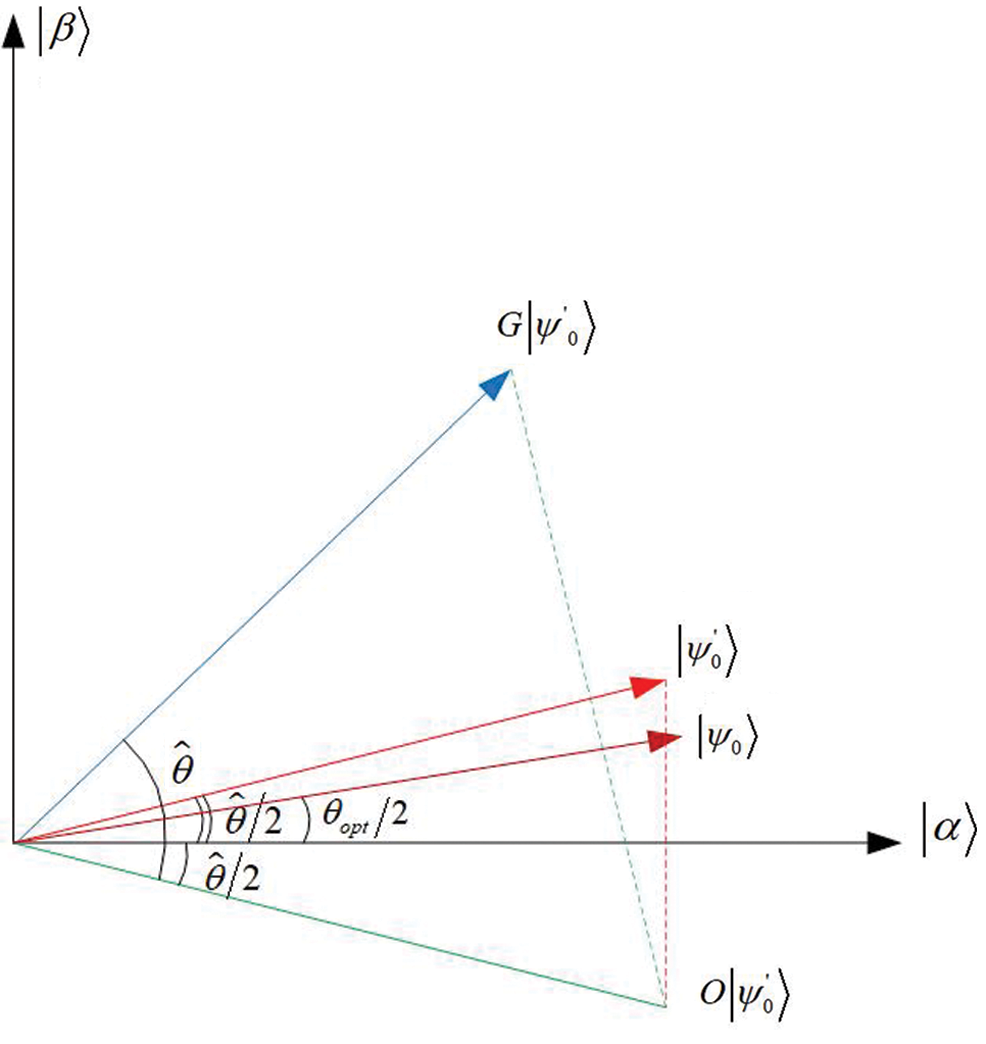
Figure 2: One iteration’s rotation for error estimation by 
As a result, the correct probability of the measurement results using the estimated QD algorithm is
4 Numerical Simulation for Estimating the Number of Solutions
In this section, we simulate the MPD problem using the effect of evaluation. The number of experiments is C, and each experiment simulation produces a specific MPD task. The real value of the corresponding number of solutions is calculated by experiment, and the correct probability of measurement results is calculated.
For an MPD problem, we need to specify the probability of a successful appointment and the number of users in advance when we don’t know which time of the parties is free. And we generally set the success rate as a lower value of 50% and a higher value of 90%. Similarly, due to the exponential growth of resources consumed in MPD simulation, the number of users should be set to consider the value more suitable for the simulation environment. For the number of experiments, a smaller value and a larger value are selected to facilitate comparison. So the simulation involves the following settings: (1) the success rate of appointment P is set to be 50% or 90%; (2) the number of users K is set to 6 or 12; (3) the number of experiments C is set to 10 or 1000.
Figs. 3 to 5 show the actual number of solutions produced in each experiment, and the distribution of probability of getting the correct results after every measurement using the estimation method. It can be seen from the experimental results that, except for the MPD problem without solution, the estimation method can always give the answer with a certain probability as long as the solution can be found. By observing their distribution, most of them can achieve the correct results of measurement with a probability greater than 0.5. Further, using the above results for calculation, we can get more intuitive results in Tabs. 2 and 3 (here, we consider the case where the correct probability is greater than 0.6 and 0.8 respectively).
Figure 3: Estimation results when params change as K = 6 with P = 50%, K = 6 with P = 90%, K = 12 with P = 50% and K = 12 with P = 90% (four columns from left to right), C = 10 for all
Figure 4: Estimation results when params change as K = 20 with P = 50% & C = 10, K = 20 with P = 90% & C = 10, K = 6 with P = 50% & C = 1000 and K = 6 with P = 90% & C = 1000 (four columns from left to right)
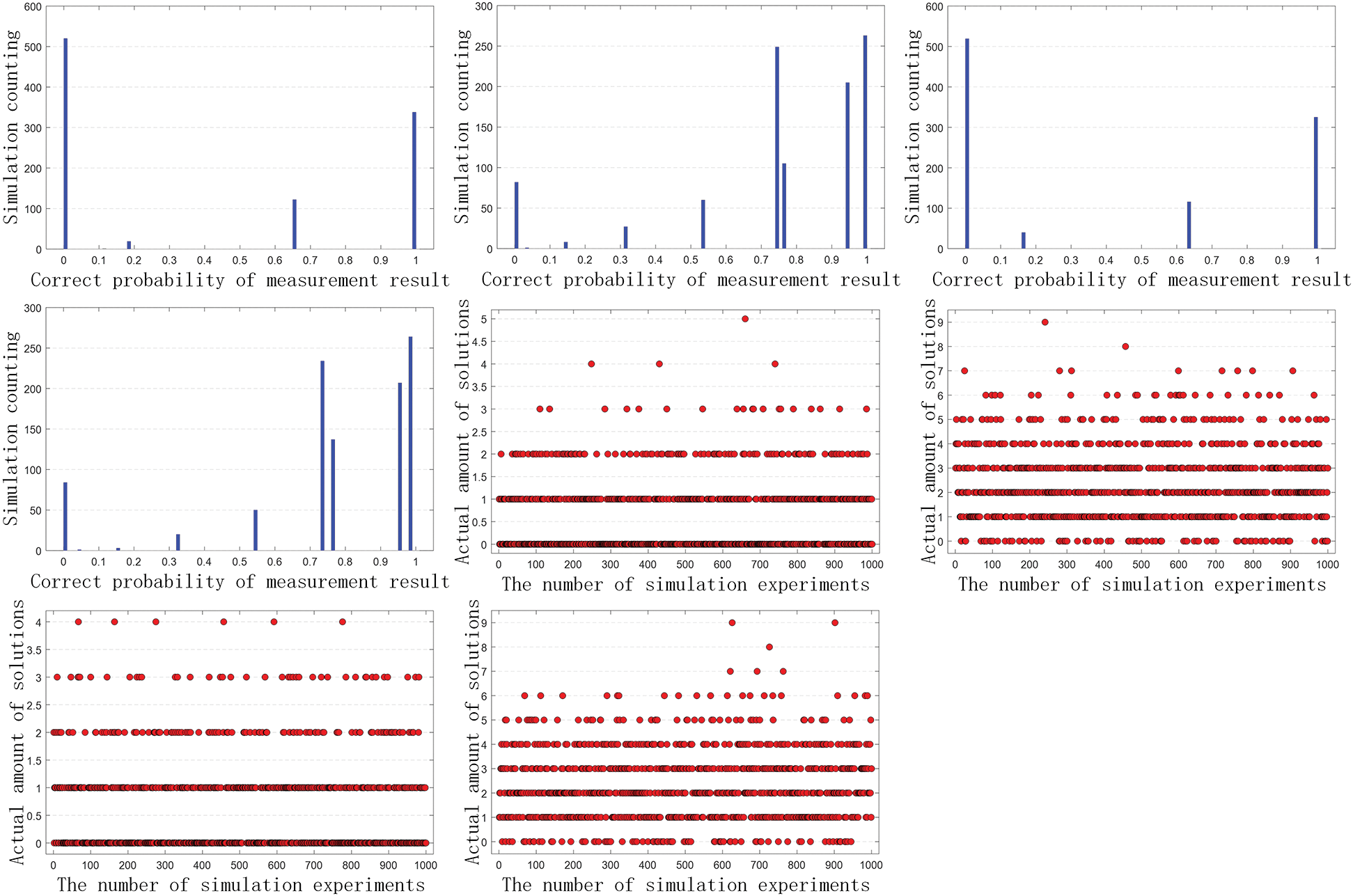
Figure 5: Estimation results when params change as K = 12 with P = 50%, K = 12 with P = 90%, K = 20 with P = 50% and K = 20 with P = 90% (four columns from left to right), C = 1000 for all
Table 2: The rate of correct results of 10 experiments (exclude zero-solution cases)
Table 3: The rate of correct results of 1000 experiments (exclude zero-solution cases)
When the number of experiments is equal to 10, we can clearly see the distribution of the number of solutions from Figs. 3 and 4. However, in the comparison of Tabs. 2 and 3, we can find that the stability of the results of 10 experiments is significantly less than that of 1000 experiments. In the distribution of more than 0.6, the results of 1000 experiments were basically stable at about 90%, but 10 experiments did not get the similar result.
As is shown in Tabs. 2 and 3, except that the actual number of solutions is zero, the correct probability obtained in each experiment can basically fall in a higher probability interval. This shows that except for the actual number of solutions is zero, the correct measurement results can be obtained by solving MPD problem with high probability by using estimation method. According to the characteristics of Grover’s search algorithm, for an example with a certain correct probability (a fixed value with a correct probability greater than 0), the probability of getting the correct result will be close to 1 if the same algorithm process is repeated several times [2]. For the case that the actual number of solutions is zero, no matter how repetitive the operation is, the measurement output of solving MPD problem by using the estimation method will be solvable, which is consistent with the actual number of solutions being 0.
Even if the quantum parallelism can speed many algorithms of multi-party computing up the realization of a quantum distributed algorithm still has been limited by solution’s amount estimation. It must be assured that the total communication complexity should not increase after apply solution’s amount estimation. Based on our study on the phase estimation algorithm for MPC problem the result shows it is possible to make a phase estimation without any complexity increasing. Theorem 1 presents that the communication complexity of phase estimation algorithm is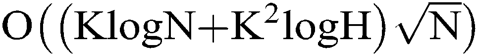 
, which means the communication cost is as the same level as MPC itself. Therefore, no more communication complexity induced by apply proposed estimation algorithm. Additionally, by utilizing the special attributes of MPD problem we able to estimate the number of solutions in advance without any communication. Because that the MPD has a known probabilistic distribution of Bernoulli. It only cost a few local iterations to get the result and dramatically degrades the communication complexity to 0. Amount of simulations for MPD example show the efficiency when the quantum algorithm applied.
Acknowledgement: Thank for being partially supported by the China–USA Computer Science Research Center.
Funding Statement: Supported by the National Natural Science Foundation of China under Grant Nos. 61501247, 61373131 and 61702277, the Six Talent Peaks Project of Jiangsu Province (Grant No. 2015-XXRJ-013), Natural Science Foundation of Jiangsu Province (Grant No. BK20171458), the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (China under Grant No. 16KJB520030), the NUIST Research Foundation for Talented Scholars under Grant Nos. 2015r014, PAPD and CICAEET funds. This work is also funded in part by the Science and Technology Development Fund, Macau SAR (File No. SKL-IOTSC-2018-2020, 0018/2019/AKP, 0 0 08/2019/AGJ, and FDCT/194/2017/A3), in part by the University of Macau under Grant Nos. MYRG2018-00248-FST and MYRG2019-0137-FST.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. H. Hsu, J. Lee, T. Q. S. Quek and J. C. Chen. (2018). “Reconfigurable security: Edge-computing-based framework for IoT,” IEEE Networks, vol. 32, no. 5, pp. 92–99.
2. M. Nielsen and I. Chuang. (2010). Quantum Computation and Quantum Information. 10th ed. Cambridge, UK: Cambridge University Press.
3. Z. G. Qu, Z. Y. Li, G. Xu, S. Y. Wu and X. J. Wang. (2019). “Quantum image steganography protocol based on quantum image expansion and Grover search algorithm,” IEEE Access, vol. 7, pp. 50849–50857.
4. Z. G. Qu, Z. W. Cheng and X. J. Wang. (2019). “Matrix coding-based quantum image steganography algorithm,” IEEE Access, vol. 7, pp. 35684–35698.
5. Z. G. Qu, T. C. Zhu, J. W. Wang and X. J. Wang. (2018). “A novel quantum steganography based on brown states,” Computers, Materials & Continua, vol. 56, no. 1, pp. 47–59.
6. W. J. Liu, Y. Xu, C. N. Yang, P. P. Gao and W. B. Yu. (2018). “An efficient and secure arbitrary n-party quantum key agreement protocol using bell states,” International Journal of Theoretical Physics, vol. 57, no. 1, pp. 195–207.
7. W. J. Liu, H. B. Wang, G. L. Yuan, Y. Xu, Z. Y. Hen, et al. (2016). , “Multiparty quantum sealed-bid auction using single photons as message carrier,” Quantum Information Processing, vol. 15, no. 2, pp. 869–879.
8. W. J. Liu, Z. Y. Chen, J. S. Liu, Z. F. Su and L. H. Chi. (2018). “Full-blind delegating private quantum computation,” Computers, Materials & Continua, vol. 56, no. 2, pp. 211–223.
9. M. M. Wang, C. Yang and R. Mousoli. (2018). “Controlled cyclic remote state preparation of arbitrary qubit states,” Computers, Materials & Continua, vol. 55, no. 2, pp. 321–329.
10. Z. G. Qu, S. Y. Wu, M. M. Wang, L. Sun and X. J. Wang. (2017). “Effect of quantum noise on deterministic remote state preparation of an arbitrary two-particle state via various quantum entangled channels,” Quantum Information Processing, vol. 16, no. 306, pp. 1–25. [Google Scholar]
11. W. J. Liu, P. P. Gao, W. B. Yu, Z. G. Qu, C. N. Yang, et al. (2018). , “Quantum relief algorithm,” Quantum Information Processing, vol. 17, no. 10, pp. pp.–280. [Google Scholar]
12. A. C. C. Yao. (1979). “Some complexity questions related to distributed computing,” in Proc. of STOC, New York, USA, pp. 209–213. [Google Scholar]
13. A. C.–C. Yao. (1993). “Quantum circuit complexity,” in Proc. of FOCS, Palo Alto, CA, USA, pp. 352–361. [Google Scholar]
14. G. Brassard. (2003). “Quantum communication complexity,” Foundations of Physics, vol. 33, no. 11, pp. 1593–1616. [Google Scholar]
15. P. W. Shor. (1997). “Polynomial time algorithms for prime factorization and discrete logarithms on a quantum computer,” SIAM Journal on Computing., vol. 26, no. 5, pp. 1484–1590. [Google Scholar]
16. L. Grover. (1996). “A fast quantum mechanical algorithm for database search,” in Proc. of STOC, Philadelphia, PA, USA, pp. 212–219. [Google Scholar]
17. L. Grover. (1998). “Quantum computers can search rapidly by using almost any transformation,” Physical Review Letters, vol. 80, no. 19, pp. 4329–4332. [Google Scholar]
18. L. Grover. (2005). “Fixed-point quantum search,” Physical Review Letters, vol. 95, no. 15, pp. 150501–150507. [Google Scholar]
19. P. Høyer. (2000). “Arbitrary phases in quantum amplitude amplification,” Physical Review A , vol. 62, no. 5, pp. 052304–052309. [Google Scholar]
20. M. Mosca. (1998). “Quantum searching, counting and amplitude amplification by eigenvector analysis,” in Proc. of MFCS, Brno, Czech Republic, pp. 90–100. [Google Scholar]
21. A. Younes, J. Rowe and J. Miller. (2006). “A hybrid quantum search engine: a fast quantum algorithm for multiple matches,” in Proc. of ICENCO, Cairo, Egypt. [Google Scholar]
22. A. Younes, J. Rowe and J. Miller. (2004). “Quantum search algorithm with more reliable behaviour using partial diffusion,” in Proc. of QCMC, Glasgow, UK, pp. 171. [Google Scholar]
23. H. Buhrman, R. Cleve and A. Wigderson. (1998). “Quantum vs. classical communication and computation,” in Proc. of STOC, Dallas, TX, USA, pp. 63–68. [Google Scholar]
24. E. Shakshuki, H. Koo, D. Benoit and D. Silver. (2008). “A distributed multi-agent meeting scheduler,” Journal of Computer and System Sciences, vol. 74, no. 2, pp. 279–296. [Google Scholar]
25. D. Wang, V. Venkataraman, Z. Wang, W. Qin, H. Wanget al. (2009). , “Accelerating multi-party scheduling for transaction-level modeling,” in Proc. of GLSVLSI, Boston Area, MA, USA, pp. 339–344. [Google Scholar]
26. S. Han, N. Kim, K. Choi and J. Kim. (2007). “Design of multi-party meeting system for interactive collaboration,” in Proc. of COMSWARE, Bangalore, India, pp. 1–8. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |