DOI:10.32604/cmc.2021.012351
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012351 | |
| Article |
Application of Metaheuristic Algorithms for Optimizing Longitudinal Square Porous Fins
1College of Computing and Informatics, Saudi Electronic University, Riyadh, 11673, Saudi Arabia
2Department of Mechanical Engineering, College of Engineering, Prince Mohammad bin Fahd University, Al Khobar, 31952, Saudi Arabia
3Department of Basic Sciences, College of Science and Theoretical Studies, Saudi Electronic University, Riyadh, 11673, Saudi Arabia
*Corresponding Author: Nawaf N. Hamadneh. Email: nwwaf977@gmail.com
Received: 27 June 2020; Accepted: 25 July 2020
Abstract: The objectives of this study involve the optimization of longitudinal porous fins of square cross-section using metaheuristic algorithms. A generalized nonlinear ordinary differential equation is derived using Darcy and Fourier’s laws in the energy balance around a control volume and is solved numerically using RFK 45 method. The temperature of the base surface is higher than the fin surface, and the fin tip is kept adiabatic or cooled by convection heat transfer. The other pertinent parameters include Rayleigh number (100 ≤ Ra ≤ 104), Darcy number, (10−4 ≤ Da ≤ 10−2), relative thermal conductivity ratio of solid phase to fluid (1000 ≤ kr ≤ 8000), Nusselt number (10 ≤ Nu ≤ 100), porosity (0.1 ≤ φ ≤ 0.9). The impacts of these parameters on the entropy generation rate are investigated and optimized using metaheuristic algorithms. In computer science, metaheuristic algorithms are one of the most widely used techniques for optimization problems. In this research, three metaheuristic algorithms, including the firefly algorithm (FFA), particle swarm algorithm (PSO), and hybrid algorithm (FFA-PSO) are employed to examine the performance of square fins. It is demonstrated that FFA-PSO takes fewer iterations and less computational time to converge compared to other algorithms.
Keywords: Optimization; firefly algorithm; particle swarm algorithm; hybrid algorithms; porous media; entropy generation rate
The heat transfer rate from a solid surface can be enhanced with the help of the fins of different shapes. They are employed in numerous appliances such as microelectronics and heat exchangers. The geometry of the fin plays a key role in improving the overall performance that needs to enhance the efficiency of the fin. Several researchers, including [1–5] have examined several fins shapes for the longitudinal and annular fins and optimized the thermal performance of these fins. Porous fins have been widely used as a viable thermal candidate for effective cooling. The research on the performance and efficiency of porous fins is a new dimension of research in the field of heat transfer. Porous fins enhance the heat transfer rate by increasing the surface area by convection through the pores in addition to reducing the weight of the assembly. The thermal performance of the Porous fins is excellent compared with the thermal performance of conventional equal weight solids, where many studies have examined the thermal performance of the porous fins [6–9].
In 2001, Kiwan et al. [10] proposed a new method that enhances the heat transfer from a given surface by using porous fins. They found that the performance of the porous fin leads to much more improvement in the heat transfer coefficient compared to the performance of the conventional fin. Ghasemi et al. [11] solved the nonlinear temperature distribution equation in solid and porous longitudinal fin with temperature using differential transformation method (DTM). Their results reveal that the technique is highly effective and convenient. Kundu et al. [12] studied the thermal performance of porous fin of various shapes working in a convection environment. They investigated the Straight fins (rectangular, convex parabolic and two exponential types). Kiwan [13] proposed a new method to study the performance of porous fins in a natural convection environment. He found that the rate of heat transfer from the porous fin could exceed the rate of the solid fin. Kiwan [14] studied the problem of laminar natural convection heat transfer from a porous fin attached to a vertical surface. Gorla et al. [15] examined the effects of heat transfer and convection in rectangular porous media. Kundu et al. [16] proposed a computational model to determine the best performance and optimal dimensions of porous fins. They also studied the effects of all parameters on performance and conditions for improvement. Hatami et al. [17] found that the thermal performance of rectangular profiles was better compared to convex and triangular shapes.
The primary purpose of any optimization algorithm is to detect the optimal value of system parameters under various conditions. An optimization algorithm is desired to be robust, has a low computational cost, is able to rapidly reach the globally optimal values of a problem, has very few control parameters, and easy to implement in different problem paradigms [18]. In the last two decades, nature-inspired metaheuristic algorithms have become very popular because of their ability to solve several real-world optimization problems in artificial intelligence (AI), optimization, engineering applications, computational intelligence, data mining, and machine learning. These metaheuristic algorithms are now one of the most widely used techniques for optimization. They are incredibly diverse and include Particle Swarm Optimization (PSO), Firefly Algorithm (FFA), Simulated Annealing, Differential Evolution, Genetic Algorithms, Harmony Search, Ant and Bee algorithm, and others.
Hatami et al. [19] used the Least Square Method and fourth-order Runge–Kutta method to predict the temperature distribution in circular convective-radiative porous fins. Hatami et al. [20] used three analytical methods for predicting the temperature distribution in a rectangular porous fin with temperature-dependent internal heat generation. The methods are the Differential Transformation Method, Collocation Method, and Least Square Method. Das et al. [21] used a simulated annealing method to choose parameters of a rectangular porous fin, which can meet the desired temperature distribution. Deshamukhya et al. [22] used FFA to optimize the important parameters of rectangular porous fins with the reflective boundary condition. They have used three metaheuristic optimization algorithms, namely FFA, PSO, and Gravitational Search Algorithm (GSA). They optimized the parameters responsible for transferring heat from the porous fin subjected to convective tip conditions and insulated end condition.
The above literature review reveals that there is no single study that investigates the modeling and optimization of a longitudinal square fin using metaheuristic algorithms. To fill this gap, mathematical models are developed for the heat transfer and optimization of a longitudinal square fin. For optimization, PSO, FFA, and their hybrid algorithms were employed to obtain the optimum values of the governing parameters for the minimum average entropy generation rate.
Consider a longitudinal porous fin of square cross-section, which is attached to a base plate, as shown in Fig. 1. The side of the square fin is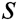 
, and the length is 
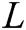, and the fluid (air) is flowing axially along the fin length. Two different materials (Aluminum and copper) are used for the porous fin. The fin surface transfers heat to ambient by convection through fin pores and solid surface. The fluid flow rate is assumed to be 
, the ambient temperature is 
, and the heat transfer coefficient is 
. The fin tip is considered to be either adiabatic or convectively cooled. This analysis is based on the following assumptions:
1. The porous fin is homogeneous, isotropic, and saturated with the single-phase ambient fluid.
2. The thermophysical properties are constant,
3. The entire system is in local thermodynamic equilibrium,
4. The heat conduction occurs only in the axial direction, and
5. The fluid velocity is modeled by Darcy’s law.
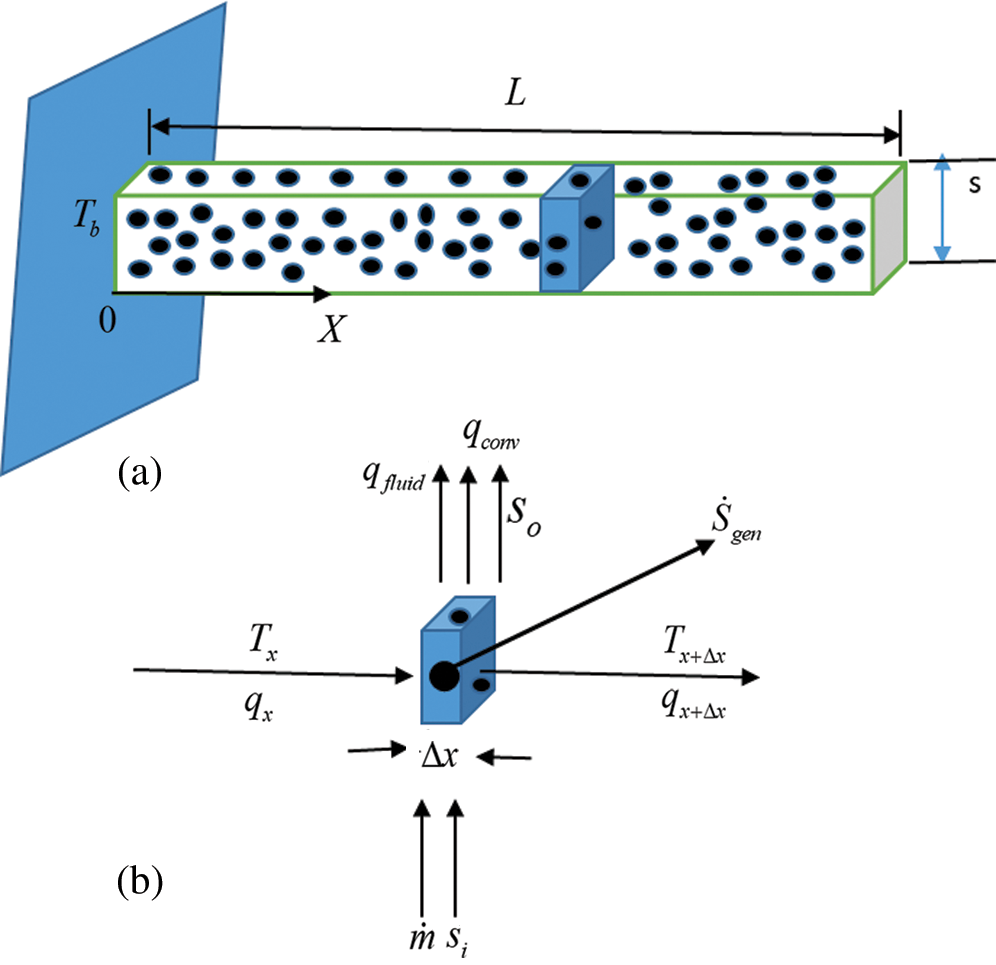
Figure 1: (a) Schematic diagram of porous longitudinal fin of square cross-section (b) Control volume of porous fin for energy and entropy balance
We get the following dimensionless equation for a longitudinal fin of arbitrary profile with uniform cross-section:
where 
and 
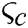are the porous and convective parameters respectively and can be written as:
The porous parameter 
shows the effect of the permeability of the porous medium, while the convective parameter 
shows the effect of convection heat transfer from the fin surface and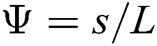 
is the dimensionless geometry parameter. The dimensionless temperature and the efficiency of the fin are plotted in terms of these two parameters. Eq. (2) is subjected to the following dimensionless boundary conditions:
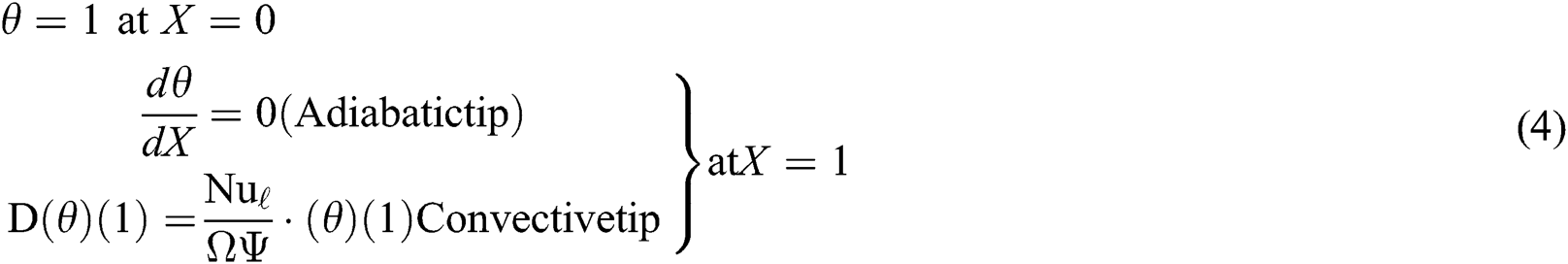
The second-order differential Eq. (2) with boundary conditions (4) can be solved numerically by the finite difference method or analytically by the homotopy perturbation method. Thus, the dimensionless distribution within the porous square fin up to first order for adiabatic tip boundary condition can be written as:
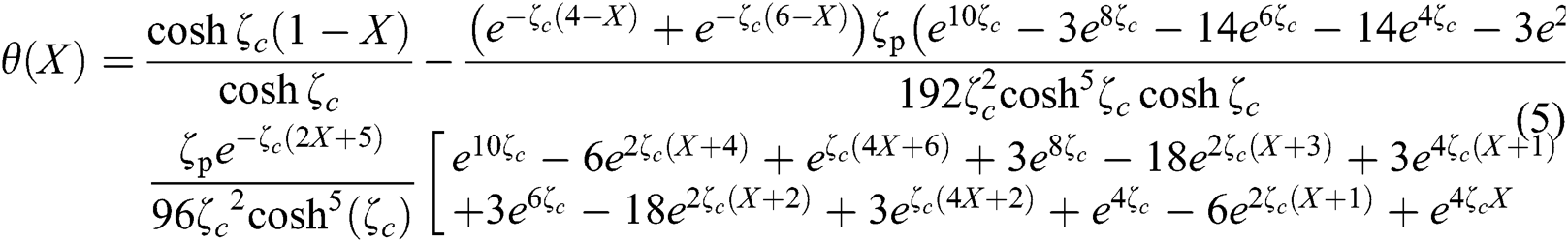
Similarly, the dimensionless distribution within the porous square fin up to first order for convective tip boundary condition can be written as:
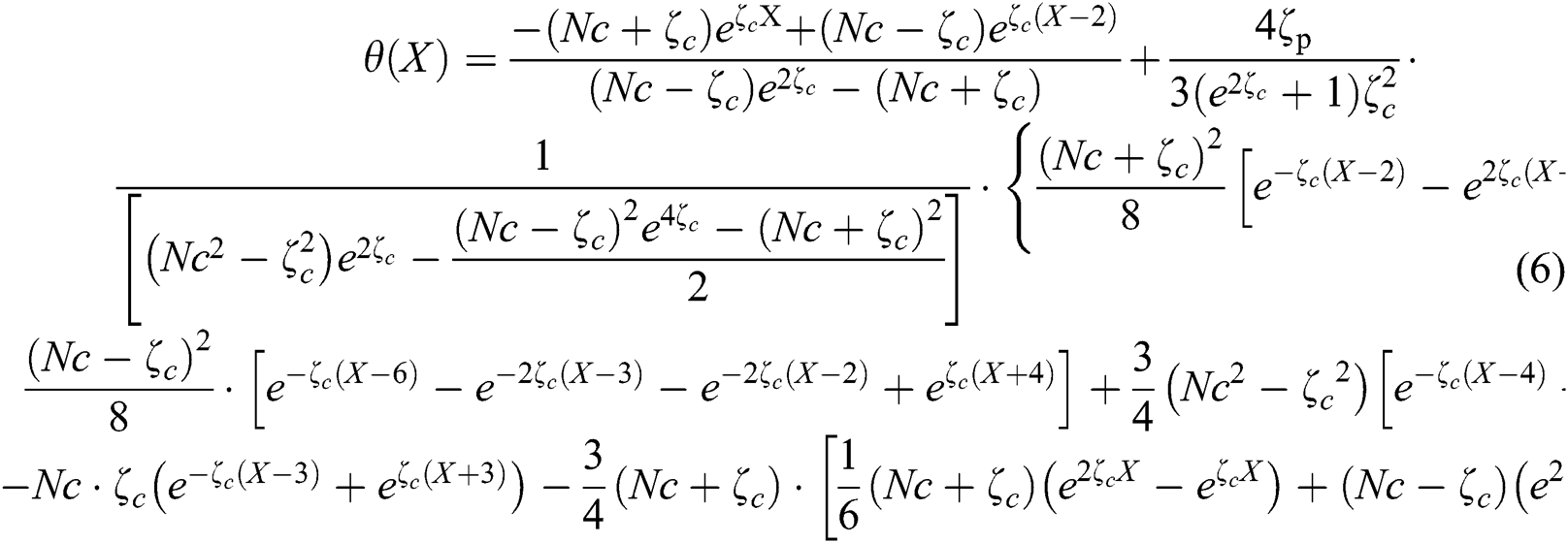
These temperature distributions depend upon the porous and convective parameters. They can be used to determine the heat transfer rate from the porous fins and the efficiency that will be defined in the next section.
Following [23], the actual heat transfer rate, maximum heat transfer rate, and the heat transfer rate of the un-finned surface can be written as:
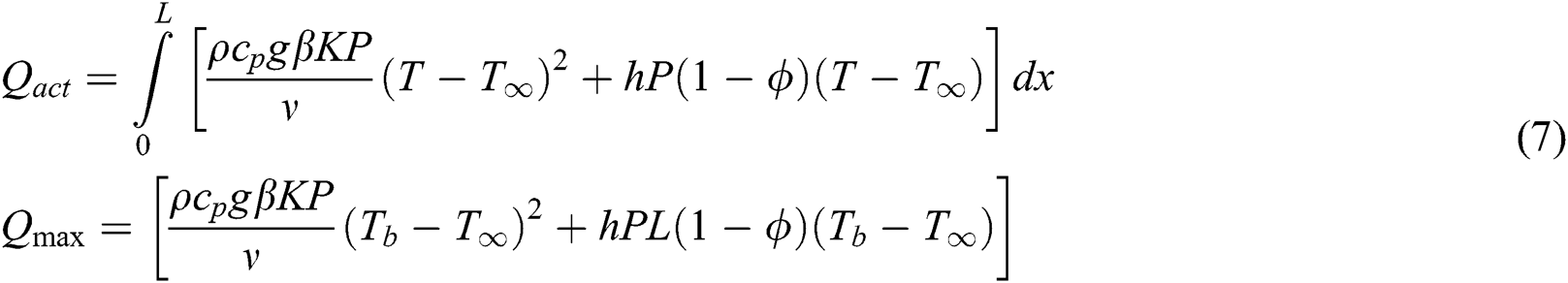
The efficiency of the porous fin is defined as the ratio of the actual rate of heat transfer of the fin to the maximum heat transfer rate and can be written as:
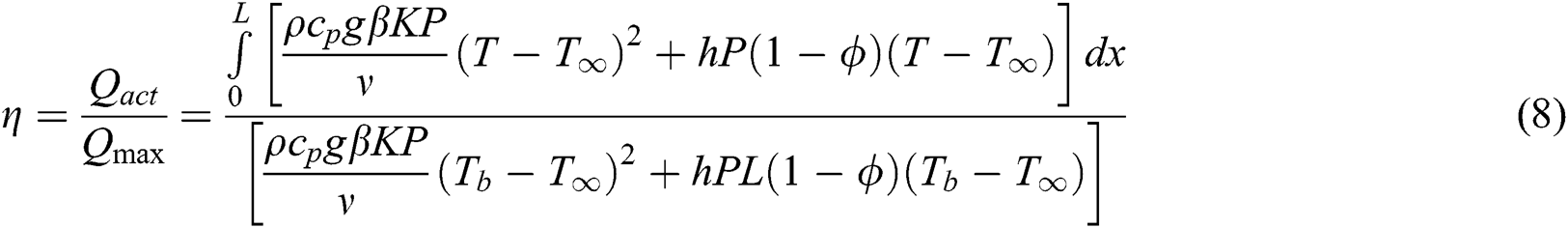
Using dimensionless variables, Eq. (8), and simplifying, we get
Thus, the efficiency of the porous fin depends on the porosity, as well as Rayleigh, Darcy, and Nusselt numbers. The selection of these dimensionless numbers is very vital in improving the efficiency of porous fins.
Following [24], the entropy generation rate for steady flow can be obtained from entropy balance across the control volume (Fig. 1) and can be written as:
Assuming uniform pressure across the control volume, and following [25], the change in entropy can be written as:
Considering the limiting case, 
and using Eqs. (11) and (12) gives:
Using Darcy’ law, the mass flow rate through the porous fin can be written as:
Using Fourier’s law of conduction and Eq. (13), the entropy generation rate can be written as:
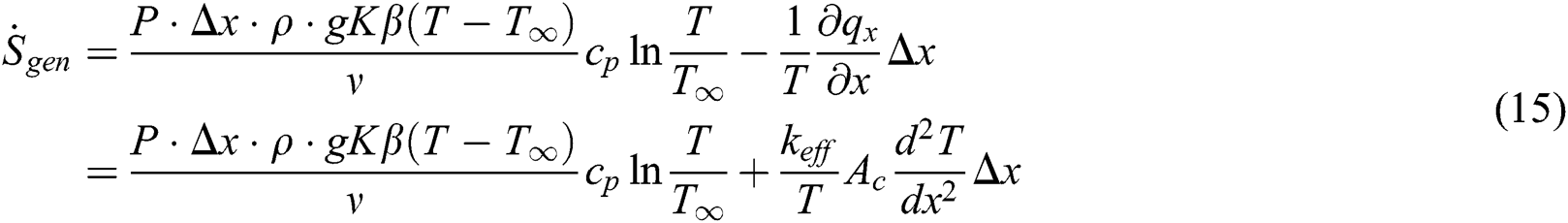
Thus, the entropy generation rate per unit volume of the longitudinal porous fin of the arbitrary cross-section can be written as:
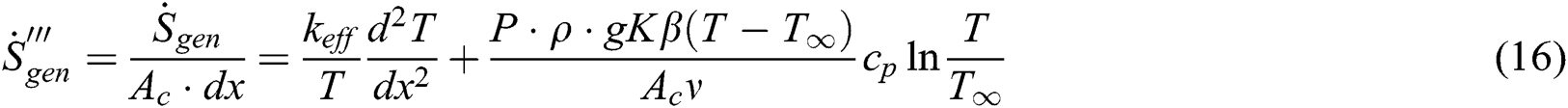
In dimensionless form, the total entropy generation rate can be written as:
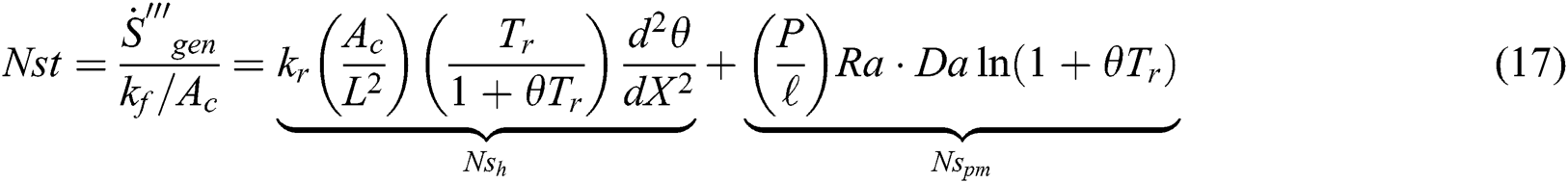
where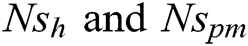 
are the dimensionless entropy generation rates due to heat and porous medium, 
and 
are the dimensionless ratios and defined as:
while the characteristic length 
, cross-sectional area 
and the perimeter 
of the square fin are defined as:
The average entropy generation rate in the longitudinal fin can be determined from:
The irreversibility ratio also known as Bejan number [26] is defined as:
Concerning the entropy generation analysis of convective heat transfer problems, Bejan presented the expression of irreversibility distribution ratio as follows [26]:
It is noteworthy to underline that when 
, the porous medium irreversibility 
is the major source, whereas if 
the heat transfer irreversibility 
is dominant when 
the irreversibility due to heat transfer (
) and due to porous medium (
) have the same share.
The optimization algorithms, searching for optimal solutions, are based on the information they collect through several iterations [27]. To avoid local search, three metaheuristic algorithms, including firefly algorithm (FFA), particle swarm optimization (PSO), and hybrid PSO-FFA algorithms are used for global optimization. The general optimization procedure and the essential aspects of each algorithm will be presented in the coming sections.
In this study, the dimensionless average entropy generation rate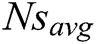 
is the objective function (fitness function) that is to be minimized subject to the following constraints. So, the mathematical model for the optimization of 
can be written as:
Subject to
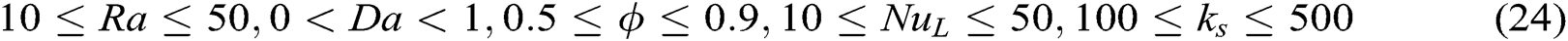
We focus on finding the optimal values of the above parameters through the selected algorithms. The other fixed parameters are given in Tab. 1.
Table 1: Constant values of fixed parameters
Based on the behavior of fireflies, Yang [28] presented the FFA as a very effective algorithm. The FFA is flexible to both continuous and clustering problems because of its several characteristics [29,30]. The key advantages of FFA arise in two main parts: The ability to deal with the automatic subdivision and multimodality. Therefore, the population of FFA is automatically divided into groups, with each group trying to achieve the optimal local position.
The main idea of the FFA relies on the attraction of fireflies to each other depending on the strength of brightness, aware that sceneries will determine the strength of the brightness of an objective function. According to that, the fireflies are going to move to the brighter ones, whereas a firefly will have a random movement if there are no brighter fireflies. According to Yang [28], the new position of a firefly i in reference to a brighter firefly j is given by:
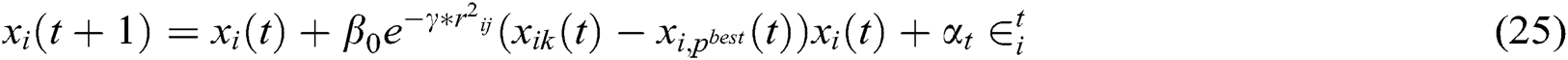
where 
represents the position of the firefly 
at time t (i = 1, 2, …, N), where N is the number of fireflies. 
represents the attractiveness at a distance of 
and if 
, then the firefly 
has a random walk, 
represents the brightness absorption parameter, α represents a random vector over the interval [0,1],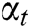 
and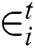 
represent random parameter and vector, respectively, at time t [31]. FFA techniques and practical steps are briefly summarized in the following.
1. The FFA starts with N initial solutions (N fireflies) that are generated randomly. Note that initial solutions provide the initial values of the optimal variables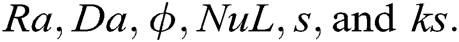 
These initial solutions will develop over time to create a new generation. Furthermore, the random vector α and the brightness absorption parameter 
are assigned fixed parameters. Here, the parameter 
defines the convergence speed between the fireflies and contributes to how the FFA behaves.
2. The optimization process starts by generating initial populations. In every iteration, the attractiveness (β) and the distance (r) values of the fireflies are computed from the best firefly.
3. The value of light intensity 
changes with the firefly movements. This means that the positions of the fireflies are affected depending on their performance given the attractiveness and distance values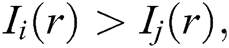 
then the firefly 
will move towards the firefly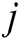 
; otherwise, the firefly 
will move randomly.
4. Announce the optimal solution (optimal value of 
). Fig. 2 illustrates the structure of the FFA algorithm.
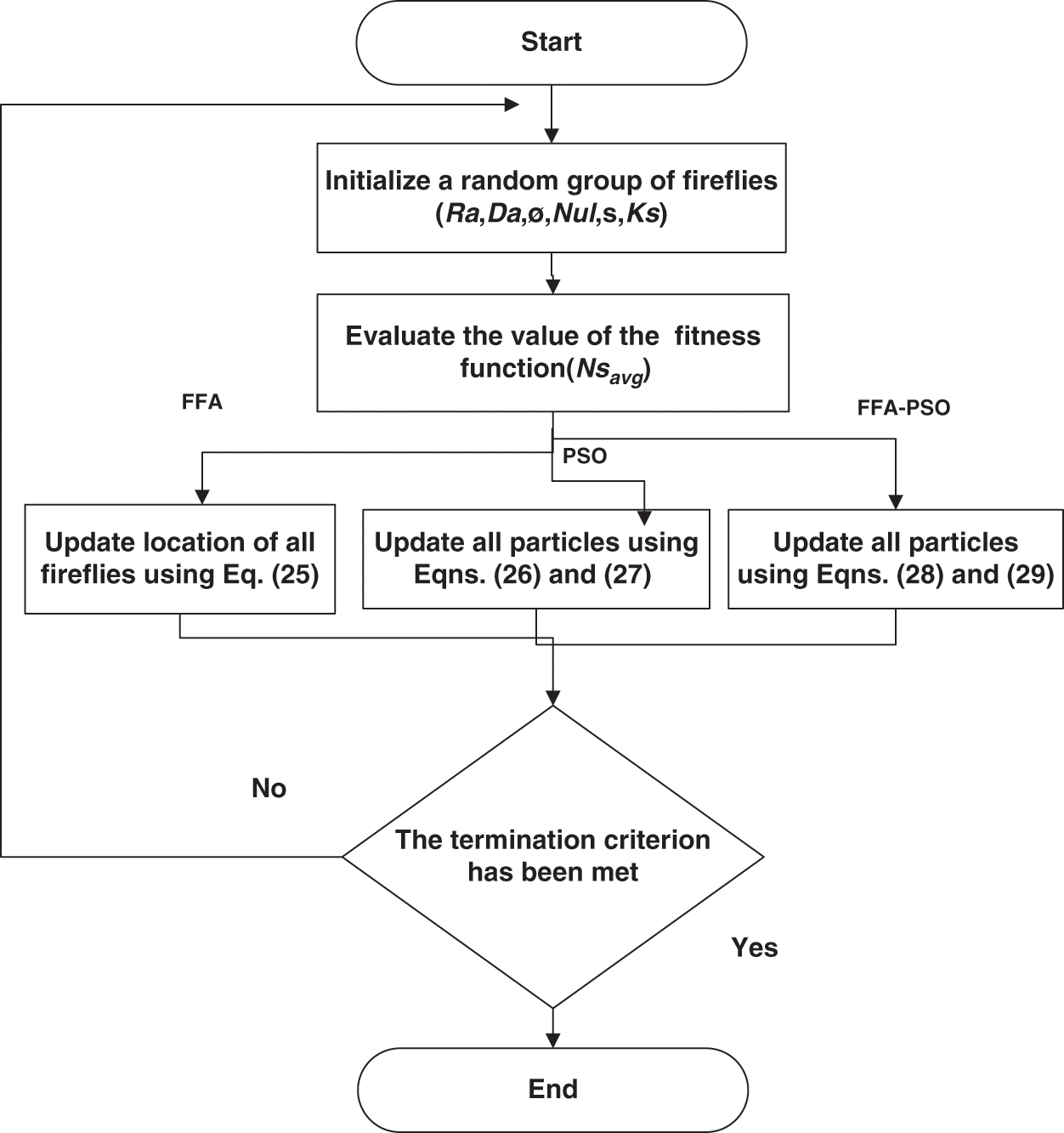
Figure 2: Structure of FFA, PSO, and hybrid FFA-PSO algorithms
5.3 Particle Swarm Optimization Algorithm
The working principle of the PSO algorithm was inspired by the birds flock’s social behavior and the fish’s shoaling behavior [32,33]. The solutions generated by the PSO algorithm have the name particles. Note that particles of this work are the values of Ra, Da, ϕ, Nul, s, and Ks. Using the Eqs. (26) and (27), each particle flies according to the change in its velocity vector v and its position x [32,34]:
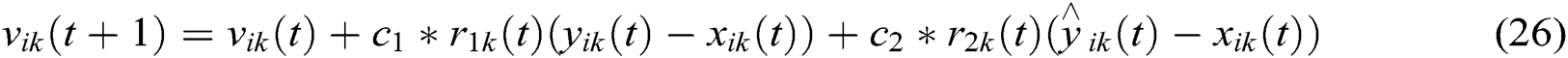
where 
, and 
are the position, the velocity, the best personal position (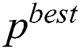
), and the global best position (
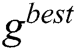) of each respectively, while 
and 
are the learning factors (acceleration coefficients) of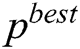 
in the interval [0,2], 
and 
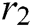are the random numbers in the interval [0,1].
Kennedy and Eberhart suggested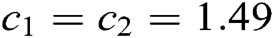 
in his calculations [35]. Note that, when the best particle, i.e., the solution with the best performance (optimal value of 
), is determined, the other particles will follow it. Additionally, each particle will retain the best position it achieved before.
The purpose of using of PSO-FFA is improving the overall performance of FFA and PSO algorithm in a research field by combining the two algorithms together so that the weaknesses of one algorithm are compensated by the strengths of other algorithm [36]. The new position vectors of the FFA-PSO is generated randomly by using the following equations [36].
where 
is the Cartesian distance between 
. 
is the Cartesian distance between 
and 
.
This study demonstrates the mathematical modeling and optimization of longitudinal porous fins of square cross-section. For the modeling, the first and second laws of thermodynamics together with Darcy and Fourier’s laws, are employed, whereas three metaheuristic algorithms are utilized to minimize the entropy generation rate. The dimensionless nonlinear differential equations are solved analytically using Homotopy Perturbation Method (HPM) for the two selected fin tip boundary conditions. The effects of dimensionless numbers, including Rayleigh, Darcy, Nusselt numbers on the dimensionless temperature, fin efficiency, total entropy generation rate, and Bejan number, are investigated theoretically. In each case, it is assumed that 
.
Figs. 3(a) and 3(b) display the effects of Rayleigh and Darcy numbers on the dimensionless temperature along the fin surface for the adiabatic and convective tip conditions. The Rayleigh number plays the same role in free convection, as Reynolds number plays in the forced convection. The dimensionless temperature is found to be maximum at the base surface and decreases along the fin surface. As the Rayleigh number increases, the dimensionless temperature decreases in each case. For convective fin tip condition, the Rayleigh number enables a better heat transfer rate at higher values of 
. The Darcy number signifies the comparative impact of the permeability of the porous medium. It is observed that the dimensionless temperature decreases with an increase in the Darcy number, see Figs. 3(a) and 3(b). The variation of fin efficiency with both Ra and Da along the fin surface is depicted in Figs. 4(a) and 4(b) for both boundary conditions, respectively. Like temperature, the fin efficiency is maximum at the base surface and decreases along the fin surface. Both Ra and Da tend to reduce the efficiency of the fin. As Da increases, the ideal heat transfer rate increases, which reduces the fin efficiency.
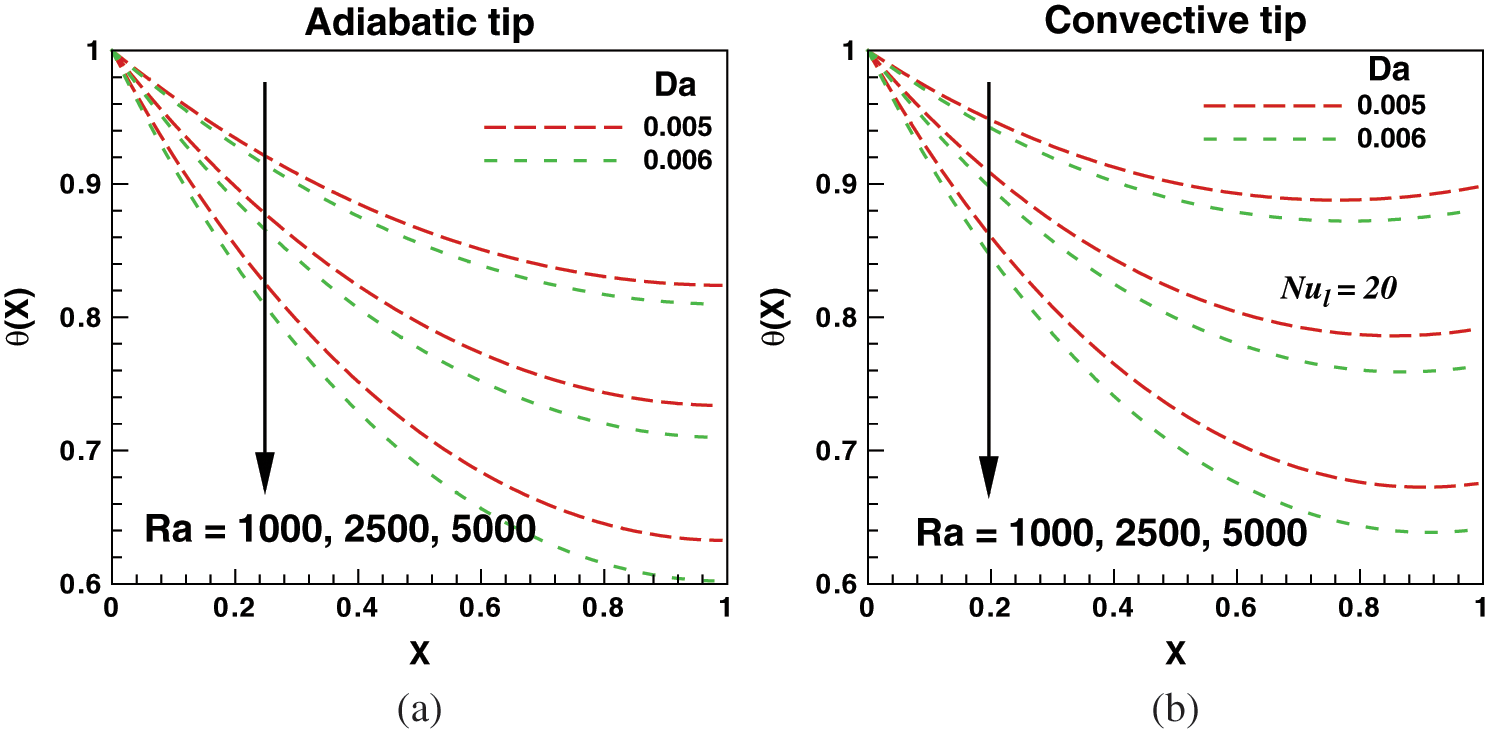
Figure 3: Effects of Rayleigh and Darcy numbers on dimensionless temperature for (a) adiabatic tip and (b) convective tip condition
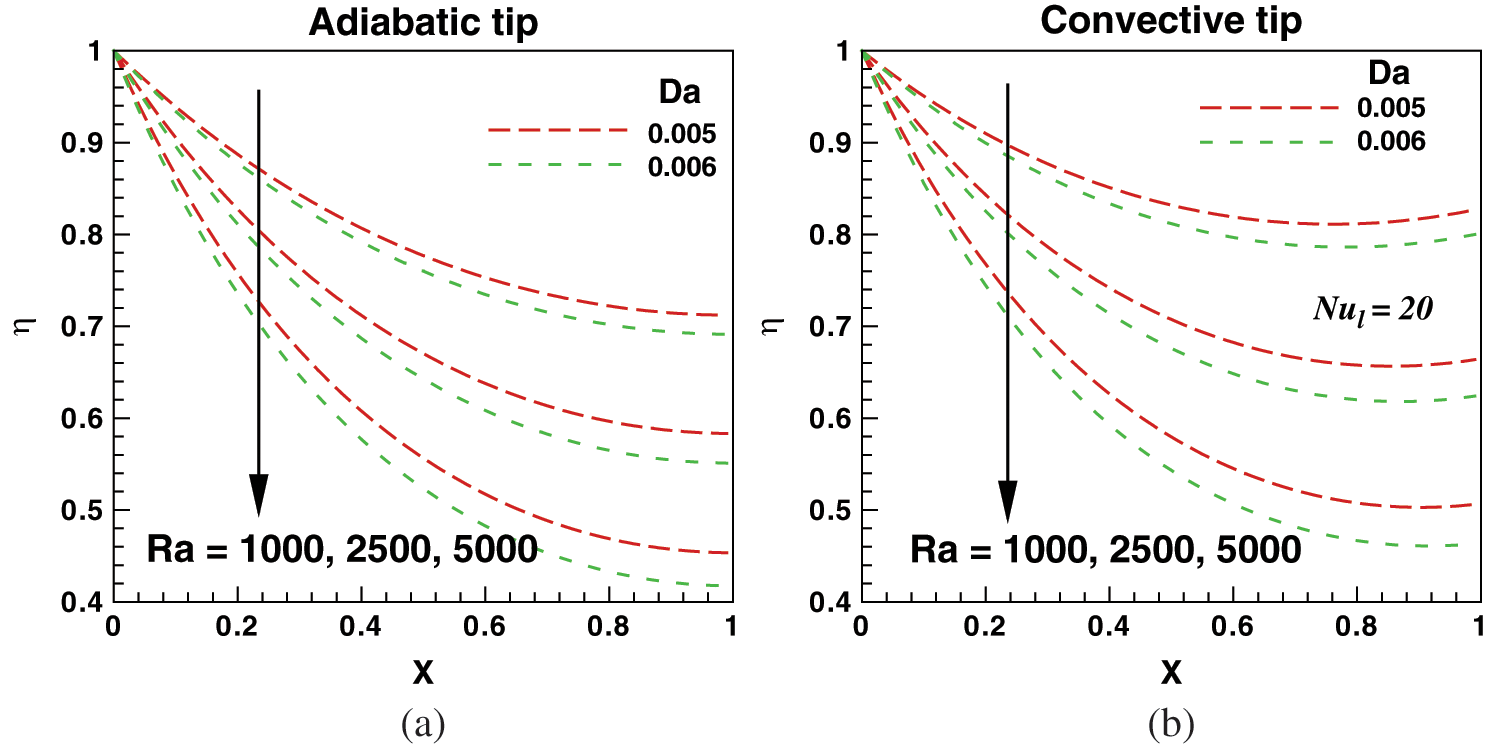
Figure 4: Effects of Rayleigh and Darcy numbers on fin efficiency for (a) adiabatic tip and (b) convective tip condition
The total dimensionless entropy generation rate Nst includes the entropy generation due to heat transfer 
and porous medium 
. In the porous medium, the entropy generation rate depends upon Ra and Da. The total dimensionless entropy generation rate is plotted versus the fin length in Figs. 5(a) and 5(b) for both tip boundary conditions. In each case, the effects of Ra and Da on 
are displayed for the same fixed parameters. As expected, the total dimensionless entropy generation rate is maximum at the base surface and decreases along the fin length. As the Rayleigh number increases, the total dimensionless entropy generation rate decreases due to the decrease in temperature gradients. As the Darcy number decreases, the permeability of the porous medium decreases, and as a result, the entropy generation rate also decreases. The Bejan number is plotted versus fin length in Figs. 6(a) and 6(b) for both boundary conditions. The effect of Ra and Da on the Bejan number are displayed. It is shown that the Bejan number decreases with an increase in the Ra, but increases with Da. In fact, Bejan number shows the relative measure of irreversibility due to heat transfer over irreversibility due to porous medium. In both cases, the Bejan number is close to unity which indicates the dominance of irreversibility due to heat transfer, see Fig. 6.
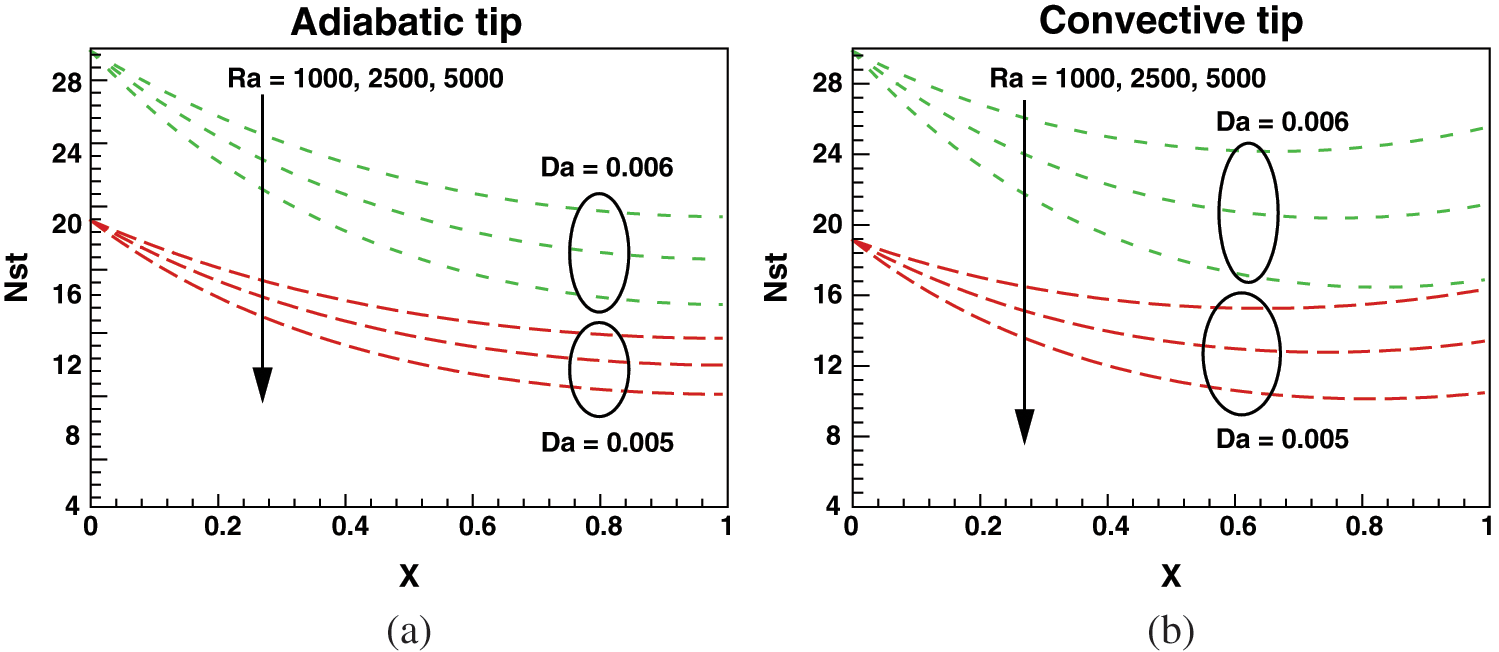
Figure 5: Effects of Rayleigh and Darcy numbers on total dimensionless EGR for (a) adiabatic tip and (b) convective tip condition
Figure 6: Effects of Rayleigh and Darcy numbers on Bejan number for (a) adiabatic tip and (b) convective tip condition
In this study, a longitudinal square cross-section porous fin is modeled and optimized using three robust metaheuristic algorithms, namely, PSO, FFA, and hybrid PSO-FFA, for the two selected boundary conditions. The personal and global best values of 
are plotted in Fig. 7(a) adiabatic tip and Fig. 7(b) convective tip conditions using the PSO algorithm. During the optimization process, the position of each particle will be automatically adjusted in the direction based on the best position founded by itself (personal best), and the other is the best position in the whole swarm (Global best) [32]. In each iteration, the algorithms memorized the personal best value of the fitness function (the lowest value of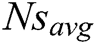 
founded by that iteration). Moreover, each iteration memorized the Global best value of the fitness function (the lowest value of 
found so far). These curves show a decreasing trend from first iteration until a point that has no more improvement, and then there is convergence in the algorithms. For the adiabatic tip condition, the global best value of 
is found after 8 iterations, whereas for the convective tip condition, the global best value of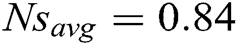 
is found after 38 iterations.
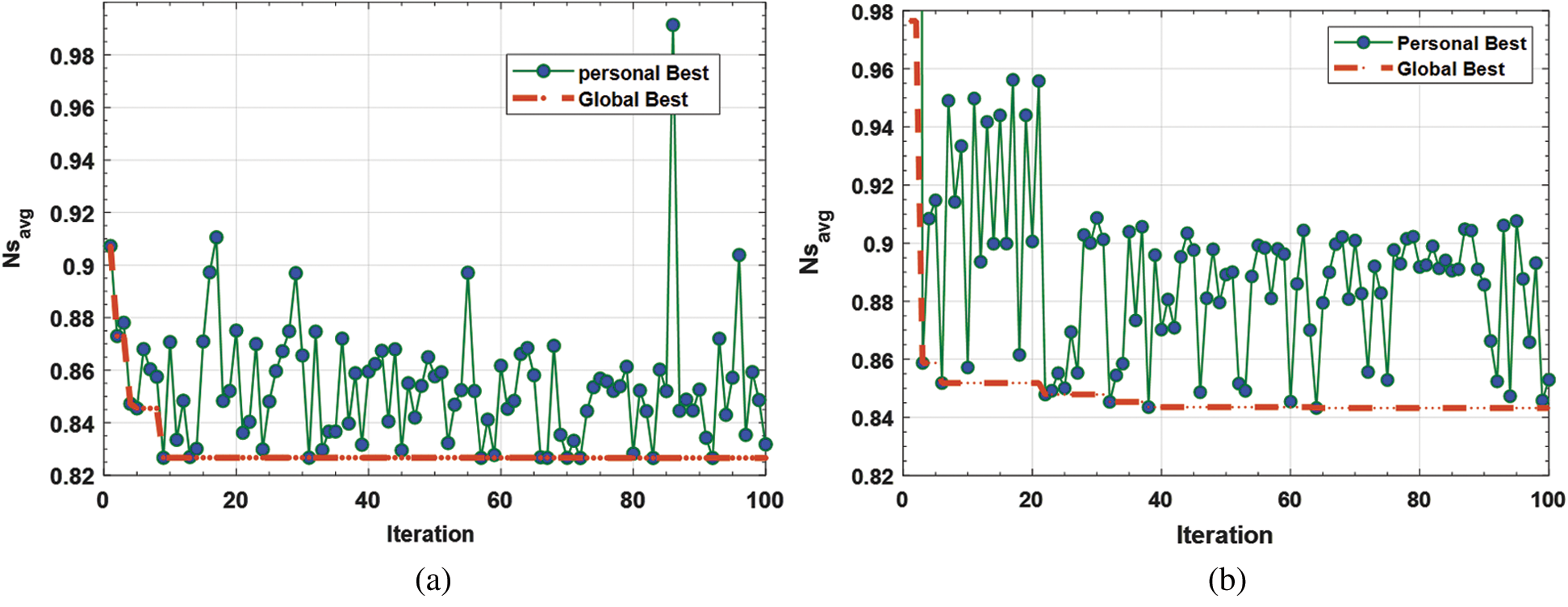
Figure 7: Personal and global best values of 
using PSO algorithm for (a) adiabatic tip and (b) convective tip conditions
Figs. 8 and 9 display the convergence of 
using PSO for both fin tip conditions, respectively. The constriction factors (
and 
) were introduced into PSO to improve its search performance, where 
has been suggested by Zeng et al. [35]. The constriction factors represent jumping steps that affect finding the best solutions. In order to find appropriate values for the constriction factors (PSO algorithm parameters), we examined different values for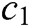 
and 
find the optimum value of 
As a result, we found that the best values for the parameters for both boundary conditions are 
as shown in Fig. 8(a) adiabatic tip and Fig. 8(b) convective tip conditions. The initial population that we have used is 80, and the number of iterations is 100. As a result, the best values of PSO algorithm parameters are 
PSO algorithm parameters represent jumping steps that affect finding the minimum possible value.
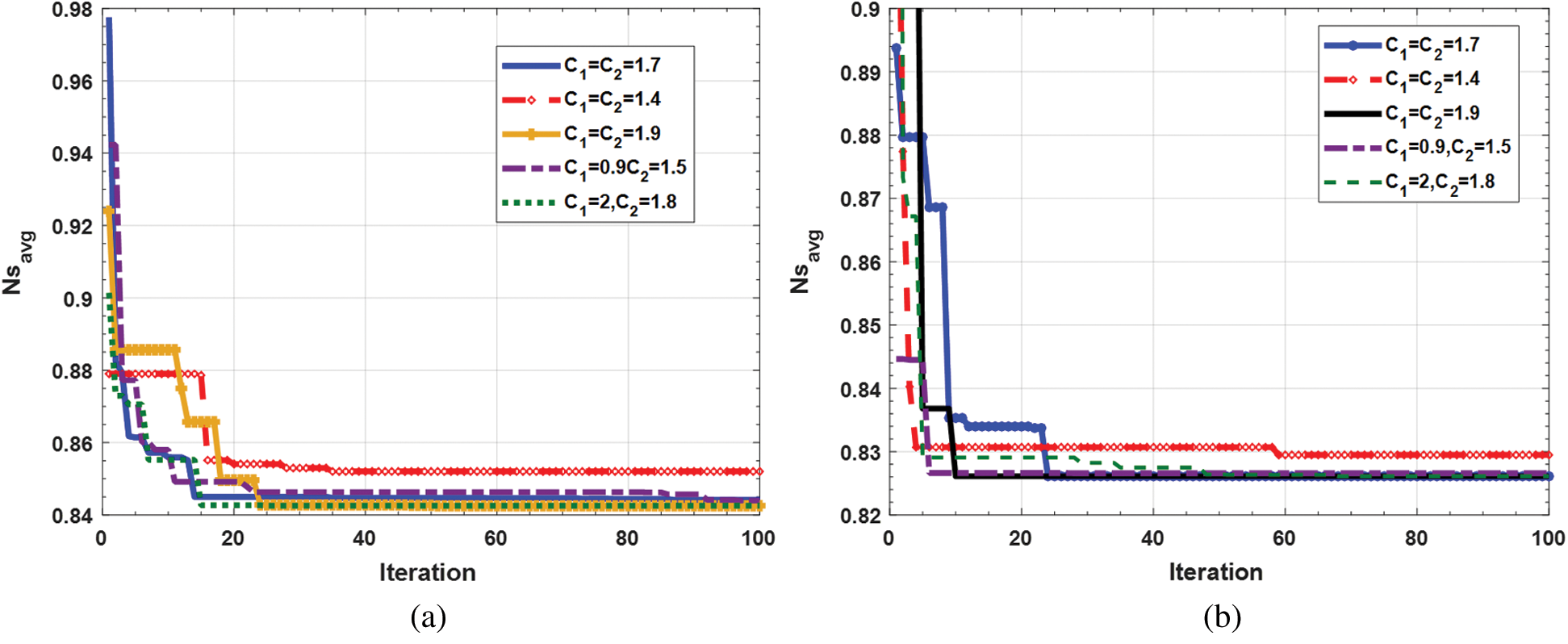
Figure 8: (a) Convergence of 
for adiabatic tip condition using PSO algorithm, (b) Convergence of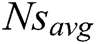 
for convective tip condition using PSO algorithm
Figure 9: (a) Convergence of 
for adiabatic tip condition-comparison of three Mas, (b) Convergence of 
for convective tip condition-comparison of three Mas
In addition to the PSO algorithm, we also made an effort to improve the objective function 
of longitudinal porous fins by calculating optimal values using FFA and hybrid PSO-FFA. The initial population starts by 80, and the number of iterations is determined by 100, while 
and 
In the first experiment (adiabatic tip condition), the optimal value of 
is 0.8261, and the corresponding value of 
is 0.91.
Fig. 9(a) adiabatic tip and Fig. 9(b) convective tip conditions demonstrate the convergence of the fitness functions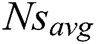 
for both fin tip conditions using three selected MAs. The best results or the minimum entropy generation rate obtained after all the runs have been shown in both figures. MAs examine the whole domain for improved combinations of design variables, which would give the minimum value of 
is observed that hybrid PSO-FFA converges after 5 iterations, then PSO converges after 16 iterations, and FFA converges after 80 iterations for the adiabatic fin tip condition. Therefore, PSO-FFA has performed better than FFA and PSO in terms of convergence speed and computational effort. However, for the convective fin tip condition, the convergence rate is found slow. Note that the three algorithms determine the same optimal value. As a result, the best values of the parameters for adiabatic tip conditions are 
and 
(Fig. 9(a)).
On the other hand, the optimal value of 
for the convective tip condition is 0.8425, as shown in Fig. 9(b). This figure shows that the optimum value obtained is the same value that was determined using the three algorithms. In addition, the best values of the parameters are 
, and 
.
Metaheuristic algorithms have been used to optimize the thermal performance of longitudinal porous fins with a square cross-section using the entropy generation model. The information of the local and global best positions is exploited to update the particle’s velocity in each iteration. The effects of two different tip boundary conditions on the performance of fins are examined. The following important conclusions are drawn from this study:
Rayleigh and Darcy’s numbers reduce the dimensionless temperature and fin efficiency along the fin surface.
The convective tip condition provides higher efficiency than the adiabatic tip condition.
• The Rayleigh number reduces the total entropy generation rate, whereas the Darcy number increases the entropy generation rate.
• The optimum value obtained is the same value that was determined using the three algorithms
• The hybrid PSO-FFA is found to be more efficient than PSO or FFA algorithms in terms of convergence speed and computational efforts.
• The global best values for both fin tip conditions are found to be very close.
Funding Statement: This research is supported by the Deanship of Scientific Research/Saudi Electronic University [Research No. 7704-CAI-2019-1-2-r]. Initials of authors who received the grant: S. H. Atawneh; N. N. Hamadneh; W. A. Khan.
Conflict of Interest: All authors declare that they have no conflict of interest.
References
1. S. Pashah, A. Moinuddin and S. M. Zubair. (2016). “Thermal performance and optimization of hyperbolic annular fins under dehumidifying operating conditions—Analytical and numerical solutions,” International Journal of Refrigeration, vol. 65, pp. 42–54.
2. M. Hajmohammadi, A. Doustahadi and M. Ahmadian-Elmi. (2020). “Heat transfer enhancement by a circumferentially non-uniform array of longitudinal fins assembled inside a circular channel,” International Journal of Heat and Mass Transfer, vol. 158, pp. 1–8.
3. W. Khan and A. Aziz. (2012). “Transient heat transfer in a functionally graded convecting longitudinal fin,” Heat and Mass Transfer, vol. 48, no. 10, pp. 1745–1753.
4. A. Aziz and T. Fang. (2010). “Alternative solutions for longitudinal fins of rectangular, trapezoidal, and concave parabolic profiles,” Energy Conversion and Management, vol. 51, no. 11, pp. 2188–2194.
5. C. H. Huang and Y. L. Chung. (2018). “Optimal design of annular fin shapes with temperature-dependent properties,” Journal of Thermophysics and Heat Transfer, vol. 32, no. 1, pp. 18–26.
6. S. Hoseinzadeh, A. Moafi, A. Shirkhani and A. J. Chamkha. (2019). “Numerical validation heat transfer of rectangular cross-section porous fins,” Journal of Thermophysics and Heat Transfer, vol. 33, no. 3, pp. 698–704.
7. M. Sobamowo, O. Kamiyo and O. Adeleye. (2017). “Thermal performance analysis of a natural convection porous fin with temperature-dependent thermal conductivity and internal heat generation,” Thermal Science and Engineering Progress, vol. 1, pp. 39–52.
8. G. Oguntala, G. Sobamowo, R. Abd-Alhameed and J. Noras. (2019). “Numerical investigation of inclination on the thermal performance of porous fin heatsink using pseudospectral collocation method,” Karbala International Journal of Modern Science, vol. 5, no. 1, pp. 19–26.
9. Y. Zhao. (2019). “Application of Euler-Poincare characteristic in the prediction of permeability of porous media,” Intelligent Automation and Soft Computing, vol. 25, no. 4, pp. 835–845.
10. S. Kiwan and M. Al-Nimr. (2001). “Using porous fins for heat transfer enhancement,” Journal of Heat Transfer, vol. 123, no. 4, pp. 790–795. [Google Scholar]
11. S. Ghasemi, P. Valipour, M. Hatami and D. Ganji. (2014). “Heat transfer study on solid and porous convective fins with temperature-dependent heat generation using efficient analytical method,” Journal of Central South University, vol. 21, no. 12, pp. 4592–4598. [Google Scholar]
12. B. Kundu, D. Bhanja and K. S. Lee. (2012). “A model on the basis of analytics for computing maximum heat transfer in porous fins,” International Journal of Heat and Mass Transfer, vol. 55, no. 25, pp. 7611–7622. [Google Scholar]
13. S. Kiwan. (2007). “Thermal analysis of natural convection porous fins,” Transport in Porous Media, vol. 67, no. 1, pp. 17–29. [Google Scholar]
14. S. Kiwan. (2007). “Effect of radiative losses on the heat transfer from porous fins,” International Journal of Thermal Sciences, vol. 46, no. 10, pp. 1046–1055. [Google Scholar]
15. R. S. R. Gorla and A. Bakier. (2011). “Thermal analysis of natural convection and radiation in porous fins,” International Communications in Heat and Mass Transfer, vol. 38, no. 5, pp. 638–645. [Google Scholar]
16. B. Kundu and D. Bhanja. (2011). “An analytical prediction for performance and optimum design analysis of porous fins,” International Journal of Refrigeration, vol. 34, no. 1, pp. 337–352. [Google Scholar]
17. M. Hatami and D. Ganji. (2014). “Investigation of refrigeration efficiency for fully wet circular porous fins with variable sections by combined heat and mass transfer analysis,” International Journal of Refrigeration, vol. 40, pp. 140–151. [Google Scholar]
18. W. Yu, X. Li, H. Yang and B. Huang. (2018). “A multi-objective metaheuristics study on solving constrained relay node deployment problem in WSNS,” Intelligent Automation and Soft Computing, vol. 24, no. 2, pp. 367–376. [Google Scholar]
19. M. Hatami and D. Ganji. (2013). “Thermal performance of circular convective-radiative porous fins with different section shapes and materials,” Energy Conversion and Management, vol. 76, pp. 185–193. [Google Scholar]
20. M. Hatami, A. Hasanpour and D. Ganji. (2013). “Heat transfer study through porous fins (Si3N4 and AL) with temperature-dependent heat generation,” Energy Conversion and Management, vol. 74, pp. 9–16. [Google Scholar]
21. R. Das and K. Ooi. (2013). “Predicting multiple combination of parameters for designing a porous fin subjected to a given temperature requirement,” Energy Conversion and Management, vol. 66, pp. 211–219. [Google Scholar]
22. T. Deshamukhya, R. Nath, S. A. Hazarika, D. Bhanja and S. Nath. (2019). “A modified firefly algorithm to maximize heat dissipation of a rectangular porous fin in heat exchangers exposed to both convective and radiative environment,” in Proc. of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, vol. 233, no. 6, pp. 1203–1216. [Google Scholar]
23. Y. A. Cengel and M. A. Boles. (2011). Thermodynamics: An Engineering Approach, 7th ed. New York: McGraw-Hill. [Google Scholar]
24. G. Oguntala, G. Sobamowo, Y. Ahmed and R. Abd-Alhameed. (2019). “Thermal prediction of convective-radiative porous fin heatsink of functionally graded material using adomian decomposition method,” Computation, vol. 7, no. 1, pp. 1–17. [Google Scholar]
25. M. J. Moran, H. N. Shapiro, D. D. Boettner and M. B. Bailey. (2010). Fundamentals of Engineering Thermodynamics. Hoboken, New Jersey, USA: John Wiley & Sons. [Google Scholar]
26. M. W. A. Khan, M. I. Khan, T. Hayat and A. Alsaedi. (2018). “Entropy generation minimization (EGM) of nanofluid flow by a thin moving needle with nonlinear thermal radiation,” Physica B: Condensed Matter, vol. 534, pp. 113–119. [Google Scholar]
27. X. S. Yang and X. S. He. (2019). “Introduction to optimization,” in Mathematical Foundations of Nature-Inspired Algorithms. Switzerland: Springer, pp. 1–20. [Google Scholar]
28. X. S. Yang. (2010). Nature-Inspired Metaheuristic Algorithms. Luniver Press. [Google Scholar]
29. N. Hamadneh. (2020). “Dead sea water levels analysis using artificial neural networks and firefly algorithm,” International Journal of Swarm Intelligence Research, vol. 11, no. 3, pp. 1–11. [Google Scholar]
30. S. L. Tilahun, J. M. T. Ngnotchouye and N. N. Hamadneh. (2019). “Continuous versions of firefly algorithm: A review,” Artificial Intelligence Review, vol. 51, no. 3, pp. 445–492. [Google Scholar]
31. W. A. Khan, N. N. Hamadneh, S. L. Tilahun and J. Ngnotchouye. (2016). “A review and comparative study of firefly algorithm and its modified versions,” Optimization Algorithms-Methods and Applications, pp. 281–313. [Google Scholar]
32. N. Hamadneh, W. A. Khan, S. Sathasivam and H. C. Ong. (2013). “Design optimization of pin fin geometry using particle swarm optimization algorithm,” PLoS One, vol. 8, no. 5, e66080. [Google Scholar]
33. N. N. Hamadneh, W. A. Khan, I. Khan and A. S. Alsagri. (2019). “Modeling and optimization of gaseous thermal slip flow in rectangular microducts using a particle swarm optimization algorithm,” Symmetry, vol. 11, no. 4, pp. 1–13. [Google Scholar]
34. J. Liang, S. Ge, B. Qu, K. Yu and F. Liu et al. (2020). , “Classified perturbation mutation based particle swarm optimization algorithm for parameters extraction of photovoltaic models,” Energy Conversion and Management, vol. 203, pp. 1–20. [Google Scholar]
35. N. Zeng, Z. Wang, H. Zhang and F. E. Alsaadi. (2016). “A novel switching delayed PSO algorithm for estimating unknown parameters of lateral flow immunoassay,” Cognitive Computation, vol. 8, no. 2, pp. 143–152. [Google Scholar]
36. P. Kora and K. S. R. Krishna. (2016). “Hybrid firefly and particle swarm optimization algorithm for the detection of bundle branch block,” International Journal of the Cardiovascular Academy, vol. 2, no. 1, pp. 44–48. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |