DOI:10.32604/cmc.2021.012000
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012000 | |
| Article |
Analysis of Magnetic Resistive Flow of Generalized Brinkman Type Nanofluid Containing Carbon Nanotubes with Ramped Heating
1Department of Mathematical Sciences, Faculty of Science, Universiti Teknologi Malaysia, Johor Bahru, 81310, Malaysia
2Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
3Center of Excellence for Research in Engineering Materials (CEREM), King Saud University, Al-Riyadh, 11421, Saudi Arabia
4Department of Physical Chemistry, Electrochemistry and Corrosion Laboratory, National Research Centre, Cairo, 12622, Egypt
*Corresponding Author: Ilyas Khan. Email: ilyaskhan@tdtu.edu.vn
Received: 09 June 2020; Accepted: 16 July 2020
Abstract: In recent times, scientists and engineers have been most attracted to electrically conducted nanofluids due to their numerous applications in various fields of science and engineering. For example, they are used in cancer treatment (hyperthermia), magnetic resonance imaging (MRI), drug-delivery, and magnetic refrigeration (MR). Bearing in mind the significance and importance of electrically conducted nanofluids, this article aims to study an electrically conducted water-based nanofluid containing carbon nanotubes (CNTs). CNTs are of two types, single-wall carbon nanotubes (SWCNTs) and multiple-wall carbon nanotubes (MWCNTs). The CNTs (SWCNTs and MWCNTs) have been dispersed in regular water as base fluid to form water-CNTs nanofluid. The Brinkman Type nanofluid model is developed in terms of time-fractional domain. The ramped heating and sinusoidal oscillations conditions have been taken at the boundary. The model has been solved for exact analytical solutions via the fractional Laplace transform method. The exact solutions have been graphically studied to explore the physics of various pertinent flow parameters on velocity and temperature fields. The empirical results reveal that the temperature and velocity fields decreased with increasing values of fractional parameters due to variation in thermal and momentum boundary layers. It is also indicated that the isothermal velocity and temperature are higher than ramped velocity and temperature.
Keywords: Nanofluid; fractional derivatives; Brinkman type fluid; exact solutions
In recent decades, technology has been growing exponentially in numerous fields of science and engineering such as power generation and electronics where heat transport is an essential phenomenon. The extraordinary growth in technologies needs revolutionary and innovative heat transport management. In this case, advanced and innovative cooling procedures are required to be invented. As the heat transfer management in industries and electronic devices gained prominence, the research community tried to develop an efficient heat transfer medium. Numerous conventional techniques such as mini channel and increasing the surface area had been applied but failed due to scientific limitations. Despite that, enrichment in material science provides specialness to heat transfer fluid by dissolving nano-sized particles in the base fluid. This phenomenon of dispersion of nano-sized particles in host fluid had been revealed by Choi et al. [1]. Thereby, numerous investigators characterized, prepared, and examined different nanofluids in heat transport applications [2,3]. Many experimental and numerical studies indicated a different combination of nanoparticle and base fluids. Amongst the many types of nanoparticles, carbide ceramic, metal oxide, metals, nitride ceramic, semiconductor, and carbon in the various forms are commonly used in the traditional fluids such as water, oil, alcohol, and polymer solutions [4]. However, some recent studies indicated that carbon nanotubes (CNTs) are more efficient in convection heat transfer due to their high thermal conductivity.
CNTs nanoparticles are in a cylindrical shape with superior thermal characteristics (higher electrical and thermal conductivities and low density) compared to spherical shape nanoparticles. CNTs have incredible applications in various areas of science, which include electronics, health care, energy, cooling, heat exchanger, bio-medicine, solar collector, diesel engine, and environment [5]. Khalid et al. [6,7] investigated the magneto-hydro-dynamic (MHD) flow of Blood-CNTs nanofluid in a porous medium. In these studies, SWCNTs and MWCNTs had been considered. They reported that the temperature field increases with increasing volume concentration whereas the velocity field indicated an opposite trend. Aman et al. [8] analyzed the flow of CNTs nanofluid in a microchannel by using the perturbation method. Their results revealed that the temperature field of SWCNTs is higher than MWCNTs in different based fluids. Some more recent studies on nanofluids can be found in [9–14] and the references therein.
In the open literature, many studies had focused on convection heat transfer with constant wall temperature. But several physical situations follow arbitrary thermal conditions at the boundary. The convection heat transfer problems are effective to study with step-change thermal boundary conditions (Ramped wall thermal boundary conditions). The problems with ramped wall thermal boundary conditions can be implemented in thin-film photovoltaic devices to accomplish a certain finish of the system [15]. Ramped wall temperature is also essential for heat management in buildings such as air conditioning where the constant wall thermal conditions lead to noticeable error. Keeping in mind the importance of step-change thermal boundary conditions, this study investigates convection heat transfer with ramped boundary condition.
In the open literature, nanofluids are extensively studied without ramped wall conditions. The studies on nanofluid flow with ramped wall temperature are very rare and the flow of CNTs nanofluid with Caputo–Fabrizio time-fractional Brinkman type fluid model are not as yet reported in literature. Thereby, to fill this research gap, a Caputo time-fractional Brinkman typed fluid model is developed for the flow of CNTs (SWCNTs and MWCNTs) under the influence of the external magnetic field. In the discussed literature, the governing equations that describe the convection heat transfer in nanofluid had been modeled in terms of integer order constitutive relationship. However, with the growth of technologies, fractional calculus has reached terrific advancement due to wide range of applications. As accepted in the open literature, integer-order derivatives are local in nature, but time-fractional derivatives are non-local, which retain memory property [16]. Having such motivation, this study deals with convection heat transfer in MHD CNTs nanofluid based on the time-fractional Brinkman type fluid model. The classical Brinkman model together with energy equation have been transformed into fractional forms using Caputo time-fractional derivative. The generalized energy equation is partially coupled with the momentum equations to study the memory effect. The sinusoidal oscillating and ramped wall conditions have been imposed. The fractional model has been solved for exact solutions using the Laplace transform. The physical impact of pertinent flow parameters have been highlighted in various graphs with physical interpretation.
Consider the convection heat transfer in water-CNTs nanofluid near an infinite plate with ramped wall temperature in 
plane where the plate is selected along x-axis and y-axis is chosen normal to it. It is assumed that the fluid is electrically conducting. The magnetic Reynold is assumed to be very small, thereby, the induced magnetic field is neglected [17]. Initially, at 
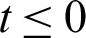, both the fluid and plate are at rest with ambient temperature 
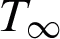. After a short interval of time t = 0+, the temperature of the plate rises from 
to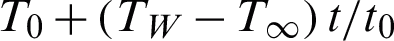 
for 0 < t < t0 or TW for t > t0. In addition, the plate starts oscillations with 
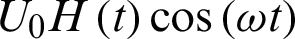where U0 is the amplitude of oscillation, 
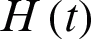is the Heaviside unit step function, 
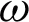is the frequency of oscillation and t is the time period. Due to the temperature gradient and plate oscillations, the mixed convection is taken place and the nanofluid begins to move in x-direction. The governing equations of the problem are given by
where 
is the density, 
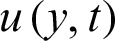is the velocity, 
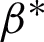is the Brinkman type fluid parameter, 
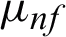is the dynamic viscosity, 
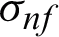is the electrical conductivity, B0 is a uniform magnetic field, g gravitational acceleration, 
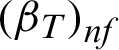is the thermal expansion, 
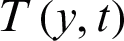is the temperature, 
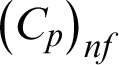is the heat capacitance, and knf is the thermal conductivity of nanofluid. The appropriate physical initial and boundary conditions are given as
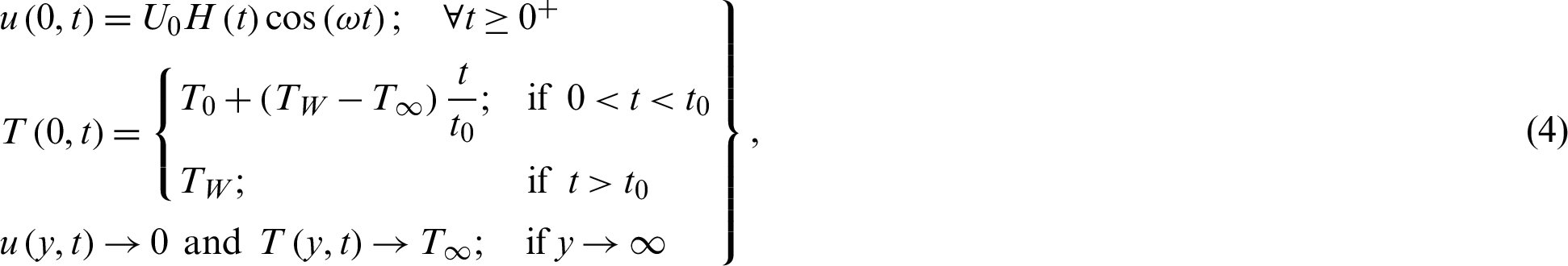
where mathematical expressions for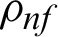 
, 
, 
, 
, 
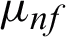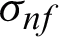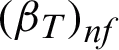and knf are given by [18].
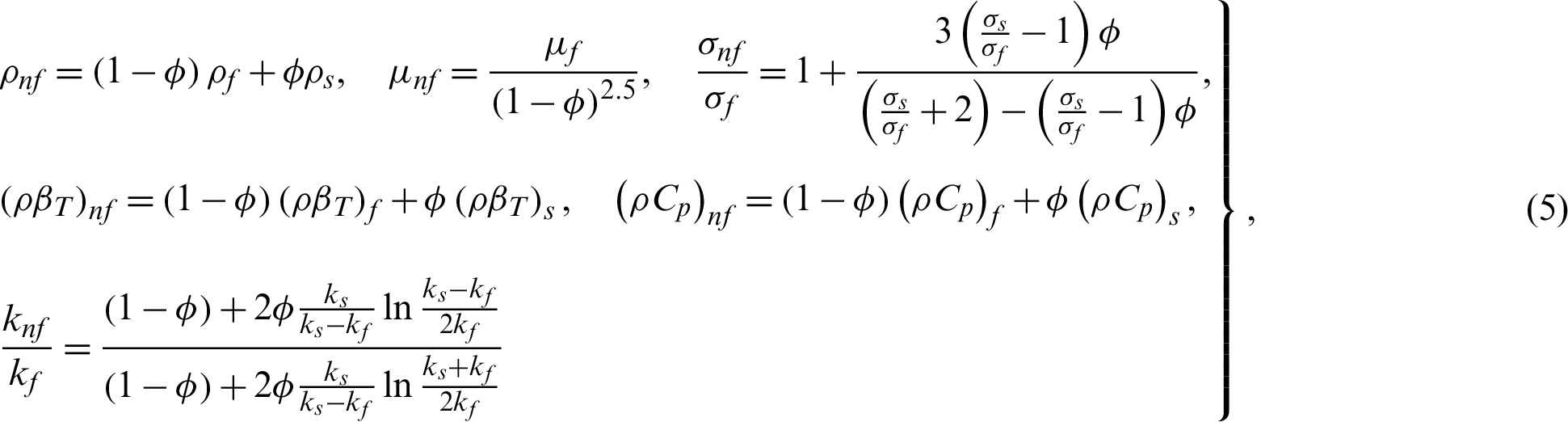
The subscripts nf, f, and s in Eqs. (5)–(10) are referred to as nanofluid, base fluid, and solid CNTs nanoparticles, respectively. The numerical values of thermophysical properties are given in Tab. 1 [6].
Table 1: Numerical values of the base fluid and solid material nanoparticles [6,7]
The dimensionless variables are introduced into governing Eqs. (1) and (2) and initial and boundary conditions (4) and (5) to minimize the number of variables and to simplify the mathematical model. Incorporating the following dimensionless variable
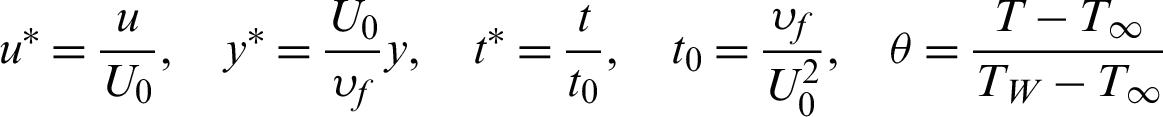
into Eqs. (1) and (4) and 
for simplicity yield to
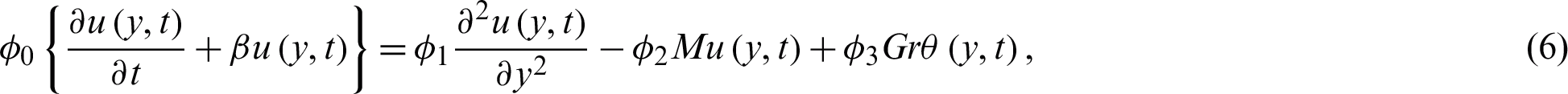
and
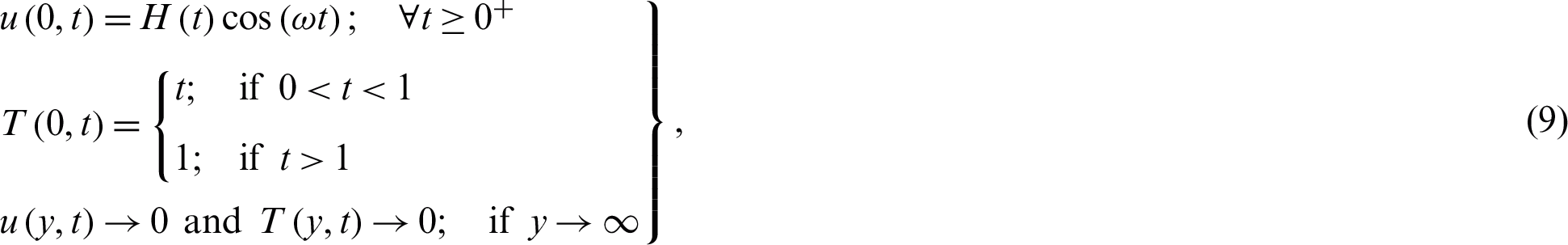
where
is the Brinkman type fluid parameter, magnetic number, thermal Grashof number, and Prandtl number respectively. In addition,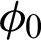 
, 
, 
, 
, 
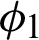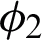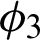and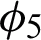 
are constant terms which are produced during the calculi. The dimensionless governing Eqs. (6) and (7) are transformed to Caputo–Fabrizio times-Fractional form as
where 
is the Caputo–Fabrizio time-fractional operator (CFTO) defined by [19]
where
The Laplace transform of Eq. (12) using Eq. (13) yield to
such that
Eq. (15) clearly indicates that the fractional order CFTO can be reduced to integer order partial differential derivatives.
In this section, the fractional Laplace transform method is adopted to solve Eqs. (10) and (11) using the initial and boundary conditions (8) and (9).
3.1 Solution for Temperature Field
Applying the Laplace transform to Eq. (11) using initial condition from (8) which yield to the following form
with the transform boundary conditions
where
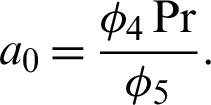
The analytical solutions of Eq. (16) in the Laplace transform domain is obtained by using the boundary conditions presented in Eq. (17) as
It is important to indicate here that Eq. (18) is the solution of the energy equation in the Laplace transform domain with ramped wall temperature. Eq. (18) is further simplified as
where
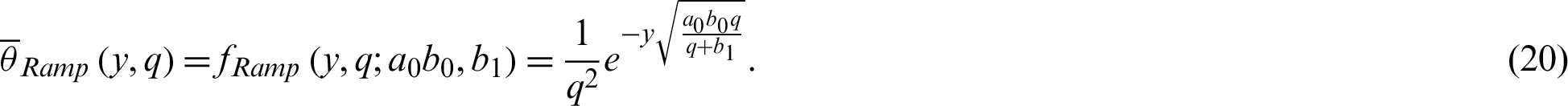
In order to transform back Eq. (19) from the Laplace transform domain, the inverse Laplace transform is employed which yield to
where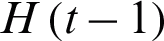 
is the Heaviside unit step function. The term 
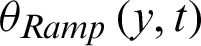is obtained as
where
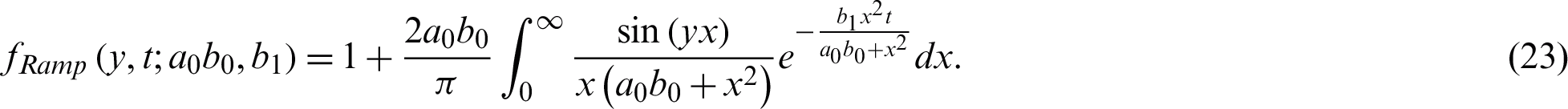
Eq. (21) corresponds to the exact solutions of energy equation (Eq. (11)) for ramped wall temperature when 
. To evaluate the isothermal temperature, Eq. (16) is again solved for isothermal temperature condition which yield to
such that
To present the solutions for isothermal temperature in the time domain, the inverse Laplace transform is applied to Eq. (25) which yield to
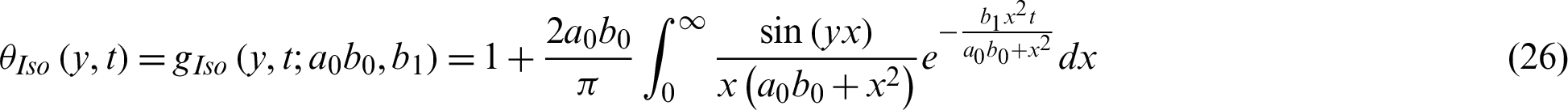
Eqs. (21) and (26) represent the exact solutions of Eq. (11) for ramped and isothermal temperature, respectively. The solutions for the velocity field for both cases, i.e., ramped and the isothermal temperature are given in the following section.
3.2 Solution for Velocity Field
In this section, the exact analytical solutions for the velocity field will be developed for both ramped and isothermal temperature. Exact expressions for these conditions will be presented. Bearing in mind Eq. (14), the Laplace transform is employed to Eq. (10) using initial conditions from Eq. (8) yield to
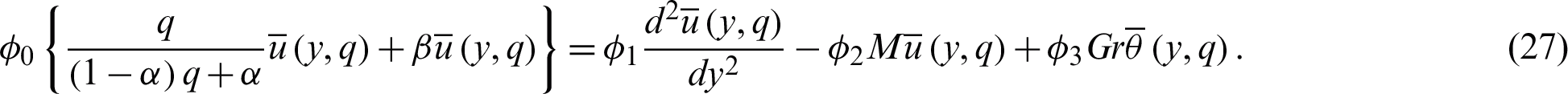
After further simplification Eq. (27) takes the following form
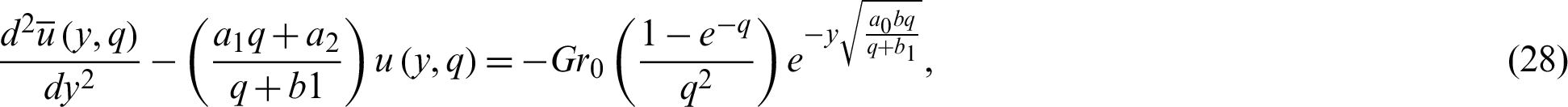
along with the velocity boundary conditions
where
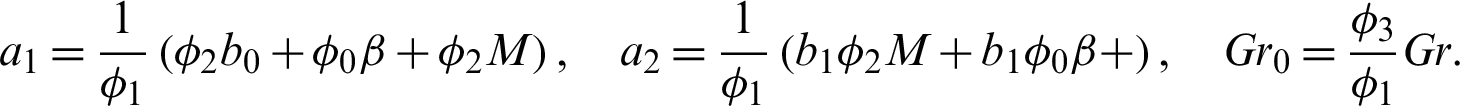
Eq. (28) is analytically solved for ramped temperature in the Laplace transform domain is given by
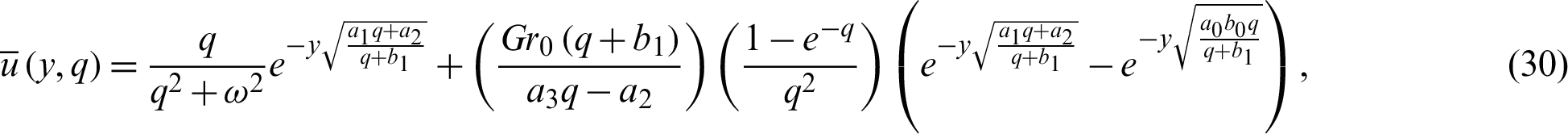
where
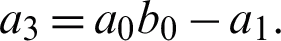
In order to find the inverse Laplace transform of Eq. (30), this equation is written in a more suitable form as
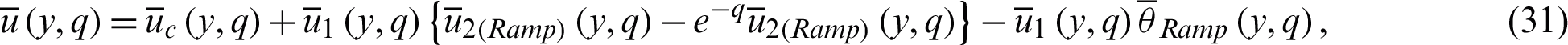
where
and 
is previously defined in Eq. (19). Now, the inverse Laplace transform is employed to transform back to Eq. (31) to the time domain as
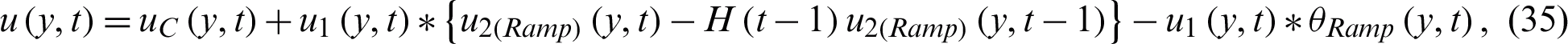
where
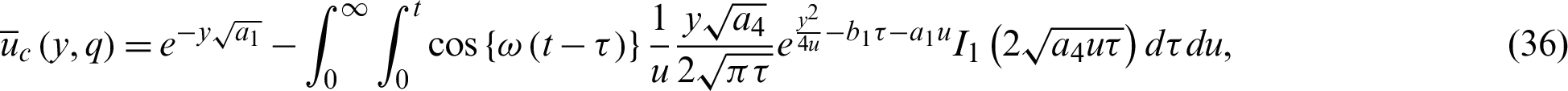
and
The symbol * presents the convolutions product.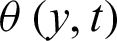 
is already defined in Eq. (21). It is important to mention here that Eq. (35) represents the ramped temperature solutions for the velocity field. Furthermore, Eq. (10) is again solved for isothermal temperature as
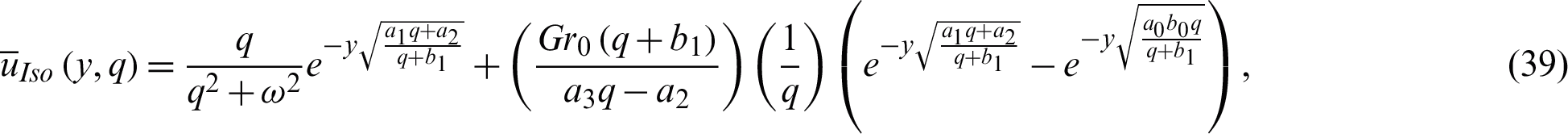
Eq. (39) is written in a simplified and convenient form as
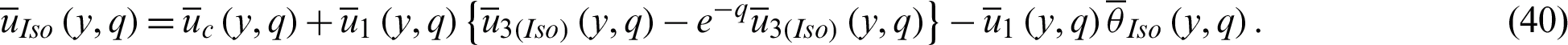
The terms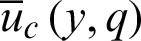 
, 
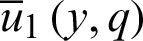and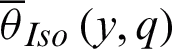 
are already defined in Eqs. (32), (33), and (24), respectively. The newly introduced term 
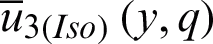is defined by
The solution for isothermal temperature is obtained by taking the inverse Laplace transform of Eq. (40) which yield to
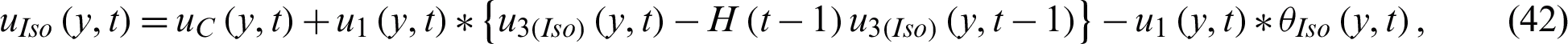
where
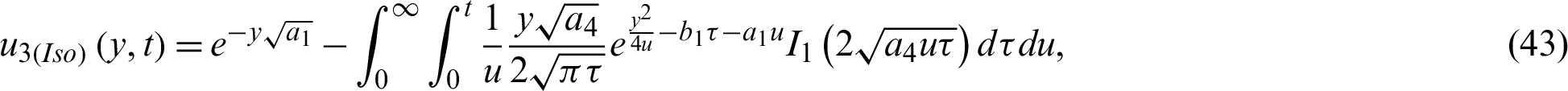
and the terms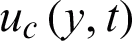 
, 
and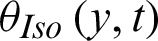 
are previously defined in Eqs. (36), (37) and (26), respectively. This complete the solutions of the proposed problem.
The solutions for velocity and temperature fields are computed for various flow parameters such as fractional parameter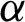 
, volume fractional of CNTs 
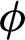, Brinkman type fluid parameter 
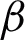, magnetic parameter M, and thermal Grashof number Gr. To explore the physical aspects of the problem, the temperature and velocity fields are graphically demonstrated in Figs. 1–9. It is important to mention here that t = 0.5 and t = 1.5 are chosen for ramped and isothermal temperature and velocity, respectively.
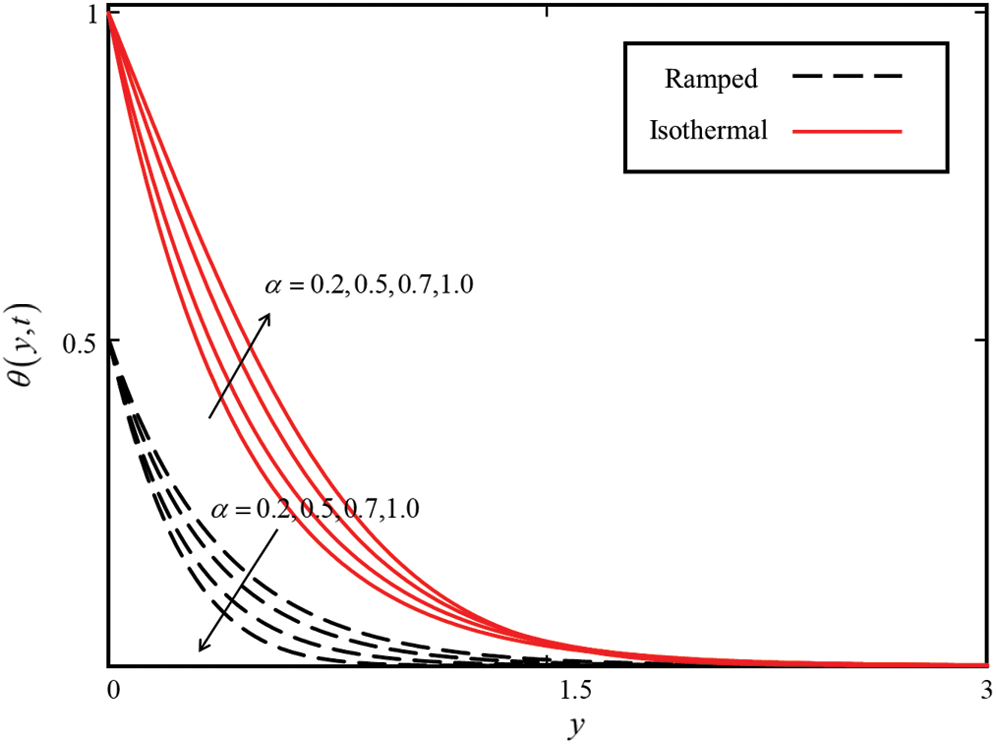
Figure 1: Consequence of 
on 
when 
for MWCNTs case
Figure 2: Consequence of 
on 
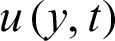when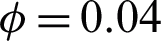 
, 
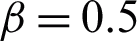, M = 0.5, Gr = 10 and 
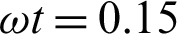for MWCNTs case
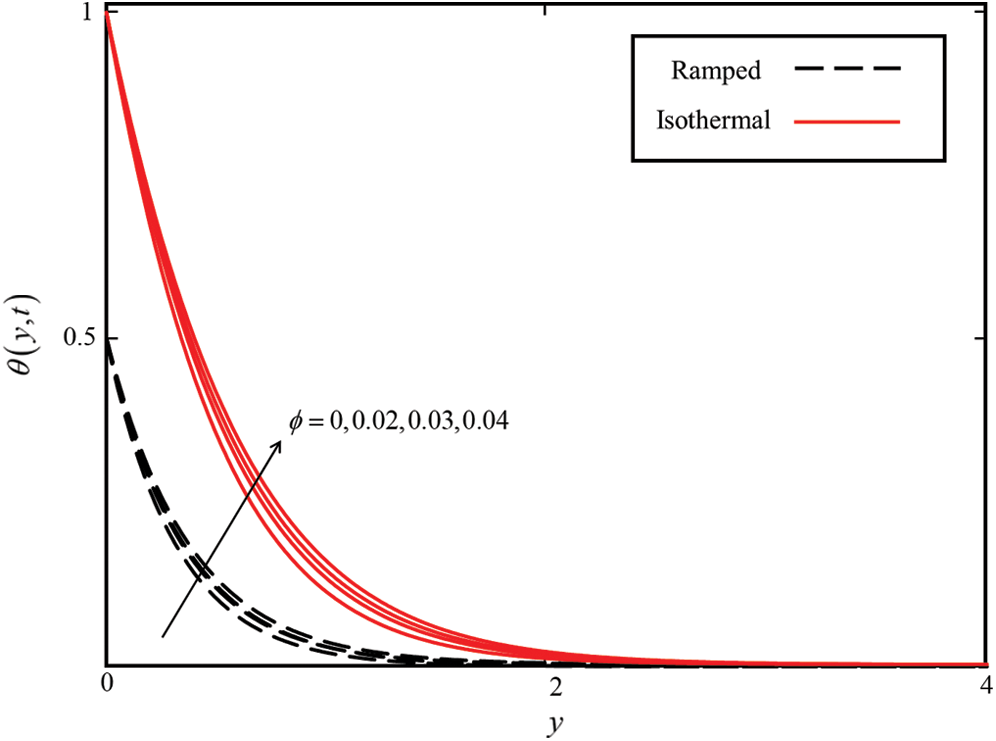
Figure 3: Consequence of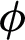 
on 
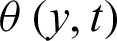when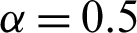 
for MWCNTs case
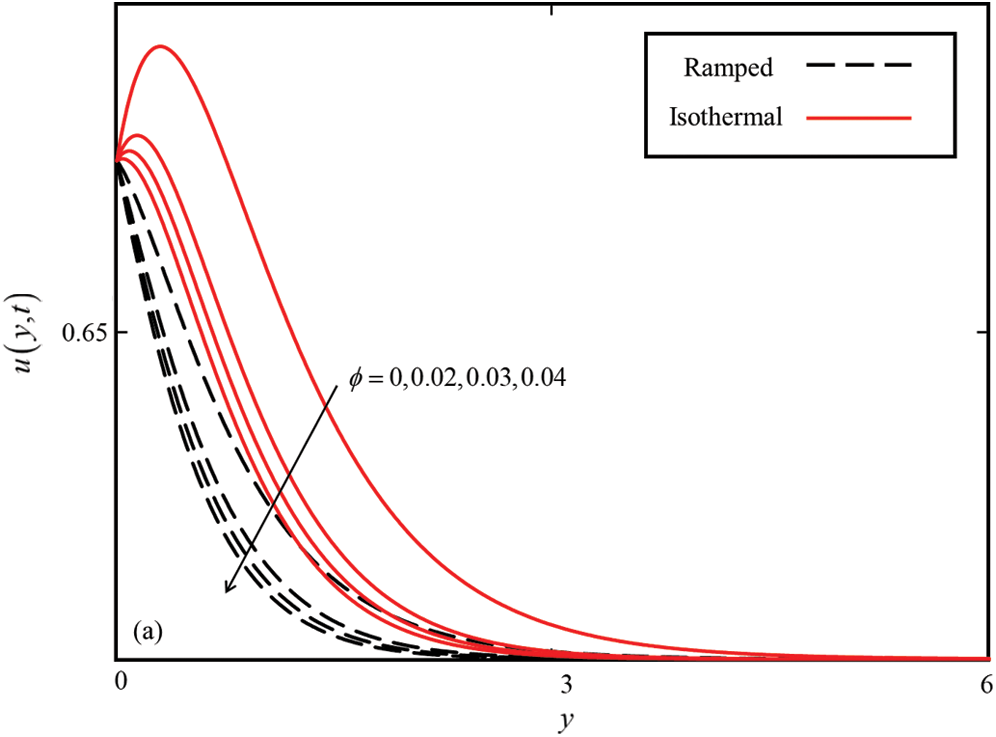
Figure 4: Consequence of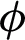 
on 
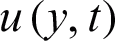when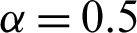 
, 
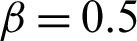, M = 0.5, Gr = 10 and 
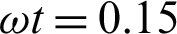for MWCNTs case
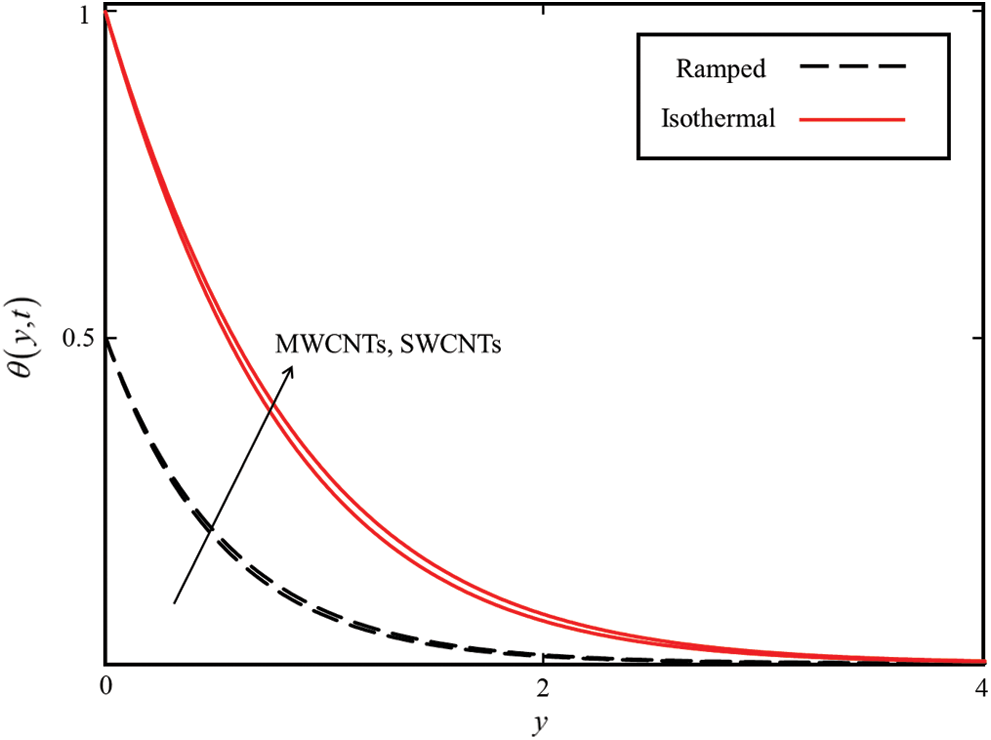
Figure 5: Comparison of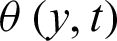 
for MWCNTs and SWCNTs when 
, and 
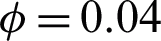
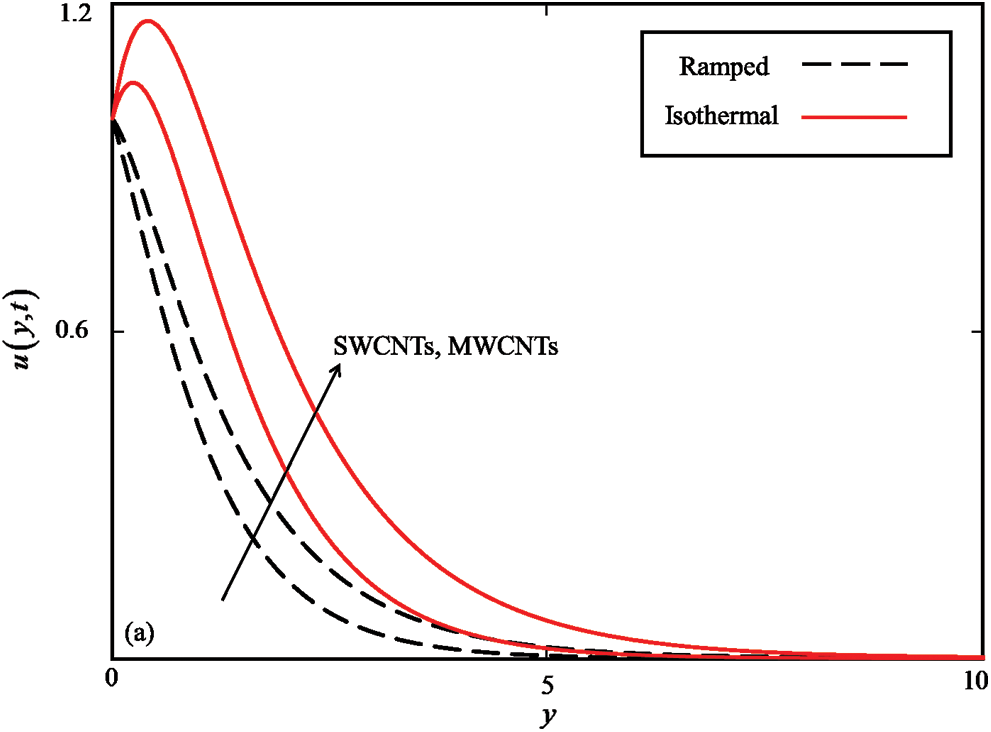
Figure 6: Comparison of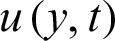 
for MWCNTs and SWCNTs when 
, 
, 
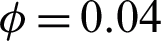, M = 0.5, Gr = 10 and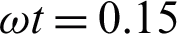 
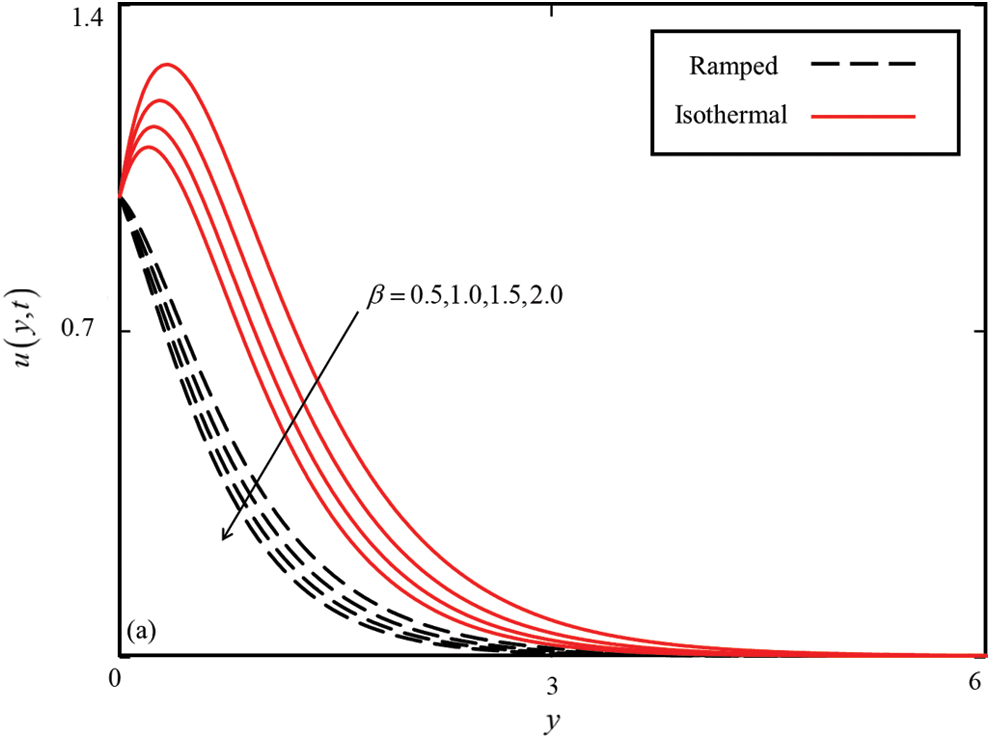
Figure 7: Consequence of 
on 
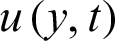when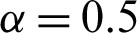 
, 
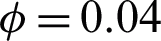, M = 0.5, Gr = 10 and 
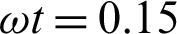for MWCNTs case
Figure 8: Consequence of M o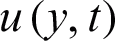n 
when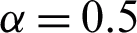 
, 
, 
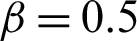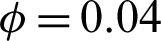, Gr = 10 and 
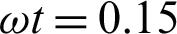for MWCNTs case
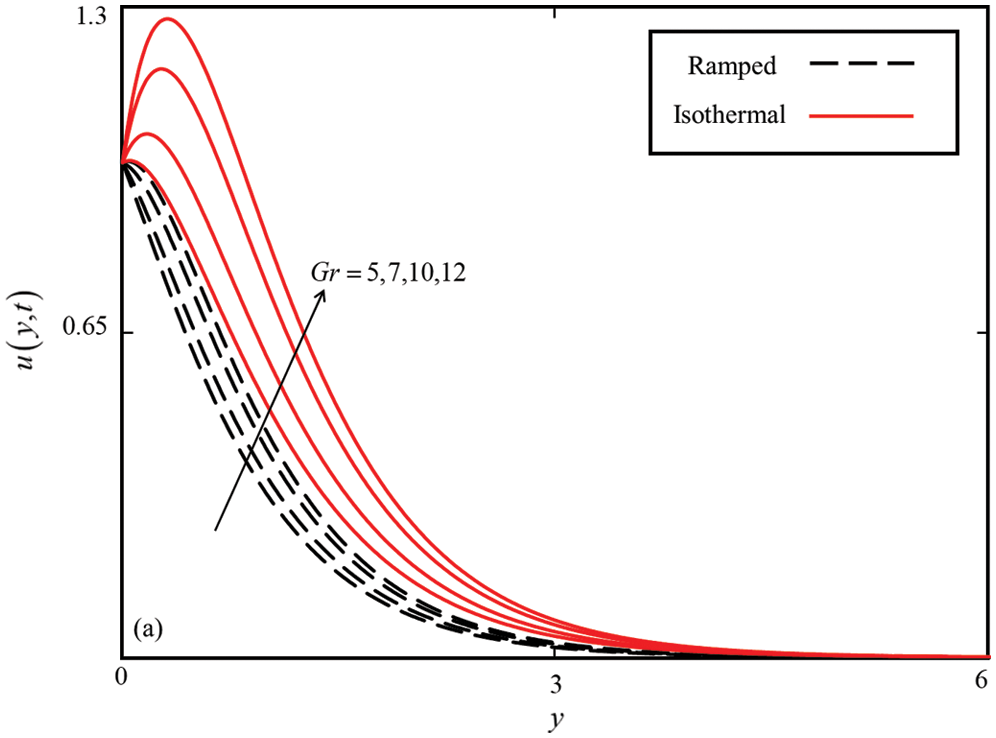
Figure 9: Consequence of Gr on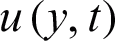 
when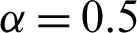 
, 
, 
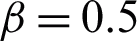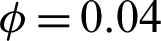, M = 0.5 and 
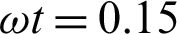for MWCNTs case
Fig. 1 depicts the effect of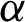 
on temperature field for both ramped and isothermal wall temperature. It is noticed that the temperature field decreased with increasing values of 
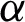in case of ramped temperature. However, in the isothermal case, the temperature field near the plate increased with increasing 
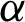. This trend reverses away from the plate. The trend of temperature field can be physically justified, as an increase in 
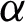causes a decrease in the thermal boundary layer, as a result, the temperature field increased. Fig. 2 presents the influence of 
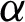on velocity profile. This figure indicates that the velocity retarded when 
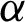is increased. This is because the velocity boundary layer decreases with an increase in 
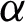. The trend of 
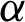on velocity and temperature field is similar to that of Ahmed et al. [20] in the case of Caputo fractional derivative.
The effect of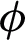 
on the temperature field is illustrated in Fig. 3. It is noticed that the temperature field enhanced with enhancement in 
for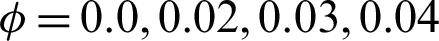 
. This is because of the effective thermal conductivity of CNTs. When 
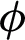increased, it caused an increment in thermal conductivity, as a result, the temperature filed increased. The impact of 
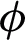on the velocity field is highlighted in Fig. 4. The velocity field decreased with an increase in 
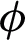due to the effective density of CNTs. Increment in 
results in an increase in the density of nanofluid, which retarded the velocity field. The effects of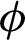 
on temperature and velocity field can be validated with [21] (Figs. 2 and 6).
In Fig. 5 the temperature field is compared for SWCNTs and MWCNTs. It is found that the temperature field of SWCNTs is higher than MWCNTs. This is due to the difference in the thermal conductivities of SWCNTs and MWCNTs. The thermal conductivity of SWCNTs (6600 k (W/mK)) is higher than the thermal conductivity of MWCNTs (3000 k (W/mK)) which correspond to the higher temperature field of SWCNTs than MWSNTs. It is noticed in Fig. 6 that the velocity of MWCNTs is higher than the velocity of SWCNTs. This is because the density and thermal conductivity of SWCNTs is greater than MWCNTs, which absorb more heat energy and are at the same time denser. Thereby, the velocity field of MWCNTs is higher than SWCNTs. The same behavior of velocity and temperature field were presented by Aman et al. [8] (Figs. 2 and 5).
The consequence of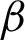 
on the velocity field is portrayed in Fig. 7. The 
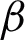is directly related to the drag force of the porous medium. Higher the 
corresponds to strengthen the drag forces which reduced the velocity field. The trend of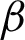 
is similar to that of [22].
The influence of M on the velocity field is studied in Fig. 8. Increasing M strengthens the Lorentz forces which resist the velocity. Therefore, the nanofluid velocity decreases with increasing values of M. Finally, the result of Gr is illustrated in Fig. 9. The Gr represent the ratio of buoyancy forces to the viscous forces. The greater the values of Gr, the stronger will be the buoyancy forces that cause an increase in the velocity field.
In this article, the Caputo time-fractional Brinkman type nanofluid model is constructed to investigate the convection heat transfer in a water-CNTs nanofluid. The time-fractional model have been solved for exact solutions using the Laplace transform method. The exact expressions for velocity and temperature field have been computed and displayed in numerous graphs with the physical explanation. The velocity and temperature fields are decreasing with increasing fractional parameters due to the reduction in the thickness of velocity and temperature boundary layers. The temperature field increased with an increase in volume concentration of CNTs whereas the velocity field performed oppositely due to thermal conductivity and density factors of CNTs. It is noticed that the temperature field of SWCNTs is higher than MWCNTs because of the thermal conductivity factor. However, the velocity field of MWCNTs is higher than SWCNTs. The velocity field decreased with an increase in Brinkman type fluid parameter due to drag forces. The magnetic parameter decreased the velocity because of Lorentz forces. Thermal Grashof number is the ratio of buoyancy force to the viscous force which increases the velocity field.
Acknowledgement: Researchers Supporting Project No. (RSP-2019/33), King Saud University, Riyadh, Saudi Arabia.
Funding Statement: The authors appreciate the obtained fund from King Saud University through Deanship of Scientific Research, Research Group Program. The authors would also like to acknowledge Ministry of Education (MOE) and Research Management Centre-UTM, Universiti Teknologi Malaysia (UTM) for the financial support through vote Nos. 5F004, 07G70, 07G72, 07G76, 07G77and 08G33 for this research.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. U. Choi and J. A. Eastman. (1995). Enhancing thermal conductivity of fluids with nanoparticles. IL, USA: Argonne National Lab.
2. T. B. Gorji and A. A. Ranjbar. (2017). “A review on optical properties and application of nanofluids indirect absorption solar collectors (DASCs),” Renewable and Sustainable Energy Reviews, vol. 72, no. 5, pp. 10–32.
3. M. U. Sajid and H. M. Ali. (2019). “Recent advances in the application of nanofluids in heat transfer devices: A critical review,” Renewable and Sustainable Energy Reviews, vol. 103, no. 4, pp. 556–592.
4. J. A. R. Babu, K. K. K. and S. S. Rao. (2017). “State-of-art review on hybrid nanofluids,” Renewable and Sustainable Energy Reviews, vol. 77, no. 9, pp. 551–565.
5. A. Baghban, M. Kahani, M. A. Nazari, M. H. Ahmadi and W. M. Yan. (2019). “Sensitivity analysis and application of machine learning methods to predict the heat transfer performance of CNT/water nanofluid flows through coils,” International Journal of Heat and Mass Transfer, vol. 128, no. 1, pp. 825–835.
6. A. Khalid, I. Khan, A. Khan, S. Shafie and I. Tlili. (2018). “Case study of MHD blood flow in a porous medium with CNTS and thermal analysis,” Case Studies in Thermal Engineering, vol. 12, no. 9, pp. 374–380.
7. A. Khalid, L. Y. Jiann, I. Khan and S. Shafie. (2017). “Exact solutions for unsteady free convection flow of carbon nanotubes over an oscillating vertical plate,” in AIP Conf. Proc., Putrajaya, Malaysia, AIP Publishing LLC, pp. 1–8.
8. S. Aman, I. Khan, Z. Ismail, M. Z. Salleh, A. S. Alshomrani et al. (2017). , “Magnetic field effect on Poiseuille flow and heat transfer of carbon nanotubes along a vertical channel filled with Casson fluid,” AIP Advances, vol. 7, no. 1, 15036.
9. I. Khan, M. Saqib and A. M. Alqahtani. (2020). “Channel flow of fractionalized H2O-based CNTs nanofluids with Newtonian heating,” Discrete & Continuous Dynamical Systems-S, vol. 13, no. 3, pp. 769–779.
10. M. Saqib, I. Khan, Y. M. Chu, A. Qushairi, S. Shafie et al. (2020). , “Multiple fractional solutions for magnetic bio-nanofluid using Oldroyd-B model in a porous medium with ramped wall heating and variable velocity,” Applied Sciences, vol. 10, no. 11, pp. 3886. [Google Scholar]
11. M. Saqib, A. R. M. Kasim, N. F. Mohammad, D. L. C. Ching and S. Shafie. (2020). “Application of fractional derivative without singular and local kernel to enhanced heat transfer in CNTs nanofluid over an inclined plate,” Symmetry, vol. 12, no. 4, pp. 1–22. [Google Scholar]
12. M. Saqib, S. Shafie, I. Khan, Y. M. Chu and K. S. Nisar. (2020). “Symmetric MHD channel flow of non-local fractional model of BTF containing hybrid nanoparticles,” Symmetry, vol. 12, no. 4, pp. 1–19. [Google Scholar]
13. M. Saqib, I. Khan and S. Shafie. (2018). “Natural convection channel flow of CMC-based CNTs nanofluid,” The European Physical Journal Plus, vol. 133, no. 12, pp. 1–16. [Google Scholar]
14. M. Saqib, I. Khan and S. Shafie. (2018). “Application of Atangana–Baleanu fractional derivative to MHD channel flow of CMC–based–CNT’s nanofluid through a porous medium,” Chaos Solitons & Fractals, vol. 116, no. 11, pp. 79–85. [Google Scholar]
15. A. Khan, I. Khan, F. Ali and S. Shafie. (2014). “Effects of wall shear stress on unsteady MHD conjugate flow in a porous medium with ramped wall temperature,” PLoS One, vol. 9, no. 3, pp. 1–12. [Google Scholar]
16. L. Liu, L. Zheng, F. Liu and X. Zhang. (2017). “Heat conduction with fractional Cattaneo–Christov upper-convective derivative flux model,” International Journal of Thermal Sciences, vol. 112, no. 2, pp. 421–426. [Google Scholar]
17. N. A. Shah, D. Vieru and C. Fetecau. (2016). “Effects of the fractional order and magnetic field on the blood flow in cylindrical domains,” Journal of Magnetism and Magnetic Materials, vol. 409, no. 7, pp. 10–19. [Google Scholar]
18. M. Saqib, I. Khan, S. Shafie and A. Qushairi. (2019). “Recent advancement in thermophysical properties of nanofluids and hybrid nanofluids: An overview,” City University International Journal of Computational Analysis, vol. 3, no. 2, pp. 16–25. [Google Scholar]
19. M. Caputo and M. Fabrizio. (2015). “A new definition of fractional derivative without singular kernel,” Progress in Fractional Differentiation Applications, vol. 1, no. 2, pp. 1–13. [Google Scholar]
20. N. Ahmed, D. Vieru, C. Fetecau and N. A. Shah. (2018). “Convective flows of generalized time-nonlocal nanofluids through a vertical rectangular channel,” Physics of Fluids, vol. 30, no. 5, pp. 1–18. [Google Scholar]
21. A. Gul, I. Khan, S. Shafie, A. Khalid and A. Khan. (2015). “Heat transfer in MHD mixed convection flow of a ferrofluid along a vertical channel,” PLoS One, vol. 10, no. 11, pp. 1–14. [Google Scholar]
22. S. A. A. Jan, F. Ali, N. A. Sheikh, I. Khan, M. Saqib et al. (2018). , “Engine oil based generalized Brinkman-type nano-liquid with molybdenum disulphide nanoparticles of spherical shape: Atangana-Baleanu fractional model,” Numerical Methods for Partial Differential Equations, vol. 34, no. 5, pp. 1472–1488. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |