DOI:10.32604/cmc.2021.014433
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014433 | |
| Article |
Brainwave Classification for Character-Writing Application Using EMD-Based GMM and KELM Approaches
1Department of Telecommunication Engineering, Rajamangala University of Technology Isan, Nakhon Ratchasima, 30000, Thailand
2School of Telecommunication Engineering, Suranaree University of Technology, Nakhon Ratchasima, 30000, Thailand
3Tianjin Key Laboratory of Cognitive Computing and Application, College of Intelligence and Computing, Tianjin University, Tianjin, 300350, China
4Department of Materials Science, Chulalongkorn University, Bangkok, 10330, Thailand
*Corresponding Author: Peerapong Uthansakul. Email: uthansakul@sut.ac.th
Received: 20 September 2020; Accepted: 18 October 2020
Abstract: A brainwave classification, which does not involve any limb movement and stimulus for character-writing applications, benefits impaired people, in terms of practical communication, because it allows users to command a device/computer directly via electroencephalogram signals. In this paper, we propose a new framework based on Empirical Mode Decomposition (EMD) features along with the Gaussian Mixture Model (GMM) and Kernel Extreme Learning Machine (KELM)-based classifiers. For this purpose, firstly, we introduce EMD to decompose EEG signals into Intrinsic Mode Functions (IMFs), which actually are used as the input features of the brainwave classification for the character-writing application. We hypothesize that EMD along with the appropriate IMF is quite powerful for the brainwave classification, in terms of character applications, because of the wavelet-like decomposition without any down sampling process. Secondly, by getting motivated with shallow learning classifiers, we can provide promising performance for the classification of binary classes, GMM and KELM, which are applied for the learning of features along with the brainwave classification. Lastly, we propose a new method by combining GMM and KELM to fuse the merits of different classifiers. Moreover, the proposed methods are validated by using the volunteer-independent 5-fold cross-validation and accuracy as a standard measurement. The experimental results showed that EMD with the proper IMF achieved better results than the conventional discrete wavelet transform (DWT) feature. Moreover, we found that the EMD feature along with the GMM/KELM-based classifier provides the average accuracy of 77.40% and 80.10%, respectively, which could perform better than the conventional methods where we use DWT along with the artificial neural network classifier in order to get the average accuracy of 80.60%. Furthermore, we obtained the improved performance by combining GMM and KELM, i.e., average accuracy of 80.60%. These outcomes exhibit the usefulness of the EMD feature combining with GMM and KELM based classifiers for the brainwave classification in terms of the Character-Writing application, which do not require any limb movement and stimulus.
Keywords: Brainwave classification; character-writing application; EMD; GMM; KELM; score combination
Human communication is an essential activity of passing and interpreting information from one person to another, i.e., exchanges of opinions, emotions, ideas, or facts. Unfortunately, traditional communication is a challenging process for impaired people who does not possess speaking power along with the muscle movements. This motivates researchers to explore the alternative systems [1,2] to help defective people in terms of communication.
So far, brain-computer interface (BCI) [3,4], which enables people to communicate with a computer, has been developed to help defective people to express their thoughts. The standard concept of BCI is to convert measured brain signals into actions such as texts and emotions [5]. Moreover, scholars have explored BCI-based researches based on three types of brain responses: Event-related potentials (ERP), steady-state visual evoked potential (SSVEP) and motor imagery (MI).
An ERP brain response is an electrophysiological response based on the direct effect of motor events. Normally, auditory [6], visual [7] and tactile stimulation [8] are introduced to evoke ERP signals. When the evoked ERP response was measuresd/analyzed, BCI system could convert the user’s intention into several actions depending on the application. For example, in [9], the authors proposed to use P300 wave being an ERP component for communication, known as P300 speller. With this speller, defective users with motor disabilities could choose alphabets based on the changed P300 wave via visual perception with the stimulus on a computer screen.
Furthermore, an SSVEP brain response is another type of visually evoked brain response, which presents natural responses in terms of human visual perception at specific frequencies (i.e., flickering stimulus [10]). When a person focuses the visual stimulus on a monitor screen at a steady flickering frequency, the electrical signals with the same frequency as the stimulus signal can be generated by the human brain. For this reason, it is believed to detect what a user is focusing on the visual stimulus such as liquid crystal display (LCD) and cathode ray tube (CRT) monitors [11]. For example, in [12], the authors presented a spelling application based on the BCI technique by using the SSVEP response. With this speller system, the 45-target characters were introduced with flickers at different frequencies and a sinusoidal stimulation approach was applied to display visual stimuli via an LCD screen. The user could select the desired character by focusing on the designed position of each character.
The final format of brain response is MI response, which is based on the mental imagination of motor behavior/movement. A conventional concept in BCI using the MI response is to convert the user’s intention based on the mental imagination. For example, in [13], a MI based BCI system was introduced for communication, known as a MI-speller. With this system, the users could perform the desired mental imagination in terms of controlling the arrow point to the specific hexagon of the desired character. In all the above mentioned BCI, a constant stimulation and limb movements are needed for generating brain responses, which may lead to non-practical applications especially for defective persons. Thus, the BCI system still requires a design where it does not require any stimulation and limb movements.
Different from the above mentioned studies, the brainwave classification without any limb movement and stimulus for character-writing applications were proposed in [14]. The aim of this system was to detect a multi-line and circle imagination characters. The experimental results showed that this method was useful to detect the circle/straight line imagination, where the estimated results could be transformed into self-designed Morse code symbols as shown in Fig. 1. However, the system relied on the pair of EEG channels (third and fourth frontal lobes: F3 and F4), which leads to the indistinct detection due to the joint decision. To address this problem, the authors of [15] proposed a simple and effective system, where the effective architecture used a single EEG channel to replace the pair of EEG channels. By comparing the pair of EEG channels, the experimental results insisted that the system using the single effective EEG channel (F3) could give better performance in terms of the average accuracy. Although the above-mentioned systems could provide the convenient and convincing communication application between human brain and computer, the exploitation of alternative feature and classifier is required to improve the detection of imagined characters.
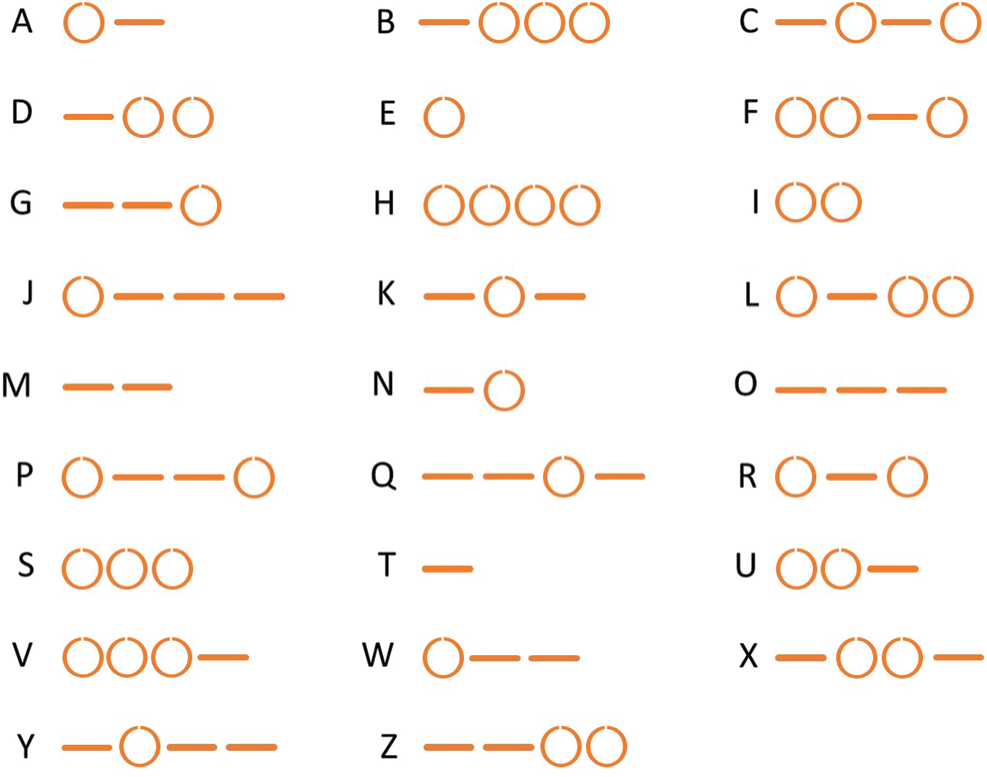
Figure 1: Morse code symbols based on circle and/or straight line characters
In this paper, we propose a new method by using EMD feature along with GMM and KELM-based classifiers. For this purpose, firstly, we explore empirical mode decomposition (EMD) to decompose the EEG signal into intrinsic mode functions (IMFs), which are used via six statistical features as the input features of the brainwave classification for the character-writing application. Secondly, by getting inspired by [16,17] that the shallow learning classifiers provide the promising performance for the classification of binary classes, Gaussian mixture model (GMM) and kernel extreme learning machine (KELM) are applied to distinguish between a circle and straight line characters. Finally, the score combination of GMM and KELM is proposed to fuse the advantages based on different classifiers. The contributions and novelties are summarized as follows:
1. EMD is first introduced to decompose EEG signals into IMFs that are used as an input feature of the brainwave classification for the character-writing application without any limb movement and stimulus. With this feature extraction method, the brainwave classification system could provide better accuracy compared to the conventional DWT information.
2. We find that the GMM and KELM methods are better classifiers compared to the conventional ANN-based classifier for distinguishing between a circle and straight line characters.
3. The score combination of GMM and KLEM is proposed in this study. It can fuse the complementary information based on different classifiers to further improve the reliability of the detection decision.
The rest of this article is organized as follows: Section 2 introduces the proposed methodology, including data collection, feature extracted by EMD, GMM-based classifier, KELM-based classifier and the score combination of GMM and KELM. Section 3 describes the experimental setup and evaluation rule for our experiment. The performances of brainwave classification are investigated and discussed in Section 4. Finally, Section 5 summarizes the paper and describes the future work.
In this section, we provide an overview of the data collection used for the experiment. In addition, the feature extraction and classifiers are described for the brainwave classification in terms of character-writing applications.
For the data collection, Emotiv EPOC Neuroheadset [18], as shown in Fig. 2, is used for imaging of neural activity of the lobes frontalis. The Raw EEG data were recorded from sixteen electrode positions, including AF3, AF4, F7, F3, F4, F8, FC5, FC6, T7, T8, P7, P3, P4, P8, O1 and O3 as seen in Fig. 3. The signals are sent through the Bluetooth technology and are sampled with a 128 Hz sampling rate.
Figure 2: Emotiv EPOC neuroheadset used as EEG signal acquisition hardware
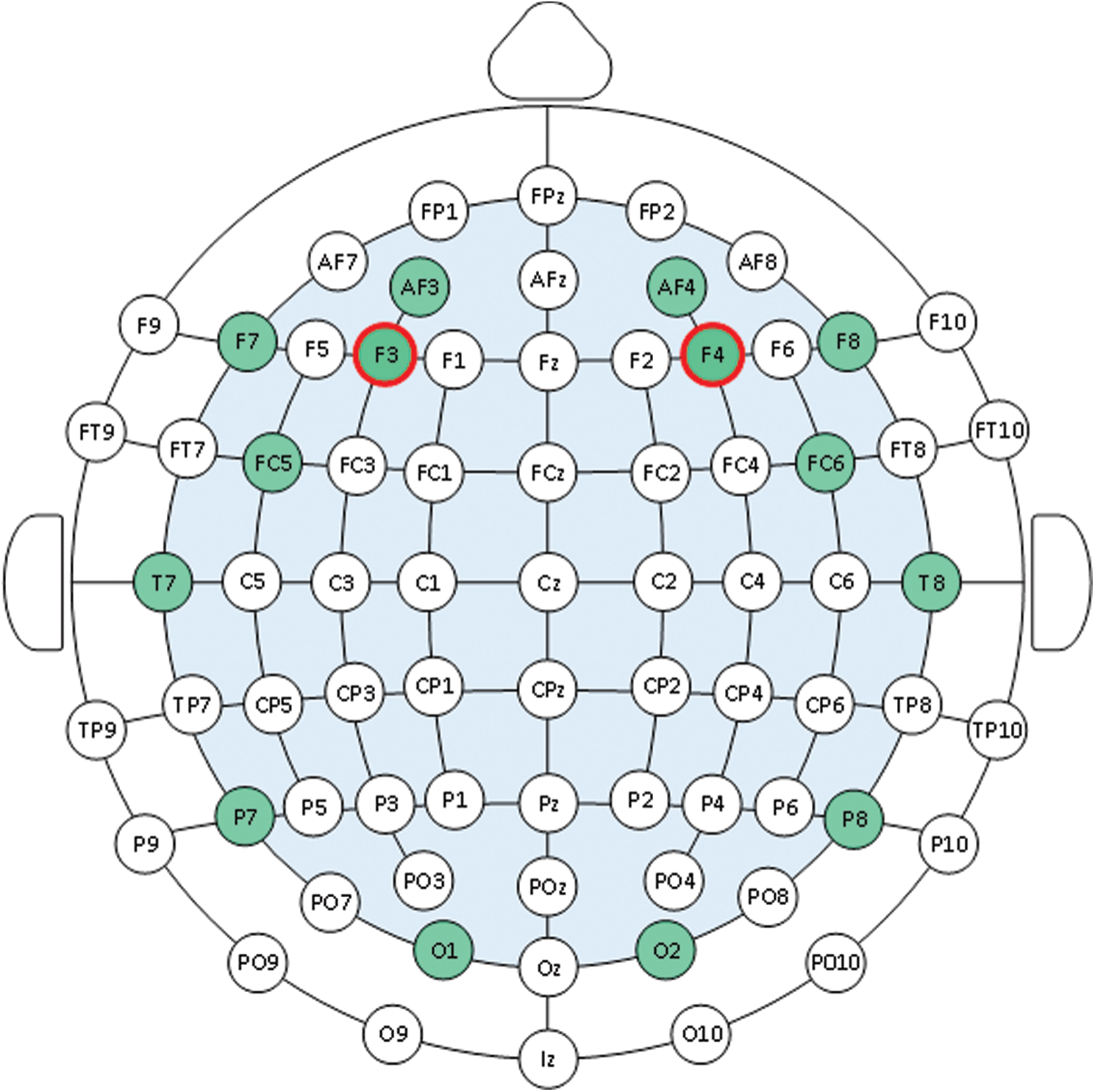
Figure 3: Electrode positions of Emotiv EPOC neuroheadset
In terms of the recording data, five healthy volunteers participated in the study. Two characters, including a circle and straight line characters are used for the animation as shown in Fig. 4. We followed the process as advised in [14]. Fig. 5 shows the procedure of the data collection. The setup is as follows: 1) A volunteer first wears Emotiv EPOC neuroheadset on his/her head and keeps on the meditation for around 60 sec as illustrated in Fig. 5a. 2) The volunteer is then tested for imagining the circle/straight line characters as illustrated in Fig. 5b. 3) the volunteer will rest for 120 s after imagining the characters for about 30 times.
Figure 4: Two characters used for the animation: (a) Circle and (b) Straight line
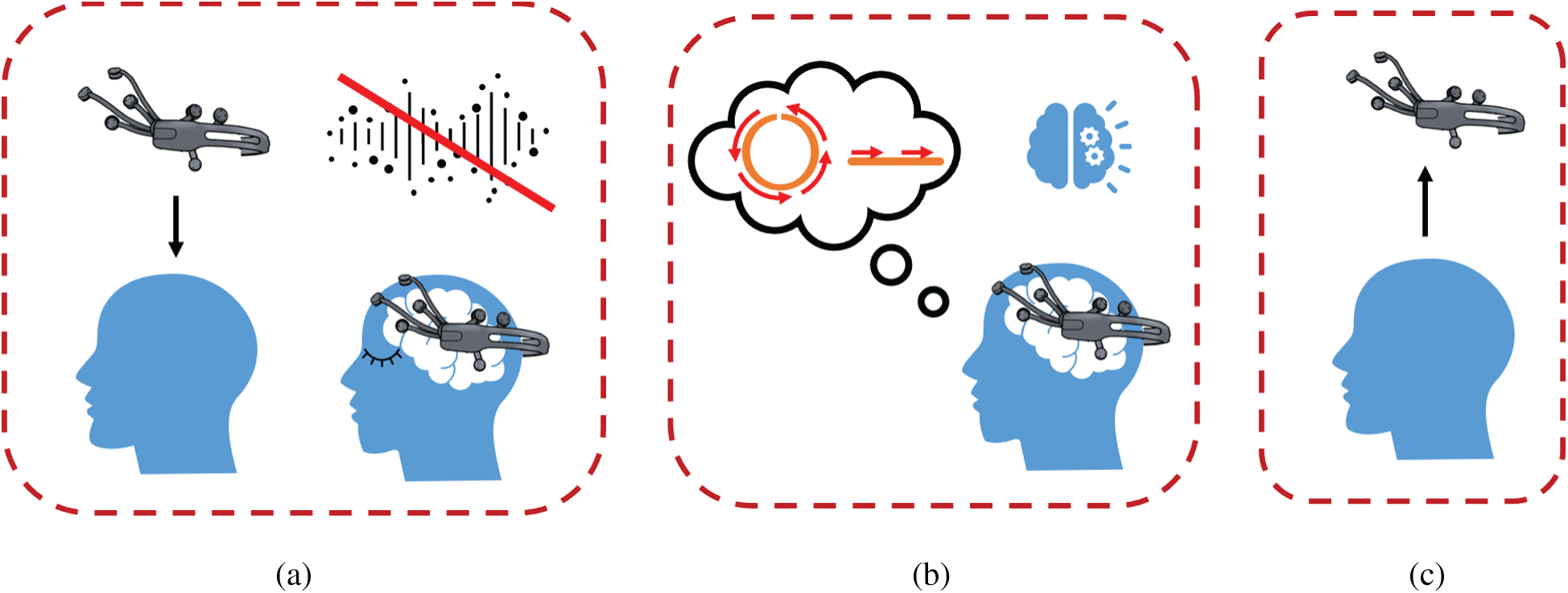
Figure 5: The procedure of the data collection consisting of three parts: (a) Preparation, (b) Imagination, (c) relaxation
EMD has been proved to be effective for non-stationary time-series analysis [19], which is one of feature extraction methods that has attracted a lot of attention, in terms of the classification of brainwaves, because of its promising adaptability [20–22]. EMD can be implemented to decompose the EEG signal into different IMFs that provide underlying intra-wave modulated components in the signal. IMFs must satisfy two conditions: 1) the difference between the total number of extreme and total number of zero-crossing is zero or one 2) the mean value of the envelope defined by the local maxima and local minima is (very close) zero.
The steps of EMD algorithm are calculated as follows:
Step 1: Detect the maximum and minimum values of the signal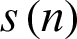 
.
Step 2: Apply the cubic spline interpolation to obtain the envelopes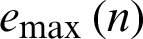 
and 
.
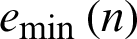Step 3: Compute the local mean as
Step 4: Subtract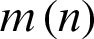 
from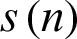 
to get the modal function 
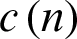as
Step 5: Acquire the residue as
Step 6: Decide whether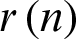 
an IMF or not based on the two basic conditions for IMFs mentioned above.
Step 7: Repeat step 1 to 6 until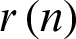 
cannot be decomposed into the IMF. Finally, the original signal is decomposed into N IMFs and the residual component as follow:
In this paper, the IMFs are not directly used as an input of classifier because of the problem of variable-sized windows. If M is the length of a sub-band,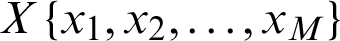 
and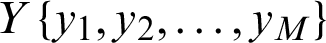 
are two adjacent sub-bands (IMFs). The information can be defined by using six statistical features [14,22] including mean, average power, standard deviation, ratio of the absolute mean values of adjacent sub bands, skewness and kurtosis. Tab. 1 shows the details of each statistical feature.
Table 1: Six statistical features
Although deep learning classifiers, such as deep neural network (DNN) [23], convolutional neural network (CNN) [24] and Long short-term memory (LSTM) [25], have been proved to be effective for the brainwave classification, it is well known that deep classifiers strongly depend on the training data. Moreover, we observe from [26] that deep neural network using multi layers cannot give convincing results for the binary classification. This motivates us to believe that shallow learning classifiers are more efficient than deep learning classifiers for the binary classification. In this paper, the GMM and KELM approaches are adopted for the brainwave classification. In addition to using the GMM/KELM approach alone, the combined scores of GMM and KELM are proposed to fuse the merits based on different classifiers. The details are described as follows.
GMM has received a great amount of attention, in terms of the brainwave classification, because of the Gaussian mixture-based ability to model complicated densities. It also provides promising results for the binary classification as suggested in [27]. In this paper, the GMM is implemented to discriminate the circle from the line imagination. It can represent each class as follow:
where O defends the feature vectors augmented by six statistical features, wk is the kth mixture weight,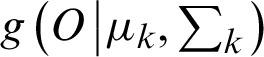 
is a D-variate Gaussian density function with m and diagonal covariance matrix, 
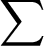and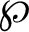 
is the number of Gaussians.
For the testing phase, the decision of circle/line imagination class is computed by the logarithmic likelihood ratio as:
where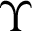 
is the testing feature vectors, 
and 
define the GMMs for circle and line imagination classes, respectively.
KELM has been proved to be an efficient algorithm for many classification tasks and can also provide an expectable performance for the brainwave classification. This is because of the good generalization, based on the original extreme learning machine (ELM) [28] and the advantage of the kernel function [29], in terms of making effective classification tasks to map nonlinear features. KELM is based on ELM where the mapping kernel function is introduced to replace the hidden layer of ELM. It achieves higher efficiency compared to other methods.
In KELM, we can directly use kernel functions for the feature mapping. Kernel matrix can be represented by using the following equation:
where H is the hidden layer output matrix. 
is a kernel function: 
.
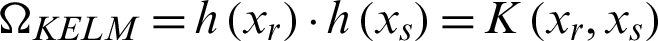Because the Moore–Penrose generalized inverse is used to compute the output weights, the output function of the KELM-based classifier can be expressed as below:
where T denotes the target (label) matrix, similar to SVM. I is the identity matrix. C denotes the regularization coefficient.
For the testing phase, the decision of circle/line imagination classes is based on the difference of two classes as below:
where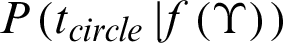 
and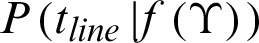 
are the posterior probability of circle and line imagination. In this paper, we employ the radial basis function as an effective kernel function. Further details of KELM can be found in [29].
2.3.3 Score Combination of GMM and KELM
Score combination gives a mechanism to fuse the merits of different classifiers in order to increase the decision performance. It has been adopted in many applications [16,30,31]. In this paper, the score combination is also used in our experiment. Fig. 6 shows the block diagram of score combination of GMM and KELM. To achieve the combined score, the scores of GMM and KLEM are linearly coupled by the following equation:
where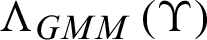 
and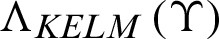 
are the scores of GMM and KELM model, respectively. Moreover, 
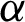is a weighing coefficient.
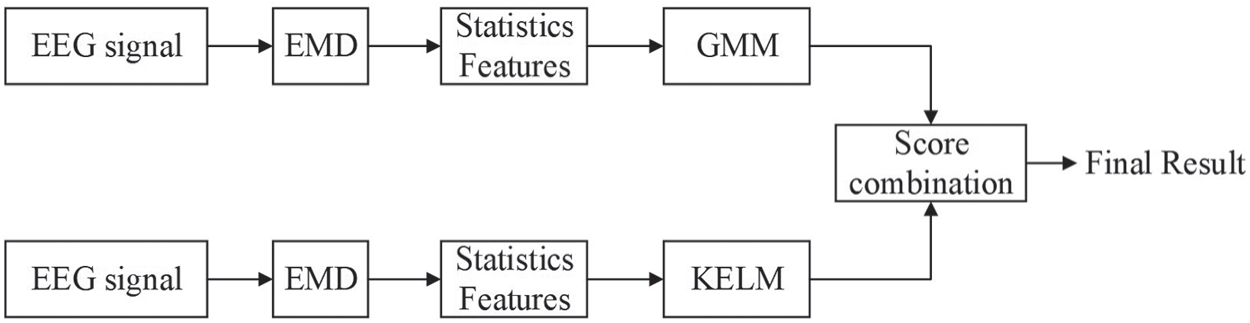
Figure 6: Block diagram of score combination of GMM and KELM
3 Experimental Setup and Evaluation Rule
In terms of recording the data, since previous work showed that the signals from two electrodes which are positioned at F3 and F4 are the suitable electrodes for the character-writing application as summarized in [14], the data from two these electrodes positions are used in our experiment. Here, the evaluation data which used in the experiment follows previous studies [14,15]. Therefore, each volunteer is required to image circle characters by 100 times and straight line characters by 100 times so that we obtain 500 circle signals and 500 straight line signals to investigate the proposed methods.
In terms of the feature extracted with the help of EMD method, we used the cubic spline interpolation to interpolate maxima and minima in order to obtain the upper and lower envelope. The first 5 IMFs based on EMD was extracted by using the six statistical methods as explained in Section 2.2. Fig. 7 shows the first 5 IMFs before the statistical methods.
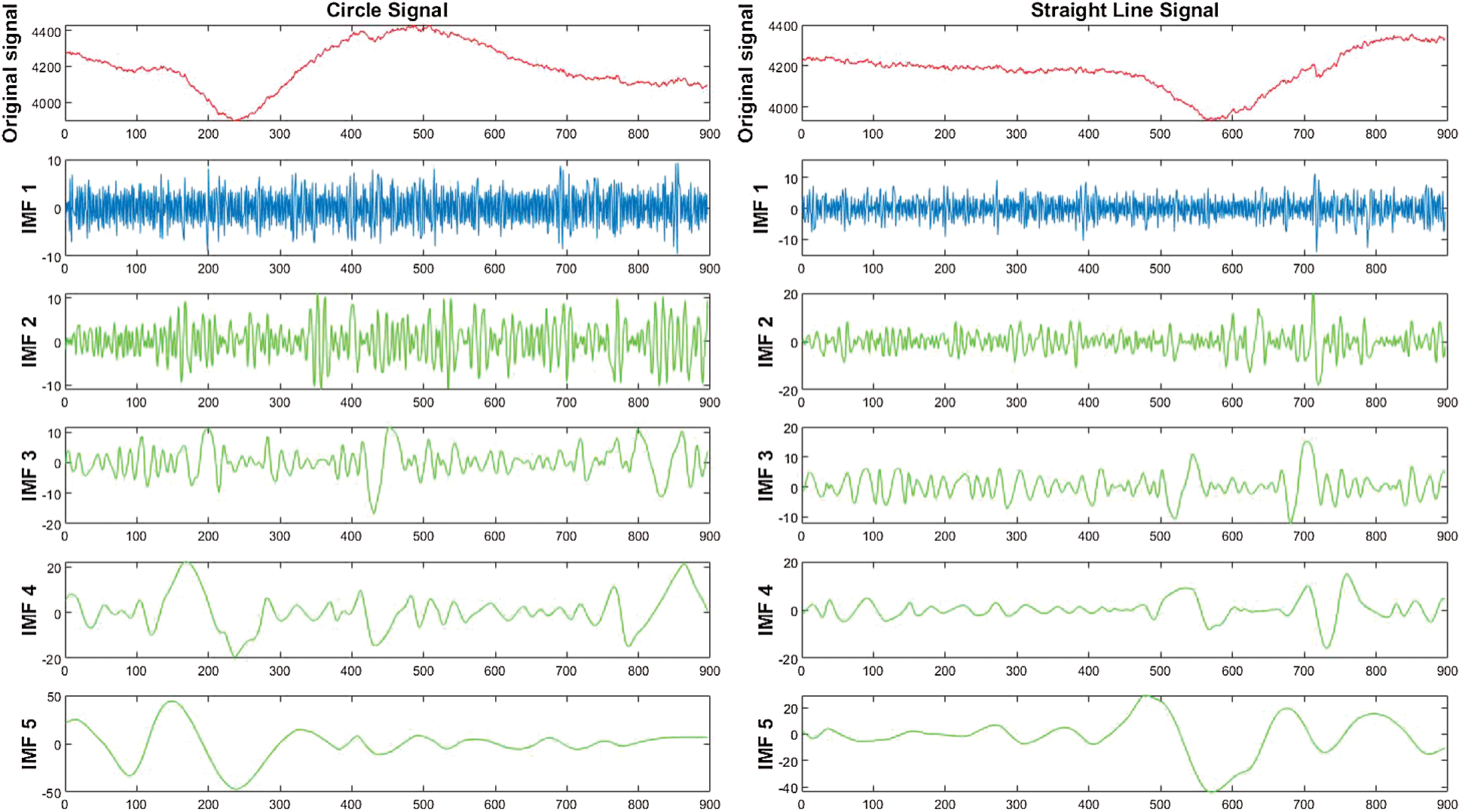
Figure 7: Signals of the first five IMFs/sub bands obtained through EMD method where (a) first columns are derived from circle characters and (b) second columns are derived from line characters
In the GMM-based classifier, the two GMMs for a circle and line imagination classes have 256-components. Motivated by [27], the expectation maximization algorithm along with the likelihood estimation is adopted to train these GMMs. For the KELM-based classifier, we found that high values of regularization coefficient and kernel parameter perform a similar performance compared with low values of regularization coefficient and kernel parameter because high values of regularization coefficient and kernel parameter are suitable for the high-dimensional feature space. As a result, minimum low values of regularization coefficient and kernel parameter with the best performance are selected. Here, the regularization coefficient and kernel parameter of the KELM were set to 100. For the score combination, the uniformly-weighted average as summarized in [32] is applied in this study, so the weighing coefficient is set to 0.5.
All the proposed classifier models were evaluated by using the volunteer-independent 5-fold cross-validation. In each fold, the data sets from four different volunteers were used to train the model and the data sets from the remaining volunteers were used to evaluate the classifier model performance. From the volunteer-independent 5-fold cross-validation, 400 circle signals and 400 straight line signals were used to train the classifier model, while 100 circle signals and 100 straight line signals where the volunteer is different from the volunteers of training datasets were used to investigate the trained model. To investigate the performance of each fold, the accuracy performance is calculated as:
where TC and TS are the true circle and true straight line where the model correctly classifies the circle and straight line classes, respectively. TN is the total number of testing trials.
4.1 Results of EMD Using Different IMF Information
Since EMD methods using different IMF information vary the accuracy of the brainwave classification system, we need to find out the suitable IMF representation. Fig. 8 shows the results of different IMF information based on the GMM-based classifier.
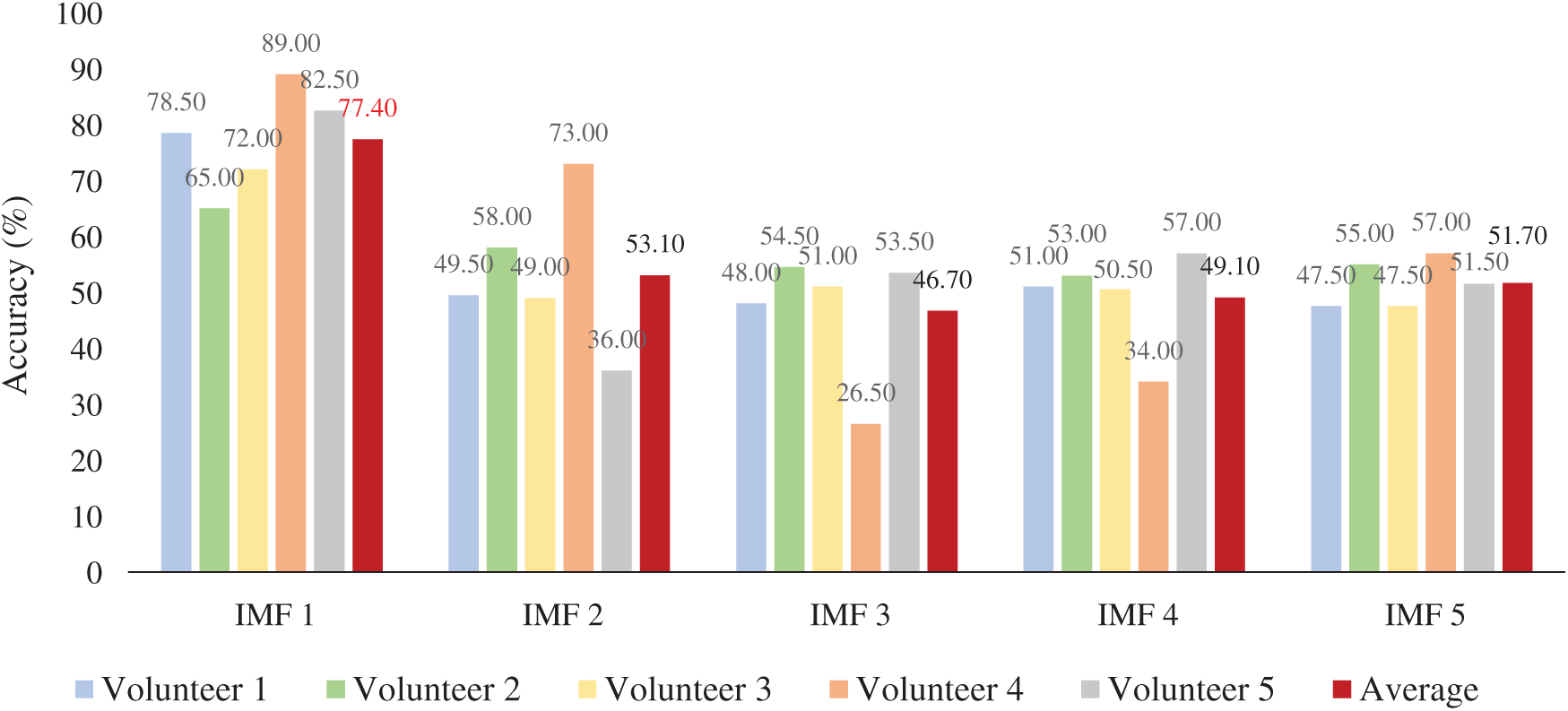
Figure 8: Performance of different IMF information
As shown in Fig. 8, based on the GMM-based classifier, we can see that IMF 1 provided the best average accuracy. This is because the IMF, obtained by the first time, has a wideband frequency, which can give the difference between the line and circle character as seen in Fig. 7 (second row). Therefore, EMD with IMF 1 was used for all the next experiments.
Although our previous work reported that the pair of F3 and F4 provide the best result, some study [15] showed that by using only one position could provide promising performance for the brainwave classification. The F3 and F4 positions were investigated to find out the suitable EEG position. Fig. 9 shows the comparison of F3 and F4 positions based on the EMD-GMM-based classifier.
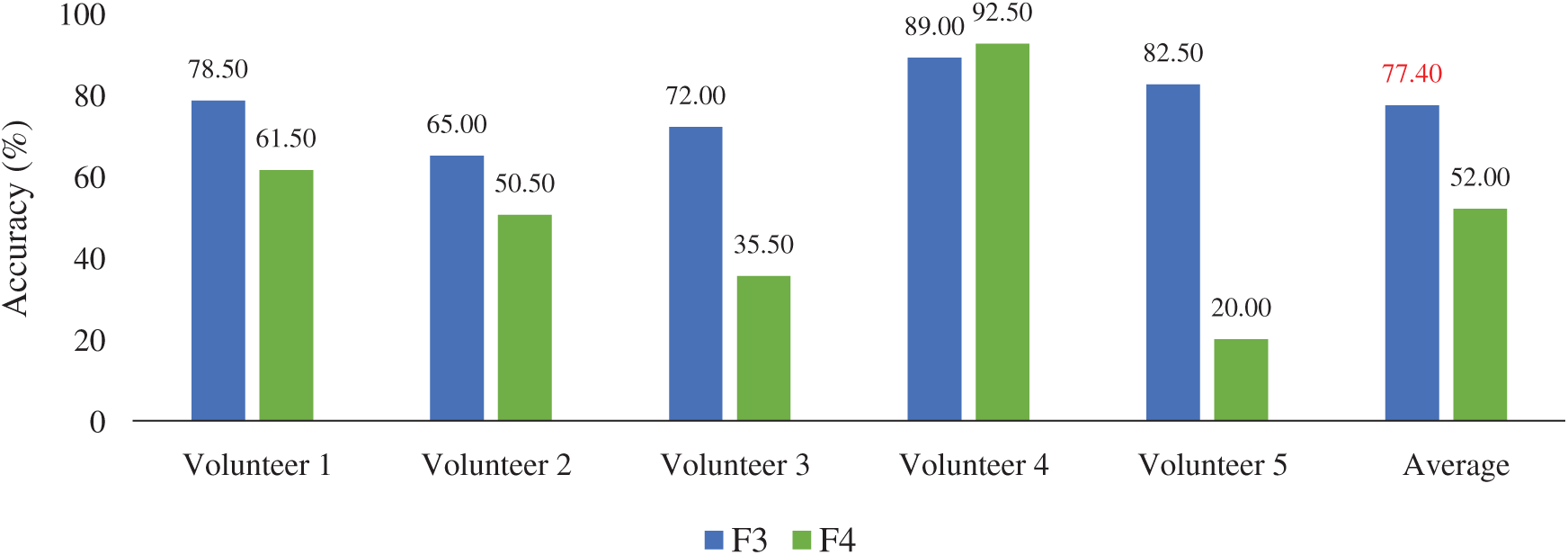
Figure 9: Performance of different EEG channels in terms of accuracy (%)
From Fig. 9, we can note that the F3 position significantly provided better average accuracy than the F4 position because the F3 position provided different information between the circle and line imagination signals. This leads to the obvious statistical features along with the efficient classifier. Similar trend can be found in [15]. Here, the best result with average accuracy has a high reliability for practical application. Therefore, the F3 position was used for all the next experiments.
4.2 Results of the Proposed Methods
In this subsection, the GMM, KELM-based classifier along with the fusion of GMM and KELM were compared for the brainwave classification. Fig. 10 shows the results of the KELM-based classifier along with the fusion of GMM and KELM.
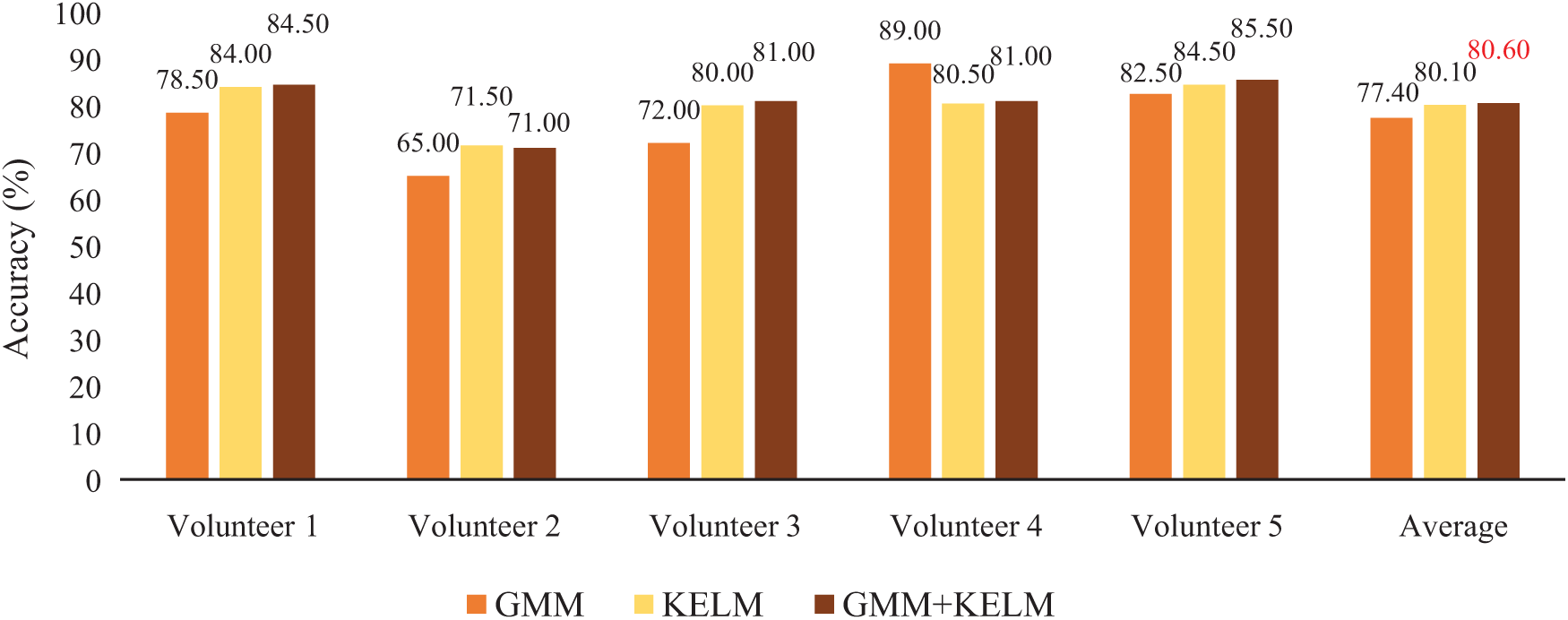
Figure 10: Performance of GMM-based classifier, KELM-based classifier, the score combination of GMM and KELM in terms of accuracy (%)
As it can be seen in Fig. 10, the KELM-based classifier performed better than the GMM-based classifier because KELM has high ability to distinguish the circle and straight line characters accurately. Next, the score fusion of GMM and KELM provided an improved performance as compared to the individual GMM and KELM-based classifiers in term of average accuracy. However, in case of the second and fourth volunteers, the score fusion can give worse performance than single classifier because the scores of two classifiers are too different to combine the decision merits. Similar trend can also be found in [33,34]. Here, the score fusion of GMM and KELM did not perform according to our expectation since the fused score of GMM and KELM provided the slightly improved performance as compared to the single KELM-based classifier. This is due to using the same input feature as summarized in [35].
4.3 Comparison with Some Previous Systems
In this subsection, our previous systems where the results of DWT feature with the ANN-based classifier was used as baseline systems [14,15] to compare the proposed system. In addition, the ANN using six statistical features extracted by EMD (IMF 1) was also used in the comparison. Tab. 2 reports the comparison of proposed systems with the referred systems.
Table 2: Comparison with some previous systems in terms of accuracy (%)
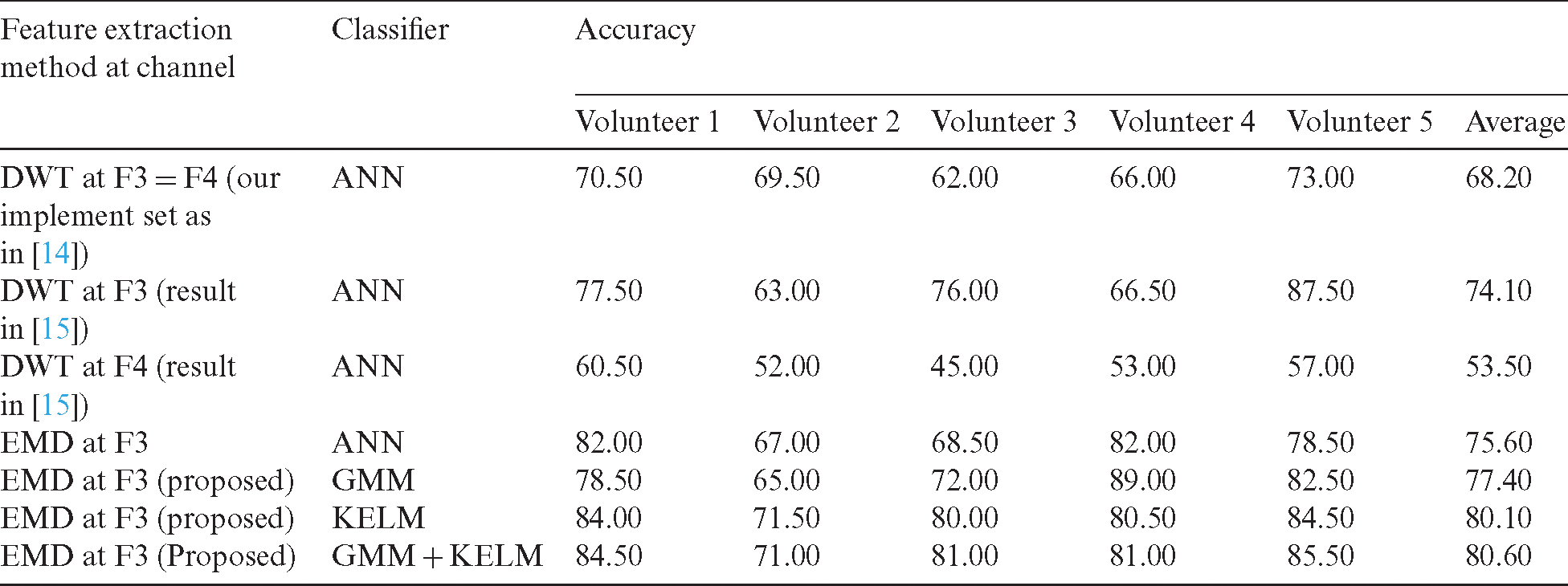
As it can be seen in Tab. 2, we can observe that the ANN using the IMF 1 information outperformed the ANN using the DTW information (Gamma) because IMF 1 can provide more distinct representation than the DTW information. This indicates that IMF 1 is powerful for the brainwave classification in terms of the character-writing application. Next, we can find that the GMM-based classifier performs better than the ANN-based classifier. This is because the MSE function in the ANN-based classifier is non-convex function, making classifier ineffective for the brainwave classification in terms of the character-writing application. In addition, the KELM-based classifier can give the best performance in terms of individual classifiers due to the advantage of kernel mapping. Finally, the score fusion of GMM and KELM provides the best accuracy at 80.60% compared to the above mentioned systems because GMM and KELM have complementary features based on different classifiers. These outcomes show the usefulness of EMD feature with GMM and KELM-based classifiers for the brainwave classification based on the character-writing application, which do not require any limb movement and stimulus.
In this paper, we proposed the brainwave classification by using EMD along with GMM and KELM for the character-writing application. For this purpose, we firstly explored the EMD method to decompose EEG signals into IMFs, which were used via statistical features as the input features of the classifiers. Secondly, the GMM and KELM methods were applied as classifiers. Finally, the score combination of GMM and KELM was proposed to fuse the merits based on different classifiers. The experimental results showed that the EMD with the proper IMF outperformed the DTW information. Furthermore, we found that by using EMD with the GMM and KELM-based classifier provided the average accuracy of 77.40% and 80.10%, respectively, which performed better than using DWT with the ANN-based classifier that gave the average accuracy of 74.10%. Moreover, the improved performance was obtained by combining the GMM and KELM at the average accuracy of 80.60%. These outcomes exhibit the usefulness of the EMD feature with GMM and KELM-based classifiers for the brainwave classification based on the character-writing application, which do not require any limb movement and stimulus.
In the future, by getting inspired by [36], we have a plan to use new neuroheadsets such as Emotiv EPOC+ and Open BCI neuroheadsets instead of EPOC neuroheadset with the aim of further improving the performance. We would also like to combine the phase feature extraction [31,37] and the neural network-based bottleneck feature extraction [38] with the proposed system in the future.
Acknowledgement: All subjects gave their informed consent for inclusion before they participated in the study. The study was conducted in accordance with the Declaration of Helsinki and the protocol was approved by the Ethics Committee of Suranaree University of Technology (License EC-61-14 COA No. 16/2561).
Funding Statement: This work is supported by the SUT research and development fund, and in part by the National Natural Science Foundation of China under Grant 61771333.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1 G. Prasad, P. Herman, D. Coyle, S. McDonough and J. Crosbie. (2010). “Applying a brain-computer interface to support motor imagery practice in people with stroke for upper limb recovery: A feasibility study,” Journal of Neuroengineering and Rehabilitation, vol. 7, no. 1, pp. 60. [Google Scholar]
2 C. Brunner, N. Birbaumer, B. Blankertz, C. Guger, A. Kübler et al. (2015). , “BNCI Horizon 2020: Towards a roadmap for the BCI community,” Brain-Computer Interfaces, vol. 2, no. 1, pp. 1–10. [Google Scholar]
3 J. R. Wolpaw, N. Birbaumer, D. J. McFarland, G. Pfurtscheller and T. M. Vaughan. (2002). “Brain-computer interfaces for communication and control,” Clinical Neurophysiology, vol. 113, no. 6, pp. 767–791. [Google Scholar]
4 G. E. Fabiani, D. J. McFarland, J. R. Wolpaw and G. Pfurtscheller. (2004). “Conversion of EEG activity into cursor movement by a brain-computer interface (BCI),” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 12, no. 3, pp. 331–338. [Google Scholar]
5 A. Al-Nafjan, M. Hosny, Y. Al-Ohali and A. Al-Wabil. (2017). “Review and classification of emotion recognition based on EEG brain-computer interface system research: A systematic review,” Applied Sciences, vol. 7, no. 12, pp. 1239. [Google Scholar]
6 G. E. Fabiani, D. J. McFarland, J. R. Wolpaw and G. Pfurtscheller. (2009). “A brain-computer interface controlled auditory event-related potential (P300) spelling system for locked-in patients,” Annals of The New York Academy of Sciences, vol. 1157, no. 1, pp. 90–100. [Google Scholar]
7 H. Hwang, V. Y. Ferreria, D. Ulrich, T. Kilic, X. Chatziliadis et al. (2015). , “A gaze independent brain-computer interface based on visual stimulation through closed eyelids,” Scientific Reports, vol. 5, pp. 15890. [Google Scholar]
8 M. Van der Waal, M. Severens, J. Geuze and P. Desain. (2012). “Introducing the tactile speller: An ERP-based brain-computer interface for communication,” Journal of Neural Engineering, vol. 9, no. 4, pp. 045002. [Google Scholar]
9 L. A. Farwell and E. Donchin. (1988). “Talking off the top of your head: Toward a mental prosthesis utilizing event-related brain potentials,” Electroencephalography and Clinical Neurophysiology, vol. 70, no. 70, pp. 510–523. [Google Scholar]
10 G. Bin, X. Gao, Y. Wang, B. Hong and S. Gao. (2009). “VEP-based brain-computer interfaces: Time, frequency and code modulations,” IEEE Computational Intelligence Magazine, vol. 4, no. 4, pp. 22–26. [Google Scholar]
11 Z. Wu, Y. Lai, Y. Xia, D. Wu and D. Yao. (2008). “Stimulator selection in SSVEP-based BCI,” Medical Engineering & Physics, vol. 30, no. 8, pp. 1079–1088. [Google Scholar]
12 X. Chen, Z. Chen, S. Gao and X. Gao. (2014). “A high-ITR SSVEP-based BCI speller,” Brain-Computer Interfaces, vol. 1, no. 3–4, pp. 181–191. [Google Scholar]
13 B. Blankertz, G. Dornhege, M. Krauledat, M. Schroder, J. Williamson et al. (2006). , “The berlin brain-computer interface presents the novel mental typewriter hex-o-spell,” in 3rd Int. Brain Computer Interface Workshop and Training Course, Graz, Austria, pp. 108–109. [Google Scholar]
14 T. Jumphoo, M. Uthansakul and P. Uthansakul. (2019). “Brainwave classification without the help of limb movement and any stimulus for character-writing application,” Cognitive Systems Research, vol. 58, pp. 375–386. [Google Scholar]
15 K. Kokkhunthod, T. Jumphoo and P. Uthansakul. (2020). “Improving brainwave classification for character-writing application using single effective EEG channel in SUT,” in Int. Virtual Conf. on Science and Technology, Nakhon Ratchasima, Thailand, pp. 142–148. [Google Scholar]
16 K. Phapatanaburi, L. Wang, R. Sakagami, Z. Zhang, X. Li et al. (2016). , “Distant-talking accent recognition by combining GMM and DNN,” Multimedia Tools and Applications, vol. 75, no. 9, pp. 5109–5124. [Google Scholar]
17 J. Cao, J. Zhu, W. Hu and A. Kummert. (2019). “Epileptic signal classification with deep EEG features by stacked CNNs,” IEEE Transactions on Cognitive and Developmental Systems, vol. 75, no. 9, pp. 1. [Google Scholar]
18 L. Vokorokos, B. Madoš, N. Ádám and A. Baláž. (2012). “Data acquisition in non-invasive brain-computer interface using emotiv Epoc neuroheadset,” Acta Electrotechnica et Informatica, vol. 12, no. 1, pp. 422. [Google Scholar]
19 N. E. Huang, Z. Shen, S. R. Long, M. C. Wu, H. H. Shih et al. (1998). , “The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis,” in Proc. of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, vol. 454, no. 1971, pp. 903–995. [Google Scholar]
20 N. Ji, L. Ma, H. Dong and X. Zhang. (2019). “EEG signals feature extraction based on DWT and EMD combined with approximate entropy,” Brain Sciences, vol. 9, no. 8, pp. 201. [Google Scholar]
21 P. A. Muñoz-Gutiérrez, E. Giraldo and M. Bueno-López. (2018). “Localization of active brain sources from EEG signals using empirical mode decomposition: A comparative study,” Frontiers in Integrative Neuroscience, vol. 19, pp. 55.
22 A. Subasi, S. Jukic and J. Kevric. (2019). “Comparison of EMD, DWT and WPD for the localization of epileptogenic foci using random forest classifier,” Measurement, vol. 146, pp. 846–855. [Google Scholar]
23 R. K. Tripathy and U. R. Acharya. (2018). “Use of features from RR-time series and EEG signals for automated classification of sleep stages in deep neural network framework,” Biocybernetics and Biomedical Engineering, vol. 38, no. 4, pp. 890–902. [Google Scholar]
24 Z. Tang, C. Li and S. Sun. (2017). “Single-trial EEG classification of motor imagery using deep convolutional neural networks,” Optik, vol. 130, pp. 11–18. [Google Scholar]
25 P. Wang, A. Jiang, X. Liu, J. Shang and L. Zhang. (2018). “LSTM-based EEG classification in motor imagery tasks,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 26, no. 11, pp. 2086–2095. [Google Scholar]
26 K. Phapatanaburi, L. Wang, Z. Oo, W. Li, S. Nakagawa et al. (2017). , “Noise robust voice activity detection using joint phase and magnitude based feature enhancement,” Journal of Ambient Intelligence and Humanized Computing, vol. 8, no. 6, pp. 845–859. [Google Scholar]
27 C. Hanilçi, T. Kinnunen, M. Sahidullah and A. Sizov. (2015). “Classifiers for synthetic speech detection: A comparison,” in Annual Conf. of the International Speech Communication Association, Dresden, Germany, pp. 2087–2091. [Google Scholar]
28 G. B. Huang, H. Zhou, X. Ding and R. Zhang. (2012). “Extreme learning machine for regression and multiclass classification,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 42, no. 2, pp. 513–529. [Google Scholar]
29 M. Zhang, X. Zhang, H. Wang, G. Xiong and W. Cheng. (2020). “Features fusion exaction and KELM with modified grey wolf optimizer for mixture control chart patterns recognition,” IEEE Access, vol. 8, pp. 42469–42480. [Google Scholar]
30 S. Kundu and S. Ari. (2019). “Fusion of convolutional neural networks for P300 based character recognition,” in Proc. of 2019 Int. Conf. on Information Technology, Quito, Ecuador, pp. 155–159. [Google Scholar]
31 K. Phapatanaburi, L. Wang, S. Nakagawa and M. Iwahashi. (2019). “Replay attack detection using linear prediction analysis-based relative phase features,” IEEE Access, vol. 7, pp. 183614–183625. [Google Scholar]
32 M. F. Font. (2009). “Maximum-likelihood linear regression coefficients as features for speaker recognition,” Ph.D. dissertation. Faculté des sciences d’Orsay, Universite Paris-Saclay, Essonne, Paris. [Google Scholar]
33 L. Wang, S. Nakagawa, Z. Zhang, Y. Yoshida and Y. Kawakami. (2017). “Spoofing speech detection using modified relative phase information,” IEEE Journal of Selected Topics in Signal Processing, vol. 11, no. 4, pp. 660–670. [Google Scholar]
34 M. R. Kamble and H. A. Patil. (2017). “Novel energy separation based instantaneous frequency features for spoof speech detection,” in IEEE 25th European Signal Processing Conf., Kos island, Greece, pp. 106–110. [Google Scholar]
35 Z. Chen, Z. Xie, W. Zhang and X. Xu. (2017). “ResNet and model fusion for automatic spoofing detection,” in Annual Conf. of the International Speech Communication Association, Stockholm, Sweden, pp. 102–106. [Google Scholar]
36 P. Sawangjai, S. Hompoonsup, P. Leelaarporn, S. Kongwudhikunakorn and T. Wilaiprasitporn. (2020). “Consumer grade EEG measuring sensors as research tools: A review,” IEEE Sensors Journal, vol. 20, no. 8, pp. 3996–4024. [Google Scholar]
37 Z. Oo, L. Wang, K. Phapatanaburi, M. Liu, S. Nakagawa et al. (2019). , “Replay attack detection with auditory filter-based relative phase features,” EURASIP Journal on Audio, Speech, and Music Processing, vol. 2019, no. 1, pp. 130. [Google Scholar]
38 B. Ren, L. Wang, L. Lu, Y. Ueda and A. Kai. (2016). “Combination of bottleneck feature extraction and dereverberation for distant-talking speech recognition,” Multimedia Tools and Applications, vol. 75, no. 9, pp. 5093–5108. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |