DOI:10.32604/cmc.2021.014426
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014426 | |
| Article |
Improving Reconstructed Image Quality via Hybrid Compression Techniques
1Department of Computer and Information Systems, Sadat Academy for Management Sciences, Cairo, 11742, Egypt
2Department of Computer Science, Kafr el Sheikh University, 33511, Egypt
*Corresponding Author: Nancy Awadallah Awad. Email: rarecore2002@yahoo.com
Received: 19 September 2020; Accepted: 27 October 2020
Abstract: Data compression is one of the core fields of study for applications of image and video processing. The raw data to be transmitted consumes large bandwidth and requires huge storage space as a result, it is desirable to represent the information in the data with considerably fewer bits by the mean of data compression techniques, the data must be reconstituted very similarly to the initial form. In this paper, a hybrid compression based on Discrete Cosine Transform (DCT), Discrete Wavelet Transform (DWT) is used to enhance the quality of the reconstructed image. These techniques are followed by entropy encoding such as Huffman coding to give additional compression. Huffman coding is optimal prefix code because of its implementation is more simple, faster, and easier than other codes. It needs less execution time and it is the shortest average length and the measurements for analysis are based upon Compression Ratio, Mean Square Error (MSE), and Peak Signal to Noise Ratio (PSNR). We applied a hybrid algorithm on (DWT–DCT 
, 
, 
, 
, 
) blocks. Finally, we show that by using a hybrid (DWT–DCT) compression technique, the PSNR is reconstructed for the image by using the proposed hybrid algorithm (DWT–DCT 
block) is quite high than DCT.
Keywords: Image compression; discrete cosine transform; PSNR; discrete wavelet transform; hybrid algorithm
For image compression, transform-based compression demonstrates greater robustness than spatial domain-based compression. The compression technique may be either lossless or loose. The compression ratio of data loss, however, is very high, but it suffers from lossy compression. Yet this is a high compression ratio, really.
In the lossless compression method, the decompressed image is identical to the original one, but with the compression ratio [1].
DCT cosine transforms the image from the space domain to the frequency domain, where the top left corner of the DCT matrix coefficient is the low-frequency component, and the frequency from the top left corner is decreased diagonally [2].
Discrete wavelet converts the image into four separate frequency bands called LL, LH, HL, and HH, where image characteristics are reflected by LL sub-bands and signal noise is shown by HH sub-bands [3].
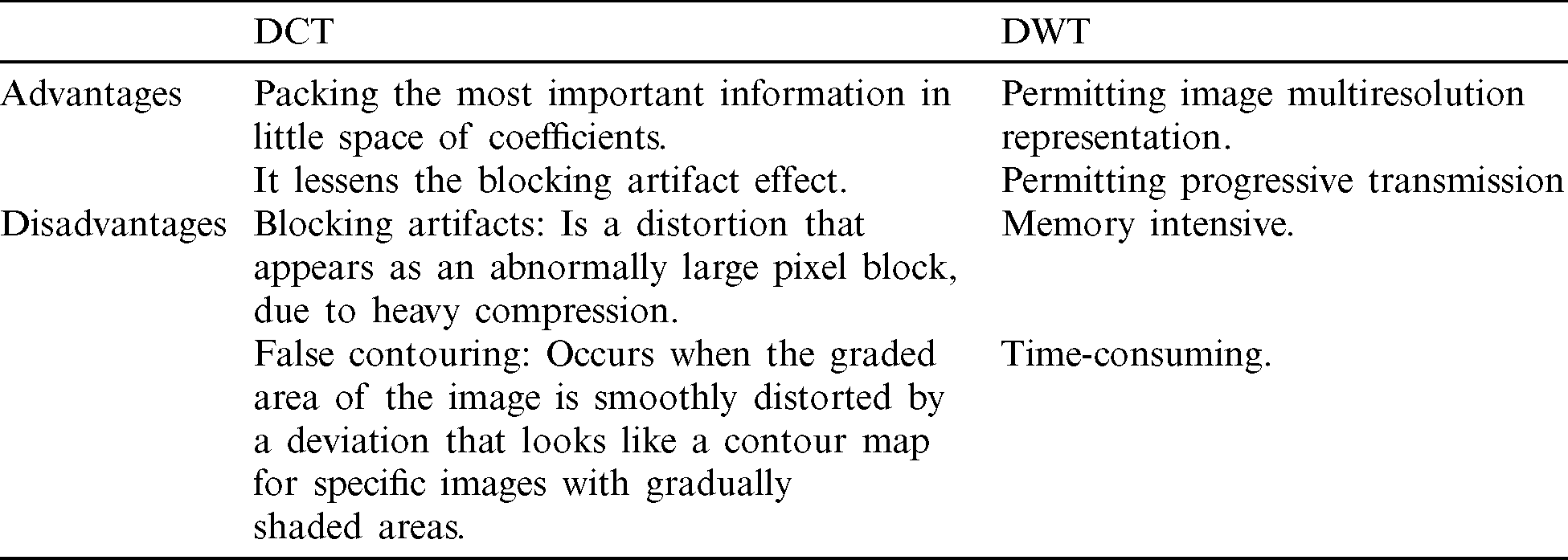
The DCT algorithm shows better energy compaction features and requires fewer computational difficulties. This removes the blocking artifact and the misleading contouring results, though DWT, it is a multi-resolution compression process but DWT’s feature of energy compaction is less and induces a ringing effect.
In this paper, the transformation techniques chosen for image compression include discrete cosine transformation (DCT) and discrete wavelet transformation (DWT). The DCT transform is used in image coding (JPEG).
DCT is an orthogonal transformation that is used for decorrelating image data. Encoding each transform coefficient is easy after using DCT without losing compression efficiency.
The quantization table option influences the compression ratio and entropy. In a lossy compression algorithm, the process of quantization is referred to throughout a stage.
The 2-D DCT is specified in Eq. (1):
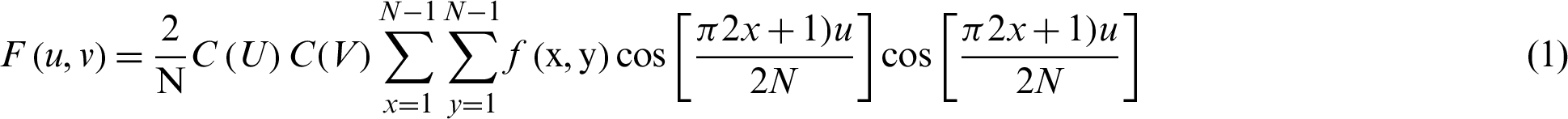
For 
and 
Coding Scheme
Compression Process
First of all, the whole image is loaded into the encoder, then transformed from RGB to YCBCR. The entire image is then divided into tiny NXN image blocks. From top to bottom or left to right, there are two directions where every block is applied to the DCT.
By dividing each transformed data item by the corresponding pixel in the quantization matrix Q, and rounding it to the nearest integer value, as shown in Eq. 2, the recompressed components of each block are obtained.
The 1D array is extracted and transmitted to the receiver from this the encoding process is completed [4]. Extra compression can be achieved by applying acceptable entropy encoding. The de-quantized matrix is displayed in Eq. 3 and then using the 2-D inverse DCT.
Decompression Procedure
The image reconstruction, the quantified DCT coefficients, are decoded and the inverse 2DDCT of the computer block is computed, then the blocks are collected in one image together. There are two important steps in this decoding process when applying the dequantization matrix to blocks: Maintaining the size of the block equals that used in the encoding method.
2.2 Discrete Wavelet Transform
For turning the coordinate system, wavelets are “a mathematical tool.” For applications where tolerable degradation and scalability are significant, they are suitable.
Multiresolution Concept and Analysis
The representation of signals is designed by the multi-resolution concept When a single occurrence is broken down into smaller, smaller specifics [5,6].
Filter Bank
It is a collection of filters. Synthesis and analysis banks are components of it. It is represented in Fig. 1
Figure 1: Filter bank
Analysis Bank
It has two filters: A high and a low pass [6]. HH, LH, LL, and HL are four bands that are produced from this passing. Those 4 bands are the decomposition’s first level. Fig. 2 illustrated finer scale and coarser scale wavelet coefficients.
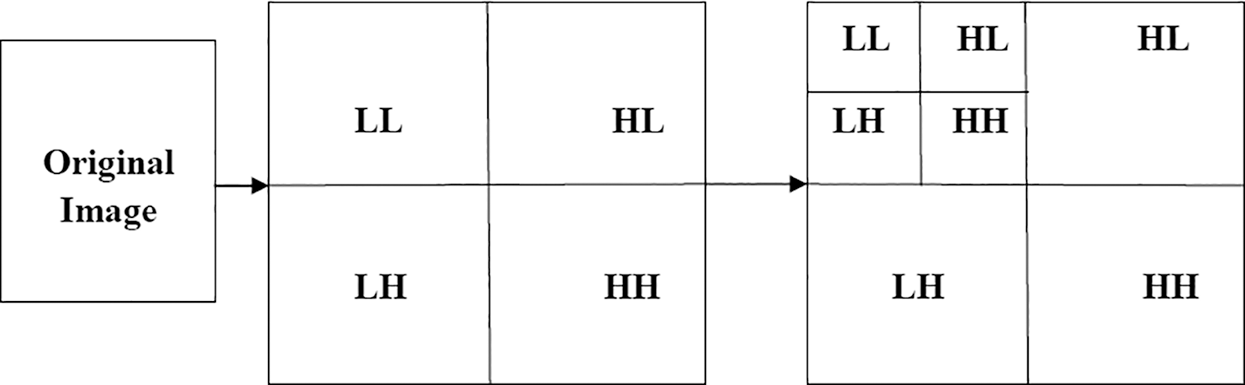
Figure 2: Wavelet coefficients finer and coarser scale
Synthesis Bank
That is the reverse of analytics bank collection. This included filtration and decimation.
Coding Scheme
Compression Process
Passing image through LPF and HPF and the Output from it is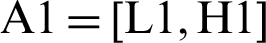 
.
Then A1 is passed over again by HPF and LPF by adding a filter to each board. The performance of [L2 and H2] is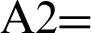 
. Now A2 is sampled down by 2 to cause a compressed image.
Through taking the actions above we can do more than one degree [7].
Decompression Process
By actually taking a higher half matrix rectangle, extracting LPF and HPF images from compressed images are an LPF image and half a rectangle down is an HPF image.
Then the two images are summed up by 2. Actually, the sum of both images is taken into 1 image named B1.
Then, by vertically splitting [8], separate the LPF picture and the HPF image. The two halves obtained are filtered through LPF and HPF, providing the reconstructed image on each block of 
blocks, summing up these halves.
In Tab. 1 illustrated the advantages and disadvantages of DCT and DWT.
Table 1: The advantages and disadvantages of DCT and DWT
3.1 Image Compression Using DCT
This section shows some previous researcher’s studies for image compression using the DCT method.
Douak et al. [9] combined DCT transform with an adaptive block scanning to compress the color image in some steps. The first step is done by conversing from RGB color space to YCbCr color space and then using the DCT transform.
Using the Bisection technique, an iterative phase involving thresholding and quantization process was done to compress an image. Reconstructing the original image was done in the reverse process. The results explain that the system was efficient and was compared to a block truncation-based coder. The proposed method’s (M-3) PSNR higher than that of JPEG by approximately 2.22 db.
Khalil [10], suggested an entropy coder for the encoding of images based on the Discrete Cosine transformation. The proposed idea is to remove the consecutive non-zero coefficients in each 
block which precede the zero coefficients. In the run-length decoder, the output is the number of coefficients of none-zero and then the coefficients themselves for each block. The method of decompression should be developed frequently. The findings of the simulation reveal that the new technique has a higher compression ratio than the previous form of entropy coding called the run process.
Chen et al. [11], proposed a modern paradigm incorporating the classical local DCT used in image compression algorithms with a regional noiseless calculation which is solved using second-order cone programming. The first step in the algorithm is to transfer DCT knowledge that is appropriate for reproducing poor-resolution image quality deterioration relative to survival, but the constraint is poor image quality.
Pandit et al. [12] proposed an efficient image compression approach depended on JPEG image compression. The objective of this research is to find the relation between image quality and compression mount. The results show that for images of size between 3 to 5 MB, the best results are got at quantization factor ranging from 25% to 30% where 80% to 85% compression can be found.
Pandey et al. [13] proposed the image compression techniques using the DCT method with different blocks and quantization methods for reducing the blocking artifacts in reconstruction images. The proposed method is subdivided into blocks (
, 
, 
, and 
) and the maximum image dimension is divided into a maximum block size & compressed the image. The performance between the original and reconstructed images is analyzed using several images and calculated with various quantization matrices with a PSNR score. From the results, it is found that when the maximum value is given by the quantization matrix then the restored image is distorted as its MSE value decreases.
Abd-Elhafiez et al. [14], the proposed compression technique is performed by RGB to YCbCr color transformation process. Second, canny edge detection is used to distinguish blocks into the edge and non-edge blocks. Using adaptive arithmetic coding, each Y, Cb, and Cr color variable is compressed, quantized, and coded by (DCT) method.
3.2 Image Compression Using DWT
This section presents the previous researcher’s studies for image compression using DWT and hybrid techniques.
Chowdhury et al. [15] proposed an image compression process with a pruning proposal depended on the basic DWT technique. The steps of the proposed compression algorithm are choosing a wavelet level, the hard threshold is applied to the detail coefficients, reconstruct the image. This algorithm supplied sufficient high compression ratios with good image quality.
Khan [16] presented several image segmentation methods, upon studying various image segmentation techniques, it is proposed that the easiest approach to solving the image segmentation problem is a hybrid method for image segmentation composed of two or more techniques.
Sathik et al. [17] proposed the hybrid image compression technique and this hybrid technique segments the image into foreground and background regions based on edges. Then the regions compressed with various quality levels. This hybrid method provides the compression ratio and gives a desired quality compressed image.
Benchikh et al. [18], a hybrid DCT–DWT image compression solution was proposed to optimize the effects of both the DCT and DWT techniques. They have shown that, where several coefficients used for image restoration are small, DWT yields a better PSNR in image compression than DCT.
Elharar et al. [19], presented a compression method developed for the specific features of the digitally registered integral image.
The compression algorithm is based on a hybrid methodology that applies a four-dimensional transformation that incorporates the discreet wavelet transformation with the discrete cosine transformation. an earlier compression method developed for MPEG integral image-based image.
Agrwal et al. [20], presented the compression technique Hybrid Integer Wavelet Transform (IWT) and Discrete Cosine Transform (DCT) to achieve better-decompressed image output relative to compression technique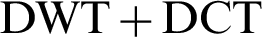 
.
The proposed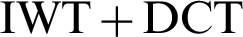 
-based hybrid compression technique reduces fractional loss relative to DWT-based compression, meaning that the proposed technique improves the image quality of decompression image with a high compression ratio comparable to DWT-based, and hybrid DWT DCT-based data compression techniques.
4 Proposed Framework for Color Images Compression Techniques
Hybrid of (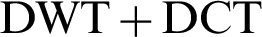
) transform lessens ringing effect, blocking artifacts, and false contouring. For every color image, each of the new three planes (Y, Cb, Cr) is partitioned into blocks after the preprocessing phase (RGB to YCbCr).
The various sizes (
, 
, 
, 
, or 
) were tested. Every block is translated to DWT and transferred to DCT after that.
Coding Scheme
In the Compression process, the input image is first converted from RGB to YCBCR, when this whole image is broken into blocks of 
pixels. Four details (LL, HL, LH, and HH) are produced after stratifying 2 D–DWT. The sub-band (LL) by 2 D–DWT is further transformed. The process continues until to get a new set of four sub-bands of size 
. After this step, we use the LL2 sub-band for computation of DCT coefficients. The output of it is then quantized and sends for coding using Huffman encoding. The other bands (HL2, LH2, and HH2) are quantized and encoded by Huffman. Fig. 3 illustrated the complete coding scheme.
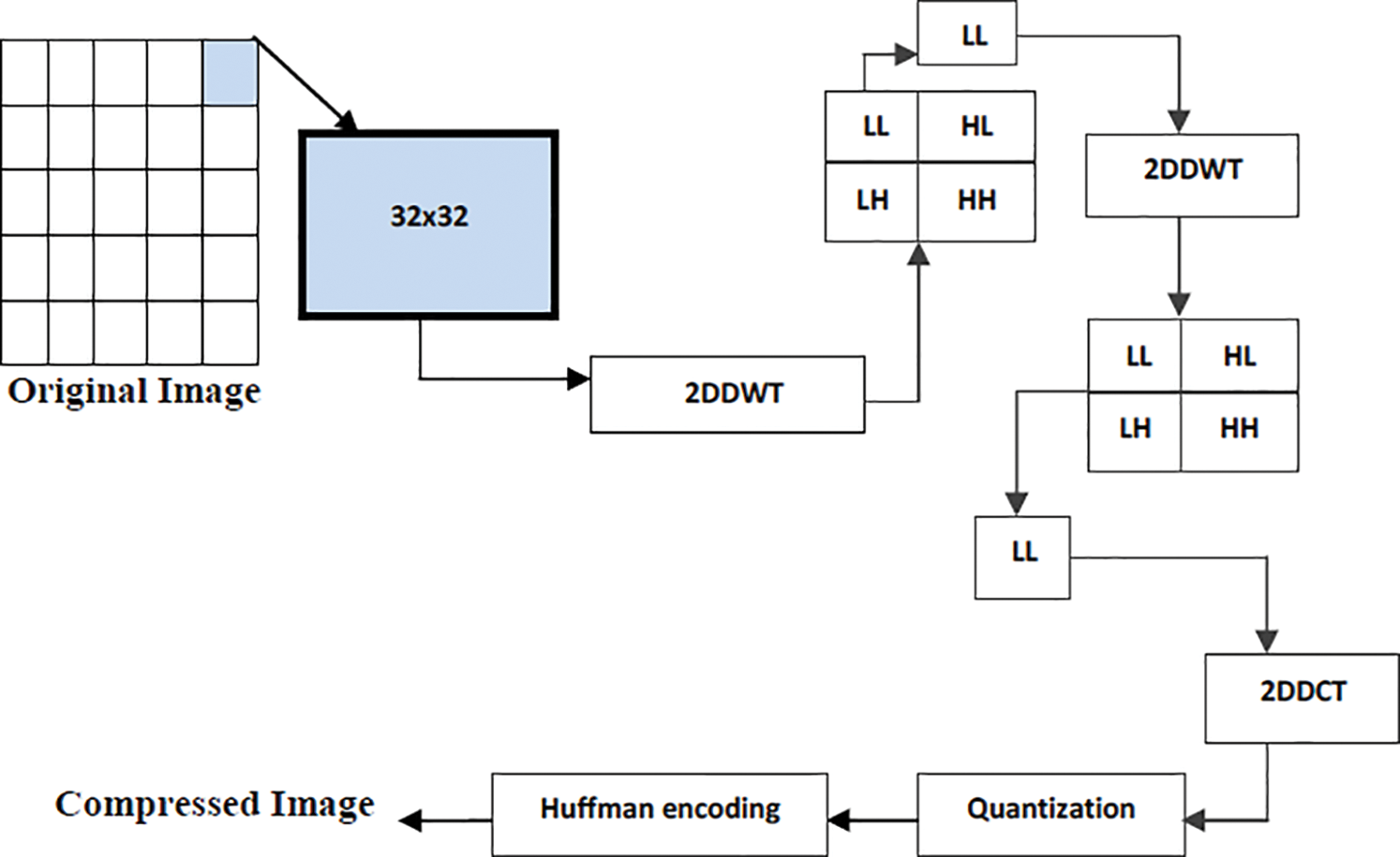
Figure 3: Compression process using hybrid DWT–DCT
In the decompression process, all the reversed processes are performed in the decompression method. We decipher the quantized DCT coefficients and measure each block’s IDCT. Block is then quantized.
5 Implementation of Color Image Compression Hybrid Techniques (DWT–DCT)
This section assesses the efficiency of various compression techniques for images. The hybrid techniques are applied to some color images. The results of (DCT, DWT) techniques, hybrid technique (DWT–DCT).
Simulation Tool
The proposed techniques were implemented using MATLAB and the evaluation parameters are CR, PSNR, and MSE.
Fig. 5 shows the reconstructed Pepper image using DCT, DWT, hybrid (DWT–DCT). Tab. 2 shows a comparison between compression techniques on Pepper image using evaluation parameters. Fig. 4 shows a chart for PSNR of different compression techniques for Pepper image.
Table 2: Comparison between compression techniques on Pepper image
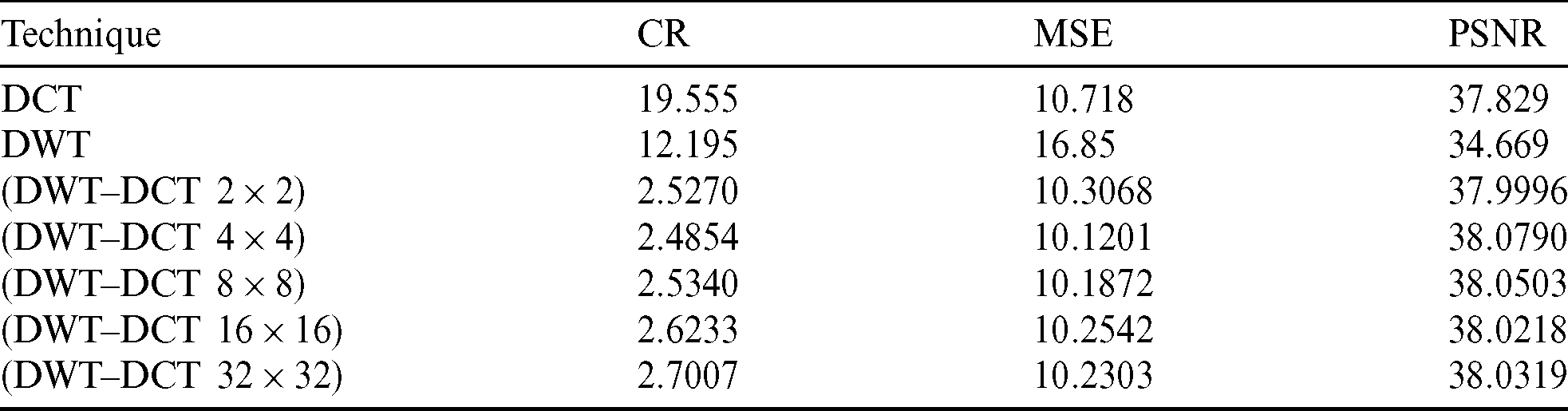
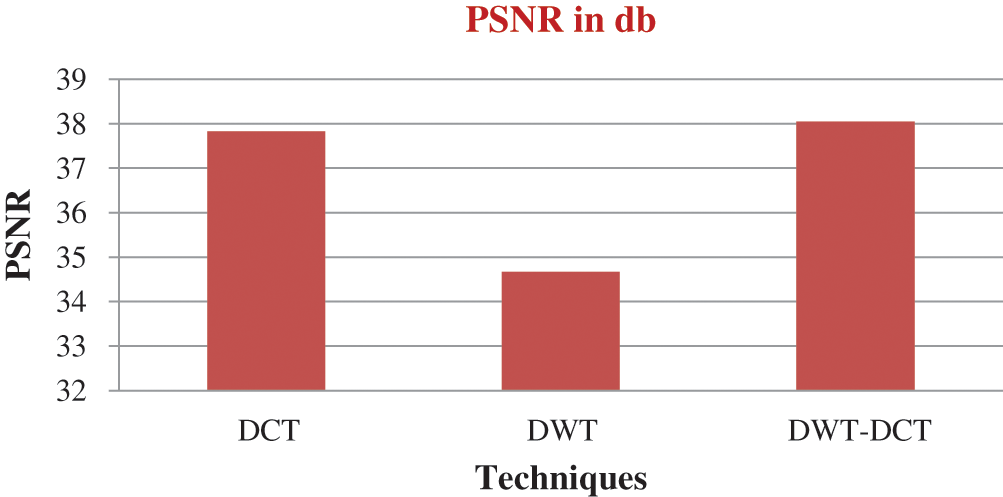
Figure 4: PSNR for pepper image of different techniques
Figure 5: The reconstructed Pepper image from techniques
From Tab. 2 and Fig. 6, we find that better PSNR than DWT is provided when the image is reconstructed using DCT, and the visual quality of the reconstructed image is better using DCT. The PSNR for the image that is reconstructed using the proposed hybrid algorithm (DWT–DCT 
block) is quite high than DCT and DWT.
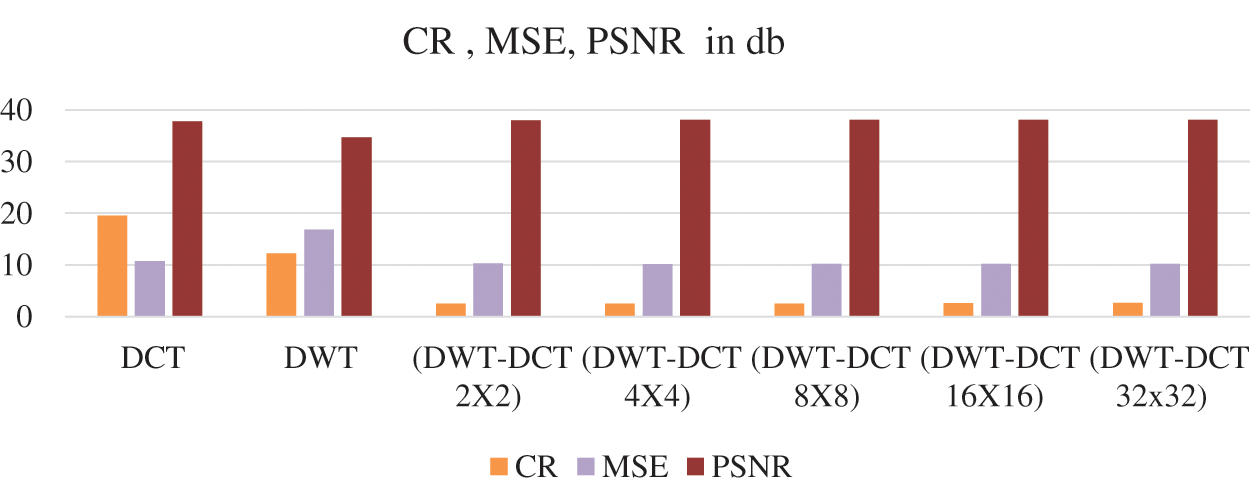
Figure 6: CR, MSE, PSNR for pepper image of different techniques
In this paper, the image compression techniques were analyzed by using the objective (PSNR, CR, and MSE) and subjective evaluation factors. Centered on the effects of the analysis set out above. For images, the suggested hybrid DWT–DCT algorithm can be shown to outperform the DCT and Daubechies-based DWT techniques. This is found that the restored images tend to be the strongest in the case of the DWT method, but with the DCT they are distorted by errors and incorrect contouring results.
The hybrid algorithm proposed has consistently higher PSNR and better quality for reconstruction.
It may also raise the impact of inaccurate contouring and images artifacts.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1 N. R. Patel and A. Kothari. (2016). “Performance analysis of medical image compression techniques,” in Proc. of Int. Conf. on ICT for Sustainable Development, Singapore: Springer, pp. 513–521. [Google Scholar]
2 P. Dosodia, A. Poonia, S. K. Gupta and S. L. Agrwal. (2015). “New Gabor-DCT feature extraction technique for facial expression recognition,” Fifth IEEE Int. Conf. on Communication Systems and Network Technologies, Gwalior, pp. 546–549. [Google Scholar]
3 K. Soni, S. K. Gupta, U. Kumar and S. L. Agrwal. (2014). “A new Gabor wavelet transform feature extraction technique for ear biometric recognition,” in 6th IEEE Power India Int. Conf., Delhi, pp. 1–3. [Google Scholar]
4 G. Vijayvargiya, S. Silakari and R. Pandey. (2013). “A survey: Various techniques of image compression,” International Journal of Computer Science and Information Security, vol. 11, no. 10, pp. 51–55. [Google Scholar]
5 C. Sun, Q. Li and J. Liu. (2010). “The study of digital image compression based on wavelets,” in Int. Conf. on Audio, Language and Image Processing, Shanghai, pp. 312–316. [Google Scholar]
6 S. Majumder, N. L. Meitei, A. D. Singh and M. Mishra. (2010). “Image compression using lifting wavelet transform,” in Int. Conf. on Advances in Communication, Network, and Computing, India, pp. 10–13. [Google Scholar]
7 B. Usevitch. (2001). “A tutorial on modern lossy wavelet image compression foundations of jpeg 2000,” IEEE Signal Processing Magazine, vol. 18, no. 5, pp. 22–35. [Google Scholar]
8 J. H. Zhao, W. J. Sun, Z. Meng and Z. H. Hao. (2004). “Wavelet transform characteristics and compression coding of remote sensing images,” Optics and Precision Engineering, vol. 12, pp. 205–210. [Google Scholar]
9 F. Douak, R. Benzid and N. Benoudjit. (2011). “Color image compression algorithm based on the DCT transform combined to an adaptive block scanning,” International Journal of Electronics and Communications, vol. 65, no. 1, pp. 16–26. [Google Scholar]
10 M. Khalil. (2010). “Image compression using new entropy coder,” International Journal of Computer Theory and Engineering, vol. 2, no. 1, pp. 39–42. [Google Scholar]
11 Z. Chen, J. Wen, Y. Han, J. Villasenor and S. Yang. (2010). “A compressive sensing image compression algorithm using quantized DCT and noiselet information,” in The 35th Int. Conf. on Acoustics, Speech, and Signal Processing, Dallas. [Google Scholar]
12 R. Pandit, N. Khosla, G. Singh and H. Sharma. (2013). “Image compression and quality factor in case of JPEG image format,” International Journal of Advanced Research in Computer and Communication Engineering, vol. 2, no. 7, pp. 2578–2581. [Google Scholar]
13 S. S. Pandey, M. P. Singh and V. Pandey. (2015). “Block wise image compression and block reduced artifacts using discrete cosine transform,” International Journal of Scientific and Research Publications, vol. 5, no. 3, pp. 1–10. [Google Scholar]
14 W. M. Abd-Elhafiez and E. O. Abdel-Rahman. (2016). “New efficient method for coding color images,” Applied Mathematics and Information Sciences an International Journal, vol. 10, no. 1, pp. 357–361. [Google Scholar]
15 M. M. Chowdhury and A. Khatun. (2012). “Image compression using discrete wavelet transform,” International Journal of Computer Science Issues, vol. 9, no. 4, pp. 327–330. [Google Scholar]
16 W. Khan. (2013). “Image segmentation techniques: A survey,” Journal of Image and Graphics, vol. 1, no. 4, pp. 166–170. [Google Scholar]
17 M. M. Sathik, K. S. Kannan and Y. J. V. Raj. (2011). “Hybrid JPEG compression using edge-based segmentation,” Signal and Image Processing: An International Journal, vol. 2, no. 1, pp. 156–176. [Google Scholar]
18 S. Benchikh and M. Corinthios. (2011). “A hybrid image compression technique based on DWT and DCT transforms,” in Int. Conf. on Advanced Infocom Technology, Wuhan, China, pp. 1–8. [Google Scholar]
19 E. Elharar, A. Stern, O. Hadar and B. Javidi. (2007). “A hybrid compression method for integral images using discrete wavelet transform and discrete cosine transform,” Journal of Display Technology, vol. 3, no. 3, pp. 321–325. [Google Scholar]
20 S. L. Agrwal, M. Sharma, D. Kumari and S. K. Gupta. (2016). “Improved image compression technique using IWT-DCT transformation,” in 2nd Int. Conf. on Next Generation Computing Technologies, Dehradun, pp. 683–686. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |