DOI:10.32604/cmc.2021.013830

| Computers, Materials & Continua DOI:10.32604/cmc.2021.013830 |  |
| Article |
Entanglement and Entropy Squeezing for Moving Two Two-Level Atoms Interaction with a Radiation Field
1Department of Mathematics, Collage of Science, Taif University, Taif, 21944, Saudi Arabia
2Department of Mathematics, Faculty of Science, Sohag University, Sohag, 82524, Egypt
3Department of Mathematics, Faculty of Science, Al-Azhar University, Cairo, Egypt
4Department of Physics, The University College at Aljamoum, Umm Al-Qura University, Makkah, Saudi Arabia
5Department of Mathematics, Faculty of Science, South Valley University, Qena, 83523, Egypt
*Corresponding Author: S. Abdel-Khalek. Email: sabotalb@tu.edu.sa; sayedquantum@yahoo.co.uk
Received: 22 August 2021; Accepted: 28 September 2020
Abstract: In this paper, we analyzed squeezing in the information entropy, quantum state fidelity, and qubit-qubit entanglement in a time-dependent system. The proposed model consists of two qubits that interact with a two-mode electromagnetic field under the dissipation effect. An analytical solution is calculated by considering the constants for the equations of motion. The effect of the general form of the time-dependent for qubit-field coupling and the dissipation term on the temporal behavior of the qubit-qubit entanglement, quantum state fidelity, entropy, and variance squeezing are examined. It is shown that the intervals of entanglement caused more squeezing for the case of considering the time-dependent parameters. Additionally, the entanglement between the qubits became more substantial for the case of time dependence. Fidelity and negativity rapidly reached the minimum values by increasing the effect of the dissipation parameter. Moreover, the amount of variance squeezing and the amplitude of the oscillations decreased considerably when the time dependence increased, but the fluctuations increased substantially. We show the relation between entropy and variance squeezing in the presence and absence of the dissipation parameter during the interaction period. This result enables new parameters to control the degree of entanglement and squeezing, especially in quantum communication.
Keywords: Entropy squeezing; variance squeezing; qubit-qubit entanglement; moving qubits
The principles of nonlocal correlation or entanglement mainly appear when two systems interact with each other; one is a pure state, and the other is mixed. Researchers utilize the von Neumann entropy to measure optimally the nonlocal correlation when a system reaches a pure condition. In this case, the density operator takes the form of a separate product state [1,2]. The linear entropy for the two symmetrical 2-level systems that interact with a 2-photon system developed in a squeezed condition is demonstrated in [3]. Additionally, a model consisting of a 2-three-level atom is investigated in [4], where the atom-atom entanglement decreases by increasing the multiplicity of the photons in the absence of a time-dependent coupling effect. A generalized model is considered to study the impact of the linear entropy of two SC-qubits with a linear system, which interacts with a thermal field [5]. Furthermore, a nonlocal correlation between subsystems has been studied. The results demonstrated that the effect of the nonlinear terms is greater than that of the linear terms. Recently, the measurement of the nonlocal correlation has achieved several purposes in the area of quantum information and computation, but the previous research considering the time independence to explain this phenomenon is limited.
The connection between the AES (atomic entropy squeezing) and entanglement has different applications in quantum computing and produces different observable physical phenomena [6–9]. The performance of the nonlocal correlation highly resembles the performance of the absorption coefficient and the GP. The AES for a 2LA coupling to fluctuating electromagnetic fields with a reflecting boundary was studied. The results showed that having the border influences the AES. Additionally, the relationship of the entanglement and FES (field entropy squeezing) of an effective 2-level system in the presence of a Stark Shift FES was studied [10]. The work has been extended to scrutinize the impact of cavity damping on the dynamics of the FES and the entanglement of the dissipation of two-photon JCM for a Kerr-like medium [11]. Recently, the relationship of the AES and entanglement between two two-level atoms and the N-level quantum system has been explored [12]. It was shown that the classical field has a potential role in the evolution of AES and nonlocal correlation. It was found that there is a strong correlation between the spin-orbit interaction and the strength of the AES, which depends on the initial state and the number of squeezed components [13]. Additionally, the relation between the atomic Fisher information and AES of the quantum system for an N-level atom that interacted with a two-level atom was also determined [14]. Experimental results in quantum physics cannot be explained using a closed system (hermitian Hamiltonian). Therefore, the results can be convincingly explained in cases of phenomena observed experimentally in the case of the open system (non-hermitian Hamiltonian) [15]. The non-hermitian generalization of Hamiltonian (NHH) can be used as a paradigm to define an open quantum system [15]. Then, we get the complex eigenvalues of energy. The aforementioned NHHs are valid as a rough and apparent description of an open quantum system, e.g., radioactive decay processes [16]. Therefore, this article explores the relation between the AES and linear entropy as a quantifier of the entanglement and purity of two qubits interacting with a two-mode electromagnetic field.
The contents of this article are arranged as follows: We present the general solution based on solving the differential equations which result from the Schrödinger equation in Section 2. The numerical results for the entropy and variance squeezing in Section 3, and the state fidelity and qubit-qubit entanglement phenomena will be discussed in Section 4. Finally, the results are presented in Section 5.
A time-dependent parameter and the atomic dissipation effect are added in our proposed model. Therefore, the Hamiltonian of the system takes the following form:

The operators 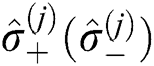 and
and 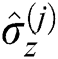
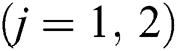 represent the Pauli matrices and fulfill the relationships of commutation
represent the Pauli matrices and fulfill the relationships of commutation  and
and 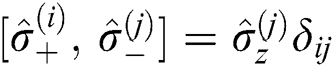 . While
. While 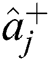 and
and 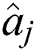 represent the operators of creation and annihilation for the cavity mode.
represent the operators of creation and annihilation for the cavity mode. 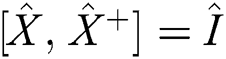 ,
,  and
and 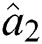 ,
, 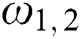 and
and 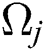 ,
, 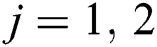 are the frequencies of the two modes and the atoms, respectively, while
are the frequencies of the two modes and the atoms, respectively, while 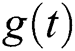 is the time-dependent coupling between the field and the atoms and
is the time-dependent coupling between the field and the atoms and 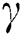 is the atomic corresponding decay rate. The behavior of the Hamiltonian (1) can be explained by calculating the wave function and solving the differential equations which are obtained from the Schrödinger formula. However, the dynamical operators can be calculated by the Heisenberg relationship. Therefore, the statistical results can be analyzed by employing these operators. The dynamical operator can be written as:
is the atomic corresponding decay rate. The behavior of the Hamiltonian (1) can be explained by calculating the wave function and solving the differential equations which are obtained from the Schrödinger formula. However, the dynamical operators can be calculated by the Heisenberg relationship. Therefore, the statistical results can be analyzed by employing these operators. The dynamical operator can be written as:
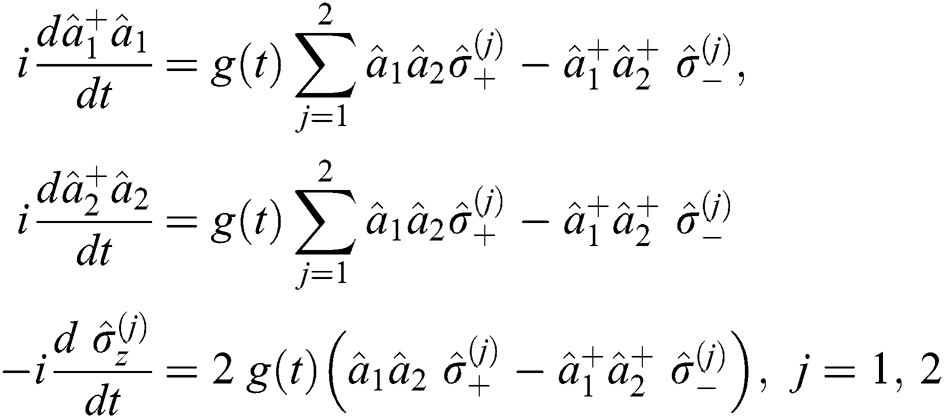
Therefore, the constants of motion are given by:
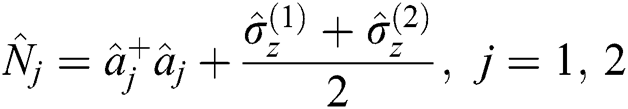
By applying Eq. (3) to the Hamiltonian system (1), we can obtain:
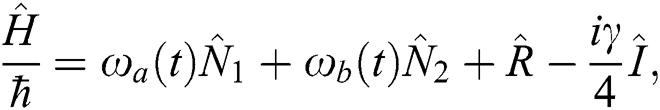
where, 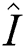 is the identity operator and
is the identity operator and 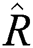 is given by:
is given by:

where 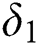 and
and 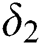 are the detuning parameters defined by:
are the detuning parameters defined by:
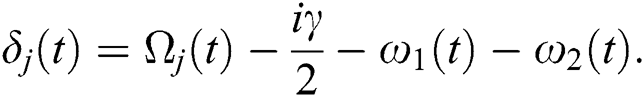
Here, we consider that 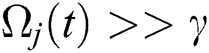 [17]. We assume that the primary conditions of the atoms and the field are:
[17]. We assume that the primary conditions of the atoms and the field are:
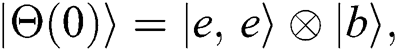
where  represents an excited state and
represents an excited state and 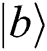 is the pair coherent state [18], which is given by:
is the pair coherent state [18], which is given by:
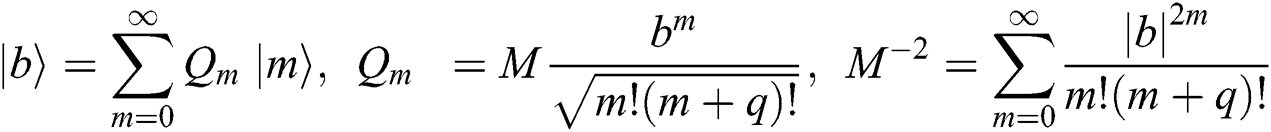
The general solution  for
for  takes the form,
takes the form,
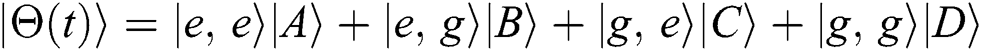
and

where  are the solution of the following system of differential equations,
are the solution of the following system of differential equations,

where 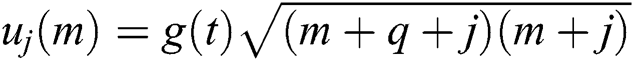
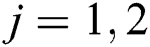
By specifying 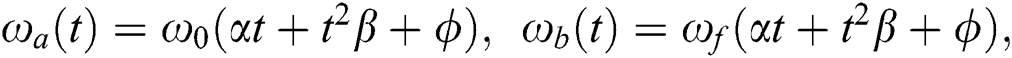
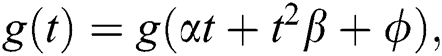 the time dependence of the coefficients
the time dependence of the coefficients 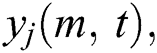
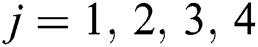 takes the following form:
takes the following form:
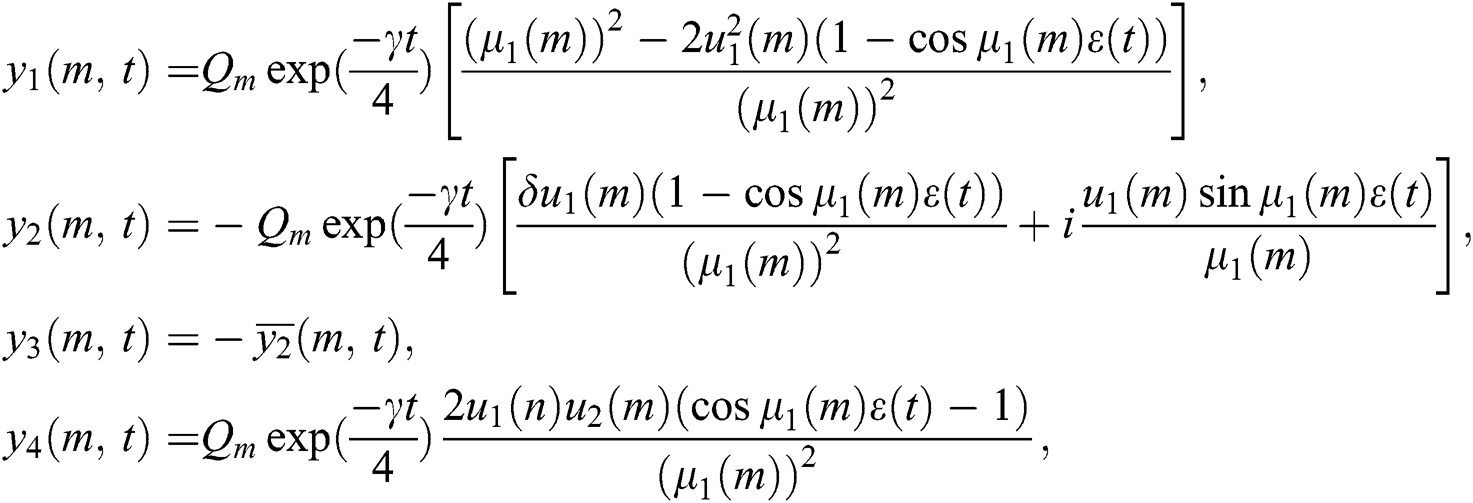
where
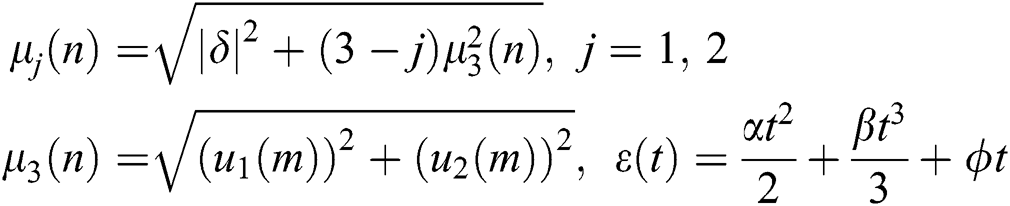
Next, the density matrix will be calculated according to various statistical quantities, and therefore, the physical phenomena can be explained. For the case where two atoms are identical and the trace is taken, we have:
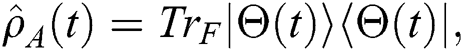
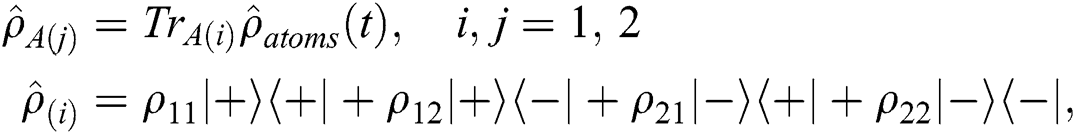
Section 3 discusses the dynamical behavior of the entropy and variance squeezing based on the single-atom density matrix (14).
3 Entropy and Variance Squeezing
The uncertainty principle, which was first introduced by Heisenberg, shows the limits of the error in the conventional measurements of non-commutating operators for measuring quantum states [19–23]. In general, the uncertainty principle for any two Hermitian operators 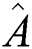 and
and 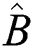 yields the relationship
yields the relationship 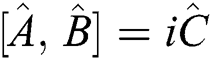 . Therefore, the Heisenberg uncertainty inequality is given by:
. Therefore, the Heisenberg uncertainty inequality is given by:
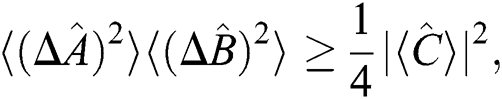
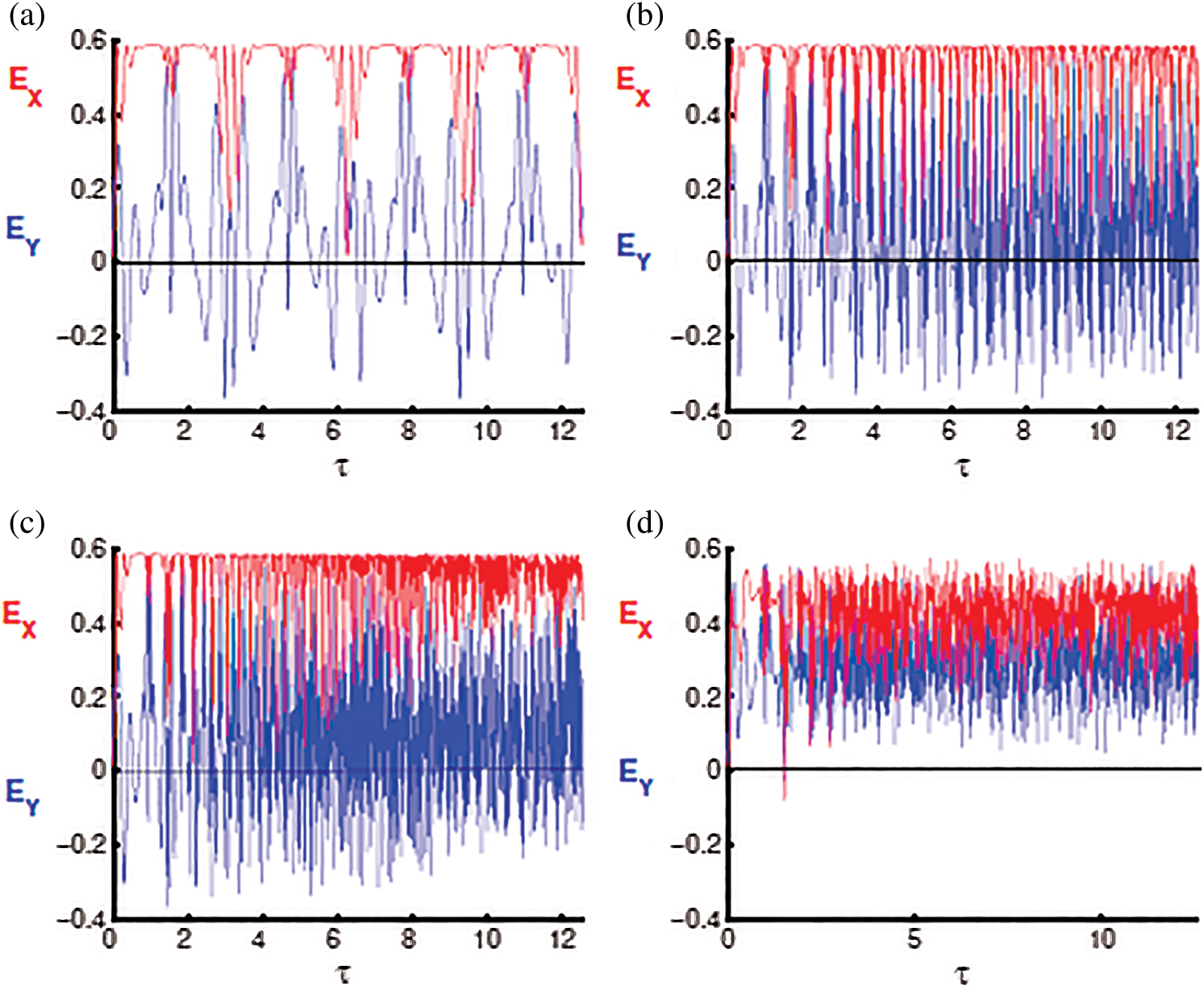
Figure 1: The dynamics of the AES components EX and EY as a function of the scaled time τ, with the atoms primarily in excited states, and the fields are prepared in a pair coherent states with γ = 0 and fixed parameter b = 5. (a) δ = 0, α = β = 0, φ = 1, (b) δ = 0, α = 1, β = 0, φ = 1, (c) δ = 0, α = 1, β = 0.5, φ = 1, and (d) δ = 4 g, α = 1, β = 0.5, φ = 1
where 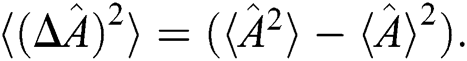 As an important application for a Pauli operator
As an important application for a Pauli operator 
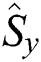 and
and  , which describe the way a two-level atom interacts with the electromagnetic field, such that
, which describe the way a two-level atom interacts with the electromagnetic field, such that 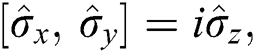 can be used to define the uncertainty as
can be used to define the uncertainty as 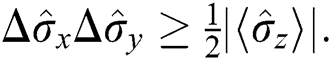 The variance squeezing (VS) for component
The variance squeezing (VS) for component  is squeezed if
is squeezed if 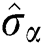 fulfills the requirement of Eq. (15),
fulfills the requirement of Eq. (15),
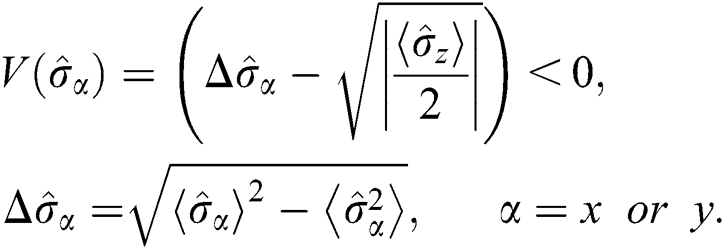
Using the next formula, the AES can be written as:
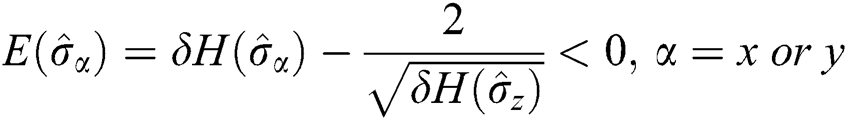
where 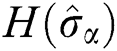 is the atomic operators’ Shannon information entropies
is the atomic operators’ Shannon information entropies  ,
,  and
and 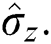
By applying the previous condition, the behavior of the ES and VS related to the uncertainty principle can be examined.
When 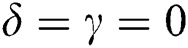 and
and 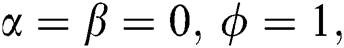 it is obvious that the AES becomes feasible for
it is obvious that the AES becomes feasible for 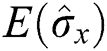 several times (at regions of collapses for the atomic population inversion [9]) and does not occur when
several times (at regions of collapses for the atomic population inversion [9]) and does not occur when 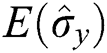 . It is noteworthy that the collapse periods have a direct relationship to the phenomenon of maximally entangled between parts of the system. These periods have applications in quantum computing [24] and quantum algorithm [25]. In addition, higher values of squeezing are found at the center of the collapse points, as seen in Fig. 1a. When considering the effect of the linear time dependence
. It is noteworthy that the collapse periods have a direct relationship to the phenomenon of maximally entangled between parts of the system. These periods have applications in quantum computing [24] and quantum algorithm [25]. In addition, higher values of squeezing are found at the center of the collapse points, as seen in Fig. 1a. When considering the effect of the linear time dependence 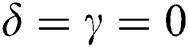 and
and 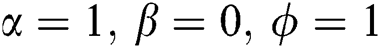 , the intervals of squeezing for the function
, the intervals of squeezing for the function 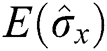 decrease to small regions, and more oscillations of the AES function are built-up (see Fig. 1b). Fig. 1c shows that the maximum values of squeezing increase, and more fluctuations in the squeezing function occur by employing the parameter
decrease to small regions, and more oscillations of the AES function are built-up (see Fig. 1b). Fig. 1c shows that the maximum values of squeezing increase, and more fluctuations in the squeezing function occur by employing the parameter 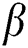 . Additionally, the fluctuations of the oscillations increase substantially by adapting
. Additionally, the fluctuations of the oscillations increase substantially by adapting 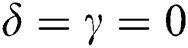 and
and 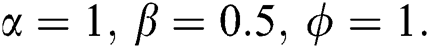 For the off-resonance case
For the off-resonance case  and
and 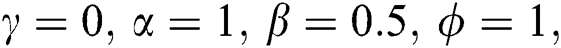 the squeezing in the previous cases deteriorates after adding the detuning term in the system. The squeezing phenomenon exists in a few regions, as shown in Fig. 1d. After inserting the dissipation term into the interaction cavity, the squeezing periods appear after the start of the interaction and decrease quickly until disappearing, as shown in Fig. 5a. Therefore, the entropy squeezing is affected by changing both the detuning and the dissipation parameters. Generally, the squeezing disappears.
the squeezing in the previous cases deteriorates after adding the detuning term in the system. The squeezing phenomenon exists in a few regions, as shown in Fig. 1d. After inserting the dissipation term into the interaction cavity, the squeezing periods appear after the start of the interaction and decrease quickly until disappearing, as shown in Fig. 5a. Therefore, the entropy squeezing is affected by changing both the detuning and the dissipation parameters. Generally, the squeezing disappears.
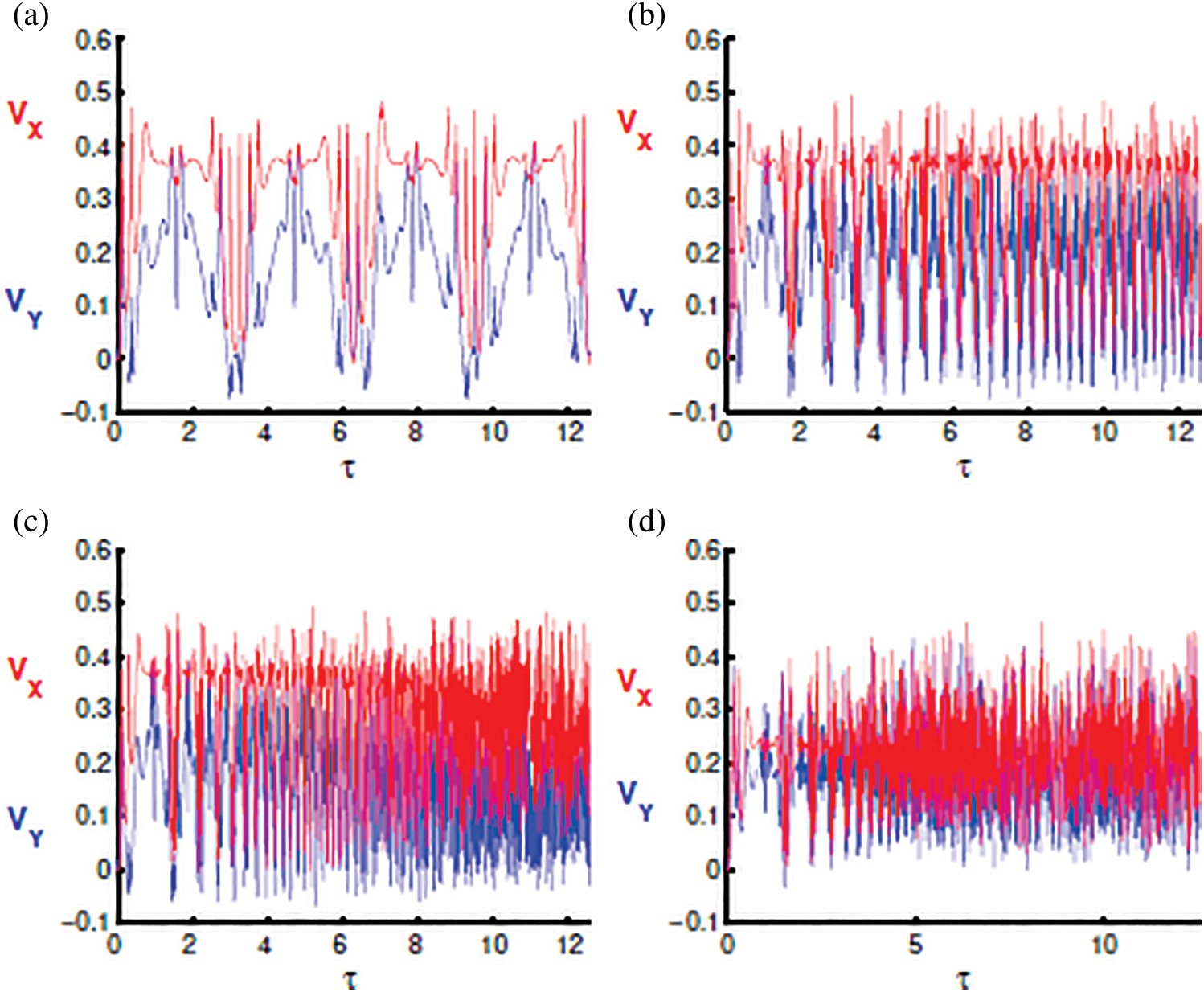
Figure 2: Variance squeezing as a function of the scaled time τ when the other conditions are the same as those in Fig. 1
Fig. 2a shows the VS when  and
and  . It is shown that the squeezing occurs in many intervals, but the regions of the VS are less than those of the ES. On the contrary, when considering the time dependence
. It is shown that the squeezing occurs in many intervals, but the regions of the VS are less than those of the ES. On the contrary, when considering the time dependence  and
and  ,
, 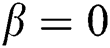 ,
, 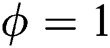 , the squeezing increases compared with the beforehand case and exists in many intervals (where the higher value of squeezing occurs at
, the squeezing increases compared with the beforehand case and exists in many intervals (where the higher value of squeezing occurs at 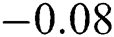 ) as shown in Fig. 2b. When
) as shown in Fig. 2b. When 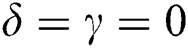 and
and 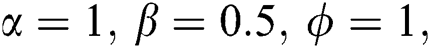 the squeezing decreases, and the maximum values reduce to
the squeezing decreases, and the maximum values reduce to 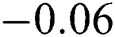 . Additionally, the fluctuations increase, with a slight shift in
. Additionally, the fluctuations increase, with a slight shift in 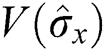 after the onset of the considered time, as shown in Fig. 2c. Finally, the amount of squeezing and the amplitude of the oscillations decrease considerably when the interaction time increases, but the fluctuations increase substantially, as shown in Fig. 2d. When we take into account the dissipation term, the squeezing periods are only fully realized in one period at the start of the interaction. The maximum values of the
after the onset of the considered time, as shown in Fig. 2c. Finally, the amount of squeezing and the amplitude of the oscillations decrease considerably when the interaction time increases, but the fluctuations increase substantially, as shown in Fig. 2d. When we take into account the dissipation term, the squeezing periods are only fully realized in one period at the start of the interaction. The maximum values of the 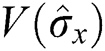 and
and 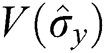 functions increase, and the amplitude of the vibrations decreases rapidly, as evident in Fig. 5d.
functions increase, and the amplitude of the vibrations decreases rapidly, as evident in Fig. 5d.
4 State Fidelity and Qubit-Qubit Entanglement
Next, we will analyze the degree of entanglement by employing fidelity since it is the primary criterion for measuring the entanglement of the system components [26–29]. Recently it has been found that the fidelity can measure the entanglement between parts of a system. It also plays an important role in quantum information in terms of estimating purity periods and partial entanglement [30]. The state fidelity of the present system can be written as
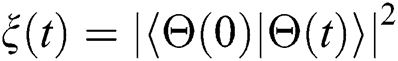
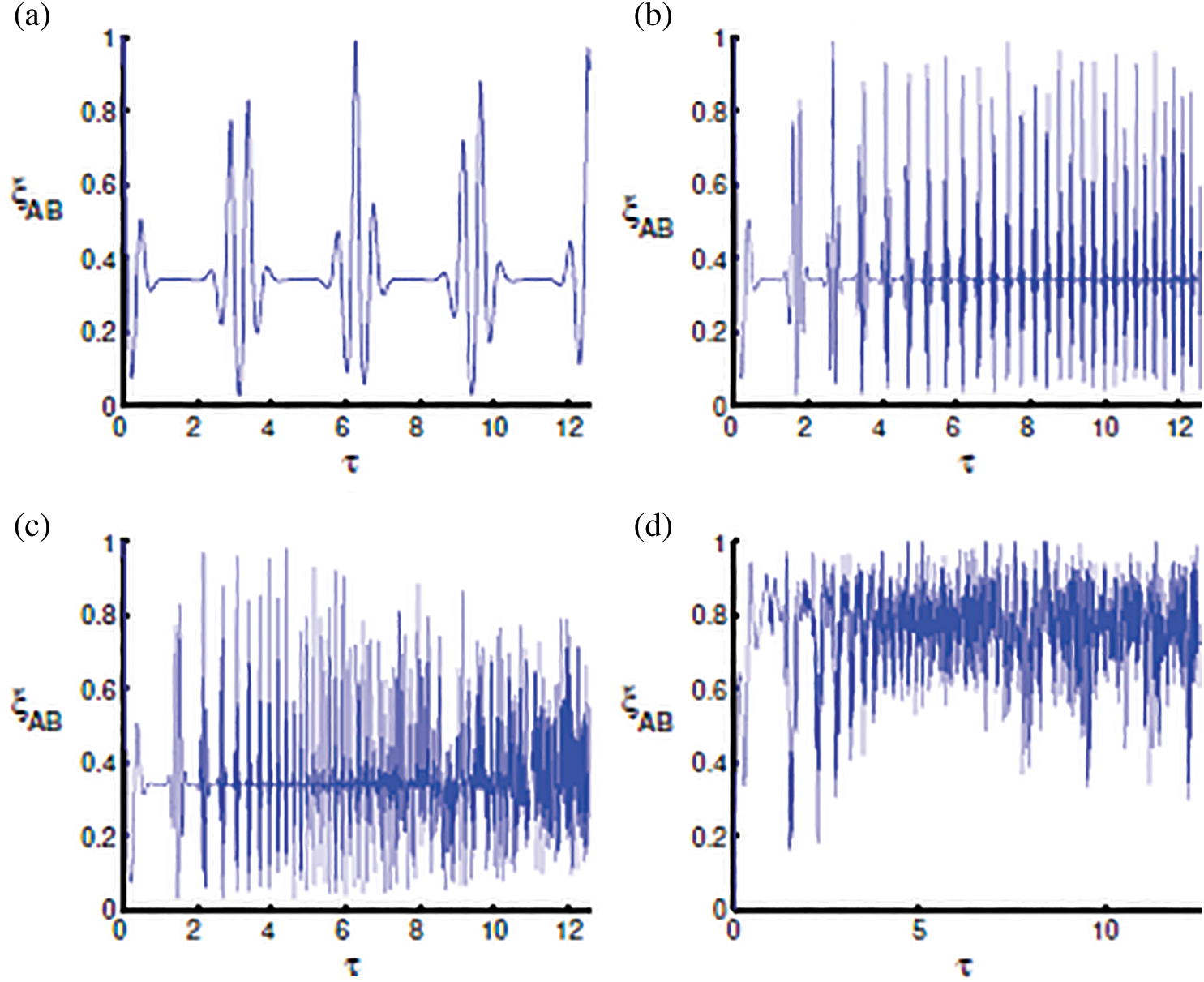
Figure 3: Fidelity as a function of the scaled time τ the other conditions are the same as those in Fig. 1
First, the case  and
and 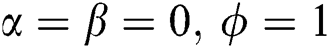 is considered. It is evident that the function
is considered. It is evident that the function 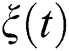 varies between 0 and 1, where fidelity starts from the pure state (
varies between 0 and 1, where fidelity starts from the pure state (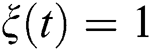 ) followed by partial entanglement. Then, the function
) followed by partial entanglement. Then, the function 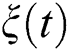 is fixed (stability) for a period, after which the function
is fixed (stability) for a period, after which the function 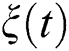 has periodically oscillations between the lower and higher values, as shown in Fig. 3a. For the case
has periodically oscillations between the lower and higher values, as shown in Fig. 3a. For the case  and
and 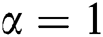 ,
, 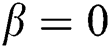 and
and 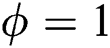 (velocity case), the oscillations increase, and the periods of the fixed intervals decrease. The results indicate that there are rapid fluctuations after adding the time dependence to the interaction cavity. Therefore, there is a strong entanglement between the parts of the system, as confirmed by Fig. 3b. While the oscillations of the function
(velocity case), the oscillations increase, and the periods of the fixed intervals decrease. The results indicate that there are rapid fluctuations after adding the time dependence to the interaction cavity. Therefore, there is a strong entanglement between the parts of the system, as confirmed by Fig. 3b. While the oscillations of the function 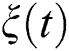 increase sharply, the maximum values decrease, and the smaller values gradually increase after taking into account the acceleration case
increase sharply, the maximum values decrease, and the smaller values gradually increase after taking into account the acceleration case 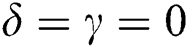 and
and 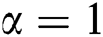 ,
, 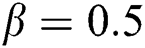 , and
, and 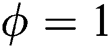 , as shown in Fig. 1c. After adding the detuning to the interaction cavity
, as shown in Fig. 1c. After adding the detuning to the interaction cavity 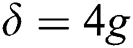 and
and 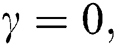
 ,
, 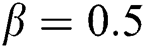 and
and 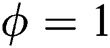 , the function
, the function 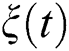 approaches the pure state compared to that of the previous cases, and the lower values increase. Thus, the entanglement decreases as expected from the effect of the detuning parameter, as shown in Fig. 3d. After the dissipation term is inserted into the interaction cavity, the maximum values decrease gradually over time. We also note that the correlation between parts of the system decreases until the function
approaches the pure state compared to that of the previous cases, and the lower values increase. Thus, the entanglement decreases as expected from the effect of the detuning parameter, as shown in Fig. 3d. After the dissipation term is inserted into the interaction cavity, the maximum values decrease gradually over time. We also note that the correlation between parts of the system decreases until the function  reaches the stability state, as is evident in Fig. 5c.
reaches the stability state, as is evident in Fig. 5c.
The quantum entanglement between the subsystems is useful in quantum computing and quantum information processing [31,32]. Using the Peres-Horodecki criterion, qubit-qubit entanglement is attained from the evolution of negativity [33,34]. In the following function
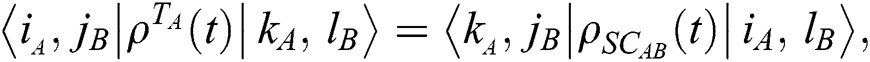
where  represents the partial transpose of
represents the partial transpose of  in terms of the first atom
in terms of the first atom 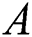 . Therefore, negativity takes the following form [35,36]
. Therefore, negativity takes the following form [35,36]
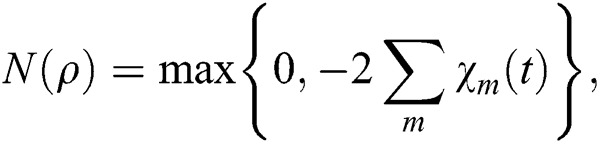

Figure 4: Negativity N(ρ) for the parameters utilized of Fig. 1
The sum is taken over each negative eigenvalue of  . The entanglement of the solid-state system takes place if
. The entanglement of the solid-state system takes place if 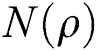 is positive. The state
is positive. The state  corresponds to the maximal entanglement, whereas
corresponds to the maximal entanglement, whereas 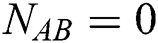 indicates that the atoms
indicates that the atoms 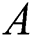 and
and 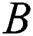 are not related.
are not related.
Using those same conditions of the previous sections, we first exclude the dissipation term, detuning, and time dependence for the velocity and acceleration. It is observed that the negativity oscillates periodically between 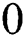 and the maximum value, and the
and the maximum value, and the 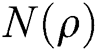 function reaches zero before and after the points
function reaches zero before and after the points 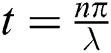 [5]. The results indicate that negativity reaches zero during the periods when the fidelity is fixed by comparing Figs. 3a and 4a. When adding the time dependence to the interaction cavity, we find that the fluctuations increase, and the oscillations become fast between the maximum and minimum values. This finding indicates that the entanglement between the qubits becomes significant for the case of time dependence (see Fig. 4b). The speed of the oscillations increases sharply, the smallest values increase, and the maximum values decrease after considering the acceleration, as seen in Fig. 4c. After adding the detuning to the interaction, the entanglement between the qubits decreases, and the center of the oscillations becomes approximately 0.25. After taking into account the dissipation term, negativity decreases gradually until it reaches its lowest value after some time as shown in Fig. 5d. In contrast, the way correlations behave can be greatly influenced by the selection of time dependence, especially the acceleration state and the parameter of dissipation term.
[5]. The results indicate that negativity reaches zero during the periods when the fidelity is fixed by comparing Figs. 3a and 4a. When adding the time dependence to the interaction cavity, we find that the fluctuations increase, and the oscillations become fast between the maximum and minimum values. This finding indicates that the entanglement between the qubits becomes significant for the case of time dependence (see Fig. 4b). The speed of the oscillations increases sharply, the smallest values increase, and the maximum values decrease after considering the acceleration, as seen in Fig. 4c. After adding the detuning to the interaction, the entanglement between the qubits decreases, and the center of the oscillations becomes approximately 0.25. After taking into account the dissipation term, negativity decreases gradually until it reaches its lowest value after some time as shown in Fig. 5d. In contrast, the way correlations behave can be greatly influenced by the selection of time dependence, especially the acceleration state and the parameter of dissipation term.
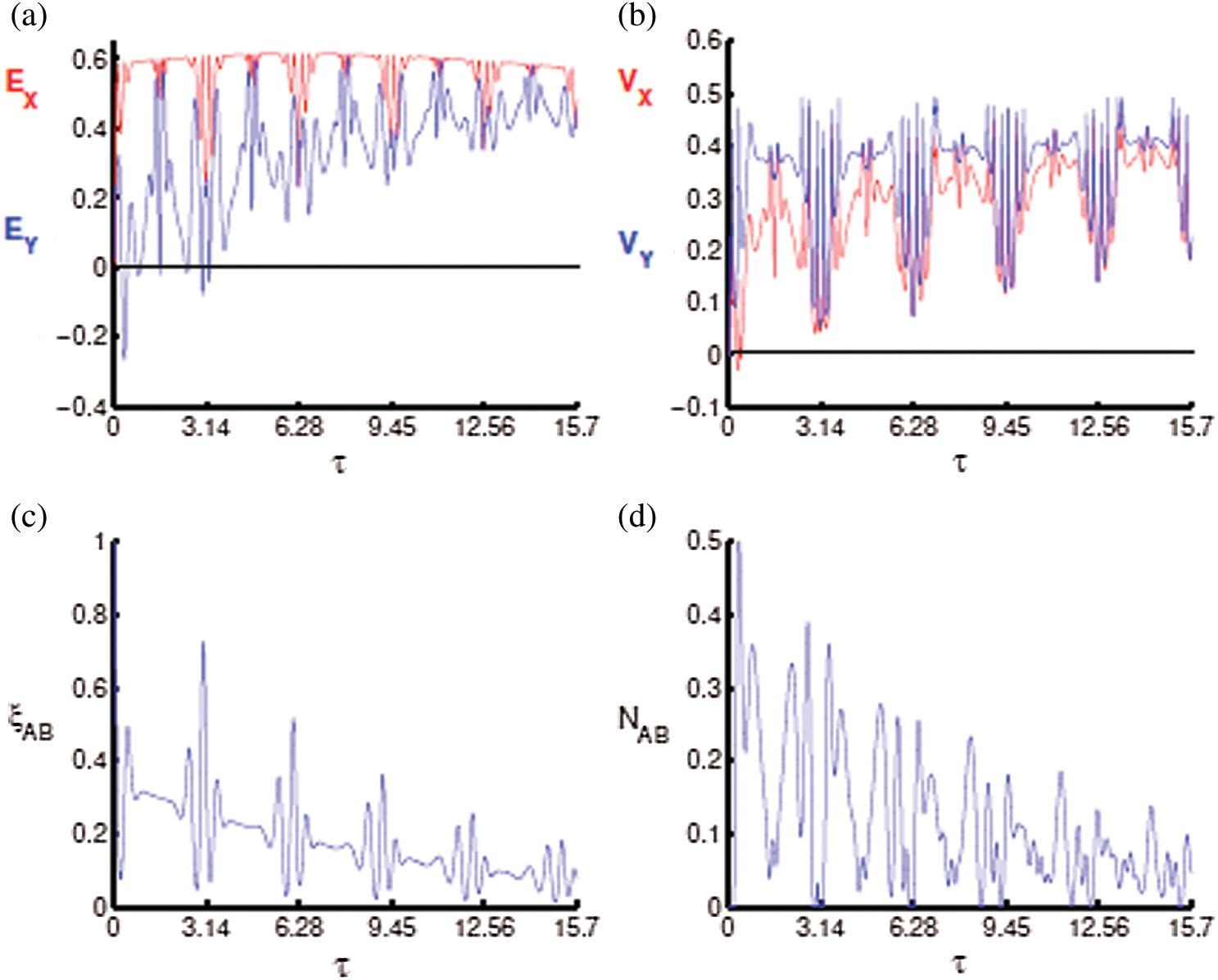
Figure 5: (a) Entropy squeezing, (b) variance squeezing, (c) fidelity and (d) negativity N(ρ) for the parameters δ = 0, α = β = 0, φ = 1, γ = 0.01
The effect of time dependence on a system containing two qubits within a cavity consisting of a pair of amplifier-type of electromagnetic fields in the presence of dissipation effect was studied. The constants of motion were calculated, and the general solution was obtained by solving the Schrödinger differential equations. The total density matrix was written via the wave function and was used to calculate and analyze the influence of the time dependence and the dissipation parameter on the entropy and variance squeezing. The results show that there was a superstructure between the atomic state fidelity and negativity based on a comparison of Figs. 3 and 4. Moreover, the degree of entanglement was proportional to the value of the time-dependent parameters. It was found that the degree of entanglement decreased after taking into account the detuning and time-dependent parameters. The dissipation parameter due to the interacting qubits and the electromagnetic field can be controlled, which helps improve and alleviate the correlation between the qubits during the interaction period. The ES and VS were examined. Furthermore, the squeezing phenomena occurred in the quadratures  and rarely occurred in the quadratures
and rarely occurred in the quadratures 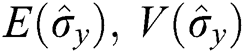 . The squeezing periods appeared after the start of the interaction and decreased quickly until disappearing after adding the dissipation term into the interaction cavity.
. The squeezing periods appeared after the start of the interaction and decreased quickly until disappearing after adding the dissipation term into the interaction cavity.
Acknowledgement: Taif University Researchers Supporting Project number (TURSP-2020/154), Taif University, Taif, Saudi Arabia.
Funding Statement: Taif University.
Conflicts of Interest: The authors declare that they have no conflicts of interest.
1. J. A. Wheeler and W. H. Zurek. (1983). Quantum theory and measurement. New Jersey: Princeton University Press. [Google Scholar]
2. M. Abdel-Aty and A. S. F. Obada. (2003). “Engineering entanglement of a general three-level system interacting with a correlated two-mode nonlinear coherent state,” European Physical Journal, vol. 23, pp. 155–165. [Google Scholar]
3. H. Moya-Cessa and A. Vidiella-Barranco. (1992). “Interaction of squeezed light with two-level atoms,” Journal of Modern Optics, vol. 39, no. 12, pp. 2481–2499. [Google Scholar]
4. S. Abdel-Khalek, S. H. A. Halawani and A. S. F. Obada. (2017). “Effect of time dependent coupling on the dynamical properties of the nonlocal correlation between two three-level atoms,” International Journal of Theoretical Physics, vol. 56, no. 9, pp. 2898–2910. [Google Scholar]
5. A. S. F. Obada, M. M. A. Ahmed, E. M. Khalil and S. I. Ali. (2013). “Entangled two two-level atoms interacting with a cavity field in the presence of the stark shift terms,” Optics Communications, vol. 287, pp. 215–223. [Google Scholar]
6. M. F. Fang, P. Zhou and S. Swain. (2000). “Entropy squeezing for a two-level atom,” Journal of Modern Optics, vol. 47, no. 6, pp. 1043–1053. [Google Scholar]
7. T. M. El-Shahat, S. Abdel-Khalek, M. Abdel-Aty and A. S. F. Obada. (2003). “Entropy squeezing of a degenerate two-photon process with a nonlinear medium,” Journal of Modern Optics, vol. 50, no. 13, pp. 2013–2030.
8. T. M. El-Shahat, S. Abdel-Khalek and A. S. F. Obada. (2005). “Entropy squeezing of a driven two-level atom in a cavity with injected squeezed vacuum,” Chaos Solitons & Fractals, vol. 26, no. 5, pp. 1293–1307.
9. M. S. Abdalla, E. M. Khalil, A. S. F. Obada, J. Peřina and J. Křepelka. (2017). “Linear entropy and squeezing of the interaction between two quantum system described by su (1,1) and su(2) Lie group in presence of two external terms,” AIP Advances, vol. 7, no. 1, 015013. [Google Scholar]
10. S. Abdel-Khalek, M. M. A. Ahmed and A. S. F. Obada. (2011). “New aspects of field entropy squeezing as an indicator for mixed state entanglement in an effective two-level system with stark shift,” Chinese Physics Letters, vol. 28, no. 12, 120305. [Google Scholar]
11. H. S. Alqannas and S. Abdel-Khalek. (2019). “Nonclassical properties and field entropy squeezing of the dissipative two-photon JCM under Kerr like medium based on dispersive approximation,” Optics & Laser Technology, vol. 111, pp. 523–529. [Google Scholar]
12. E. M. Khalil, M. S. Abdalla and A. S. F. Obada. (2010). “Pair entanglement of two-level atoms in the presence of a nondegenerate parametric amplifier,” Journal of Physics B: Quantum and Semiclassical Optics, vol. 43, no. 9, 095507. [Google Scholar]
13. E. M. Khalil, M. S. Abdalla, A. S. F. Obada and J. Perina. (2010). “Entropic uncertainty in two two-level atoms interacting with a cavity field in presence of degenerate parametric amplifier,” Journal of the Optical Society of America B, vol. 27, no. 2, pp. 266–276. [Google Scholar]
14. E. M. A. Hilal, S. Alkhateeb, S. Abdel-Khalek, E. M. Khalil and A. A. Almowalled. (2020). “Quantum scheme for N-level atom interacting with a two two-level atom: Atomic Fisher information and entropy squeezing,” Alexandria Engineering Journal, vol. 59, no. 3, pp. 1259–1264. [Google Scholar]
15. H. Eleuch and I. Rotter. (2017). “Resonances in open quantum systems,” Physical Review A, vol. 95, no. 2, 022117. [Google Scholar]
16. C. M. Bender. (2007). “Making sense of non-Hermitian Hamiltonians,” Reports on Progress in Physics, vol. 70, no. 6, pp. 947–1018. [Google Scholar]
17. S. Bose, V. Vedral and P. L. Knight. (1998). “Multiparticle generalization of entanglement swapping,” Physical Review A, vol. 57, no. 2, pp. 822–829. [Google Scholar]
18. G. S. Agarwal. (1988). “Nonclassical statistics of fields in pair coherent states,” Journal of the Optical Society of America B, vol. 5, no. 9, pp. 1940–1947. [Google Scholar]
19. A. Riccardi, C. Macchiavello and L. Maccone. (2017). “Tight entropic uncertainty relations for systems with dimension three to five,” Physical Review A, vol. 95, no. 3, 032109. [Google Scholar]
20. M. Christandl and A. Winter. (2005). “Uncertainty, monogamy, and locking of quantum correlations,” IEEE Transactions on Information Theory, vol. 51, no. 9, pp. 3159–3165.
21. E. M. Khalil and S. Abdel-Khalek. (2018). “Entangled two two-level atom in the presence of external classical fields,” International Journal of Theoretical Physics, vol. 57, no. 9, pp. 2615–2627.
22. M. S. Abdalla, A. S. F. Obada and S. Abdel-Khalek. (2008). “Entropy squeezing of time dependent single-mode Jaynes–Cummings model in presence of non-linear effect,” Chaos, Solitons & Fractals, vol. 36, no. 2, pp. 405–417.
23. E. M. Khalil, M. S. Abdalla and A. S. F. Obada. (2006). “Entropy and variance squeezing of two coupled modes interacting with a two-level atom: Frequency converter type,” Annals of Physics, vol. 321, no. 2, pp. 421–434. [Google Scholar]
24. A. Steane. (1998). “Quantum computing,” Reports on Progress in Physics, vol. 61, no. 2, pp. 117–173. [Google Scholar]
25. A. Galindo and M. A. Martin-Delgado. (2002). “Information and computation: Classical and quantum aspects,” Reviews Modern Physics, vol. 74, no. 2, pp. 347–423. [Google Scholar]
26. R. Loudon and P. L. Knight. (1987). “Squeezed light,” Journal of Modern Optics, vol. 34, no. 6, pp. 709–759. [Google Scholar]
27. S. J. D. Phoenix and P. L. Knight. (1991). “Establishment of an entangled atom-field state in the Jaynes-Cummings model,” Physical Review A, vol. 44, no. 9, pp. 6023–6029.
28. H. S. Alqannas and S. Abdel-Khalek. (2019). “Physical and nonclassical properties of the interaction between a four-level atom and field in coherent state of Morse potential,” Optical and Quantum Electronics, vol. 51, no. 3, pp. 1–12.
29. E. M. Khalil, M. S. Abdalla, A. S. F. Obada and J. Perina. (2010). “Entropic uncertainty in two two-level atoms interacting with a cavity field in presence of degenerate parametric amplifier,” Journal of the Optical Society of America B, vol. 27, no. 2, pp. 266–276. [Google Scholar]
30. D. Petrosyan, F. Motzoi, M. Saffman and K. Molmer. (2017). “High-fidelity Rydberg quantum gate via a two-atom dark state,” Physical Review A, vol. 96, no. 4, 042306. [Google Scholar]
31. H. P. Breuer and F. Petruccione. (2002). The theory of open quantum systems. Oxford: Oxford University Press, ; H. Carmichael, An open systems approach to quantum optics. Berlin: Springer, 1993. [Google Scholar]
32. E. M. Khalil. (2007). “Generation of a nonlinear two-mode stark shift via nondegenerate Raman transition,” International Journal of Modern Physics B, vol. 21, no. 30, pp. 5143–5154. [Google Scholar]
33. A. Peres. (1996). “Separability criterion for density matrices,” Physical Review Letters, vol. 77, no. 8, pp. 1413–1415. [Google Scholar]
34. P. Horodecki. (1997). “Separability criterion and inseparable mixed states with positive partial transposition,” Physics Letters A, vol. 232, no. 5, pp. 333–339. [Google Scholar]
35. G. Vidal and R. F. Werner. (2002). “Computable measure of entanglement,” Physical Review A, vol. 65, no. 3, 032314. [Google Scholar]
36. E. M. Khalil, S. Abdel-Khalek and S. Al-Awfi. (2018). “Entanglement of an su(1, 1) quantum system interacting with a single two-level atom in the presence of damping terms,” Journal of Russian Laser Research, vol. 39, no. 5, pp. 505–513. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |