DOI:10.32604/cmc.2021.013389
| Computers, Materials & Continua DOI:10.32604/cmc.2021.013389 | |
| Article |
Trade-Off between Efficiency and Effectiveness: A Late Fusion Multi-View Clustering Algorithm
1National University of Defence Technology, Changsha, China
2Department of Mathematics, Faculty of Science, University of Sargodha, Sargodha, Pakistan
*Corresponding Author: Jianzhuang Lu. Email: lujz1977@163.com
Received: 05 August 2020; Accepted: 12 September 2020
Abstract: Late fusion multi-view clustering (LFMVC) algorithms aim to integrate the base partition of each single view into a consensus partition. Base partitions can be obtained by performing kernel k-means clustering on all views. This type of method is not only computationally efficient, but also more accurate than multiple kernel k-means, and is thus widely used in the multi-view clustering context. LFMVC improves computational efficiency to the extent that the computational complexity of each iteration is reduced from 
to 
(where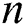 
is the number of samples). However, LFMVC also limits the search space of the optimal solution, meaning that the clustering results obtained are not ideal. Accordingly, in order to obtain more information from each base partition and thus improve the clustering performance, we propose a new late fusion multi-view clustering algorithm with a computational complexity of 
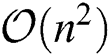. Experiments on several commonly used datasets demonstrate that the proposed algorithm can reach quickly convergence. Moreover, compared with other late fusion algorithms with computational complexity of 
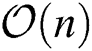, the actual time consumption of the proposed algorithm does not significantly increase. At the same time, comparisons with several other state-of-the-art algorithms reveal that the proposed algorithm also obtains the best clustering performance.
Keywords: Late fusion; kernel k-means; similarity matrix
Many real-world datasets are naturally made up of different representations or views. Given that these multiple representations often provide compatible and complementary information, it is clearly preferable to integrate them in order to obtain better performance rather than relying on a single view. However, because data represented by different views can be heterogeneous and biased, the question of how to fully utilize the multi-view information in order to obtain a consensus representation for clustering purposes remains a challenging problem in the field of multi-view clustering (MVC). In recent years, various kinds of algorithms have been developed to provide better clustering performance or higher efficiency; these include multi-view subspace clustering [1–3], multi-view spectral clustering [4–6], and multiple kernel k-means (MKKM) [7–11]. Among these, MKKM has been widely utilized due to its excellent clustering performance and strong interpretability.
Depending on the stage of multi-view data fusion involved, the existing literature on MVC can be roughly divided into two categories. The first category, which can be described as ‘early fusion’, fuses the information of all views before clustering. Huang et al. [7] optimize an optimal kernel matrix as a linear combination of a set of pre-specified kernels for clustering purposes. To reduce the redundancy of the pre-defined kernels, Liu et al. [10] propose an MKKM algorithm with matrix-induced regularization. To further enhance the clustering performance, a local kernel alignment criterion is adopted for MKKM in [10]; moreover, the algorithm proposed in [11] allows the optimal kernel to be found in the neighbor of the combinational kernels, which increases the search space of the optimal kernel.
Although the above-mentioned early fusion algorithms have greatly improved the clustering accuracy of MKKM in different respects, they also have two drawbacks that should not be overlooked. The first of these is the more intensive computational complexity, i.e., usually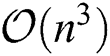 
per iteration (where 
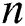is the number of samples). The second relates to the over-complicated optimization processes of these methods, which increase the risk of the algorithm becoming trapped in bad local minimums and thus lead to unsatisfying clustering performance.
The second category, which is termed as ‘late fusion’, maximizes the alignment between the consensus clustering indicator matrix and the weighted base clustering indicator matrices with orthogonal transformation, in which each clustering indicator matrix is generated by performing clustering on each single view [12,13]. This type of algorithm can improve the efficiency and clustering performance; however, these methods also simplify the search space of the optimal clustering indicator matrix, which decreases clustering performance.
Accordingly, in this paper, we propose a new late fusion framework designed to extract more information from the base clustering indicator matrix. We first assume that each base clustering indicator matrix is a feature representation after the sample is mapped from the original space to the feature space. Compared with the original features, this involves nonlinear relations between data [14]; moreover, this approach can also filter out some noise arising from the kernel matrix. Therefore, the similarity matrix constructed by the base clustering indicator matrix is superior to the original kernel matrix for clustering purposes.
We refer to the proposed method as ‘late fusion multi-view clustering with learned consensus similarity matrix’ (LF-MVCS). LF-MVCS jointly optimizes the combination coefficient of the base clustering indicator matrices and the consensus similarity matrix. This consensus similarity matrix is then used as the input of spectral clustering [15] to obtain the final result. Furthermore, we design an effective algorithm for solving the resulting optimization problem, as well as analyzing its computational complexity and convergence. Extensive experiments on 10 multi-view benchmark datasets are then conducted to evaluate the effectiveness and efficiency of our proposed method.
The contributions of this paper can be summarized as follows:
• The proposed LF-MVSC integrates the information of all views in a late fusion manner. It further optimizes the combination coefficient of each base clustering indicator matrix and consensus similarity matrix. To the best of our knowledge, this is the first time that a unified form has been obtained that can better reflect the similarity between samples via late fusion.
• The proposed optimization formulation has just one parameter to tune and avoids excessive time consumption. We therefore design an alternate optimization algorithm with proved convergence that can efficiently tackle the resultant problem. Our algorithm avoids complex computation owing to fewer optimization variables being utilized, meaning that that the objective function can converge within fewer iterations.
Let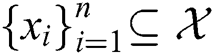 
be a dataset consisting of n samples, while
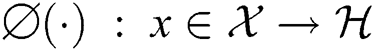is the feature mapping, which transfers 
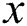into a reproducing kernel Hilbert space 
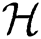. Kernel k-means clustering aims to minimize the sum-of-squares loss over the cluster assignment matrix 
, which can be formulated as follows:
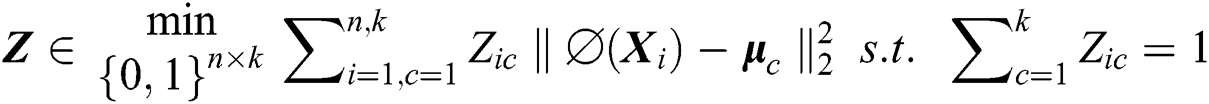
Here,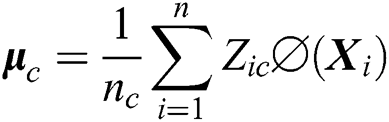 
is the centroid of the 
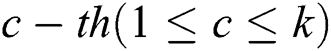cluster, while 
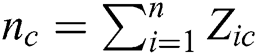is the number of samples in the corresponding cluster.
In order to optimize Eq. (1), we can transform it as follows:
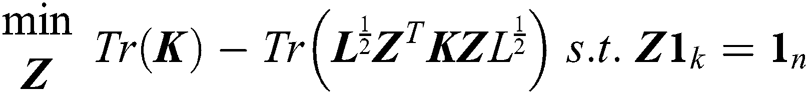
where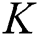 
is a kernel matrix with 
,
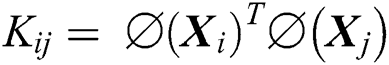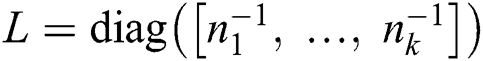, while 
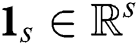denotes a vector with all elements being 1. In Eq. (2), the variables 
are discrete, which makes the optimization problem difficult to solve. Dhillon et al. [16] let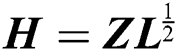 
and relaxed 
to take the arbitrary real values 
. Thus, Eq. (2) can be rewritten as follows:
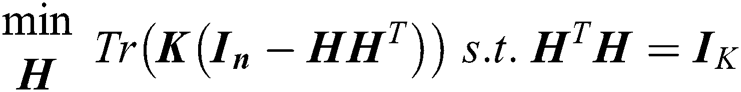
Here,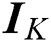 
is an identity matrix with size 
. Due to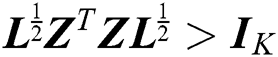 
, we impose an orthogonality constraint on 
. Finally, the optimal 
for Eq. (3) can be obtained by taking the k eigenvectors corresponding to the k largest eigenvalues of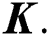 
The Lloyd’s algorithm is usually executed on 
for the clustering labels.
In multiple kernel k-means (MKKM), all samples have multiple feature representations via a group of feature mappings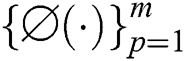 
. More specifically, each sample can be represented as 
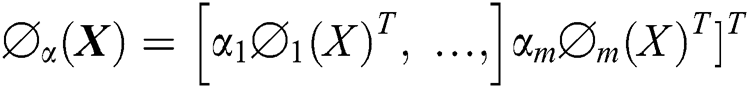, where 
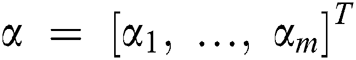are the coefficients of each base kernel. The kernel function over the above feature mappings can be written as:
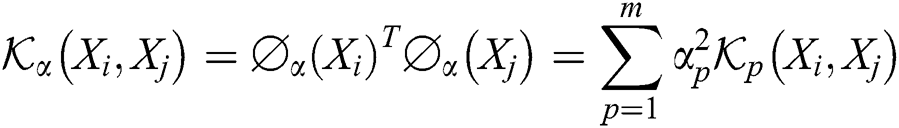
Assume that the optimal kernel matrix can be represented as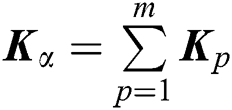 
, we obtain the optimization objective of MKKM as follows:
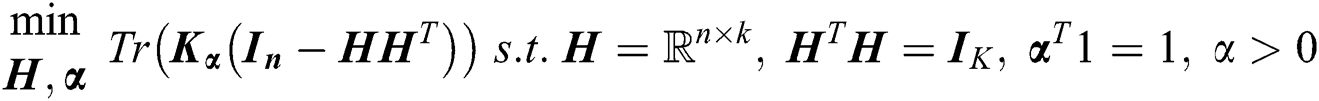
A two-step iterative algorithm can be used to optimize the Eq. (5). i) Optimize α with fixed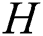 
. Eq. (5) is equivalent to:
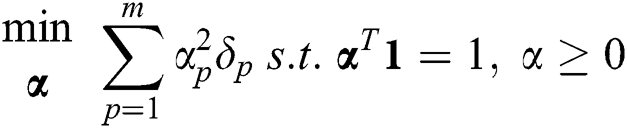
where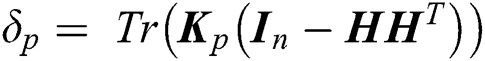 
. According to the Cauchy-Schwartz inequality, we can obtain the closed-form solution to Eq. (6) as 
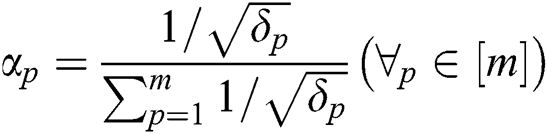. ii) Optimize 
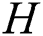with fixed α. With the kernel coefficients α fixed, 
can be optimized by taking the k eigenvectors corresponding to the k largest eigenvalues of 
.
2.2 Multi-View Clustering via Late Fusion Alignment Maximization
Multi-view clustering via late fusion alignment maximization [12] (MVC-LFA) assumes that the clustering indicator matrix obtained from each single view is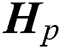 
(
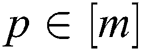), while a set of rotation matrices 
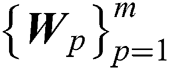are used to maximize the alignment of 
(
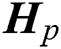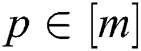) and the optimal clustering indicator matrix 
. The objective function is as follows:
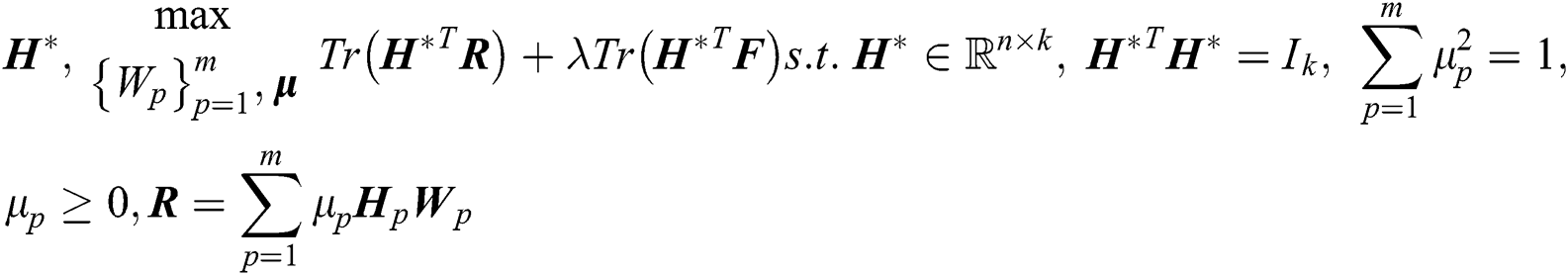
where F denotes the average clustering indicator matrix, while λ is a trade-off parameter. Moreover,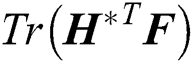 
is a regularization of the optimal clustering indicator matrix that prevents 
from being too far away from the prior average partition. This formula assumes that the optimal clustering indicator matrix 
is a linear combination of the base clustering indicator matrix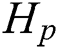 
(
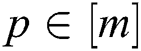). Readers are encouraged to refer to [12] for more details regarding the optimization of Eq. (7).
The drawback of MKKM is its excessive computational complexity, which is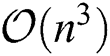 
. Although MVC-LFA does reduce the computational complexity from 
to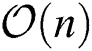 
, it also over-simplifies the search space of the optimal solution, which in turn limits the clustering performance. We therefore propose a novel late fusion multi-view clustering algorithm in Section Three, which offers a trade-off between clustering efficiency and effectiveness.
3 Multi-View Clustering Via Late Fusion Consensus Similarity Matrix
By taking the eigenvectors corresponding to the first k largest eigenvalues of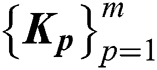 
, we can obtain the clustering indicator matrices 
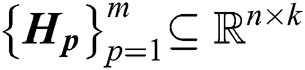. Each row of 
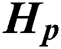can be regarded as a feature representation of each sample in the k dimension space. To construct the consensus similarity matrix 
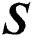, we need to construct the similarity matrix of each view. After normalizing each row of 
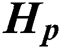(i.e., dividing by the 2-norm of the row), the 2-norm of each row of the processed 
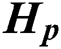becomes 1. We treat 
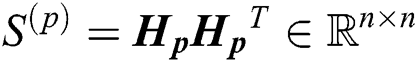as the similarity matrix of the p-th view.
Based on the assumption that the optimal consensus similarity matrix resides in the neighbor of a linear combination of all similarity matrices, our model can be expressed as follows:
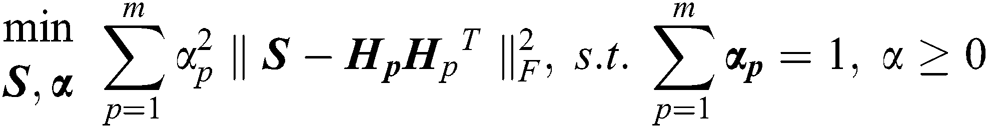
The solution to the above formula is clearly equal to a certain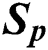 
, such that multi-view information is not fully utilized. Accordingly, inspired by [9], we introduce a regularization item capable of improving the diversity of all views for learning purposes. We let 
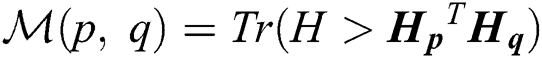. A larger 
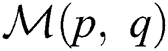is associated with a higher degree of correlation between the p-th and q-th points. Let 
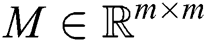be the matrix that stores diversified information of views, while 
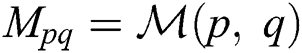. Thus, when 
is large, to avoid the information redundancy caused by similar views, we can set the coefficient of view such that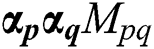 
is small. Based on the above, we add the following regularization item to the formula:
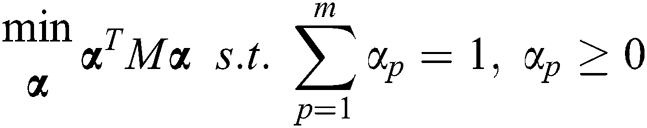
At the same time, we aim to have S satisfy the basic properties of the similarity matrix. Hence, we impose certain constraints on S, namely: i) The degree of each sample in S is greater than or equal to 0, i.e., Sij ≥ 0; ii) The degree of each sample in S is equal to 1, i.e., 
. We can accordingly obtain the following formula:
Not only can the clustering indicator matrices obtained by KKM, but also the similar basic partitions constructed by any clustering algorithms, be the input of our model. The model developed thus far represents a new multi-view clustering framework based on late fusion. Compared to other late fusion algorithms, such as [12,13], our objective formula has three key advantages, namely:
Fewer variables need to be optimized, meaning that the total number of iterations is reduced and the algorithm converges quickly.
Other late fusion algorithms hold that the optimal clustering indicator matrix is a neighbor of the average clustering indicator matrix; however, this is a heuristic assumption that may not hold true in some cases. By contrast, our assumptions in Eq. (9) are more reasonable and will be effective in any multi-view clustering task.
We further introduce a regularization item to measure the correlation of views in order to increase both the diversity and the utilization rate of multi-view information.
In the following, we construct an efficient algorithm designed to solve the optimization problem in Eq. (9). More specifically, we design a two-step algorithm to alternately solve the following:
Optimization α with fixed S.
When S is fixed, the optimization problem in Eq. (9) is equivalent to the following optimization problem:
Here, 
. Moreover, 
is a nonnegative definite matrix, meaning that the optimization in Eq. (10) w.r.t α is a quadratic programming problem with linear constraint. We can solve this using the Matlab QP toolkit.
Optimization S with fixed α.
When α is fixed, the optimization problem in Eq. (9) w.r.t S can be rewritten as follows:
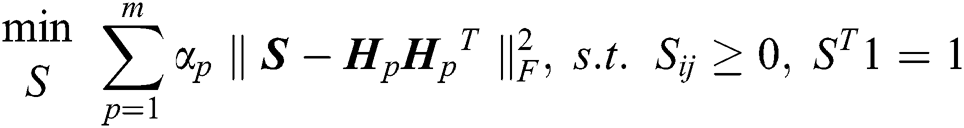
Note that the problem in Eq. (11) is independent of the value of j, meaning that we can optimize each column of S as follows:
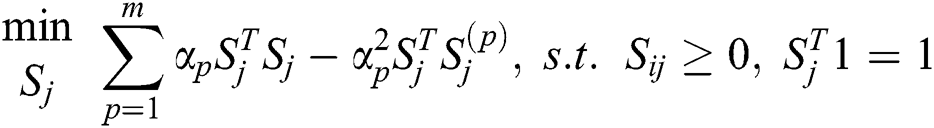
where 
is the j-th column of 
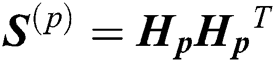. Eq. (12) is equivalent to the following function:
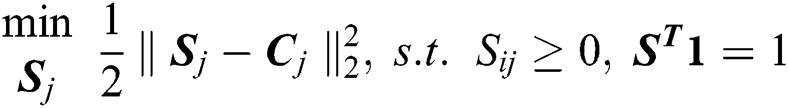
Here,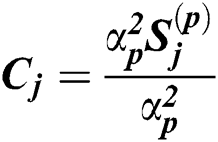 
. Eq. (13) is a problem on the simplex space, and its Lagrangian function is as follows:
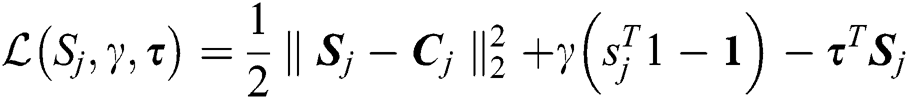
where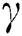 
and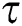 
are the Lagrangian multipliers.
According to its Karush-Kuhn-Tucker condition [17], we can obtain the optimal solution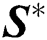 
in the form of Eq. (15):
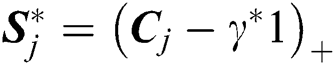
Here,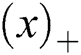 
is a signal function, which sets the elements of x that are less than 0 to 0, while 
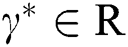makes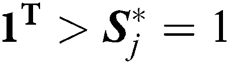 
.
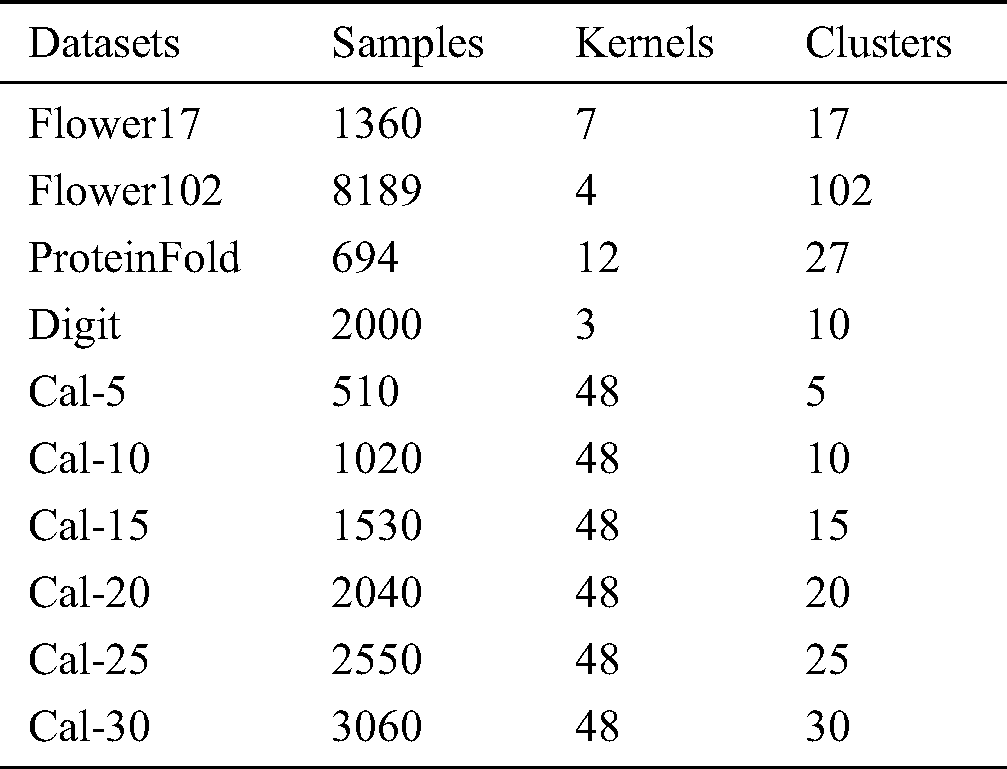
The algorithm is summarized in detail in Algorithm 1.
3.3 Complexity and Convergence
Computational Complexity. Obtaining the base clustering indicator matrices requires calculating the eigenvectors corresponding to the k largest eigenvalues of the m kernel matrices, leading to a complexity of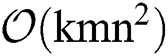 
. The proposed iterative algorithm further requires the optimization of the two variables α and S. In each iteration, the optimization of α via Eq. (10) requires the solving of a standard quadratic programming problem with linear constraint, the complexity of which is 
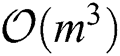. Updating each sj by Eq. (13) requires 
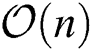time. Moreover, the complexity associated with obtaining S is 
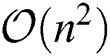per iteration, as n times are needed to calculate each sj. Overall, the total complexity of Algorithm 1 is 
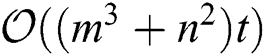, where 
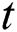is the number of iterations. Finally, executing the standard spectral clustering algorithm on S takes 
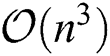time.
Convergence. In each of the optimization iterations of our proposed algorithm, the optimizations of α and S monotonically decrease the value of the objective Eq. (9). Moreover, this objective is also lower-bounded by zero. Consequently, our algorithm is guaranteed to converge to the local optimum of Eq. (9).
4.1 Datasets and Experimental Settings
Several benchmark datasets are utilized to demonstrate the effectiveness of the proposed method: namely, Flower17 (www.robots.ox.ac.uk/∼vgg/data/flowers/17/), Flower102 (www.robots.ox.ac.uk/∼vgg/data/flowers/102/), PFold (mkl.ucsd.edu/dataset/protein-fold-prediction), Digit (http://ss.sysu.edu.cn/py/), and Cal (www.vision.caltech.edu/Image Datasets/Caltech101/). Six sub-datasets, which are constructed by selecting the first 5, 10, 15, 20, 25 and 30 classes respectively from the Cal data, are also used in our experiments. More detailed information regarding these datasets is presented in Tab. 1. From this table, we can observe that the number of samples, views and categories of these datasets range from 510 to 8189, 3 to 48, and 5 to 102, respectively.
4.2 Comparison with State-of-the-Art Algorithms
In our experiments, LF-MVCS is compared with several state-of-the-art multi-view clustering methods, as outlined below.
Average multiple kernel k-means (A-MKKM): The kernel matrix, which is a linear combination of the base kernels with the same coefficients, is taken as the input of the standard kernel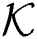 
-means algorithm.
Single best kernel k-means (SB-KKM): Stardard kernel k-means is performed on each single kernel, after which the best result is outputted.
Multiple kernel k-means (MKKM) [7]: The algorithm jointly optimizes the consensus clustering indicator matrix and the kernel coefficients.
Robust multiple kernel k-means (RMKKM) [18]: RMKC learns a robust low-rank kernel for clustering by capturing the structure of noise in multiple kernels.
Multiple kernel k-means with matrix-induced regularization (MKKM-MR) [9]: This algorithm introduces a matrix-induced regularization designed to reduce the redundancy of the kernels and enhance their diversity.
Optimal neighborhood kernel clustering with multiple kernels (ONKC) [11]: ONKC allows the optimal kernel to reside in the neighborhood of linear combination of base kernels, thereby effectively enlarging the search space of the optimal kernel.
Multi-view clustering via late fusion alignment maximization (MVC-LFA) [12]: MVC-LFA proposes maximally aligning the consensus clustering indicator matrix with the weighted base clustering indicator matrix.
Simple multiple kernel k-means (SMKKM) [19]: SimpleMKKM, or SMKKM, re-formulates the MKKM problem as a minimization-maximization problem in the kernel coefficients and the consensus clustering indicator matrix.
Figure 1: ACC, NMI and purity comparison with variations in number of classes on Cal. (left) ACC; (mid) NMI; (right) purity
In our experiments, all base kernels are first centered and then normalized; therefore, for all samples xi and the p-th kernel, we have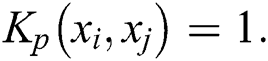 
For all datasets, the true number of clusters is known, and we set this to be the true number of classes. In addition, the parameters of RMKKM, MKKM-MR and MVC-LFA are selected by grid search according to the methods suggested in their respective papers. For the proposed algorithm, its regularization parameters λ are chosen from a large enough range 
by means of grid search. We set the allowable error 
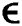to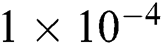 
, which is the termination condition of Algorithm 1.
The widely used metrics of clustering accuracy (ACC), normalized mutual information (NMI) and purity are applied to evaluate the clustering performance of each algorithm. For all algorithms, we repeat each experiment 50 times with random initialization (to reduce randomness caused by k-means in the final spectral clustering) and report the average result. All experiments are performed on a desktop with Intel(R) Core(TM)-i7-7820X CPU and 64 GB RAM.
Figure 2: Runtime of different algorithms on eight benchmark datasets (in seconds). The experiments are conducted on a PC with Intel(R) Core(TM)-i7-7820X CPU and 64 GB RAM in the MATLAB environment. LF-MVCS is comparably fast relative to the alternatives while also providing superior performance when compared with most other multiple kernel k-means based algorithms. Results for other datasets are omitted due to space limitations
Figure 3: The objective value of our algorithm on four datasets at each iteration
Tab. 2 reports the clustering performance of the above-mentioned algorithms on all datasets. From these results, we can make the following observations:
First, the proposed algorithm consistently demonstrates the best NMI on all datasets. For example, it exceeds the second-best method (MVC-LFA) by over 8.56% on Flower17. The superiority of our algorithm is also confirmed by the ACC and purity reported in Tab. 2.
Table 1: Empirical evaluation and comparison of SimpleMKKM with eight baseline methods on 11 datasets in terms of clustering accuracy (ACC), normalized mutual information (NMI) and purity
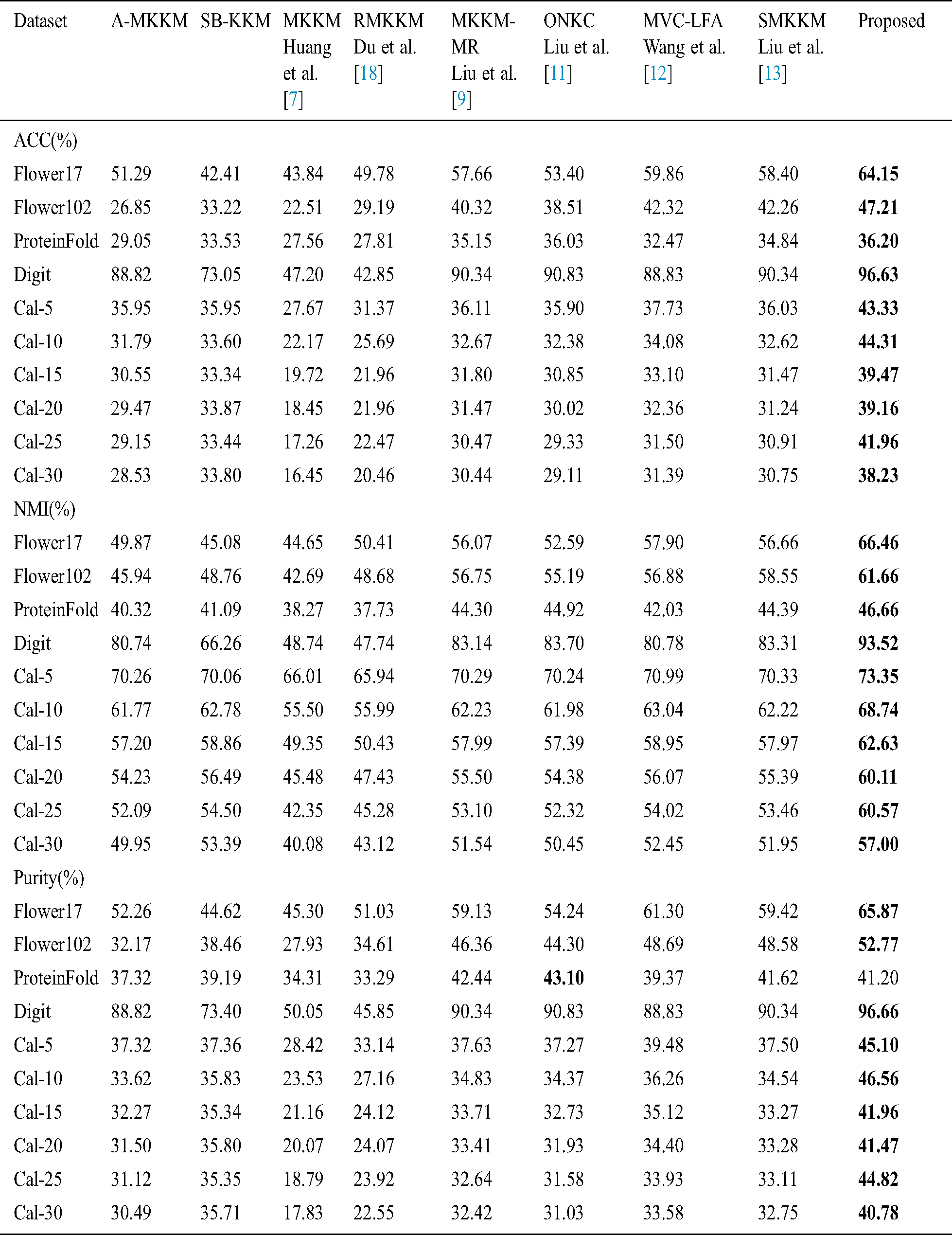
As a strong baseline, the recently proposed SMKKM [19] outperforms other comparison early-fusion multiple kernel clustering methods. However, the proposed algorithm significantly and consistently outperforms SMKKM by 9.80%, 3.11%, 2.27%, 10.21%, 3.02%, 6.52%, 4.66%, 4.72%, 7.11% and 5.05% respectively in terms of NMI on all datasets in the order listed in Tab. 1.
The late fusion algorithm MVC-LFA also outperforms most other algorithms; however, the proposed algorithm outperforms MVC-LFA by 8.56%, 4.78%, 4.63%, 12.74%, 2.36%, 5.70%, 3.68%, 4.04%, 6.55% and 4.55% respectively in terms of NMI on all datasets in the order listed in Tab. 1.
We further study the clustering performance on Cal for each algorithm depending on the number of classes, as shown in Fig. 1. As can be observed from the figure, our algorithm is consistently at the top of all sub-figures when the number of classes varies, indicating that it achieves the best performance.
In summary, our proposed LF-MVCS demonstrates superior clustering performance over all SOTA multi-view clustering algorithms. From the above experiments, we can therefore conclude that the proposed algorithm effectively learns the information from all base clustering indicator matrices, bringing significant improvements to the clustering performance.
4.5 Runtime, Convergence and Parameter Sensitivity
Figure 4: Illustration of parameter sensitivity against λ. The red curves represent the results of the proposed algorithm, while the blue lines indicate the second-best performance on the corresponding dataset
Runtime. To investigate the computational efficiency of the proposed algorithm, we record the running time of various algorithms on the benchmark datasets and report them in Fig. 2. The computational complexity of the proposed LF-MVCS is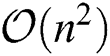 
; as can be observed, LF-MVCS has slightly higher computational complexity than the existing MVC-LFA (with a computational complexity of 
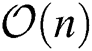). At the same time, however, the runtime of LF-MVCS is lower relative to with other kernel-based multi-view clustering algorithms.
Algorithm Convergence. We next theoretically analyze the convergence of our algorithm. Fig. 3 reflects the variation of the objective Eq. (9) with the number of iterations on four datasets: namely, Flower17, ProteinFold, Digit, and Cal-30. It can be seen that the objective function achieves convergence over very few iterations, thereby demonstrating that fewer optimization variables can make the algorithm converge faster, which makes our algorithm more efficient than other algorithms.
Parameter Sensitivity. The proposed algorithm introduces one hyper-parameter, i.e., the balancing coefficient of the diversity regularization item λ. The performance variation against λ is illustrated in Fig. 4. As the figure shows: i) λ is effective in improving the algorithm performance; ii) It also achieves good performance over a wide range of parameter settings.
Algorithm 1: Late fusion multi-view clustering with learned consensus similarity matrix
This paper proposes a simple but effective algorithm, LF-MVCS, which learns a consensus similarity matrix from all base clustering indicator matrices. We determine that each base clustering indicator matrix is a better feature representation than the original feature and kernel. Based on this finding, we derive a simple novel optimization goal for multi-view clustering, which learns a consensus similarity matrix to facilitate better clustering performance. The proposed algorithm is developed to efficiently solve the resultant optimization problem. LF-MVCS outperforms all SOTA methods significantly in terms of clustering performance. Moreover, our algorithm also reduces the computational cost on benchmark datasets when compared with other kernel-based multi-view clustering methods. In future work, we plan to extend our algorithm to a general framework, then use this framework as a platform to revisit existing multi-view algorithms in order to further improve the fusion method.
Funding Statement:This paper and research results were supported by the Hunan Provincial Science and Technology Plan Project. The specific grant number is 2018XK2102. Y. P. Zhao, W. X. Liang, J. Z. Lu and X. W. Chen all received this grant.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Gao, F. Nie, X. Li and H. Huang. (2015). “Multi-view subspace clustering,” in Proc. of the IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 4238–4246. [Google Scholar]
2. C. Zhang, Q. Hu, H. Fu, P. Zhu and X. Cao. (2017). “Latent multi-view subspace clustering,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPRHonolulu, HI, USA, pp. 4333–4341.
3. C. Zhang, H. Fu, Q. Hu, X. Cao, Y. Xie et al. (2020). , “Generalized latent multi-view subspace clustering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 1, pp. 86–99. [Google Scholar]
4. A. Kumar, P. Rai and H. Daume. (2011). “Co-regularized multi-view spectral clustering,” in Advances in Neural Information Processing Systems, Granada, Spain, pp. 1413–1421. [Google Scholar]
5. Y. Li, F. Nie, H. Huang and J. Huang. (2015). “Large-scale multi-view spectral clustering via bipartite graph,” in Proc. of the Twenty-Ninth AAAI Conf. on Artificial Intelligence, Austin, Texas, USA, pp. 2750–2756.
6. S. Zhou, X. Liu, J. Liu, X. Guo, Y. Zhao et al. (2020). , “Multi-view spectral clustering with optimal neighborhood laplacian matrix,” in Proc. of the Thirty-Fourth AAAI Conf. on Artificial Intelligence, New York, NY, USA, pp. 6965–6972. [Google Scholar]
7. H. Huang, Y. Chuang and C. Chen. (2012). “Multiple kernel fuzzy clustering,” IEEE Transactions on Fuzzy Systems, vol. 20, no. 1, pp. 120–134. [Google Scholar]
8. M. Gonen and A. A. Margolin. (2014). “Localized data fusion for kernel k-means clustering with application to cancer biology,” in Advances in Neural Information Processing Systems, Ambridge, MA, USA, pp. 1305–1313.
9. X. Liu, Y. Dou, J. Yin, L. Wang and E. Zhu. (2016). “Multiple kernel k-means clustering with matrix-induced regularization,” in Proc. of the Thirtieth Conf. on Artificial Intelligence, Phoenix, Arizona, USA, pp. 1888–1894. [Google Scholar]
10. M. Li, X. Liu, L. Wang, Y. Dou, J. Yin et al. (2016). , “Multiple kernel clustering with local kernel alignment maximization,” in Proc. of the Twenty-Fifth Int. Joint Conf. on Artificial Intelligence, New York, NY, USA, pp. 1704–1710. [Google Scholar]
11. X. Liu, S. Zhou, Y. Wang, M. Li, Y. Dou et al. (2017). , “Optimal neighborhood kernel clustering with multiple kernels,” in Proc. of the Thirty-First Conf. on Artificial Intelligence, San Francisco, California, USA, pp. 2266–2272. [Google Scholar]
12. S. Wang, X. Liu, E. Zhu, C. Tang, J. Liu et al. (2019). , “Multi- view clustering via late fusion alignment maximization,” in Proc. of the Twenty-Eighth Int. Joint Conf. on Artificial Intelligence, Macao, China, pp. 3778–3784. [Google Scholar]
13. X. Liu, M. Li, C. Tang, J. Xia, J. Xiong et al. (2020). , “Efficient and effective regularized incomplete multi-view clustering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, no. 3, pp. 3778–3784. [Google Scholar]
14. B. Schölkopf, A. Smola and K. R. Müller. (1998). “Nonlinear component analysis as a kernel eigenvalue problem,” Neural Computation, vol. 10, no. 5, pp. 1299–1319. [Google Scholar]
15. A. Y. Ng, M. I. Jordan and Y. Weiss. (2002). “On spectral clustering: Analysis and an algorithm,” in Advances in Neural Information Processing Systems, Cambridge, MA, United States, pp. 849–856. [Google Scholar]
16. I. Dhillon, Y. Guan and B. Kulis. (2004). “Kernel k-means: Spectral clustering and normalized cuts,” in Proc. of the Tenth ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, New York, NY, USA, pp. 551–556. [Google Scholar]
17. S. Boyd and L. Vandenberghe. (2004). “Basic properties and examples, operations that preserve convexity, optimization problems, & convex optimization, ” in Convex Optimization, Sao Paolo (ed.vol. 1. London, UK: Cambridge University Press, pp. 67–142. [Google Scholar]
18. L. Du, P. Zhou, L. Shi, H. Wang, M. Fan et al. (2015). , “Robust multiple kernel k-means using l21-norm,” in Twenty-Fourth Int. Joint Conf. on Artificial Intelligence, Buenos Aires, Argentina, pp. 3476–3482. [Google Scholar]
19. X. Liu, E. Zhu and J. Liu. (2020). “Simplemkkm: Simple multiple kernel k-means,” in Proc. of the 37th Int. Conf. on Machine Learning, Vienna, Austria, pp. 1–10. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |