DOI:10.32604/cmc.2021.012471
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012471 | |
| Article |
Nanofluid Flows Within Porous Enclosures Using Non-Linear Boussinesq Approximation
1Department of Mathematics, College of Science, King Khalid University, Abha, 62529, Saudi Arabia
2Department of Mathematics, South Valley University, Qena, 83523, Egypt
3Mathematics Department, College of Science, Jouf University, Sakaka, Saudi Arabia
4Electrical Engineering Department, College of Engineering, Prince Sattam Bin Abdulaziz University, Wadi Addwasir, 11991, Saudi Arabia
5Electrical Engineering Department, Aswan University, Aswan, 81542, Egypt
*Corresponding Author: Sameh E. Ahmed. Email: sehassan@kku.edu.sa
Received: 01 July 2020; Accepted: 20 October 2020
Abstract: In this paper, the Galerkin finite element method (FEM) together with the characteristic-based split (CBS) scheme are applied to study the case of the non-linear Boussinesq approximation within sinusoidal heating inclined enclosures filled with a non-Darcy porous media and nanofluids. The enclosure has an inclination angle and its side-walls have varying sinusoidal temperature distributions. The working fluid is a nanofluid that is consisting of water as a based nanofluid and Al2O3 as nanoparticles. The porous medium is modeled using the Brinkman Forchheimer extended Darcy model. The obtained results are analyzed over wide ranges of the non-linear Boussinesq parameter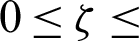 
1, the phase deviation 
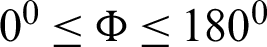, the inclination angle 
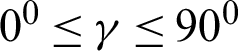, the nanoparticles volume fraction 
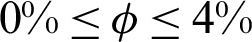, the amplitude ratio 
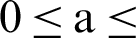1 and the Rayleigh number 
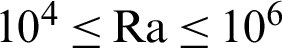. The results revealed that the average Nusselt number is enhanced by 0.73%, 26.46% and 35.42% at 
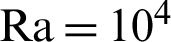, 105 and 106, respectively, when the non-linear Boussinesq parameter is varied from 0 to 1. In addition, rate of heat transfer in the case of a non-uniformly heating is higher than that of a uniformly heating. Non-linear Boussinesq parameter rises the flow speed and heat transfer in an enclosure. Phase deviation makes clear changes on the isotherms and heat transfer rate on the right wall of an enclosure. An inclination angle varies the flow speed and it has a slight effect on heat transfer in an enclosure.
Keywords: CBS scheme; non-linear Boussinesq approximation; non-uniformly heating; non-darcy flow; nanofluid
Recently, the problem of the convective flow in closed cavities with different thermal boundary conditions has been receiving many attentions. The non-uniform heating on the active walls is resulting from various factors such as the collection of solar energy and the cooling of electronic components [1–4]. In the literature, there are several cases of the non-uniform temperature distribution on the walls. Sivasankaran et al. [5] considered the distributions of the sinusoidal temperature on the convective flow of a nanofluid with variations on the amplitude and phase deviation of the sinusoidal temperature. Deng et al. [6] studied the case of two spatially varying sinusoidal temperature on vertical side walls of a rectangular enclosure. Ahmed et al. [7] presented the effects of the non-uniform temperature variations on magnetohydrodynamic (MHD) mixed convection in an inclined cavity. Roy et al. [8] used FEM method to study the effects of the uniform and non-uniform heating wall on natural convection flows. Aly et al. [9] adopted ISPH method to simulate two different cases of sinusoidal heated and isothermal walls on mixed convection flow in lid-driven cavity.
In the literatures, most of the studies working on the natural convection using Boussinesq approximation due to its rapid convergence and easy implementation. De Vahl Davis [10] introduced benchmark results for laminar flow in a square cavity. The comparison between Boussinesq approximation and Non-Boussinesq approximation was introduced by Nilesh et al. [11] and Szewc et al. [12]. Srinivasacharya et al. [13] examined the impacts of the non-linear Boussinesq approximation on the micropolar boundary layer flow with non-Newtonian heating. They noted that in the Darcy flow, the heat and mass transfer rate is more affected by the non-linear parameter compared with the non-Darcy case. Elshehabey et al. [14] used the non-linear Boussinesq approximation to study the magnetohydrodynamic flow within wavy geometries using the ferrofluids. The used scheme is based on the finite element method. They found that the non-linear parameter enhances the rate of the heat transfer while the average Bejan number is reduced. Kameswaran et al. [15] studied the effects of the non-linear Boussinesq approximation on non-Darcy nanofluid flow over a vertical wavy surface. Vasu et al. [16] considered the influences of nonlinear Boussinesq approximation on unsteady mixed flow of a nanofluid over a sphere. Kandaswamy et al. [17] used finite difference scheme to study the buoyancy–-driven nonlinear convection in a cavity with considering magnetic field effects. There are several applications from fluid flows through porous media including geothermal energy systems and oil recovery. In the recent years, there are numerous studies focused on the flow and heat transfer inside cavities filled with porous medium and nanofluids [18–26]. Alsabery et al. [27] studied numerically the natural convection flow of a nanofluid-filled inclined cavity consisting of a porous layer and a nanofluid layer.
From our investigations, there are no attempts focused on coupling between non-linear Boussinesq approximation and a non-Darcy porous media within sinusoidal heating inclined enclosures. Hence, this paper introduces a numerical study using CBS scheme [28–32] for investigating the impacts of sinusoidal heating on a non-linear Boussinesq approximation within inclined porous enclosure filled with nanofluids. In this study, the water is treated as a base fluid and Al2O3 is treated as nanoparticles. Brinkman Forchheimer extended Darcy model is used to treat the porous medium. The finding results showed that the average Nusselt number is enhanced by 0.73%, 26.46% and 35.42% at Ra = 104, 105 and 106, when the non-linear Boussinesq parameter is varied from 0 to 2. The case of non-uniformly heating gives more enhancements on the rate of heat transfer compared to the case of uniformly heating.
Fig. 1 presents an initial schematic diagram for the current physical model. Here, the square cavity has length H and it is inclined with an angle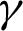 
. The assumptions of the current work are:
• The sinusoidal heating of the left and right walls are expressed as, respectively: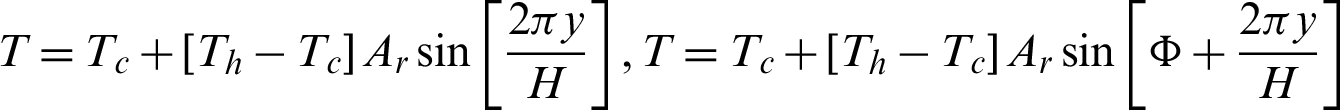 
where 
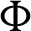is the phase deviation. In addition, the horizontal walls are considered to be adiabatic.
• The gravity acceleration vector is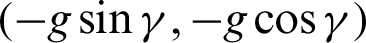 
.
• The current unsteady flow is laminar and incompressible. The base fluid is water with molecules diameter df = 0.385 nm and Al2O3 is the nanoparticles with diameter dp = 33 nm.
• The nanoparticles are considered to be having a uniform shape and equally size.
• The density is treated by the non-linear Boussinesq approximation and the other thermos-physical properties of nanofluid are constants.
• Brinkman Forchheimer extended Darcy is used to model the porous medium.
• There is a case of a local thermal equilibrium between the nanofluid and porous medium.
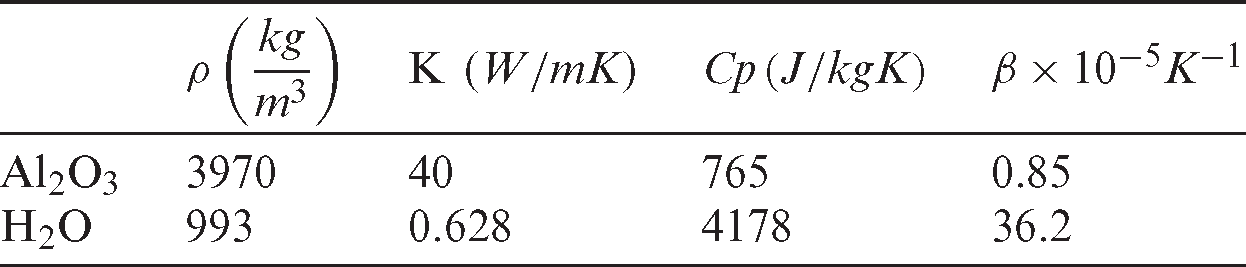
• The thermophysical properties of base fluid and nanoparticles are presented in Tab. 1.
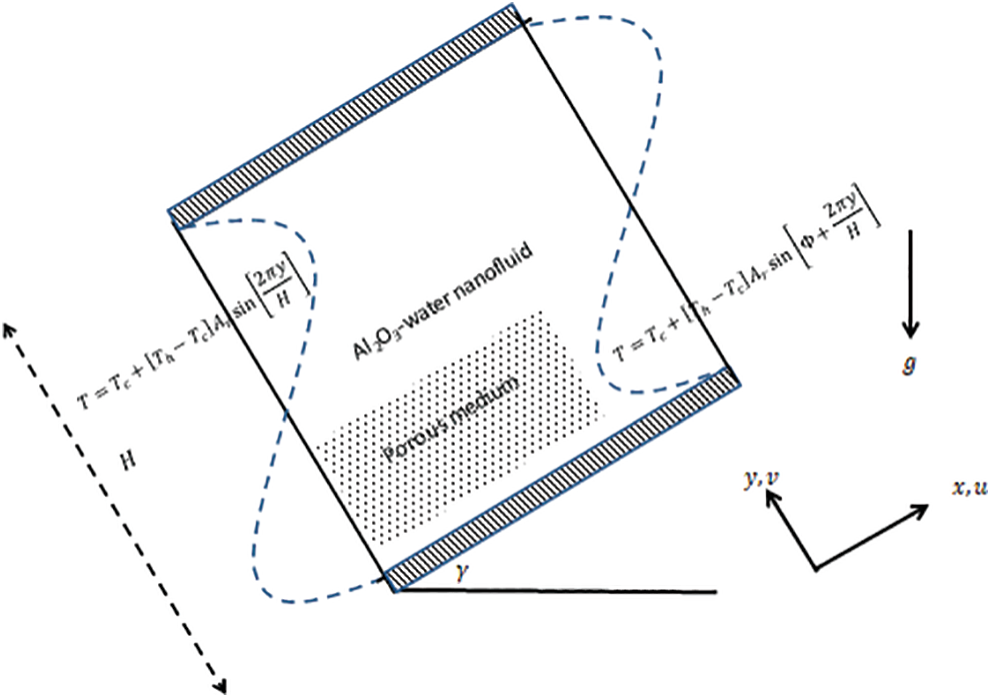
Figure 1: Physical model and coordinates system
Table 1: Thermo-physical properties of water and nanoparticles at T = 310 K
Taking into account all the previous assumptions, the partial differential equations governing this physical mode are expressed as:
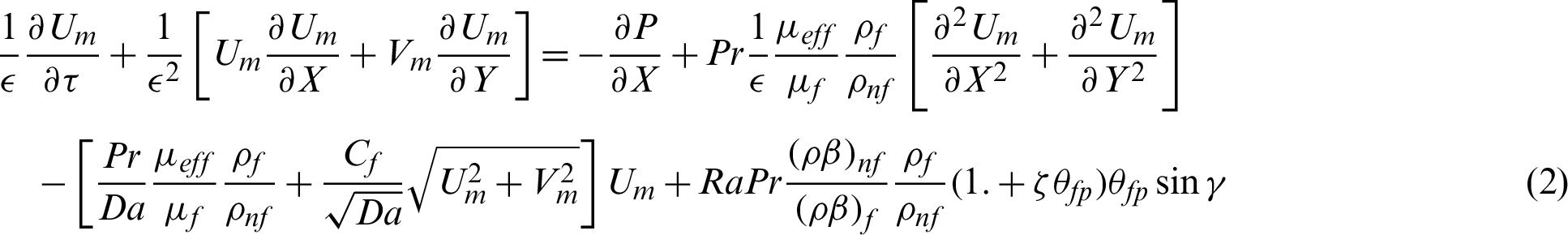
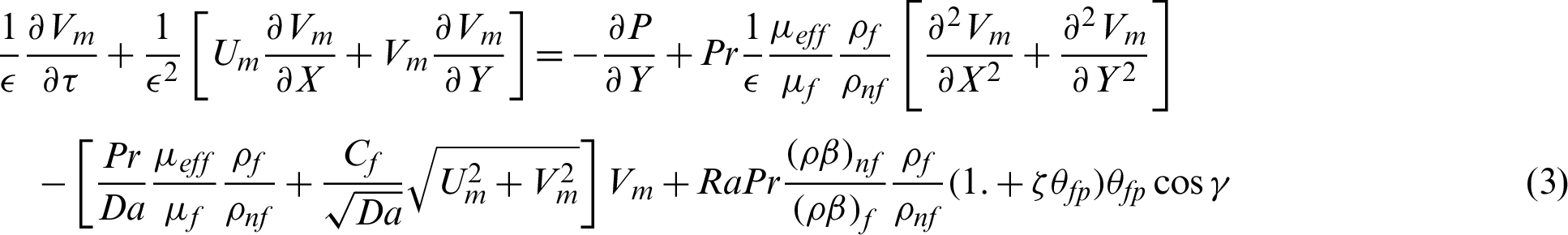
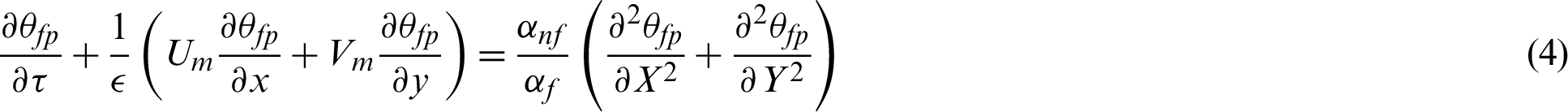
In the above system, (Um, Vm) are the velocity components in the (X, Y)directions,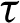 
is the dimensionless time parameter, 
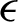is the porosity, 
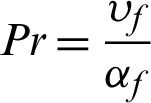is the Prandtl number, 
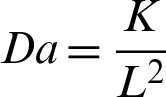is the dimensionless Darcy number, 
is the non-linear Boussinesq parameter and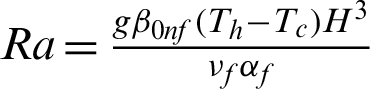 
is the Rayleigh number. Further, the initial and boundary conditions are given by:
For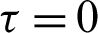 
: U = V = 0, 
: 
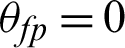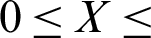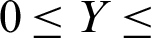1, 
1
For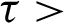 
0: U = V = 0, 
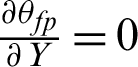: Y = 0 and 1
U = V = 0,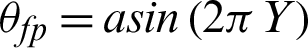 
: X = 0
where a is the amplitude of the sinusoidal heating. Here, it should be mentioned that the following dimensionless variables are used to get the previous dimensionless system:
There are numerous correlations for the nanofluids simulations were presented in the lectures. To get more realistic simulation, the thermophysical properties are expressed as functions of the nanoparticles volume fraction and diameters of the molecules of H2O and Al2O3. Following the experimental study presented by Corcione [33], the following correlations are introduced:
In the above equations, Tfr is the freezing point of water, 
is the Brownian velocity, 
is the Boltzmann’s constant,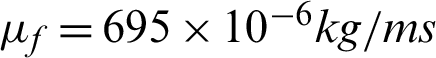 
is the dynamic viscosity of water. The local Nusselt numbers are calculated at the both left NuL and right NuR walls, those formulas are expressed as:
However, the average Nusselt numbers are calculated only on the heated parts of both side walls, as:
To obtain the numerical solutions for the current system, the characteristic-based split (CBS) scheme presented in Lewis et al. [34] is applied. This scheme consists of four steps; those are expressed as follows:
Step 1: Calculate the intermediate velocities:
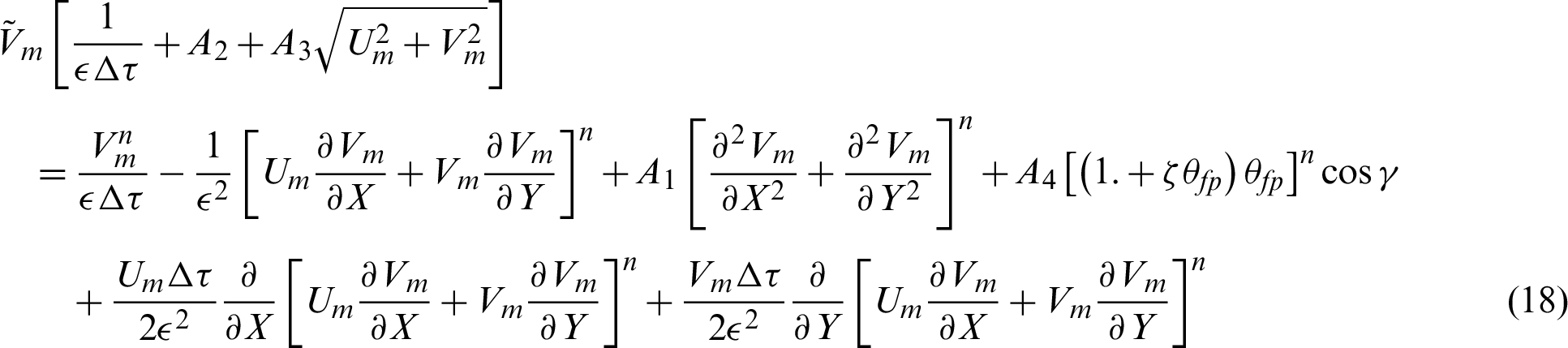
Step 2: Pressure calculations:
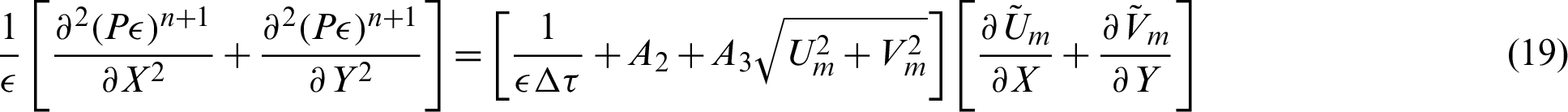
Step 3: Velocity corrections:
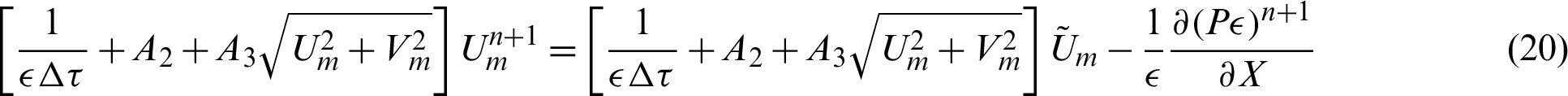
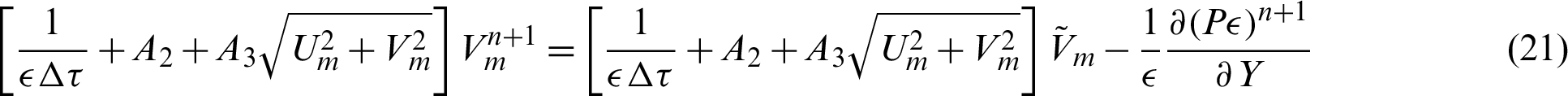
Step 4: Temperature calculations:
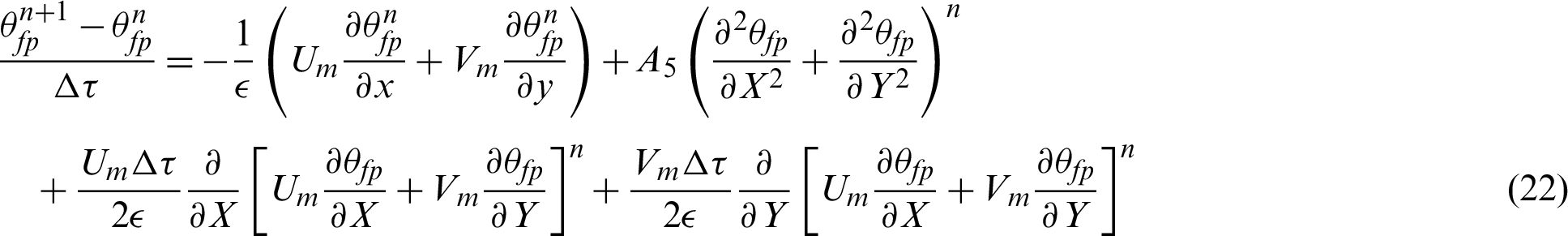
where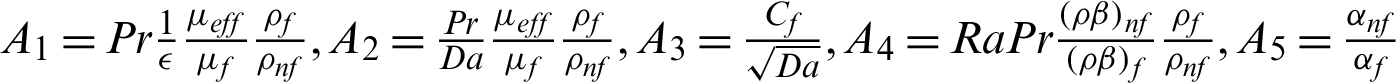 
.
Now, the Galerkin finite element method is applied to solve the previous equations. Firstly, Fig. 2 shows the mesh generation of the present model. In addition the dependent variables are expanding in terms of the shape function as:
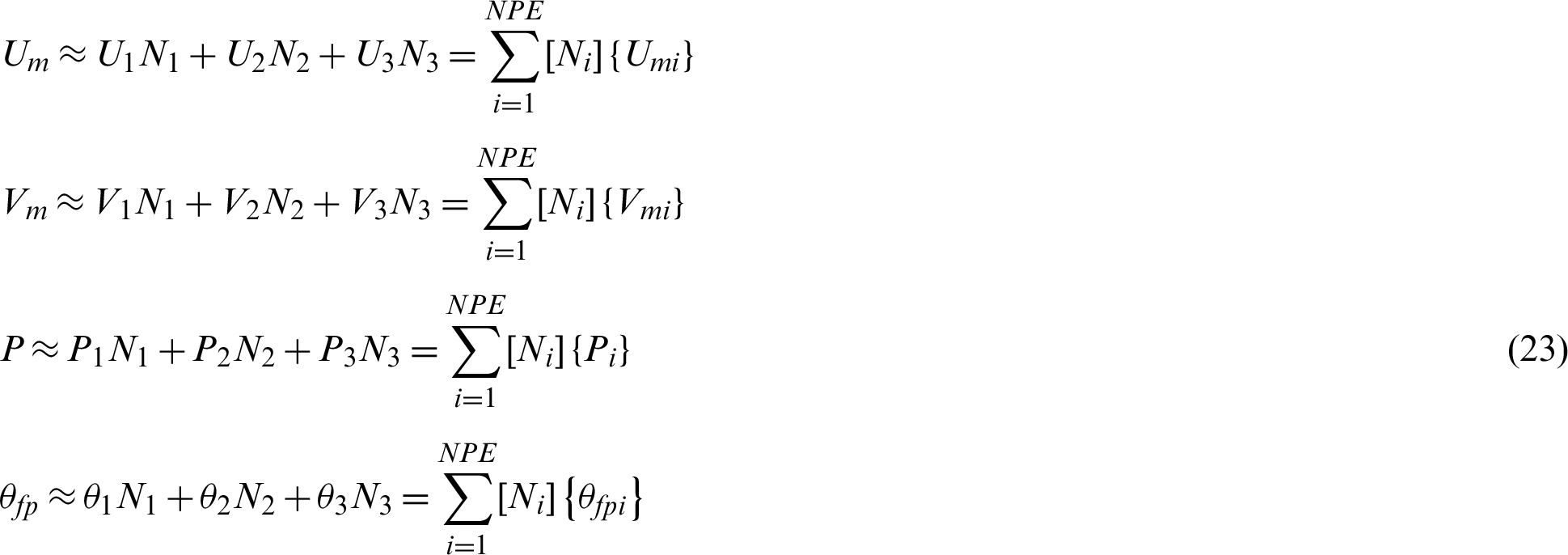
where NPE refers to the node per element. A triangular-shaped element is used in this study with an area given by:
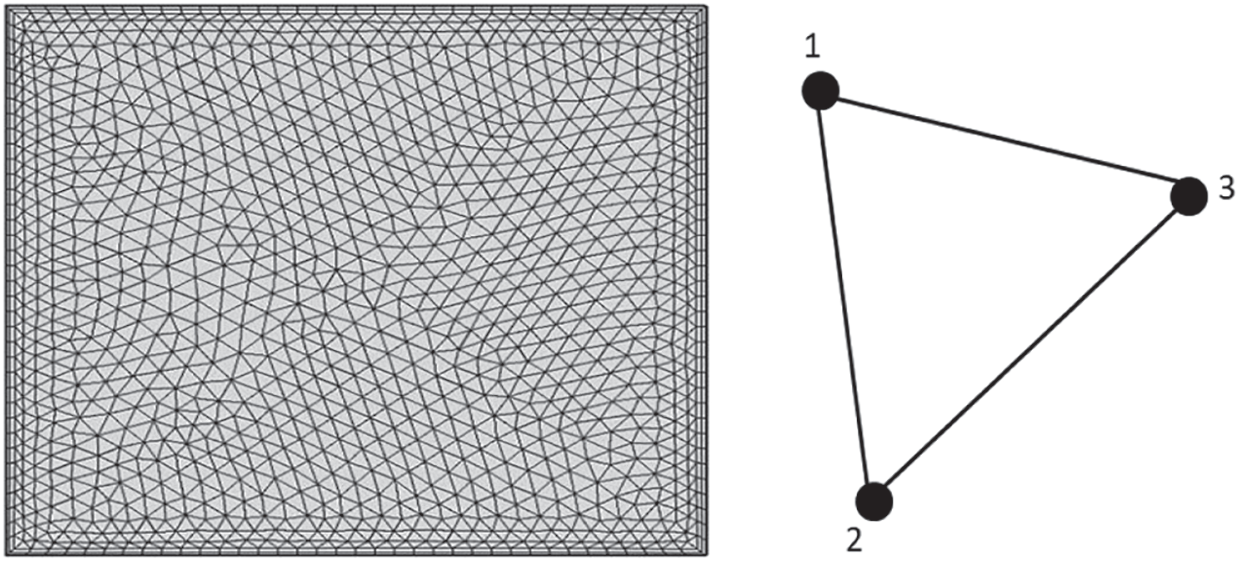
Figure 2: Mesh generation of the present physical model
The finite element discretization of the left hand side of Eqs. (17) and (18) is given by:
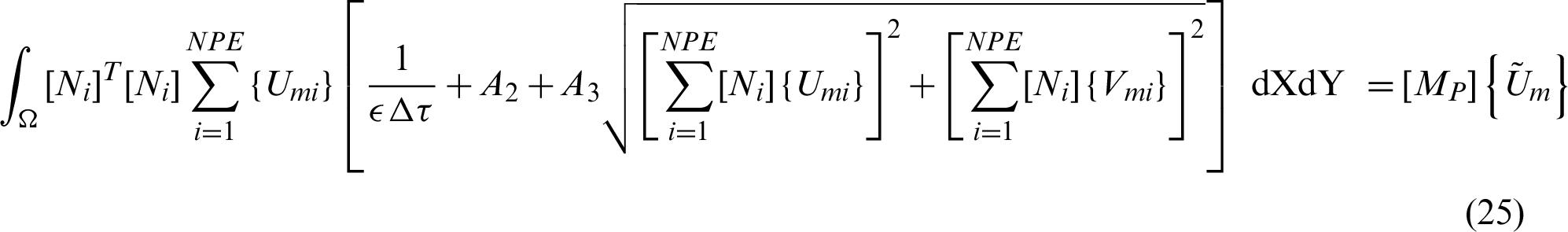
where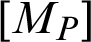 
is the mass matrix, which is given by:
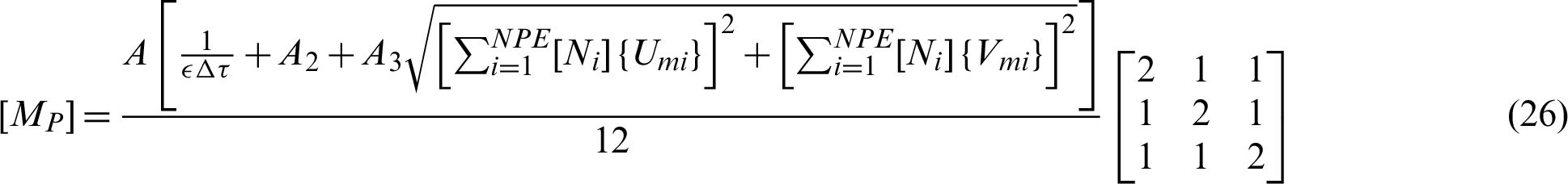
Here, as it stated by Corcione [33], the mass matrix is ‘lumped’ due to interesting in the steady state solutions as:
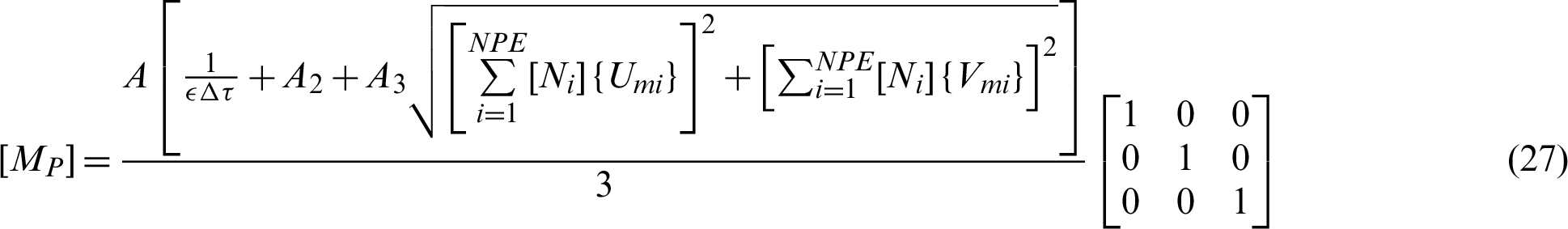
Further, details of the time step calculations, the shape functions and the convergence criteria are found in the valuable book presented by Corcione [33].
The accuracy of the current scheme is examined by valuable comparisons with previously published results. Fig. 3 presents a comparison between the present study and those obtained by Sivasankaran et al. [35] at 
. In Fig. 3, the formed four circular cells from the streamlines contours at phase deviation 
are almost similar between the current results and results of Sivasankaran et al. [35]. Then, the current numerical scheme, CBS scheme in FEM method, gives a well agreement with the previous published data.
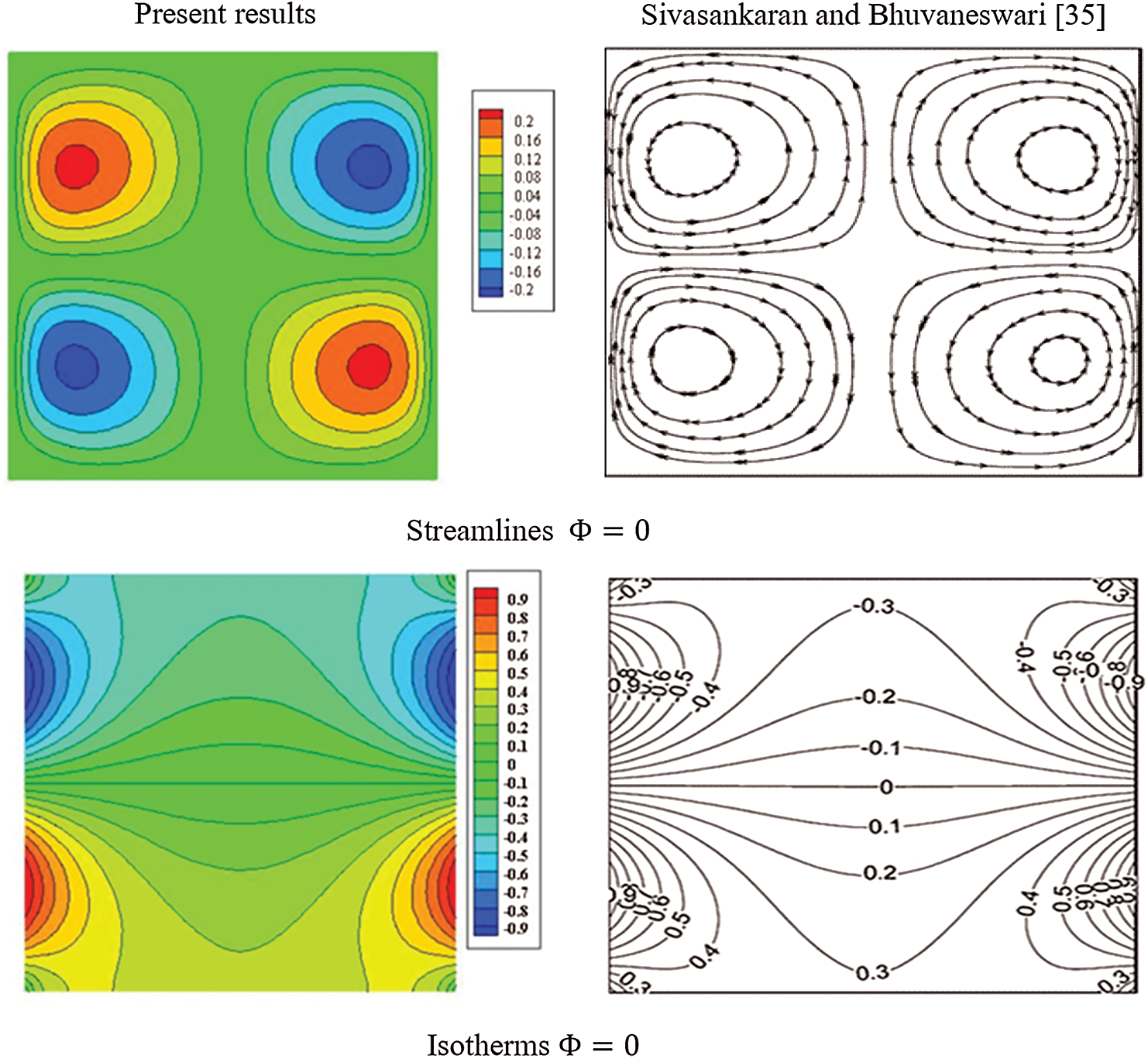
Figure 3: Comparison of the present study and those obtained by Sivasankaran et al. [35] at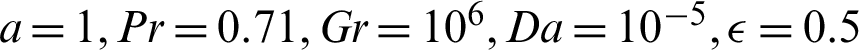 
In this section, the numerical results for impacts of the non-uniformly heating on the unsteady natural convection in an inclined cavity filled with a non-Darcy porous medium and nanofluids are discussed. The wide ranges of the current physical parameters are the Rayleigh number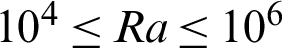 
, the amplitude ratio 
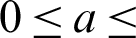1, the non-linear Boussinesq parameter 
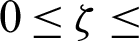2, the phase deviation 
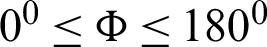, the inclination angle 
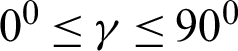and the nanoparticles volume fraction 
.
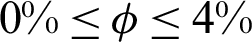Firstly, the impacts of the phase deviation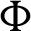 
on the streamlines and isotherms contours are introduced in Fig. 4. It is seen that, the formed cells of the streamlines contours inside the enclosure are varied according to the variations in the phase deviation 
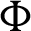. In addition, the values of the minimum and maximum of the stream function are strongly depended on the phase deviation 
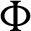. An increase of 
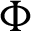from 0 to 
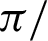2 causes that the maximum of the stream function decreases by 20.68% and the minimum of the stream function decreases from −1.5 to −2.4. The main contributions of the phase deviation on the isotherms contours appear on the right side of the cavity wall, since the phase deviation is involved in the right sinusoidal heating, only. The phase deviation 
changes the distributions of isothermal lines, while the isothermal lines on the left side remain fixed without changes. Then, the uniform distribution of the isothermal lines between the left and right walls are varied according to the variations of the phase deviation 
.
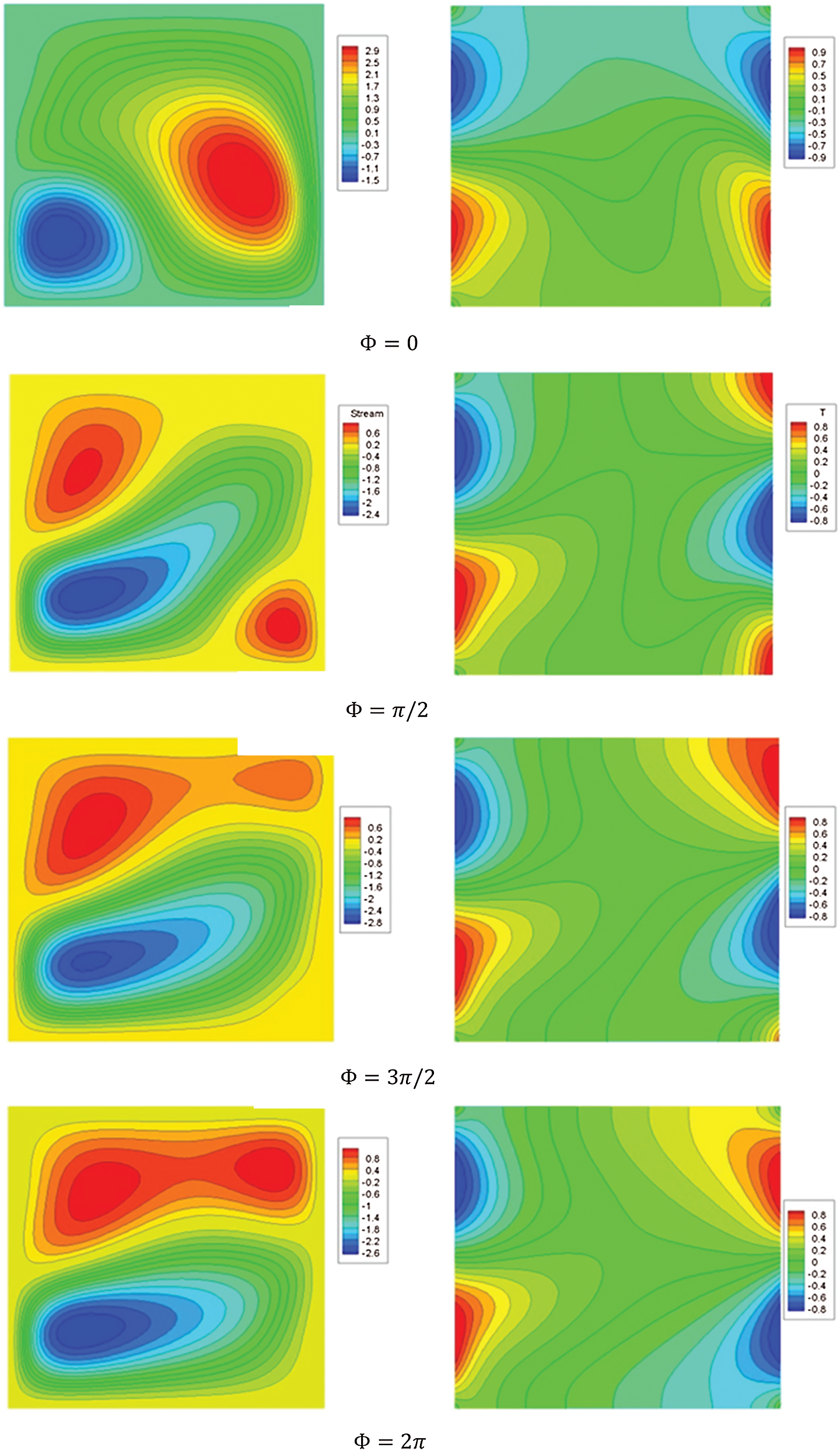
Figure 4: Streamlines and isotherms contours for variations of the phase deviation 
at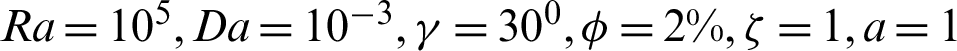 
Impacts of the non-linear Boussinesq parameter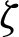 
on the streamlines and isotherms contours are shown in Fig. 5. As the non-linear Boussinesq parameter 
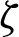increases from 0 to 1, the formed three cells of streamlines are decreased to be two formed cells. Also, the maximum of the stream function is increasing about 66.6% and the minimum value is decreasing about 60%. In addition, the temperature distributions are increasing inside the enclosure according to the increasing in the non-linear Boussinesq parameter 
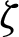. The physical explanation of these results is due to the extra buoyancy force. The effects of the inclination angle of the enclosure on the streamlines and isotherms contours are shown in Fig. 6. Here, the variations of the inclination angle change the buoyancy force and obviously, the streamlines contours and their strengths are depending strongly on the inclination angle. It seems that an increasing of the inclination angle has a slightly influence on the temperature profiles. Fig. 7 shows the impacts of the Rayleigh number on the streamlines and isotherms contours. At Ra = 104, two circular flow structures are formed with a big cell on the upper-right area and a small corner cell on the lower-left area of the enclosure. The distributions of the isothermal lines show that the convection is still weak and the conduction mode is dominant. As the Rayleigh number increases to Ra = 105, the formed two circular flow structures of the streamlines became wider with higher strengths. In this case, the convection prevails and the symmetry of the isothermal lines loses. The continuous increase of the Rayleigh number up to Ra = 106 changes the formed two circular flow structures to three circular flows. The center diagonal cell is the biggest one and the other cells are located near the top right and bottom left corners of the enclosure. The strength of the streamlines increases, strongly. Consequently, the thermal boundary layers, heating and cooling zones are shrinking along the side walls and then the heat transfer is enhanced.
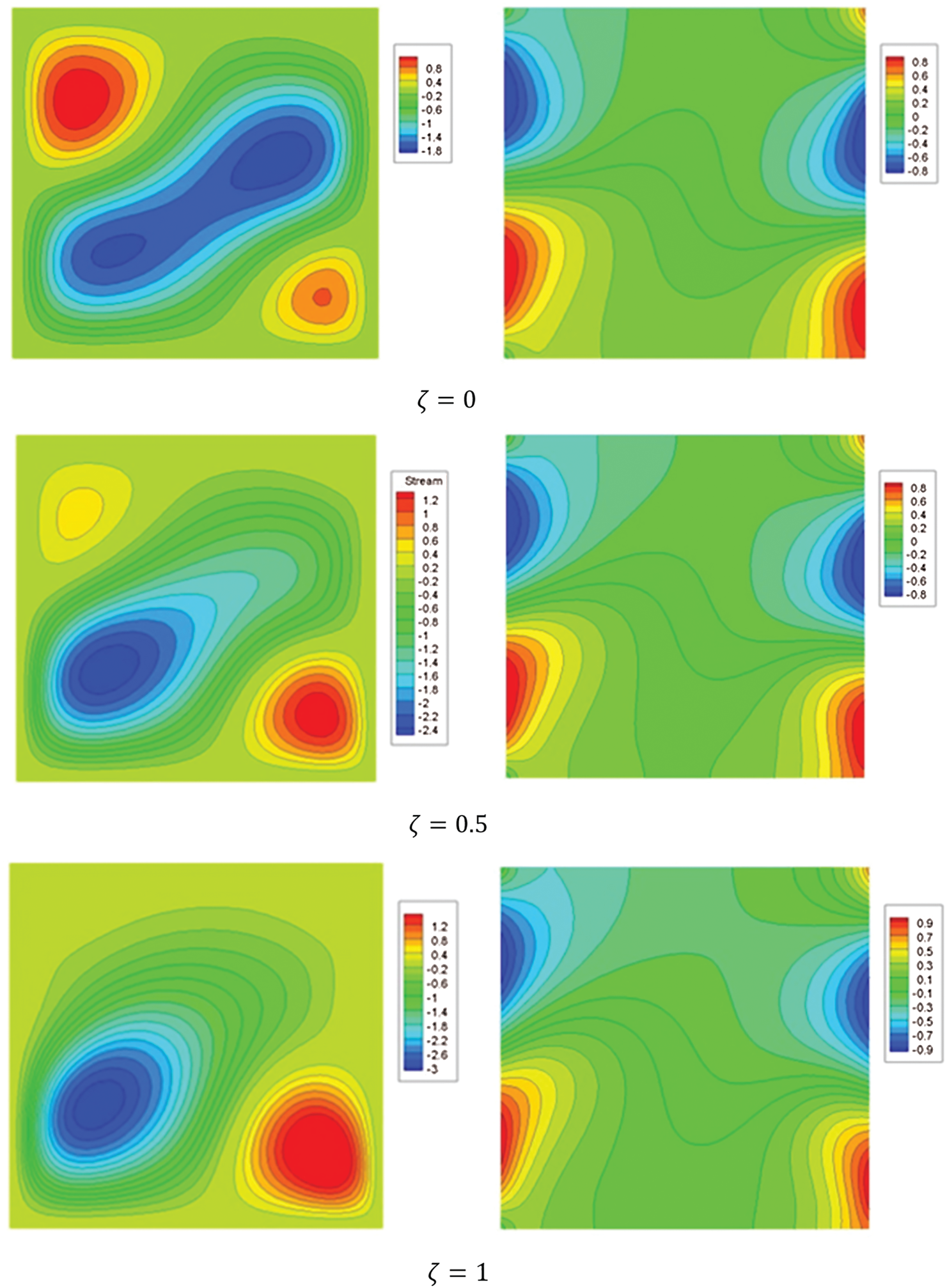
Figure 5: Streamlines and isotherms contours for the variations of 
at Ra = 105, Da = 10−3, 
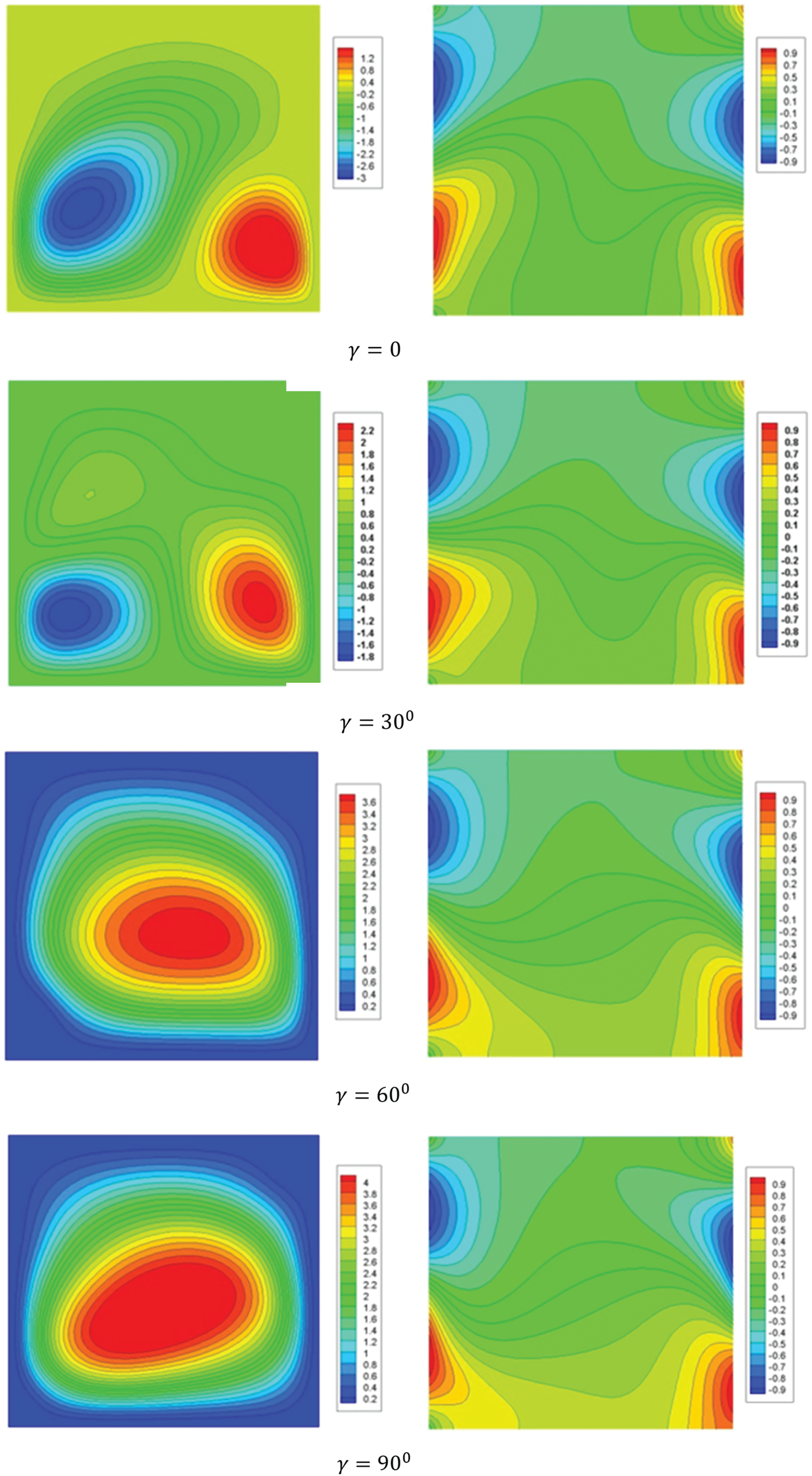
Figure 6: Streamlines and isotherms contours for variations of the inclination angle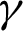 
at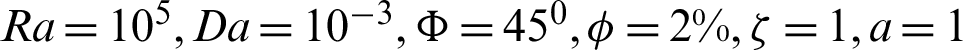 
Figure 7: Streamlines and isotherms contours for variations of the Rayleigh number Ra at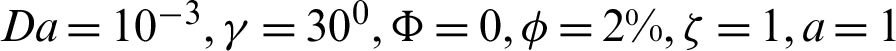 
The local Nusselt numbers along Y-axis at the left and right walls under impacts of the phase deviation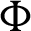 
, inclination angle 
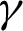and nanoparticles volume fraction 
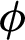are shown in Figs. 8–10, respectively. As it is expected, effects of the phase deviation 
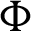on the local Nusselt number appear clearly at the right wall comparing to the left wall. On the right side, the local Nusselt number at the lower part 
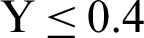increases slightly as the phase deviation 
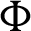increases and the reverse tendencies appear at upper part of the right wall 
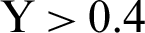. On the right wall, the local Nusselt number along 
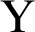-axis is significantly affected by the phase deviation 
.
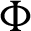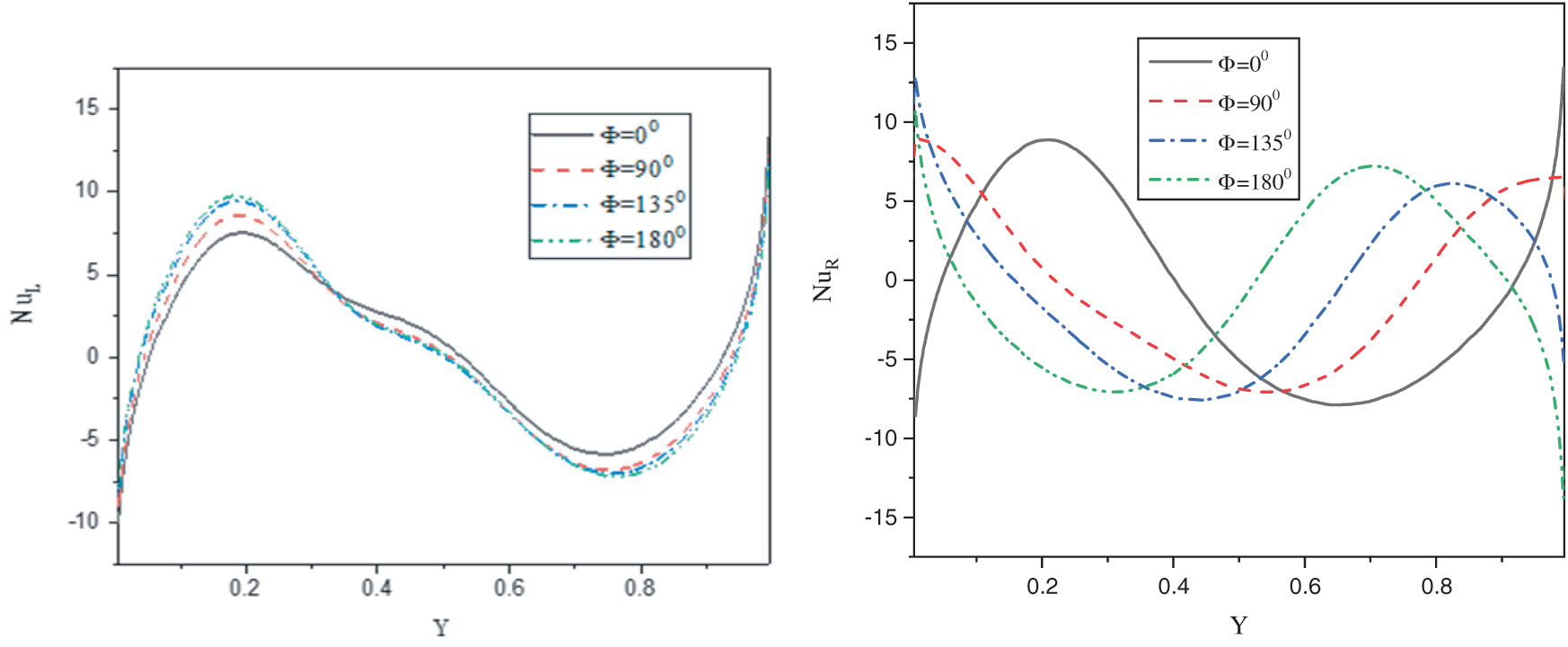
Figure 8: Impacts of the phase deviation 
on the local Nusselt number at the left and right walls when 
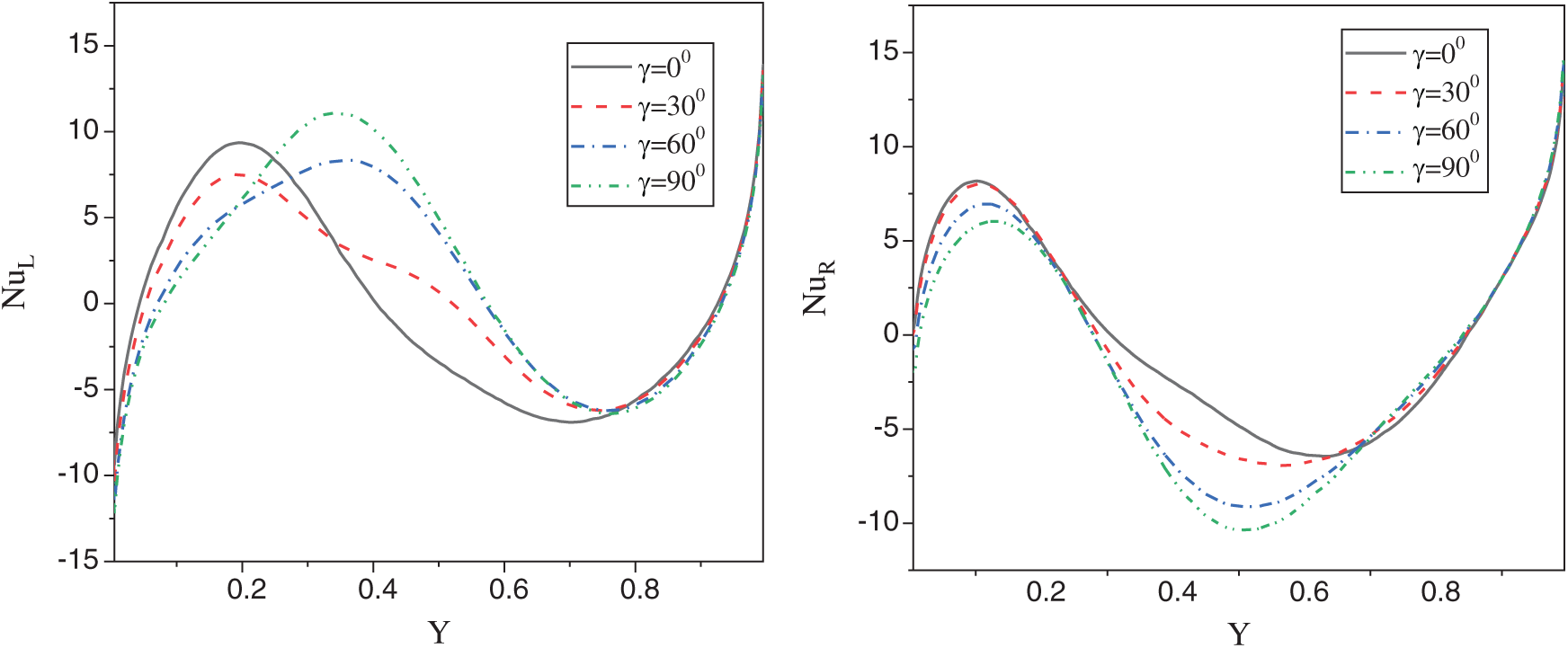
Figure 9: Impacts of the inclination angle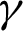 
on the local Nusselt number at the left and right walls when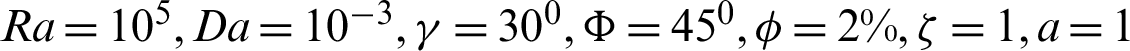 
Figure 10: Impacts of the nanoparticles volume fraction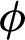 
on the local Nusselt number at the left and right walls when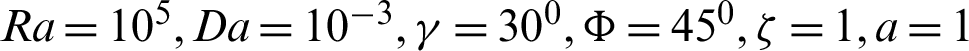 
It is seen that as the phase deviation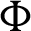 
changes from 00 to 1800, the heating zone moves upward and the cooling zone moves downward and consequently, the local Nusselt number oscillating according to the variation of 
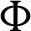. The physical reason of these results return to the sinousiodal heating on both left and right side-walls. In addition, the local Nusselt number along 
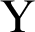-axis at the left and right walls varies according to the vaiation of the inclination angle 
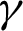. It is observed that the tendency of the local Nusselt number at the left wall is different from the local Nusselt number at the right wall under the impact of inclination angle 
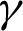and these behaviors are due to the variation of the sinusoidal heating at different values of 
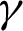. Fig. 10 shows the impacts of the nanoparticles volume fraction 
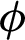on the local Nusselt number at the left and right walls when 
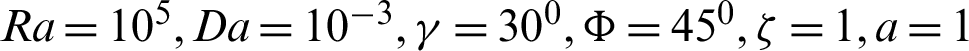. It seems that adding the nanoparticles by 4%, leads to slightly changes in the local Nusslet number along Y-axis, since the convection domeninant at Ra = 105 and also the presence of the porous medium try to decrease the influence of the nanoparticles concentration on the heat transfer. Fig. 11 presents the comparisons between the linear Boussinesq approximation and non-linear Boussinesq approximation for local Nusselt number on the left and right walls at 
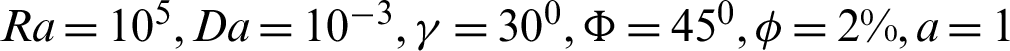. This comparison shows clearly the impact of using non-linear Boussinesq approximation on the rate of heat transfer. It is seen that, the non-linear Boussinesq approximation has clear effects on the local Nusselt number. As the non-linear Boussinesq approximation increases, then the local Nusselt number increases dramatically.
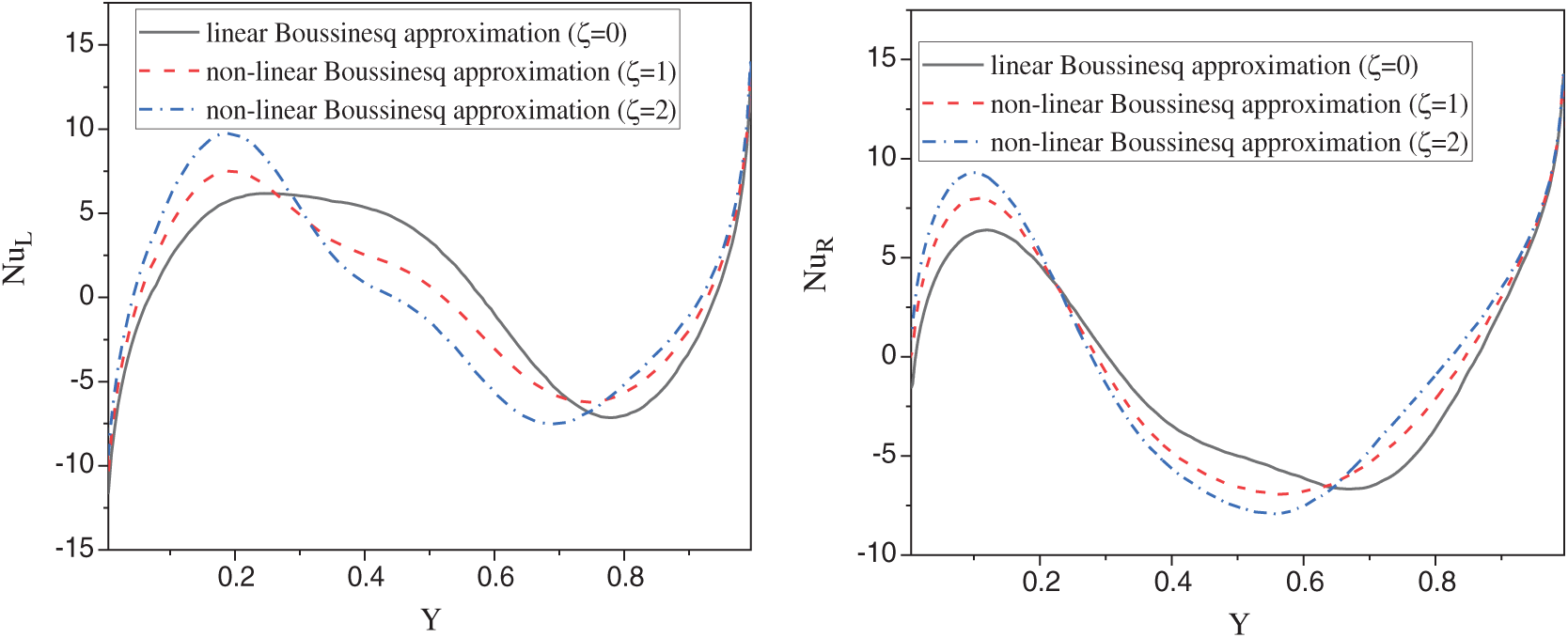
Figure 11: Comparisons between the linear Boussinesq approximation and non-linear Boussinesq approximation for local Nusselt number on the left and right walls at Ra = 105, Da = 10−3,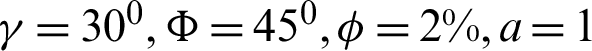 
Figs. 12 and 13 show the average Nusselt number under the effects of the amplitude ratio a with the phase deviation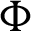 
and Rayleigh number Ra with the non-linear Boussinesq parameter 
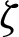, respectively. In Fig. 12, an increase of the amplitude ratio 
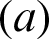increases the average Nusselt number, while the phase deviation is slightly changing the average Nusselt number. In Fig. 13, the maximum values of the average Nusselt number appear at a higher non-linear Boussinesq parameter 
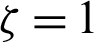and a higher Rayleigh number Ra = 106. Also, effect of the non-linear Boussinesq parameter appears clearly at higher values of the Rayleigh number.
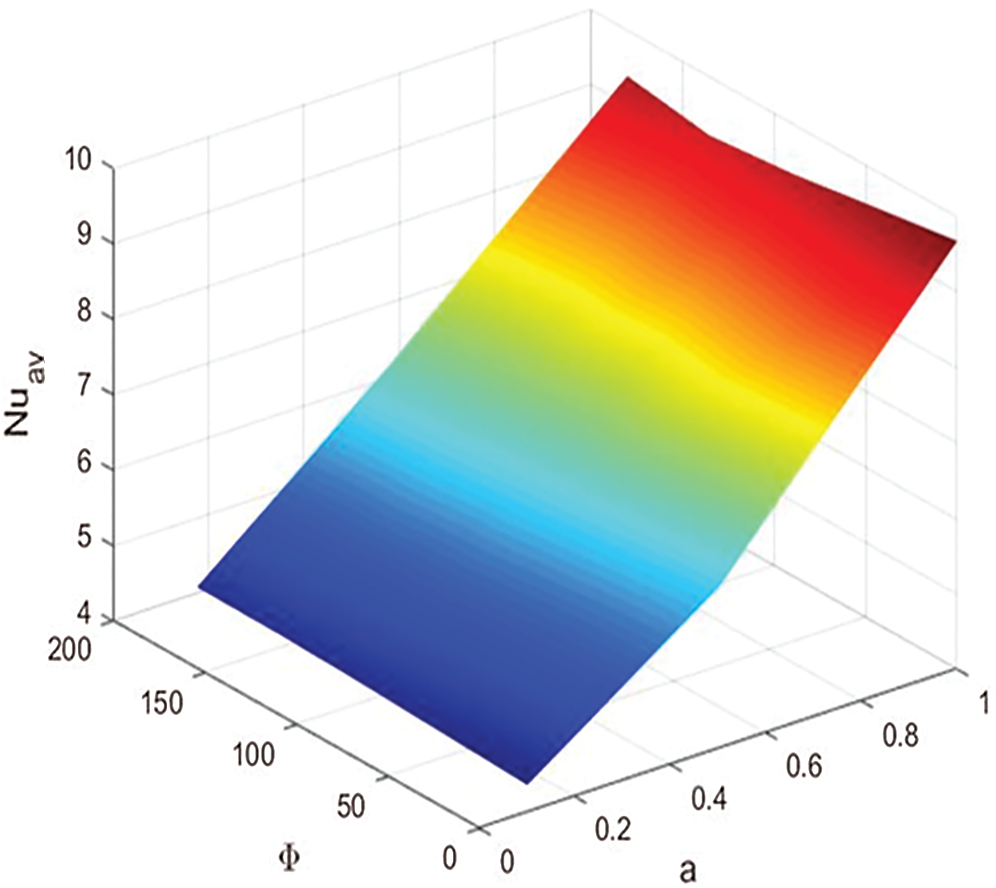
Figure 12: Impacts of the amplitude ratio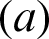 
and the phase deviation 
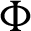on the average Nusselt number at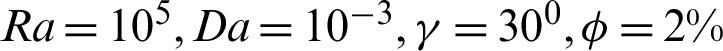 
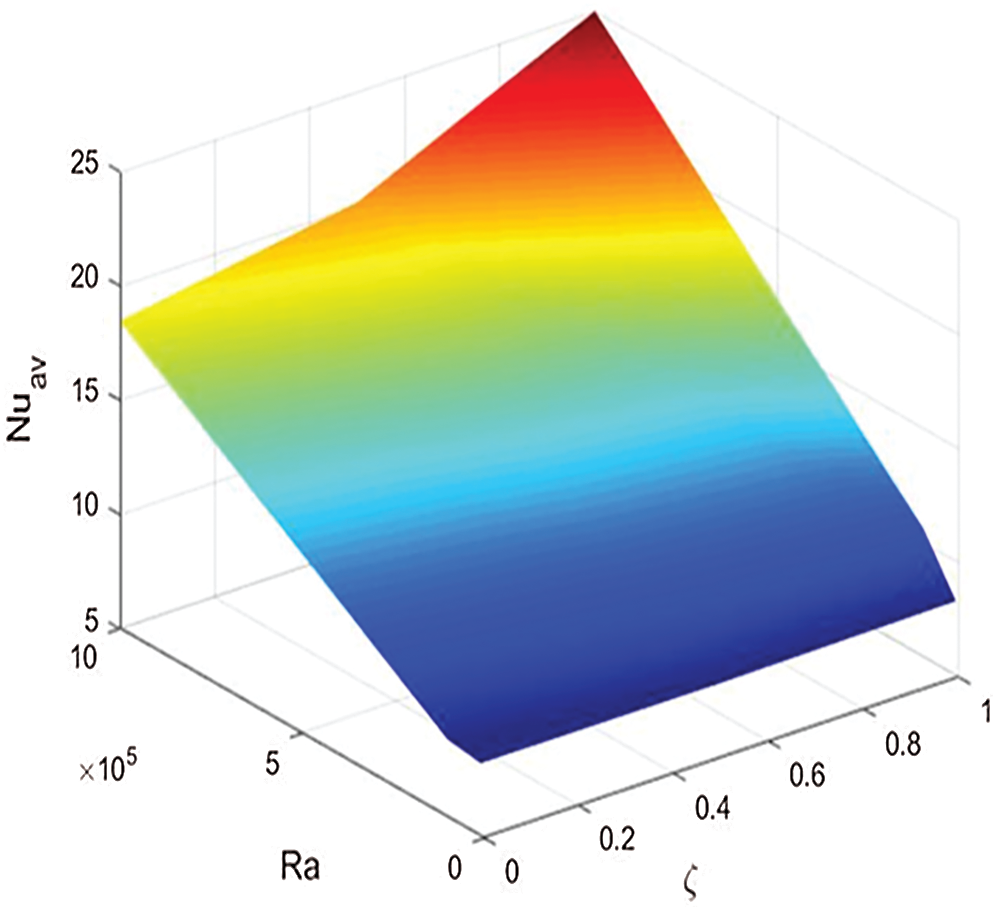
Figure 13: Impacts of the Rayleigh number Ra and the non-linear Boussinesq parameter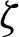 
on the average Nusselt number at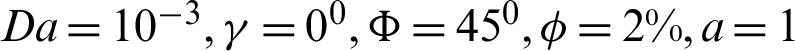 
The main objective of the current work is adapting CBS scheme in FEM method for investigating the influences of the non-linear Boussinesq approximation and sinusoidal heating on a nanofluid flow-filled a porous enclosure. The enclosure is inclined and it has varying sinusoidal temperature distributions on the side walls. Al2O3 is taken as nanoparticles and the water is taken as a base fluid. The main attentions of this work are focusing on the influences of the physical parameters including phase deviation, non-linear Boussinesq parameter, Rayleigh number, an inclination angle, the nanoparticles volume fraction and the amplitude ratio. In addition, the main findings of this study are:
• The location of phase deviation decides its contributions. The phase deviation varies the isothermal lines and heat transfer at the right-side wall and the phase deviation has a slight effect on the isothermal lines at the left-side wall.
• Amplitude ratio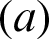 
growths the heat transfer and consequently the case of the non-uniformly heating enhances the heat transfer comparing to the uniformly heating.
• The non-linear Boussinesq parameter raises the buoyancy force which strengths the fluid flow and heat transfer inside the enclosure.
• The average Nusselt number is enhanced as the Rayleigh number increases when the non-linear Boussinesq parameter varies from 0 to 1.
• The inclination angle varies the flow speed and it has a slight impact on the heat transfer inside the inclined enclosure.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under Grant Number (R.G.P2/72/41).
1 S. E. Ahmed and H. M. Elshehabey. (2018). “Buoyancy-driven flow of nanofluids in an inclined enclosure containing an adiabatic obstacle with heat generation/absorption: Effects of periodic thermal conditions,” International Journal of Heat and Mass Transfer, vol. 124, pp. 58–73. [Google Scholar]
2 Y. Wang, Q. Liu, J. Lei and H. Jin. (2015). “Performance analysis of a parabolic trough solar collector with non-uniform solar flux conditions,” International Journal of Heat and Mass Transfer, vol. 82, pp. 236–249.
3 F. Wu, W. Zhou and X. Ma. (2015). “Natural convection in a porous rectangular enclosure with sinusoidal temperature distributions on both side walls using a thermal non-equilibrium model,” International Journal of Heat and Mass Transfer, vol. 85, pp. 756–771.
4 S. H. Lee, Y. M. Seo, H. S. Yoon and M. Y. Ha. (2016). “Three-dimensional natural convection around an inner circular cylinder located in a cubic enclosure with sinusoidal thermal boundary condition,” International Journal of Heat and Mass Transfer, vol. 101, pp. 807–823. [Google Scholar]
5 S. Sivasankaran and K. L. Pan. (2014). “Natural convection of nanofluids in a cavity with nonuniform temperature distributions on side walls,” Numerical Heat Transfer, Part A: Applications, vol. 65, no. 3, pp. 247–268. [Google Scholar]
6 Q. H. Deng and J. J. Chang. (2008). “Natural convection in a rectangular enclosure with sinusoidal temperature distributions on both side walls,” Numerical Heat Transfer, Part A: Applications, vol. 54, no. 5, pp. 507–524. [Google Scholar]
7 S. E. Ahmed, M. A. Mansour and A. Mahdy. (2013). “MHD mixed convection in an inclined lid-driven cavity with opposing thermal buoyancy force: Effect of non-uniform heating on both side walls,” Nuclear Engineering and Design, vol. 265, pp. 938–948. [Google Scholar]
8 S. Roy and T. Basak. (2005). “Finite element analysis of natural convection flows in a square cavity with non-uniformly heated wall(s),” International Journal of Engineering Science, vol. 43, no. 8–9, pp. 668–680. [Google Scholar]
9 A. M. Aly, A. J. Chamkha, S. W. Lee and A. F. Al-Mudhaf. (2016). “On mixed convection in an inclined lid-driven cavity with sinusoidal heated walls using the isph method,” Computational Thermal Sciences: An International Journal, vol. 8, no. 4, pp. 337–354. [Google Scholar]
10 G. De Vahl Davis. (1983). “Natural convection of air in a square cavity: A bench mark numerical solution,” International Journal for Numerical Methods in Fluids, vol. 3, no. 3, pp. 249–264. [Google Scholar]
11 A. Nilesh, S. M. Ali, K. Velusamy and S. Das. (2010). “Numerical study of natural convection in an enclosure with and without boussinesq assumption–-A comparative study,” in Proc. of the 37th National & 4th Int. Conf. on Fluid Mechanics and Fluid Power, Chennai, India, pp. 16–18. [Google Scholar]
12 K. Szewc, J. Pozorski and A. Taniere. (2011). “Modeling of natural convection with smoothed particle hydrodynamics: Non-Boussinesq formulation,” International Journal of Heat and Mass Transfer, vol. 54, no. 23–24, pp. 4807–4816. [Google Scholar]
13 D. Srinivasacharya, C. RamReddy and P. Naveen. (2019). “Effects of nonlinear Boussinesq approximation and double dispersion on a micropolar fluid flow under convective thermal condition,” Heat Transfer-Asian Research, vol. 48, no. 1, pp. 414–434. [Google Scholar]
14 H. M. Elshehabey, Z. Raizah, H. F. Öztop and S. E. Ahmed. (2020). “MHD natural convective flow of Fe3O4–H2O ferrofluids in an inclined partial open complex-wavy-walls ringed enclosures using non-linear boussinesq approximation,” International Journal of Mechanical Sciences, vol. 170, pp. 105352. [Google Scholar]
15 P. K. Kameswaran, B. Vasu, P. V. S. N. Murthy and R. S. R. Gorla. (2016). “Mixed convection from a wavy surface embedded in a thermally stratified nanofluid saturated porous medium with non-linear boussinesq approximation,” International Communications in Heat and Mass Transfer, vol. 77, pp. 78–86. [Google Scholar]
16 B. Vasu, R. S. R. Gorla, O. A. Bég, P. Murthy, V. Prasad et al. (2018). “Unsteady flow of a nanofluid over a sphere with nonlinear Boussinesq approximation,” Journal of Thermophysics and Heat Transfer, vol. 33, no. 2, pp. 343–355. [Google Scholar]
17 P. Kandaswamy and K. Kumar. (1999). “Buoyancy-driven nonlinear convection in a square cavity in the presence of a magnetic field,” Acta Mechanica, vol. 136, no. 1–2, pp. 29–39. [Google Scholar]
18 A. J. Chamkha and M. A. Ismael. (2013). “Conjugate heat transfer in a porous cavity filled with nanofluids and heated by a triangular thick wall,” International Journal of Thermal Sciences, vol. 67, pp. 135–151. [Google Scholar]
19 M. A. Sheremet and I. Pop. (2014). “Conjugate natural convection in a square porous cavity filled by a nanofluid using Buongiorno’s mathematical model,” International Journal of Heat and Mass Transfer, vol. 79, pp. 137–145.
20 M. T. Nguyen, A. M. Aly and S.-W. Lee. (2015). “Natural convection in a non-darcy porous cavity filled with Cu–water nanofluid using the characteristic-based split procedure in finite-element method,” Numerical Heat Transfer, Part A: Applications, vol. 67, no. 2, pp. 224–247.
21 M. A. Sheremet, T. Grosan and I. Pop. (2015). “Free convection in a square cavity filled with a porous medium saturated by nanofluid using tiwari and das’ nanofluid model,” Transport in Porous Media, vol. 106, no. 3, pp. 595–610.
22 M. A. Sheremet, I. Pop and R. Nazar. (2015). “Natural convection in a square cavity filled with a porous medium saturated with a nanofluid using the thermal nonequilibrium model with a tiwari and das nanofluid model,” International Journal of Mechanical Sciences, vol. 100, pp. 312–321.
23 A. Rashad, M. Rashidi, G. Lorenzini, S. E. Ahmed and A. M. Aly. (2017). “Magnetic field and internal heat generation effects on the free convection in a rectangular cavity filled with a porous medium saturated with cu-water nanofluid,” International Journal of Heat and Mass Transfer, vol. 104, pp. 878–889.
24 Z. A. S. Raizah, A. M. Aly and S. E. Ahmed. (2018). “Natural convection flow of a power-law non-Newtonian nanofluid in inclined open shallow cavities filled with porous media,” International Journal of Mechanical Sciences, vol. 140, pp. 376–393.
25 Z. Z. Rashed, S. E. Ahmed and A. M. Aly. (2019). “Heat transfer enhancement in the complex geometries filled with porous media,” Thermal Science, pp. 166.
26 A. M. Aly and Z. A. S. Raizah. (2020). “Incompressible smoothed particle hydrodynamics simulation of natural convection in a nanofluid-filled complex wavy porous cavity with inner solid particles,” Physica A: Statistical Mechanics and Its Applications, vol. 537, pp. 122623. [Google Scholar]
27 A. Alsabery, A. Chamkha, H. Saleh and I. Hashim. (2017). “Natural convection flow of a nanofluid in an inclined square enclosure partially filled with a porous medium,” Scientific Reports, vol. 7, pp. 2357. [Google Scholar]
28 N. Massarotti, P. Nithiarasu and O. Zienkiewicz. (1998). “Characteristic-based-split (CBS) algorithm for incompressible flow problems with heat transfer,” International Journal of Numerical Methods for Heat & Fluid Flow, vol. 8, no. 8, pp. 969–990. [Google Scholar]
29 N. Massarotti, P. Nithiarasu and O. Zienkiewicz. (2001). “Natural convection in porous medium-fluid interface problems–-A finite element analysis by using the CBS procedure,” International Journal of Numerical Methods for Heat & Fluid Flow, vol. 11, no. 5, pp. 473–490.
30 P. Nithiarasu. (2003). “An efficient artificial compressibility (AC) scheme based on the characteristic based split (CBS) method for incompressible flows,” International Journal for Numerical Methods in Engineering, vol. 56, no. 13, pp. 1815–1845.
31 P. Nithiarasu, J. Mathur, N. Weatherill and K. Morgan. (2004). “Three-dimensional incompressible flow calculations using the characteristic based split (CBS) scheme,” International Journal for Numerical Methods in Fluids, vol. 44, no. 11, pp. 1207–1229.
32 S. E. Ahmed. (2020). “Fem-cbs algorithm for convective transport of nanofluids in inclined enclosures filled with anisotropic non-darcy porous media using ltnem,” International Journal of Numerical Methods for Heat & Fluid Flow. [Google Scholar]
33 M. Corcione. (2011). “Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids,” Energy Conversion Management, vol. 52, no. 1, pp. 789–793. [Google Scholar]
34 R. W. Lewis, P. Nithiarasu and K. N. Seetharamu, Fundamentals of the Finite Element Method for Heat and FLuid Flow. 1 edition. Wiley, USA, New Jersey. [Google Scholar]
35 S. Sivasankaran and M. Bhuvaneswari. (2013). “Natural convection in a porous cavity with sinusoidal heating on both sidewalls,” Numerical Heat Transfer, Part A: Applications, vol. 63, no. 1, pp. 14–30. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |