DOI:10.32604/cmc.2021.012470
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012470 | |
| Article |
Two-Phase Flow of Blood with Magnetic Dusty Particles in Cylindrical Region: A Caputo Fabrizio Fractional Model
1Department of Mathematics, City University of Science and Information Technology, Peshawar, 25000, Pakistan
2Computational Analysis Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam
3Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
4Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
5Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, 11991, Saudi Arabia
*Corresponding Author: Farhad Ali. Email: farhad.ali@tdtu.edu.vn
Received: 01 July 2020; Accepted: 25 September 2020
Abstract: The present study is focused on the unsteady two-phase flow of blood in a cylindrical region. Blood is taken as a counter-example of Brinkman type fluid containing magnetic (dust) particles. The oscillating pressure gradient has been considered because for blood flow it is necessary to investigate in the form of a diastolic and systolic pressure. The transverse magnetic field has been applied externally to the cylindrical tube to study its impact on both fluids as well as particles. The system of derived governing equations based on Navier Stoke’s, Maxwell and heat equations has been generalized using the well-known Caputo–Fabrizio (C–F) fractional derivative. The considered fractional model has been solved analytically using the joint Laplace and Hankel (L&H) transformations. The effect of various physical parameters such as fractional parameter, Gr, M and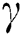 
on blood and magnetic particles has been shown graphically using the Mathcad software. The fluid behaviour is thinner in fractional order as compared to the classical one.
Keywords: Two-phase blood flow; dusty fluid; Brinkman type model; magnetic dusty particles; heat transfer; C–F derivative
Biomagnetic fluid dynamic (BFD) is a new area in fluid mechanics. It focuses on the usage of the magnetic particles as drug carriers in magnetic drug targeting, cancer tumor treatment and many more [1–3]. The Biomagnetic fluid occurs in all living organisms and for its investigation, the BFD model was initially recommended by Haik et al. [4]. Fluids that show non-linear relation between shear stress and strain are termed as non-Newtonian fluids e.g., blood. Blood is the only biological electrically conducting fluid and its mobility is influenced by an applied magnetic field. It contains plasma and red blood cells (RBC) that are oxides of iron and have hemoglobin fragments in high concentrations [5,6]. Due to the oxygenated state, blood exhibits a magnetic nature [7,8]. The non-Newtonian behaviour of blood due to the suspension of red blood cells in plasma and human thoracic aorta is analyzed by Caballero et al. [9]. Tripathi et al. [10] have examined the Non-Newtonian blood in a channel and attained analytical solutions for the velocity, volumetric flow rate and wavelength. In the human left ventricle (LV), the significance of the non-Newtonian blood has examined by Doost et al. [11]. Kumar et al. [12] evaluated the difference between Newtonian and non-Newtonian blood models and concluded that the non-Newtonian blood has more/less augmented wall shear stress as compared to the Newtonian blood.
Since blood is a biological fluid, biological heating is significant for metabolic heat generation [13]. The phenomenon in biological fluids was first discussed by Bernard in 1876. Afterwards, bioheat transfer became a topic applied in the practice of biology in a wide variety of applications such as chemotherapy [14,15], human thermoregulation system [16] and others [17]. Sharifi et al. [18] investigated the heat transfer applications in peripheral vascular disease using FHD principle through two inclined permanent magnets in a channel. Jimoh et al. [19] studied third-grade fluid in hematocrit with slip velocity. Dutta et al. [20] have developed an analytical study of heat propagation in biological tissues for constant and variable heat flux at the skin surface with hypothermia treatment. Fu et al. [21] reviewed the heat transfer modelling in thermoregulatory responses in the human body. Kengne et al. [22] discussed the bioheat transfer in the spherical biological tissues. Zhang et al. [23] discussed the heat transfer in LN2 cryoprobe systems and obtained effective results. David et al. [24] used the heat transfer in the warming of simulated blood by the generation of electronic components. Zainol et al. [25] investigated the heat transfer model for the prediction of human skin temperature using the bioheat equation.
The consideration of Two-phase flow is due to the presence of numerous interfaces separating two immiscible phases. The blood flow through a tiny tube at a very low shear is responsible for the two-phase flow surrounded by a cell-depleted peripheral layer. Different types of particles have been considered as the second phase in blood flow, but the most recommended and suitable particles are magnetic particles. The magnetic particles in blood have a vital role in numerous medical applications [26,27]. In drug delivery, a specific number of magnetic particles are used to transport the maximum number of a drug to the area of its choice. Due to the mentioned applications of magnetic particles, several researchers used the two-phase blood flow along with magnetic particles. Verma et al. [28] described a dual-phase blood flow model in thin pipes with the fundamental core of deferred erythrocytes and cell unrestricted film and found the results for the nonlinear problem numerically. The thermal and mass concentration effect of the multiphase blood model in a stenosed artery has been investigated by Tripathi et al. [29]. An analytical approach has been used for the results to comprehend the comportment of blood flow rate, wall shear stress and flow resistivity. Arribas et al. [30] created a reliable two-phase RBC model for the blood vessel and calculated the viscosity, phase dispersals and volume fractions using the depletion theory. They have associated their results with numerical as well as experimental study and found extraordinary conclusions. A two-phase model of blood with mild stenosis magnetic field and thermal effects has been explored by Ponalagusamy et al. [31]. They have concluded that thermal and shear stress slow down with increase in the levels of the plasma layer thickness and they are very effective for the diseased arterial treatment. Ali et al. [32] examined the two-phase dusty fluid with heat transfer in a fluctuating plate, and found that by enhancing the number of embedded particles, the dusty fluid velocity increases.
Due to multidimensional features, the non-integer order calculus is attracting the attention of scientists and researchers [33,34]. Fractional calculus is an important and fruitful tool for describing many systems including memory effects. In the preceding few decades, fractional calculus is used for many purposes in various fields, such as electrochemistry, transportation of water in ground level, electromagnetism, elasticity, diffusion and in conduction of heat process [35]. In 2015, Caputo et al. [36] worked together in the field of non-integer order calculus and presented a new expression for the non-integer order derivative with the non-singular kernel. So, keeping in sight the importance of CF operators, many researchers used the CF operator in their studies such as in physics, biological mathematics, and many more. Ali et al. [37] examined the magnetic flow of Walter’s-B fluid by using the CF non-singular operator. Salah Uddin et al. [38] investigated the CF model of blood flow with Ferro particles in cylindrical coordinates and their results were in agreement with the previously published works. Ali et al. [39,40] studied the fractionalized model of blood flow having magnetic particles in cylindrical coordinates.
There is no attempt found in the literature relevant to Caputo–Fabrizio fractional approach to find the closed-form solution for magnetite particles-based blood flow with thermal concentration. Hence, in the present article, the work of Saqib et al. [41] has been generalized by taking the flow of blood as a Brinkman type fluid with magnetic particles in cylinder. The governing equations for both fluid and particles are modelled and using the Caputo–Fabrizio fractional-order approach, the closed-form solutions have been obtained by using joint Laplace and Hankel transformations. The impact of different embedded parameters on blood and particles velocities have been examined through graphs.
The blood flow is considered in a vertical cylinder having a radius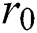 
as represented in Fig. 1.
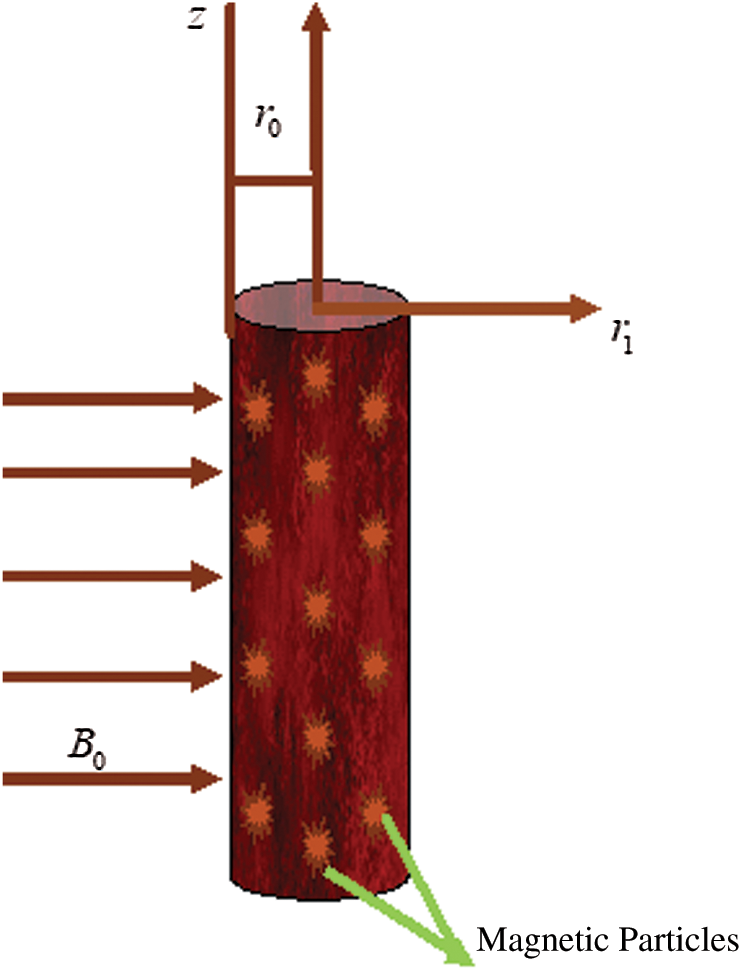
Figure 1: The geometry of the flow
The magnetic particles are equally distributed throughout the blood flow. The cylinder has been considered along the z-axis and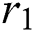 
-axis is chosen perpendicular to it. The direction of the motion of the blood and magnetic particles are along the z-axis. The biological thermal effect has also been considered and the radiation has been neglected. The induced magnetic field due to a very slight Reynold number has been ignored [42]. For a time 
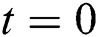, the system is considered to be at rest with ambient temperature 
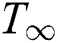. For 
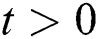the temperature rises to 
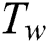. The force 
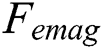is described by [43,44]
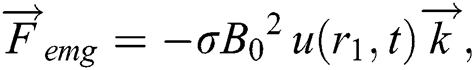
where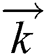 
denotes the direction along the z-axis and 
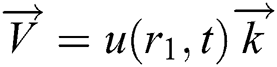shows blood velocity.
The unsteady Brinkman-type blood flow in a cylinder is specified by:
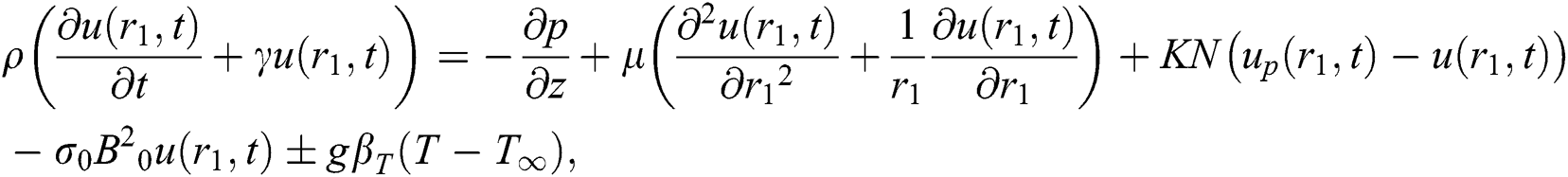
the oscillating pressure gradient [45] is
where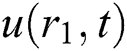 
is the blood velocity, 
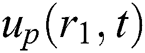is the magnetic particles velocity. The term 
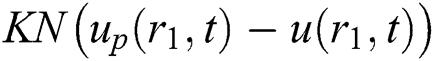is the force between the fluid and particle due to relative motion and magnetic particles flow is conducted [46]:
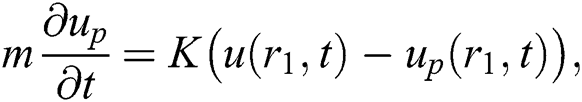
The thermal equation is specified by:
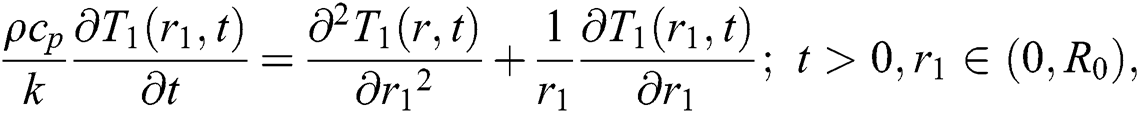
subjected to the following IBCs
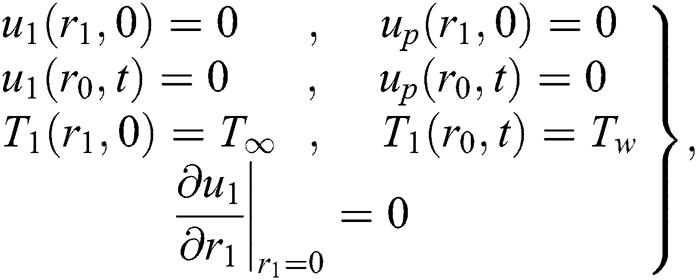
By incorporating the Non-dimensional variables
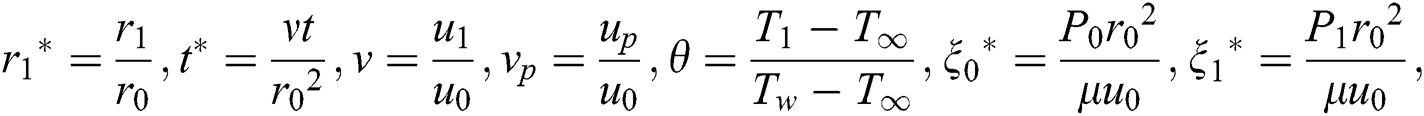
into Eqs. (2)–(5), then ignoring the * notation, we obtain:
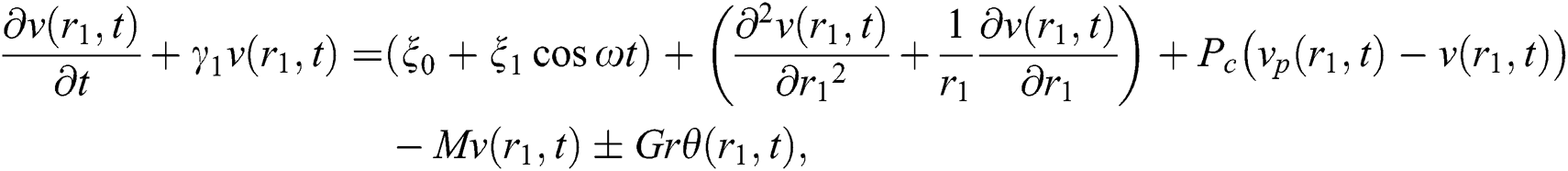
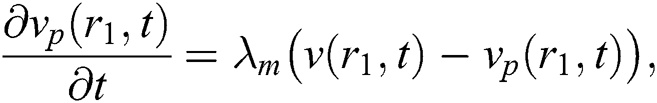
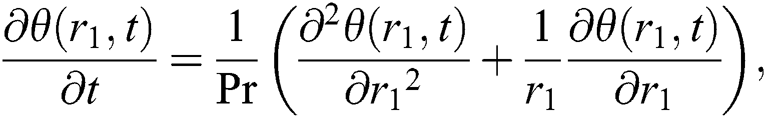
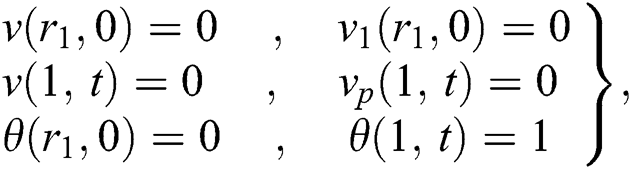
For a generalized fractional model, the newly developed CF time-fractional derivative has been used to covert the linear model to the fractional model, therefore Eqs. (8)–(10) reduces to:
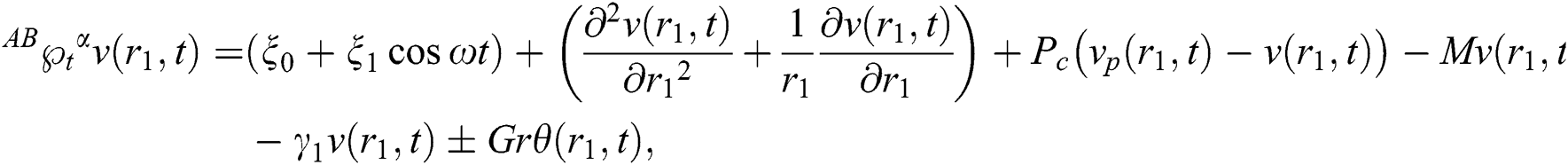
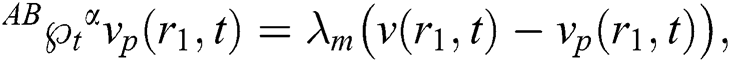
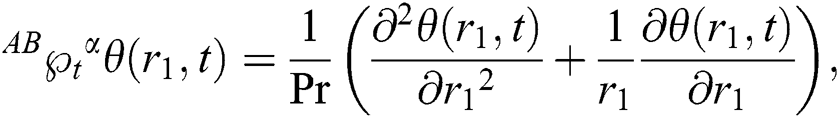
where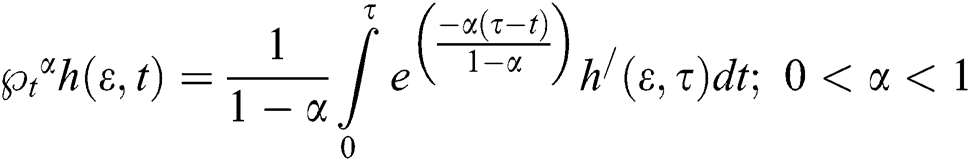 
is the CF operator is [36]:
For the solution of Eqs. (14)–(16) the non-dimensional IBC’s from Eq. (11) and the Laplace and Hankel transformations are utilized.
Applying the joint L&H transforms using Eqs. (11)–(14), we get
where
and 
is the Hankel Transform of 
[39,40].
Applying inverse L&H transformations to Eq. (15), and by using Lorenzo and Hartley’s’ and Robotnov and Hartley’s’ functions, respectively [43], yields:
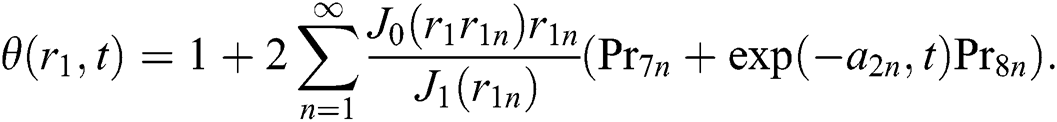
The Non-dimensional Nusselt number is given by
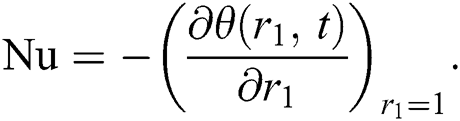
3.2 Solution of the Blood and Particle Velocities
To obtain the solution for the blood velocity and Magnetic particles velocity, the Laplace and Hankel transforms have been applied on Eq. (15) using the corresponding transformed boundary conditions by letting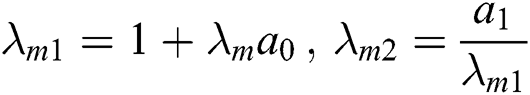 
and we get:
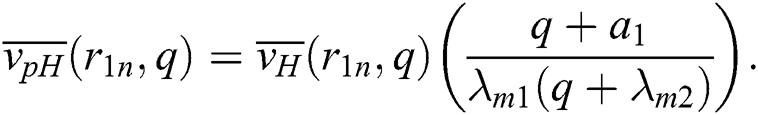
Now for the blood velocity, Eq. (18) has been incorporated into Eq. (12) using the corresponding transformations and boundary condition 
which yields:
The simplified form of Eq. (19) is
After further simplification the Eq. (20) will take the following form as
where
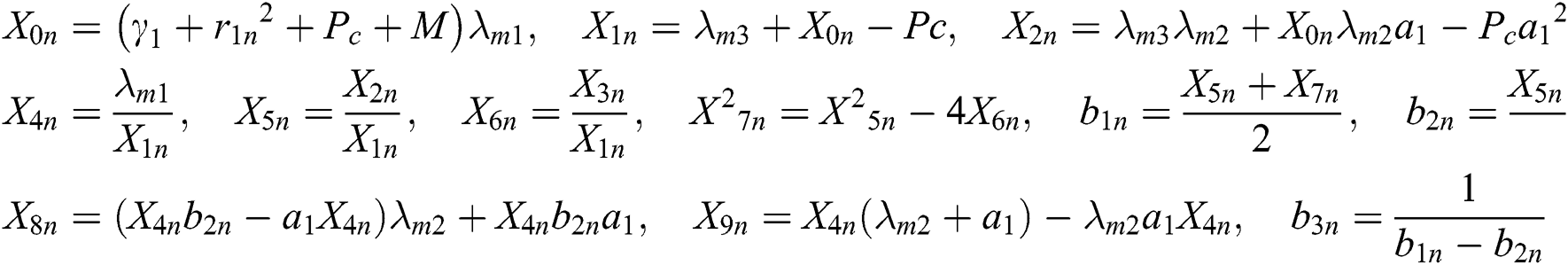
In component form Eq. (21) is expressed as:
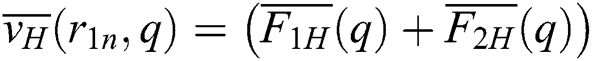
where
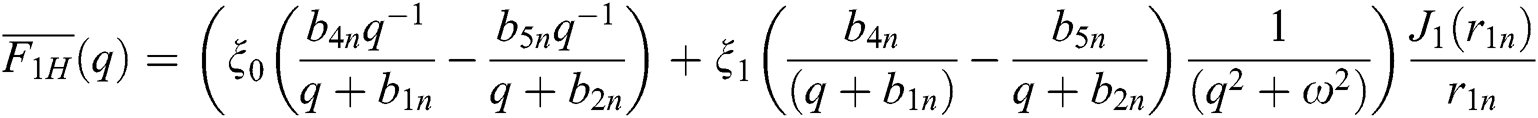
and
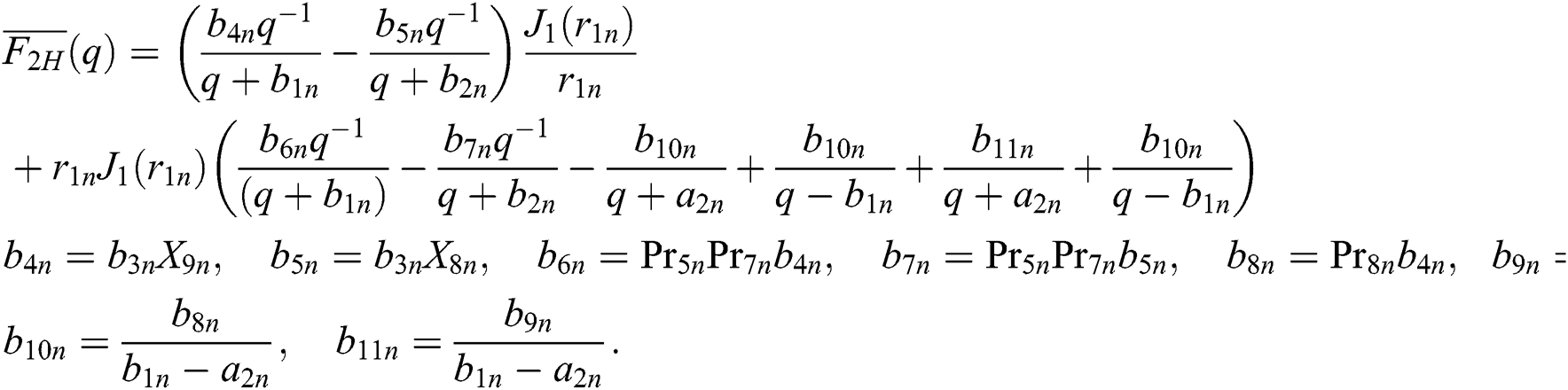
By applying inverse Laplace transform to Eq. (22), by using the Lorenzo and Hartley’s’ respectively [46],
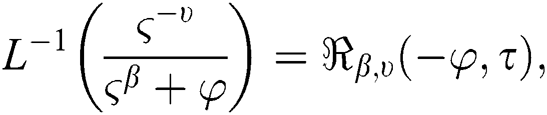
we get
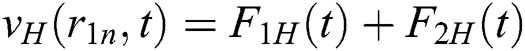
where
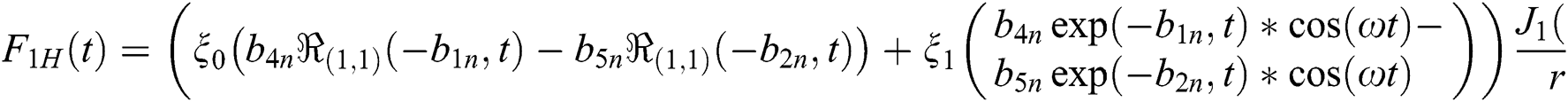
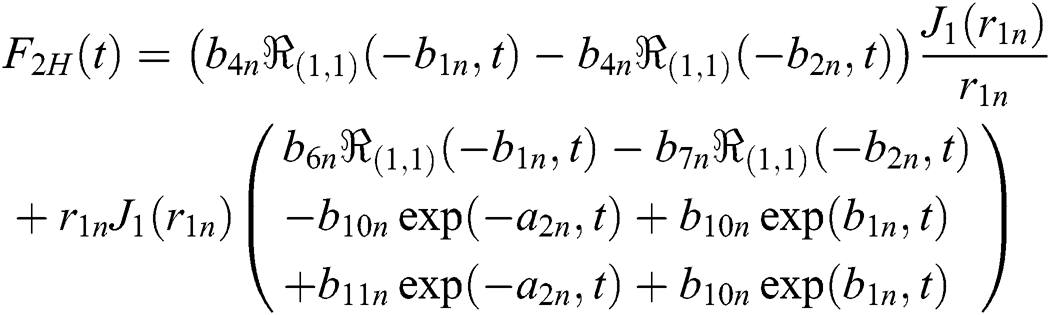
Applying the finite Hankel transform of order zero to Eq. (23), we get
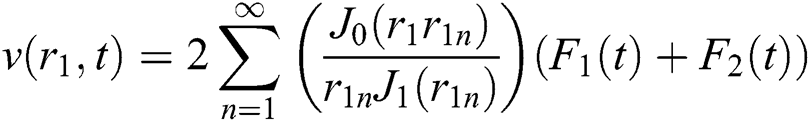
where
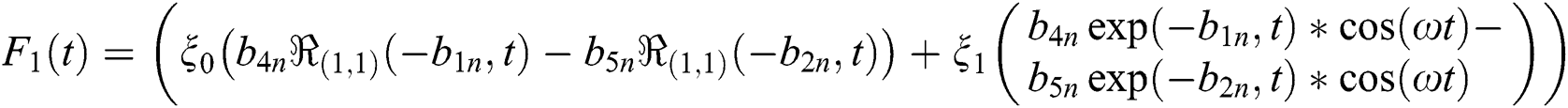
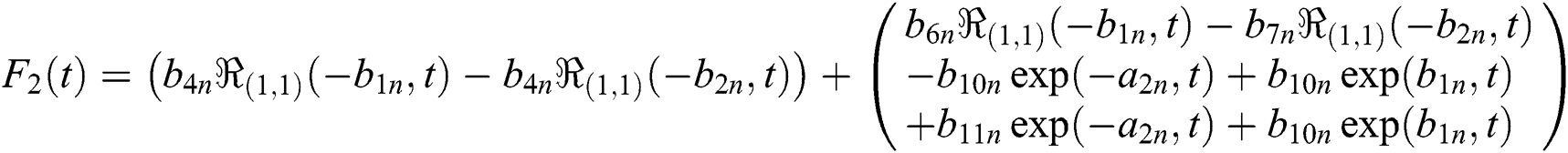
Now for the solution of magnetic particles velocity applying the inverse L&H transformations to Eq. (16), yields:
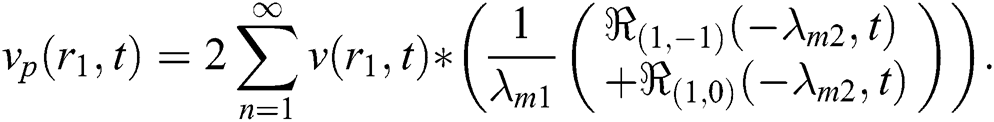
From Tab. 1 it can be seen that by growing the fractional parameter an enhancement in (Nu) occurs for time.
Table 1: Time and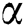 
variation on Nusselt number
4 Graphical Results and Discussion
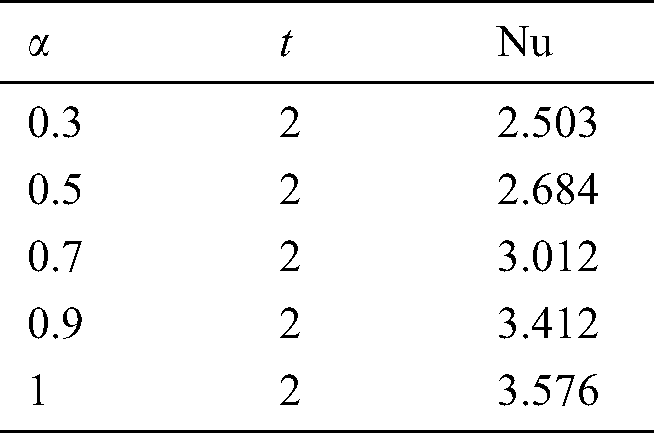
The considered work aims to study the generalized two-phase blood flow of Brinkman type fluid in a cylindrical tube. The analytical solutions have been attained for energy, velocity as well as for the magnetic particles contained in the blood. Various parameters have been discussed physically on velocities of the blood, particles and temperature. Fig. 1 shows the physical model of the considered problem. Fig. 2 shows the effect of fractional parameter on the temperature profile. It can be concluded from the figure that by using the fractional parameter, we obtained different temperature profiles by keeping the other parameters constant and this effect is called the memory effect, which is impossible in integer-order. In this graph, we obtained dual behaviour of temperature memory for different values of 
and the same behaviour has been noticed as reported by Ali et al. [39].
Figure 2: Variation in Temperature for diverse values of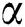 
for Pr = 22.64 at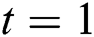 
Fig. 3 shows the effect of the fractional parameter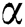 
on velocity profiles. The corresponding results for regular blood and particles velocity are compared with the fractional order in a fixed time and with classical order and the fluid and particles memory has been discussed.
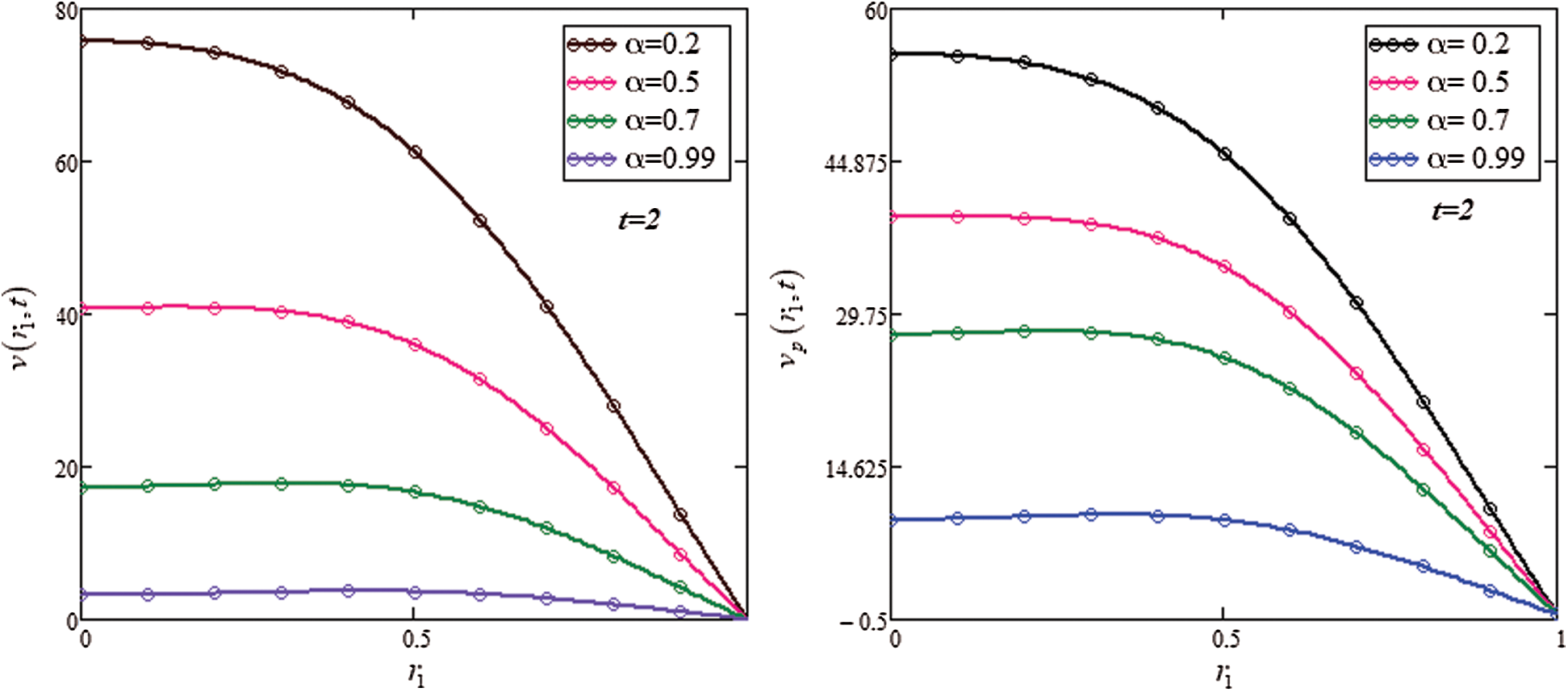
Figure 3: Blood and Particle velocities sketch of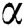 
at t = 2,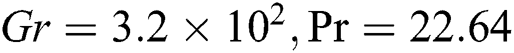 
Fig. 4 shows the impact of the Magnetic parameter on blood velocity and particle velocity. From the figures, it has been concluded that for the higher values of M, the flow of blood, as well as magnetic particles, retards. It is physically true that by increasing M, the Lorentz forces increase, which produces resistive forces due to which the flow retards. This effect is very useful in various medical fields such as Magnetic drug targeting and separation techniques by the magnetic field for the cure of different types of diseases and to maintain the normal aspects of the human body.
Figure 4: Blood velocity sketch of M at t = 2, 
Fig. 5 shows the impact of the Brinkman type parameter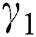 
on the velocities of blood and particles. It is observed that the velocity decreases with the increasing values of 
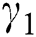. This is because 
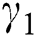is the ratio between resistive forces and density. By increasing 
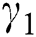, the opposite forces increase, which retards the fluid velocity and is directly related to the blood flow. These results are strongly in agreement with Saqib et al. [41].
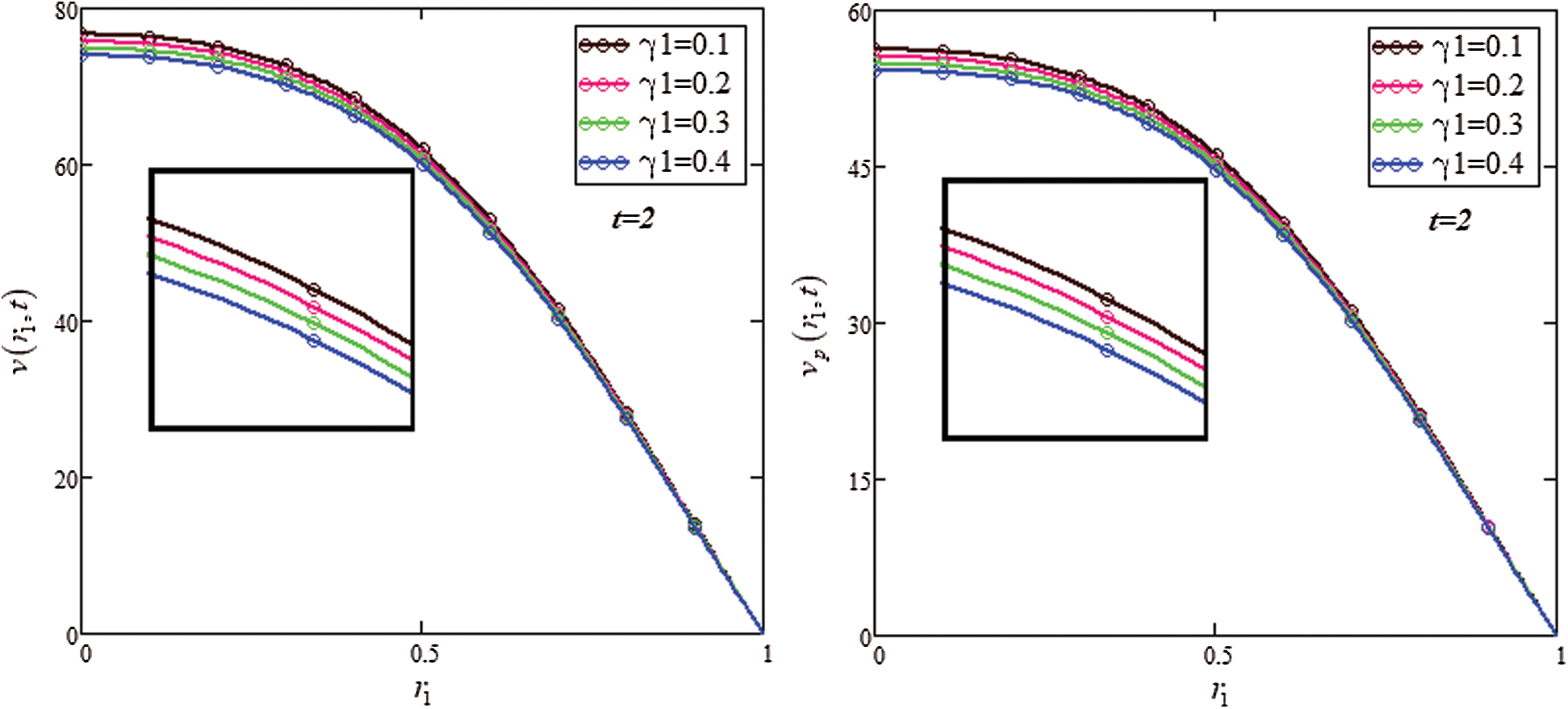
Figure 5: Blood velocity graph of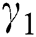 
at t = 2,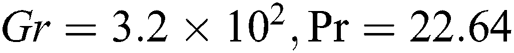 
The Caputo–Fabrizio time-fractional derivative has been used. The effect of relative parameters has been shown graphically. Closed-form expressions have been obtained by using the Laplace transform and Hankel transform techniques. Based on the graphical study, it has been concluded that the velocity profile decreases in the response of an external applied magnetic field and Brinkman parameter. This phenomenon might play an important role in Magnetic wounds. Furthermore, by increasing the fractional parameter, the fluid memory becomes thicker.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. El-Boubbou. (2018). “Magnetic iron oxide nanoparticles as drug carriers: Clinical relevance,” Nanomedicine, vol. 13, no. 8, pp. 953–971. [Google Scholar]
2. A. M. Morega, A. A. Dobre, M. Morega and A. Săndoiu. (2018). “Constructal optimization of magnetic field source in magnetic drug targeting therapy,” in Proc. of the Romanian Academy: Series A, vol. 19, pp. 123–128.
3. S. Rashidi, J. A. Esfahani and M. Maskaniyan. (2017). “Applications of magnetohydrodynamics in biological systems: A review on the numerical studies,” Journal of Magnetism and Magnetic Materials, vol. 439, pp. 358–372. [Google Scholar]
4. Y. Haik, V. Pai and C. J. Chen. (1999). “Biomagnetic fluid dynamics,” in Fluid Dynamics at Interfaces, Cambridge, UK: Cambridge University Press, pp. 439–452, . [Online]. Available: https://books.google.com.pk/books. [Google Scholar]
5. M. Sheikholeslami. (2018). “Application of Darcy law for nanofluid flow in a porous cavity under the impact of lorentz forces,” Journal of Molecular Liquids, vol. 266, pp. 495–503. [Google Scholar]
6. S. Sharma, U. Singh and V. K. Katiyar. (2018). “Magnetic field effect on flow parameters of blood along with magnetic particles in a cylindrical tube,” Journal of Magnetism and Magnetic Materials, vol. 377, pp. 395–401. [Google Scholar]
7. J. C. Misra, A. Sinha and G. C. Shit. (2011). “Mathematical modeling of blood flow in a porous vessel having double stenoses in the presence of an external magnetic field,” International Journal of Biomathematics, vol. 4, no. 2, pp. 207–225. [Google Scholar]
8. C. Y. Lin, P. L. Wei, W. J. Chang, Y. K. Huang, S. W. Feng et al. (2013). , “Slow freezing coupled static magnetic field exposure enhances cry preservative efficiency: A study on human erythrocytes,” PLoS One, vol. 8, no. 3, e58988. [Google Scholar]
9. A. D. Caballero and S. Laín. (2015). “Numerical simulation of non-Newtonian blood flow dynamics in human thoracic aorta,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 18, no. 11, pp. 1200–1216. [Google Scholar]
10. D. Tripathi, A. Yadav, O. A. Bég and R. Kumar. (2018). “Study of microvascular non-Newtonian blood flow modulated by electroosmosis,” Microvascular Research, vol. 117, pp. 28–36. [Google Scholar]
11. S. N. Doost, L. Zhong, B. Su and Y. S. Morsi. (2016). “The numerical analysis of non-Newtonian blood flow in human patient-specific left ventricle,” Computer Methods and Programs in Biomedicine, vol. 127, pp. 232–247. [Google Scholar]
12. D. Kumar, R. Vinoth and V. S. Ravi raj Adhikari. (2017). “Non-Newtonian and Newtonian blood flow in human aorta: A transient analysis,” An International Journal of Medical Sciences, vol. 28, no. 7, pp. 3194–3203. [Google Scholar]
13. P. Hooshmand, A. Moradi and B. Khezry. (2015). “Bioheat transfer analysis of biological tissues induced by laser irradiation,” International Journal of Thermal Sciences, vol. 90, pp. 214–223. [Google Scholar]
14. W. G. Weng, X. F. Han and M. Fu. (2014). “An extended multi-segmented human bioheat model for high temperature environments,” International Journal of Heat and Mass Transfer, vol. 75, pp. 504–513. [Google Scholar]
15. W. K. Marsh, B. Gershenson and A. J. Rothschild. (2015). “Symptom severity of bipolar disorder during the menopausal transition,” International Journal of Bipolar Disorders, vol. 3, no. 1, pp. 17. [Google Scholar]
16. J. González-Alonso. (2012). “Human thermoregulation and the cardiovascular system,” Experimental Physiology, vol. 97, no. 3, pp. 340–346. [Google Scholar]
17. E. Majchrzak. (2013). “Application of different variants of the BEM in numerical modeling of bioheat transfer problems,” Molecular & Cellular Biomechanics, vol. 10, no. 3, pp. 201. [Google Scholar]
18. A. Sharifi, S. Y. Motlagh and H. Badfar. (2019). “Ferro hydro dynamic analysis of heat transfer and biomagnetic fluid flow in channel under the effect of two inclined permanent magnets,” Journal of Magnetism and Magnetic Materials, vol. 472, pp. 115–122. [Google Scholar]
19. A. Jimoh, G. T. Okedayo and T. Aboiyar. (2019). “Hematocrit and slip velocity influence on third grade blood flow and heat transfer through a stenosed artery,” Journal of Applied Mathematics and Physics, vol. 7, no. 3, pp. 638. [Google Scholar]
20. J. Dutta and B. Kundu. (2018). “Thermal wave propagation in blood perfused tissues under hyperthermia treatment for unique oscillatory heat flux at skin surface and appropriate initial condition,” Heat and Mass Transfer, vol. 54, no. 11, pp. 3199–3217. [Google Scholar]
21. M. Fu, W. Weng, W. Chen and N. Luo. (2016). “Review on modeling heat transfer and thermoregulatory responses in human body,” Journal of Thermal Biology, vol. 62, pp. 189–200. [Google Scholar]
22. E. Kengne and A. Lakhssassi. (2015). “Bioheat transfer problem for one-dimensional spherical biological tissues,” Mathematical Biosciences, vol. 269, pp. 1–9. [Google Scholar]
23. X. Zhang, S. C. Hossain, Q. Wang, B. Qiu and G. Zhao. (2019). “Two-phase flow and heat transfer in a self-developed MRI compatible LN2 cryoprobe and its experimental evaluation,” International Journal of Heat and Mass Transfer, vol. 136, pp. 709–718. [Google Scholar]
24. D. N. Broussard, G. M. Charles, W. Jerry, D. O. Clifford, Y. Liu. (2019). et al., “Warming of simulated blood using waste heat generated by electronic components,” U.S. Patent Application, vol. 16, no. 058, pp. 134. [Google Scholar]
25. Z. N. Zainol, M. M. Tap, H. M. Kamar and N. Kamsah. (2019). “Heat transfer model to predict human skin temperature under comfort level by using bioheat equation,” International Journal of Online Engineering, vol. 15, no. 10, pp. 52. [Google Scholar]
26. S. P. Nanda and B. B. Mallik. (2012). “A non-Newtonian two-phase fluid model for blood flow through arteries under stenotic condition,” International Journal of Pharma and Bio Sciences, vol. 2, no. 2, pp. 237–247. [Google Scholar]
27. B. Namgung, M. Ju, P. Cabrales and S. Kim. (2013). “Two-phase model for prediction of cell-free layer width in blood flow,” Microvascular Research, vol. 85, pp. 68–76. [Google Scholar]
28. S. R. Verma and A. Srivastava. (2014). “Analytical study of a two-phase model for steady flow of blood in a circular tube,” International Journal of Engineering Research and Applications, vol. 4, no. 10, pp. 1–10. [Google Scholar]
29. B. Tripathi, B. K. Sharma and M. Sharma. (2017). “MHD pulsatile two-phase blood flow through a stenosed artery with heat and mass transfer”, arXiv Preprint arXiv: 1705. 09794, vol. 2, pp. 1–24. [Google Scholar]
30. E. Arribas and M. S. Celebi. (2020). “A thermal based RBC Aggregation model for two-phase blood flow,” Korea-Australia Rheology Journal, vol. 32, no. 2, pp. 121–136. [Google Scholar]
31. R. Ponalagusamy and R. T. Selvi. (2015). “Influence of magnetic field and heat transfer on two-phase fluid model for oscillatory blood flow in an arterial stenosis,” Meccanica, vol. 50, no. 4, pp. 927–943. [Google Scholar]
32. F. Ali, M. Bilal, N. A. Sheikh, I. Khan and K. S. Nisar. (2019). “Two-phase fluctuating flow of dusty viscoelastic fluid between non-conducting rigid plates with heat transfer,” IEEE Access, vol. 7, pp. 123299–123306. [Google Scholar]
33. A. B. Malinowska, T. Odzijewicz and D. F. Torres. (2015). Advanced Methods in the Fractional Calculus of Variations. Cham: Springer, . [Online]. Available: https://link.springer.com/book/10.1007/978-3-319-14756-7#authorsandaffiliationsbook. [Google Scholar]
34. H. Sun, Y. Zhang, D. Baleanu, W. Chen and Y. Chen. (2018). “A new collection of real-world applications of fractional calculus in science and engineering,” Communications in Nonlinear Science and Numerical Simulation, vol. 64, pp. 213–231. [Google Scholar]
35. F. Mainardi. (2010). Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. London: World Scientific, Imperial College Press, . [Online]. Available: https://www.springer.com/gp/book/9783319147550. [Google Scholar]
36. M. Caputo and M. Fabrizio. (2015). “A new definition of fractional derivative without singular kernel,” Progress in Fractional Differentiation and Applications, vol. 1, no. 2, pp. 1–13. [Google Scholar]
37. F. Ali, M. Saqib, I. Khan and N. A. Sheikh. (2016). “Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-b fluid model,” European Physical Journal Plus, vol. 131, no. 10, pp. 377. [Google Scholar]
38. S. Uddin, M. Mohamad, K. Khalid, M. Abdul hammed, M. S. Rusiman. (2018). et al., “Blood flow problem in the presence of magnetic particles through a circular cylinder using Caputo-Fabrizio fractional derivative,” Journal of Physics, vol. 995, pp. 1–9. [Google Scholar]
39. F. Ali, A. Imtiaz, I. Khan, N. A. Sheikh and D. L. C. Ching. (2018). “Hemodynamic flow in a vertical cylinder with heat transfer: Two-phase Caputo Fabrizio fractional model,” Journal of Magnetics, vol. 23, no. 2, pp. 179–191. [Google Scholar]
40. F. Ali, A. Imtiaz, I. Khan and N. A. Sheikh. (2018). “Flow of magnetic particles in blood with isothermal heating: A fractional model for two-phase flow,” Journal of Magnetism and Magnetic Materials, vol. 456, pp. 413–422. [Google Scholar]
41. M. Saqib, I. Khan and S. Shafie. (2019). “Generalized magnetic blood flow in a cylindrical tube with magnetite dusty particles,” Journal of Magnetism and Magnetic Materials, vol. 484, pp. 490–496. [Google Scholar]
42. M. Kothandapani, J. Prakash and V. Pushparaj. (2015). “Analysis of heat and mass transfer on MHD peristaltic flow through a tapered asymmetric channel,” Journal of Fluids, vol. 2015, no. 3, pp. 1–9. [Google Scholar]
43. S. Sharma, U. Singh and V. K. Katiyar. (2015). “Magnetic field effect on flow parameters of blood along with magnetic particles in a cylindrical tube,” Journal of Magnetism and Magnetic Materials, vol. 377, pp. 395–401. [Google Scholar]
44. M. Zhao, S. Wang and S. Wei. (2013). “Transient electro-osmotic flow of Oldroyd-b fluids in a straight pipe of circular cross section,” Journal of Non-Newtonian Fluid Mechanics, vol. 201, pp. 135–139. [Google Scholar]
45. T. Hayat, H. Yasmin and A. Alsaedi. (2015). “Convective heat transfer analysis for peristaltic flow of power-law fluid in a channel,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, vol. 37, no. 2, pp. 463–477. [Google Scholar]
46. N. A. Shah, D. Vieru and C. Fetecau. (2016). “Effects of the fractional order and magnetic field on the blood flow in cylindrical domains,” Journal of Magnetism and Magnetic Materials, vol. 409, pp. 10–19. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |